Визуализация численных методов. Решение обыкновенных дифференциальных уравнений

Сибирский государственный университет телекоммуникации

и информатики

Уральский технический институт связи и информатики

Кафедра физики, прикладной математики и информатики.

Курсовая работа

по информатике

Визуализация численных методов.

Решение обыкновенных дифференциальных уравнений

Введение

дифференциальный уравнение программа

Информатика - это области человеческой деятельности, связанная с процессами преобразования информации с помощью компьютеров и их взаимодействием со средой применения.

Информатика в таком понимании нацелена на разработку общих методологических принципов построения информационных моделей. Поэтому методы информатики применимы по - всюду, где существует возможность описания объекта, явления, процесса и т.п. с помощью информационных моделей. Таким образом, информатика намного ускоряет решение математических задач.

Уравнения, связывающие независимую переменную, искомую функцию и её производные называют дифференциальным уравнением. Решение дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Цель и задача данной курсовой работы заключается в том чтобы рассчитать и научиться пользоваться несколькими способами решение дифференциального уравнения, добиться вывода графических изображений в программах используемых для этой работы.

.Убедиться в том, что данные методы решений совпадают и сделать вывод о сходимости.

.Проанализировать результаты, которые получатся в обоих методах

.Также в соответствующих программах создать данные формы объекта

1. Постановка задачи

Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Часто в задаче Коши в роли независимой переменной выступает время.

Задачу Коши можно сформулировать следующим образом.

Пусть дано дифференциальное уравнение

и начальное условие y(x₀) = y₀. Требуется найти функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию.

Численное решение задачи Коши сводится к табулированию искомой функции.

График решения дифференциального уравнения называется интегральной кривой.

Геометрический смысл задачи:

 - тангенс угла наклона касательной к графику решения в точке (x, y) к оси ОХ, - угловой коэффициент (рис.1).

Существование решения:

Если правая часть f(x,y) непрерывна в некоторой области R, определяемой неравенствами

|x - x₀| < a ; |y - y₀| < b ,

то существует, по меньшей мере, одно решение y = y(x), определённое в окрестности |x - x₀| < h, где h - положительное число.

Это решение единственно, если в R выполнено условие Липшица

где N - некоторая постоянная (константа Липшица), зависящая, в общем случае, от a и b. Если f(x, y)имеет ограниченную производную  в R, то можно положить

N = max|| при  .

Моя задача:

Решить методами Эйлера модифицированного и Рунге Кутта 4 порядка задачу Коши для дифференциального уравнения 1-го порядка на отрезке [X₀; X_k] с шагом h и начальным условием: Y(X₀) = Y₀.

Ответ должен быть получен в виде таблицы результатов:

Где Y⁽¹⁾, Y⁽²⁾ - решения, полученные различными численными методами, Y^T - точное решение дифференциального уравнения.

Возможно представление результатов решения не в виде таблицы, а в виде списков.

Данные таблицы визуализировать на форме в виде графиков.

Перед вычислением последнего столбца таблицы результатов необходимо из начальных условий вычесть значение коэффициента c, используемого в общем решении.

2. Описание методов решения

Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Часто в задаче Коши в роли независимой переменной выступает время. Задачу Коши можно сформулировать следующим образом:

Пусть дано дифференциальное уравнение

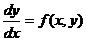
и начальное условие y(x₀) = у₀. Требуется найти функцию у(x), удовлетворяющую как указанному уравнению, так и начальному условию.

Численное решение задачи Коши сводится к табулированию искомой функции. График решения дифференциального уравнения называется интегральной кривой.

. Метод Эйлера модифицированный

Для уменьшения погрешности вычислений часто используется модифицированный метод Эйлера. Этот метод имеет так же следующие названия: метод Эйлера-Коши или метод Рунге-Кутта второго порядка точности.

Пусть дано дифференциальное уравнение первого порядка

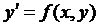
с начальным условием:

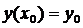
Выберем шаг h и введём обозначения:

x_i = x₀ + ih и y_i = y(x_i),

где i = 0, 1, 2, ...,

x_i - узлы сетки,

y_i - значение интегральной функции в узлах.

При использовании модифицированного метода Эйлера шаг h делится на два отрезка.

Иллюстрации к решению приведены на рисунке 4.

Проведем решение в несколько этапов:

1. Обозначим точки: А(х_i, y_i,), C(x_i + h/2, y_i + h/2 ∙ f(x_i, y_i)) и B(x_i+1, y_i+1);

2. Через точку А проведем прямую под углом б, где tg б = f(x_i, y_i);

3. На этой прямой найдем точку С(х_i + h/2, y_i + h/2 ∙ f(x_i, y_i));

4. Через точку С проведем прямую под углом б1, где tg б1 = f(x_i + h/2,y_i + h/2 ∙ f(x_i, y_i));

5. Через точку А проведем прямую, параллельную последней прямой;

6. Найдем точку B(x_i+1, y_i+1). Будем считать B(x_i+1, y_i+1) решением дифференциального уравнения при х = x_i+1;

7. После проведения вычислений, аналогичных вычислениям, описанным в методе Эйлера, получим формулу для определения значения у_i+1:

y_i+1 = y_i + h ∙ f(x_i + h/2, y_i + h/2 ∙ f(x_i, y_i)).

Модифицированный метод Эйлера дает меньшую погрешность. На рисунке 4 это хорошо видно. Так величина еl характеризует погрешность метода Эйлера, а е - погрешность метода Эйлера модифицированного.

Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным приведена на рисунке 5.

F(x, у) - заданная функция - должна

быть описана отдельно.

Входные параметры:Х0, XК - начальное и конечное

значения независимой

переменной;

Y0 - значение y₀ из начального условия

y(x₀)=y₀;

N - количество отрезков разбиения;

Рисунок 4. Метод Эйлера модифицированный.

Выходные параметры:

Y - массив значений искомого решения

в узлах сетки.

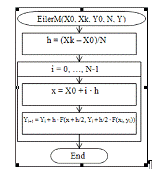
Рисунок 5. Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным.

4. Метод Рунге-Кутта 4 порядка

Пусть дано дифференциальное уравнение первого порядка 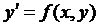 с начальным условием y(x₀)=y_0. Выберем шаг h и введем обозначения:

x_i = x₀ + ih и y_i = y(x_i), где i = 0, 1, 2, ... .

Аналогично описанному выше методу производится решение

дифференциального уравнения. Отличие состоит в делении шага на 4 части.

Согласно методу Рунге-Кутта четвертого порядка, последовательные значения y_i искомой функции y определяются по формуле:

y_i+1 = y_i +∆y_i

где i = 0, 1, 2 ...

∆y=(k1+2*k2+2*k3+k4)/6

a числа k1, k2 ,k3, k4 на каждом шаге вычисляются по формулам:

k1 = h*f(x_i, y_i )= f (x_i +h/2, y_i +k1 /2)*h= F(x_i +h/2, y_i +k2 /2)*h= F(x_i +h, y_i +k3 )*h

Это явный четырехэтапный метод 4 порядка точности.

Блок-схема процедуры решения дифференциального уравнения методом Рунге-Кутта приведена на рисунке 6.

F(x, у) - заданная функция - должна быть описана отдельно.

Входные параметры:

Х0, XК - начальное и конечное

значения независимой

переменной;

Y0 - значение y₀ из начального условия

y(x₀)=y₀;

N - количество отрезков разбиения;

Выходные параметры:

Y - массив значений искомого решения

в узлах сетки.

Алгоритм решения задачи

Решение в MathCAD

Формы

Листинг программы на языке Visual Basic

Dim xr(), yr(), xe(), ye(), xo(), yo() As Singlex0, y0, h, xk, k1, k2, c, k3, k4, yd As Singlen, i As IntegerFunction f(ByVal a, ByVal b) As Single= -(a - b) / aFunctionSub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click= Val(TextBox1.Text)= Val(TextBox2.Text)= Val(TextBox4.Text)= Val(TextBox3.Text)= (xk - x0) / h= y0 / x0 + Math.Log(x0)xr(n)yr(n)xe(n)ye(n)xo(n)yo(n)(0) = x0(0) = y0(0) = x0(0) = y0(0) = x0(0) = y0.ColumnCount = 4.RowCount = n + 2.Item(0, 0).Value = "x".Item(1, 0).Value = "Общее".Item(2, 0).Value = "Ейлер М".Item(3, 0).Value = "Рунге Кутт"i = 0 To n - 1(i) = Math.Round((xe(0) + i * h), 2)(i + 1) = ye(i) + h * f(xe(i) + h / 2, ye(i) + h / 2 * f(xe(i), ye(i))).Item(2, 1).Value = ye(0).Item(0, 1).Value = xe(0).Item(0, i + 1).Value = xe(i).Item(2, i + 1).Value = Str(ye(i))i = 0 To n - 1(i) = Math.Round((xe(0) + i * h), 2)= h * f(xr(i), yr(i))= h * f(xr(i) + h / 2, yr(i) + k1 / 2)= h * f(xr(i) + h / 2, yr(i) + k2 / 2)= h * f(xr(i) + h, yr(i) + k3)= (k1 + 2 * k2 + 2 * k3 + k4) / 6(i + 1) = yr(i) + yd.Item(3, 1).Value = yr(0).Item(3, i + 1).Value = Str(yr(i))i = 0 To n - 1(i) = Math.Round((xe(0) + i * h), 2)(i) = xo(i) * (c - Math.Log(xo(i))).Item(1, 1).Value = yo(0).Item(1, i + 1).Value = Str(yo(i)).Series.Add("Общее решение").Series("Общее решение").ChartType = SeriesChartType.Linei = 0 To n - 1.Series("Общее решение").Points.AddXY(xo(i), yo(i)).Series("Общее решение").ChartArea = "ChartArea1"i.Series.Add("Эйлер М").Series("Эйлер М").ChartType = SeriesChartType.Pointi = 0 To n - 1.Series("Эйлер М").Points.AddXY(xe(i), ye(i)).Series("Эйлер М").ChartArea = "ChartArea1".Series("Эйлер М").Color = Color.Bluei.Series.Add("Рунге Кутт").Series("Рунге Кутт").ChartType = SeriesChartType.Linei = 0 To n - 1.Series("Рунге Кутт").Points.AddXY(xr(i), yr(i)).Series("Рунге Кутт").ChartArea = "ChartArea1".Series("Рунге Кутт").Color = Color.Green i

End Sub

Заключение

Выполняя курсовую работу, я решил данное мне дифференциальное уравнение с помощью численных методов (Рунге-Кутта и Эйлера модифицированного) и общего решения построил графики их решения в программе Microsoft Visual Basic 10. Как и следовало ожидать графики, построенные с помощью метода Эйлера модифицированного и Рунге-Кутта, полностью совпали с графиком точного решения. Точность методов достаточно высока, следовательно, их можно применять в ситуации, когда нет возможности вычислить интеграл, и получить ответ с незначительной погрешностью.

Список литературы

1.      Минина Е.Е. Информатика: методические указания для курсовой работы для студентов очной формы обучения. Екатеринбург: УрТИСИ ГОУ ВПО «СибГУТИ».

.        http://msdn.microsoft.com/ru-ru/library/