Оцінка роботи системи пожежогасіння
Вступ
Під системою
«людина-машина» розуміють систему, яка включає людину-оператора (групу
операторів) і сукупність технічних засобів, за допомогою яких здійснюється
трудова діяльність. За структурою машинного компонента системи «людина-машина»
можуть бути різного рівня складності:
інструментальні системи
«людина-машина», в яких технічними пристроями є інструменти і прилади;
прості системи
«людина-машина», які включають стаціонарні і нестаціонарні технічні пристрої і
людину, що використовує ці пристрої;
складні системи
«людина-машина», в яких людина управляє сукупністю технологічно
взаємопов’язаних, але різних за функціональним призначенням апаратів, пристроїв
і машин. Керування технологічним процесом забезпечується локальними системами
автоматичного управління;
система «людина-машина»
у вигляді системотехнічних комплексів. Це складні системи, в яких людина
взаємодіє не тільки з технічними пристроями, але й іншими людьми.
Системотехнічні комплекси можна подати як ієрархію більш простих
людино-машинних систем.
За типом взаємодії
людини і машини виділяються системи неперервної та епізодичної взаємодії.
Незалежно від рівня
автоматизації системи «людина-машина» основною ланкою є людина, яка ставить
мету, планує, направляє і контролює весь процес її функціонування.
До взаємодії людини і
технічних засобів ставляться підвищені вимоги, що вимагає пристосування техніки
до людини (конструювання машин з врахуванням людських можливостей) і людини до
машини (відбір і підготовка спеціалістів).
Завдання
1
Потрібно визначити
статистичні ймовірності безвідмовної роботи P(t) і відмови Q(t)
сповіщувачів для заданого значення t0, зазначеного в табл. 1.
Далі необхідно розрахувати значення ймовірності безвідмовної роботи Р*(t)
пo першим 20 значенням наробітку до відмови, зазначеним для відповідного
варіанта в табл. 1. Потім для заданого наробітку t0 потрібно
розрахувати математичне очікування кількості працездатних сповіщувачів 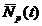 при
загальній кількості сповіщувачів N*, які знаходились в експлуатації
(табл. 2).
при
загальній кількості сповіщувачів N*, які знаходились в експлуатації
(табл. 2).
Таблиця 1.
Значення наробки до відмови і задані значення t0 та Т0
|
Варіант
|
Масив значень наробки до відмови
Т, 103год.
|
Задане значення t0, 103
год.
|
Значення Т0, 103
год.
|
|
8
|
7, 7, 11, 14, 6, 3, 8, 10, 7, 12,
8, 9, 4, 9, 6, 5, 13, 6, 8, 7, 9, 10, 5, 6, 8, 10, 9, 13, 8, 3, 7, 4, 9, 8,
11, 4, 7, 11, 6, 8, 10, 12, 7, 3, 9, 11, 5, 10, 3, 6
|
8,5
|
2,5
|
|
|
|
|
|
Таблиця
2. Обсяг партії сповіщувачів і задане значення k
|
Варіант
|
8
|
|
Обсяг партії N*
|
700
|
|
Значення k
|
3
|
Таблиця
3. Кількість сповіщувачів,
працездатних на момент часу t0
|
Значення наробки до відмови Т,
103год.
|
t0, 103 год.
|
значення Т, що перевищують t0,
103 год.
|
Значення наробки до відмови Т,
103год.
|
t0, 103 год.
|
значення Т, що перевищують t0,
103 год.
|
|
7
|
8,5
|
|
10
|
8,5
|
10
|
|
7
|
8,5
|
|
9
|
8,5
|
9
|
|
11
|
8,5
|
11
|
13
|
8,5
|
13
|
|
14
|
8,5
|
14
|
8
|
8,5
|
|
|
6
|
8,5
|
|
3
|
8,5
|
|
|
3
|
8,5
|
|
7
|
8,5
|
|
|
8
|
8,5
|
|
4
|
8,5
|
|
|
10
|
8,5
|
10
|
9
|
8,5
|
9
|
|
7
|
8,5
|
|
8
|
8,5
|
|
|
12
|
8,5
|
12
|
11
|
8,5
|
11
|
|
8
|
8,5
|
|
4
|
8,5
|
|
|
9
|
8,5
|
9
|
7
|
8,5
|
|
|
4
|
8,5
|
|
11
|
8,5
|
11
|
|
9
|
8,5
|
9
|
6
|
8,5
|
|
|
6
|
8,5
|
|
8
|
8,5
|
|
|
5
|
8,5
|
|
10
|
8,5
|
10
|
|
13
|
8,5
|
13
|
12
|
8,5
|
12
|
|
6
|
8,5
|
|
7
|
8,5
|
|
|
8
|
8,5
|
|
3
|
8,5
|
|
|
7
|
8,5
|
|
9
|
8,5
|
9
|
|
9
|
8,5
|
9
|
11
|
8,5
|
11
|
|
10
|
8,5
|
10
|
5
|
8,5
|
|
|
5
|
8,5
|
|
10
|
8,5
|
10
|
|
6
|
8,5
|
|
3
|
8,5
|
|
|
8
|
8,5
|
|
6
|
8,5
|
|
|
|
|
N=50
|
|
Nпр(t0)=20
|
 ,
,
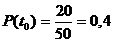 ,
,
Імовірність
відмови сповіщувача за період наробки t0
статистично визначається як
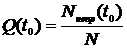
де Nнепр(t0) - кількість сповіщувачів, непрацездатних до наробки t0. Для
визначення Nнепр(t0) з табл. 1 слід
вибрати значення Т, менші t0.
 ,
,
Сума ймовірностей
дорівнює:
P(t) +
Q(t) = 0,4+0,6= 1
Оцінку
ймовірності безвідмовної роботи сповіщувачів по першим 20-ти значенням
наробки до відмови позначимо як Р*(t0). Її значення
визначається також за формулою (1), але при цьому N = 20, і кількість
працездатних об'єктів Nпр(t0) вибирається з цієї
сукупності. Результати вибору доцільно приставити у вигляді табл. 4.
Таблиця
4. Кількість сповіщувачів, працездатних на момент часу t0 з
перших 20-ти значень наробки до відмови
|
Значення наробки до відмови Т,
103год.
|
t0, 103 год.
|
значення Т, що перевищують t0,
103 год.
|
|
7
|
8,5
|
|
|
7
|
8,5
|
|
|
11
|
8,5
|
11
|
|
14
|
8,5
|
14
|
|
6
|
8,5
|
|
|
3
|
8,5
|
|
|
8
|
8,5
|
|
|
10
|
8,5
|
10
|
|
7
|
8,5
|
|
|
12
|
8,5
|
12
|
|
8
|
8,5
|
|
|
9
|
8,5
|
9
|
|
4
|
8,5
|
|
|
9
|
8,5
|
9
|
|
6
|
8,5
|
|
|
5
|
8,5
|
|
|
13
|
8,5
|
13
|
|
6
|
8,5
|
|
|
8
|
8,5
|
|
|
7
|
8,5
|
|
|
N=20
|
|
Nпр(t0)=7
|
Р*(t0)=
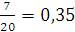
Будемо
вважати, що умови дослідження, яке включає 50 спостережень, дозволили
однозначно визначити ймовірність безвідмовної роботи сповіщувачів, тобто
(t) = 1
- F(t).
Де F(t) -
функція розподілу випадкової величини «наробка до відмови» - імовірність, що
визначає, події 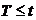 при
при
 .
.
Математичне
очікування кількості сповіщувачів Nпр(t0),
працездатних до наробки t0, визначається як:
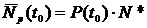

де N*
- обсяг партії сповіщувачів, згідно табл. 2.
Висновки.
Можлива відмінність значень P(t0) і Р*(t0) обумовлена
в першу чергу кількістю об'єктів, що перевіряються, адже чим більше об'єктів ми
перевіримо тим більше несправних виявимо і отже середнє значення буде точніше.
Завдання
2
Потрібно
розрахувати середню наробку до відмови  розглянутих
сповіщувачів. Спочатку обчислення зробити безпосередньо за вибірковими
значенням Т, зазначеним у табл. 1, а потім з використанням статистичного
ряду.
розглянутих
сповіщувачів. Спочатку обчислення зробити безпосередньо за вибірковими
значенням Т, зазначеним у табл. 1, а потім з використанням статистичного
ряду.
Для розрахунку
середнього значення  випадкової
величини Т безпосередньо по її вибіркових значеннях
випадкової
величини Т безпосередньо по її вибіркових значеннях  використовують
формулу
використовують
формулу
 .
.
дорівнює
кількості значень Т у табл. 1
 1. Метод прямого
обчислення
1. Метод прямого
обчислення
 =
= 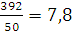
. Метод непрямого
обчислювання
Таблиця
5. Перетворення значень наробки до відмови у статистичний ряд
|
Інтервал
|
Число влучень в інтервал
|
Загальна кількість влучень
|
Статистична ймовірність
|
|
№
|
Нижня та верхня межа, 103
год
|
|
|
|
|
1
|
2,5 ¸ 5,5
|
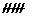  n1=10q1=
0,2 n1=10q1=
0,2
|
|
|
|
2
|
5,5 ¸ 8,5
|
 ////n2=19q2=
0,4 ////n2=19q2=
0,4
|
|
|
|
3
|
8,5 ¸ 11,5
|
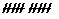 ////n3=14q3=
0,3 ////n3=14q3=
0,3
|
|
|
|
4
|
11,5 ¸ 14,5
|
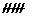 n4=5q4=0,1 n4=5q4=0,1
|
|
|
|
|
|
 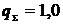
|
|
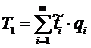 =
4х0,2+7х0,4+10х0,3+13х0,1=7,9* 103 год.
=
4х0,2+7х0,4+10х0,3+13х0,1=7,9* 103 год.
Розрахунки
з використанням формули (4) вносять деяку методичну помилку. Однак її значення,
як правило, знехтуване. Цю помилку у Ваших розрахунках оцініть за формулою:
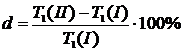 = 0,01
= 0,01
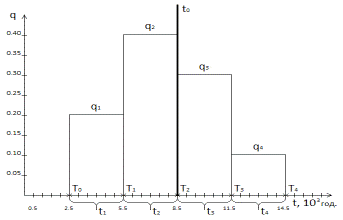
Рис. 1 Статистичний ряд
Висновки. Похибку у
розрахунках за другим методом можна зменшити, збільшивши кількість інтервалів у
статистичному ряді, цим самим зменшивши кількість потраплянь величини наробки
до відмови у певний інтервал.
Завдання
3
Потрібно
розрахувати інтенсивність відмов l(t) для заданих
значень t0 іDt.
Потім у
припущенні, що безвідмовність будь-якого блоку в електронній системі керування
пожежогасінням характеризується інтенсивністю відмов, чисельно рівної
розрахованої, причому ця інтенсивність не змінюється протягом усього строку
його служби, необхідно визначити середню наробку до відмови ТБ
такого блоку.
Підсистема
управління включає в себе k=3 послідовно з’єднаних електронних
блоків
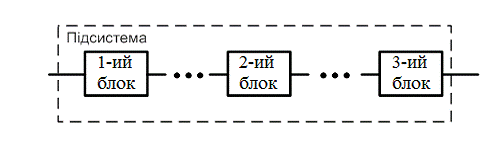
Рис. 2
Підсистема керування з послідовно включеними блоками
Ці блоки мають
однакову інтенсивність відмов, чисельно рівною розрахованої. Потрібно визначити
інтенсивність відмов підсистеми lп і середню наробку її до відмови 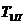 , побудувати залежності
ймовірності безвідмовної роботи одного блоку РБ(t) і
підсистеми PП(t) від наробки та визначити ймовірності
безвідмовної роботи блоку PБ(t) і підсистеми PП(t)
до наробки t=T1П. Значення k наведене в табл. 2
, побудувати залежності
ймовірності безвідмовної роботи одного блоку РБ(t) і
підсистеми PП(t) від наробки та визначити ймовірності
безвідмовної роботи блоку PБ(t) і підсистеми PП(t)
до наробки t=T1П. Значення k наведене в табл. 2
Інтенсивність
відмов l(t) розраховується за
формулою:
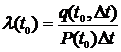 ,
, 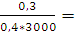 2,5
*10-4
2,5
*10-4
де q(t0,
Dt)
- статистична ймовірність відмов обладнання на інтервалі] t0, t0+Dt]  або інакше кажучи -
статистична ймовірність влучення на зазначений інтервал випадкової величини Т;
P(t0)=0,4 - імовірність безвідмовної роботи обладнання, яка
розрахована під час виконання завдання 1.
або інакше кажучи -
статистична ймовірність влучення на зазначений інтервал випадкової величини Т;
P(t0)=0,4 - імовірність безвідмовної роботи обладнання, яка
розрахована під час виконання завдання 1.

Якщо
інтенсивність відмов не змінюється протягом терміну служби об'єкта тобто l(t0) = l
= const, то наробка до відмови розподілена по експоненційному
(показниковому) закону.
У цьому
випадку ймовірність безвідмовної роботи блоку
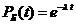 ,
,
а
середня наробка блоку до відмови знаходиться як
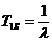 ,
,  =
0,4*10-3
=
0,4*10-3
Якщо
інтенсивності відмов усіх блоків однакові, то інтенсивність відмов підсистеми
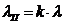 , 3*0,00025= 7,5*10-4
, 3*0,00025= 7,5*10-4
а
ймовірність безвідмовної роботи підсистеми
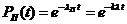 .
.
Середня
наробка підсистеми до відмови визначається як
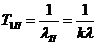
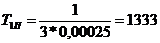
Для
будь-якого розподілу наробки до відмови ймовірність безвідмовної роботи
підсистеми, яка складається з k послідовно з'єднаних блоків, пов'язана з
ймовірностями безвідмовної роботи цих блоків наступним співвідношенням:
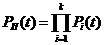 .
.
Якщо
блоки рівнонадійні, як прийнято в завданні, то
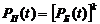
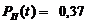
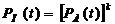 = (е-лt)3 = е-лt*3
= (е-лt)3 = е-лt*3
Таблиця 6.
Розрахункові значення PБ(t) і PП(t)
|
t
|
PБ(t)
|
PП(t)
|
|
0
|
1
|
1
|
|
400
|
0,904837418
|
0,740818221
|
|
800
|
0,818730753
|
0,548811636
|
|
1200
|
0,740818221
|
0,40656966
|
|
1600
|
0,670320046
|
0,301194212
|
|
2000
|
0,60653066
|
0,22313016
|
|
2400
|
0,548811636
|
0,165298888
|
|
2800
|
0,496585304
|
0,122456428
|
|
3200
|
0,449328964
|
0,090717953
|
|
3600
|
0,40656966
|
0,067205513
|
|
4000
|
0,367879441
|
0,049787068
|
|
4400
|
0,332871084
|
0,036883167
|
|
4800
|
0,301194212
|
0,027323722
|
|
5200
|
0,272531793
|
0,020241911
|
Висновки. При наближенні
до граничного стану - інтенсивність відмов об'єктів як правило різко та
неухильно зростає, тому що при послідовному з’єднанні блоків з однаковою
ймовірністю відмови, ймовірність відмови всієї систем збільшується.
Завдання
4
Для наробки 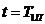 потрібно
розрахувати ймовірність безвідмовної роботи
потрібно
розрахувати ймовірність безвідмовної роботи  системи пожежогасіння
(рис. 3), що складається з двох підсистем, одна з яких є резервною.
системи пожежогасіння
(рис. 3), що складається з двох підсистем, одна з яких є резервною.
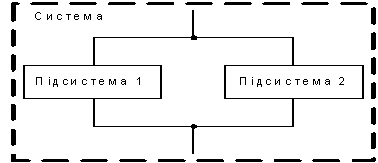
Рис. 3 Схема
системи з резервуванням
наробка
безвідмовний сповіщувач пожежогасіння
Проведемо розрахунки з
припущенням, що відмови кожної з двох підсистеми незалежні, тобто відмова
першої підсистеми не порушує працездатність другої, і навпаки.
Імовірності
безвідмовної роботи кожної підсистеми однакові та дорівнюють 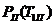 .
Тоді ймовірність відмови однієї підсистеми
.
Тоді ймовірність відмови однієї підсистеми
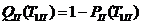 .
.
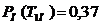
Імовірність
відмови всієї системи  визначається
з умови, що відмовила й перша, і друга підсистеми, тобто:
визначається
з умови, що відмовила й перша, і друга підсистеми, тобто:
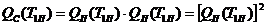 = 0,632≈
0,4
= 0,632≈
0,4
Тоді
ймовірність безвідмовної роботи системи:
 ,
,
або
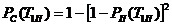 = 1-0,4=0,6
= 1-0,4=0,6
Висновки: Перше
це - збільшення навантаження на блок, що залишився в разі виходу з ладу
одного з них. Друге - неможливість розриву ланцюга в разі несправності в замкнутому
стані будь-якої з підсистем. Зменшення пропускної здатності.
Завдання 5
За даними табл. 7
потрібно визначити залежності математичного очікування (середнього значення)
зношування шатунних шийок колінчатого валу ДВЗ 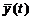 і дисперсії зношування
D (у(t)) від наробки (пробігу пожежної машини). Отримані рівняння необхідно
записати. Параметри шуканих залежностей слід розрахувати з використанням
правила визначення рівняння прямої, що проходить через дві точки з відомими
координатами.
і дисперсії зношування
D (у(t)) від наробки (пробігу пожежної машини). Отримані рівняння необхідно
записати. Параметри шуканих залежностей слід розрахувати з використанням
правила визначення рівняння прямої, що проходить через дві точки з відомими
координатами.
Дане завдання
виконується з припущенням, що математичне очікування (середнє значення) і
дисперсія зношування шатунних шийок колінчатого вала представляють собою
лінійні функції пробігу пожежної машини. Це підтверджується дослідженнями,
проведеними в різних відділеннях аварійно-рятувальної служби та обробкою
статистичних даних.
Позначимо
зношування шийок як деяку змінну величину Y. Залежність Y від наробки (пробігу
пожежної машини) представляє собою випадкову фу-нкцію, реалізації якої є
монотонними неспадними функціями. Для опису такої випадкової функції часто
цілком достатньо знати, як змінюється залежно від наробки її математичне
очікування (середнє значення) і дисперсія: и D (у(t)).
Дослідження,
проведені в різних відділеннях аварійно-рятувальної служби, показують, що для
опису залежності зношування від пробігу пожежної машини можуть бути використані
лінійні функції
 , (у мм)
, (у мм)
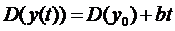 (у мм2
(у мм2
де і D(у0)
відповідно - середнє значення та дисперсія зношування шийок при t=0, при цьому
початком відліку є останнє обточування колінчатих валів;
а - середня
швидкість збільшення зношування, мм/тис. км;- швидкість збільшення дисперсії
зношування, мм2/тис. км;- пробіг пожежної машини, тис. км
Таблиця 7
Результати обробки виміру зношування шатунних шийок колінчатих валів двигуна
пожежної машини
|
Варіант
|
Розрахункова величина
|
|
Перше вимірювання
|
Друге вимірювання
|
|
Пробіг t1, тис. км
|
Середнє зношування 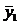 ,
ммДисперсія зношування D(у1), мм2Пробіг t2,
тис. кмСереднє зношування ,
ммДисперсія зношування D(у1), мм2Пробіг t2,
тис. кмСереднє зношування 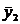 , ммДисперсія зношування D(у2), мм2 , ммДисперсія зношування D(у2), мм2
|
|
|
|
|
|
8
|
35
|
0,9
|
0,06
|
150
|
2,1
|
0,154
|
Передбачається,
що масиви даних про зношування шийок для кожного ti вже
оброблені. Вважається також можливим визначити шукані лінійні залежності,
користуючись координатами тільки двох точок.
У
такому випадку параметри а і b залежностей можуть бути визначені
відповідно
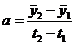
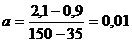
та
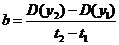

Після цього,
використовуючи координати кожної з відомих двох точок, наприклад, другій  або
або
 ,
можна знайти два інших параметра
,
можна знайти два інших параметра
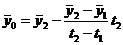 ;
;
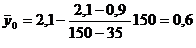

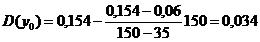
Підставивши
значення отримаємо вирази, що визначають залежності від пробігу середнього
зношування шатунних шийок ДВЗ та дисперсії зношування


та
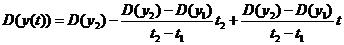 .
.
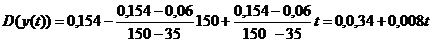
Висновки:
Теоретично в разі ідеального обточування і без пробігу вихідні значення
середнього прокату і дисперсії бандажів можуть дорівнювати нулю, на практиці
швидше за все ні, від’ємними також.
Завдання 6
Потрібно розрахувати
середні значення, дисперсії та середні квадратичні відхилення зношування для
декількох значеннях пробігу, користуючись залежностями, отриманими під час
виконання попереднього завдання. Потім потрібно для тих же значень пробігу
визначити нижню y(ti) min і верхню y(ti) max, межі практично можливих значень
зношування. Результати розрахунків слід занести в таблицю, виконану за формою
табл. 8, і побудувати по них лінії, що представляють собою залежність
середнього зношування шийок від пробігу, нижню і верхню межу практично можливих
значень зношування
Таблиця 8 Результати
розрахунків середніх значень, дисперсій і середніх квадратичних відхилень
зношування шийок колінчатих валів
|
Величина
|
Пробіг, тис. км
|
|
0
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
|
1
|
Середнє зношування 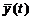 , мм0,61,11,62,12,63,13,64,1 , мм0,61,11,62,12,63,13,64,1
|
|
|
|
|
|
|
|
|
|
2
|
Дисперсія зношування 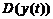 , мм20,030,070,110,150,190,230,270,31 , мм20,030,070,110,150,190,230,270,31
|
|
|
|
|
|
|
|
|
|
3
|
Середнє квадратичне відхилення
зношування 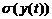 ,
мм0,170,260,330,390,440,480,520,56 ,
мм0,170,260,330,390,440,480,520,56
|
|
|
|
|
|
|
|
|
|
4
|
Потроєне значення  , мм0,510,780,991,171,321,441,561,68 , мм0,510,780,991,171,321,441,561,68
|
|
|
|
|
|
|
|
|
|
5
|
Нижня межа y(t)mах
|
1,15
|
1,92
|
2,61
|
3,28
|
3,92
|
4,55
|
5,17
|
5,78
|
|
6
|
Верхня межа y(t)mіn
|
0,005
|
0,28
|
0,59
|
0,92
|
1,28
|
1,65
|
2,03
|
2,42
|
Граничне значення упр
зношування шийок колінчатих валів ДВЗ типу ЧН21/21 встановлене рівним 1,7 мм.
На практиці обточування прагнуть робити при прокаті 1,5 мм, тому при виконанні
курсового проекту прийміть упр. рівним 1,5 мм. Заданий пробіг
зазначений у табл. 9.
Таблиця
9. Задана серія та пробіг Тзад
|
Варіант
|
8
|
|
Заданий пробіг Тзад,
тис. км
|
260
|
Заповнюємо
таблицю, послідовно виконуючі обчислення за формулами, отриманими під час
виконання завдання 5, для різних значень пробігу пожежної машини. Розрахунки
середньоквадратичних відхилень зробіть за формулою
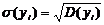 ,
,
де і
- номер інтервалу в табл. 8.
Прийнятої
моделі процесу зношування шейки, відповідає таке поступове збільшення
зношування, при якому середнє значення та дисперсія збільшення зношування за
деякий інтервал пробігу Dt пропорційні
довжині цього інтервалу й не залежать від досягнутого значення у. У
такому випадку цілком припустиме, ґрунтуючись на основних теоремах теорії
ймовірностей, вважати, що для будь-якого ti (поки y < уПР)
значення зношування розподілені за нормальним законом з густиною розподілу:
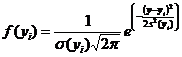 .
.
Звуження
області визначення функції f(yi) до інтервалу] 0, упр]
практично не впливає на результати розрахунків. Для знаходження області
практично можливих значень випадкової величини уi,
розподіленої за нормальним законом, користуються «правилом трьох сигм».
Відповідно до цього правила для кожного пробігу пожежної машини ti
верхня і нижня межа практично можливих значень зношування шийок визначають як
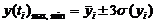 .
.
Криві,
що показують верхню і нижню межу практично можливих значень зношування,
визначаються виразами:
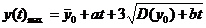 ,
,

Висновки: Ні, оскільки
зміна йде лінійно
Завдання
7
Потрібно
розрахувати 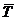 -
середній пробіг (наробку) до поточного ремонту, а також найменший Тн
і критичний (найбільший) Тк - практично можливі пробіги до
обточування шийок колінчатих валів внаслідок зношування.
-
середній пробіг (наробку) до поточного ремонту, а також найменший Тн
і критичний (найбільший) Тк - практично можливі пробіги до
обточування шийок колінчатих валів внаслідок зношування.
Далі необхідно
розрахувати Y - імовірність того, що до заданого
пробігу Тзад буде зроблено обточування шийок колінчатого вала
по зношуванню.
Поточний ремонт
представляє собою обточування шатунних шийок колінчатих валів з розбиранням
ДВЗ. Факторами, що визначають необхідність проведення обточування шатунних
шийок, можуть бути:
збільшення
зношування до граничного значення,
прояв дефектів на
поверхні ковзання,
необхідність
зрівняти діаметри шийок колінчатих валів для постановки вкладишів ремонтних
градацій тощо.
У даній роботі
будемо вважати, що основною причиною постановки пожежної машини на ремонт є
збільшення зношування шийок, що цілком відповідає практиці роботи більшості
відділень аварійно-рятувальної служби.
За таких умов
середній пробіг до поточного ремонту можна розрахувати, підставивши у вираз
(14) значення y(t) = упр:
 .
.
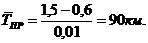
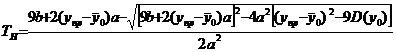 , тис. км;
, тис. км;
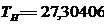 тис. км.
тис. км.
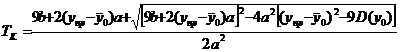 , тис. км.
, тис. км.
Тк = 237,7393 тис. км.
Ймовірність
того, що до пробігу Тзад вже буде зроблено обточування шийок
знаходиться як
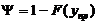 ,
,
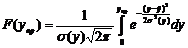 .
.

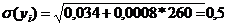
Виразити
функцію розподілу через нормальну функцію розподілу можна за допомогою виразу:
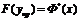 ,
,
де х
знаходиться в результаті заміни змінної як
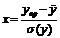
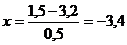
За розрахованим
значенням X знаходимо по таблиці нормальної функції розподілу, значення Ф*(х)
і далі Y.
Ф*(х)= -3,4, тоді
Ф*(х)=0,5+
Ф*(-х)= 0,5 - Ф(х)=0,5 - Ф (3,4)=0,5-0,49=0,01.
Y=
1-0,01=0,99
Висновки:
Ймовірність проведення обточування шийок колінчатих валів к моменту Тпр=
90 км.
Завдання
8
На
випробуванні знаходилось N0 = 1 000 зразків електричних ламп,
які належать до класу неремонтованої апаратури. Кількість відмов n(Dt) фіксувалося через
кожні 100 год. роботи (Dt=100 ч).
Дані
про відмови по варіантах шифру наведені в табл. 10.
Потрібно
обчислити кількісні характеристики надійності та побудувати залежності
характеристик від часу.
Таблиця
10. Дані про відмови
|
Dti
|
0 100
|
100 200
|
200 300
|
300 400
|
400 500
|
500 600
|
600. 700
|
700 800
|
800 900
|
900 1000
|
1000 1100
|
1100 1200
|
1200 1300
|
1300 1400
|
1400 1500
|
1500 1600
|
1600 1700
|
1700 1800
|
1800 1900
|
1900 2000
|
2000 2100
|
2100 2200
|
2200 2300
|
2300 2400
|
2400 2500
|
2500 2600
|
2600 2700
|
2700 2800
|
2800 2900
|
2900 3000
|
|
n(ti) вар. 8
|
49
|
39
|
31
|
23
|
18
|
15
|
14
|
14
|
13
|
12
|
13
|
12
|
12
|
11
|
12
|
11
|
11
|
11
|
12
|
10
|
10
|
11
|
10
|
11
|
12
|
14
|
18
|
23
|
28
|
38
|
Електричні
лампи належать до класу невідновлюваних виробів. Тому критеріями надійності
будуть P(t); f(t), l(t), Tcp.
Обчислимо
P(t).

Для розрахунків
характеристик f(t) і l(t) застосовуються формули:

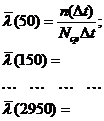
де 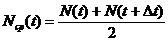 -
середня кількість працездатних елементів на інтервалі [t, t + Dt].
-
середня кількість працездатних елементів на інтервалі [t, t + Dt].
Значення,
обчислені для всіх Dti,
зводимо в таблицю наступної форми (табл. 11):
Таблиця 11.
Обчислені значення 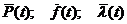
|
Dti,
год
|
P(t)
|
 , 1/год , 1/год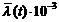 ,
1/год ,
1/год
|
|
|
0…100
|
0,951
|
0,49
|
11,13636
|
|
100…200
|
0,912
|
0,39
|
11,14286
|
|
200…300
|
0,881
|
0,31
|
11,48148
|
|
300…400
|
0,858
|
0,23
|
11,21951
|
|
400…500
|
0,84
|
0,18
|
10,90909
|
|
500…600
|
0,825
|
0,15
|
10,34483
|
|
600…700
|
0,811
|
0,14
|
10
|
|
700…800
|
0,797
|
0,14
|
10,37037
|
|
800…900
|
0,784
|
0,13
|
10,4
|
|
900…1000
|
0,772
|
0,12
|
9,6
|
|
1000…1100
|
0,759
|
0,13
|
10,4
|
|
1100…1200
|
0,747
|
0,12
|
10
|
|
1200…1300
|
0,735
|
0,12
|
10,43478
|
|
1300…1400
|
0,724
|
0,11
|
9,565217
|
|
1400…1500
|
0,712
|
0,12
|
10,43478
|
|
1500…1600
|
0,701
|
0,11
|
10
|
|
1600…1700
|
0,69
|
0,11
|
10
|
|
1700…1800
|
0,679
|
0,11
|
9,565217
|
|
1800…1900
|
0,667
|
0,12
|
10,90909
|
|
1900…2000
|
0,657
|
0,1
|
10
|
|
2000…2100
|
0,647
|
0,1
|
9,52381
|
|
2100…2200
|
0,636
|
0,11
|
10,47619
|
|
2200…2300
|
0,626
|
0,1
|
9,52381
|
|
2300…2400
|
0,615
|
0,11
|
9,565217
|
|
2400…2500
|
0,603
|
0,12
|
9,230769
|
|
2500…2600
|
0,589
|
0,14
|
8,75
|
|
2600…2700
|
0,571
|
0,18
|
8,780488
|
|
2700…2800
|
0,548
|
0,23
|
9,387755
|
|
2800…2900 2900…3000
|
0,522
|
0,26
|
8,125
|
|
2900…3000 2900…3000
|
0,484
|
0,38
|
10
|
За
даними, наведеними у табл. 11, будуються на міліметровому папері, або на
комп’ютері за допомогою прикладних програм залежності P(t); f(t), l(t).
Обчислимо
середній час безвідмовної роботи, припустивши, що на випробуванні знаходились
тільки ті зразки, які відмовили:
 =1378
год.
=1378
год.
Література
1. Пискунов Н.С. Дифференцальные и интегральные исчисления для вызов. т. 2. Учебное
пособие для вузов. - 13-е изд.-М: Наука, Главная редакция физико-математической
литературы, 1985.-560 с.
2. ВентцельЕ.С.
Теорія вероятностей.-М.: Наука, 1969.-576 с.
. Гумбель Еге.
Статистика екстремальних значень.-М.:Мир, 1965.-450 с.
. Болотин В.В.,
Чирков В.П. Асимптотические оцінки для ймовірності безвідмовної роботи за
моделями типунагрузка-сопротивление // Проблеми машинобудування й надійності
машин, 1992, №6 с. 3-10