Основные понятия математической статистики
Содержание
Введение
. Статистическая обработка результатов выборочных наблюдений
.1 Постановка задачи
.2 Вычисление основных числовых характеристик выборочных
наблюдений
.3 Результаты вычисления интервальных оценок для математического
ожидания и дисперсии
.4 Ранжирование выборочных данных, вычисление моды и медианы
.5 Параметрическая оценка функции плотности распределения
.6 Проверка гипотезы о нормальном распределении случайной величины
по критерию Пирсона
. Расчет аналитических показателей ряда динамики
.1 Ряды динамики и их аналитические показатели
.2 Пример расчета показателей ряда динамики
. Статистика денежного обращения
.1 Понятия денежного обращения и денежной массы
.2 Система показателей денежной массы
.3 Структура денежной массы и ее виды
.4 Понятие денежной базы и её составляющие
.5 Статистический анализ оборачиваемости денежной массы
Заключение
Список литературы
Введение
Статистические данные являются
важнейшей частью глобальной информационной системы государства.
Многовековая и древняя история
статистики (от латинского слова status - «состояние и положение вещей»)
свидетельствует о крайней важности существования данной науки.
Актуальность работы вызвана тем, что
в наше время важность правильной, рациональной организации и реализации
статистических методов вошла в повседневный обиход современной жизни. Это
неудивительно. Статистика является корреляционной наукой. Она включает в себя
разделы как теоретические, так и прикладные (экономическая, социальная,
отраслевая статистика). В этой связи статистика представляет собой необходимое
звено в системе организации и функционирования, как малого субъекта бизнеса,
так и страны в целом.
Курсовая работа состоит из трех
разделов. Первый раздел призван обеспечить анализ количественной стороны
массовых явлений, служит основой для принятия соответствующих управленческих
решений. Также в данном разделе рассматривается определение функции плотности и
построение ее графика, сравнение экспериментальной и теоретической вероятности.
Третий раздел раскрывает понятие денежного обращения и денежной массы, в нем
рассмотрено понятие денежной базы и ее составляющих, рассмотрены показатели, с
помощью которых определяется оборачиваемость денежной массы и ее монетизация.
Целью курсового
проекта является изучение и усвоение основных понятий математической
статистики, овладение методикой статистического оценивания числовых
характеристик случайной величины и нормального закона распределения, знакомство
с методикой применения статистических критериев для проверки гипотез.
1. Статистическая
обработка результатов выборочных наблюдений
.1 Постановка задачи
По выборке объема n провести статистическую обработку
результатов выборочных наблюдений (статистических наблюдений).
Цель работы:
изучить и усвоить основные понятия
дасциплины “Статистика”;
овладеть методикой статистического
оценивания числовых характеристик случайной величины и нормального закона
распределения;
ознакомиться с методикой применения
статистических критериев для проверки гипотез.
Пусть проведено выборочное исследование
(эксперимент) и имеются выборочные значения объема n = 60, которые представляют собой
реализацию случайной величины Х. Исходные данные представлены в табл. 1.1.1
Таблица 1.1.1 Исходные данные
|
1
|
4,7229
|
11
|
3,6843
|
21
|
3,9105
|
31
|
5,4419
|
41
|
3,6265
|
51
|
4,9232
|
|
2
|
4,0395
|
12
|
4,9778
|
22
|
2,9767
|
32
|
4,6723
|
42
|
3,1680
|
52
|
3,8214
|
|
3
|
5,5413
|
13
|
4,0183
|
23
|
4,9375
|
33
|
4,1387
|
43
|
4,2869
|
53
|
3,4783
|
|
4
|
2,2989
|
14
|
4,8180
|
24
|
2,8683
|
34
|
3,1405
|
44
|
2,1811
|
54
|
5,4320
|
|
5
|
2,9663
|
15
|
4,7023
|
25
|
3,2893
|
35
|
3,2477
|
45
|
2,4269
|
55
|
3,1299
|
|
6
|
3,2363
|
16
|
3,7687
|
26
|
2,8305
|
36
|
5,2296
|
46
|
6,0157
|
56
|
4,8075
|
|
7
|
6,1764
|
17
|
3,8863
|
27
|
5,0654
|
37
|
5,1508
|
47
|
3,9280
|
57
|
3,4894
|
|
8
|
4,4316
|
18
|
4,1279
|
28
|
3,3196
|
38
|
3,3920
|
48
|
6,6289
|
58
|
4,7435
|
|
9
|
3,5562
|
19
|
3,2006
|
29
|
2,2742
|
39
|
4,8062
|
49
|
3,7567
|
59
|
4,8479
|
|
10
|
4,0300
|
20
|
3,7614
|
30
|
4,8132
|
40
|
4,2171
|
50
|
4,1733
|
60
|
3,1701
|
1.2 Вычисление основных
числовых характеристик выборочных наблюдений
.Среднее арифметическое случайной
величины Х

 i
=
i
= 
 = 4,06
= 4,06
. Среднее линейное
отклонение
d
= 
 =
= 
 = 0,79
= 0,79
. Смещённая оценка
дисперсии случайной величины Х

4. Несмещённая оценка
дисперсии случайной величины Х
D[X] = 𝞂2 = 
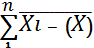
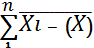 2 =
2 = 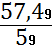
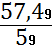 = 0,97
= 0,97
. Смещённое среднее
квадратическое отклонение

 =
= 
 =
= 
 2 =
2 = 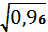
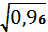 = 0,98
= 0,98
. Несмещённое среднее
квадратическое отклонение
𝞂
= 
 =
= 
 2 =
2 = 
 = 0,98
= 0,98
. Коэффициент вариации
V
= 
 100% =
100% = 
 = 24,13%
= 24,13%
. Коэффициент асимметрии
случайной величины Х

 3 =
3 = 
 = 0,29
= 0,29
𝞂3
= ( 0,98)3= 0,94
As
= 
 =
= 
 = 0,31
= 0,31
. Коэффициент эксцесса
случайной величины Х

 4 =
4 = 
 = 2,51
= 2,51
Es
= 
 - 3 =
- 3 = 
 - 3 = - 0,27
- 3 = - 0,27
. Вариационный размах
R
= Xmax - Xmin = X48 - X44 = 6,63 - 2,18 = 4,45
На основании полученных
вычислений можно сделать следующие выводы:
.Необходимое условие V < 33% для того, чтобы выборка имела нормальный закон
распределения, выполняется:
V
= 24,13% < 33%
. Для нормального
распределения коэффициенты асимметрии и эксцесса должны быть равны нулю:
As
= E = 0
По результатам
вычислений асимметрия близка к нулю 
 s
= 0,31 > 0 - это означает, что длинная часть функции плотности расположена
справа от математического ожидания.
s
= 0,31 > 0 - это означает, что длинная часть функции плотности расположена
справа от математического ожидания.
Коэффициент эксцесса
равен 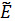
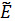 s
= - 0,27. Он отрицательный, а это означает, что функция плотности имеет более
низкую и плоскую вершину, чем плотность нормального распределения.
s
= - 0,27. Он отрицательный, а это означает, что функция плотности имеет более
низкую и плоскую вершину, чем плотность нормального распределения.
1.3 Результаты
вычисления интервальных оценок для математического ожидания и дисперсии
Для вычисления
интервальной оценки математического ожидания воспользуемся формулой:

 - tn-1,p *
- tn-1,p * 
 < a <
< a < 
 + tn-1,p *
+ tn-1,p * 

где a = M(X) - математическое ожидание, tn-1,p - процентная точка распределения Стьюдента с n-1 степенью свободы; р - доверительная вероятность.
Подставим в формулу
вычисленные ранее значения 
 ,
, 
 и n.
и n.
В результате получим:
,06 - t59,p * 
 < a < 4,06 + t59,p *
< a < 4,06 + t59,p * 

Зададимся доверительной
вероятностью:
Р1 = 0,95; Р2 = 0,99
При р1 = 0,95 находим t59, 0,95 = 2 и доверительный интервал для a
= M(X) имеет вид:
,81 < a < 4,31
При р2 = 0,99 находим t59, 0,99 = 2,66 и доверительный интервал для a = M(X) имеет вид:
,72 < a < 4,40
Для интервальной оценки
дисперсии существуют следующие неравенства:

Подставив в неравенство
известные значения n и 
 2, получим неравенство,
в котором неизвестны х12 и х22 :
2, получим неравенство,
в котором неизвестны х12 и х22 :

Задаваясь доверительной
вероятностью pi (или уровнем значимости a),
вычисляем значения (1 - pi)/2
и (1 + pi)/2. Используем эти два значения и степень свободы v = n - 1 находим  и
и
 :
:
x12
=  x22 =
x22 = 
Для р1 = 0,95, (1 - рi)/2 = 0,025, (1 + рi)/2
= 0,975 и v = 59 находим:
x12
= x20,975; 59 = 40,48
x22
= x20,025; 59 = 83,30
Подставляя в неравенства
х12 и х22 и производя вычисления, получим интервальную оценку:

 < 𝞂2 <
< 𝞂2 <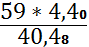
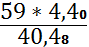
,12< 𝞂2 <6,41
Для интервальной оценки
среднего квадратического отклонения имеем:

При р1 = 0,95 получаем
доверительный интервал:

 =
= 
 = 7,68
= 7,68

 = 0,98
= 0,98

 * 𝞂 = 7,68 * 0,98 = 7,53
* 𝞂 = 7,68 * 0,98 = 7,53

 < 𝞂 <
< 𝞂 < 

,82511 < 𝞂 < 1,18359
При р2 = 0,99 получаем
доверительный интервал:

 < 𝞂 <
< 𝞂 < 
 ;
;
,78527 < 𝞂 < 1,26342
1.4 Ранжирование
выборочных данных, вычисление моды и медианы
Используя исходные
данные, запишем все заданные значения выборки в виде неубывающей
последовательности значений случайной величины Х.
Интервал [2,1811;
6,6289], содержащий все элементы выборки, разобьем на частичные интервалы,
используя при этом формулу Стерджеса для определения оптимальной длины и границ
этих частичных интервалов.
По формуле Стерджеса
длина частичного интервала равна:
h
= 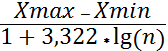
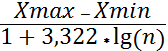 =
= 
 = 0,64
= 0,64
Для удобства и простоты
расчетов округлим величину h.
В нашем случае выбираем h
= 0,6 и вычисляем границы интервалов.
Таблица 1.4.1
Ранжированный ряд
|
1
|
2,1811
|
11
|
3,1680
|
21
|
3,5562
|
31
|
4,0183
|
41
|
4,7023
|
51
|
4,9778
|
|
2
|
2,2742
|
12
|
3,1701
|
22
|
3,6265
|
32
|
4,0300
|
42
|
4,7229
|
52
|
5,0654
|
|
3
|
2,2989
|
13
|
3,2006
|
23
|
3,6843
|
33
|
4,0395
|
43
|
4,7435
|
53
|
5,1508
|
|
4
|
2,4269
|
14
|
3,2363
|
24
|
3,7567
|
34
|
4,1279
|
44
|
4,8062
|
54
|
5,2296
|
|
5
|
2,8305
|
15
|
3,2477
|
25
|
3,7614
|
35
|
4,1387
|
45
|
4,8075
|
55
|
5,4320
|
|
6
|
2,8683
|
16
|
3,2893
|
26
|
3,7687
|
36
|
4,1733
|
46
|
4,8132
|
56
|
5,4419
|
|
7
|
2,9663
|
17
|
3,3196
|
27
|
3,8214
|
37
|
4,2171
|
47
|
4,8180
|
57
|
5,5413
|
|
8
|
2,9767
|
18
|
3,3920
|
28
|
3,8863
|
38
|
4,2869
|
48
|
4,8479
|
58
|
6,0157
|
|
9
|
3,1299
|
19
|
3,4783
|
29
|
3,9105
|
39
|
4,4316
|
49
|
4,9232
|
59
|
6,1764
|
|
10
|
3,1405
|
20
|
3,4894
|
30
|
3,9280
|
40
|
4,6723
|
50
|
4,9375
|
60
|
6,6289
|
За начало первого интервала
принимаем значение:
которое округляем до
целого значения и принимаем х0 = 2. Далее вычисляем границы интервалов:
х1 = х0 + h = 2 + 0,6 = 2,6
х2 = х1 + h = 2,6 + 0,6 = 3,2
х3 = х2 + h = 3,2 + 0,6 = 3,8
х4 = х3 + h = 3,8 + 0,6 = 4,4
х5 = х4 + h = 4,4 + 0,6 = 5
х6 = х5 + h = 5 + 0,6 = 5,6
х7 = х6 + h = 5,6 + 0,6 = 6,2
х8 = х0 + n*h
х8 = 2 +8*0,6 = 6,8
Вычисление границ
заканчиваем, как только выполняется неравенство:
Xn
> Xmax
то есть x8 = 6,8 > Xmax
= 6,6289
По результатам
вычислений составим табл. 1.4.2 значений выборочной функции плотности.
Таблица 1.4.2 Значения
выборочной функции плотности
|
[xi-1;xi)
|
[2;2,6)
|
[2,6;3,2)
|
[3,2;3,8)
|
[3,8;4,4)
|
[4,4;5)
|
[5;5,6)
|
[5,6;6,2)
|
[6,2;6,8)
|
|
  I = I =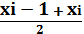 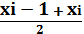 2,32,93,54,14,75,35,96,5 2,32,93,54,14,75,35,96,5
|
|
|
|
|
|
|
|
|
|
ni
|
4
|
8
|
14
|
12
|
13
|
6
|
2
|
1
|
|
Wi =
|
0,06666
|
0,13333
|
0,23333
|
0,2
|
0,21666
|
0,1
|
0,03333
|
0,01666
|
|
 0,11110,222210,388880,333330,36110,166660,055550,02776 0,11110,222210,388880,333330,36110,166660,055550,02776
|
|
|
|
|
|
|
|
|
В первую строку таблицы поместим
частичные интервалы, во вторую строку - середины интервалов, в третью строку
запишем частоты - количество элементов выборки, попавших в каждый частичный
интервал, в четвертую строку запишем относительные частоты, в пятую строку
запишем значения плотности относительных частот или значения выборочной,
экспериментальной функции плотности.
По результатам вычислений функции
плотности, представленным в табл.1.4.2, можно сделать вывод, что мода имеет
один локальный максимум в окрестностях точки х = 3,5 с частотой ni = 14.
Оценку медианы находим, используя
вариационный ряд, для которого n = 2k = 60 и k = 30:
Me = 1/2(xk + xk+1) = 1/2( x30 + x31) = 1/2(3,9280 + 4,0183) = 3,97
Сравнение оценок медианы
Me = 3,97 и оценки математического ожидания  =
4,06 показывает, что они отличаются на 2,26%.
=
4,06 показывает, что они отличаются на 2,26%.
1.5 Параметрическая
оценка функции плотности распределения
Исходя из гипотезы, что
заданная выборка имеет нормальный закон распределения, найдем параметрическую
оценку функции плотности, используя формулу для плотности распределения
вероятности нормального закона:

где  =
4,06 и 𝞂2 = 0,98
=
4,06 и 𝞂2 = 0,98
Значения этой функции
вычисляют для середин частичных интервалов, т.е. при х = 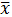
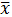 i.
На практике для упрощения вычислений функции ⱷ(
i.
На практике для упрощения вычислений функции ⱷ(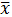
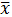 i),
где i = 1,2,…,k,
пользуются таблицами значений функции плотности стандартной нормальной
величины.
i),
где i = 1,2,…,k,
пользуются таблицами значений функции плотности стандартной нормальной
величины.
Для этого вычислим
значения:
zi
= 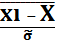
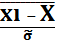 для i = 1,2,…k:
для i = 1,2,…k:
z1
= 
 =
= 
 = -1,85
= -1,85
z2
= 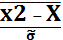
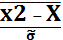 =
= 
 = -1,18
= -1,18
z3
= 
 =
= 
 = -0,57
= -0,57
z4
= 
 =
= 
 = 0,04
= 0,04
z5
= 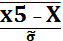
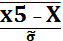 =
= 
 = 0,65
= 0,65
z6
= 
 =
= 
 = 1,26
= 1,26
z7
= 
 =
= 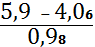
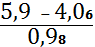 = 1,88
= 1,88
z8
= 
 =
= 
 = 2,49
= 2,49
Затем по таблице находим
значения функции плотности стандартной нормальной величины:
f(zi) = e - 

Имеем:
f(z1) = 0,07
f(z2)
= 0,21(z3) = 0,34(z4) = 0,39(z5) = 0,32(z6) = 0,18(z7) = 0,06
f(z8) = 0,01
После этого, разделив
значения функции f(zi) на 
 , получим значения
теоретической функции плотности ⱷ(
, получим значения
теоретической функции плотности ⱷ(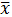
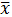 i):
i):
ⱷ(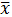
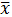 i) =
i) = 
 f(zi)
f(zi)
Имеем:
ⱷ(
 1) =
1) = 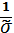
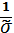 f(z1) =
f(z1) = 
 = 0,07
= 0,07
ⱷ(
 2) =
2) = 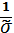
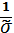 f(z2) =
f(z2) = 
 = 0,21
= 0,21
ⱷ(
 3) =
3) = 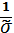
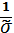 f(z3) =
f(z3) = 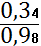
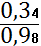 = 0,35
= 0,35
ⱷ(
 4) =
4) = 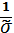
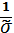 f(z4) =
f(z4) = 
 = 0,4
= 0,4
ⱷ(
 5) =
5) = 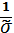
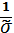 f(z5) =
f(z5) = 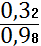
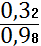 = 0,33
= 0,33
ⱷ(
 6) =
6) = 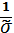
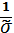 f(z6) =
f(z6) = 
 = 0,18
= 0,18
ⱷ(
 7) =
7) = 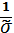
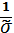 f(z7) =
f(z7) = 
 = 0,06
= 0,06
ⱷ(
 8) =
8) = 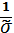
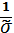 f(z8) =
f(z8) = 
 = 0,01
= 0,01
Вычислим теоретические
вероятности:
P1T = 0,6 * 0,07 = 0,042
P2T = 0,6 * 0,21 = 0,126
P3T
= 0,6 * 0,35 = 0,21T = 0,6 * 0,4 = 0,24T = 0,6 * 0,33 = 0,198T = 0,6 * 0,18 =
0,108T = 0,6 * 0,06 = 0,0368T
= 0,6 * 0,01 = 0,006
Вычислим теоретические
частоты niT для n = 60:
n1T
= 0,042 * 60 = 2,52T = 0,126 * 60 = 7,56T = 0,21 * 60 = 12,6T = 0,24 * 60 =
14,4T = 0,198 * 60 = 11,886T
= 0,108 * 60 = 6,48
n7T = 0,036 * 60 = 2,16
n8T = 0,006 * 60 = 0,36
Результаты вычислений
вероятностей и соответствующих частот приведены в табл. 1.5.1.
В первом столбце таблицы
расположены k частичных интервалов, во втором столбце расположены наблюдаемые
частоты ni , в третьем столбце расположены координаты середины частичных
интервалов, в четвертом столбце расположены относительные частоты, в пятом
столбце расположены значения экспериментальной функции плотности, в шестом
столбце расположены значения zi
, в седьмом столбце расположены значения теоретической функции плотности,
вычисленные в середине частичных интервалов, в восьмом столбце расположен
значения теоретических вероятностей, в девятом столбце расположены значения
теоретических частот.
Таблица 1.5.1 Результаты
вычисления экспериментальных теоретических вероятностей и частот
|
[xi-1;xi)
|
ni
|
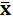 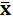 I = I =   рi = рi =   ( ( -i)ziⱷ( -i)ziⱷ(  i)piTniT i)piTniT
|
|
|
|
|
|
|
|
[2;2,6)
|
4
|
2,3
|
0,06666
|
0,1111
|
-1,85
|
0,07
|
0,042
|
2,52
|
|
[2,6;3,2)
|
8
|
2,9
|
0,13333
|
0,22221
|
-1,18
|
0,21
|
0,126
|
7,56
|
|
[3,2;3,8)
|
14
|
3,5
|
0,23333
|
0,38888
|
-0,57
|
0,35
|
0,21
|
12,6
|
|
[3,8;4,4)
|
12
|
4,1
|
0,2
|
0,33333
|
0,04
|
0,4
|
0,24
|
14,4
|
|
[4,4;5)
|
13
|
4,7
|
0,21666
|
0,3611
|
0,65
|
0,33
|
0,198
|
11,88
|
|
[5;5,6)
|
6
|
5,3
|
0,1
|
0,16666
|
1,26
|
0,18
|
0,108
|
6,48
|
|
[5,6;6,2)
|
2
|
5,9
|
0,03333
|
0,05555
|
1,88
|
0,06
|
0,036
|
2,16
|
|
[6,2;6,8)
|
1
|
6,5
|
0,01666
|
0,02776
|
2,49
|
0,01
|
0,006
|
0,36
|
|
∑
|
60
|
|
0,99997
|
|
|
|
0,966
|
57,96
|

Рис. 1.5.1 Теоретическая и
экспериментальная функция плотности вероятностей
1.6 Проверка гипотезы о
нормальном распределении случайной величины по критерию Пирсона
В теории математической статистики
доказывается, что проверку гипотезы о модели закона распределения по критерию
Пирсона можно делать только в том случае, если выполняются следующие условия: n >50, niT > 5, где i = 1,2, …,k.
Из результатов вычислений,
приведенных в табл. 1.5.1, следует, что необходимое условие для применения
критерия согласия Пирсона не выполнено, так как в некоторых группах niT < 5. Поэтому те
группы вариационного ряда, для которых необходимое условие не выполняется,
объединяют с соседними и уменьшают число групп; при этом частоты объединенных
групп суммируются. Так объединяют все группы с частотами niT < 5 до тех пор, пока
для каждой новой группы не будет выполняться условие: niT > 5.
При уменьшении числа групп ля
теоретических частот соответственно уменьшают и число групп для эмпирических частот.
После объединения групп в формуле для числа степеней свободы v = k - 3, где в качестве k принимают новое число групп,
полученное после объединения частот.
Таблица 1.6.1 Результаты объединения
интервалов и теоретических частот
|
[xi-1;xi)
|
piT
|
niT
|
ni
|
(ni - niT )2
|

|
|
[2;3,2)
|
0,168
|
10,08
|
12
|
3,6864
|
0,36571429
|
|
[3,2;3,8)
|
0,21
|
12,6
|
14
|
1,96
|
0,15555556
|
|
[3,8;4,4)
|
0,24
|
14,4
|
12
|
5,76
|
0,4
|
|
[4,4;5)
|
0,198
|
11,88
|
13
|
1,2544
|
0,10558923
|
|
[5;6,8)
|
0,15
|
9
|
9
|
0
|
0
|
|
|
∑ piT=0,966
|
∑niT=57,96
|
∑ ni=60
|
|
1,02685908
|
При выбранном уровне значимости α = 0,05 и числе групп k = 5 число степеней свободы v = 2, по таблице для α = 0,5 и v = 2 находим:
Х2крит = 5,99147.
Для Х2наб = 1,02685908 , которое
найдем по результатам вычислений, приведенных в табл. 1.6.1, имеем:
Х2наб = 1,02685908 < Х2крит =
5,99147.
Следовательно, выдвинутая гипотеза о
теоретическом законе распределения не противоречит выборке наблюдения при
заданном уровне значимости и нет оснований отвергать гипотезу о нормальном
распределении случайной величины.
2. Расчет аналитических
показателей динамики
.1 Ряды динамики и их
аналитические показатели
Процесс развития, движения
социально-экономических явлений во времени в статистике принято называть
динамикой. Для отображения динамики строят ряды динамики (хронологические,
временные), которые представляют собой ряды изменяющихся во времени значений
статистического показателя, расположенных в хронологическом порядке. В нем
процесс экономического развития изображается в виде совокупности перерывов
непрерывного, позволяющих детально проанализировать особенности развития при
помощи характеристик, отражающих изменение параметров экономической системы во
времени.
Составными элементами ряда динамики
являются показатели уровней ряда и показатели времени (годы, кварталы, месяцы,
сутки) или моменты (даты) времени.
Уровни ряда обычно обозначаются
через «y», моменты или периоды времени, к которым относятся - через «t».
Анализ скорости и интенсивности
развития явления во времени осуществляется с помощью статистических
показателей, которые получаются в результате сравнения уровней между собой. К
таким показателям относятся: абсолютный прирост, темп роста и прироста,
абсолютное значение одного процента прироста. При этом принято сравниваемый
уровень называть отчетным, а уровень, с которым происходит сравнение -
базисным.
Абсолютный прирост (Δу) характеризует размер
увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он
равен разности двух сравниваемых уровней и выражает абсолютную скорость роста:
Δi = уi-yi-k
где i=1,2,3,...,n
Если k=1, то уровень yi-1 является
предыдущим для данного уровня, а абсолютные приросты изменения уровня будут
цепными. Если же k постоянны для данного ряда, то абсолютные приросты будут
базисными.
Интенсивность изменения уровня
оценивается отношением отчетного уровня к базисному, которое всегда
представляет собой положительное число.
Показатель интенсивности изменения
уровня ряда - в зависимости от того, выражается ли он в виде коэффициента или в
процентах, принято называть коэффициентом роста или темпом роста. Иными
словами, коэффициент роста и темп роста представляют собой две формы выражения
интенсивности изменения уровня. Однако необходимо отметить, что ненужно
пользоваться одновременно двумя формами, которые по существу идентичны. Разница
между ними заключается только в единице измерения.
Коэффициент роста показывает во
сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент
больше единицы) или какую часть базисного уровня составляет уровень текущего
периода за некоторый промежуток времени (если он меньше единицы). В качестве
базисного уровня в зависимости от цели исследования может приниматься какой-то
постоянный для всех уровень (часто начальный уровень ряда), либо для каждого
последующего предшествующий ему:
Tрб
= 
 *100 или Трц =
*100 или Трц = 
 *100
*100
В первом случае говорят
о базисных темпах роста, во втором - о цепных темпах роста.
Наряду с темпом роста можно
рассчитать показатель темпа прироста, характеризующий относительную скорость
изменения уровня ряда в единицу времени. Темп прироста показывает, на какую
долю (или процент) уровень данного периода или момента времени больше (или
меньше) базисного уровня.
Темп прироста есть отношение
абсолютного прироста к уровню ряда, принятого за базу:
Tпрц = 
 =
= 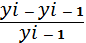
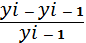 *100 = (Kpi/i-1 -
1)*100 = Tpi/i-1 - 100
*100 = (Kpi/i-1 -
1)*100 = Tpi/i-1 - 100
Если темп роста всегда
положительное число, то темп прироста может быть положительным, отрицательным и
равным нулю.
В статистической
практике часто вместо расчета и анализа темпов роста и прироста рассматривают
абсолютное значение одного процента прироста. Оно представляет собой одну сотую
часть базисного уровня и в то же время - отношение абсолютного прироста к
соответствующему темпу прироста:
|%| = 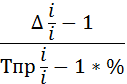
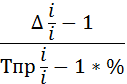 =
= 
 =
= 
 = 0,01*yi-1
= 0,01*yi-1
где |%| - обозначение
абсолютного значения одного процента прироста.
Абсолютное значение
одного процента прироста служит косвенной мерой базисного уровня и вместе с
темпом прироста позволяет рассчитать абсолютный прирост уровня за
рассматриваемый период.
2.2 Пример расчета
показателей динамики
Расчет показателей
динамики в области лесоводства по РФ:
Таблица 2.1
|
год
|
лесовосстановление
|
защита лесов от вредных организмов
|
|
|
биологич. способ
|
хим.способ
|
|
2005
|
812,3
|
511
|
128,3
|
|
2006
|
877,3
|
520,1
|
46,9
|
|
2007
|
872,5
|
419,6
|
14,6
|
|
2008
|
828,4
|
317,3
|
42,1
|
|
2009
|
836,7
|
150,4
|
15,5
|
|
2010
|
811,5
|
226,6
|
49
|
|
2011
|
860
|
161,7
|
13,8
|
Абсолютный прирост (цепной):
Абсолютный прирост (базисный):

 у2006 = 877,3 - 812,3 =
65
у2006 = 877,3 - 812,3 =
65 
 у2006 = 877,3 - 812,3 =
65
у2006 = 877,3 - 812,3 =
65

 у2007 = 872,5 - 877,3 =
-4,8
у2007 = 872,5 - 877,3 =
-4,8 
 у2007 = 872,5 - 812,3 =
60,2
у2007 = 872,5 - 812,3 =
60,2

 у2008 = 828,4 - 872,5 =
-44,1
у2008 = 828,4 - 872,5 =
-44,1 
 у2008 = 828,4 - 812,3 =
16,1
у2008 = 828,4 - 812,3 =
16,1

 у2009 = 836,7 - 828,4 =
8,3
у2009 = 836,7 - 828,4 =
8,3 
 у2009 = 836,7 - 812,3 =
24,4
у2009 = 836,7 - 812,3 =
24,4

 у2010 = 811,5 - 836,7 =
-25,2
у2010 = 811,5 - 836,7 =
-25,2 
 у2010 = 811,5 - 812,3 =
-0,8
у2010 = 811,5 - 812,3 =
-0,8

 у2011 =860 - 811,5 =
48,5
у2011 =860 - 811,5 =
48,5 
 у2011 = 860 - 812,3 =
47,7
у2011 = 860 - 812,3 =
47,7
Коэффициент роста(цепной):
Коэффициент роста(базисный):
Кр2006 = 877,3/812,3 =
1,08 Кр2006 = 877,3/812,3 =1,08
Кр2007 = 872,5/877,3 =
0,99 Кр2007 = 872,5/812,3 =1,07
Кр2008 = 828,4/872,5 =
0,94 Кр2008 = 828,4/812,3 =1,01
Кр2009 = 836,7/828,4 =
1,01 Кр2009 = 836,7/812,3 =1,03
Кр2010 = 811,5/836,7 =
0,96 Кр2010 = 811,5/812,3 =0,99
Кр2011 = 860/811,5 =
1,09 Кр2011 = 860/812,3 =1,05
Темп роста(цепной): Темп
роста(базисный):
Тр2006 = 108% Тр2006 =
108%
Тр2007 = 99% Тр2007 =
107%
Тр2008 = 94% Тр2008 =
101%
Тр2009 = 101% Тр2009 =
103%
Тр2010 = 96% Тр2010 =
99%
Тр2011 = 109% Тр2011 =
105%
Темп прироста(базисный):
Тпр2006 = 65/812,3* 100
= 8%
Тр2007 = 60,2/812,3 *100
= 7,4%
Тр2008 = 16,1/812,3*100
= 1,98%
Тр2009 = 24,4/812,3*100
= 3%
Тр2010 = -0,8/812,3 *100
= -0,09%
Тр2011 = 47,7/812,3*100
= 5,8%
Абсолютное значение
1%-го прироста:
А%2006 = 65/8 = 8,125
А%2010 = -0,8/-0,09 = 8,8
А%2007 = 60,2/7,4 = 8,13
А%2011 = 47,7/5,8 =8,22
А%2008 =16,1/1,98 = 8,13
А%2009 =24,4/3 = 8,1

Рисунок 2.1 Абсолютный прирост

Рисунок 2.2 Коэффициент роста
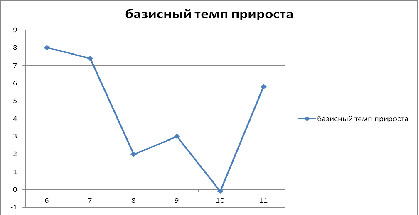
Рисунок 2.3 Темп прироста

Рисунок 2.4 Абсолютное значение 1%
прироста
3. Статистика денежного
обращения
3.1 Понятия денежного
обращения и денежной массы
Сменяя форму стоимости (товар на
деньги, деньги на товар), деньги находятся в постоянном движении между тремя
субъектами: физическими лицами, хозяйствующими субъектами и органами
государственной власти. Движение денег при выполнении ими своих функций в
наличной и безналичной формах представляет собой денежное обращение.
Товарно-денежные отношения требуют
определенного количества денег для обращения.
Закон денежного обращения
устанавливает количество денег, нужное для выполнения ими функций средств
обращения и средства платежа.
Денежный мультипликатор - это
величина множителя (коэффициента), на которую увеличивается количество денег в
обращении в результате операций на монетарном рынке. Коэффициент денежного
мультипликатора означает, во сколько раз возрастает эффективность денежной
базы. Его величина является обратной величиной нормы обязательных резервов, а
также соотношением между объемами наличности и депозитов. Это свидетельствует о
том, что с увеличением резервной нормы или при более высоком соотношении
наличных относительно депозитов величина денежного мультипликатора уменьшаться.
Система показателей статистики
денежного обращения включает: денежный оборот, денежную массу, наличные деньги
внебанковской системы, безналичные средства, скорость обращения денежных
средств, продолжительность одного оборота, купюрное строение денежной массы,
индекс-дефлятор, покупательную способность рубля и др.
Преобладающей частью денежного
оборота является безналичный денежный оборот (деньги выступают только в функции
средств платежа - перечисление денежных средств по счетам кредитных учреждений,
зачет взаимных требований).
В Российской Федерации форма
безналичных расчетов определяется правилами банка России, действующими в
соответствии с законодательством.
Под налично-денежным оборотом
понимают движение наличных денег в сфере обращения и выполнения ими функций
средств платежа и средства обращения. Наличные деньги используются для
кругооборота товаров и услуг, расчетов по выплате заработной платы, премий,
пособий, выплаты страховых возмещений по договорам страхования, при оплате
ценных бумаг и выплат по ним дохода, при платежах населения за коммунальные
услуги.
Налично-денежное движение
осуществляется с помощью различных видов денег: банкнот, металлических монет,
векселей, чеков, кредитных карточек.
Эмиссию наличных денег осуществляет
Центральный банк РФ. Он выпускает и изымает наличные деньги из обращения в
случае их ветхости или производит замену старых купюр на новые (по номиналу).
Таким образом, наличное и
безналичное обращения образуют общий денежный оборот страны, в котором
действуют единые деньги одного наименования и унифицированной нарицательной
стоимости. В процессе денежного оборота постоянно происходит преобразование
наличных денежных потоков в безналичные.
Важнейшим количественным показателем
денежного обращения является денежная масса, представляющая собой совокупный
объем покупательных и платежных средств, обслуживающих хозяйственный оборот и
принадлежащих частным лицам, предприятиям и государству.
Денежная масса - это совокупность
наличных и безналичных покупательных и платежных средств, обеспечивающих
обращение товаров и услуг в народном хозяйстве, которым располагают частные
лица, институциональные собственники и государство. В структуре денежной массы
выделяется активная часть, к которой относятся денежные средства, реально
обслуживающие хозяйственный оборот, и пассивная часть, включающая денежные
накопления, остатки на счетах, которые потенциально могут служить расчетными
средствами.
Таким образом, структура
денежной массы достаточно сложна и не совпадает со стереотипом, который
сложился в сознании рядового потребителя, считающего деньгами прежде всего
наличные средства - денежные знаки (банкноты) и мелкую разменочную монету. На
деле доля банкнот в денежной массе весьма низка (менее 25%), а основная часть
сделок между предпринимателями и организациями, даже в розничной торговле
<#"607548.files/image106.gif">
где ВВП - валовой
внутренний продукт в текущих ценах (ВВП = ∑p1q1);
М2 - совокупный объем
денежной массы в изучаемом периоде, определяемой как средние остатки денег за
период.
Этот показатель
характеризует скорость оборота денежной массы, т.е. сколько в среднем за год
оборотов совершила денежная масса (прямая характеристика оборачиваемости
денег). Иначе говоря, он показывает, сколько раз за год использовался рубль для
получения товаров и услуг.
.Продолжительность
одного оборота денежной массы рассчитывается по формуле:
t
= M2 : 

где Д - число
календарных дней в периоде.
Показателем, с помощью
которого можно измерить запас денежной массы на 1 руб. ВВП (%), является
показатель монетаризации экономики (Мэ ), который исчисляется как отношение
совокупного объема денежной массы в изучаемом периоде (М2 ) к величине валового
внутреннего продукта в текущих ценах (ВВП):

В развитых странах Мэ =
60-80% считается нормой.
Таблица 3.3
|
Год
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
|
Валовой внутренний продукт, млрд. руб.
|
33410,5
|
36134,6
|
39218,7
|
41276,8
|
38048,6
|
39699,9
|
41421,0
|
|
Денежная масса М2, млрд. руб.
|
4353,9
|
6032,1
|
8970,7
|
12869
|
12975,9
|
15267,6
|
20011,9
|
)Количество оборотов денег за год:
V
= 

В 2005 г.: V0 = 
 = 7,67
= 7,67
В 2006 г.: V1 = 
 = 5,99
= 5,99
В 2007 г.: V2 = 
 = 4,37
= 4,37
В 2008 г.: V3 = 
 = 3,20
= 3,20
В 2009 г.: V4 = 
 = 2,93
= 2,93
В 2010 г.: V5 = 
 = 2,60
= 2,60
В 2011 г.: V6 = 
 = 2,06
= 2,06
)Продолжительность
одного оборота в днях:
В 2005 г.: t0 = 
 = 47
= 47
В 2006 г.: t1 = 
 = 60
= 60
В 2007 г.: t2 = 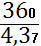
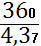 = 82,3
= 82,3
В 2008 г.: t3 = 
 = 112,5
= 112,5
В 2009 г.: t4 = 
 = 123
= 123
В 2010 г.: t5 = 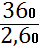
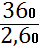 = 138,4
= 138,4
В 2011 г.: t6 = 
 = 175.
= 175.
)Монетаризация
экономики:
Мэ = 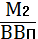
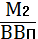 * 100%
* 100%
В 2005 г.: М0 = 
 * 100% = 13%
* 100% = 13%
В 2006 г.: М1 = 
 * 100% = 16,6%
* 100% = 16,6%
В 2007 г.: М2 = 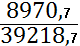
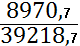 * 100% = 22,8%
* 100% = 22,8%
В 2008 г.: М3 = 
 * 100% = 31,1%
* 100% = 31,1%
В 2009 г.: М4 = 
 * 100% = 34,1%
* 100% = 34,1%
В 2010 г.: М5 = 
 * 100%= 38,4%
* 100%= 38,4%
В 2011 г.: М6 = 
 * 100% = 48,3%
* 100% = 48,3%
Заключение
В результате проведенной
работы, мной были усвоены основные навыки анализа рядов динамики, а так же,
рассмотрена статистика денежной системы и России, в частности.
Работа имеет высокую
актуальность, так как в ней использовались данные за ближайшие годы, а
содержащийся анализ по основным параметрам денежного обращения может иметь
широкое практическое применение.
Список литературы
статистика динамика
распределение денежный
1. Гусаров В.М. Статистика: учеб. пособие для вузов. - М.:
ЮНИТИ-ДАНА, 2008. - 463 с.
.Елисеева И.И., Юзбашев М.М Общая теория статистики: Учебник - 5-е
изд., перераб. И доп. - М.: Финансы и статистика, 2004. - 656 с.
. В.Г. Минашкин, Р.А. Шмойлова, Н.А. Садовникова, Л.Г. Моисейкина,
Е.С. Рыбакова Теория статистики: Учебно-методический комплекс. - М.: Изд. центр
ЕАОИ, 2008. - 296 с.
. Поляк Г.Б. Финансы. Денежное обращение. Кредит: учебник. - М.:
ЮНИТИ-ДАНА, 2007. - 512 с.
. Статистика: учеб. / И.И. Елисеева [и др.]; под ред. И.И.
Елисеевой. - М.: Проспект, 2010. - 448 с.
.Теория статистики: Учебник/Под ред. Р.А. Шмойловой. - 3-е изд.,
перераб. - М.: Финансы и статистика, 2001. - 560 с.
. Статистика: учебник для студ. сред. проф. учеб. заведений/[ В.С.
Мхитарян, Т.А. Дуброва, В.Г. Минашкин и др.]; под ред. В.С. Мхитаряна. - 4-е
изд., стер. - М.: Издательский центр “Академия”, 2006. - 272 с.