Комбинаторные алгоритмы. Поиск кратчайшего пути на графе
ФГБОУ ВПО
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ
Курсовой
проект
«Комбинаторные
алгоритмы. Поиск кратчайшего пути на графе.»
Дисциплина:
«Структуры и алгоритмы компьютерной обработки данных »
Москва 2013
Содержание
Задача о ходе коня
Методы
решения
Описание
алгоритмов
Итеративная
программа
Рекурсивная
программа
Генерация перестановок из n элементов
Постановка
задачи
Методы
решения и описание алгоритмов
Построение эйлерова цикла на графе
Постановка
задачи
Методы
решения и описания алгоритма
Поиск кратчайшего пути на графе
Постановка
задачи
Описание
задачи
Программная
реализация
Используемая литература
Приложение
Задача о ходе коня
Постановка задачи. Дана доска nxn. Конь, который ходит согласно шахматным правилам,
помещается на поле с начальными координатами x0, y0.
Нужно покрыть всю доску ходами коня, т.е. вычислить обход доски, если он
существует, такой, что каждое поле посещается ровно один раз.
Методы решения
Метод Эйлера
Метод Эйлера состоит в том, что сначала конь двигается по произвольному
маршруту, пока не исчерпает все возможные ходы. Затем оставшиеся не пройденными
клетки добавляются в сделанный маршрут, после специальной перестановки его
элементов.
Метод Вандермонда
Вандермонд попытался свести задачу к арифметической. Для этого он
обозначал маршрут коня по доске в виде последовательности дробей x/y , где x и y - координаты поля на доске. Очевидно, что в
последовательности дробей, соответствующей ходам коня, разность числителей двух
соседних дробей может быть только 1 или 2, при том, что разность их
знаменателей составляет соответственно 2 или 1. Кроме того, числитель и
знаменатель не могут быть меньше 1 и больше 8.
Его метод нахождения подходящей последовательности аналогичен методу Эйлера,
но позволяет находить маршруты коня только для досок чётной размерности.
Правило Варнсдорфа
Правило Варнсдорфа, являющееся разновидностью жадного алгоритма для
отыскания маршрута коня, формулируется так: При обходе доски конь следует на то
поле, с которого можно пойти на минимальное число ещё не пройденных полей. Если
таких полей несколько, то можно пойти на любое из них. Долгое время считалось,
что правило Варнсдорфа работает безукоризненно. Позднее с помощью компьютеров
была установлена неточность во второй его части: если существует несколько
подходящих полей, то не все они равноценны, и произвольный выбор поля может
завести коня в тупик. На практике однако вероятность попадания в тупик невелика
даже при вольном пользовании второй частью правила Варнсдорфа.
Со времен Эйлера известен так называемый "раздельный ход коня";
который заключается в нахождении пути по одной половине доски, его симметричном
дублировании и соединении обеих путей вместе(рис.1) .
Многие решения опираются на создание симметричного маршрута, пример
одного из них на рисунке 2.
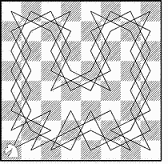
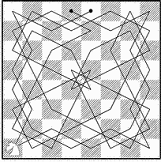
Если говорить о графиках маршрутов коня, то здесь придумано множество
необычных решений, изображающих различные предметы, буквы или знаки (известен
даже график, посвященный Наполеону). Два достопримечательных примера такого
рода приведены ниже. График одного маршрута (он является замкнутым) напоминает
собой вазу, а график другого подобен цветку, части которого расположены в высшей
степени симметрично( см. рис.3 и 4)
Описание алгоритмов
Данная задача из области «искусственного интеллекта». Здесь нужно строить
алгоритмы, которые находят решение задачи не по фиксированным правилам
вычисления, а методом проб и ошибок. Процесс проб и ошибок можно рассматривать
в общем виде как поисковый процесс, который постепенно строит и просматривает
(а так же обрезает) дерево подазадач. Во многих случаях такие деревья поиска
растут очень быстро, обычно экспоненциально, в зависимости от заданного
параметра. Так как мы хотим сохранять историю последовательного «захвата»
доски, то мы будем представлять каждое поле доски целым числом, по которому
можно судить посещалось ли поле и на каком ходу.
Итеративная программа
Полный перебор
Идея алгоритма для итеративной программы заключается в следующем:
· на каждом шаге ищется фрагмент пути, начинающийся из текущей
клетки и не включающий уже пройденные;
· при совершении хода из массива возможных ходов извлекается
очередной элемент, который приводит в незанятую клетку, находящуюся в пределах
доски;
· если ход невозможен, то происходит возврат в предыдущую
клетку (отмена хода);
· поиск пути считается успешным тогда, когда номер текущего
хода станет равным количеству клеток на доске. Если из начальной клетки
перебраны все возможные ходы, то пути не существует.
Ниже приведена структура функции, выполняющей перебор:
void find_path()
{( move_num = 1 ; move_num <= max_moves ; )
{( make_move() ) // Сделать
ход.
move_num++ ;// Ход невозможен.
if( move_num > 1 )
{_move() ; // Отменить ход._num-- ;
}; // Обход невозможен.
}
}
Номер использованного варианта хода для каждого из ходов запоминается в
массиве, размер которого выбирается в соответствии с размером доски.
Описанный алгоритм осуществляет перебор вариантов и находит решение, если
оно имеется. Отсутствие решения приводит к полному перебору всех вариантов.
Оценить сложность данного алгоритма трудно. Для некоторых клеток
программа работает чрезвычайно медленно уже при небольших размерах доски.
Например, для доски 6 * 6 при старте из клетки (5,2) поиск пути требует более
290 миллионов возвратов.
Рекурсивная программа
Наиболее известное решение для задачи обхода конем - рекурсивное . При
этом структура функции, выполняющей перебор, имеет следующий вид:
int find_path( int cur_x, int cur_y, int move_num )
{_state[cur_x][cur_y] = move_num ; // Запомнить ход.( move_num
> max_moves ) return
1 ; // Проверить завершение обхода.
// Проверить каждый возможный ход из текущей клетки.
for( int i = 0 ; i < 8 ; i++ )
{next_x = cur_x + possible_moves[i][0] ; // Определить
следующее поле.next_y = cur_y + possible_moves[i][1] ;( (move_possible( next_x,
next_y ) && find_path( next_x, next_y, move_num+1 )) return 1 ;
}
// Возврат._state[cur_x][cur_y] = 0 ;_ret++ ;
return
0 ;
}
Оптимизированный алгоритм
. Определение клеток, обход из которых невозможен
Если количество клеток доски нечетно (число белых и черных клеток
отличается на единицу), то обход из некоторых клеток не существует. Отметим,
что путь коня проходит по клеткам, чередующимся по цвету. Если общее число
клеток доски нечетно, то первая и последняя клетки пути, пройденного конем,
будут одного и того же цвета. Таким образом, обход будет существовать только
тогда, когда он начнется клеткой того цвета, который имеют наибольшее число
клеток.
Выполнение этого условия проверяется следующей функцией:
solution_impossible()
{
// Если произведение сторон доски нечетно и сумма координат начальной
позиции
return ((size_x*size_y) % 2 != 0) && ((start_x+start_y) % 2 != 0) ;
}
Однако приведенное правило не охватывает всех клеток, для которых обхода
не существует. Так, для доски размером 3*7, помимо тех клеток, для которых выполняется
приведенное правило, обход невозможен также из клетки (2,4).
. Выявление заблокированных клеток
Если при очередном ходе образуется клетка, куда можно войти, но откуда
нельзя выйти, то такой ход недопустим, за исключением предпоследнего в обходе.
Данный метод оптимизации позволяет значительно сократить число возвратов, в том
числе и при совместном использовании с правилом Варнсдорфа.
Развитием этого метода является определение групп заблокированных клеток,
связанных друг с другом, но отрезанных от остальной части доски. В
рассматриваемой программе определяются группы из двух заблокированных клеток,
что значительно уменьшает количество возвратов для небольших досок, а при
использовании вместе с правилом Варнсдорфа - и для больших (например, размером
100*100 клеток).
. Применение правила Варнсдорфа
Среди многих эвристических методов , используемых для сокращения
перебора, правило Варнсдорфа является наиболее простым. В соответствии с ним
при обходе доски коня следует каждый раз ставить на то поле, из которого он
может сделать наименьшее число ходов по еще не пройденным полям. Если таких
полей несколько, то можно выбрать любое из них, что может, однако, завести коня
в тупик и потребовать возврата . Отметим, что наилучшим образом правило
Варнсдорфа работает для угловых полей.
. Использование различных массивов ходов коня
Ходы коня могут быть заданы, например, в виде следующего
массива:possible_moves_sh[][2] = {
{-1, -2}, {-2, -1}, {-2, 1}, { 1, -2},
{-1, 2}, { 2, -1}, { 1, 2}, { 2, 1} };
Каждый его элемент определяет один возможный ход коня и содержит
изменения его координат на доске при совершении хода.
В написанной программе используется массив ходов и правило Варнсдорфа.
Программа находится в приложении.
Генерация перестановок из n
элементов
Постановка задачи
Дано число n, n > 1. Получить все перестановки элементов множества {1,
2, ..., n}.
Перестановка- это упорядоченный набор чисел 1, 2, ..., n , которая числу
i ставит соответствие i-й элемент из набора. Число n при этом называется
порядком перестановки.
Перестановка - это упорядоченный набор элементов. Это означает, что
порядок элементов в наборе имеет значение. И две перестановки, состоящие из
одних элементов, расположенных в разном порядке различными.
Методы решения и описание алгоритмов
Количество различных перестановок множества, состоящего из n элементов
равно n!. В этом нетрудно убедиться: на первом месте в перестановке может
стоять любой из n элементов множества, после того, как мы на первом месте
зафиксировали какой-либо элемент, на втором месте может стоять любой из n - 1
оставшегося элемента и т.д. Таким образом, общее количество вариантов равно n(n
- 1)(n - 2)...3*2*1 = n!
итеративный
рекурсивный программный граф
Генерация всех перестановок по индексам
Алгоритм заключается в поиске n-факториального представления числа i и восстановлению перестановки по найденному представлению.
Мы не будем рассматривать его подробно, так как время работы данного алгоритма
есть O(nn!), что не является оптимальным, как в случае следующих
алгоритмов.
Циклический сдвиг
Циклический сдвиг заключается в последовательном сдвиге по циклу на один
разряд всех n элементов. При завершении круга,
т.е. возвращении к исходной перестановке, осуществляется сдвиг первых n-1 элементов, далее, если и этот шаг
возвращает нас к уже полученной перестановке, сдвигаем на один разряд первые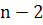 
элементов и т.д.
Алгоритм генерации перестановок в антилексикографическом порядке
Алгоритм для генерации перестановок в антилексикографическом порядке
может базироваться на двух утверждениях:
. Если множество перестановок P упорядочено антилексикографически,
то начальная и конечная перестановки - это соответственно (1, 2, …, n) и (n,
n-1,…,1).
. Упорядоченная антилексикографически последовательность
перестановок по значению последнего элемента в них может быть разбита на n
блоков длины (n-1)!. При этом q-й блок на последнем месте имеет элемент, равный
(n-q+1), а первые n-1 позиций этого блока определяют последовательность
перестановок множества {1,2,…,n}\{q} в антилексикографическом порядке.
Алгоритм генерации перестановок в лексикографическом порядке:
При генерации перестановок в лексикографическом порядке, начиная с
тождественной перестановки (1,2,..,n), требуется переходить от уже построенное перестановки a=(a1,…an) к
непосредственно следующей за ней перестановкой b=(b1,..bn) до тех пор, пока не получим
наибольшую перестановку (n,n-1…,1)(относительно
лексикографического порядка).
Рассмотрим способ построения такой перестановки b.Просматриваем справа налево перестановку a=(a1,…an) в
поисках самой правой позиции i
такой, что ai<ai+1.Если такой позиции нет, то a1>a2>...>an,т.е. a=(n,n-1,…,1) и генерировать больше нечего.
Поэтому считаем, что такая позиция i есть. Значит , ai<ai+1>ai+2>…>an. Далее ищем первую позицию j при переходе от позиции n к позиции i такую, что ai<aj. Тогда i<j.
Затем меняем местами элементы ai и aj, а в полученной перестановке a,=(a`1,…,a`n)отрезок a`1,…,a`n-1, a`n переворачиваем.
Построенную перестановку обозначим через b. Например, пусть a=(2,6,5,8,7,4,3,1). Тогда ai=5 и aj=7. Поменяем местами эти элементы,
повернем отрезок (8,5,4,3,1) и получим перестановку b=(2,6,7,1,3,4,5,8).
Сложность такого алгоритма - O(n!).
Программа, демонстрирующая генерации перестановок в лексикографическом
порядке представлена в приложении.
Построение эйлерова цикла на графе
Постановка задачи
Необходимо найти эйлеров цикл на графе.
Эйлеровым циклом называется замкнутый маршрут, в котором каждое ребро
графа встречается точно один раз. Для существования такого маршрута в связном
графе необходимо и достаточно, чтобы степени всех вершин были четными.
Методы решения и описания алгоритма
Алгоритм Флери
Один из алгоритмов поиска эйлерова цикла. Он заключается в следующем:
выходим из произвольной вершины графа, соблюдая два правила:
•все рёбра, по которым мы проходим, стираются, так же как и появившиеся в
результате изолированные вершины;
•на каждом шаге идём по мосту только тогда, когда нет других возможностей
(мост - это такое ребро графа, при стирании которого граф становится
несвязным).
Другой алгоритм похож на алгоритм поиска в глубину: начиная с произвольно
выбранной стартовой вершины a,
строим путь, выбирая каждый раз для дальнейшего продвижения еще не пройденное
ребро. Главное отличие от поиска в глубину состоит в том, что как пройденные
помечаются именно ребра, а не вершины. Поэтому одна и та же вершина может
посещаться несколько раз, но каждое ребро проходится не более одного раза, так
что в полученном маршруте ребра не будут повторяться. Вершины пути накапливаются
в стеке S. Через некоторое количество шагов
неизбежно наступит тупик - все ребра, инцидентные активной (последней
посещенной) вершине x, уже пройдены.
Так как степени всех вершин графа четны, в этот момент x=a и пройденные
ребра образуют цикл, но он может включать не все ребра графа. Для обнаружения
еще не пройденных ребер возвращаемся по пройденному пути, перекладывая вершины
из стека S в другой стек C , пока не встретим вершину x , которой инцидентно непройденное
ребро. Так как граф связен, такая вершина обязательно встретится. Тогда
возобновляем движение вперед по не пройденным ребрам, пока не дойдем до нового
тупика и т.д. Процесс заканчивается, когда в очередном тупике обнаруживается,
что S пуст. В этот момент в стеке C находится последовательность вершин
эйлерова цикла.
Алгоритм построения эйлерова цикла:
. выбрать произвольно вершину a
2. aàS
. while S=! 0 do
4. x=top(S)
. if имеется непройденное ребро (x,y)
. then пометить ребро (x,y) как пройденное
7. yàS
. else переместить вершину x из S в C
Программа представлена в приложении.
Поиск кратчайшего пути на графе
Кратчайший путь рассматривается при помощи математического объекта,
называемого графом.
Существуют три наиболее эффективных алгоритма нахождения кратчайшего
пути:
) Алгоритм Дейкстры;
) Алгоритм Флойда - Уоршелла;
) Алгоритм Беллмана - Форда.
Принцип работы некоторых из указанных алгоритмов будет рассмотрен в
рамках данной работы.
Постановка задачи
Задачей является программная реализация алгоритма поиска кратчайшего пути
между двумя любыми вершинами графа.
Пользователь вводит количество вершин и длины рёбер графа, а после
обработки этих данных на экран выводится кратчайший путь между двумя ранее
заданными вершинами и его длина.
Описание задачи
Алгоритм Дейкстры
Данный алгоритм был изобретён нидерландским ученым Э. Дейкстрой в 1959
году.
Каждой вершине сопоставим метку - минимальное известное расстояние от
этой вершины до начальной, с которой мы начинаем поиск кратчайшего пути.
Алгоритм работает пошагово - на каждом шаге он посещает одну вершину и пытается
уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
Инициализация. Метка начальной вершины полагается равной 0, метки
остальных вершин - бесконечности. Это отражает то, что расстояния от начальной
до других вершин пока неизвестны. Все вершины графа помечаются как
непосещённые.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В
противном случае, из ещё не посещённых вершин выбирается вершина, имеющая
минимальную метку. Обозначим её за U. Мы рассматриваем всевозможные маршруты, в которых U является предпоследним пунктом.
Вершины, в которые ведут рёбра из U, назовем соседями этой вершины. Для каждого соседа вершины U, кроме отмеченных как посещённые,
рассмотрим новую длину пути, равную сумме значений текущей метки U и длины ребра, соединяющего U с этим соседом. Если полученное
значение длины меньше значения метки соседа, заменим значение метки полученным
значением длины. Рассмотрев всех соседей, пометим вершину U как посещенную и повторим шаг
алгоритма.
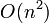
Сложность алгоритма в простейшем случае, когда для поиска вершины с
минимальным d[v] просматривается все множество вершин, время работы алгоритма
есть
Алгоритм Флойда - Уоршелла
Предложен независимо Ричардом Беллманом и Лестером Фордом.
За время O(|V| × |E|) алгоритм находит кратчайшие пути от
одной вершины графа до всех остальных. В отличие от алгоритма Дейкстры,
алгоритм Беллмана-Форда допускает рёбра с отрицательным весом.
Программная реализация
В рамках данной работы мною реализован алгоритм Дейкстры. Проведем
машинный эксперимент. Запустим программу, после чего введем количество вершин.
Далее, поочередно будем вводить длину пути или «цену» между указанными
вершинами. Если вершины не соединены между собой напрямую, то необходимо ввести
ноль. После окончания ввода программа построит матрицу смежности и предложит
ввести начальную и конечную координату.
Далее, введем начальную и конечную вершины, после чего программа найдет
кратчайший путь и выведет его на экран. Результат получен.
Используемая литература
• Алгоритмы+структуры
данных=программы. Вирт Н. - М.: Мир, 1989.
• ru.wikipedia.org
• Комбинаторные
алгоритмы: Учебное пособие. Т.И. Федоряева, Новосиб.гос.ун-т. Новосибирск, 2011
• Комбинаторика
для программистов / Липский В. - М.: Мир, 1988.
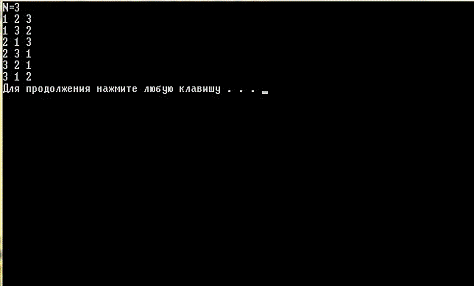
Приложение 2. Генерация перестановок из n элементов
Программа
#include "stdafx.h"
#include <iostream>namespace std;X[100];N;Swap(int
a,int b)
{t=X[a];[a]=X[b];[b]=t;
}Generate(int k)
{(k==N)
{(int i=0;i<N;i++)<<X[i]<<"
";<<"\n";
}
{(int j=k;j<N;j++)
{(k,j);(k+1);(k,j);
}
}
}_tmain(int argc, _TCHAR* argv[])
{<<"N=";>>N;(int
i=0;i<N;i++)[i]=i+1;(0);<<"Press any button";.get();
return 0;
}
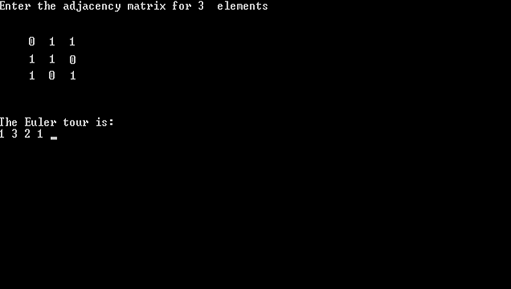
Приложение 3. Построение эйлерова цикла на графе
#include "stdafx.h"
#include <stack>
#include <iostream>namespace std;main()
{<int> stackArray;
int N=3;<<"Enter the adjacency matrix for 3
elements"<<'\n';vertexArray[N]; // массив вершинadjacencyArray[N][N]; // матрица смежности(int i=0; i<N; i++)
{k=0;(int j=0; j<N; j++)
{>>adjacencyArray[i][j];(adjacencyArray[i][j]!=0) k++;
}[i]=k;
}(int i=0; i<N; i++)(vertexArray[i]%2!=0)
{<<"There is no Euler tour."; // Если кол-во единиц нечетно - пути Эйлера
нет
return 0;
}<<"The Euler tour is:"<<'\n'; // Если четно - путь
есть, выводим на экран сам путь.push(0); // Принцип работы стека - последний
зашел - первый вышел
while (!stackArray.empty())
{topOfStack=stackArray.top();(vertexArray[topOfStack]==0)
{.pop();<<topOfStack+1<<" "; // Выводим
на экран
}
else
{i=0; while (adjacencyArray[topOfStack][i]==0)
i++;.push(i);[topOfStack][i]=adjacencyArray[i][topOfStack]=0;[topOfStack]--;
vertexArray[i]--;
}
}ab;::cin >> ab;
return 0;
}
Приложение 4. Поиск кратчайшего пути на графе. Алгоритм
Дейкстры
Исходный код программы на языке программирования C++
#include "StdAfx.h"
#include <iostream>namespace std;i, j, n, num,
start_pos, end_pos;infinity =
99999;visit[15];matrix[15][15];lenght[15];s[100];path[100][15];_tmain()
{(LC_ALL,"Russian");<<"Введите количество вершин: ";
cin>>n;
cout<<"\n";(i=0;i<n;i++)(j=0;j<n;j++)
matrix[i][j]=0;(i=0;i<n;i++)(j=i+1;j<n;j++)
{<<"Расстояние от "<<i+1<<" до
"<<j+1<<": ";
cin>>matrix[i][j];
}<<"\n\n ";(i=0;i<n;i++)
cout<<"
X"<<i+1;<<endl<<endl;<<"\n";(i=0;i<n;i++)
{("X%d",i+1);(j=0;j<n;j++)
{("%6d",matrix[i][j]);[j][i]=matrix[i][j];
}("\n\n");
}(i=0;i<n;i++)(j=0;j<n;j++)(matrix[i][j]==0)
matrix[i][j]=infinity;
cout<<"\n";(;;)
{<<"Введите начальную вершину: ";
cin>>start_pos;(start_pos<1 || start_pos>n)
{.clear();(stdin);<<"Некорректный ввод. Введите
номер вершины в интервале от 1 до "<<n<<"\n";
}break;
}_pos--;(;;)
{<<"Введите конечную вершину: ";>>end_pos;
if(end_pos<1 || end_pos>n)
{.clear();(stdin);<<"Некорректный ввод. Введите
номер вершины в интервале от 1 до "<<n<<"\n";
}break;
}_pos--;<<"\n";(start_pos==end_pos)
{<<"Начальная и конечная точка совпадают\n"<<endl;
return;
{[i]=0;[i]=infinity;
}[start_pos]=0;[start_pos]=1;=start_pos;(start_pos+1,s,10);(i=1;i<=n;i++)
{(path[i],"X");(path[i],s);
}
{(i=0;i<n;i++)((matrix[num][i]!=infinity)&&(!visit[i])&&(i!=num))
{(lenght[i]>lenght[num]+matrix[num][i])
{(i+1,s,10);(path[i+1],path[num+1]);(path[i+1],"-X");(path[i+1],s);
}(lenght[i]>lenght[num]+matrix[num][i]) {[i] =
lenght[num]+matrix[num][i];
}
}(i=0;i<n;i++)(!(visit[i]))
num=i;(i=0;i<n;i++)((lenght[num]>lenght[i])&&(!visit[i]))
num=i;[num]=1;
}(num!=end_pos);(lenght[num]!=infinity)
{<<"Путь: "<<path[num+1]<<endl;<<"Длина пути:
"<<lenght[num]<<endl<<endl;
}<<"Такого пути не существует"<<endl<<endl;
}