Использование алгоритма муравья для решения задачи коммивояжера
Содержание
Введение
. Специальная часть
.1 Постановка задачи и анализ исходных данных
.2 Обзор известных алгоритмов для решения поставленной задачи
.2.1 Алгоритм А*
.2.2 Метод ветвей и границ
.2.3 Метод ближайшего соседа
.2.4 Алгоритм поиска в глубину (ширину)
.2.5 Алгоритм Дейкстры
.2.6 Алгоритм Джонсона
.2.7 Алгоритм муравья.
.3 Алгоритм муравья, основные понятия.
.3.1 Биологические основы
.3.2 Начальная популяция
.3.3 Движение муравья
.3.4 Пример итерации
.3.5 Разновидности алгоритма муравья
.4 Построение алгоритма движения муравья и моделирование
этого алгоритма на ЭВМ
.4.1 Ограничения, накладываемые на агента в стандартной
постановке задачи коммивояжера
.4.2 Алгоритм обхода препятствий
.4.3 Пример работы алгоритма обхода препятствий
.4.4 Структура данных алгоритма муравья
.4.5 Использование графа видимости в алгоритме муравья
.4.6 Моделирование алгоритма муравья на ЭВМ
.5 Анализ полученных результатов
. Экономическая часть
.1 Определение целесообразности разработки алгоритма
.2 Определение трудоемкости разработки алгоритма и ПП.
.3 Календарное планирование
.4 Расчет заработной платы основного персонала
.5 Определение затрат на создание алгоритмов и ПП
.6 Расчет экономической эффективности
.7 Выводы
. Охрана труда и окружающей среды
.1 Введение
.2 Санитарно-гигиенические факторы
.2.1 Микроклимат
.2.2 Освещение
.2.3 Электробезопасность
.2.4 Шум
.2.5 Вибрация
.2.6 Электромагнитные излучения (ЭМИ)
.2 Эргономика рабочего места
.3 Психофизиологические факторы
.4 Расчет освещенности
Выводы
Заключение
Список использованной литературы
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Введение
В данной дипломной работе рассматривается использование алгоритма муравья
для решения задачи коммивояжера.
В основу алгоритма муравья положена имитация жизнедеятельности муравьиных
колоний. При этом колония рассматривается как многоагентная система, в которой
каждый агент (муравей) действует автономно по определенным правилам. Поскольку
в основе алгоритма лежит моделирование передвижения муравьев по различным
путям, такой подход может стать эффективным способом поиска рациональных
решений для задач оптимизации, допускающих графовую интерпретацию.
Задача коммивояжера - traveling salesman problem (TSP) - является
NP-сложной задачей дискретной оптимизации. Для нее еще не найдено и возможно не
существует быстрых полиномиальных алгоритмов. В общем виде на графах задача
формулируется следующим образом: необходимо найти минимальный маршрут,
проходящий через указанные узлы графа хотя бы по одному разу с последующим
возвратом в исходный узел.
В настоящее время задача коммивояжера находит много практических
применений в таких областях как:
- Оптимизация в сетях
- Оптимизация маршрутов
- Приложения в кристаллографии
- Управление роботами
- Обработка печатных плат
- Исследование ДНК
Городами в различных задачах могут выступать как физические объекты, так
и процессы, и другие сущности.
В частности, задача коммивояжера практически без изменений может
применяться для составления маршрута облета местности летательным аппаратом.
Таким образом, поиск точных и приближенных способов решения задачи
коммивояжера остается актуальным и с теоретической и с практической точек
зрения.
На практике при облете местности могут появиться условные препятствия,
которые располагаются на пути облета точек маршрута летательным аппаратом.
Такими условными препятствиями могут оказаться объекты, над которыми запрещен
полет, например населенные пункты, лесистая местность, задымленная местность,
любые опасные участки. В данной дипломной работе рассмотрена задача построения
минимального маршрута при условии наличия препятствий.
Научная новизна
Для достижения поставленных целей решены следующие задачи:
. Разработан алгоритм обхода препятствий, позволяющий строить
возможные маршруты, не пересекающие границы препятствий.
. Разработанный алгоритм обхода препятствий применен к алгоритму
муравья для решения задачи коммивояжера.
1. Специальная часть
.1 Постановка
задачи и анализ исходных данных
В данной дипломной работе рассматривается использование алгоритма муравья
для решения задачи коммивояжера.
Существует замкнутый и незамкнутый варианты задачи коммивояжера. В
замкнутом варианте задачи коммивояжера требуется посетить все вершины графа,
после чего вернуться в исходную вершину. Незамкнутый вариант отличается от
замкнутого тем, что в нём не требуется возвращаться в стартовую вершину. В
данной работе решается незамкнутый вариант задачи коммивояжера.
Обычно, в целях упрощения задачи и гарантии существования маршрута в
задаче коммивояжера считается, что граф, описывающий задачу, является полностью
связным, то есть, что между произвольной парой вершин существует ребро. В
данной дипломной работе это упрощение опущено, граф, описывающий задачу, имеет
ограничения, т.е. существуют не все ребра графа.
По условию задачи на пути условных точек маршрута расположено три
препятствия. Препятствия представляют собой геометрические фигуры: треугольник,
прямоугольник и восьмиугольник. Вершины препятствий являются узлами графа.
Координаты вершин препятствий и точек маршрута (в дальнейшем - городов)
заданы дипломным руководителем. Количество городов меняется от 5 до 25 с шагом
5.
Целью дипломной работы является решение задачи коммивояжера и построение
минимального маршрута при заданной конфигурации препятствий и городов с помощью
алгоритма муравья. Маршрут не должен пересекать границы препятствий, но может
проходить по их границам.
1.2 Обзор известных алгоритмов для решения поставленной задачи
.2.1 Алгоритм
А*
Поиск A* - алгоритм поиска по первому наилучшему совпадению на графе,
который находит маршрут с наименьшей стоимостью от одной вершины (начальной) к
другой (целевой, конечной).
Порядок обхода вершин определяется эвристической функцией «расстояние +
стоимость» (обычно обозначаемой как f(x). Эта функция - сумма двух других:
функции стоимости достижения рассматриваемой вершины (x) из начальной (обычно
обозначается как g(x) и может быть как эвристической, так и нет) и
эвристической оценки расстояния от рассматриваемой вершины к конечной
(обозначается как h(x)).
Функция h(x) должна быть допустимой эвристической оценкой, то есть не
должна переоценивать расстояния к целевой вершине. Например, для задачи
маршрутизации h(x) может представлять собой расстояние до цели по прямой линии,
так как это физически наименьшее возможное расстояние между двумя точками.
Описание алгоритма* пошагово просматривает все пути, ведущие от начальной
вершины в конечную, пока не найдёт минимальный. Как и все информированные
алгоритмы поиска, он просматривает сначала те маршруты, которые «кажутся»
ведущими к цели. От жадного алгоритма (который тоже является алгоритмом поиска
по первому лучшему совпадению) его отличает то, что при выборе вершины он
учитывает, помимо прочего, весь пройденный до неё путь (составляющая g(x) - это
стоимость пути от начальной вершины, а не от предыдущей, как в жадном
алгоритме).
В начале работы просматриваются узлы, смежные с начальным; выбирается тот
из них, который имеет минимальное значение f(x), после чего этот узел
раскрывается. На каждом этапе алгоритм оперирует с множеством путей из
начальной точки до всех ещё не раскрытых (листовых) вершин графа («множеством
частных решений»), которое размещается в очереди с приоритетом. Приоритет пути
определяется по значению f(x) = g(x) + h(x). Алгоритм продолжает свою работу до
тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое
значение в очереди (либо пока всё дерево не будет просмотрено). Из
множественных решений выбирается решение с наименьшей стоимостью.
Множество уже пройденных вершин можно опустить (при этом алгоритм
превратится в поиск по дереву решений), если известно, что решение существует,
либо если алгоритм поиска оптимального маршрута умеет отсекать циклы.
Свойства
Алгоритм А* всегда находит решение, если таковое существует.
Если эвристическая функция h допустима, то есть никогда не переоценивает
действительную минимальную стоимость достижения цели, то A* сам является
допустимым (или оптимальным), также при условии, что мы не отсекаем пройденные
вершины. Если же мы это делаем, то для оптимальности алгоритма требуется, чтобы
h(x) была ещё и монотонной, или преемственной эвристикой. Свойство монотонности
означает, что если существуют пути A-B-C и A-C (не обязательно через B), то
оценка стоимости пути от A до C должна быть меньше, либо равна сумме оценок
путей A-B и B-C. (Монотонность также известна как неравенство треугольника:
одна сторона треугольника не может быть длиннее, чем сумма двух других сторон.)
Математически, для всех путей x, y (где y - потомок x) выполняется:
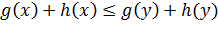 (1)
(1)
* также оптимально эффективен для заданной эвристики h. Это значит, что
любой другой алгоритм исследует не меньше узлов, чем A* (за исключением
случаев, когда существует несколько частных решений с одинаковой эвристикой,
точно соответствующей стоимости оптимального пути).
Частные случаи
В общем случае, поиск в глубину и поиск в ширину являются двумя частными
случаями алгоритма A*. Для поиска в глубину возьмём глобальную
переменную-счётчик, инициализировав её неким большим значением. Всякий раз при
раскрытии вершины будем присваивать значение счётчика смежным вершинам,
уменьшая его на единицу после каждого присваивания. Таким образом, чем раньше
будет открыта вершина, тем большее значение h(x) она получит, а значит, будет
просмотрена в последнюю очередь. Если положить h(x) = 0 для всех вершин, то мы
получим ещё один специальный случай - алгоритм Дейкстры.
Особенности реализации
Существует несколько особенностей реализации и приёмов, которые могут
значительно повлиять на эффективность алгоритма. Первое, на что не мешает обратить
внимание - это то, как очередь с приоритетом обрабатывает связи между
вершинами. Если вершины добавляются в неё так, что очередь работает по принципу
«первый пришел - последний ушел», то в случае вершин с одинаковой оценкой A*
«пойдёт» в глубину. Если же при добавлении вершин реализуется принцип «первый
пришел - первый ушел», то для вершин с одинаковой оценкой алгоритм, напротив,
будет реализовывать поиск в ширину. В некоторых случаях это обстоятельство
может оказывать существенное значение на производительность.
В случае если по окончании работы от алгоритма требуется маршрут, вместе
с каждой вершиной обычно хранят ссылку на родительский узел. Эти ссылки
позволяют реконструировать оптимальный маршрут. Если так, тогда важно, чтобы
одна и та же вершина не встречалась в очереди дважды (имея при этом свой
маршрут и свою оценку стоимости). Обычно для решения этой проблемы при
добавлении вершины проверяют, нет ли записи о ней в очереди. Если она есть, то
запись обновляют так, чтобы она соответствовала минимальной стоимости из двух.
Для поиска вершины в сортирующем дереве многие стандартные алгоритмы требуют
времени O(n). Если усовершенствовать дерево с помощью хеш-таблицы, то можно
уменьшить это время.
Оценка сложности
Временная сложность алгоритма A* зависит от эвристики. В худшем случае,
число вершин, исследуемых алгоритмом, растёт экспоненциально по сравнению с
длиной оптимального пути, но сложность становится полиномиальной, когда
эвристика удовлетворяет следующему условию:
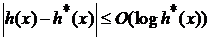 (2)
(2)
передвижение муравей задача коммивояжер
где
h* - оптимальная эвристика, то есть точная оценка расстояния из вершины x к
цели. Другими словами, ошибка h(x) не должна расти быстрее, чем логарифм от
оптимальной эвристики.
Но
ещё большую проблему, чем временная сложность, представляют собой потребляемые
алгоритмом ресурсы памяти. В худшем случае ему приходится помнить
экспоненциальное количество узлов. Для борьбы с этим было предложено несколько
вариаций алгоритма, таких как алгоритм A* с итеративным углублением (iterative
deeping A*, IDA*), A* с ограничением памяти (memory-bounded A*, MA*),
упрощённый MA* (simplified MA*, SMA*) и рекурсивный поиск по первому наилучшему
совпадению (recursive best-first search, RBFS). /1/
.2.2 Метод
ветвей и границ
Метод ветвей и границ - общий алгоритмический метод для нахождения
оптимальных решений различных задач оптимизации, особенно дискретной и
комбинаторной оптимизации. По существу, метод является комбинаторным (алгоритм
перебора) с отсевом подмножеств допустимых решений, не содержащих оптимальных
решений.
Общая идея метода может быть описана на примере поиска минимума и
максимума функции f(x) на множестве допустимых значений x. Функция f и x могут
быть произвольной природы. Для метода ветвей и границ необходимы две процедуры:
ветвление и нахождение оценок (границ).
Процедура ветвления состоит в разбиении области допустимых решений на
подобласти меньших размеров. Процедуру можно рекурсивно применять к
подобластям. Полученные подобласти образуют дерево, называемое деревом поиска
или деревом ветвей и границ. Узлами этого дерева являются построенные
подобласти.
Процедура нахождения оценок заключается в поиске верхних и нижних границ
для оптимального значения на подобласти допустимых решений.
В основе метода ветвей и границ лежит следующая идея (для задачи
минимизации): если нижняя граница для подобласти A дерева поиска больше, чем
верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть
исключена из дальнейшего рассмотрения (правило отсева). Обычно минимальную из
полученных верхних оценок записывают в глобальную переменную m. Любой узел
дерева поиска, нижняя граница которого больше значения m, может быть исключен
из дальнейшего рассмотрения.
Если нижняя граница для узла дерева совпадает с верхней границей, то это
значение является минимумом функции и достигается на соответствующей
подобласти. /2/
.2.3 Метод
ближайшего соседа
Алгоритм ближайшего соседа - один из простейших эвристических методов
решения задачи коммивояжёра. Относится к категории «жадных» алгоритмов.
Формулируется следующим образом:
Пункты обхода плана последовательно включаются в маршрут, причем, каждый
очередной включаемый пункт должен быть ближайшим к последнему выбранному пункту
среди всех остальных, ещё не включенных в состав маршрута.
Алгоритм прост в реализации, быстро выполняется, но, как и другие
«жадные» алгоритмы, может выдавать неоптимальные решения. Одним из
эвристических критериев оценки решения является правило: если путь, пройденный
на последних шагах алгоритма, сравним с путём, пройденным на начальных шагах,
то можно условно считать найденный маршрут приемлемым, иначе, вероятно,
существуют более оптимальные решения. Другой вариант оценки решения заключается
в использовании алгоритма нижней граничной оценки (lower bound algorithm).
Для любого количества городов в задаче коммивояжёра можно подобрать такое
расположение городов (значение расстояний между вершинами графа и указание
начальной вершины), что алгоритм ближайшего соседа будет выдавать наихудшее
решение, и в этом его главный недостаток. Вместе с тем этот алгоритм отличается
наибольший простотой.
.2.4 Алгоритм
поиска в глубину (ширину)
Поиск в глубину (DFS) - один из методов обхода графа. Алгоритм поиска
описывается следующим образом: для каждой непройденной вершины необходимо найти
все непройденные смежные вершины и повторить поиск для них. Используется в
качестве подпрограммы в алгоритмах поиска одно- и двусвязных компонент,
топологической сортировки. Пример порядка обхода дерева в глубину представлен
на рисунке 1.
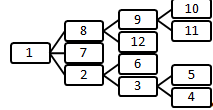
Рисунок 1. Порядок обхода дерева в глубину
Описание
Пусть задан граф G = (V,E), где V - множество вершин графа, E - множество
ребер графа. Предположим, что в начальный момент времени все вершины графа
окрашены в белый цвет. Выполним следующие действия:
. Из множества всех белых вершин выберем любую вершину, обозначим
её v1.
. Выполняем для нее процедуру DFS(v1).
. Перекрашиваем ее в черный цвет.
. Повторяем шаги 1-3 до тех пор, пока множество белых вершин не
пусто.
Процедура DFS (параметр - вершина 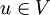 )
)
. Перекрашиваем вершину u в серый цвет.
. Для всякой вершины w, смежной с вершиной u, выполняем следующие
два шага:
. Если вершина w окрашена в белый цвет, выполняем процедуру
DFS(w).
. Окрашиваем w в черный цвет.
Поиск в ширину (BFS) - другой метод обхода и разметки вершин графа. Поиск
в ширину выполняется в следующем порядке: началу обхода s приписывается метка
0, смежным с ней вершинам - метка 1. Затем поочередно рассматривается окружение
всех вершин с метками 1, и каждой из входящих в эти окружения вершин
приписываем метку 2 и т. д. Пример порядка обхода дерева в глубину представлен
на рисунке 2.

Рисунок 2. Порядок обхода дерева в ширину
Если исходный граф связный, то поиск в ширину пометит все его вершины.
Дуги вида (i, i+1) порождают остовный бесконтурный ориентированный граф,
содержащий в качестве своей части остовное ориентированное дерево, называемое
поисковым деревом.
Легко увидеть, что с помощью поиска в ширину можно также занумеровать
вершины, нумеруя вначале вершины с меткой 1, затем с меткой 2 и т. д.
Двунаправленный поиск в ширину
Алгоритм часто улучшает простой поиск в ширину тем, что запускаются два
одновременных поиска в ширину из стартового и конечного узлов и
останавливается, когда узел из одного фронта поиска находит соседний узел из
другого фронта. Подобный поиск может улучшить простой поиск в ширину (обычно в
2 раза).
Наиболее сложным случаем для двунаправленного поиска является такая
задача, в которой для проверки цели дано только неявное описание некоторого
(возможно очень большого) множества целевых состояний, например всех состояний,
соответствующих проверки цели "Мат" в шахматах. При обратном поиске
потребовалось бы создать компактные описания всех состояний, которые позволяют
поставить мат с помощью ходов q1,q2,q3... и т.д.; и эти описания нужно было бы
сверять с состояниями, формируемыми при прямом поиске. Общего способа
эффективного решения такой проблемы не существует, и в этом недостаток данного
алгоритма.
.2.5 Алгоритм
Дейкстры
Алгоритм Дейкстры - алгоритм на графах, изобретенный Э. Дейкстрой.
Находит кратчайшее расстояние от одной из вершин графа до всех остальных.
Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм
широко применяется в программировании и технологиях. Например, его использует
протокол OSPF для устранения кольцевых маршрутов. Известен также под названием
кратчайший путь - первый (Shortest Path First).
Формулировка задачи
Дан простой взвешенный граф G(V,E) без петель и дуг отрицательного веса.
Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин
этого графа.
Инициализация
Каждой вершине из V сопоставим метку - минимальное известное расстояние
от этой вершины до a. Алгоритм работает пошагово - на каждом шаге он «посещает»
одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда
все вершины посещены. Метка самой вершины a полагается равной 0, метки
остальных вершин - бесконечности. Это отражает то, что расстояния от a до
других вершин пока неизвестны. Все вершины графа помечаются как не посещенные.
Шаг алгоритма
Если все вершины посещены, алгоритм завершается. В противном случае из
еще не посещенных вершин выбирается вершина u, имеющая минимальную метку. Мы
рассматриваем всевозможные маршруты, в которых u является предпоследним
пунктом. Вершины, соединенные с вершиной u ребрами, назовем соседями этой
вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей
метки u и длины ребра, соединяющего u с этим соседом. Если полученная длина
меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей,
пометим вершину u как посещенную и повторим шаг.
Алгоритм
Обозначения:
· V - множество вершин графа
· E - множество ребер графа
· w[ij] - вес (длина) ребра ij
· a - вершина, расстояния от которой ищутся
· U - множество посещенных вершин
· d[u] - по окончанию работы алгоритма равно длине кратчайшего
пути из a до вершины u
· p[u] - по окончании работы алгоритма содержит кратчайший путь
из a в u
Псевдокод
Присвоим

Для
всех 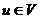 отличных от a
отличных от a
присвоим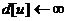
Пока
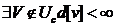
Пусть
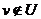 - вершина с минимальным d[v] (3)
- вершина с минимальным d[v] (3)
Добавим
вершину v к U
Для
всех 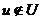 таких, что
таких, что 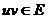
если
d[u] > d[v] + w[vu] то
изменим
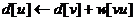
изменим
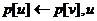
Описание.
В простейшей реализации для хранения чисел d[i] можно использовать массив
чисел, а для хранения принадлежности элемента множеству U - массив булевских
переменных.
В начале алгоритма расстояние для начальной вершины полагается равным
нулю, а все остальные расстояния заполняются большим положительным числом
(больше максимального возможного пути в графе). Массив флагов заполняется
нулями. Затем запускается основной цикл.
На
каждом шаге цикла мы ищем вершину с минимальным расстоянием и флагом равным
нулю. Затем мы устанавливаем в ней флаг в 1 и проверяем все соседние с ней
вершины. Если в ней расстояние больше, чем сумма расстояния до текущей вершины
и длины ребра, то уменьшаем его. Цикл завершается, когда флаги всех вершин
становятся равны 1, либо когда у всех вершин с флагом 0 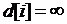 . Последний случай возможен, если граф G несвязан.
. Последний случай возможен, если граф G несвязан.
Подводя короткий итог, можно сказать, что достоинством данного алгоритма
является не только учет длины пути от исходной i-той вершины к следующей j-той
вершине (как это было в алгоритме ближайшего соседа), а сумма этой длины и
минимально известного расстояния до начального пункта a , указанного в метке вершины
j.
.2.6 Алгоритм
Джонсона
Алгоритм Джонсона позволяет найти кратчайшие пути между всеми парами
вершин взвешенного ориентированного графа. Данный алгоритм работает, если в
графе содержатся ребра с положительным или отрицательным весом, но отсутствуют
циклы с отрицательным весом.
Алгоритм
Дан граф 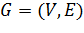 с весовой функцией
с весовой функцией 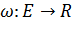 . Если веса всех ребер
. Если веса всех ребер 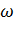 в графе неотрицательные, можно найти
кратчайшие пути между всеми парами вершин, запустив алгоритм Дейкстры один раз
для каждой вершины. Если в графе содержатся ребра с отрицательным весом, но
отсутствуют циклы с отрицательным весом, можно вычислить новое множество ребер
с неотрицательными весами, позволяющее воспользоваться предыдущим методом.
Новое множество, состоящее из весов ребер
в графе неотрицательные, можно найти
кратчайшие пути между всеми парами вершин, запустив алгоритм Дейкстры один раз
для каждой вершины. Если в графе содержатся ребра с отрицательным весом, но
отсутствуют циклы с отрицательным весом, можно вычислить новое множество ребер
с неотрицательными весами, позволяющее воспользоваться предыдущим методом.
Новое множество, состоящее из весов ребер 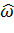 должно удовлетворять следующим
свойствам.
должно удовлетворять следующим
свойствам.
· Для всех ребер  новый вес
новый вес  .
.
· Для всех пар вершин 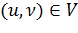 путь
путь 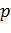 является кратчайшим путем из вершины
является кратчайшим путем из вершины
 в вершину
в вершину 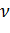 с использованием весовой функции
с использованием весовой функции 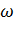 тогда и только тогда, когда
тогда и только тогда, когда 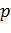 - также кратчайший путь из вершины
- также кратчайший путь из вершины 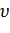 в вершину
в вершину 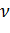 с весовой функцией
с весовой функцией 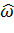 .
.
Сохранение кратчайших путей
Пусть дан взвешенный ориентированный граф 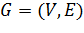 с весовой функцией
с весовой функцией 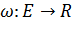 , и пусть
, и пусть 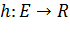 - произвольная функция, отображающая
вершины на действительные числа. Для каждого ребра
- произвольная функция, отображающая
вершины на действительные числа. Для каждого ребра  определим:
определим:
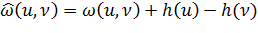 (4)
(4)
Пусть 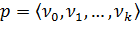 - произвольный путь из вершины
- произвольный путь из вершины  в вершину
в вершину 
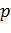 является кратчайшим путем с весовой
функцией
является кратчайшим путем с весовой
функцией 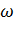 тогда и только тогда, когда он
является кратчайшим путем с весовой функцией
тогда и только тогда, когда он
является кратчайшим путем с весовой функцией 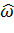 , то есть равенство
, то есть равенство 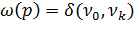 равносильно равенству
равносильно равенству 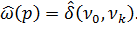 Кроме того, граф
Кроме того, граф 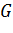 содержит цикл с отрицательным весом
с использованием весовой функции
содержит цикл с отрицательным весом
с использованием весовой функции 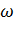 тогда и только тогда, когда он
содержит цикл с отрицательным весом с использованием весовой функции
тогда и только тогда, когда он
содержит цикл с отрицательным весом с использованием весовой функции 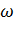 .
.
Изменение веса
. Для данного графа создадим новый граф 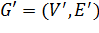 , где
, где 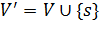 , для некоторой новой вершины
, для некоторой новой вершины  , а
, а  .
.
. Расширим весовую функцию 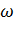 таким образом, чтобы для всех вершин
таким образом, чтобы для всех вершин
 выполнялось равенство
выполнялось равенство 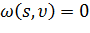 .
.
. Далее определим для всех вершин 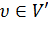 величину
величину 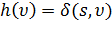 и новые веса для всех ребер
и новые веса для всех ребер 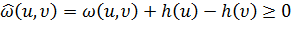 .
.
Недостатком этого алгоритма является то, что в общем случае работа
алгоритма может занять значительное время. /3/
.2.7 Алгоритм
муравья
Главная идея алгоритма муравья (метода муравьиных колоний) состоит в
моделировании поведения колонии муравьев, которые способны находить кратчайший
путь от муравейника до источника пищи и приспосабливаться к изменяющимся
условиям внешней среды, находя новый кратчайший путь, если старый в силу
каких-либо обстоятельств оказывается недоступным. При движении муравей
откладывает феромон, отмечая свой путь, и эту информацию используют другие
муравьи. Таким образом, взаимодействие между агентами (муравьями) происходит
посредством непрямой коммуникации. /22/
Если моделировать перемещение муравьев на некотором графе, ребра которого
представляют собой пути возможного перемещения муравьев, то помимо
положительной обратной связи (откладывания феромона) необходимо моделировать
отрицательную обратную связь, т.е. испарение феромона. Наличие отрицательной
обратной связи гарантирует, что муравьи будут искать другие пути от колонии до
источника пищи, т.е. найденное локально оптимальное решение не будет
единственным. Решением задачи будет наиболее обогащенный феромоном путь на
ребрах графа, который является оптимальным.
Муравьиные алгоритмы позволяют получить решения многих дискретных
комбинаторных задач не хуже вышеперечисленных алгоритмов. Чрезвычайно хорошие
результаты муравьиной оптимизации получаются для распределенных систем,
параметры которых изменяются во времени. Особенностью муравьиных алгоритмов
является не-конвергентность - даже после многих итераций одновременно
исследуется множество разных решений, что позволяет не застревать в локальных
оптимумах. /4/
В данной работе для решения задачи коммивояжера был выбран алгоритм
муравья.
1.3 Алгоритм
муравья, основные понятия
.3.1
Биологические основы
Известно, что насекомые, включая муравьев различных
видов, термитов и некоторые виды пчел и ос, живут в колониях, составленных из
большого количества взаимодействующих индивидуумов. Колонии насекомых способны
к решению различных задач оптимизации, которые ни одно насекомое не было бы
способно решить отдельно (например, нахождение кратчайших путей в процессе
добывания корма, решения задачи при назначении рабочей силы и кластеризация при
организации гнезд).
Для роя насекомых необходима некоторая форма связи,
чтобы сотрудничать при решении задачи. Эта связь между индивидуумами колонии
может быть более или менее прямой, в зависимости от определённых
разновидностей. Когда пчела находит источник продовольствия, она сообщает
направление и расстояние до местоположения, где она нашла продовольствие другим
пчелам, выполняя характерный танец. Это пример прямой связи, поскольку другие
пчелы должны чувствовать танец, который выполняет одна пчела, чтобы определить
местонахождение источника продовольствия. Другие формы прямой связи:
возбуждение физическим контактом или обменом продовольствием или жидкостью.
Косвенная связь между индивидуумами колонии является
более тонкой и требует, чтобы один индивидуум изменил окружающую среду таким
способом, чтобы это изменило поведение индивидуумов, проходящих через эту
измененную окружающую среду в будущем.
Одним из примеров косвенной связи является наложение
следов феромона, выполняемое некоторыми разновидностями муравьев. Муравей при
добывании корма отмечает дорожку, оставляя определённое количество феромона в
след за собой, за счёт чего побуждает следовать по его пути другого муравья,
который также занимается кормодобыванием.
Принцип изменения окружающей среды как средство связи
для изменения поведения называют stigmergy. Он является основным в организации
в муравьиных колониях. Хотя муравьи имеют королеву, специализированного
муравья, она является ответственным только за кладку яиц и не имеет никакой
управляющей функции. Вместо этого, муравьиные колонии самоорганизуются.
Термин самоорганизация (СО) используется, чтобы
описать сложное поведение, которое возникает при взаимодействии сравнительно
простых агентов. С помощью СО муравьи способны решить сложные задачи, с
которыми они сталкиваются ежедневно. Выгоды СО при решении задачи особенно
очевидны в её распределенном и здравом характере. Муравьиная колония может
эффективно поддерживать осмысленное поведение, даже если большое количество
муравьев неспособно к содействию.
Чтобы лучше понять механизм и способность муравьиных колоний сходиться к
хорошим решениям при поиске кратчайшего пути от гнезда к источнику
продовольствия были проведены некоторые эксперименты. /22/ При проведении
экспериментов колонии муравьёв Аргентины Linep-ithema humile давали два пути
идентичной длины, и после того, как прошло некоторое время, было замечено, что
муравьи сходились к одной из дорожек, после чего фактически была исключена
альтернатива. Чтобы проверить, сходился ли бы этот вид муравьёв к наиболее
короткому из множества путей, был проведен двойной эксперимент моста, где
муравьи должны были выбирать дважды между коротким и длинным путями (рис. 1.1).
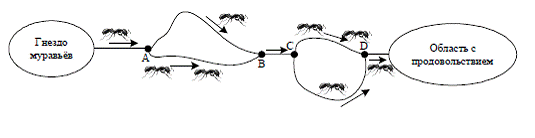
Рисунок 3. Двойной эксперимент моста
Муравей Аргентины является фактически слепым, поэтому
он не имеет никаких непосредственных средств идентификации короткого пути.
Однако, несмотря на этот недостаток, как показали результаты эксперимента,
колония муравьев способна к обнаружению кратчайшего пути, соединяющего гнездо с
областью, содержащей продовольствие.
Первоначально, все муравьи расположены на участке
гнезда. Множество муравьев отправляется от гнезда в поиске продовольствия,
каждый муравей оставляет феромон на своём пути, и достигает первой вилки в
точке A. Так как муравьи не имеют никакой информации о том, какой путь выбрать,
то есть никакой другой муравей не проходил тут ранее и не оставлял за собой
след феромона, каждый муравей будет выбирать идти или вправо или влево с равной
вероятностью.
Впоследствии приблизительно одна половина муравьев
выберет более короткий путь, остальные - более длинный маршрут к пересечению с
B. Муравьи, которые выберут более короткий путь, достигнут этого пересечения
быстрее, и должны будут решить, какой способ выбрать, чтобы вернуться.
Снова нет никакой информации для муравьев, чтобы
использовать её как ориентир, поэтому половина муравьев, достигших пересечения
B, возвратится к гнезду, в то время как остальные продолжают перемещение к
области, содержащей продовольствие.
Муравьи на более длинном участке между пересечениями A
и B, незатронутом другими муравьями, которых они встретили ранее на прямом
участке, достигают пересечения B и также разделятся; однако, так как
интенсивность следа феромона, который находится на пути назад к гнезду
приблизительно вдвое больше, чем следа феромона, достигающего области с
продовольствием, большинство возвратится к гнезду, прибывая туда в то же время
как и другие муравьи, которые выбрали длинный путь. Интересно, что так как
больше муравьев теперь шло по короткому участку между пересечениями A и B по
сравнению с длинным, следующие муравьи, покидающие гнездо теперь уже будут
более склонны выбрать короткий путь, который является первым удачным выбором
при поиске самого короткого пути.
Поведение муравьев на втором мосту в пересечениях
между C и D фактически идентично поведению, показанному прежде на первом мосту
между пересечениями A и B. В конечном счете, множество муравьев достигнет
продовольствия и соберет некоторое количество продовольствия, чтобы принести
назад к гнезду.
Достигая пересечения D, муравьи предпочтут короткий
участок по тем же самым причинам, что и муравьи, начинающие перемещение из
гнезда, и то же самое происходит снова в пересечении B.
Так как количество феромона в пересечениях A и C на
пути назад к гнезду примерно равно сумме количества феромона на этих двух
участках от гнезда, то также наиболее вероятен самый короткий полный путь от
области с продовольствием назад к гнезду при выборе муравьёв при возвращении.
Поскольку муравьи непрерывно распределяют феромон во
время своего перемещения, короткий путь непрерывно усиливается все большим
количеством муравьёв, пока количество феромона, помещенного в дальнейшем,
относительно других альтернативных маршрутов не станет настолько низким, что
фактически все муравьи будут использовать самый короткий путь, то есть система
сойдётся к самому короткому пути через самоукрепление.
Заметим, что феромон, используемый муравьями, медленно испаряется через
какое-то время, что не оставляет сомнений при объяснении двойного эксперимента
моста. Действительно, длины путей, которые не были выбраны в течение некоторого
времени, неизменно большие, и эти пути не будут содержать почти никаких следов
феромона из-за их испарения после определённого промежутка времени, далее
увеличивается вероятность выбора муравьями коротких путей. Следует обратить
внимание, что количество феромона на самом коротком пути имеет максимальную
ценность, которая достигнута большим количеством феромона, оставленным
муравьями. Укрупненная схема работы алгоритму муравья представлена на рисунке
4.
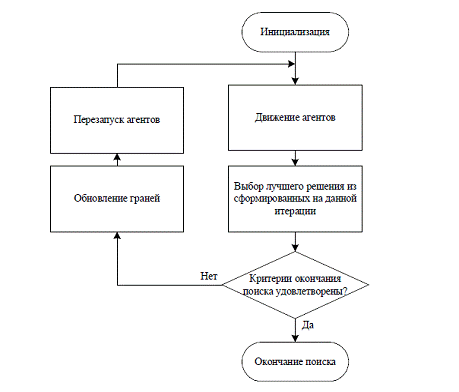
Рисунок 4. Укрупненная схема работы алгоритма муравья
Первой задачей, к которой был применён метод
муравьиных колоний (алгоритм муравья), была задача коммивояжёра (Traveling
Salesman Problem, TSP). Основной причиной, по которой была выбрана данная
задача, является то, что в ней необходимо находить кратчайший путь, поэтому аналогия
метода муравьиных колоний легко приспосабливается для решения данной задачи.
Для решения данной задачи было разработано несколько
различных методов, основанных на оптимизации с помощью муравьиных колоний.
Первым методом был метод муравьиных систем (Ant System
- AS). /23/ /24/ В дальнейшем этот метод послужил основой для многих других
методов, работающих на принципе муравьиных колоний.
В методе муравьиных систем агент формирует своё
решение в процессе перемещения от одного узла к другому на графе решений. Метод
работает до выполнения  итераций. На каждой итерации агенты составляют свои решения
за n шагов, на каждом из которых применяется правило выбора следующего узла -
правило выбора агентом, находящимся в узле
итераций. На каждой итерации агенты составляют свои решения
за n шагов, на каждом из которых применяется правило выбора следующего узла -
правило выбора агентом, находящимся в узле  , следующего узла для перемещения в него.
, следующего узла для перемещения в него.
Первоначально Марком Дориго было предложено три метода
муравьиных систем, различных между собой способом обновления путей - рёбер. Эти
методы назывались: плотностный (ant-density), количественный (ant-quantity) и
циклический (ant-cycle) методы муравьиных систем. В плотностном и
количественном методах агенты оставляли феромоны в процессе составления
решения, в то время как в циклическом методе агенты оставляли феромоны после
окончания перемещения, т.е. после составления решения.
Проведенные эксперименты по решению тестовых задач
/25/ показали, что циклический метод имел значительно лучшие результаты по
сравнению с другими двумя. В связи с этим, два худших метода были отброшены.
Поэтому, в дальнейшем, под методом муравьиных колоний понимается именно
циклический метод муравьиных систем. /5/
.3.2
Начальная популяция
После создания популяция муравьев поровну
распределяется по узлам сети. Необходимо равное разделение муравьев между
узлами, чтобы все узлы имели одинаковые шансы стать отправной точкой. Если все
муравьи начнут движение из одной точки, это будет означать, что данная точка
является оптимальной для старта, а на самом деле мы этого не знаем.
Для каждого муравья переход из города  в город
в город  зависит от трех составляющих: памяти
муравья списка TabuList , видимости и виртуального следа феромона.(память
муравья) - это список, в котором хранится битовый массив, с помощью которого
определяются посещённые и не посещённые узлы. Таким образом, агент должен
проходить через каждый узел только один раз. Узлы в списке “текущего
путешествия” Path располагаются в том порядке, в котором агент посещал их.
Позже список используется для определения протяженности пути между узлами.
Ясно, что список tabu возрастает при совершении маршрута и обнуляется в начале
каждой итерации алгоритма. Обозначим через
зависит от трех составляющих: памяти
муравья списка TabuList , видимости и виртуального следа феромона.(память
муравья) - это список, в котором хранится битовый массив, с помощью которого
определяются посещённые и не посещённые узлы. Таким образом, агент должен
проходить через каждый узел только один раз. Узлы в списке “текущего
путешествия” Path располагаются в том порядке, в котором агент посещал их.
Позже список используется для определения протяженности пути между узлами.
Ясно, что список tabu возрастает при совершении маршрута и обнуляется в начале
каждой итерации алгоритма. Обозначим через 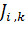 список городов, которые еще
необходимо посетить муравью
список городов, которые еще
необходимо посетить муравью 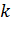 , находящемуся в городе
, находящемуся в городе  .
.
Видимость - величина, обратная расстоянию: 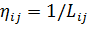 , где
, где 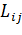 - расстояние между городами
- расстояние между городами  и
и 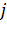 . Видимость - это локальная
статическая информация, выражающая эвристическое желание посетить город
. Видимость - это локальная
статическая информация, выражающая эвристическое желание посетить город 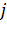 из города
из города  - чем ближе город, тем больше
желание посетить его. Использование только видимости, конечно, является
недостаточным для нахождения оптимального маршрута.
- чем ближе город, тем больше
желание посетить его. Использование только видимости, конечно, является
недостаточным для нахождения оптимального маршрута.
Виртуальный след феромона на ребре (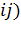 представляет подтвержденное
муравьиным опытом желание посетить город j из города
представляет подтвержденное
муравьиным опытом желание посетить город j из города  . Этот параметр характеризует
преимущество выбора данной грани по сравнению с другими при перемещении.
Информация о феромонах граней изменяется в процессе составления решений. При
этом количество феромонов, оставляемое агентами, пропорционально качеству
решения, составленного соответствующим агентом: чем меньше путь, тем больше
будет оставлено феромона, и наоборот, чем длиннее путь, тем меньше будет
оставлено феромона на соответствующих рёбрах. Такой подход позволяет обеспечить
непосредственный поиск в направлении нахождения лучшего решения.
. Этот параметр характеризует
преимущество выбора данной грани по сравнению с другими при перемещении.
Информация о феромонах граней изменяется в процессе составления решений. При
этом количество феромонов, оставляемое агентами, пропорционально качеству
решения, составленного соответствующим агентом: чем меньше путь, тем больше
будет оставлено феромона, и наоборот, чем длиннее путь, тем меньше будет
оставлено феромона на соответствующих рёбрах. Такой подход позволяет обеспечить
непосредственный поиск в направлении нахождения лучшего решения.
В отличие от видимости след феромона является более
глобальной и динамичной информацией - она изменяется после каждой итерации
алгоритма, отражая приобретенный муравьями опыт. Количество виртуального феромона
на ребре 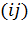 на итерации
на итерации 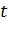 обозначим через
обозначим через 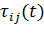 . /6/
. /6/
.3.3 Движение
муравья
Движение муравья основывается на одном
вероятностно-пропорциональном правиле, которое определяет вероятность перехода
k-го муравья из города  в город
в город 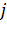 , если муравей еще не закончил путь (path), то есть не
посетил все узлы сети:
, если муравей еще не закончил путь (path), то есть не
посетил все узлы сети:
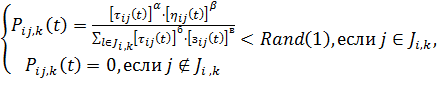 (5)
(5)
где:
- 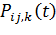 - вероятность того, что муравей
- вероятность того, что муравей 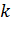 переместиться в
переместиться в 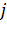 узел из
узел из  узла.
узла.
-  - случайное число в интервале (0; 1);
- случайное число в интервале (0; 1);
-  - параметр, задающий веса следа
феромона при выборе маршрута. При
- параметр, задающий веса следа
феромона при выборе маршрута. При  будет выбран ближайший город, что
соответствует жадному алгоритму в классической теории оптимизации.
будет выбран ближайший город, что
соответствует жадному алгоритму в классической теории оптимизации.
- 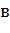 - параметр, задающий веса видимости
(расстояний). Если
- параметр, задающий веса видимости
(расстояний). Если 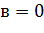 , тогда работает лишь феромонное усиление, что влечет за
собой быстрое вырождение маршрутов к одному субоптимальному решению.
, тогда работает лишь феромонное усиление, что влечет за
собой быстрое вырождение маршрутов к одному субоптимальному решению.
Обратим внимание, что правило (5) определяет лишь
вероятности выбора того или иного города. Собственно выбор города
осуществляется по принципу «колеса рулетки»: каждый город на ней имеет свой
сектор с площадью, пропорциональной вероятности (5). Для выбора города нужно
бросить шарик на рулетку - сгенерировать случайное число, и определить сектор,
на котором этот шарик остановится.
Заметим, что хотя правило (5) не изменяется на
протяжении итерации, значения вероятностей 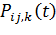 для двух муравьев в одном и том же
городе могут отличаться, т. к.
для двух муравьев в одном и том же
городе могут отличаться, т. к. 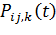 - функция от
- функция от 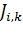 - списка еще не посещенных городов муравьем
- списка еще не посещенных городов муравьем 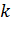 .
.
Пройденный муравьем путь заканчивается, когда муравей
посетит все узлы графа. Обратите внимание, что циклы запрещены, поскольку в
алгоритм включен список табу. После завершения длина пути может быть подсчитана
- она равна сумме всех граней, по которым путешествовал муравей. Уравнение (6)
показывает количество фермента, который был оставлен на каждой грани пути для
муравья 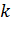 . Переменная
. Переменная 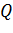 является константой.
является константой.
 (6)
(6)
где 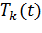 - маршрут, пройденный муравьем
- маршрут, пройденный муравьем 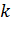 на итерации
на итерации 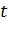 ;
; 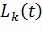 - длина этого маршрута;
- длина этого маршрута; 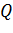 - регулируемый параметр, значение
которого выбирают одного порядка с длиной оптимального маршрута.
- регулируемый параметр, значение
которого выбирают одного порядка с длиной оптимального маршрута.
Результат уравнения является средством измерения пути,
- короткий путь характеризуется высокой концентрацией фермента, а более длинный
путь - более низкой. Затем полученный результат используется в уравнении (7),
чтобы увеличить количество фермента вдоль каждой грани пройденного муравьем 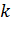 пути.
пути.
 (7)
(7)
где 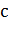 - коэффициент испарения феромона,
- коэффициент испарения феромона,  ;
;  и
и 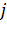 - узлы, образующие грани, которые посетил
- узлы, образующие грани, которые посетил 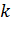 -ый муравей;
-ый муравей;  - общее количество агентов,
посетивших грань
- общее количество агентов,
посетивших грань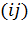 .
.
Следует обратить внимание, что данное уравнение
применяется ко всему пути, при этом каждая грань помечается ферментом пропорционально
длине пути. Поэтому следует дождаться, пока муравей закончит путешествие и
только потом обновить уровни фермента, в противном случае истинная длина пути
останется неизвестной.
В начале пути у каждой грани есть шанс быть выбранной.
Чтобы постепенно удалить грани, которые входят в худшие пути в сети, ко всем
граням применяется процедура испарения фермента (Pheromone evaporation).
Используя константу 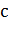 из уравнения (7), мы получаем формулу (8).
из уравнения (7), мы получаем формулу (8).
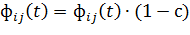 (8)
(8)
В начале оптимизации количество феромона принимается равным небольшому
положительному числу 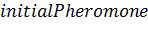 . Общее количество муравьев в колонии остается постоянным на
протяжении выполнения алгоритма. Многочисленная колония приводит к быстрому
усилению субоптимальных маршрутов, а когда муравьев мало, возникает опасность
потери кооперативности поведения через ограниченное взаимодействие и быстрое
испарения феромона. Обычно число муравьев назначают равным количеству городов -
каждый муравей начинает маршрут со своего города.
. Общее количество муравьев в колонии остается постоянным на
протяжении выполнения алгоритма. Многочисленная колония приводит к быстрому
усилению субоптимальных маршрутов, а когда муравьев мало, возникает опасность
потери кооперативности поведения через ограниченное взаимодействие и быстрое
испарения феромона. Обычно число муравьев назначают равным количеству городов -
каждый муравей начинает маршрут со своего города.
После того как путь муравья завершен, грани обновлены в соответствии с
длиной пути и произошло испарение фермента на всех гранях, алгоритм запускается
повторно. Список табу очищается, и длина пути обнуляется. Муравьям разрешается
перемещаться по сети, основывая выбор грани на уравнении (5).
Этот процесс может выполняться для постоянного
количества путей или до момента, когда на протяжении нескольких запусков не
было отмечено повторных изменений. Затем определяется лучший путь, который и
является решением. /7/
.3.4 Пример
итерации
Разберем функционирование алгоритма на простом примере, чтобы увидеть,
как работают уравнения. Рассмотрим простой сценарий с двумя муравьями, которые
выбирают два разных пути для достижения одной цели. На рисунке 6 показан этот
пример с двумя гранями между двумя узлами (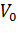 и
и 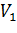 ).
).
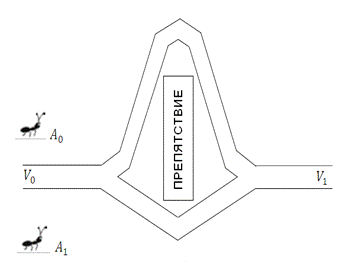
Рисунок 6. Начальная конфигурация проблемы
Каждая грань инициализируется и имеет одинаковые шансы на то, чтобы быть
выбранной. Короткий путь составляет 10 шагов, длинный путь составляет 20 шагов.
В качестве параметров алгоритма примем следующие значения:
- вес следа феромона, 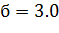 ;
;
- вес видимости,  ;
;
- коэффициент испарения феромона, 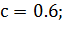
- регулируемый параметр 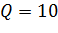 ;
;
- начальное значение феромона 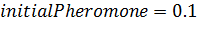 .
.
Два муравья находятся в узле 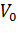 и помечаются как
и помечаются как 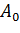 и
и 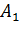 . Так как вероятность выбора любого
пути одинакова, в этом цикле мы проигнорируем уравнение выбора пути. На рисунке
7 каждый муравей выбирает свой путь (муравей
. Так как вероятность выбора любого
пути одинакова, в этом цикле мы проигнорируем уравнение выбора пути. На рисунке
7 каждый муравей выбирает свой путь (муравей 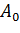 идет по верхнему пути, а муравей
идет по верхнему пути, а муравей  - по нижнему).
- по нижнему).
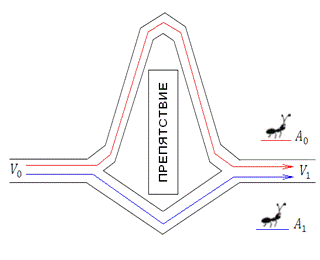
Рисунок 7. Путь муравья завершен
По уравнению (6) рассчитывается количество фермента, которое должно быть
"нанесено".
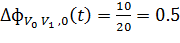
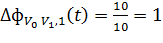
Далее по уравнению (7) рассчитывается количество фермента, которое будет
применено. Для муравьев 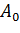 и
и 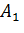 результат соответственно составляет:
результат соответственно составляет:
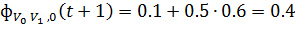
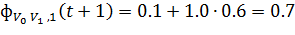 .
.
Далее с помощью уравнения (8) определяется, какая
часть фермента испарится и, соответственно, сколько останется. Результаты (для
каждого пути) составляют:
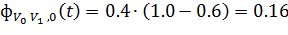
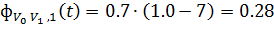 .
.
Эти значения представляют новое количество фермента для каждого пути
(верхнего и нижнего, соответственно). Теперь переместим Муравьев обратно в узел
V0 воспользуемся вероятностным уравнением выбора пути (5), чтобы
определить, какой путь должны выбрать муравьи.
Вероятность того, что муравей выберет верхний путь (представленный
количеством фермента 0.16), составляет:
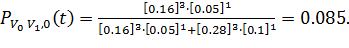
Вероятность того, что муравей выберет нижний путь (представленный
количеством фермента 0.28), составляет
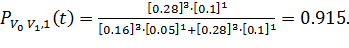
При сопоставлении двух вероятностей оба муравья выберут нижний путь,
который является наиболее оптимальным. /8/
В таблице 1 указаны основные параметры алгоритма, характеризующие данный
пример.
|
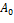
|
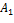
|
|
Пройденное расстояние, 
|
20
|
10
|
|
Уровень фермента/пройденное расстояние, 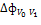
|
0.5
|
1.0
|
|
Количество фермента, которое было применено, 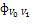
|
0.4
|
0.7
|
|
Количество фермента, которое испарилось, 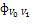
|
0.16
|
0.28
|
|
Вероятность выбора верхнего/нижнего пути
|
0.085/0.915
|
0.085/0.915
|
Таблица 1. Характеристики пройденного пути
.3.5
Разновидности алгоритма муравья
В связи с возможностью различного математического
описания поведения муравьёв были разработаны расширения алгоритма муравья
(также называемого методом муравьиных систем). К ним относятся: метод
муравьиных систем, основанный на элитной стратегии; метод муравьиных систем,
основанный на ранжировании (ASrank); метод системы муравьиных
колоний; макси-минный метод муравьиных систем (MAX-MIN AS - MMAS).
Первым расширением метода муравьиных систем была
элитная стратегия. Данный подход основывается на дополнительном увеличении
количества феромонов для лучшего глобального пути в данный момент времени t.
Таким образом, процедура добавления феромона для дуг, которые входят лучший на
данный момент времени путь, выполняется повторно, при этом количество
добавляемого феромона рассчитывается в соответствии с длиной лучшего пути.
Далее был предложен метод муравьиных систем, основанный на ранжировании
(ASrank). Данный метод по своей сути является расширением элитной
стратегии и заключается в следующем: агенты сортируются по длине составленных
ими путей, после чего на глобально лучшем пути феромоны увеличиваются с весом
w, а также увеличение феромонов производится также только для дуг, вошедших в
пути (w-1) лучших агентов; при этом k-ый лучший агент будет добавлять феромон с
весом (w-k) в соответствии с (9):
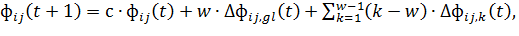 (9)
(9)
где  - длина лучшего глобального пути.
- длина лучшего глобального пути.
Метод системы муравьиных колоний (Ant Colony System -
ACS) улучшает алгоритм муравья путём использования информации, полученной
предыдущими агентами, для изучения пространства поиска. Это достигается с
помощью двух механизмов. Во-первых, используется строгая элитная стратегия при
обновлении феромонов на гранях. Во-вторых, агенты выбирают следующий город для
перемещения, используя так называемое, псевдослучайное пропорциональное
правило: с вероятностью 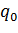 агент перемещается в пункт
агент перемещается в пункт 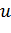 , для которого произведение
количества феромонов и эвристической информации является максимальным:
, для которого произведение
количества феромонов и эвристической информации является максимальным: 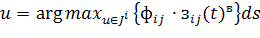 , в то время как с вероятностью
, в то время как с вероятностью 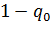 будет применён базовый подход при
определении следующего пункта для перехода, описанный в методе муравьиных
систем. Значение
будет применён базовый подход при
определении следующего пункта для перехода, описанный в методе муравьиных
систем. Значение 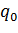 является константой. При этом если
является константой. При этом если 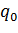 стремится к
стремится к 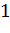 , то используется только
псевдослучайное пропорциональное правило, когда же
, то используется только
псевдослучайное пропорциональное правило, когда же  , тогда метод муравьиных колоний
работает по принципу метода муравьиных систем.
, тогда метод муравьиных колоний
работает по принципу метода муравьиных систем.
При обновлении путей, как было сказано выше, применяется строгая элитная
стратегия, в соответствии с которой только агент, составивший лучшее решение,
вырабатывает феромон на пути своего перемещения. Тогда количество феромонов на
гранях изменяется в соответствии с формулой (10):
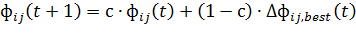 (10)
(10)
В качестве лучшего агента может использоваться агент,
получивший лучшее решение на данной итерации, или глобально лучший агент,
получивший лучшее решение на всех итерациях от начала работы метода.
Последним отличием метода системы муравьиных колоний является то, что
агенты обновляют количество феромонов в процессе составления решения (подобно
плотностному и количественному методам муравьиных систем). Такой подход
приводит к уменьшению вероятности выбора одинаковых путей всеми агентами. За
счёт этого понижается вероятность зацикливания в локальном оптимуме.
Макси-минный метод муравьиных систем (MAX-MIN AS - MMAS) вводит нижнюю и
верхнюю границу для возможных значений феромонов на грани, а также данный метод
отличается подходом к определению их значения при инициализации. Практически в
MMAS используется интервал значений феромонов, ограниченный 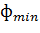 и
и 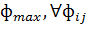 , т.е.
, т.е. 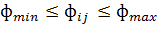 . Количество феромонов граней при
инициализации задаётся равным нижней границе интервала, что обеспечивает лучшее
исследование пространства решений. В MMAS, также как и в ACS, только лучший
агент (глобально лучший или локально) выполняет добавление феромонов после
каждой итерации метода. Результаты вычислений /26/ показали, что лучшие
результаты получаются, когда обновление феромонов выполняется с использованием
глобально лучшего решения. В MMAS также часто применяется локальный поиск для улучшения
его свойств. /9/
. Количество феромонов граней при
инициализации задаётся равным нижней границе интервала, что обеспечивает лучшее
исследование пространства решений. В MMAS, также как и в ACS, только лучший
агент (глобально лучший или локально) выполняет добавление феромонов после
каждой итерации метода. Результаты вычислений /26/ показали, что лучшие
результаты получаются, когда обновление феромонов выполняется с использованием
глобально лучшего решения. В MMAS также часто применяется локальный поиск для улучшения
его свойств. /9/
В общем виде различия между разновидностями метода муравьиных колоний
можно отобразить в таблице 2.
|
Критерий
|
AS
|
ASrank
|
ACS
|
MMAS
|
|
Добавление феромона
|
После получения решения
|
После получения решения
|
В процессе получения решения
|
В процессе получения решения
|
|
Динамическое изменение коэффициента 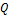
|
Отсутствует
|
Отсутствует
|
Отсутствует
|
Отсутствует
|
|
Правило выбора следующего пункта
|
Традиционный подход
|
Псевдослучайное пропорциональное правило
|
Традиционный подход
|
Традиционный подход
|
|
Применение элитной стратегии
|
Все агенты участвуют в обновлении путей
|
Обновление выполняют 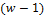 локально лучших агентов и
глобально лучший агент локально лучших агентов и
глобально лучший агент
|
Обновление выполняет только лучший (глобально или локально)
агент
|
|
Использование ограничений для различных параметров
|
Отсутствуют
|
Ограничение на количество агентов, участвующих в обновлении
путей
|
Отсутствует
|
Используется интервал значений феромонов
|
|
Применение локальной оптимизации
|
Отсутствуют
|
Отсутствуют
|
Используются традиционные методы локальной оптимизации
|
Отсутствует
|
|
Решаемые задачи
|
Задача коммивояжёра, квадратичная задача о назначениях,
задача календарного планирования, транспортная задача
|
Задача коммивояжёра
|
Задача коммивояжёра, задача календарного планирования
|
Задача коммивояжёра, квадратичная задача о назначениях
|
|
Влияние количества агентов на нахождение результата
|
Сильное
|
Среднее
|
Слабое
|
Слабое
|
Таблица 2. Различия между разновидностями метода муравьиных колоний
.4 Построение
алгоритма движения муравья и моделирование этого алгоритма на ЭВМ
.4.1
Ограничения, накладываемые на агента в стандартной постановке задачи коммивояжера
Алгоритм
муравья - один из эффективных полиномиальных алгоритмов для нахождения
приближённых решений задачи коммивояжёра
<#"607393.files/image115.gif">
Рисунок
7. Иллюстрация работы со списком TabuList
В
данном примере решается задача коммивояжера для пяти городов. На рисунке
представлен третий шаг алгоритма, когда агент 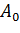 находится
в третьем городе,
находится
в третьем городе, 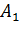 в пятом. На данном шаге список TabuList будет
выглядеть в соответствии с таблицей 3:
в пятом. На данном шаге список TabuList будет
выглядеть в соответствии с таблицей 3:
|
агент город
|
1
|
2
|
3
|
4
|
5
|
1
|
0
|
0
|
1
|
1
|
|
|
1
|
1
|
1
|
0
|
0
|
Таблица 3. Содержание списка TabuList на третьем шагу.
В данном списке  между двумя узлами (
между двумя узлами (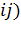 соответствует не посещенному городу,
соответствует не посещенному городу,
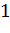 соответствует посещенному городу.
При выборе пути агентом происходит считывание данного массива и расчет
производится только для городов, которым соответствует
соответствует посещенному городу.
При выборе пути агентом происходит считывание данного массива и расчет
производится только для городов, которым соответствует 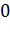 в списке TabuList.
в списке TabuList.
.4.2 Алгоритм
обхода препятствий
В
данной дипломной работе необходимо решить задачу коммивояжера, на которую
наложено дополнительное ограничение в виде препятствий. Препятствия представлены
в виде прямоугольной, треугольной и восьмиугольной фигур (в общем случае,
найдено решение для препятствий любой выпуклой формы). Координаты вершин
препятствий являются узлами графа. Агент не должен пересекать границы
препятствий, но может посещать их узлы. Данное дополнительное ограничение
описывается списком obstacles, в котором хранится битовый массив возможных
перемещений агента. В некоторых источниках граф, описываемый данным массивом
также называется графом видимости (visibility graph). /27 <#"607393.files/image116.gif"> между двумя узлами (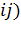 соответствует видимой грани,
соответствует видимой грани, 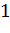 соответствует
не видимой грани. Очевидно, что при отсутствии препятствий, данный массив
должен быть заполнен нулями.
соответствует
не видимой грани. Очевидно, что при отсутствии препятствий, данный массив
должен быть заполнен нулями.
Для
того чтобы заполнить список obstacles, используется алгоритм обхода
препятствий, который рассчитывает граф видимости. В Приложении 1 расположен
исходный код программы на Delphi, решающий задачу коммивояжера с препятствиями.
В данном коде комплекс функций InitialFullFill, FullFillNeighbour,
NotTemporary, Intersect, PreIntersect, FinalTrans рассчитывает граф видимости и
заполняет массив obstacles, позволяя алгоритму муравья обходить препятствий.
Массив
obstacles так же как и массив TabuList заполняется нулями и единицами. К
примеру, если элемент массива obstacles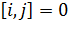 , то
грань между узлами
, то
грань между узлами 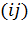 видима, если элемент массива obstacles
видима, если элемент массива obstacles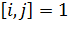 , то грань между узлами
, то грань между узлами 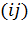 не
видима (пересекает какое-то препятствие).
не
видима (пересекает какое-то препятствие).
Первым
шагом функция InitialFullFill заполняет массив obstacles некой первоначальной
величиной, которая соответствует непроверенному ребру. В качестве такой
величины была выбрана  . Если элемент массива obstacles
. Если элемент массива obstacles , то ребро между узлами
, то ребро между узлами 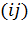 еще не
проверено на пересечение с препятствиями. Функция InitialFullFill также
записывает
еще не
проверено на пересечение с препятствиями. Функция InitialFullFill также
записывает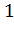 в элементы массива, расположенные на его диагонали.
Это объясняется тем, что когда в алгоритме муравья агент переходит в узел
в элементы массива, расположенные на его диагонали.
Это объясняется тем, что когда в алгоритме муравья агент переходит в узел  , он записывает этот узел в список табу и уже не может
его посетить. Значит, находясь в узле
, он записывает этот узел в список табу и уже не может
его посетить. Значит, находясь в узле  и
выбирая следующий узел для движения, агент не может выбрать текущий узел
и
выбирая следующий узел для движения, агент не может выбрать текущий узел  для посещения. Элементы, стоящие на диагонали массива
как раз и соответствуют переходу из узла
для посещения. Элементы, стоящие на диагонали массива
как раз и соответствуют переходу из узла  в узел
в узел 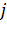 при условии что
при условии что 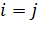 , поэтому
из значения приравниваются
, поэтому
из значения приравниваются 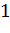 .
.
Далее
функция FullFillNeighbour заполняет элементы массива, которые соответствуют
соседним узлам препятствия, значением 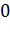 . Таким
образом, агент может передвигаться по границе препятствия, не пересекая её.
. Таким
образом, агент может передвигаться по границе препятствия, не пересекая её.
Функция
PreIntersect передает функции Intersect координаты  узлов одного непроверенного ребра графа и координаты
всех узлов, которые образуют грани препятствия. Если непроверенное ребро графа
с узлами
узлов одного непроверенного ребра графа и координаты
всех узлов, которые образуют грани препятствия. Если непроверенное ребро графа
с узлами 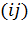 не пересекает ни одной грани препятствия, то это
означает, что ребро между узлами
не пересекает ни одной грани препятствия, то это
означает, что ребро между узлами  видимо и
значение массива obstacles
видимо и
значение массива obstacles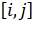 не меняется. Если же непроверенное ребро графа с
узлами
не меняется. Если же непроверенное ребро графа с
узлами 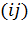 пересекает хотя бы одну грань хотя бы одного
препятствия, то в массив obstacles
пересекает хотя бы одну грань хотя бы одного
препятствия, то в массив obstacles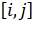 записывается
записывается 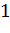 , то есть ребро между узлами
, то есть ребро между узлами  не видимо.
не видимо.
Функция
FinalTrans вызывается в конце, когда в массив obstacles записаны все
ограничения. Функция изменяет все элементы массива, значение которых осталось
равно 2, на новое значение - 0.
.4.3 Пример
работы алгоритма обхода препятствий
Для иллюстрации работы алгоритма обход препятствий, рассмотрим следующий
пример, показанный на рисунке 8.
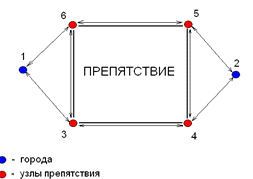
Рисунок 8. Задача с двумя городами и препятствием
На рисунке 8 представлен простой пример, на котором изображены два города
и препятствие.
На первом шаге функция InitialFullFill заполняет массив obstacles цифрами
два, а по диагонали цифрами один. На первом шаге массив obstacles примет
следующий вид (таблица 4):
|
Узлы
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
|
2
|
2
|
1
|
2
|
2
|
2
|
2
|
|
3
|
2
|
2
|
1
|
2
|
2
|
2
|
|
4
|
2
|
2
|
2
|
1
|
2
|
2
|
|
5
|
2
|
2
|
2
|
2
|
1
|
2
|
|
6
|
2
|
2
|
2
|
2
|
2
|
1
|
Таблица 4. Массив obstacles после функции InitialFullFill
Далее FullFillNeighbour заполняет элементы массива, которые соответствуют
соседним узлам препятствия, значением 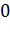 . В данном примере соседними узлами
препятствия являются следующие пары узлов:
. В данном примере соседними узлами
препятствия являются следующие пары узлов: 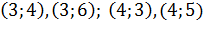 ;
; 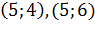 ;
; 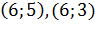 . Массив obstacles примет следующий
вид (таблица 5):
. Массив obstacles примет следующий
вид (таблица 5):
Таблица 5. Массив obstacles после функции FullFillNeighbour
|
Узлы
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
|
2
|
2
|
1
|
2
|
2
|
2
|
2
|
|
3
|
2
|
2
|
1
|
0
|
2
|
0
|
|
4
|
2
|
2
|
0
|
1
|
0
|
2
|
|
5
|
2
|
2
|
2
|
0
|
1
|
0
|
|
6
|
2
|
2
|
0
|
2
|
0
|
1
|
Рассмотрим работу функции PreIntersect. Она поочередно проверяет,
является ли ребро графа проверенным или нет. Если нет, то она передает функции
Intersect координаты узлов непроверенного ребра и координаты узлов всех ребер
препятствий.
Таким образом, на первом шаге функция проверяет элемент массива obstacles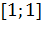 , который равен единице. Это
означает, что ребро
, который равен единице. Это
означает, что ребро 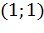 является невидимым, происходит переход к следующему ребру
obstacles
является невидимым, происходит переход к следующему ребру
obstacles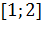 .
.
На втором шаге функция проверяет ребро  , которое является непроверенным,
поэтому функция PreIntersect передает функции Intersect координаты узлов этого
непроверенного ребра и координаты узлов всех ребер препятствий. Функция
Intersect возвращает значение типа Boolean; true соответствует тому, что ребра
пересекаются, false соответствует тому, что ребра не пересекаются.
, которое является непроверенным,
поэтому функция PreIntersect передает функции Intersect координаты узлов этого
непроверенного ребра и координаты узлов всех ребер препятствий. Функция
Intersect возвращает значение типа Boolean; true соответствует тому, что ребра
пересекаются, false соответствует тому, что ребра не пересекаются.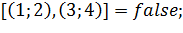 (ребро
(ребро  не пересекает ребро
не пересекает ребро 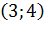 препятствия).
препятствия).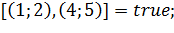 (ребро
(ребро  пересекает ребро
пересекает ребро 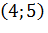 препятствия, следовательно ребро
препятствия, следовательно ребро является не видимым (запрещенным),
поэтому в элемент массива obstacles
является не видимым (запрещенным),
поэтому в элемент массива obstacles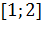 записывается
записывается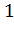 .
.
На третьем шаге функция проверяет ребро 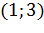 , которое также является
непроверенным, поэтому функция PreIntersect передает функции Intersect
координаты узлов этого непроверенного ребра и координаты узлов всех ребер
препятствий.
, которое также является
непроверенным, поэтому функция PreIntersect передает функции Intersect
координаты узлов этого непроверенного ребра и координаты узлов всех ребер
препятствий. (ребро
(ребро 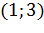 не пересекает ребро
не пересекает ребро 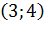 препятствия).
препятствия).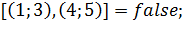 (ребро
(ребро 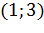 не пересекает ребро
не пересекает ребро 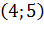 препятствия).
препятствия).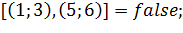 (ребро
(ребро 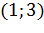 не пересекает ребро
не пересекает ребро 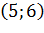 препятствия).
препятствия). (ребро
(ребро 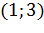 не пересекает ребро
не пересекает ребро 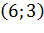 препятствия).
препятствия).
Таким образом, ребро 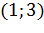 не пересекает ребер препятствия, следовательно, ребро
является видимым (разрешенным), поэтому в элемент массива obstacles
не пересекает ребер препятствия, следовательно, ребро
является видимым (разрешенным), поэтому в элемент массива obstacles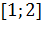 не записывается
не записывается 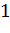 (остается прежнее значение
(остается прежнее значение  . Цикл продолжается, пока не будут
проверены все ребра. Ребра, лежащие внутри препятствий, помечаются не видимые
(не разрешенные).
. Цикл продолжается, пока не будут
проверены все ребра. Ребра, лежащие внутри препятствий, помечаются не видимые
(не разрешенные).
Массив obstacles примет следующий вид (6):
|
Узлы
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
1
|
1
|
2
|
1
|
1
|
2
|
|
2
|
1
|
1
|
1
|
2
|
2
|
1
|
|
3
|
2
|
1
|
1
|
0
|
1
|
0
|
|
4
|
1
|
2
|
0
|
1
|
0
|
1
|
|
5
|
1
|
2
|
1
|
0
|
1
|
0
|
|
6
|
2
|
1
|
0
|
1
|
0
|
1
|
Таблица 6. Массив obstacles после функции PreIntersect
Функция FinalTrans производит окончательное преобразование массива
obstacles, изменяя все элементы массива, значение которых осталось равно цифре
два, на новое значение - цифре ноль.
Массив obstacles примет следующий вид (таблица 7):
|
Узлы
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
|
2
|
1
|
1
|
1
|
0
|
0
|
1
|
|
3
|
0
|
1
|
1
|
0
|
1
|
0
|
|
4
|
1
|
0
|
0
|
1
|
0
|
1
|
|
5
|
1
|
0
|
1
|
0
|
1
|
0
|
|
6
|
0
|
1
|
0
|
1
|
0
|
1
|
Таблица 7. Массив obstacles после функции FinalTrans
Итоговый массив описывает все возможные перемещения из всех узлов графа и
используется далее в алгоритме муравья.
.4.4
Структура данных алгоритма муравья
Сначала изучим структуру данных как для городов и узлов препятствий, так
и для агентов, которые будут по ним путешествовать:
Константы:
- MAX_OBSTACLE_NODES - параметр, отвечающий за количество узлов
препятствий;
- MAX_CITIES - параметр, отвечающий за количество городов;
- MAX_NODES=MAX_OBSTACLE_NODES+MAX_CITIES - параметр,
отвечающий за общее количество узлов препятствий и городов.
- MAX_DISTANCE - параметр, отвечающий за максимальную дистанцию
между городами;
- MAX_ANTS - параметр, отвечающий за максимальное количество
муравьев.
- ALPHA, BETA, RHO, QVAL - параметры алгоритма муравья,
подробно описанные выше;
- MAX_TOURS - параметр, отвечающий максимальную длину тура;
- MAX_TIME - параметр, отвечающий за количество итераций
алгоритма;
- INIT_PHEROMONE - начальное значение феромона;
- NK - количество препятствий
Структура данных antType:
- curCity - параметр, отвечающий за текущий город, в котором
находится агент;
- NextCity - параметр, отвечающий за следующий город, в который
переходит агент;
- PathIndex - счетчик посещенных узлов препятствий;
- PathIndex_city - счетчик посещенных городов;
- Tabu - массив посещенных городов;
- Path - массив последовательности посещенных городов;
- TourLength - длина маршрута.
Структура данных cityType:
- X - координата X;
- Y - координата X;
Глобальная структура данных
- Distance - массив расстояний между городами и узлами препятствий;
- Cities - массив с координатами городов и координатами узлов
препятствий;
- ants - массив, в котором записана информация про каждого
агента. Элемент массива содержит минимальный путь;
- Obstacles - массив, содержащий информацию о графе видимости;
- pheromone: массив, в котором записана информация о количестве
феромонов на видимых ребрах графа;
- best - наименьшая длина маршрута;
- bestIndex - номер агента с наименьшей длиной маршрут
- curTime - счетчик итераций;
- denom - используется для расчета формулы (4.1);
- Inf:array - массив, содержащий информацию о количестве
городов, о количества препятствий и о количестве их ребер.
Структура cityType используется для определения
координат городов и узлов препятствий. Структура antType представляет одного
муравья. Кроме отслеживания текущего и следующего города на пути (поля curCity
и nextCity) каждый муравей также должен учитывать города, которые уже были
посещены (массив tabu), узлы, которые можно посетить, находясь в текущем узле
(учесть массив obstacles), а также длину пройденного пути. Наконец, общая длина
пуп сохраняется в поле tourLength.
Структуры данных в алгоритме включают также специальный двумерный массив
distance, который содержит предварительно рассчитанные расстояния от одного
города до всех других. Уровни фермента сохраняются в массиве pheromone. Каждый
двумерный массив в алгоритме использует первый индекс в качестве начала ребра,
то есть исходного города, а второй - в качестве конечного.
.4.5
Использование графа видимости в алгоритме муравья
Как уже отмечалось выше, в стандартной постановке задачи коммивояжера при
движении по графу на агента накладывается только одно ограничение: каждый город
может быть посещен только один раз. В дополнение к этому, в задаче,
поставленной в данной дипломной работе, необходимо учесть наличие препятствий.
Для этого используется массив obstacles. О том, как этот массив заполняется,
было подробно написано выше.
В данном пункте рассмотрим то, как использовать граф видимости в
алгоритме муравья. В Приложении 1 расположен исходный код программы на Delphi,
сейчас же остановимся на основных этапах построения алгоритма движения муравья.
Сначала функция init выполняет три базовых действия,
которые требуются для подготовки алгоритма муравья. Первое действие - это
считывание координат городов. Кроме того, во время считывания городов
одновременно очищаются массивы distance и pheromone.
Далее, немного оптимизируя алгоритм, выполняется предварительный расчет
расстояний между всеми городами и узлами препятствий. Расстояния вычисляется с
помощью обычной двумерной геометрии координат (теорема Пифагора).
Наконец, инициализируется массив ant. Муравьи должны
быть равномерно распределены по всем городам. Для этого используется переменная
to1 в качестве счетчика псевдоцикла. Когда значение переменной to1 становится
равным номеру последнего города, она возвращается к первому городу, и процесс
повторяется. Поле curcity в структуре ant устанавливается в значение текущего
города (первого города для муравья). Затем очищаются списки tabu и path. Ноль в
массиве tabu обозначает, что город еще не был посещен; единица свидетельствует,
что город уже включен в путь муравья. В массив path помещается номер текущего
города для муравья, и очищается поле tourLength (длина пути).
После завершения пути каждый муравей должен быть повторно
инициализирован, а затем распределен по графу. Это выполняет функция
restartAnts.
Во время повторной инициализации самая оптимальная длина пути
сохраняется, чтобы можно было оценить прогресс муравьев. Затем структура
алгоритма очищается и повторно инициализируется - начинается следующее
путешествие.
Функция selectNextCity позволяет выбрать следующий город для составления
пути. Она вызывает функцию antProduct, которая используется для расчета
уравнения (5).
Функция selectNextCity вызывается для заданного
муравья и определяет, которую из граней можно выбрать в соответствии со списком
tabu. На этом шаге список tabu уже включает в себя информацию обо всех видимых
и невидимых гранях. Выбор грани основывается на вероятностном уравнении (5),
которое вычисляет коэффициент заданного пути от суммы других путей. Первой
задачей функции selectNextCity является расчет знаменателя выражения. После
этого все ребра, которые агент может посетить из данного узла, проверяются с
помощью уравнения (5), чтобы муравей мог выбрать путь. Как только ребро
найдено, функция определяет город, к которому перейдет муравей. Следующая
функция, simulateAnts, рассчитывает движения муравьев по графу.
Функция simulateAnts добавляет в список tabu, который
содержит информацию о посещенных городах, информацию о видимых из текущего узла
ребрах графа из массива obstacles. Затем функция проверяет, есть ли для агента,
находящегося в текущем узле, следующий ход. Если агенту некуда идти, то есть в
списке tabu нет  , то функция рассматривает следующего агента. Если списке
tabu есть хотя бы один
, то функция рассматривает следующего агента. Если списке
tabu есть хотя бы один  , значит, муравей может совершить еще один ход. Если муравей
еще не посетил все города, то есть если переменная pathIndex_city не равна
MAX_CITIES, то в этом случае вызывается функция selectNextCity, которая
определяет следующую грань. Затем выбранный узел сохраняется в переменной
nextcity, а также в массивах path и tabu. Увеличивается на единицу переменная
pathIndex, а если выбранный узел оказался городом, то увеличивается на единицу
переменная pathIndex_city. Рассчитывается значение tourLength, чтобы сохранить
длину пути.
, значит, муравей может совершить еще один ход. Если муравей
еще не посетил все города, то есть если переменная pathIndex_city не равна
MAX_CITIES, то в этом случае вызывается функция selectNextCity, которая
определяет следующую грань. Затем выбранный узел сохраняется в переменной
nextcity, а также в массивах path и tabu. Увеличивается на единицу переменная
pathIndex, а если выбранный узел оказался городом, то увеличивается на единицу
переменная pathIndex_city. Рассчитывается значение tourLength, чтобы сохранить
длину пути.
Один вызов функции simulateAnts позволяет каждому
муравью перейти от одного узла к другому. Функция simulateAnts возвращает нуль,
если посещены все города, в противном случае - значение, отличное от нуля.
После завершения пути выполняется процесс обновления путей. Он включает
не только обновление путей по количеству фермента, оставленного агентами, но и
существующего фермента, часть которого испарилась. Эту часть алгоритма
выполняет функция updateTrails.
Первая задача функции updateTrails заключается в том,
чтобы испарить часть фермента, который уже находится на пути. Она выполняется
на всех видимых ребрах графа с помощью уравнения (8). Следующая задача -
получение нового фермента на путях, пройденных муравьями во время последних
перемещений. Для этого необходимо пройти по элементам массива ant и,
руководствуясь значением поля path, «распылить» новый фермент на посещенной
муравьем грани в соответствии с уравнением (6). Затем следует применить
параметр RHO, чтобы снизить интенсивность фермента, который выделяют муравьи.
После инициализации генератора случайных чисел и установки начальных
значений параметров алгоритма запускается симуляция для количества шагов,
заданного константой MAX_TIME. Когда муравей завершает путь (который он
проходит с помощью функции simulateAnts), вызывается функция updateTrails для
того, чтобы изменить окружающую среду.
Следует обратить внимание, что каждый раз при завершении пути вызывается
функция restartAnts. Это делается для того, чтобы подготовиться к следующему
путешествию по графу. Функция restartAnts не вызывается только в случае,
если симуляция уже завершена. Дело в том, что функция уничтожает информацию о
пути муравья, которую необходимо сохранить в самом конце, чтобы определить
наилучший путь.
.4.6
Моделирование алгоритма муравья на ЭВМ
В данном разделе представлены результаты моделирования алгоритма муравья
на примере задачи коммивояжера с препятствиями.
Моделирование производилось с двумя целями:
- изучение влияния параметров  ,
,  ,
, 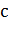 на сходимость алгоритма к оптимальному решению
на сходимость алгоритма к оптимальному решению
- сравнение с алгоритмом Дейкстры.
Для изучения влияния параметров было произведено моделирование алгоритма
муравья при различных значениях параметров  ,
,  ,
, 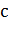 . Тестируемые значения параметров выбирались в соответствии с
рекомендациями основателя алгоритма Марко Дориго. /28/ Параметр Q не
рассматривался, т.к. согласно данной работе величина Q не влияет на
производительность алгоритма. В качестве постоянного значения Q было выбрано
значение 20. Во всех экспериментах количество муравьев было равно количеству
городов. Каждый муравей начинал свой путь из города, а не из вершины
препятствия. Менялась величина одного параметра, при этом величина других
параметров оставалась неизменной. В качестве постоянных параметров
использовались следующие значения:
. Тестируемые значения параметров выбирались в соответствии с
рекомендациями основателя алгоритма Марко Дориго. /28/ Параметр Q не
рассматривался, т.к. согласно данной работе величина Q не влияет на
производительность алгоритма. В качестве постоянного значения Q было выбрано
значение 20. Во всех экспериментах количество муравьев было равно количеству
городов. Каждый муравей начинал свой путь из города, а не из вершины
препятствия. Менялась величина одного параметра, при этом величина других
параметров оставалась неизменной. В качестве постоянных параметров
использовались следующие значения: 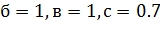 . В каждом эксперименте изменялась
величина только одного параметра. Изменяемые значения параметров:
. В каждом эксперименте изменялась
величина только одного параметра. Изменяемые значения параметров: 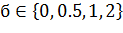 ,
,  ,
, 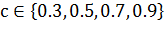 . Количество циклов алгоритма в
каждом эксперименте менялось пропорционально количеству городов и равнялось
MAX_TOURS * MAX_CITIES*10. Каждая комбинация параметров тестировалась десять
раз.
. Количество циклов алгоритма в
каждом эксперименте менялось пропорционально количеству городов и равнялось
MAX_TOURS * MAX_CITIES*10. Каждая комбинация параметров тестировалась десять
раз.
Моделирование производилось на персональном компьютере на базе процессора
Intel Core 2 Duo 2.67 GHz, с объемом оперативной памяти 2GB. Количество городов
изменялось от 5 до 25 городов с шагом 5. Количество препятствий равнялось трем,
конфигурация препятствий: треугольник, прямоугольник и восьмиугольник.
Конфигурация препятствий, их координаты и координаты городов были заданы
дипломным руководителем и представлены в Приложении 2.
Подробные результаты каждого эксперимента и все временные диаграммы, характеризующие
влияние параметров  ,
,  ,
,  расположены в Приложении 3. Анализ полученных результатов
будет произведен в следующем разделе. В данном разделе остановимся на лучших
решениях, которые были получены.
расположены в Приложении 3. Анализ полученных результатов
будет произведен в следующем разделе. В данном разделе остановимся на лучших
решениях, которые были получены.
Вариант задачи с пятью городами
В связи с маленьким количеством городов, при всех комбинациях параметров,
кроме 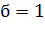 ,
, 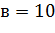 ,
, 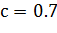 была найдена минимальная длина пути:
199,361. Результат работы алгоритма проиллюстрированы на рисунке (9):
была найдена минимальная длина пути:
199,361. Результат работы алгоритма проиллюстрированы на рисунке (9):
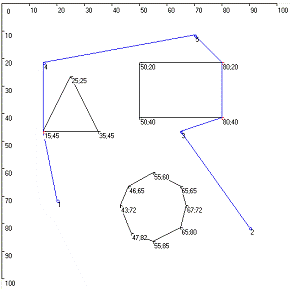
Рисунок 9. Результат работы алгоритма муравья для 5 городов.
Вариант задачи с десятью городами
В данном примере минимальная найденная длина пути составила: 262,045.
Параметры, при которых она был найден:
 ,
, 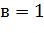 ,
, 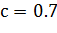
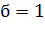 ,
, 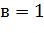 ,
, 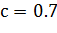
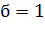 ,
, 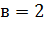 ,
, 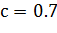
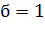 ,
, 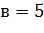 ,
, 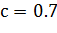
Результат работы алгоритма проиллюстрированы на рисунке (10):
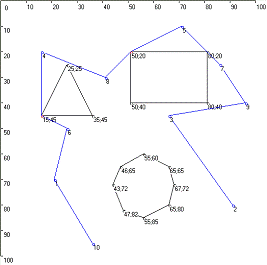
Рисунок 10. Результат работы алгоритма муравья для 10 городов.
Вариант задачи с пятнадцатью городами
В данном примере минимальная найденная длина пути составила: 303,926.
Параметры, при которых оно был найден:
 ,
, 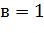 ,
, 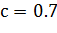
Результат работы алгоритма проиллюстрированы на рисунке (11):
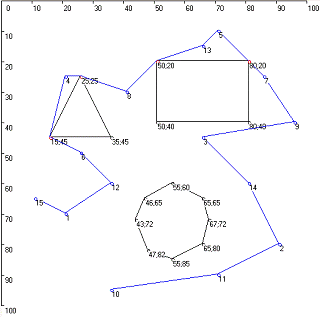
Рисунок 11. Результат работы алгоритма муравья для 15 городов.
Вариант задачи с двадцатью городами
В данном примере минимальная найденная длина пути составила: 341,038.
Параметры, при которых она была найдена:
 ,
, 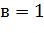 ,
, 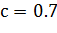
Результат работы алгоритма проиллюстрированы на рисунке (12):
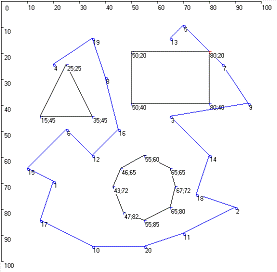
Рисунок 12. Результат работы алгоритма муравья для 20 городов.
Вариант задачи с двадцатью пятью городами
В данном примере минимальная найденная длина пути составила: 375,068.
Параметры, при которых она была найдена:
 ,
, 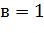 ,
, 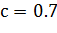
Результат работы алгоритма проиллюстрированы на рисунке (13):
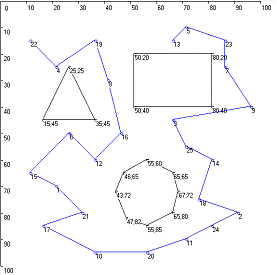
Рисунок 13. Результат работы алгоритма муравья для 25 городов.
Для сравнения с алгоритмом Дейкстры была рассмотрена работа аспиранта 301
кафедры МАИ Чжо Мьо Хана. /10/ В данной работе задача коммивояжера с
препятствиями решена с помощью алгоритма Дейкстры. Для обхода препятствий
использовалась диаграмма Вороного. Данная задача используется в качестве
тестовой для сравнения её с алгоритмом муравья. Исходный код программы
представлен в Приложении 4. Задача изображена на рисунке 14:
Рисунок 14. Тестовая задача, решенная с помощью алгоритма Дейкстры
Минимальный путь, найденный алгоритмом Дейкстры для данной задачи,
составил 170,32.
Задача с такой же конфигурацией городов и препятствий была решена
алгоритмом муравья. Использовались следующие параметры алгоритма:
 ,
, 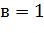 ,
, 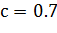
Число муравьев равнялось количеству городов. Количество циклов алгоритма
было задано равным 2400. Результаты моделирования представлены на рисунке 15:
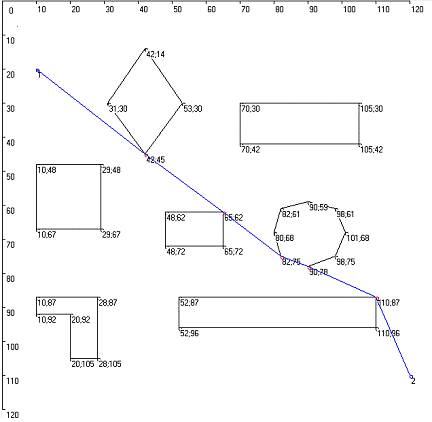
Рисунок 15. Тестовая задача, решенная алгоритмом муравья
Минимальный путь, найденный алгоритмом муравья, составил 146,165. Таким
образом, можно сделать вывод, что алгоритм муравья справился с тестовой задачей
лучше.
1.5 Анализ
полученных результатов
В данном подразделе проанализировано влияние параметров  ,
,  ,
,  на сходимость алгоритма муравья к оптимальному решению.
на сходимость алгоритма муравья к оптимальному решению.
В варианте задачи с пятью городами алгоритм муравья показывает наилучшие
результаты (в десяти случаях из десяти) при следующих значениях параметров:  ,
,  ,
, 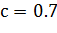 . В дальнейшем будем называть эту
комбинацию параметров набором номер один. Следует отметить, что в связи с
относительно малым количеством городов, алгоритм достаточно хорошо сходится к
минимальному решению и при всех остальных значениях параметров
. В дальнейшем будем называть эту
комбинацию параметров набором номер один. Следует отметить, что в связи с
относительно малым количеством городов, алгоритм достаточно хорошо сходится к
минимальному решению и при всех остальных значениях параметров  ,
, 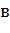 ,
, 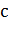 , кроме следующего:
, кроме следующего: 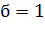 ,
, 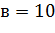 ,
, 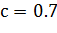 . Причина этого будет описана ниже.
. Причина этого будет описана ниже.
С увеличением городов до десяти алгоритм муравья по-прежнему показывает
наилучшие результаты при наборе параметров номер один. Средний путь составляет
256, 176. Алгоритм муравья находит близкие к этому найденному минимальному
решению результаты (266, 306; 268, 173) при следующих значениях параметров: 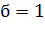 ,
, 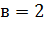 ,
, 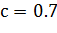 и
и 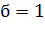 ,
, 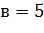 ,
, 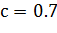 . В дальнейшем будем называть их
набором параметров номер два и три соответственно. При всех остальных значениях
параметров алгоритм находит решения со средним значением, отличающимся от
минимального найденного, в большую сторону более чем на 10.
. В дальнейшем будем называть их
набором параметров номер два и три соответственно. При всех остальных значениях
параметров алгоритм находит решения со средним значением, отличающимся от
минимального найденного, в большую сторону более чем на 10.
На рисунке 16 в графическом виде представлена зависимость среднего
найденного пути от нескольких наборов параметров.
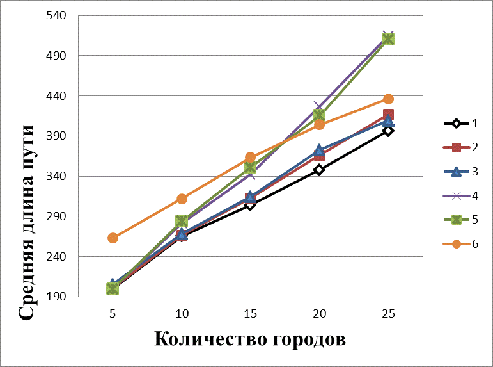
Рисунок 16. Влияние параметров алгоритма на среднюю длину пути.
На данном рисунке:
график под номером 1 ( ) соответствует набору параметров номер один:
) соответствует набору параметров номер один:  ,
, 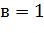 ,
, 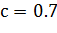 ;
;
график под номером 2 ( ) соответствует набору параметров номер два:
) соответствует набору параметров номер два: 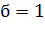 ,
, 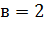 ,
, 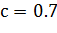 ;
;
график под номером 3 ( ) соответствует набору параметров номер три:
) соответствует набору параметров номер три:
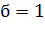 ,
, 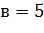 ,
, 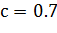 ;
;
график под номером 4 ( ) соответствует следующему набору параметров:
) соответствует следующему набору параметров:
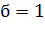 ,
, 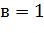 ,
, 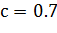 ;
;
график под номером 5 ( ) соответствует следующему набору параметров:
) соответствует следующему набору параметров:
график под номером 6 ( ) соответствует следующему набору параметров:
) соответствует следующему набору параметров:
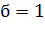 ,
, 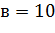 ,
, 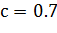 .
.
Зависимость длины среднего найденного пути от всех протестированных
наборов параметров в графическом виде представлена на рисунке 22 в Приложении
3.
Как видно из рисунка 16, наилучший результат во всех пяти задачах
достигается при наборе параметров номер один, затем при наборе параметров номер
два и три. Следует отметить, что с увеличением количества городов увеличивается
разница между длиной среднего пути, найденной при наборе параметров номер один
и между длинами средних путей, найденных при всех остальных наборах параметров.
При этом если для набора параметров номер и два и три эта разница не велика (не
более 20), то для всех других наборов параметров (кроме нижеописанного) разница
более существенна (более 50).
Единственным исключением является следующий набор параметров: 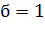 ,
, 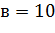 ,
, 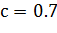 . В нем с увеличением количества
городов разница с минимальной найденной длиной пути уменьшается. Это можно
объяснить тем, что параметр
. В нем с увеличением количества
городов разница с минимальной найденной длиной пути уменьшается. Это можно
объяснить тем, что параметр 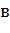 определяет вес расстояния при расчете вероятности по формуле
(5). С увеличением количества городов увеличивается и минимальное расстояние,
находимое алгоритмом муравья. Следовательно, увеличивается влияние параметра
определяет вес расстояния при расчете вероятности по формуле
(5). С увеличением количества городов увеличивается и минимальное расстояние,
находимое алгоритмом муравья. Следовательно, увеличивается влияние параметра 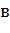 на найденное решение. Таким образом,
при малом количестве городов (при пяти) влияние параметра
на найденное решение. Таким образом,
при малом количестве городов (при пяти) влияние параметра 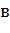 мало и при значении
мало и при значении 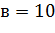 алгоритм сходится к неоптимальному
решению. При увеличении количества городов (более 15) влияние параметра
алгоритм сходится к неоптимальному
решению. При увеличении количества городов (более 15) влияние параметра 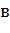 увеличивается и разница с
минимальной найденной длиной пути уменьшается.
увеличивается и разница с
минимальной найденной длиной пути уменьшается.
Таким образом, можно заключить, что при дальнейшем увеличении количества
городов следует использовать набор параметров номер один, либо набор параметров
номер 6.
Время выполнения программы можно оценивать только в пределах одного
варианта задачи, т.к. с увеличением количества городов пропорционально
увеличивается количество циклов выполнения алгоритма. Как и следовало ожидать,
при дробных значениях параметров  и
и 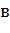 увеличивается время выполнения
программы, т.к. эти параметры входят в уравнение (5) в качестве степеней. В
зависимости от количества городов при дробных значениях параметров
увеличивается время выполнения
программы, т.к. эти параметры входят в уравнение (5) в качестве степеней. В
зависимости от количества городов при дробных значениях параметров  и
и 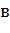 это время увеличиваются на 30-50% по
сравнению со временем выполнения программы при целых значениях
это время увеличиваются на 30-50% по
сравнению со временем выполнения программы при целых значениях  и
и 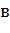 .
.
2. Экономическая часть
.1
Определение целесообразности разработки алгоритма
Целью дипломной работы является разработка алгоритма муравья для решения
задачи коммивояжера. Разработка алгоритма, его применение, задание исходных
данных для его работы, моделирование и анализ результатов проводятся на
персональном компьютере.
Для экономической эффективности разрабатываемых алгоритмов и программного
продукта (ПП) необходимо:
определить целесообразность выполнения разработки;
определить трудоемкость и затраты на создание ПП;
определить показатели экономической эффективности разработки ПП.
Для того чтобы обосновать целесообразность разработки ПП, дать оценку
технической прогрессивности и качеству реализации, необходимо сравнить ее с
одним из существующих аналогов, который принят в качестве базового. В качестве
такого аналога будем рассматривать алгоритм Дейкстры, применяемый в настоящее
время для решения задачи коммивояжера.
Анализируемые характеристики качества алгоритмов и программных продуктов
представлены в таблице 8.
Таблица 8. Характеристики качества алгоритмов и программных продуктов.
|
№
|
Характеристики качества ПП
|
Единица измерения
|
Значения характеристик качества ПП
|
Значимость характеристик
|
|
|
|
аналог
|
новый вариант
|
|
|
1
|
Универсальность
|
Относительные единицы
|
1
|
2
|
0.2
|
|
2
|
Точность
|
|
1
|
1.3
|
0.2
|
|
3
|
Надежность
|
|
1
|
1.5
|
0.2
|
|
4
|
Возможность модернизации
|
|
1
|
4
|
0.4
|
Определим индекс технического уровня разработки по формуле:
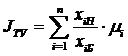
где
xiН, xiБ - уровень i-ой функциональной характеристики
соответственно нового и базового ПП;
μi -
значимость i-ой функциональной характеристики;- количество рассматриваемых
функциональных характеристик.
Значимость
i-ой функциональной характеристики определяется экспертным путем, при этом
учитывается условие:
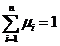 .
.
Таким
образом, индекс технического уровня равен:
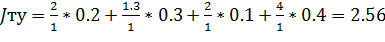
Индекс
технического уровня разрабатываемого ПП больше единицы, следовательно, делаем
заключение о целесообразности разработки.
.2
Определение трудоемкости разработки алгоритма и ПП
В процессе планирования разработки ПП определяется трудоемкость его
создания. При традиционном программировании каждый элемент ПП содержит все
этапы решения задачи, начиная с ввода исходных данных и кончая выводом
результатов. Для этого случая затраты труда в чел.-час определяются по формуле:
ПП = tО + tИ + tА + tК + tОТ
+ tД ,
где tО - затраты труда на подготовку описания задачи;И
- затраты труда на изучение описания задачи;А - затраты труда на
разработку алгоритма решения задачи;К - затраты труда на составление
программы;ОТ - затраты труда на отладку программы;Д -
затраты труда на подготовку документации по ПП.
Условное количество команд в программе определяется следующим образом:
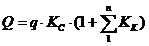 ,
,
где=
1200- - предполагаемое количество команд,
КС
- коэффициент сложности программы, характеризует относительную сложность
программы по отношению к так называемой типовой задаче, реализующей стандартные
методы решения, сложность которой принята равной единице (величина с лежит в
пределах от 1,25 до 2). Для программного продукта, реализующего алгоритм,
сложность задачи возьмем 1,6.
КК
- коэффициент коррекции программы в ходе разработки, т.е. увеличение объема
работ за счет внесения изменений в алгоритм или программу по результатам
уточнения постановок. В данном случае заказчик хорошо представлял себе, что он
хочет получить, это не требовало многочисленных доработок. С учетом этого
возьмем коэффициент равный 0,07.
Таким
образом, условное количество команд в разрабатываемой программе:
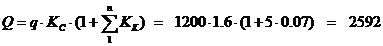
Составляющие
затрат труда рассчитываются по формулам:
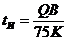 ;
;
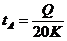 ;
;
 ;
;
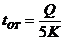 ;
;
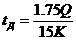 ,
,
где
В - коэффициент увеличения затрат труда на изучение и постановку задачи
вследствие их сложности и новизны (В = 1.2 - 3.0);
К=1
- коэффициент квалификации разработчика, определяется в зависимости от стажа
работы и составляет:
- для работающих до двух лет - 0,8;
от двух до трех лет - 1,0;
от трех до пяти лет - 1,1 - 1,2;
от пяти до семи - 1,3 - 1,4;
свыше семи лет - 1,5 - 1,6.
Разработчик, которому было поручено это задание, имел опыт работы по
специальности 2.5 года.
Цифры, находящиеся в знаменателях формул, характеризуют среднюю
производительность труда программистов (число команд или операторов в час).
Таким образом, составляющие трудоемкости разрабатываемого ПП (чел.-час.):
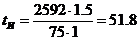 ;
;
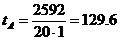 ;
;
 ;
;
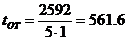 ;
;
 ;
;
Значение
tO примем равным 20 чел.-час.
Тогда
общие затраты труда составляют:ПП= 20 + 51.8 + 129.6 + 280.8 + 561.6
+ 327.6 = 1319.6 чел.-час.
.3
Календарное планирование
Календарное планирование создания ПП производится на основе данных о
трудоемкости работ по его созданию.
Производственный цикл каждого этапа определяется по формуле:
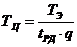 ;
;
где
ТЭ - трудоемкость этапа, чел.-час.;РД - продолжительность
рабочего дня, ч. (tРД = 8ч.);- количество работников одновременно
участвующих в выполнении работ, чел.
Пересчет
длительности производственного цикла, выраженной в человеко-часах, в
календарные дни осуществляют умножением ее на коэффициент 1.4, т.е:
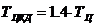 .
.
Произведем
расчет длительности каждого этапа:
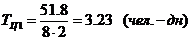 ;
; 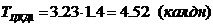 ;
;
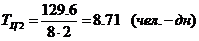 ;
; 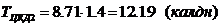 ;
;
 ;
; 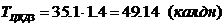 ;
;
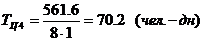 ;
; 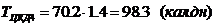 ;
;
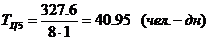 ;
; 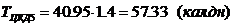 ;
;
Результаты
расчета и директивный график представлены в таблице 9.
|
Наименование этапов
|
Удельный вес, %
|
Трудоемкость этапа, чел.-час.
|
Количество исполнителей
|
Длительность этапа, кал. дни
|
Календарные дни
|
|
|
|
|
|
30
|
60
|
90
|
120
|
150
|
180
|
210
|
240
|
|
изучение описания задачи
|
3.9
|
51.8
|
2
|
4.52
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разработка алгоритма
|
9.7
|
129.6
|
2
|
12.19
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составление программы
|
21.5
|
280.8
|
1
|
49.14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отладка программы
|
41
|
561.6
|
1
|
98.3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подготовка документации
|
23.9
|
327.6
|
1
|
57.33
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всего
|
100
|
1351.4
|
|
221.4
|
|
|
|
|
|
|
|
|
Таблица 9. Календарное планирование
.4 Расчет
заработной платы основного персонала
Заработная плата разработчиков программы рассчитывается на основе
трудоемкости стадий работ. Часовые ставки определяются на основе должностных
окладов разработчиков и разрядов работ (часовых тарифных ставок). Расчет
заработной платы представлен в таблице 10.
|
№
|
Стадии (этапы)
|
Трудоемкость стадий, чел.-дн.
|
Исполнители
|
Днев. ставка руб.
|
Сред. днев. ставка руб.
|
З/п, руб.
|
З/п с уч. премий руб.
|
|
|
|
Должность
|
Кол-во.
|
|
|
|
|
|
1
|
Подготовка описания и изучение задачи
|
5
|
программист
|
1
|
1000
|
1100
|
5500
|
7700
|
|
|
|
ведущий специалист
|
1
|
1200
|
|
|
|
|
2
|
Разработка алгоритма
|
13
|
программист
|
1
|
1000
|
1100
|
14300
|
20020
|
|
|
|
ведущий специалист
|
1
|
1200
|
|
|
|
|
3
|
Составление программы
|
49
|
программист
|
1
|
1000
|
1000
|
49000
|
68600
|
|
4
|
Отладка программы
|
98
|
программист
|
1
|
1000
|
1000
|
98000
|
137200
|
|
5
|
Подготовка документации
|
57
|
программист
|
1
|
1000
|
1000
|
57000
|
79800
|
|
Всего
|
222
|
|
|
|
|
223800
|
313500
|
Таблица 10. Расчет заработной платы основного персонала
Премия составляет 40% от заработной платы. Заработная плата основного
персонала рассчитана по формуле:
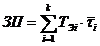 ,
,
где
k - количество этапов;
ТЭi
- трудоемкость i-го этапа;
 -
средняя часовая тарифная ставка оплаты труда работ i-го этапа.
-
средняя часовая тарифная ставка оплаты труда работ i-го этапа.
.5
Определение затрат на создание алгоритмов и ПП
Затраты на создание алгоритмов и ПП определяются по следующим статьям:
1. заработная плата основных исполнителей;
2. отчисления на социальные нужды;
. накладные расходы;
. прочие расходы.
Заработная плата основных исполнителей
Заработная плата основных исполнителей рассчитана в пункте 2.4 и, с
учетом премий, составляет ЗПП = 313500 р.
Отчисления на социальные службы
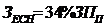
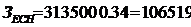 р.
р.
Накладные
расходы
 ,
,
 р.
р.
Прочие
расходы
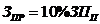 ,
,
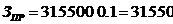 р.
р.
Сводная таблица затрат
Затраты на создание алгоритмов и ПП сведены в таблицу 11.
|
№
|
Наименование статей затрат
|
Затраты, руб.
|
Удельный вес, %
|
|
1
|
Заработная плата основных исполнителей
|
315500
|
38
|
|
2
|
Отчисления на социальные нужды
|
106519
|
12.9
|
|
3
|
Накладные расходы
|
376200
|
45.3
|
|
4
|
Прочие расходы
|
31550
|
3.8
|
|
Итого:
|
829769
|
100
|
Таблица 11. Структура затрат на создание алгоритмов и ПП
Цена предложения
Цена первоначально разработанных алгоритмов и ПП с учётом рентабельности
разработки:
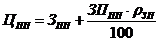 ,
,
где
ЗПП - затраты на создание алгоритмов и ПП;
ЗППП
- заработная плата основных исполнителей;
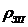 -
рентабельность разработки ПП по отношению к оплате труда персонала,
обеспечивающая безубыточную деятельность (
-
рентабельность разработки ПП по отношению к оплате труда персонала,
обеспечивающая безубыточную деятельность (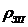 =200-400%; выберем значение - 250%)
=200-400%; выберем значение - 250%)
Таким
образом:
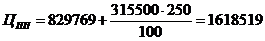 р.
р.
.6 Расчет
экономической эффективности
Показатель годового экономического эффекта определяется по формуле:
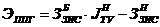 ,
,
где
 - годовые эксплуатационные затраты в информационной
системе по базовому и новому варианту соответственно, руб.
- годовые эксплуатационные затраты в информационной
системе по базовому и новому варианту соответственно, руб.
Таким
образом:
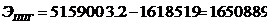 руб.
руб.
Для
разрабатываемого ПП уровень экономической эффективности капиталовложений
составляет:
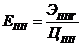 ,
,
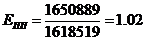 .
.
Срок
окупаемости затрат на создание алгоритмов и ПП определяется как величина,
обратная ЕПП:
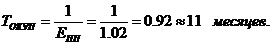
.7 Выводы
В данном разделе был проведен расчет затрат на разработку алгоритма
муравья для решения задачи коммивояжера. На основании величины уровня
экономической эффективности (ЕПП=1.02), а также срока окупаемости
затрат на создание алгоритма и ПП (около 11 месяцев) можно сделать вывод о том,
что разработка и внедрение данного ПП являются экономически целесообразными и
эффективными.
3. Охрана
труда и окружающей среды
.1 Введение
Темой моей дипломной работы является использование алгоритма муравья для
решения задачи коммивояжера. Разработка алгоритма, его применение, задание
исходных данных для его работы, моделирование и анализ результатов проводятся в
вычислительном центре (лаборатории) на персональном компьютере. Все эти этапы
требуют достаточно продолжительного пребывания за компьютером. В данном разделе
необходимо провести анализ условий труда инженера-программиста, рассмотреть все
вредные факторы, вытекающие из условий длительной работы за компьютером.
Характеристика технических средств.
В рабочем помещении размещены следующие технические средства:
. Персональный компьютер, количество: 12.
Характеристики персонального компьютера предоставлены в таблице 12:
|
системный блок
|
U = 220 В, L = 35 дБ, P = 500 Вт
|
|
ЖК-монитор
|
U = 220 В, P = 35 Вт
|
|
клавиатура
|
U = 5 В, P = 1 Вт
|
|
манипулятор типа “мышь”
|
U = 5 В, P = 1 Вт
|
Таблица 12. Характеристики персонального компьютера.
. Лазерный принтер, количество: 1.
Характеристики:
U = 220 В, L = 40 дБ:, P = 150 Вт.
3. Кондиционер, количество: 1.
Характеристики:
U = 220 В, L = 37-44 дБ:, P = 1550 Вт в режиме
охлаждения, Р = 1420 Вт в режиме нагрева.
Характеристика помещения предоставлены в таблице 13:
|
Длина:
|
7 м
|
|
Ширина:
|
6 м
|
|
Высота:
|
3 м
|
|
Общая площадь комнаты:
|
42 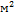
|
|
Количество рабочих мест в помещении:
|
12
|
|
Площадь, приходящаяся на одного работника
|
3.5 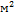
|
|
Объем, приходящийся на одного работника
|
10.5 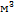
|
Таблица 13. Характеристика помещения
Естественное освещение осуществляется с помощью трех окон размером 1.5 х
2.5 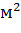 .
.
Искусственное освещение осуществляется с помощью четырех светильников с
четырьмя люминесцентными лампами.
Для поддержания благоприятных микроклиматических условий помещение
оборудовано системой отопления и кондиционирования.
Анализ
условий труда
Анализ условий труда будем осуществлять по следующей схеме:
Санитарно- гигиенические факторы:
Микроклимат
Освещение
Электробезосопасность
Шум
Вибрации
Электромагнитные излучения (ЭМИ)
Эргономика рабочего места
Психофизиологические факторы
Рассмотрим отдельно каждый из вредных факторов.
.2.
Санитарно- гигиенические факторы
.2.1 Микроклимат
Вычислительная техника является источником существенных тепловыделений,
что может привести к повышению температуры и снижению относительной влажности в
помещении. Требования к микроклимату определяются ГОСТ 12.1.005-88 "Воздух
рабочей зоны".
Работа по разработке алгоритма относится к категории
Iа «Легкая физическая», т.к. работа производится сидя и не требует физического
напряжения. Ниже, в таблице 14, приведены оптимальные параметры микроклимата
согласно ГОСТ 12.1.005-88 «Воздух рабочей зоны».
|
Период года
|
Категория работ
|
Температура воздуха на рабочих местах
|
Относительная влажность
|
Скорость движения воздуха, м/с
|
|
Холодный
|
Легкая - I а
|
22-24
|
40 - 60
|
0,1
|
|
Теплый
|
Легкая - I а
|
23-25
|
40 - 60
|
0,1
|
Таблица 14. Оптимальные параметры микроклимата для помещений с ПЭВМ
Температура в помещении, в котором производится разработка алгоритма,
составляет 23…24°С в теплый и 22…23°С в холодный периоды года. Относительная
влажность - 45…60 %. Скорость движения воздуха - 0.08…0.1 м/с.
Для
поддержания и контроля нормальных параметров микроклимата в рабочей зоне в
холодное время применяют водяную систему отопления. В теплое время года
применяется система кондиционирования воздуха, кондиционер AEG KWI 50i/KWA 50i.
<#"607393.files/image218.gif">. По форме она может быть прямоугольной, иметь вырез для
корпуса работающего или углубление для клавиатуры. Под столом должно иметься
пространство для ног с размерами по глубине 650 мм. Под столешницей рабочего
стола предусматривается свободное пространство для ног размерами: по высоте -
не менее 600 мм, по ширине - 500 мм, по глубине - 650 мм. Удаленность
клавиатуры от переднего края стола до нижнего ряда клавиатура составляет 80-100
мм.
Рабочий стул программиста должен быть снабжен подъемно-поворотным
механизмом. Высота сиденья должна регулироваться в пределах 400 - 550 мм,
глубина в пределах 380 - 420 мм, а ширина - в пределах 400-450 мм. Высота
верхней кромки спинки относительно сидения должна составлять 320 мм, ширина
-360 - 400 мм. Угол наклона спинки стула к плоскости сиденья должен изменяться
в пределах 95 - 110°.
В данном помещении соблюдено оптимальное расположение
оборудования, входящего в состав рабочего места. Обеспечено достаточное рабочее
пространство, позволяющее выполнять все необходимые движения и перемещения
согласно ГОСТ 12.2.032-78. Рабочее место соответствует характеристикам
оптимального размещения предметов труда в зоне досягаемости рук программиста.
Конструкции рабочих поверхностей соответствуют требованиям СанПиН
2.2.2/2.4.1340-03. Конструкция рабочего стола, рабочего стула обеспечивают
оптимальное положение оператора в рациональной позе сидя. Высота сиденья
регулируется в пределах 400-600 мм. ЖК-монитор соответствует требованиям ГОСТ
Р52324-2005. Следовательно, можно сделать вывод о том, что в рабочем помещении
выполняются требования к эргономике.
.3
Психофизиологические факторы
При работе с персональным компьютером очень важную роль играет соблюдение
правильного режима труда и отдыха. В противном случае у персонала отмечаются
значительное напряжение зрительного аппарата с появлением жалоб на
неудовлетворенность работой, головные боли, раздражительность, нарушение сна,
усталость и болезненные ощущения в глазах, в пояснице, в области шеи и руках.
Все психофизиологические факторы включают в себя физическую и
нервно-психологическую (интеллектуальную или сенсорную) нагрузки на человека в
процессе труда.
- Повышение уровня механизации и автоматизации
трудоемких производственных процессов, использование современной
высокопроизводительной техники;
- Совершенствование организации рабочих мест;
Организация приемов и методов труда;
Оптимизация темпа работы;
Оптимизация режима труда и отдыха;
Научно обоснованное установление норм
обслуживания оборудования и норм времени его обслуживания с учетом объема
информации, который работник может правильно воспринять, переработать и принять
своевременное и правильное решение;
Чередование работ, требующих участия разных
анализаторов (слуха, зрения, осязания и др.);
Чередования работ, требующих преимущественно
умственных нагрузок с работами физическими;
Чередование работ разной сложности и
интенсивности;
Оптимизация режимов труда и отдыха;
Ритмизация труда (работа по графику с
пониженной на 10-15% нагрузкой в первый и последний часы рабочей смены);
3.4. Расчет
освещенности
Расчет освещенности рабочего места сводится к выбору системы
освещения, определению необходимого числа светильников, их типа и размещения.
Исходя из этого, рассчитаем параметры искусственного освещения.
Обычно искусственное освещение выполняется посредством
электрических источников света двух видов: ламп накаливания и люминесцентных
ламп. Будем использовать люминесцентные лампы, которые по сравнению с лампами
накаливания имеют ряд существенных преимуществ:
- по спектральному составу света они близки к
дневному, естественному свету;
- обладают более высоким КПД (в 1,5-2раза выше,
чем КПД ламп накаливания);
обладают повышенной светоотдачей (в 3-4 раза
выше, чем у ламп накаливания);
более длительный срок службы.
Расчет освещения производится для комнаты площадью 42
м2, длиной 7 м и шириной 6 м.
Расчет
освещения будем производить по методу коэффициента использования светового
потока. Рассматриваемый метод позволяет производить расчет осветительной
установки (ОУ) с учетом прямой и отраженной составляющих освещенности и
применяется для расчета общего равномерного освещения
<#"607393.files/image219.gif">, где
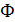 -
рассчитываемый световой поток, лм;
-
рассчитываемый световой поток, лм;
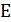 -
нормированная минимальная освещенность, лк. В соответствии с пунктом 1.1.2,
-
нормированная минимальная освещенность, лк. В соответствии с пунктом 1.1.2,  ;
;
 -
площадь освещаемого помещения (в нашем случае S =42 м2);
-
площадь освещаемого помещения (в нашем случае S =42 м2);
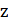 -коэффициент
минимальной освещенности, характеризует неравномерность освещения и составляет
1.1 для люминесцентных ламп.
-коэффициент
минимальной освещенности, характеризует неравномерность освещения и составляет
1.1 для люминесцентных ламп.
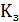 -
коэффициент запаса, учитывающий уменьшение светового потока лампы в результате
загрязнения светильников в процессе эксплуатации (его значение зависит от типа
помещения и характера проводимых в нем работ; в нашем случае производственное
помещение: лаборатория, искусственное освещение: газоразрядные лампы,
-
коэффициент запаса, учитывающий уменьшение светового потока лампы в результате
загрязнения светильников в процессе эксплуатации (его значение зависит от типа
помещения и характера проводимых в нем работ; в нашем случае производственное
помещение: лаборатория, искусственное освещение: газоразрядные лампы, 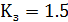 );
);
 -
установленное число светильников,
-
установленное число светильников,  ;
;
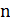 - число
ламп в светильнике,
- число
ламп в светильнике,  ;
;
 -
коэффициент использования светового потока, выражается отношением светового
потока, падающего на расчетную поверхность, к суммарному потоку всех ламп и
исчисляется в долях единицы; зависит от характеристик светильника, размеров
помещения, окраски стен и потолка, характеризуемых коэффициентами отражения от
стен
-
коэффициент использования светового потока, выражается отношением светового
потока, падающего на расчетную поверхность, к суммарному потоку всех ламп и
исчисляется в долях единицы; зависит от характеристик светильника, размеров
помещения, окраски стен и потолка, характеризуемых коэффициентами отражения от
стен  , потолка
, потолка 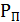 и
расчетной поверхности
и
расчетной поверхности 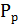 ; значение коэффициентов:
; значение коэффициентов: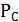 =0.5,
=0.5, 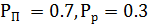 (в
помещениях, где находится компьютер, необходимо обеспечить следующие величины
коэффициента отражения: для потолка: 80... 90%, для стен: 50... 60%, для пола:
около 30%. Для других поверхностей и рабочей мебели: 30... 40%).
(в
помещениях, где находится компьютер, необходимо обеспечить следующие величины
коэффициента отражения: для потолка: 80... 90%, для стен: 50... 60%, для пола:
около 30%. Для других поверхностей и рабочей мебели: 30... 40%).
Индекс
помещения:
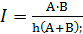 , где
, где
 - площадь
помещения,
- площадь
помещения,  ;
;
 -
расчетная высота подвеса,
-
расчетная высота подвеса, 
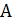 - ширина
помещения,
- ширина
помещения,  ;
;
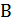 - длина
помещения,
- длина
помещения, 
Подставив
значения, получим: 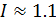 .
.
Зная
индекс помещения  , по таблице 2 приложения 3 Методических указаний «Производственное
освещение авиастроительных предприятий», находим
, по таблице 2 приложения 3 Методических указаний «Производственное
освещение авиастроительных предприятий», находим 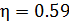 .
.
Подставим
все значения в формулу для определения светового потока  и получим следующее значение:
и получим следующее значение: 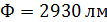 .
.
В помещении используются люминесцентные лампы типа ЛБ-40, световой поток
которых 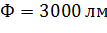 .
.
Таким образом, используемые лампы дневного света удовлетворяют
требованиям.
Выводы
В разделе «Охрана труда и окружающей среды» изложены основные требования
безопасности для обеспечения работы инженера-программиста, произведен анализ
сформированных условий труда на соответствие нормативным значениям. Сделан
вывод о соблюдении в помещении правил электробезопасности, о соответствии
электромагнитного излучения, шума, вибрации, освещенности и микроклимата
нормам.
Фактор освещенности признан основным. Произведен анализ условий труда и
расчет освещенности вычислительного центра (лаборатории). Оптимальными для
освещения помещения являются лампы ЛБ-40 (лампы люминесцентные белого света,
мощность - 40 Вт, световой поток - 3000 лм). Показатель освещенности в данном
помещении не отклоняется от нормы. Шум и вибрация в помещении соответствуют
нормам.
Созданные условия должны обеспечить комфортную работу, что позволит
сохранить хорошую работоспособность в течение всего рабочего дня.
Заключение
В данной дипломной работе была рассмотрена задача коммивояжера с тремя
препятствиями заданной конфигурации и количеством городов, изменяющимся от 5 до
25 с шагом 5. Для решения задачи был использован алгоритм муравья.
Для каждого варианта задачи был успешно найден кратчайший маршрут. Было
оценено время выполнения программы. При дробных значениях параметров  и
и  время выполнения программы
увеличивается на 30-50%, в зависимости от количества городов.
время выполнения программы
увеличивается на 30-50%, в зависимости от количества городов.
Проанализировано влияние коэффициентов  ,
,  ,
,  на сходимость алгоритма к минимальному решению. Для всех
вариантов задачи наилучший результат был найден при следующих параметрах:
на сходимость алгоритма к минимальному решению. Для всех
вариантов задачи наилучший результат был найден при следующих параметрах:  ,
, 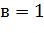 ,
, 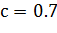 . На основании анализа влияния
параметров алгоритма на его сходимость к минимальному решению, сделан вывод,
что при дальнейшем увеличении количества городов увеличивается влияние параметра
. На основании анализа влияния
параметров алгоритма на его сходимость к минимальному решению, сделан вывод,
что при дальнейшем увеличении количества городов увеличивается влияние параметра
 на сходимость к минимальному
решению.
на сходимость к минимальному
решению.
Разработанную программу можно применять для задач с любым количеством
городов и с любым количеством препятствий.
В экономической части дипломной работы был проведен расчет затрат на
разработку алгоритма муравья для решения задачи коммивояжера. На основании
величины уровня экономической эффективности (ЕПП=1.02), а также
срока окупаемости затрат на создание алгоритма и ПП (около 11 месяцев) можно
сделать вывод о том, что разработка и внедрение данного ПП являются
экономически целесообразными и эффективными.
В разделе «Охрана труда и окружающей среды» изложены основные требования
безопасности для обеспечения работы инженера-программиста, произведен анализ
сформированных условий труда на соответствие нормативным значениям. Сделан
вывод о соблюдении в помещении правил электробезопасности, о соответствии
электромагнитного излучения, шума, вибрации, освещенности и микроклимата
нормам.
Фактор освещенности признан основным. Произведен анализ условий труда и
расчет освещенности вычислительного центра (лаборатории). Оптимальными для
освещения помещения являются лампы ЛБ-40 (лампы люминесцентные белого света,
мощность - 40 Вт, световой поток - 3000 лм). Показатель освещенности в данном
помещении не отклоняется от нормы. Шум и вибрация в помещении соответствуют
нормам.
Созданные условия должны обеспечить комфортную работу, что позволит
сохранить хорошую работоспособность в течение всего рабочего дня.
передвижение муравей задача коммивояжер
Список использованной литературы
1. Рассел
С. Дж., Норвиг, П. Искусственный интеллект: современный подход - М.: Вильямс,
2006. 2006.
. А.Левитин.
Алгоритмы. Введение в разработку и анализ, 2006.
. Томас
Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы. Построение
и анализ - М. «Вильямс», 2005.
. Павленко
А.И., Титов Ю.П. Метод муравьиной оптимизации в задачах распределения ресурсов
- МАИ, 2008.
5. Субботин С.А.,
Олейник Ан.А., Олейник Ал.А. Интеллектуальные мультиагентные методы (swarm
intelligence) - <#"607393.files/image250.gif">
Минимальная длина пути
|
Время,  с с
|
Средняя длина пути
|
Среднее время,  с с
|
|
0
|
1
|
0.7
|
203,599 200,820 199,361 199,361 207,902 202,074 200,820
199,361 199,361 203,599
|
188 156 186 186 156 171 186 171 171 188
|
201,709
|
176
|
|
0.5
|
1
|
0.7
|
200,886 199,361 202,074 200,820 199,361 202,074 200,886
199,361 199,361 200,820
|
281 281 281 296 279 281 295 281 279 281
|
200,5
|
283
|
|
1
|
1
|
0.7
|
202,074 199,361 199,361 199,361 200,886 199,361 199,361
199,361 199,361 199,361
|
203 201 203 202 201 203 203 201 201 203
|
199,785
|
202
|
|
2
|
1
|
0.7
|
199,361 199,361 199,361 199,361 199,361 199,361 199,361
199,361 199,361 199,361
|
203 203 203 201 201 203 203 203 203 203
|
199,361
|
203
|
Таблица 17. Моделирование алгоритма муравья для задачи коммивояжера с 5
городами с варьированием параметра α
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
0.5
|
0.7
|
200,886 199,361 199,361 199,361 199,361 209,506 200,886
200,886 199,361 199,361
|
296 281 296 296 296 296 296 279 281 296
|
200,833
|
291
|
|
1
|
1
|
0.7
|
199,361 199,361 199,361 200,886 199,361 199,361 199,361
199,361 199,361 199,361
|
203 203 203 201 203 203 203 203 203 203
|
199,513
|
203
|
|
1
|
2
|
0.7
|
202,074 202,074 202,074 199,361 199,361 202,074 199,361
199,361 202,074 199,361
|
188 187 201 187 203 186 203 203 188 187
|
200,718
|
193
|
|
1
|
5
|
0.7
|
209,361 202,496 202,496 209,361 202,496 202,496 202,496
207,902 209,361 202,496
|
171 188 171 172 171 170 172 171 187 172
|
205,242
|
174
|
|
1
|
10
|
0.7
|
245,681 278,425 270,599 269,917 271,668 230,835 274,446
271,668 234,216 283,341
|
156 156 156 171 156 156 171 156 155 156
|
263,08
|
158
|
Таблица 18. Моделирование алгоритма муравья для задачи коммивояжера с 5
городами с варьированием параметра β
|
α
|
β
|

|
Минимальная длина пути
|
Время,  с с
|
Средняя длина пути
|
Среднее время,  с с
|
|
1
|
1
|
0.3
|
199,361 199,361 199,361 200,886 199,361 200,886 199,361
199,361 199,361 199,361
|
218 203 218 203 203 201 218 203 201 203
|
199,666
|
207
|
|
1
|
1
|
0.5
|
199,361 199,361 199,361 199,361 199,361 199,361 199,361
199,361 199,361 199,361
|
218 218 203 218 203 233 201 218 203 218
|
199,361
|
213
|
|
1
|
1
|
0.7
|
199,361 199,361 199,361 199,361 200,820 200,886 199,361
199,361 199,361 199,361
|
203 218 218 203 218 203 218 233 234 203
|
199,660
|
215
|
|
1
|
1
|
0.9
|
199,361 199,361 200,820 199,361 199,361 199,361 199,361
202,074 199,361 199,361
|
203 219 203 203 233 201 218 203 219 202
|
199,779
|
210
|
Таблица 19. Моделирование алгоритма муравья для задачи коммивояжера с 5
городами с варьированием параметра 
В таблицах 20-22 представлены результаты моделирования для задачи
коммивояжера с 10 городами.
|
α
|
β
|

|
Минимальная длина пути
|
Время,  с с
|
Средняя длина пути
|
Среднее время,  с с
|
|
0
|
1
|
0.7
|
321,870 308,068 327,015 312,675 328,514 311,903 319,955
300,741 309,831 329,653
|
1559 1467 1527 1465 1513 1528 1482 1482 1498 1512
|
317,022
|
1503
|
|
0.5
|
1
|
0.7
|
284,406 287,922 283,283 282,414 282,153 309,718 290,238
270,586 298,913 283,216
|
2604 2635 2604 2652 2621 2621 2636 2604 2621 2621
|
287,284
|
2622
|
|
1
|
1
|
0.7
|
294,993 289,701 289,210 284,039 298,934 262,045 262,045
291,317 276,750 273,7605
|
1856 1825 1841 1825 1855 1825 1840 1825 1825 1839
|
282,279
|
1835
|
|
2
|
1
|
0.7
|
262,045 262,111 269,493 262,111 262,443 262,443 269,559
269,493 262,111 269,956
|
1778 1825 1763 1793 1778 1793 1778 1809 1793 1763
|
265,176
|
1787
|
Таблица 20. Моделирование алгоритма муравья для задачи коммивояжера с 10
городами с варьированием параметра α
|
α
|
β
|

|
Минимальная длина пути
|
Время,  с с
|
Средняя длина пути
|
Среднее время,  с с
|
|
1
|
0.5
|
0.7
|
301,973 314,680 287,527 289,109 297,898 294,584 286,253
291,363 319,092 284,295
|
2621 2604 2637 2589 2635 2589 2636 2621 2588 2589
|
296,677
|
2611
|
|
1
|
1
|
0.7
|
294,993 289,701 289,210 284,039 298,934 262,045 262,045
291,317 276,750 273,7605
|
1856 1825 1831 1825 1855 1821 1865 1825 1898 1832
|
281,279
|
1843
|
|
1
|
2
|
0.7
|
273,006 262,111 262,509 273,006 262,111 269,891 269,956
262,509 265,459 262,509
|
1732 1715 1732 1715 1732 1732 1716 1716 1748 1715
|
266,306
|
1725
|
|
1
|
5
|
0.7
|
262,509 269,956 262,509 269,956 262,509 262,509 269,956
269,956 275,364 276,506
|
1560 1545 1575 1543 1575 1574 1543 1560 1545 1575
|
268,173
|
1556
|
|
1
|
10
|
0.7
|
282,962 321,249 307,475 311,575 324,241 324,241 315,346
324,241 324,241 282,962
|
1482 1512 1482 1512 1482 1513 1498 1497 1513 1481
|
311,853
|
1497
|
Таблица 21. Моделирование алгоритма муравья для задачи коммивояжера с 10
городами с варьированием параметра β
|
α
|
β
|

|
Минимальная длина пути
|
Время,  с с
|
Средняя длина пути
|
Среднее время,  с с
|
|
1
|
1
|
0.3
|
277,575 291,751 308,649 284,866 269,891 282,169 269,559
299,115 275,185 278,432
|
1840 1825 1840 1825 1855 1825 1825 1856 1810 1825
|
283,719
|
1832
|
|
1
|
1
|
0.5
|
289,641 269,956 276,108 275,292 282,874 275,366 296,734
271,943 288,706 272,255
|
1872 1856 1825 1840 1826 1856 1855 1825 1841 1855
|
279,887
|
1845
|
|
1
|
1
|
0.7
|
287,978 288,639 282,219 281,251 280,876 269,956 274,079
276,108 269,956 284,039
|
1865 1872 1825 1872 1853 1812 1825 1825 1856 1872
|
277,510
|
1847
|
|
1
|
1
|
0.9
|
283,337 296,342 273,826 276,815 287,075 284,707 272,940
282,551 292,145 280,637
|
1810 1808 1840 1809 1856 1810 1808 1841 1810 1808
|
283,037
|
1820
|
Таблица 22. Моделирование алгоритма муравья для задачи коммивояжера с 10
городами с варьированием параметра 
В таблицах 23-25 представлены результаты моделирования для задачи
коммивояжера с 5 городами.
|
α
|
β
|

|
Минимальная длина пути
|
Время,  с с
|
Средняя длина пути
|
Среднее время,  с с
|
|
0
|
1
|
0.7
|
381,689 365,390 366,435 401,345 410,885 399,004 379,142
402,691 385,457 403,215
|
5008 5054 5211 5195 5211 5211 5148 5023 5022 5257
|
389,525
|
5134
|
|
0.5
|
1
|
0.7
|
366,429 377,882 373,726 375,055 376,235 372,726 349,039
380,588 345,543 344,261
|
9640 9626 9671 9656 9640 9703 9688 9624 9686 9734
|
366,148
|
9666
|
|
1
|
1
|
0.7
|
341,031 352,595 340,877 328,224 340,450 349,184 345,377
347,027 339,949 337,622
|
6224 6224 6240 6240 6208 6240 6285 6287 6240 6333
|
342,233
|
6252
|
|
2
|
1
|
0.7
|
304,471 304,471 303,926 303,926 304,471 304,471 303,926
303,926 303,926 303,926
|
5397 5819 5335 5771 5599 5585 5663 5506 5553 5429
|
304,14
|
5565
|
Таблица 23. Моделирование алгоритма муравья для задачи коммивояжера с 15
городами с варьированием параметра α
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
0.5
|
0.7
|
402,111 392,230 395,262 412,370 388,0031 380,193 383,730
367,022 394,486 398,120
|
9671 9952 9764 9734 9781 9750 9780 9719 9781 9703
|
391,352
|
9763
|
|
1
|
1
|
0.7
|
328,224 352,595 340,877 328,224 340,450 349,184 345,377
347,027 352,595 337,622
|
6224 6323 6240 6240 6238 6424 6285 6284 6240 6333
|
342,217
|
6283
|
|
1
|
2
|
0.7
|
311,791 311,395 312,564 313,759 318,585 312,264 309,150
314,608 318,085 305,591
|
5912 5959 5928 5959 5959 5880 5928 5880 5990 5990
|
312,779
|
5938
|
|
1
|
5
|
0.7
|
320,058 311,395 316,238 320,058 311,040 305,591 315,128
317,629 320,058 305,591
|
5600 5677 5647 5616 5600 5646 5677 5647 5710 5817
|
314,278
|
5663
|
|
1
|
10
|
0.7
|
359,717 359,717 367,599 375,769 357,571 368,638 358,555
373,190 337,072 375,7693
|
363,359
|
5557
|
Таблица 24. Моделирование алгоритма муравья для задачи коммивояжера с 15
городами с варьированием параметра β
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
1
|
0.3
|
362,189 326,495 332,287 355,794 355,174 348,673 362,679
352,648 349,888 363,414
|
6162 6145 6225 6318 6192 6224 6239 6178 6145 6255
|
350,924
|
6208
|
|
1
|
1
|
0.5
|
347,340 344,958 333,566 325,062 356,268 341,849 327,046
352,326 337,591 345,583
|
6535 6068 6145 6162 6162 6145 6130 6208 6068 6208
|
341,158
|
6183
|
|
1
|
1
|
0.7
|
337,622 352,595 340,877 328,224 340,450 349,184 345,377
347,027 339,949 340,450
|
6224 6224 6230 6240 6208 6210 6255 6297 6220 6333
|
342,175
|
6244
|
|
1
|
1
|
0.9
|
357,629 344,132 342,803 356,439 348,374 348,120 323,829
343,084 356,795 336,178
|
6099 6193 6192 6162 6224 6177 6317 6131 6162 6208
|
345,738
|
6186
|
Таблица 24. Моделирование алгоритма муравья для задачи коммивояжера с 15
городами с варьированием параметра 
В таблицах 25-27 представлены результаты моделирования для задачи
коммивояжера с 20 городами.
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
0
|
1
|
0.7
|
499,394 486,626 486,626 505,397 516,337 461,955 519,651
489,683 470,891 495,061
|
15927 16129 16068 16178 16130 16145 16426 15943 16068 16160
|
493,162
|
16117
|
|
0.5
|
1
|
0.7
|
446,739 470,199 490,320 446,486 452,234 476,644 466,741
441,192 436,684 442,349
|
29187 29281 29344 29204 29234 29234 29484 29484 29375 29296
|
456,958
|
29312
|
|
1
|
1
|
0.7
|
429,654 425,935 423,685 428,559 408,697 435,610 441,373
430,971 410,478 432,241
|
19796 19842 19857 19922 19890 19874 19873 19967 19889 20015
|
426,720
|
19892
|
|
2
|
1
|
0.7
|
349,831 345,244 341,038 349,411 341,038 361,389 344,364
357,777 347,195 341,038
|
17051 17237 17439 17284 17394 17096 17861 17424 18110 17253
|
347,832
|
17414
|
Таблица 25. Моделирование алгоритма муравья для задачи коммивояжера с 20
городами с варьированием параметра α
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
0.5
|
0.7
|
487,488 501,848 493,917 526,844 507,671 507,671 502,857
491,566 499,218 486,229
|
28406 28501 28736 28656 28688 28688 28907 28642 28502 28454
|
500,530
|
28618
|
|
1
|
1
|
0.7
|
429,654 432,241 423,685 428,559 408,697 435,610 441,373
423,685 408,697 432,241
|
19796 19832 19857 19952 19890 19434 19873 19967 19219 20015
|
426,444
|
19783
|
|
1
|
2
|
0.7
|
372,438 369,060 346,436 367,952 370,689 354,513 367,341
368,199 367,341 378,024
|
19016 18984 19156 18953 18890 18906 18923 18891 19000 18860
|
366,199
|
18957
|
|
1
|
5
|
0.7
|
374,991 377,238 368,249 364,750 381,300 374,053 374,971
364,216 374,798 372,290
|
17580 17674 17488 17409 17690 17549 17487 17425 17456 17612
|
372,685
|
17537
|
|
1
|
10
|
0.7
|
400,703 405,334 395,637 412,306 414,298 414,298 407,675
399,084 399,084 390,833
|
17004 49233 250520 16941 17222 36862 17301 17191 17097
167216
|
403,925
|
60658
|
Таблица 26. Моделирование алгоритма муравья для задачи коммивояжера с 20
городами с варьированием параметра β
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
1
|
0.3
|
372,899 409,014 387,071 414,344 411,111 438,301 418,373
432,340 431,232 436,710
|
19671 19672 19765 19748 19749 19687 19656 19687 19687 19827
|
415,139
|
19714
|
|
1
|
1
|
0.5
|
441,271 443,077 428,994 413,778 422,292 396,416 448,667
443,501 427,269 439,990
|
19842 19671 19625 19671 19624 19609 19624 19609 19873 19701
|
430,525
|
19684
|
|
1
|
1
|
0.7
|
429,654 425,935 410,478 428,559 428,559 435,610 425,935
430,971 410,478 432,241
|
19796 19832 19817 19922 19890 19874 19863 19967 19339 20045
|
426,842
|
19834
|
|
1
|
1
|
0.9
|
452,622 438,295 436,301 388,593 430,213 417,868 426,566
437,035 429,3842 446,605
|
19702 19749 19734 19765 19781 19719 19717 19781 19717 19905
|
430,348
|
19757
|
Таблица 27. Моделирование алгоритма муравья для задачи коммивояжера с 20
городами с варьированием параметра 
В таблицах 28-30 представлены результаты моделирования для задачи
коммивояжера с 25 городами.
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
0
|
1
|
0.7
|
606,182 570,806 580,729 595,103 623,546 608,281 553,164
501,322 603,956 613,422
|
35957 35941 36004 36862 36082 35896 35974 36224 36191 35910
|
585,651
|
36104
|
|
0.5
|
1
|
0.7
|
570,731 566,232 535,265 547,427 527,484 502,115 543,282
544,595 555,640 566,888
|
65628 66907 65941 65691 65598 65675 65785 65644 65723 65551
|
545,965
|
65814
|
|
1
|
1
|
0.7
|
525,001 508,422 527,881 512,607 516,170 501,925 500,261
512,514 506,092 534,947
|
44445 45037 44585 45256 44585 44522 44570 43992 44632 44585
|
514,582
|
44620
|
|
2
|
1
|
0.7
|
408,374 396,215 391,746 392,329 412,053 375,068 417,862
389,223 406,984 375,068
|
37798 38096 38376 38422 38595 38033 38579 38875 38594 38016
|
396,492
|
38338
|
Таблица 28. Моделирование алгоритма муравья для задачи коммивояжера с 25
городами с варьированием параметра α
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
0.5
|
0.7
|
619,137 632,135 598,434 628,177 597,788 634,564 637,260
611,795 627,146 616,642
|
63383 63508 63383 63321 63600 63491 63413 63227 63944 63460
|
620,30
|
63473
|
|
1
|
1
|
0.7
|
525,001 501,925 506,092 512,607 516,170 501,925 527,881
512,514 506,092 534,947
|
44445 45123 44585 45256 45585 44534 44570 42923 44632 44585
|
514,515
|
44623
|
|
1
|
2
|
0.7
|
413,457 417,487 418,535 418,635 414,218 417,561 409,579
407,456 423,981 425,543
|
42042 42010 42120 42306 41980 42026 42011 41980 42119 42042
|
416,645
|
42063
|
|
1
|
5
|
0.7
|
411,128 407,367 410,372 406,943 413,612 407,218 413,779
414,828 401,566 404,230
|
39092 39140 39094 39109 39765 78717 39529 39077 39468 39265
|
409,104
|
43225
|
|
1
|
10
|
0.7
|
437,036 449,886 436,766 423,885 425,185 431,411 439,998
446,258 437,036 434,819
|
38016 38016 38001 38203 38048 38064 38033 37985 37986 38406
|
436,228
|
38075
|
Таблица 29. Моделирование алгоритма муравья для задачи коммивояжера с 25
городами с варьированием параметра β
|
αβ Минимальная длина путиВремя, Минимальная длина путиВремя,  сСредняя длина путиСреднее время, сСредняя длина путиСреднее время,  с с
|
|
|
|
|
|
|
|
1
|
1
|
0.3
|
535,693 520,596 483,727 514,275 509,050 514,302 531,892
490,102 506,197 498,491
|
44117 44257 44508 44117 44115 44382 44100 44382 44132 44397
|
510,432
|
44250
|
|
1
|
1
|
0.5
|
521,860 518,299 525,348 477,727 507,674 471,031 520,677
508,273 470,320 508,193
|
43992 44428 44069 44194 44240 44227 44320 44366 44273 44320
|
502,940
|
44242
|
|
1
|
1
|
0.7
|
525,001 534,947 527,881 512,607 512,607 501,925 500,261
508,422 506,092 534,947
|
44445 45033 44585 45256 44585 44522 44554 43923 44632 46585
|
516,469
|
44812
|
|
1
|
1
|
0.9
|
506,665 500,077 492,521 494,121 510,830 515,789 525,415
523,760 517,404 515,264
|
44756 44413 44428 44724 44709 44601 44443 44679 44490 44617
|
510,184
|
4458
|
Таблица 30. Моделирование алгоритма муравья для задачи коммивояжера с 5
городами с варьированием параметра 
В таблице 31 представлена информация обо всех найденных средних путях для
пяти задач при всех наборах параметров  ,
, 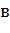 ,
, 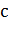 .
.
|
Номер графика
|

|

|

|
Количество городов Средняя длина пути
|
|
|
|
|
5
|
10
|
15
|
20
|
25
|
|
1
|
0
|
1
|
1
|
201,709
|
317,022
|
389,525
|
493,162
|
585,651
|
|
2
|
0,5
|
1
|
1
|
200,5
|
287,284
|
366,148
|
456,958
|
545,965
|
|
3
|
1
|
1
|
1
|
199,785
|
282,279
|
342,233
|
426,72
|
514,582
|
|
4
|
2
|
1
|
1
|
199,361
|
265,176
|
304,14
|
347,832
|
396,492
|
|
5
|
1
|
0,5
|
1
|
200,833
|
296,677
|
391,352
|
500,53
|
620,3
|
|
6
|
1
|
1
|
1
|
199,513
|
281,279
|
342,217
|
426,444
|
514,515
|
|
7
|
1
|
2
|
1
|
200,718
|
266,306
|
312,779
|
366,199
|
416,645
|
|
8
|
1
|
5
|
1
|
205,242
|
268,173
|
314,278
|
372,685
|
409,104
|
|
9
|
1
|
10
|
1
|
263,08
|
311,853
|
363,359
|
403,925
|
436,228
|
|
10
|
1
|
1
|
0,3
|
199,666
|
283,719
|
350,924
|
415,139
|
510,432
|
|
11
|
1
|
1
|
0,5
|
199,361
|
279,887
|
341,158
|
430,525
|
502,94
|
|
12
|
1
|
1
|
0,7
|
199,66
|
277,51
|
342,175
|
426,842
|
516,469
|
|
13
|
1
|
0,9
|
199,779
|
283,037
|
345,738
|
430,348
|
510,184
|
Таблица 31. Зависимость найденных средних длин путей для пяти задач при
всех наборах параметров  ,
, 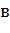 ,
, 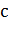
На рисунке 22 в графическом виде представлена зависимость среднего
найденного пути от всех протестированных наборов параметров. Номер графика
соответствует номеру набора параметров, представленном в таблице 31.

Рисунок 22. Зависимость среднего найденного пути от всех протестированных
наборов параметров
Приложение 4
Исходный код программы на Matlab, решающий задачу коммивояжера алгоритмом
Дейкстры
алгоритм Дейкстры[r_path, r_cost] = dijkstra(pathS, pathE, transmat)
% This version support detecting _cyclic-paths_
%
% USAGE:
% [path, cost]= dijkstra(pathStart, pathEnd, transMatrix)
%
% PARAMETERS:
% pathS : the index of start node, indexing from 1
% pathE : the index of end node, indexing from 1
% transmat: the transition matrix, or adjacent matrix
%
% Ensure the transition matrix is square
%( size(transmat,1) ~= size(transmat,2) )( 'detect_cycles:Dijkstra_SC',
...
'transmat has different width and heights' );
% Initialization:
% noOfNode : nodes in the graph
% parent(i) : record the parent of node i
% distance(i) : the shortest distance from i to pathS
% queue : for width-first traveling of the graph= size(transmat, 1);i =
1:noOfNode(i) = 0;(i) = Inf;= [];
% Start from pathSi=1:noOfNodetransmat(pathS, i)~=Inf(i) =
transmat(pathS, i);(i) = pathS;= [queue i];
% Width-first exploring the whole graph
%length(queue) ~= 0= queue(1);= queue(2:end);hopE =
1:noOfNodedistance(hopE) > distance(hopS) + transmat(hopS,hopE)(hopE) =
distance(hopS) + transmat(hopS,hopE);(hopE) = hopS;= [queue hopE];
% Back-trace the shortest-path
%_path = [pathE];= parent(pathE);i~=pathS && i~=0_path = [i
r_path];= parent(i);i==pathS_path = [i r_path];_path = []
% Return cost
%_cost = distance(pathE);
программа в Matlab для
модификация диаграммы
Вороногоall=50:10:70;=ones(1,length(xu)).*75;=xu;=ones(1,length(xu)).*60;=60:5:75;=ones(1,length(yyu)).*50;=ones(1,length(yyu)).*70;=60:30:120;=ones(1,length(bxu)).*40;=bxu;=ones(1,length(bxl)).*20;=20:10:40;=ones(1,length(byyu)).*60;=ones(1,length(byyu)).*120;=80:20:120;=ones(1,length(dxu)).*110;=dxu;=ones(1,length(dxl)).*90;=90:10:110;=ones(1,length(dyyu)).*80;=ones(1,length(dyyu)).*120;=0:60:360;=deg2rad(dd);=cos(d).*10+100;=sin(d).*10+70;=deg2rad(0:30:360);=cos(g).*10+100;=sin(g).*10+70;=15:10:35;=ones(1,length(exu)).*100;=exu;=ones(1,length(exl)).*70;=70:10:100;=ones(1,length(eyyu)).*15;=ones(1,length(eyyu)).*35;=0:10:150;=ones(1,length(wallu))*5;=ones(1,length(wallu))*125;=0:10:150;=ones(1,length(cwall))*10;=ones(1,length(cwall))*135;on(xu,yu,'-r','LineWidth',3)(xl,yl,'-r','LineWidth',3)(xxu,yyu,'r','LineWidth',3)(xxl,yyu,'r','LineWidth',3)(bxu,byu,'r','LineWidth',3)(bxl,byl,'r','LineWidth',3)(bxxu,byyu,'r','LineWidth',3)(bxxl,byyu,'r','LineWidth',3)(dxu,dyu,'r','LineWidth',3)(dxl,dyl,'r','LineWidth',3)(dxxu,dyyu,'r','LineWidth',3)(dxxl,dyyu,'r','LineWidth',3)(cxx,cyy,'r','LineWidth',3)(exu,eyu,'r','LineWidth',3)(exl,eyl,'r','LineWidth',3)(exxu,eyyu,'r','LineWidth',3)(exxl,eyyu,'r','LineWidth',3)=[65
8 90 45 90 130 20 125]=[10 65 10 25 115 100 110 105]=[xu xl xxu xxl bxu bxl
bxxu bxxl cx dxu dxl dxxu dxxl exu exl exxu exxl wallu wallu cwall1 cwall2
];=[yu yl yyu yyu byu byl byyu byyu cy dyu dyl dyyu dyyu eyu eyl eyyu eyyu
wall1 wall2 cwall cwall ];
[a,b]=voronoi(xa,ya);pppp=1:4X
Y newxx newyy newx newy lengthofsize xx yy distancess dist xhh r TOTALDIS path
Paths matrix totaldis R netXloc netYloctotalCost=[a(1,:) a(2,:)];=[b(1,:)
b(2,:)];=1;i=1:length(X);X(1,i)>140 || Y(1,i)>140 || X(1,i)<0 ||
Y(1,i)<0=0;(1,mm)=X(1,i);(1,mm)=Y(1,i);=mm+1;X
Y=nX;=nY;=1;i=1:length(X)=X(1,i);=Y(1,i);p>=60 && p<=120
&& q>=20 && q<=40=1;p>=50 && p<=70
&& q>=60 && q<=75=1;p>=80 && p<=120
&& q>=90 && q<=110=1;p>=15 && p<=35
&& q>=70 && q<=100=1;p>=95 && p<=105
&& q>=65 && q<=75=1;=0;z==0(1,j)=p;(1,j)=q;=j+1;=1;(newxx,newyy,'*g')([0
150 0 150])=length(newyy);i=1:lengthofsize
[yyyyyy,ind]=min(newyy);(1,i)=newxx(1,ind);(1,i)=newyy(1,ind);(1,ind)=inf;(1,ind)=inf;=[xcor(1,pppp)
newx xcor(1,pppp+4)];yy=[ycor(1,pppp) newy ycor(1,pppp+4)];=length(xx);u=1:nv=1:n=1;=sqrt((xx(1,v)-xx(1,u))^2+(yy(1,v)-yy(1,u))^2);=distancess;=(yy(1,v)-yy(1,u))/(xx(1,v)-xx(1,u));abs(slobe)<0.01yy(1,v)>19.5
&& yy(1,v)<40.5=1;yy(1,v)>59.5 &&
yy(1,v)<75.5=1;yy(1,v)>69.5 && yy(1,v)<100.5=1;yy(1,v)>89.5
&& yy(1,v)<110.5=1;=0;abs(slobe)>100xx(1,v)>59.5 &&
xx(1,v)<120.5=1;xx(1,v)>49.5 && xx(1,v)<70.5=1;xx(1,v)>14.5
&& xx(1,v)<35.5=1;xx(1,v)>79.5 &&
xx(1,v)<120.5=1;=0;=0;dist==0=2;tyty==1=2;=yy(1,u)-slobe*xx(1,u);=xx(1,u);=2;=(abs(xx(1,u)-xx(1,v)))/0.05;=round(nn);=1;slobe>0=1;=-1;i=1:nn=slobe*(xhh+0.05*k*coe)+c;=xhh+0.05*k*coe;=1;slobe==0=2;xh>=59
&& xh<=121 && chy>=19 && chy<=41=2;xh>=49
&& xh<=71 && chy>=59 && chy<=76=2;xh>=79
&& xh<=121 && chy>=89 && chy<=111=2;xh>=14
&& xh<=36 && chy>=69 && chy<=101=2;xh>=92
&& xh<=108 && chy>=62 &&
chy<=79=2;=k+1;bbb==2;(u,v)=inf;(u,v)=distancess;path;
[path,
totalCost]=dijkstra1(1,n,r);(1,pppp)=totalCost;yyyy=1:length(path)(pppp,yyyy)=path(1,yyyy);;pppp==1i
= 1:(length(path)-1)path(length(path)-1)==0;([xx(path(i)) xx(path(i+1))],
[yy(path(i)) yy(path(i+1))], 'Color','b','LineWidth', 0.75, 'LineStyle',
'-');;pppp==2i = 1:(length(path)-1)path(length(path)-1)==0;([xx(path(i))
xx(path(i+1))], [yy(path(i)) yy(path(i+1))], 'Color','r','LineWidth', 0.75,
'LineStyle', '--');;;pppp==3i = 1:(length(path)-1)path(length(path)-1)==0;([xx(path(i))
xx(path(i+1))], [yy(path(i)) yy(path(i+1))], 'Color','c','LineWidth', 0.75,
'LineStyle', '-');;;i = 1:(length(path)-1)path(length(path)-1)==0;([xx(path(i))
xx(path(i+1))], [yy(path(i)) yy(path(i+1))], 'Color','k','LineWidth', 0.75,
'LineStyle', '-.');; ; ; onpppp==1([xcor(1,pppp) xcor(1,pppp+4)],[ycor(1,pppp)
ycor(1,pppp+4)],'bd')pppp==2([xcor(1,pppp) xcor(1,pppp+4)],[ycor(1,pppp)
ycor(1,pppp+4)],'rs')pppp==3([xcor(1,pppp) xcor(1,pppp+4)],[ycor(1,pppp)
ycor(1,pppp+4)],'co')([xcor(1,pppp) xcor(1,pppp+4)],[ycor(1,pppp)
ycor(1,pppp+4)],'kd');on;