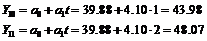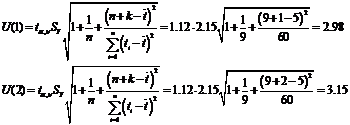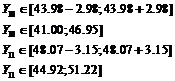|
Тип
сырья
|
Нормы
расхода сырья на ед. продукции
|
Запасы
сырья
|
|
1вид
|
II вид
|
III вид
|
|
|
I
|
1
|
2
|
1
|
430
|
|
II
|
3
|
0
|
2
|
460
|
|
III
|
1
|
4
|
0
|
420
|
|
Цена
изделия
|
3
|
2
|
5
|
|
Требуется:
) сформулировать прямую
оптимизационную задачу на максимум выручки от реализации готовой продукции,
получить оптимальный план выпуска продукции;
) сформулировать двойственную
задачу и найти ее оптимальный план с помощью теорем двойственности;
) Пояснить нулевые значения
переменных в оптимальном плане;
) на основе свойств
двойственных оценок и теорем двойственности:
· проанализировать использование
ресурсов в оптимальном плане исходной задачи;
· определить, как
изменится выручка от реализации продукции и план ее выпуска, если запас сырья I
вида увеличить на 5 ед., а II
- уменьшить на 5 ед.;
· определить
целесообразность включения в план изделия четвертого вида ценой 7 у.е., если
нормы затрат сырья 2, 4 и 3 единицы
Решение
. Сформулируем
прямую оптимизационную задачу на максимум выручки от реализации готовой
продукции:
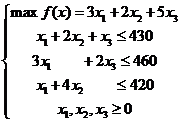
Получим оптимальный план выпуска
продукции:
Для этого приводим эту задачу к каноническому
виду и решаем симплекс-методом с естественным базисом с оформлением расчетов в
симплекс-таблицах:
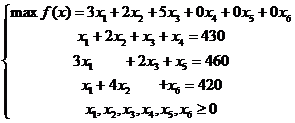
КЗЛП имеет необходимое число
единичных столбцов, т.е. обладает очевидным начальным опорным планом
(0,0,0,1,1,1)
|
Номер
симплекс-таблицы
|
Базис
|
Сj
Ci
|
B
|
3
|
2
|
5
|
0
|
0
|
0
|
Q
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
A5
|
A6
|
|
|
0
|
A4
|
0
|
430
|
1
|
2
|
1
|
1
|
0
|
0
|
430
|
|
←A5
|
0
|
460
|
3
|
0
|
2
|
0
|
1
|
0
|
230
|
|
A6
|
0
|
420
|
1
|
4
|
0
|
0
|
0
|
1
|
|
|
∆φ
|
-
|
0
|
-3
|
-2
|
-5
|
0
|
0
|
0
|
-
|
|
1
|
←A5
|
0
|
200
|
-0,5
|
2
|
0
|
1
|
-0,5
|
0
|
100
|
|
→A3
|
3
|
230
|
1,5
|
0
|
1
|
0
|
0,5
|
0
|
|
|
A6
|
0
|
420
|
1
|
4
|
0
|
0
|
0
|
1
|
105
|
|
∆φ
|
-
|
1150
|
4,5
|
-2
|
0
|
0
|
2,5
|
0
|
-
|
|
2
|
→A2
|
7
|
100
|
-0,25
|
1
|
0
|
0,5
|
-0,25
|
0
|
|
|
A3
|
3
|
230
|
1,5
|
0
|
1
|
0
|
0,5
|
0
|
|
|
←A6
|
0
|
20
|
2
|
0
|
0
|
-2
|
1
|
1
|
|
|
∆φ
|
-
|
1350
|
4
|
0
|
0
|
1
|
2
|
0
|
-
|
В симплекс-таблице 2 получен оптимальный опорный
план, поскольку все симплекс-разности (оценки) ∆j≥0
j = 1, 2, 3, 4, 5, 6
. Оптимальные значения переменных равны: x1=0,
x2
=100 , x3=230
(основные переменные), x4=
0, x5
=0, x6
=20 (дополнительные переменные). Максимальное значение целевой функции равно
1350 ден.ед.
Оптимальный план 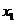 =0,
=0,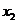 =100,
=100,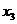 =230,
выручка составит 1350 ден.ед.
=230,
выручка составит 1350 ден.ед.
2. Проверим, как
удовлетворяется система функциональных ограничений оптимальным планом X* = (х1
= 0, х2 =100, х3 = 230)
+2*100+230=430
*0+0+2*230=460 (*)
+ 4*100=400<420
Значение целевой функции на этом
плане равно
f(X)
=3*0+2*100+5*230=200+1150=1350
Двойственная задача имеет вид:
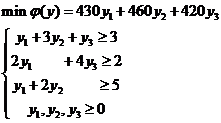
Для нахождения оценок у1
у2, у3 используем вторую теорему двойственности.
Поскольку третье ограничение в (*) выполняется как строгое неравенство, то у3
= 0. Так как х3 > 0 и х2> 0, то:

Итак, для получения двойственных
оценок имеем систему линейных уравнений:
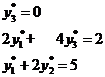
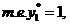
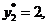
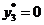
Вычислим значение целевой функции
двойственной задачи:

По первой теореме двойственности мы
можем утверждать, что действительно найдены оптимальные значения двойственных
переменных.
Оптимальный план двойственной задачи


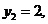
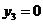
3. Поясним
нулевые значения переменных в оптимальном плане
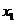 =0, т.е. производить продукцию 1
вида нецелесообразно, т.к. на ее производство затрачивается большое количество
ресурсов всех видов.
=0, т.е. производить продукцию 1
вида нецелесообразно, т.к. на ее производство затрачивается большое количество
ресурсов всех видов.
4. на
основе свойств двойственных оценок и теорем двойственности:
· проанализируем использование
ресурсов в оптимальном плане исходной задачи:
1. Величина двойственной оценки того или иного
ресурса показывает насколько возросло бы максимальное значение целевой функции,
если бы объем данного ресурса увеличился на одну единицу(двойственные оценки
измеряют эффективность малых приращений объемов ресурсов в конкретных условиях
данной задачи).
В рассматриваемом примере увеличение
запасов сырья I типа, на 1
привело бы к росту максимальной суммы выручки на 
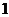 у.е. (у1 =
у.е. (у1 =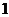 ), а
увеличение сырьевых ресурсов II типа на 1 привело бы к росту
максимальной суммы выручки на
), а
увеличение сырьевых ресурсов II типа на 1 привело бы к росту
максимальной суммы выручки на 
 у.е. Тогда как увеличение сырьевых
ресурсов III типа не
повлияет на оптимальный план выпуска продукции и сумму выручки.
у.е. Тогда как увеличение сырьевых
ресурсов III типа не
повлияет на оптимальный план выпуска продукции и сумму выручки.
Сказанное позволяет выявить
направления «расшивки» узких мест, обеспечивающие получение наибольшего
экономического эффекта, а также целесообразность изменения в структуре выпуска
продукции с позиций общего оптимума.
. Двойственные оценки отражают
сравнительную дефицитность различных видов ресурсов в отношении принятого в
задаче показателя эффективности. Оценки показывают, какие ресурсы являются
более дефицитными (они будут иметь самые высокие оценки), какие менее
дефицитными и какие совсем недефицитны (избыточны).
В данном случае недефицитным
ресурсом является сырье III типа, поскольку у3
= 0.
Острее ощущается дефицитность
ресурса сырья II типа (у2
= ) - он более
дефицитен, чем ресурс I типа (у1 =1).
) - он более
дефицитен, чем ресурс I типа (у1 =1).
Двойственные оценки позволяют
определять своеобразные «нормы заменяемости ресурсов»: имеется в виду не
абсолютная заменяемость ресурсов, а относительная, т.е. заменяемость с точки
зрения конечного эффекта и лишь в конкретных условиях данной задачи.
В нашем примере относительная
заменяемость ресурсов определяется соотношением (нормой) 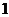 :
: .
.
· определим,
как изменится выручка от реализации продукции и план ее выпуска, если запас
сырья I
вида увеличить на 5 ед., а II
- уменьшить на 5 ед.:
Найдем пределы устойчивости двойственных оценок
для сырьевых ресурсов I
и II типов
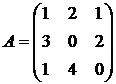
После приведения задачи к
канонической форме матрица А примет вид
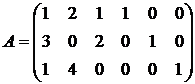
С ненулевыми значениями в
оптимальный план вошли 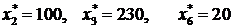 ,
следовательно матрица А* будет составлена из второго, третьего и
шестого столбцов матрицы А
,
следовательно матрица А* будет составлена из второго, третьего и
шестого столбцов матрицы А
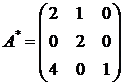
Для вычисления интервалов
устойчивости необходимо найти обратную матрицу
D=A*-1
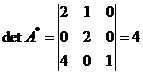
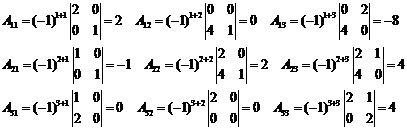
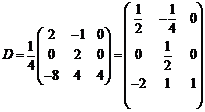
При вычислении интервала
устойчивости по формулам
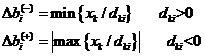
Примем x2*=100=xk=1, x3*=230=xk=2, x6*=20= xk=3
Интервал устойчивости первого
ресурса сырье I типа
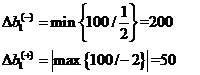
Интервал устойчивости
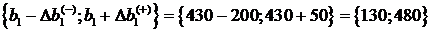
Интервал устойчивости второго
ресурса сырье II типа

Интервал устойчивости
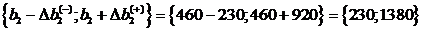
Определим, как изменится выручка от
реализации продукции и план ее выпуска, если запас сырья I вида
увеличить на 5 ед., а II - уменьшить на 5 ед. Эти
изменения (430+5=435; 460-5=455) находятся в интервалах устойчивости двойственных
оценок
План выпуска
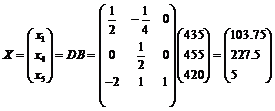
x1*=103,75, x2*=27,5, x3*=5
Объем прибыли f(X) =
3*103,75+2*227,5+5*5=791,25 уменьшится на
,75 ден.ед.
· определить целесообразность
включения в план изделия четвертого вида ценой 7 у.е., если нормы затрат сырья
2, 4 и 3 единицы.
Двойственные оценки служат
инструментом определения эффективности отдельных хозяйственных решений
(технологических способов), с их помощью можно определять выгодность
производства новых изделий, эффективность новых технологических способов:
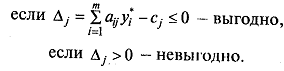
В рассматриваемом примере
следует решить вопрос о целесообразности включения в план изделия пятого вида
ценой 7 ден.ед, если нормы затрат сырья 2, 4 и 3 ден. ед.

невыгодно расширение ассортимента.
Задача 3
Используя балансовый метод
планирования и модель Леонтьева, построить баланс производства и распределения
продукции предприятий.
Промышленная группа предприятий
(холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий
группы специализируется на выпуске продукции одного вида: первое предприятие
специализируется на выпуске продукции первого вида, второе предприятие -
продукции второго вида; третье предприятие - продукции третьего вида. Часть
выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее
потребление), остальная часть поставляется за его пределы (внешним
потребителям, является конечным продуктом). Специалистами управляющей компании
получены экономические оценки аij (i=1,2,3; j=1,2,3)
элементов технологической матрицы А (норм расхода, коэффициентов прямых
материальных затрат) и элементов  вектора конечной продукции Y.
вектора конечной продукции Y.
Требуется:
1) Проверить продуктивность
технологической матрицы А=( аij) (матрицы
коэффициентров прямых материальных затрат).
) Построить баланс (заполнить
таблицу) производства и распределения продукции предприятий холдинга.
|
Предприятия
(виды продукции)
|
Коэффициенты
прямых затрат аij
|
Конечный
продукт, Y
|
|
1
|
2
|
3
|
|
|
1
|
0,0
|
0,4
|
0,1
|
160
|
|
2
|
0,4
|
0,1
|
0,0
|
180
|
|
3
|
0,3
|
0,0
|
0,1
|
150
|
Решение:
1) проверим
продуктивность матрицы А;
Для продуктивности матрицы А
необходимо и достаточно, чтобы выполнялось условие (первый признак). Матрица (Е
- А) неотрицательно обратима, т.е. существует обратная матрица (Е - А)-1
и все ее элементы неотрицательны.
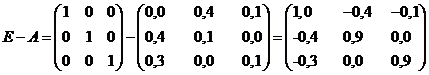
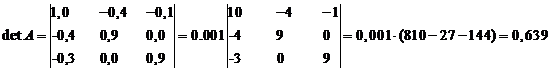
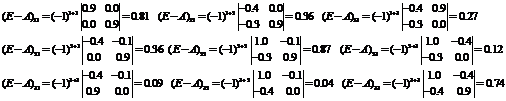
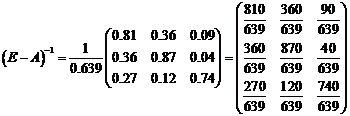
Матрица E-A
неотрицательно обратима, значит матрица А продуктивна
2) построим баланс
производства и распределения продукции предприятий холдинга.
Модель баланса производства и
распределения продукции предприятия можно представить следующей системой
уравнений:
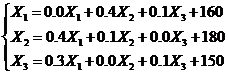

Отсюда определяем валовую продукцию
предприятий:
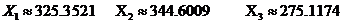
Распределение продукции между
предприятиями на внутреннее потребление определяем из соотношения
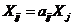
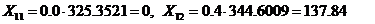 и т.д.
и т.д.
В итоге плановая модель - баланс
производства и распределения продукции предприятий холдинга - будет иметь
следующий вид (см. табл.)
|
Межпродуктовый
баланс производства и распределения продукции
|
|
Производящие
структуры
|
Потребляющие
структуры
|
Конечный
продукт
|
Валовой
продукт
|
|
1
|
3
|
|
|
|
1
|
0
|
137.84
|
27.51
|
160
|
325,3521
|
|
2
|
130.14
|
34.46
|
0
|
180
|
344,6009
|
|
3
|
97.60
|
0
|
27.51
|
150
|
275,1174
|
|
Итого
|
227.74
|
172.3
|
55.02
|
490
|
945,0704
|
Задача 4
Исследовать
динамику экономического показателя на основе анализа одномерного временного
ряда
В течение девяти
последовательных недель фиксировался спрос Y(t)
(млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t)
этого показателя приведен ниже в таблице
|
Номер
варианта
|
Номер
наблюдения (t = 1,
2, , 9)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
8
|
8
|
13
|
15
|
19
|
25
|
27
|
33
|
35
|
40
|
Требуется:
) проверить наличие аномальных
наблюдений;
) построить линейную модель Ŷ(t)
= aQ + a1t,,
параметры которой оценить МНК (Ŷ(t)-
расчетные, смоделированные значения временного ряда);
3) построить адаптивную модель
Брауна Ŷ (t) = а0 + a1t с
параметром сглаживания  = 0,4 и
= 0,4 и  = 0,7;
выбрать лучшее значение
= 0,7;
выбрать лучшее значение  ;
;
) оценить адекватность построенных
моделей используя: свойства независимости остаточной компоненты, случайности и
соответствия нормальному закону распределения (при использовании R/S-критерия
взять табулированные границы 2.7-3.7).
5) Оценить
точность модели на основе использования средней относительной ошибки
аппроксимации;
6) по
двум построенным моделям осуществить прогноз спроса на следующие две недели
(доверительный интервал прогноза рассчитать при доверительной вероятности p=70%).
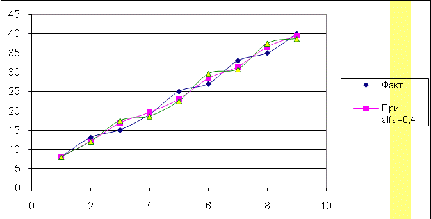
7) Фактические
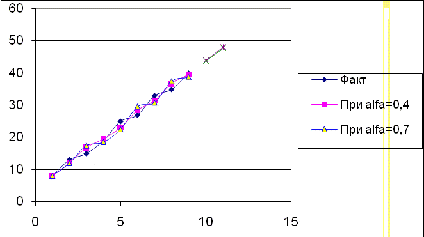
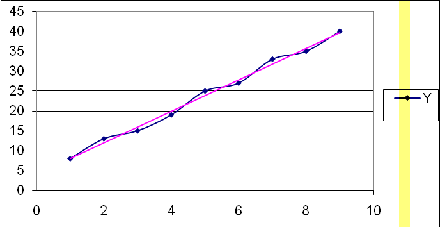
значения показателя, результату моделирования и прогнозирования представить на
графике
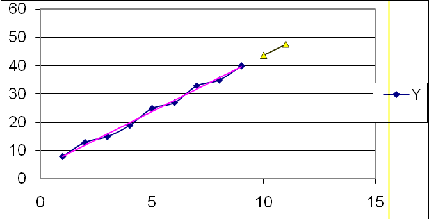
1)
проверим наличие аномальных наблюдений
Проверим наличие аномальных
наблюдений, для чего построим график временного ряда
стоимость рацион
производство распределение
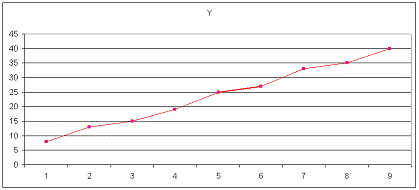
Визуальный анализ графика
позволяет сделать вывод, что аномальных наблюдений не обнаружено.
2) построим
линейную модель Ŷ(t)
= aQ
+ a1t,,
параметры которой оценить МНК (Ŷ(t)-
расчетные, смоделированные значения временного ряда):
При вычислении «вручную» по
формуле

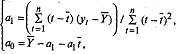
Промежуточные расчеты
параметров линейной модели приведены в табл.
|
t
|
Yt
|
t-tср
|
(t-tср)2
|
y-yср
|
(y-yср)(t-tср)
|
Yлин
|
|
1
|
8
|
-4
|
16
|
-15,89
|
63,56
|
8,02
|
|
2
|
13
|
-3
|
9
|
-10,89
|
32,67
|
11,99
|
|
3
|
15
|
-2
|
4
|
-8,89
|
17,78
|
15,96
|
|
4
|
19
|
-1
|
1
|
-4,89
|
4,89
|
19,92
|
|
5
|
25
|
0
|
0
|
1,11
|
0,00
|
23,89
|
|
6
|
27
|
1
|
1
|
3,11
|
3,11
|
27,86
|
|
7
|
33
|
2
|
4
|
9,11
|
18,22
|
31,82
|
|
8
|
35
|
3
|
9
|
11,11
|
33,33
|
35,79
|
|
9
|
40
|
4
|
16
|
16,11
|
64,44
|
39,76
|
|
Сумма
|
45
|
215
|
0
|
60
|
0
|
238
|
|
|
средн
|
5
|
23,89
|
|
|
|
|
|

Уравнение регрессии зависимости у от
t имеет вид
Y(t)=4.06+3.97t
3) построим адаптивную модель Брауна
Yp(t) = а0
+ a1t с
параметром сглаживания  = 0,4 и
= 0,4 и  = 0,7;
выберем лучшее значение
= 0,7;
выберем лучшее значение  ;
;
Адаптивными методами прогнозирования
принято называть такие методы, процесс реализации которых заключается в
вычислении последовательных во времени значений прогнозируемого показателя с
учетом степени влияния предшествующих уровней. При краткосрочном
прогнозировании наиболее важным является не тенденция развития исследуемого
процесса, сложившаяся в среднем на всем периоде предыстории, а последние
значения этого процесса. Свойство динамичности развития экономического явления
здесь преобладает над свойством его инерционности. Поэтому при краткосрочном
прогнозировании, как правило, более эффективными оказываются адаптивные методы,
учитывающие неравноценность уровней временного ряда и быстро приспосабливающие
свою структуру и параметры к изменяющимся условиям.
Рассмотрим один из таких методов -
метод Брауна.
Расчетное значение в момент времени
получается по формуле
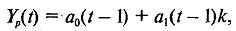
где k -
количество шагов прогнозирования (обычно k = 1).
Это значение сравнивается с
фактическим уровнем, и полученная ошибка прогноза E(t)=Y(t) - Yp(t)
используется для корректировки модели. Корректировка параметров осуществляется
по формулам:

где  - коэффициент дисконтирования данных,
отражающий большую степень доверия к более поздним данным. Его значение должно
быть в интервале от 0 до 1. Процесс модификации модели (t- 1,2,..., N) в
зависимости от текущих прогнозных качеств обеспечивает ее адаптацию к новым
закономерностям развития. Начальные оценки параметров получим по первым пяти
точкам при помощи метода наименьших квадратов
- коэффициент дисконтирования данных,
отражающий большую степень доверия к более поздним данным. Его значение должно
быть в интервале от 0 до 1. Процесс модификации модели (t- 1,2,..., N) в
зависимости от текущих прогнозных качеств обеспечивает ее адаптацию к новым
закономерностям развития. Начальные оценки параметров получим по первым пяти
точкам при помощи метода наименьших квадратов
|
t
|
Yt
|
t-tср
|
(t-tср)^2
|
y-yср
|
(y-yср)(t-tср)
|
|
|
|
|
|
|
|
|
1
|
8
|
-2,00
|
4,00
|
-8,00
|
16,00
|
|
2
|
13
|
-1,00
|
1,00
|
-3,00
|
3,00
|
|
3
|
15
|
0,00
|
0,00
|
-1,00
|
0,00
|
|
4
|
19
|
1,00
|
1,00
|
3,00
|
3,00
|
|
5
|
25
|
2,00
|
4,00
|
9,00
|
18,00
|
|
Сумма
|
15
|
80,00
|
0,00
|
10,00
|
0,00
|
40,00
|
|
средн
|
3
|
16,00
|
|
|
|
|
a0=4
a1=4,
При  =0,4;
=0,4; 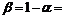 0,6
0,6
|
Время
t
|
Факт
Y
|
a0
|
a1
|
Расчет
|
Отклонение
|
|
|
4
|
4,00
|
|
|
|
1
|
8
|
8,00
|
4,00
|
8,00
|
0,00
|
|
2
|
13
|
12,64
|
4,16
|
12,00
|
1,00
|
|
3
|
15
|
15,65
|
3,87
|
16,80
|
-1,80
|
|
4
|
19
|
19,19
|
3,79
|
19,52
|
-0,52
|
|
5
|
25
|
24,27
|
4,11
|
22,98
|
2,02
|
|
6
|
27
|
27,50
|
3,89
|
28,38
|
-1,38
|
|
7
|
33
|
32,42
|
4,15
|
31,39
|
1,61
|
|
8
|
35
|
35,56
|
3,90
|
36,57
|
-1,57
|
|
9
|
40
|
39,81
|
3,98
|
39,46
|
0,537
|
|
Среднее
значение
|
|
|
|
|
-0,01
|
При  =0,7;
=0,7; 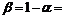 0,3
0,3
|
Время
t
|
Факт
Y
|
a0
|
a1
|
Расчет
|
Отклонение
|
|
|
4
|
4,00
|
|
|
|
1
|
8
|
8,00
|
4,00
|
8,00
|
0,00
|
|
2
|
13
|
12,91
|
4,49
|
12,00
|
1,00
|
|
3
|
15
|
15,22
|
3,31
|
17,40
|
-2,40
|
|
4
|
19
|
18,96
|
3,54
|
18,53
|
0,47
|
|
5
|
25
|
24,78
|
4,77
|
22,50
|
2,50
|
|
6
|
27
|
27,23
|
3,52
|
29,54
|
-2,54
|
|
7
|
33
|
32,80
|
4,62
|
30,75
|
2,25
|
|
8
|
35
|
35,22
|
3,44
|
37,42
|
-2,42
|
|
9
|
40
|
39,88
|
4,10
|
38,66
|
1,34
|
|
Среднее
значение
|
|
|
|
|
0,02
|
4) оценим адекватность построенных
моделей:
Для того чтобы модель была адекватна
исследуемому процессу, ряд остатков E(t)
должен обладать свойствами случайности, независимости последовательных уровней,
нормальности распределения.
· случайности остаточной
компоненты по критерию пиков;
Проверку случайности уровней остаточной
компоненты проводим на основе критерия поворотных точек. Для этого каждый
уровень ряда E(t)
сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних
уровней, то точка считается поворотной и в гр. точки поворота табл. для этой
строки ставится 1, в противном случае - 0. В первой и последней строке гр.
ставится прочерк или иной знак, так как у этого уровня нет двух соседних
уровней. Для линейной модели
|
Промежуточные
расчеты для оценки адекватности и точности модели
|
|
t
|
Отклон,
E(t)
|
Точки
поворота
|
E(t)2
|
[E(t)-E(t-1)]2
|
E(t)*E(t-1)
|
|E(t)/Y(t)|
|
|
1
|
-0,02
|
0,00
|
-
|
-
|
0,00
|
|
2
|
1,01
|
1
|
1,02
|
1,07
|
-0,02
|
0,08
|
|
3
|
-0,96
|
1
|
0,91
|
3,87
|
-0,97
|
0,06
|
|
4
|
-0,92
|
0
|
0,85
|
0,00
|
0,88
|
0,05
|
|
5
|
1,11
|
1
|
1,23
|
4,13
|
-1,02
|
0,04
|
|
6
|
-0,86
|
1
|
0,73
|
3,87
|
-0,95
|
0,03
|
|
7
|
1,18
|
1
|
1,39
|
4,13
|
-1,01
|
0,04
|
|
8
|
-0,79
|
1
|
0,62
|
3,87
|
-0,93
|
0,02
|
|
9
|
0,24
|
***
|
0,06
|
1,07
|
-0,19
|
0,01
|
|
сумма
|
0,0000000000000036
|
6
|
6,82
|
22,01
|
-4,21
|
0,33
|
Общее число поворотных точек в нашем примере
равно р = 6.
Рассчитаем значение q:
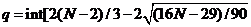 .
.
Функция int означает,
что от полученного значения берется только целая часть. При N = 9
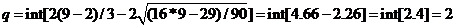 .
.
Если количество поворотных точек р
больше q, то условие
случайности уровней выполнено. В нашем случае р = 6, q = 2, значит
условие случайности уровней ряда остатков выполнено. Модель по этому критерию
адекватна.
Для адаптивной модели Брауна  =0,4
=0,4
|
Промежуточные
расчеты для оценки адекватности и точности модели
|
|
t
|
Отклон,
E(t)
|
Точки
поворота
|
E(t)2
|
[E(t)-E(t-1)]2
|
E(t)*E(t-1)
|
|E(t)/Y(t)|
|
|
1
|
0,00
|
***
|
0,00
|
-
|
-
|
0,00
|
|
2
|
1,00
|
1
|
1,00
|
1,00
|
0,00
|
0,08
|
|
3
|
-1,80
|
1
|
3,24
|
7,84
|
-1,80
|
0,12
|
|
4
|
-0,52
|
0
|
0,27
|
1,64
|
0,94
|
0,03
|
|
5
|
2,02
|
1
|
4,10
|
6,47
|
-1,05
|
0,08
|
|
6
|
-1,38
|
1
|
1,92
|
11,61
|
-2,80
|
0,05
|
|
7
|
1,61
|
1
|
2,59
|
8,97
|
-2,23
|
0,05
|
|
8
|
-1,57
|
1
|
2,46
|
10,11
|
-2,53
|
0,04
|
|
9
|
0,54
|
***
|
0,29
|
4,44
|
-0,84
|
0,01
|
|
сумма
|
-0,10
|
6
|
15,87
|
52,08
|
-10,32
|
0,46
|
Общее число поворотных точек равно р = 6.
Значение q=2.
p>q значит
условие случайности уровней ряда остатков выполнено. Модель по этому критерию
адекватна. Для адаптивной модели Брауна  =0,7
=0,7
|
Промежуточные
расчеты для оценки адекватности и точности модели
|
|
t
|
Отклон,
E(t)
|
Точки
поворота
|
E(t)2
|
[E(t)-E(t-1)]2
|
E(t)*E(t-1)
|
|E(t)/Y(t)|
|
|
1
|
0,00
|
***
|
0,00
|
-
|
-
|
0,00
|
|
2
|
1,00
|
1
|
1,00
|
1,00
|
0,00
|
0,08
|
|
3
|
-2,40
|
1
|
5,76
|
11,56
|
-2,40
|
0,16
|
|
4
|
0,47
|
0
|
0,22
|
8,24
|
-1,13
|
0,02
|
|
5
|
2,50
|
1
|
6,24
|
4,11
|
1,17
|
0,10
|
|
6
|
-2,54
|
1
|
6,47
|
25,42
|
-6,35
|
0,09
|
|
7
|
2,25
|
1
|
5,06
|
22,97
|
-5,72
|
0,07
|
|
8
|
-2,42
|
1
|
5,86
|
21,82
|
-5,45
|
0,07
|
|
9
|
1,34
|
***
|
1,81
|
14,18
|
-3,26
|
0,03
|
|
сумма
|
0,20
|
6
|
32,42
|
109,30
|
-23,13
|
0,63
|
Общее число поворотных точек равно р = 6.
Значение q=2.
p>q
значит условие случайности уровней ряда остатков выполнено. Модель по этому
критерию адекватна.
· Проверка равенства математического ожидания
уровней ряда остатков нулю осуществляется в ходе проверки
соответствующей нулевой гипотезы. Для чего строится е-статистика:
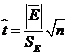
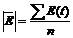
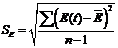
Для линейной модели

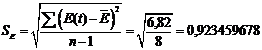

Полученное значение сравним с
табличным значением 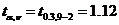
Так как  <
< то гипотеза
принимается.
то гипотеза
принимается.
Для адаптивной модели Брауна  =0,4
=0,4
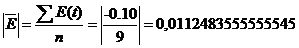
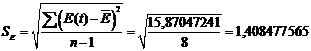

Полученное значение сравним с табличным
значением 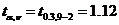
Так как 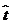 <
< то гипотеза
принимается.
то гипотеза
принимается.
Для адаптивной модели Брауна  =0,7
=0,7
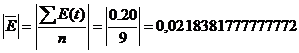
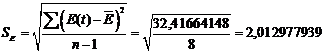
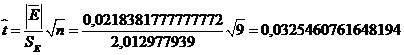
Полученное значение сравним с
табличным значением 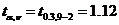
Так как 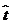 <
< то гипотеза
принимается.
то гипотеза
принимается.
· независимости уровней ряда
остатков по d-критерию
(в качестве критических используйте уровни d1
= 1,08 и d2
=1,36) или по первому коэффициенту корреляции, критический уровень которого r(1)
= 0,36;
Проверку проводим двумя методами:
) по d-критерию;
) по первому коэффициенту автокорреляции r(1).
Для линейной модели
)
 =
22.01/6.82
= 3.23
=
22.01/6.82
= 3.23
Примечание. В случае если полученное значение
больше 2, значит имеет место отрицательная автокорреляция. В таком случае
величину d уточняют, вычитая
полученное значение из 4.
Уточним величину d=4-3.23=0.77
Полученное (или уточненное) значение d
сравнивают с табличными значениями d1
и d2. Для нашего
случая d1=l,08,
a d2=1.36.
Если 0<d<d1,
то уровни автокоррелированы, то есть зависимы, модель неадекватна.
Если d1<d<d2,
то критерий Дарбина-Уотсона не дает ответа на вопрос о независимости уровней
ряда остатков. В таком случае необходимо воспользоваться другими критериями
(например, проверить независимость уровней по первому коэффициенту
автокорреляции).
Если d2<d<2
, то уровни ряда остатков являются независимыми.
В нашем случае 0.77<1.08, следовательно, то
уровни ряда остатков являются зависимыми, модель неадекватна.
) 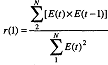 =
-4,21/6.82 = -0.62
=
-4,21/6.82 = -0.62
Если модуль рассчитанного значения первого
коэффициента автокорреляции меньше критического значения |r(1)|<rтаб,
то уровни ряда остатков независимы. Для нашей задачи критический уровень rтаб
= 0,36. Имеем: |r(1)| = 0,62
> rтаб
= 0,36, значит уровни зависимы, модель неадекватна
Для адаптивной модели Брауна  =0,4
=0,4
1) 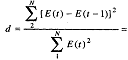 =52.08/10.32=3,28=4-3.28=0.72
=52.08/10.32=3,28=4-3.28=0.72
В
нашем случае 0.72<1.08, следовательно, то уровни ряда остатков являются
зависимыми, модель неадекватна.
)
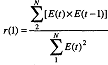 =-10.32/15.87=-0.65
=-10.32/15.87=-0.65
Имеем: |r(1)|
= 0,65 > rтаб
= 0,36, значит уровни зависимы, модель неадекватна по этому критерию
Для адаптивной модели Брауна  =0,7
=0,7
1) 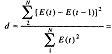 =109.30/32.42=3,37
=109.30/32.42=3,37
d=4-3.37=0.63
В нашем случае 0.63<l,08,
следовательно, то уровни ряда остатков являются зависимыми, модель неадекватна.
)  =-23.13/32.42=-0.713
=-23.13/32.42=-0.713
Имеем: |r(1)|
= 0,713 > rтаб
= 0,36 - значит уровни зависимы, модель неадекватна по этому критерию
· нормальности распределения
остаточной компоненты по R/S-критерию
с критическими уровнями 2,7-3,7;
Рассчитаем значение RS:
RS = (Emax-Emin)/
S,
где Emin
- максимальное значение уровней ряда остатков E(t);
Emax
- минимальное значение уровней ряда остатков E(t)
S - среднее
квадратическое отклонение.
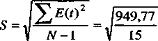
Для линейной модели
Emax= 1,18= -0,96Emin
= 2,13= 0,92= 2,31
Полученное значение RS
сравнивают с табличными значениями, которые зависят от количества точек N и
уровня значимости. Для N=9 и 5%-го уровня значимости значение RS
для нормального распределения должно находиться в интервале от 2,7 до 3,7.
Так как 2.31<2,7, полученное значение RS
не попало в заданный интервал. Значит, уровни ряда остатков не подчиняются
нормальному распределению, модель неадекватна.
Для адаптивной модели Брауна  =0,4
=0,4
E
max = 2,02min = -1,80max - Emin = 3,82 =
1,41
RS = 2,72
Так как 2,7<2,72<3.7, полученное значение RS
попало в заданный интервал. Значит, уровни ряда остатков подчиняются
нормальному распределению, модель адекватна по этому критерию.
Для адаптивной модели Брауна  =0,7
=0,7
Emax
= 2,50= -2,54- Emin = 5,04= 2,01, RS = 2,50
Так как 2,5<2.7, полученное значение RS
непопало в заданный интервал. Значит, уровни ряда остатков не подчиняются
нормальному распределению, модель неадекватна по данному критерию.
5) Оценить
точность модели на основе использования средней относительной ошибки
аппроксимации;
Оценка точности модели имеет
смысл только для адекватных моделей. В случае временных рядов точность модели
определяется как разность меду фактическим и расчетным значениями. В качестве
статистических показателей точности чаще всего применяют стандартную ошибку
прогнозируемого показателя, или среднеквадратическое отклонение от линии
тренда:
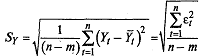
где т - число параметров
модели, и среднюю относительную ошибку аппроксимации -
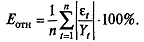
Если ошибка не превосходит 15%,
точность модели считается приемлемой. В общем случае допустимый уровень
точности, а значит и надежности устанавливает пользователь модели, который в
результате содержательного анализа проблемы выясняет, насколько она
чувствительна к точности решения и насколько велики потери из-за неточного
решения.
Для линейной модели
(Неадекватная модель)

Условия точности выполнены
Для адаптивной модели Брауна  =0,4
(Неадекватная модель)
=0,4
(Неадекватная модель)
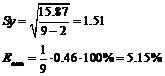
Условия точности выполнены
Для адаптивной модели Брауна  =0,7
(Неадекватная модель)
=0,7
(Неадекватная модель)
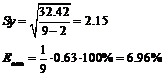
Условия точности выполнены
Показатели точности лучше при  =0,4 меньше,
чем при
=0,4 меньше,
чем при  =0,7, значит
можно сделать вывод, что значение
=0,7, значит
можно сделать вывод, что значение  =0,4 лучше.
=0,4 лучше.
6) По двум построенным моделям
осуществить прогноз спроса на следующие две недели (доверительный интервал
прогноза рассчитать при доверительной вероятности p=70%).
Для линейной модели
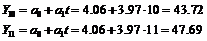
Для учета случайных колебаний при
прогнозировании рассчитываются доверительные интервалы, зависящие от
стандартной ошибки 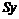 , горизонта
прогнозирования k, длины временного ряда n и уровня
значимости прогноза а. Будущие значения Yn+k c
вероятностью (1 - а) попадут в интервал
, горизонта
прогнозирования k, длины временного ряда n и уровня
значимости прогноза а. Будущие значения Yn+k c
вероятностью (1 - а) попадут в интервал
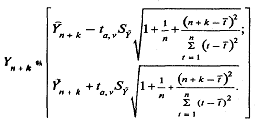
Примем значение уровня
значимости а = 0,3, а значит, доверительную вероятность - 70%. В этом случае
критерий Стьюдента (при v=
n- 2 = 7) равен
ta,v
=
1.12.
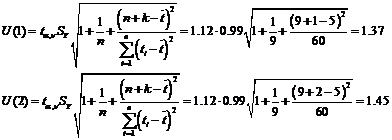
Получим интервальный прогноз

Построение прогноза
по модели Брауна
Для прогнозирования
используется модель, полученная на последнем шаге (при t
= N). Прогнозные
оценки по модели (5.3.1) получаются путем подстановки в нее значения k
= 1, 2; а интервальные - по тем же формулам, что и для кривых роста:
Для адаптивной модели Брауна  =0,4
=0,4
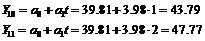
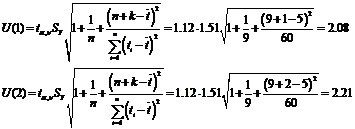

Для адаптивной модели Брауна  =0,7
=0,7