Геометрические операции над изображением
Северо-Кавказский
горно-металлургический институт
Практическая
работа
По
предмету: «Компьютерная графика»
Тема:
«Геометрические операции над изображением»
Выполнил: Теблоев В.Н.
Проверила: Соколова Е.А.
Владикавказ
2012 г.
Введение
Целью моей работы является написание программы, реализующей поворот
изображения на заданный градус по любой из осей координат, смещение также по
любой из осей.
1. Компьютерная графика
Компьютерная графика - это область информатики, занимающаяся проблемами
получения различных изображений (рисунков, чертежей, мультипликации) на
компьютере.
Работа с компьютерной графикой - одно из самых популярных направлений
использования персонального компьютера, причем занимаются этой работой не
только профессиональные художники и дизайнеры. На любом предприятии время от
времени возникает необходимость в подаче рекламных объявлений в газеты и
журналы, в выпуске рекламной листовки или буклета. Иногда предприятия
заказывают такую работу специальным дизайнерским бюро или рекламным агентствам,
но часто обходятся собственными силами и доступными программными средствами.
Без компьютерной графики не обходится ни одна современная программа.
Работа над графикой занимает до 90% рабочего времени программистских
коллективов, выпускающих программы массового применения.
Основные трудозатраты в работе редакций и издательств тоже составляют
художественные и оформительские работы с графическими программами.
Необходимость широкого использования графических программных средств
стала особенно ощутимой в связи с развитием Интернета и, в первую очередь,
благодаря службе World Wide Web, связавшей в единую "паутину"
миллионы "домашних страниц". У страницы, оформленной без компьютерной
графики мало шансов привлечь к себе массовое внимание. Область применения
компьютерной графики не ограничивается одними художественными эффектами. Во
всех отраслях науки, техники, медицины, в коммерческой и управленческой
деятельности используются построенные с помощью компьютера схемы, графики,
диаграммы, предназначенные для наглядного отображения разнообразной информации.
Конструкторы, разрабатывая новые модели автомобилей и самолетов, используют
трехмерные графические объекты, чтобы представить окончательный вид изделия.
Архитекторы создают на экране монитора объемное изображение здания, и это
позволяет им увидеть, как оно впишется в ландшафт.
2. История развития компьютерной графики
компьютерный
графика пиксельный изображение
Практически с самого момента появления компьютеров появилась и
компьютерная графика. В настоящее время можно сказать, что нет ни одной области
в деятельности человека, где бы она ни применялась.
Редко какой фильм обходится без компьютерной графики, не говоря уж о
рекламе, издательском деле, анимации и компьютерных играх. Виртуальная
реальность находит свою нишу в индустрии развлечений и видеоиграх. Число
виртуальных галерей и развлекательных парков быстро растет. Практически ни одно
производство не обходится без компьютерной графики. Такая отрасль как
космическая, пользуется компьютерной графикой с самого её появления, особенно с
приходом автоматических пилотируемых аппаратов.
"Классическая" векторная графика до сих пор используется в
различных приложениях бизнеса, включая разработку концепции, тестирование и
создание новых продуктов. Можно считать, что первые системы компьютерной
графики появились вместе с первыми цифровыми компьютерами. Сейчас ее
рассматривают как средство, которое обеспечивает мощную взаимосвязь между
человеком и компьютером, заставляя компьютер говорить с человеком на языке изображений.
Прошло несколько лет, пока компьютерная графика стала основным средством
связи между человеком и компьютером, постоянно расширяющим сферы своего
применения. Проект "вихрь" Массачусетского технологического института
был отмечен как начало эры компьютерной графики. "Вихрь" стал основой
создания опытного образца командноуправляемой системы воздушной защиты,
разработанной как средство преобразования данных, полученных от радара, в
наглядную форму.
В конце шестидесятых - начале семидесятых в области компьютерной графики
начали работать новые фирмы. Если ранее для выполнения каких-либо работ
покупателям приходилось устанавливать уникальное оборудование и разрабатывать
новое программное обеспечение, то с появлением разнообразных пакетов программ,
облегчающих процесс создания изображений, чертежей и интерфейсов, ситуация
существенно изменилась. За десятилетие системы стали настолько совершенны, что
почти полностью изолировали пользователя от проблем, связанных с программным
обеспечением.
В конце семидесятых в компьютерной графике произошли значительные
изменения. Появилась возможность создания растровых дисплеев, имеющих множество
преимуществ: вывод больших массивов данных, устойчивое, немерцающее
изображение, работа с цветом. Впервые стало возможным получение цветовой гаммы.
Растровая технология в конце семидесятых стала явно доминирующей. Наиболее
знаменательным событием в области компьютерной графики было создание конце
семидесятых персонального компьютера.
В 1977 году компания Apple создала Apple-II. Появление этого устройства
вызывало смешанные чувства: графика была ужасной, а процессоры медленными.
Однако персональные компьютеры стимулировали процесс разработки периферийных
устройств. Конечно, персональные компьютеры развивались как важная часть машинной
графики, особенно с появлением в 1984 году модели Apple Macintosh с их
графическим интерфейсом пользователя. Первоначально областью применения
персонального компьютера были не графические приложения, а работа с текстовыми
процессорами и электронными таблицами, но его возможности как графического
устройства побуждали к разработке относительно недорогих программ как в области
CAD/CAM, так и в более общих областях бизнеса и искусства.
К концу 80-х программное обеспечение имелось для всех сфер применения: от
комплексов управления до настольных издательств. В конце восьмидесятых возникло
новое направление рынка на развитие аппаратных и программных систем
сканирования, автоматической оцифровки. Оригинальный толчок в таких системах
должна была создать магическая машина Ozalid, которая бы сканировала и
автоматически векторизовала чертеж на бумаге, преобразуя его в стандартные
форматы.
В 90-х стираются отличия между компьютерной графикой и обработкой
изображения. Машинная графика часто имеет дело с векторными данными, а основой
для обработки изображений является пиксельная информация. Еще несколько лет
назад каждый пользователь требовал рабочую станцию с уникальной архитектурой, а
сейчас процессоры рабочих станций имеют быстродействие, достаточное для того,
чтобы управлять как векторной, так и растровой информацией.
Кроме того, появляется возможность работы с видео. Прибавьте аудио
возможности - и вы имеете компьютерную среду мультимедиа. Все области
применения - будь то инженерная или научная, бизнес или искусство - являются
сферой применения компьютерной графики. Возрастающий потенциал персональных
компьютеров и их громадное число - порядка 100 миллионов - обеспечивает
устойчивый рост индустрии в данной отрасли. Графика все шире проникает в бизнес
- сегодня фактически нет документов, созданных без использования какого-либо
графического элемента.
Художники, архитекторы, дизайнеры, уже не мыслят своей работы без
использования компьютерной графики. Трехмерная графика позволяет смоделировать
архитектурный объект и позволяет оценить его достоинства более объективно, чем
это, возможно, сделать на основе чертежей или макетов. Дизайнер по интерьерам
сейчас может предложить заказчику почти фотографическое изображение его
будущего жилья, тогда как раньше, возможно было довольствоваться только
эскизами.
Особенно часто в повседневной жизни мы сталкиваемся с векторными
изображениями. Почти на любом изделии есть логотип компании-изготовителя.
Разрабатывается логотип в векторах. Но нельзя и переоценивать возможности
компьютера. Ведь это всего лишь инструмент, каким бы совершенным он не был.
Компьютер лишь облегчает работу человека с графическими изображениями, но не
создает их. Сначала можно было создавать лишь простые векторные объекты -
изображения, состоящие из, так называемых, «векторов» - функций, которые
позволяют вычислить положение точки на экране или бумаге. Например, функция,
графиком которой является круг, прямая линия или другие более сложные кривые.
С развитием компьютерной техники и технологий появилось множество
способов выполнения графических изображений. Примерно в 1995 году в России
появились свои разработчики мультимедиа программ, зародились электронные
издательства. Качественный уровень программных продуктов, выполненных
российскими художниками и программистами не уступал, а иногда и превосходил
качество программ зарубежных авторов. Ещё одним направлением современной
компьютерной графики стал «Веб-Дизайн». С 1995 года во всём мире наблюдается
развёртывание глобальной мировой компьютерной сети - Интернет.
Интернет является самым большим в мире хранилищем информации и связывает
сегодня почти 80% всех компьютерных систем мира. По нашему мнению, Интернет
стал новым направлением для компьютерных художников-дизайнеров. По своему жанру
он очень близок к книжной и журнальной графике. Заметим, что художественная
графика, предназначенная для Интернет, должна быть лаконична. Это связано,
прежде всего, с ограничениями в скорости передачи данных по телефонным и
кабельным сетям, через которые осуществляется связь между компьютерами. Однако
этого вполне достаточно для того, чтобы осуществлять передачу видеоданных.
3. Геометрические операции
Геометрические преобразования - это такие преобразования графических
объектов, при которых изменяется направление, масштаб и положение координатной
системы, используемой для определения местонахождения точек в пространстве. При
этом само пространство не подвергается каким-либо изменениям; т.е. сама
структура графического изображения сохраняется. Следовательно, при
геометрических преобразованиях неважен тип объекта, так как в преобразованиях
участвуют точки.
Основными операциями, которые относятся к геометрическим преобразованиям
двумерных графических объектов, являются:
перенос начала координат;
масштабирование;
поворот осей координат.
Теперь подробнее об этих операциях.
3.1 Поворот
Рассмотрим частный случай поворота в пространстве XYZ - поворот
относительно оси Z, проходящей перпендикулярно плоскости XY.
Предположим, что центр вращения совпадает с началом координат. Тогда, при
повороте системы координат XY в декартовой плоскости на некоторый произвольный
угол а относительно центра вращения, координаты произвольной точки С в системе
координат (x’,y’) можно выразить через координаты этой точки в изначальной
системе координат (x, y):
x' = x cos w + y sin w,' = -x sin w + y cos w.
Для выполнения операции поворота используется матрица:
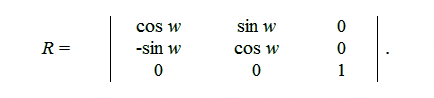
3.2 Перенос
При выполнении данной операции происходит перенос начала координат на
некоторую величину.
Обозначим старую систему координат - СК1, новую - СК2. При переносе новое
начало координат в системе координат СК1 лежит в точке (Tx, Ty), в новой же
системе СК2 старое начало координат является точкой (-Tx, -Ty). Начало
координат (x,y) системы СК1 в системе СК2 станет точкой (x-Tx, y-Ty).
Стоит упомянуть, что при переносе сохраняются как направление осей
координат, так и масштаб.
Матрица, необходимая для выполнения операции переноса имеет вид:
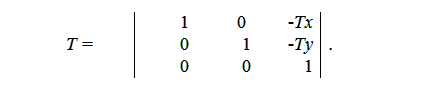
3.3 Масштабирование
При выполнении операции масштабирования отрезок единичной длины на оси X
становится отрезком длиной Sx на оси X’; отрезок единичной длины на оси Y
становится отрезком длиной Sy на оси Y’. Получается, что в новой системе точка
с координатой (1,1) преобразуется в точку (Sx, Sy), точка (x,y) будет иметь
координаты (x*Sx, y*Sy).
Стоит отметить, что при масштабировании начало координат и направление
осей новой и старой систем координат совпадают, меняется лишь масштаб по осям.
Матрица, необходимая для выполнения операции масштабирования имеет вид:
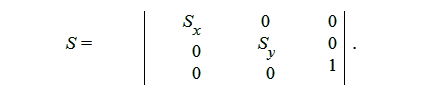
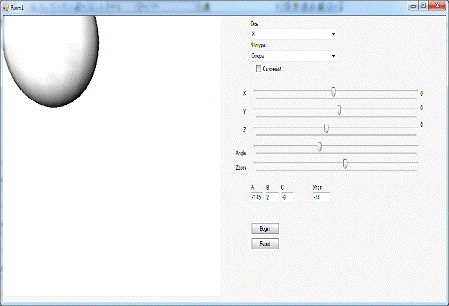
4. Пример работы
программы
До:
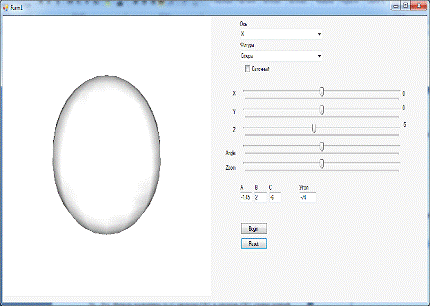
После:
5. Листинг программы
System;System.Collections.Generic;System.ComponentModel;System.Data;System.Drawing;System.Linq;System.Text;System.Windows.Forms;Tao.OpenGl;Tao.FreeGlut;Tao.Platform.Windows;Tao
{partial class Form1 : Form
{Form1()
{();.InitializeContexts();
}a = 0, b = 0, c = -5, d = 0, zoom = 1;os_x = 1, os_y = 0, os_z = 0;Wire
= false;void Form1_Load(object sender, EventArgs e)
{.glutInit();.glutInitDisplayMode(Glut.GLUT_RGB |
Glut.GLUT_DOUBLE);.glClearColor(255, 255, 255, 1);.glViewport(0, 0, AnT.Width,
AnT.Height);.glMatrixMode(Gl.GL_PROJECTION);.glLoadIdentity();.gluPerspective(45,
(float)AnT.Width / (float)AnT.Height, 0.1,
200);.glMatrixMode(Gl.GL_MODELVIEW);.glLoadIdentity();.glEnable(Gl.GL_DEPTH_TEST);.glEnable(Gl.GL_LIGHTING);.glEnable(Gl.GL_LIGHT0);.SelectedIndex
= 0;.SelectedIndex = 0;.Start();
}void simpleOpenGlControl1_Load(object sender, EventArgs e)
{
}void button1_Click(object sender, EventArgs e)
{.glClear(Gl.GL_COLOR_BUFFER_BIT
Gl.GL_DEPTH_BUFFER_BIT);.glLoadIdentity();.glColor3f(1.0f, 0,
0);.glPushMatrix();.glTranslated(0, 0, -6);.glRotated(45, 1, 1,
0);.glutWireSphere(1, 12,
16);.glutWireCube(10);.glPopMatrix();.glFlush();.Invalidate();
}void RenderTimer_Tick(object sender, EventArgs e)
{();
{= (double)trackBar1.Value / 1000.0;.Text = a.ToString();
}void trackBar2_Scroll(object sender, EventArgs e)
{= (double)trackBar2.Value / 1000.0;.Text = b.ToString();
}void trackBar3_Scroll(object sender, EventArgs e)
{= (double)trackBar3.Value / 1000.0;.Text = c.ToString();
}void checkBox1_CheckedChanged(object sender, EventArgs e)
{(checkBox1.Checked)= true;= false;
}void trackBar5_Scroll(object sender, EventArgs e)
{= (double)trackBar5.Value / 1000.0;
}void trackBar4_Scroll(object sender, EventArgs e)
{= (double)trackBar4.Value;
}void Draw()
{.glClear(Gl.GL_COLOR_BUFFER_BIT|
Gl.GL_DEPTH_BUFFER_BIT);.glClearColor(255, 255, 255,
1);.glLoadIdentity();.glPushMatrix();.glTranslated(a, b, c);.glRotated(d, os_x,
os_y, os_z);.glScaled(zoom, zoom, zoom);(comboBox2.SelectedIndex)
{0:
{(Wire).glutWireSphere(2, 16,
16);.glutSolidSphere(2, 16, 16);;
}1:
{(Wire).glutWireCylinder(1,
2, 32, 32);.glutSolidCylinder(1, 2, 32, 32);;
}2:
{(Wire).glutWireCube(2);.glutSolidCube(2);;
}3:
{(Wire).glutWireCone(2, 3,
32, 32);.glutSolidCone(2, 3, 32, 32);;
}4:
{(Wire).glutWireTorus(0.2,
2.2, 32, 32);.glutSolidTorus(0.2, 2.2, 32, 32);;
}
}.glPopMatrix();.glFlush();.Invalidate();
}void
comboBox1_SelectedIndexChanged(object sender, EventArgs e)
{(comboBox1.SelectedIndex)
{0:
{_x = 1;_y = 0;_z = 0;;
}1:
{_x = 0;_y = 1;_z = 0;;
}2:
{_x = 0;_y = 0;_z = 1;;
}
}
}void button2_Click(object
sender, EventArgs e)
{.Value = 0;.Value = 0;.Value
= -5000;.Value = 0;.Value = 0;= (double)trackBar1.Value / 1000.0;.Text =
a.ToString();= (double)trackBar2.Value / 1000.0;.Text = b.ToString();=
(double)trackBar3.Value / 1000.0;.Text = c.ToString();
}void button3_Click(object
sender, EventArgs e)
{=
Convert.ToDouble(textBox1.Text);.Value = (int)(a * 1000);=
Convert.ToDouble(textBox2.Text);.Value = (int)(b * 1000);=
Convert.ToDouble(textBox3.Text);.Value = (int)(c * 1000);= Convert.ToDouble(textBox4.Text);.Value
= (int)(d);
}
}
}
Список использованных
источников
1) Интернет-портал
ru.wikipedia.org
) Интернет-портал
habrahabr.ru
) Интернет-портал
stackoverflow.com
) Интернет-портал
cyberforum.ru
) Интернет-портал
programmersheaven.com
) Интернет-портал
esate.ru
) Интернет-портал
google.com