Алгоритмы Краскала и Прима

Содержание

Введение

1 Алгоритм Краскала

1.1 Описание алгоритма Краскала

1.2 Псевдокод алгоритма

1.3 Блок-схема алгоритма

1.4 Сложность алгоритма

2. Алгоритм Прима

2.1 Описание алгоритма Прима

2.2 Псевдокод алгоритма

2.3 Блок-схема алгоритма

2.4 Код программы

2.5 Оценка сложности

Заключение

Список использованных источников

Введение

Объектом исследования курсовой работы стала реализация алгоритма Краскалы.

Целями работы являлись:

) ознакомление с алгоритмом Краскалы, его историей;

) реализация алгоритма, для построения минимального остовного дерева;

) анализ трудоёмкости алгоритма;

) тестирование алгоритма.

Минимальным остовным деревом (МОД) связного взвешенного графа называется его связный подграф, состоящий из всех вершин исходного дерева и некоторых его ребер, причем сумма весов ребер максимально возможная. Если исходный граф несвязен, то описываемую ниже процедуру можно применять поочередно к каждой его компоненте связности, получая тем самым минимальные остовные деревья для этих компонент.

Алгоритм Краскала (или алгоритм Крускала) - алгоритм построения минимального отовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джзефом Крускалом в 1956 году.

Алгоритм Краскала может строить дерево одновременно для нескольких компонент связности, которые в процессе решения объединяются в одно связанное дерево.

Полный граф задается списком ребер. Перед работой список ребер сортируется по возрастанию длины. На каждом шаге просматривается список ребер, начиная с ребра, следующего за вошедшим в решение на предыдущем шаге, и к строящемуся поддереву присоединяют то ребро, которое не образует цикла с ребрами, уже включенными в решение.

Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: есть n городов, через которые можно проложить маршрут так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Требуется найти такой маршрут, чтобы стоимость проезда была максимальной.

На практике алгоритм Краскалы применятся в работе авиалиний при нахождении наименьшего воздушного пути из одного пункта назначения в другой.

Алгоритм Прима - алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые был открыт в 1930 году чешским математиком Войцехом Ярником, позже переоткрыт Робертом Примом в 1957 году, и, независимо от них, Э. Дейкстрой в 1959 году.

Построение начинается с дерева, включающего в себя одну (произвольную) вершину. В течение работы алгоритма дерево разрастается, пока не охватит все вершины исходного графа. На каждом шаге алгоритма к текущему дереву присоединяется самое лёгкое из рёбер, соединяющих вершину из построенного дерева и вершину не из дерева.

1 Алгоритм Краскала

1.1 Описание алгоритма Краскала

Формулировка.

Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса.

Алгоритм состоит из следующей последовательности действий:

.        Создается список ребер E, содержащий длину ребра, номер исходной вершины ребра (i), номер конечной вершины ребра (j), признак включения данного ребра в дерево.

2.      Данный список упорядочивается в порядке возрастания длин ребер.

.        Просматривается список E и выбирается из него ребро с максимальной длиной, еще не включенное в результирующее дерево и не образующее цикла с уже построенными ребрами.

.        Если все вершины включены в дерево и количество ребер на единицу меньше количества вершин, то алгоритм свою работу закончил. В противном случае осуществляется возврат к пункту 3.

1.2 Псевдокод алгоритма

Отсортировать ребра в порядке возрастания весов

инициализировать структуру разбиений

edgeCount=l

while edgeCount<=E and includedCount<=М-l do

parentl=FindRoot (edge [edgeCount]. start)=FindRoot (edge [edgeCount]. end)parentl/=parent2 then

добавить edge [edgeCount] в остовное дерево=includedCount=l(parent1,parent2)if=edgeCount+lwhile. - число ребер в графе;

V - число вершин в графе

edgeCount - переменная;

includedCount - переменная;- массив, в котором под каждый элемент множества, с которым мы собираемся работать, отведена одна ячейка;

FindRoot (x) - (x элемент, для которого мы хотим найти корень части, его содержащей) процедура, начинающая с ячейки Parent [x], в которой хранится номер непосредственного предка элемента x;- функция, выполняющая объединение двух частей в одну.

1.3 Блок-схема алгоритма

На рисунке 1 представлена общая схема алгоритма.

алгоритм краскал прим псевдокод

Рисунок 1 - Общая схема

На рисунке 2 представлена блок-схема алгоритма сортировки вставками.

Рисунок 2 - Блок-схема алгоритма сортировки вставками

На рисунке 3 представлена блок-схема алгоритма Краскала

Рисунок 3 - Блок-схема алгоритма Краскала

1.4 Сложность алгоритма

Сложность этого алгоритма совпадает со сложностью используемого алгоритма сортировки, поскольку число операций в цикле while линейно по числу ребер. Поэтому сложность алгоритма Крускала поиска МОД равна O (E\og Е).

2. Алгоритм Прима

2.1 Описание алгоритма Прима

Описание.

Сам алгоритм имеет очень простой вид. Искомый минимальный остов строится постепенно, добавлением в него рёбер по одному. Изначально остов полагается состоящим из единственной вершины (её можно выбрать произвольно). Затем выбирается ребро минимального веса, исходящее из этой вершины, и добавляется в минимальный остов. После этого остов содержит уже две вершины, и теперь ищется и добавляется ребро минимального веса, имеющее один конец в одной из двух выбранных вершин, а другой - наоборот, во всех остальных, кроме этих двух. И так далее, т.е. всякий раз ищется минимальное по весу ребро, один конец которого - уже взятая в остов вершина, а другой конец - ещё не взятая, и это ребро добавляется в остов (если таких рёбер несколько, можно взять любое). Этот процесс повторяется до тех пор, пока остов не станет содержать все вершины (или, что то же самое, n-1 ребро). В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связен, то остов найден не будет (количество выбранных рёбер останется меньше n-1).

Вход: Связный неориентированный граф G (V,E)

Выход: Множество T рёбер минимального остовного дерева

Алгоритм.

·        Множество остовных вершин - исходная вершины

·        Множество оставшихся - все вершины за исключением исходной

·        Пока множество оставшихся не пусто:

o   Ищем ребро соединяющее множество остовных и множество оставшихся и имеющее наименьший вес

o   Для найденного ребра, вершину принадлежащую множеству оставшихся:

·        Вычеркиваем из множества оставшихся.

·        Добавляем к множеству остовных.

сформировать начальную кайму, состоящую из вершин,

соседних с начальным узломв графе есть вершины, не попавшие в дерево do

выбрать ребро из дерева в кайму с наименьшим весом

добавить конец ребра к дереву

изменить кайму, для чего

добавить в кайму вершины, соседние с новой

обновить список ребер из дерева в кайму так,

чтобы он состоял из ребер наименьшего веса

end while

2.2 Псевдокод алгоритма

MST_PRIM (G, w, r)

for (Для) каждой вершины u є V [G]

2 do key [u] " - INFINITY

prev [u] " - NIL

key [r] " - 0

Q " - V [G]

while Q не пустая

do u " - Extract_Min (Q)

8 for (Для) каждой вершины v є Adj [u]

9 do if v є Q и w (u,v) < key [v]

10 then prev [v] " - u

key [v] " - w (u, v)

2.3 Блок-схема алгоритма

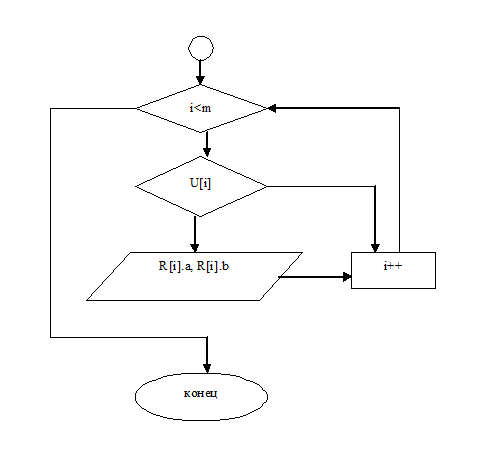
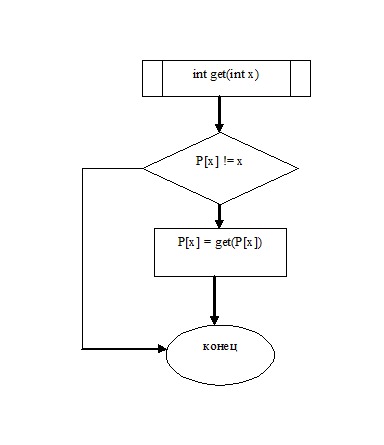
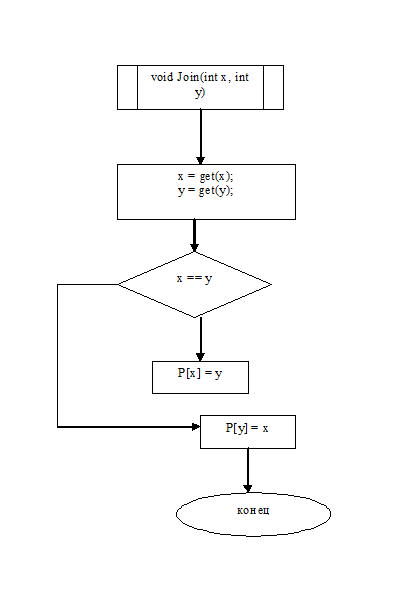
2.4 Код программы

2.5 Оценка сложности

Время работы алгоритма Прима зависит от выбранной реализации очереди с приоритетами Q. Если реализовать ее как бинарную пирамиду, то для выполнения инициализации в строках 1-5 потребуется времени О (V). Тело цикла while выполняется |V| раз, а поскольку каждая операция Extract_Min занимает время О (lg V), общее время всех вызовов процедур Extract__Min составляет О (V*lg V). Цикл for в строках 8-11 выполняется всего О (Е) раз, поскольку сумма длин всех списков смежности равна 2|Е|. Внутри цикла for проверка на принадлежность Q в строке 9 может быть реализована за постоянное время, если воспользоваться для каждой вершины битом, указывающим, находится ли она в Q, и обновлять этот бит при удалении вершины из Q. Присвоение в строке 11 неявно включает операцию Decrease_Key над пирамидой. Время выполнения этой операции - О (lg V). Таким образом, общее время работы алгоритма Прима составляет o (V * lg V + Е * lg V) = o (Е * lg V), что асимптотически совпадает со временем работы алгоритма Крускала.

Заключение

В курсовом проекте был изучен алгоритм Краскала. Рассмотрены блок-схема, псевдокод данного алгоритма. Разработана программа, реализующая алгоритм Краскала, поиск минимального остовного дерева. Изучен алгоритм Прима.

Список использованных источников

1.       Свободная энциклопедия ВикипедиЯ [Электронный ресурс]. - Режим доступа: http://ru. wikipedia.org/. - Загл. с экрана.

2.      Алгоритмы, методы, исходники [Электронный ресурс]. - Режим доступа: http://algolist. manual.ru/. - Загл. с экрана.

3.       Макконелл Дж. Основы современных алгоритмов: 2-е дополненное издание М.: Техносфера, 2004. - 368с. ISBN 5-94836-005-9.

.         [Электронный ресурс]. - Режим доступа: http://www.lotos-khv. narod.ru/. - Загл. с экрана.