Точный закон сохранения энергии
Точный закон
сохранения энергии
Океанов
Е.Н.
Одномерное геометрическое
пространство, например, вдоль оси 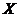 , можно рассматривать, как частный
случай трехмерного пространства без участия массы. Этот частный случай
позволяет выявить одно важное свойство сугубо математического - геометрического
- пространства.
, можно рассматривать, как частный
случай трехмерного пространства без участия массы. Этот частный случай
позволяет выявить одно важное свойство сугубо математического - геометрического
- пространства.
Пусть в этом пространстве существует
интеграл 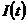 :
:
закон сохранение энергия
геометрическое
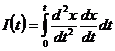 (1)
(1)
Его легко преобразовать к виду:
 (2)
(2)
и проинтегрировать по частям:
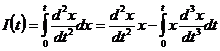 (3)
(3)
Но интеграл (1) можно, очевидно,
представить и в ином виде, удобном для непосредственного интегрирования:
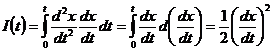 (4)
(4)
Из сравнения выражений (3) и (4)
следует равенство:
 (5)
(5)
Это равенство и является выражением
важного свойства геометрического пространства. И вот почему. Интеграл (1) легко
превратить в энергетическую характеристику физического пространства с помощью
множителя  ,
выражающего некую массу в этом пространстве:
,
выражающего некую массу в этом пространстве:
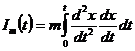 (6)
(6)
Тогда равенство (5) приобретает
смысл баланса энергий в одномерном физическом пространстве:
 (7)
(7)
Действительно, если учесть, что сила
 и скорость
и скорость 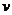 равны,
соответственно:
равны,
соответственно:
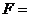
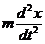 и
и 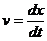 ,
,
 , (8)
, (8)
в котором левая часть выражает
потенциальную энергию  :
:
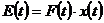 ,
,
а второе слагаемое в правой части
выражает кинетическую энергию  :
:
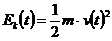
Первое слагаемое правой части
уместно переписать в виде:
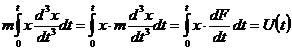 , (9)
, (9)
а производную силы  по времени
по времени  , входящую в
подынтегральное выражение, понимать, как усилие (по аналогии с ускорением).
Тогда можно полагать, что энергию
, входящую в
подынтегральное выражение, понимать, как усилие (по аналогии с ускорением).
Тогда можно полагать, что энергию 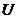 усилия выражает равенство (9) и
баланс энергий (8) принимает вид:
усилия выражает равенство (9) и
баланс энергий (8) принимает вид:
 (10)
(10)
Равенство (10) выражает, как
представляется, точный закон сохранения энергии для случая постоянной массы, в
соответствии с которым потенциальная энергия равна сумме кинетической энергии и
энергии усилия. Традиционный - неточный - закон сохранения энергии предполагает
равенство потенциальной и кинетической энергий. В точном законе это равенство
достигается только при обязательном условии:
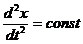 (11)
(11)
Но тогда надо объяснить, чем
отличается неточный закон сохранения энергии от выведенного здесь точного.
В работе [1] весьма подробно
рассмотрен интеграл  действия,
на основе которого и выводились в дальнейшем понятия кинетической и
потенциальной энергий. Уместно привести цитату из этой работы:
действия,
на основе которого и выводились в дальнейшем понятия кинетической и
потенциальной энергий. Уместно привести цитату из этой работы:
«Изменение S при замене 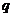 на
на  дается
разностью:
дается
разностью:
 .
.
Разложение этой разности по степеням
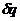 и
и  (в
подынтегральном выражении) начинается с членов первого порядка. Необходимым
условием минимальности
(в
подынтегральном выражении) начинается с членов первого порядка. Необходимым
условием минимальности  является
обращение в нуль совокупности этих членов; ее называют первой вариацией (или
просто вариацией) интеграла».
является
обращение в нуль совокупности этих членов; ее называют первой вариацией (или
просто вариацией) интеграла».
Эта вариация в работе принимает вид:

И далее вторая цитата:
«Таким образом, мы получаем
уравнение
Из первой цитаты следует, что
исследование интеграла действия почти двести лет тому назад производилось с
точностью до линейных членов разложения функции Лагранжа. Пусть эта точность
здесь определяется как точность до макромира, когда о микромире никто еще даже
не задумывался. Только к концу XIX века микромир стал
привлекать внимание ученых. Но микромир требовал точность, на несколько (более
10) порядков лучшую, когда уже нельзя пренебрегать членами разложения более
высоких степеней, нежели первая степень. Однако ревизией интеграла действия с
учетом новых реалий никто не занимался, хотя в 1969 году в работе [1] уже не
только можно было, но и должно было пересмотреть интеграл действия с точностью
до микромира. Тогда уравнение из второй цитаты (уравнение Лагранжа) оказалось
бы неоднородным, и на этой основе последующий анализ сохранения энергии
осуществлялся бы с точностью до микромира. Но проще было постулировать, что в
микромире закон сохранения энергии не всегда выполняется (когда эксперименты
обнаруживали этот досадный факт). Между тем, закон сохранения энергии есть
объективная реальность и, если он не выполняется почему-либо, надо искать тому
субъективные причины. Объективных причин быть не может - это же закон, и он
выполняется всегда с точностью до постоянного слагаемого. Полезно выявить хотя
бы несколько из этих субъективных причин.
Во-первых, упомянутое в первой
цитате разложение по степеням уместно представить в виде:
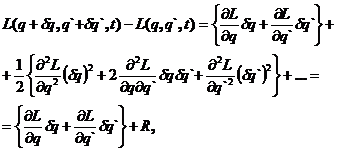
где  - сумма всех членов разложения
порядка 2 и более. Это - точное разложение. Во-вторых, - полезное замечание о
параметре. Суть его сводится к следующему. Пусть некая характеристика
- сумма всех членов разложения
порядка 2 и более. Это - точное разложение. Во-вторых, - полезное замечание о
параметре. Суть его сводится к следующему. Пусть некая характеристика 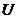 в системе
координат
в системе
координат  является
функцией этих координат:
является
функцией этих координат:
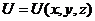 ,
,
а сами координаты являются функциями
параметра  :
:
 ,
, 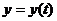 ,
, 
Тогда производная функции 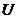 по
параметру
по
параметру  принимает
вид:
принимает
вид:
 (12)
(12)
Пусть эта же характеристика 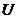 в системе
координат
в системе
координат  является
функцией этих координат:
является
функцией этих координат:
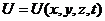 ,
,
а сами координаты являются функциями
координаты 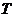 :
:
 ,
, 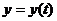 ,
,  ,
, 
Тогда производная функции 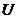 по
координате
по
координате 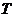 принимает
вид:
принимает
вид:
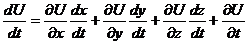 (13)
(13)
Как легко заметить, выражение (13)
отличается от выражения (12) дополнительным слагаемым в виде частной
производной функции 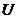 по
координате
по
координате 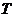 . Это
означает, что независимая переменная в статусе параметра порождает одну
функцию, а в статусе координаты - совершенно иную функцию даже для одной и той
же характеристики, описываемой этими функциями. Поэтому введение параметра в
число независимых переменных по принципу «каши маслом не испортишь»
представляется недопустимым, поскольку изменяет статус этой переменной и
подменяет поставленную для решения задачу совершенно другой задачей. В
рассматриваемом же случае время выступает в качестве параметра, а не
координаты, и именно потому в приведенном разложении отсутствует частная
производная функции Лагранжа по времени (тогда как формально она должна была бы
быть, поскольку в цитируемой работе время непосредственно входит в число
независимых переменных этой функции). Отсутствует она и в приведенной вариации,
что и дает основание полагать время параметром, а не координатой.
. Это
означает, что независимая переменная в статусе параметра порождает одну
функцию, а в статусе координаты - совершенно иную функцию даже для одной и той
же характеристики, описываемой этими функциями. Поэтому введение параметра в
число независимых переменных по принципу «каши маслом не испортишь»
представляется недопустимым, поскольку изменяет статус этой переменной и
подменяет поставленную для решения задачу совершенно другой задачей. В
рассматриваемом же случае время выступает в качестве параметра, а не
координаты, и именно потому в приведенном разложении отсутствует частная
производная функции Лагранжа по времени (тогда как формально она должна была бы
быть, поскольку в цитируемой работе время непосредственно входит в число
независимых переменных этой функции). Отсутствует она и в приведенной вариации,
что и дает основание полагать время параметром, а не координатой.
Теперь надо заметить, что именно из
указанной вариации выводится дифференциальное уравнение Лагранжа, решение
которого в указанной работе и приводит не к балансу энергии, а к равенству
потенциальной и кинетической энергий. Но приводит только лишь при неявном
условии 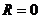 , которое
скрыто в цитируемой фразе. Однако это условие превращает общую задачу в частный
случай. Как раз в тот частный случай постоянного ускорения, при котором усилие
отсутствует. В параграфе 5 цитируемой работы функция Лагранжа для системы
частиц в этом частном случае имеет вид:
, которое
скрыто в цитируемой фразе. Однако это условие превращает общую задачу в частный
случай. Как раз в тот частный случай постоянного ускорения, при котором усилие
отсутствует. В параграфе 5 цитируемой работы функция Лагранжа для системы
частиц в этом частном случае имеет вид:

а в общем случае должна иметь вид:
 ,
,

Но рассмотренный одномерный случай
баланса (10) энергии как раз такой вид и имеет, что позволяет полагать
справедливыми равенствами:
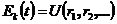 ,
,  и
и 
На основании изложенного можно
утверждать, что традиционный закон сохранения энергии оказывается приближенным
(неточным) по субъективным причинам, тогда как вывод точного закона сохранения
энергии с произволом субъекта не связан, а опирается на объективное свойство
геометрического пространства.
Литература
1. Ландау Л.Д. и Лифшиц Е.М.
Механика и электродинамика - Изд. «Наука», Главная редакция
физико-математической литературы. М., 1969.