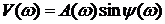Передаточная функция для заданной RLC цепи
1. Вывести передаточную функцию для заданной RLC-цепи
Согласно закону Ома отношение напряжения к току равно
сопротивлению
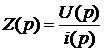 (1)
(1)

Рис.1 Последовательное и параллельное включение сопротивлений
Последняя формула определяет импеданс комплексного
сопротивления как отношение изображений.
В случае последовательного включения (рис.1а) через  и
и 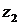 протекает общий ток и падения напряжений на сопротивлениях
соответственно равны
протекает общий ток и падения напряжений на сопротивлениях
соответственно равны 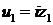 и
и 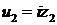 . Общее падение напряжения согласно второму закону Кирхгофа равно
сумме
. Общее падение напряжения согласно второму закону Кирхгофа равно
сумме 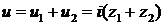 . Отсюда по закону Ома эквивалентное
сопротивление цепи (рис.3.1в) равно сумме сопротивлений
. Отсюда по закону Ома эквивалентное
сопротивление цепи (рис.3.1в) равно сумме сопротивлений
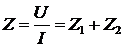 . (2)
. (2)
В случае параллельного включения (рис.1б) через сопротивления
протекают токи  и
и 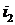 , создавая одинаковые падения напряжения
, создавая одинаковые падения напряжения 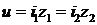 . Согласно первому закону Кирхгофа общий
ток равен сумме,
. Согласно первому закону Кирхгофа общий
ток равен сумме,
где
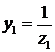
и

Отсюда по закону Ома эквивалентная проводимость по Лапласу равна
сумме проводимостей
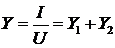 . (3)
. (3)
Переходя к сопротивлениям по Лапласу, получим
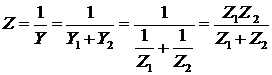 (4)
(4)
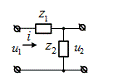
Рис.2. Делитель напряжения
В случае делителя напряжения (рис.2) ток 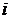 протекает через
протекает через  и
и 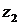 последовательно.
последовательно.
Поэтому
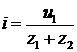 (5)
(5)
Выходное напряжение схемы является падением напряжения на
сопротивлении 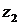 .
.
Умножим (3.5) на 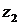
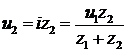 . (6)
. (6)
Отсюда передаточная функция делителя напряжения
 . (7)
. (7)

Рис.3. Активное, емкостное индуктивное сопротивления
Из физики для активного, емкостного и индуктивного
сопротивлений (рис.3.3) в области оригиналов имеем
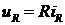 ;
; 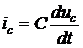 ;
; 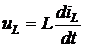 . (8)
. (8)
При переходе к изображениям при нулевых начальных условиях соответственно получим
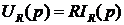 ;
; 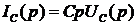 ;
; 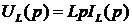 .
.
Отсюда по закону Ома для импеданцев сопротивлений получим
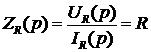 ;
; 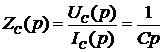 ;
; 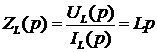 . (9)
. (9)
Пример выполнения задания.
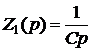 ,
, 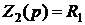
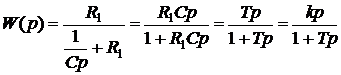 ,
,

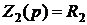
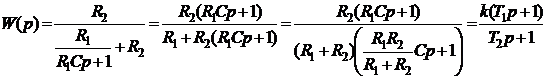 ,
,
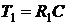 ,
, 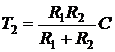 ,
, 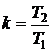
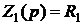
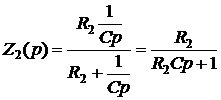
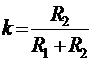 ,
, 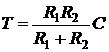
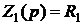
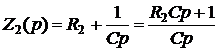
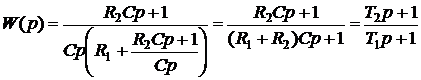 ,
,
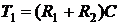 ,
, 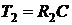 ,
, 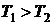
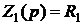
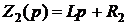
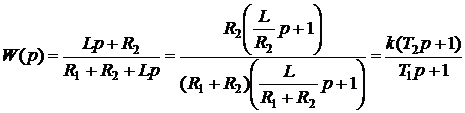 ,
,
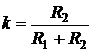 ,
,  ,
, 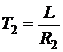
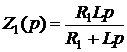
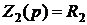
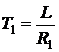 ,
, 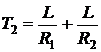
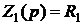
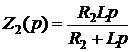
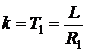 ,
, 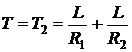
2. По передаточной функции
записать
дифференциальное уравнение, однородное дифференциальное уравнение,
характеристическое уравнение, характеристический полином.
. Записать общее решение дифференциального уравнения по п.2.
4. По заданному в символической форме дифференциальному уравнению
записать его в классической форме, записать однородное дифференциальное
уравнение, характеристическое уравнение, характеристический полином и
передаточную функцию. Найти корни характеристического уравнения. По корням
записать общее решение дифференциального уравнения, определить 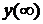 , указать расположение корней на плоскости
и по их расположению отметить характер переходного процесса (монотонный,
немонотонный). Определить устойчивость системы.
, указать расположение корней на плоскости
и по их расположению отметить характер переходного процесса (монотонный,
немонотонный). Определить устойчивость системы.
Непрерывные линейные системы описываются обыкновенными линейными
дифференциальными уравнениями с постоянными коэффициентами вида
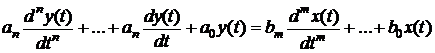 , (2.2.1)
, (2.2.1)
где x(t) -
входная величина (сигнал); y(t) - выходная величина (реакция, или отклик системы).
Как видно из (2.2.1), дифференциальным уравнением называют
уравнение, которое связывает выходную величину (или ошибку) и ее производные с
входной величиной и ее производными (в частном случае только со входной
переменной).
Если обозначить оператор дифференцирования буквой р:
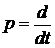 (2.2.2)
(2.2.2)
то уравнение (2.2.1) можно записать в символической форме
(anpn +…+ a0)y(t) = (bmpm +…+ b0)x(t), (2.2.3)
A(p)y(t) = В(p)x(t), (2.2.4)
где
А(p) = anpn +…+ a0 ; B(p) = bmpm +…+ b0 .
Система находится в свободном состоянии, если входной сигнал
равен нулю. Соответственно движение системы в свободном состоянии описывается
однородным дифференциальным уравнением, т.е. уравнением с нулевой правой
частью:
А(р) y(t) = 0. (2.2.5)
Известно, что решение дифференциального уравнения (2.2.4) можно
представить в виде суммы общего и частного, т.е.
y(t) = yобщ(t)+yчас(t) = 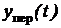 +
+ 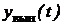 , (2.2.6)
, (2.2.6)
где yобщ(t) является решением однородного дифференциального уравнения
(2.2.5) и поэтому характеризует собственное движение системы, находящейся в
свободном состоянии. Поэтому в литературе по теории автоматического
регулирования иногда используется обозначение 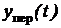 . Второе слагаемое в (2.2.6) характеризует движение под действием
вынуждающей силы - внешнего воздействия. Поэтому в теории автоматического
регулирования иногда используется обозначение
. Второе слагаемое в (2.2.6) характеризует движение под действием
вынуждающей силы - внешнего воздействия. Поэтому в теории автоматического
регулирования иногда используется обозначение 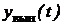 . Найдем общее решение, т.е. решение однородного дифференциального
уравнения (2.2.5), полагая, что его можно представить в виде
. Найдем общее решение, т.е. решение однородного дифференциального
уравнения (2.2.5), полагая, что его можно представить в виде
yобщ(t) = еpt, (2.2.7)
где
р = а +jb
Подставляя (2.2.7) и производные
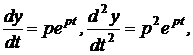
в уравнение (2.2.5) и сокращая на 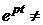 0, получим
тождество
0, получим
тождество
А(р) = an pn+…+a0 = 0, (2.2.8)
которое характеризует общее решение и потому называется
характеристическим уравнением (с переменной р = а + jb - комплексным в общем случае числом).
Характеристическое уравнение - это алгебраическое уравнение n-й степени, которое на основании основной теоремы алгебры
имеет n корней p1,…., pn.. Корни в общем случае являются
комплексными. Так как коэффициенты уравнения действительные, а не комплексные
числа, то комплексные корни могут быть только комплексно-сопряженными. То есть
каждому корню вида рi = аi +jbi соответствует сопряженный корень (с
противоположной по знаку мнимой частью) вида рi+1 = аi - jbi.
По теореме Безу характеристический полином можно представить в
виде
D(p) = anpn +…+ a0 = an(p - p1)×××(p - pn). (2.2.9)
Два комплексно-сопряженных множителя дают трехчлен с
действительными коэффициентами [р - (аi+ jbi)][р - (аi - jbi)] = [(p - аi) - jbi][(p - аi) + jbi] = = ( p - аi)2 + bi2, или p 2- 2 аi р + (аi2 + bi)2. Действительный корень дает двучлен (р - аi). Следовательно, в
случае действительных и комплексно-сопряженных корней произведение двучленов и
трехчленов дает многочлен с действительными коэффициентами. Отсюда, обратно,
следует наличие комплексно-сопряженных корней в случае характеристического
полинома с действительными коэффициентами.
Так как характеристическое уравнение имеет n корней, то и сумма решений вида (2.2.7) с разными рi будет удовлетворять однородному дифференциальному
уравнению, т.е. быть его решением. Поэтому окончательно общее решение следует
представить в виде суммы линейно-независимых решений
 , (2.2.10)
, (2.2.10)
где Сi
- произвольные постоянные,
зависящие от начальных условий.
Преобразование Лапласа.
Для сигнала x(t) (x(t)  0 при t < 0) изображение определяется по
формуле одностороннего преобразования Лапласа
0 при t < 0) изображение определяется по
формуле одностороннего преобразования Лапласа
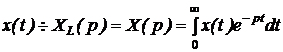 , (2.2.11)
, (2.2.11)
где р = 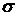 +j
+j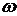 - переменная преобразования Лапласа.
Согласно введенным обозначениям величина
- переменная преобразования Лапласа.
Согласно введенным обозначениям величина 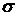 комплексной переменной
комплексной переменной 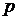 является абсциссой абсолютной сходимости. Если
является абсциссой абсолютной сходимости. Если 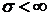 , то результатом интегрирования (2.2.11)
будет конечное значение, которое является решением и оригиналу
, то результатом интегрирования (2.2.11)
будет конечное значение, которое является решением и оригиналу 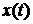 будет соответствовать изображение
будет соответствовать изображение 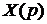 . Здесь применено обозначение переменной
преобразования Лапласа все той же буквой р. В математической литературе, как
правило, переменная преобразования Лапласа обозначается буквой s. p = s - это третий смысл переменной р в зависимости от
контекста.
. Здесь применено обозначение переменной
преобразования Лапласа все той же буквой р. В математической литературе, как
правило, переменная преобразования Лапласа обозначается буквой s. p = s - это третий смысл переменной р в зависимости от
контекста.
Преобразование Лапласа обладает свойством линейности,
заключающемся в том, что изображение суммы сигналов равно сумме их изображений,
и если оригинал умножается на постоянную величину, то и изображение также.
Другими словами, если z(t) = ax(t) + bу(t), то и Z(p)
= aX(p) + bY(р). Согласно теореме об изображении производных при нулевых
начальных условиях имеем
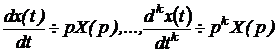 . (2.2.12)
. (2.2.12)
Дополнительно отметим: теорему запаздывания
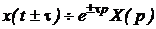 ,
,
где 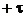 - время упреждения, а
- время упреждения, а 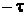 - время запаздывания сигнала;
- время запаздывания сигнала;
- теорему свертки:
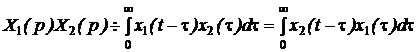 .
.
Изображения непрерывных сигналов по Лапласу приведены в
табл.2.2.1.
Оригиналы и изображения непрерывных сигналов по Лапласу
|
№
|
x(t)
|
X(p)
|
|
1
|
d(t)
|
1
|
|
2
|
1(t)
|
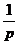
|
|
3
|
t
|

|
|
4
|
 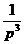
|
|
|
5
|
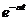 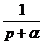
|
|
|
6
|
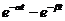 
|
|
|
7
|
 
|
|
Перейдем теперь от дифференциального уравнения (2.2.3), как
от уравнения для оригиналов (функций действительного аргумента t - в данном
случае времени) к уравнению для изображений по Лапласу. Воспользовавшись
свойством линейности, соотношениями (2.2.12) и аналогичными соотношениями для
реакции системы после почленного перехода от оригиналов к изображениям при
нулевых начальных условиях получим уравнение для изображений
(anpn+…+a0)Y(p) = (bmpm+…+b0)X(p), (2.2.13)
Или
(p)Y(р) = B(p)X(p). (2.2.14)
Данные уравнения по внешнему виду напоминают уравнения
(2.2.3), (2.2.4) для оригиналов. Однако переменная р в них им
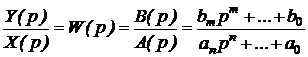 . (2.2.15)
. (2.2.15)
сопротивление цепь преобразование лаплас
Это отношение изображения выхода Y(p) к изображению входа X(p) по Лапласу
при нулевых начальных условиях называется передаточной функцией системы.
Из (2.2.15) следует, что
Y(p) = X(p)W(p), (2.2.16)
т.е. в области изображений определение реакции сводится к
алгебраической операции умножения, что упрощает нахождение реакции.
Операторный метод решения (с помощью преобразования Лапласа)
сводится к трем действиям:
1. От оригинала x(t) по формуле
(2.2.11) переходят к изображению Х(р).
. Пo формуле (2.2.16) находят изображение реакции.
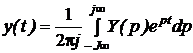 (2.2.17)
(2.2.17)
Заметим, что изложенная методика позволяет при известной
передаточной функции найти реакцию системы при нулевых начальных условиях. Если
начальные условия не нулевые, то при переходе от дифференциального уравнения к
изображениям необходимо воспользоваться изображениями производных при ненулевых
начальных условиях.
На практике переход от оригиналов к изображениям и обратно
осуществляется с помощью таблицы преобразования Лапласа.
Примеры выполнения заданий.
Пункт 2
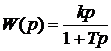
Дифференциальное уравнение в символьной форме
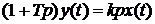
Дифференциальное уравнение в классической форме

Однородное дифференциальное уравнение
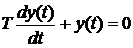
Характеристическое уравнение

Характеристический полином
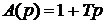
Пункт 3
Характеристическое уравнение

Корни характеристического уравнения
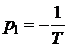
Общее решение дифференциального уравнения
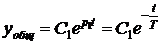
Пункт 4

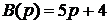
Дифференциальное уравнение в символической форме
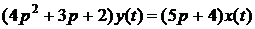
Дифференциальное уравнение в классической форме

Однородное дифференциальное уравнение
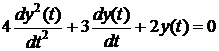
Характеристическое уравнение
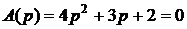
Характеристический полином
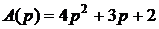
Передаточная функция

Корни характеристического уравнения:

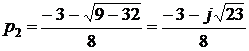
Общее решение дифференциального уравнения
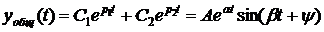 ,
,
где 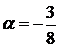 ,
, 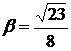
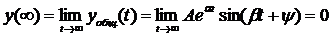
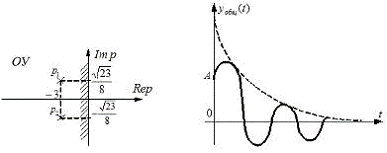
Так как корни являются комплексными попарно сопряженными, то
характер переходного процесса является немонотонным (колебательным).
Корни характеристического уравнения находятся в левой
полуплоскости. Система устойчива.
Частотную передаточную функцию, или комплексный коэффициент
усиления W(j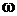 ), можно ввести двумя способами:
), можно ввести двумя способами:
1. Путем нахождения реакции на синусоидальный
(гармонический сигнал).
2. С помощью преобразования Фурье.
Начнем с первого способа и найдем реакцию системы (2.2.1) на
гармонический сигнал, который представим в показательной форме
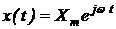 ,(2.4.11)
,(2.4.11)
где Хm и 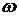 - амплитуда и
круговая частота.
- амплитуда и
круговая частота.
Так как в линейной системе отсутствуют нелинейные искажения, то в
установившемся режиме на выходе также будет гармонический сигнал той же частоты
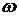 , в общем случае с другими амплитудой и фазой, т.е.
, в общем случае с другими амплитудой и фазой, т.е.
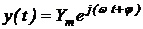 .(2.4.12)
.(2.4.12)
Для определения амплитуды и фазы подставим выражения сигналов (2.4.11),
(2.4.12) и их производных в дифференциальное уравнение и после сокращения на еj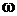 t
t  0 и элементарных преобразований получим
тождество
0 и элементарных преобразований получим
тождество
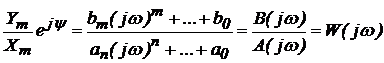 .(2.4.13)
.(2.4.13)
Отсюда
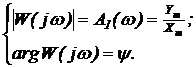 (2.4.14)
(2.4.14)
Эти соотношения можно рассматривать как определение частотной
передаточной функции. В них заключается физический смысл частотной передаточной
функции и из них вытекает способ её экспериментального нахождения путем
измерения амплитуд гармонических сигналов на входе и выходе и сдвига по фазе
между ними для одной и той же частоты.
В случае второго способа определения частотной передаточной
функции сравним (2.4.13) и (2.2.15). Из сравнения следует, что частотная
передаточная функция является частным случаем передаточной функции по Лапласу
при р = j , т.е.
, т.е.
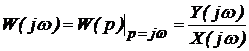 . (2.4.15)
. (2.4.15)
Так как передаточная функция по Лапласу применима к сигналам произвольной
(любой) формы, то и частотная передаточная функция применима для нахождения
реакции на сигнал произвольной формы, а не обязательно гармонический. Из
(2.4.5) для Фурье-изображения реакции имеем
 . (2.4.16)
. (2.4.16)
Сама реакция, то есть оригинал, находится по формуле обращения
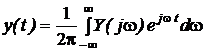 .(2.4.17)
.(2.4.17)
Таким образом, из второго определения частотной передаточной
функции вытекает частотный метод (метод преобразования Фурье) нахождения
реакции:
. Для заданного входного сигнала находим изображение по Фурье
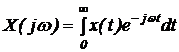 . (2.4.19)
. (2.4.19)
(jw) = X(jw)×W(jw). (2.4.20)
. По формуле обращения (обратного преобразования Фурье) находим
реакцию
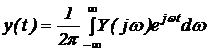 . (2.4.21)
. (2.4.21)
Характер преобразования входного сигнала звеном или системой
определяется частотной передаточной функцией или соответствующими ей частотными
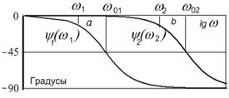
характеристиками. Виды частотных характеристик тесно связаны с формами записи
комплексных чисел, поскольку для 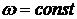 частотная передаточная функция является комплексным числом.
частотная передаточная функция является комплексным числом.
Основные частотные характеристики (рис.2.4.3-2.4.6).
. Амплитудно-фазовая характеристика (АФХ) - зависимость W(jw) на комплексной плоскости при изменении w от от -¥ до +¥ (Рис.
2.4.3). Так как Wх(w) = Wх(-w) - четная функция, а Wу(w) = Wу(-w) - нечетная функция, то АФХ для w < 0 симметрична относительно вещественной оси характеристике
для w>0 и ее обычно не изображают.

. Вещественная Wх(w) и мнимая Wу(w) частотные
характеристики (рис. 2.4.4) - зависимости вещественной и мнимой части от
частоты. Имея в виду четность вещественной характеристики и нечетность мнимой,
их для w
< 0 обычно не изображают. Четность Wх(w) и нечетность Wу(w) вытекают из правила
(2.4.22) их выделения из W(jw), так как в знаменателе четная функция, а в
числителе jw в четной степени - действительное число (отходит к Wх(w)), а в нечетной -мнимое
(отходит к Wy(w)).
. Амплитудная (АЧХ) и фазовая (ФЧХ) частотные характеристики
- зависимости А(w) и y(w) от частоты (рис.2.4.5).
В силу четности А(w) и нечетности y(w), их для w < 0 обычно не
изображают. Амплитудная частотная характеристика определяет инерционность
(пропускную способность) звена или системы. Фазовая частотная характеристика
определяет величину фазового сдвига на соответствующей круговой частоте.
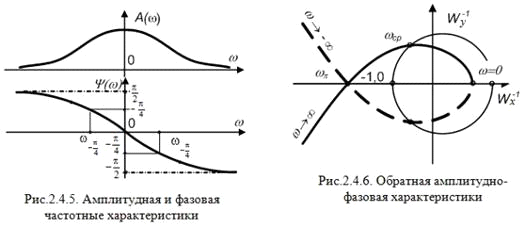
. Обратная частотная характеристика W-1(jw) = 1/ W(jw). Определяя амплитуду и
аргумент (фазу) для дроби по правилу (2.4.6), найдем
 . (2.4.22)
. (2.4.22)
Из связи между формами записи комплексных чисел вытекает, что по
АФХ можно построить Wх(w), Wу(w) или А(w), y(w), а также W-1(jw) и наоборот. На рис.2.4.6 изображена
обратная для характеристики на рис.2.4.3 характеристика. На рисунке построена
окружность единичного радиуса. В соответствии с правилом (2.4.22) точки,
соответствующие А(w) > 1, лежат
внутри круга единичного радиуса. Точка А(w) = 1 остается на окружности, но фаза меняется на противоположную
(на 180°).
Тем не менее, рассматриваются звенья, для которых условие
физической осуществимости не выполняется. Это правомерно в определенном диапазоне
частот. Если спектр сигнала на входе звена выходит за пределы этого диапазона,
то возникнут искажения в реакции, не предусмотренные передаточной функцией
звена.
. Логарифмические частотные характеристики.
Наиболее широкое применение нашли логарифмические
характеристики. Для их объяснения представим частотную передаточную функцию в
показательной форме и возьмем натуральный логарифм от:
 .
.
Он равен комплексному выражению; вещественная его часть является
логарифмом от модуля, а мнимая - фазой.
На практике берется десятичный логарифм, так что
логарифмические амплитудная (ЛАХ) и фазовая (ЛФХ) характеристики определяются
выражениями:
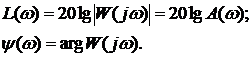 (2.4.23)
(2.4.23)
По оси абсцисс на графиках откладывается частота в логарифмическом
масштабе, т.е. lg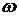 . Однако желательно делать оцифровку
непосредственно в значениях круговой частоты
. Однако желательно делать оцифровку
непосредственно в значениях круговой частоты 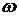 , а для разметки
можно воспользоваться табл.2.4.1. Значения
, а для разметки
можно воспользоваться табл.2.4.1. Значения 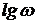
Таблица 2.4.1
|
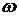 12345678910 12345678910
|
|
|
|
|
|
|
|
|
|
|
|
lg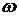 00.3010.4770.6020.6990.7780.8450.9030.9541 00.3010.4770.6020.6990.7780.8450.9030.9541
|
|
|
|
|
|
|
|
|
|
|
Амплитуда измеряется в децибелах, фаза - в градусах. Для
разметки оси абсцисс непосредственно в значениях w (рад/с) можно
воспользоваться любой из трех шкал (основной, квадратичной и кубической)
логарифмической линейки (рис.2.4.7).
Если взять за декаду D мм, то,
например, 0.301 дек (соответствует  = 2 рад/с) составит 0.301D мм, 1.301 дек (соответствует
= 2 рад/с) составит 0.301D мм, 1.301 дек (соответствует  20 рад/с) составит D+0.301D мм и т.д. Таким образом, точки с оцифровкой в пределах от
1 до 10 смещаем вправо на декаду и оцифровываем от 10 до 100 и т.д.
(рис.2.4.7), смещаем влево от исходного положения на одну декаду и оцифровываем
от 0.1 до 1 и т.д.
20 рад/с) составит D+0.301D мм и т.д. Таким образом, точки с оцифровкой в пределах от
1 до 10 смещаем вправо на декаду и оцифровываем от 10 до 100 и т.д.
(рис.2.4.7), смещаем влево от исходного положения на одну декаду и оцифровываем
от 0.1 до 1 и т.д.
Если w2 /w1 = 10, то расстояние
между частотами равно одной декаде (lg10=1), если w2 /w1 = 2, то расстояние
равно одной октаве.
Так как lg(w = 0) = -¥, то точка w = 0 находится на
бесконечности слева. Поэтому ось ординат проводят в любом месте с таким
расчетом, чтобы на график попал интересующий диапазон частот. Так как 20lg1 =
0, то L(w)
> 0, если А(w)>1 и L(w) < 0, если А(w ) < 1. Если А(w)® 0, то L(w)® -¥.
Рассмотрим
ЛАХ инерционного звена. Имеем
A(w) = 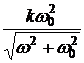 ;
;  . (2.4.24)
. (2.4.24)
Левее частоты сопряжения w0, т.е. в случае w < w0, пренебрежем под знаком радикала величиной w2 по сравнению с w02. Тогда
L(w) » 20lg(k). (2.4.25)
Следовательно, левее w0 асимптотическая ЛАХ
представляет собой горизонтальную прямую на высоте 20lg(k). Если k = 1, то эта
прямая совпадает с осью частот.
Правее частоты сопряжения w0, где w > w0, аналогично получим
прямую с наклоном -20 дБ/дек, так как по оси абсцисс откладывается lgw.
L(w) » 20lg(k) - 20lgw,
(2.4.26)
В точке w0 имеем погрешность замены точной (реальной)
характеристики на асимптотическую, равную
 .
.
Так как
Lточ(w 0)=Lприб(w 0)+DL(w 0),
то реальная характеристика в точке w0 расположена ниже
асимптотической на 3дБ. На практике погрешность в 3дБ считается небольшой и не
учитывается.
Логарифмические характеристики звеньев
Таблица 2.4.6
|
№ п/п
|
Название звена
|
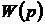 ЛАХ, ЛФХ ЛАХ, ЛФХ
|
|
|
1
|
Идеальное
интегрирующее
|
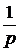 
|
|
|
2
|
Инерционное
|
 
|
|
|
3
|
Колебательное
|
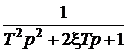 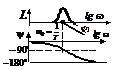
|
|
|
4
|
Идеальное
дифференцирующее
|
 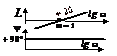
|
|
|
5
|
Форсирующее
|
 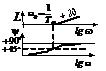
|
|
|
6
|
Обратное
колебательному
|
 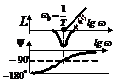
|
|
Из табл.2.4.6 следует:
1. Наклон и соответственно сдвиг по фазе на низких частотах
могут дать только интегрирующие или дифференцирующие звенья. Если, например, в
передаточной функции имеется r интегрирующих
звеньев, то наклон ЛАХ на низких частотах равен 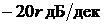 , а сдвиг по фазе соответственно
, а сдвиг по фазе соответственно 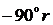 .
.
2. n корням знаменателя (полюсам передаточной функции), т.е.
степени знаменателя n, соответствует наклон ЛАХ на верхних
частотах, равный 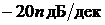 , и в случае минимально фазовой системы -
соответственно сдвиг по фазе на высоких частотах, равных
, и в случае минимально фазовой системы -
соответственно сдвиг по фазе на высоких частотах, равных 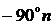 .
.
.  корням числителя (нулям передаточной
функции) на высоких частотах аналогично соответствуют наклон ЛАХ, равный
корням числителя (нулям передаточной
функции) на высоких частотах аналогично соответствуют наклон ЛАХ, равный 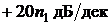 , и сдвиг по фазе
, и сдвиг по фазе  .
.
. В случае передаточной функции
минимально-фазовой системы с n полюсами и n1 нулями наклон
ЛАХ на высоких частотах равен  , а сдвиг по фазе равен
, а сдвиг по фазе равен 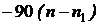 градусов.
градусов.
Построение логарифмических характеристик систем
и восстановление передаточной функции по ЛАХ
Если звенья системы соединены последовательно, то
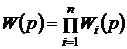
и для модуля и аргумента комплексного коэффициента усиления
разомкнутой системы соответственно имеем:
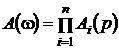 ;
; 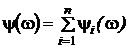 . (2.4.38)
. (2.4.38)
Очевидно,
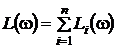 . (2.4.39)
. (2.4.39)
Следовательно, для построения ЛАХ и ЛФХ нужно просуммировать
соответствующие характеристики отдельных звеньев.
Пример 2.4.3. Построить ЛАХ и ЛФХ по передаточной функции
 ,
,
где 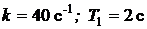 ;
; 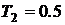 с;
с; 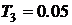 с. Соответственно сопрягающие частоты
равны
с. Соответственно сопрягающие частоты
равны  ;
; 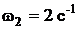 ;
;
 .
.
Передаточную функцию представим в виде произведения передаточных
функций интегрирующего звена
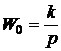 ;
;
инерционных звеньев
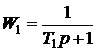
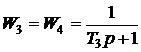
и форсирующего
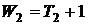 .
.
Логарифмические амплитудные и фазовые характеристики отдельных
звеньев, а также результирующие ЛАХ и ЛФХ системы построены на рис.2.4.13 и
2.4.14.
На рис.2.4.13 жирными линиями показаны асимптотические ЛАХ
звеньев. Характеристики двух инерционных звеньев с передаточными функциями 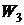 и
и  на графиках сливаются, но их необходимо учитывать дважды. Это
касается также и ЛФХ этих звеньев. Для построения результирующей ЛАХ к ЛАХ
интегрирующего звена последовательно добавлялись характеристики остальных
звеньев при перемещении вдоль оси частот слева направо по мере встречи сопрягающих
частот. После очередной частоты сопряжения наклон ЛАХ изменялся на
на графиках сливаются, но их необходимо учитывать дважды. Это
касается также и ЛФХ этих звеньев. Для построения результирующей ЛАХ к ЛАХ
интегрирующего звена последовательно добавлялись характеристики остальных
звеньев при перемещении вдоль оси частот слева направо по мере встречи сопрягающих
частот. После очередной частоты сопряжения наклон ЛАХ изменялся на 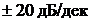 . Приращение наклона соответствовало
звену, которому принадлежала сопрягающая частота.
. Приращение наклона соответствовало
звену, которому принадлежала сопрягающая частота.
Анализируя результаты примера и характеристики типовых звеньев
(табл.2.4.6), можно сделать вывод, что ЛАХ разомкнутой системы можно построить
сразу, минуя промежуточные построения ЛАХ звеньев и суммирование их, по
правилу:
. Найти сопрягающие частоты и отложить их на оси частот. Ось
ординат провести для удобства левее самой низкой сопрягающей частоты.
. При ω = 1 отложить
20 lgk и через эту точку провести прямую с
наклоном -20 дБ/дек, если в системе имеется
дБ/дек, если в системе имеется  интегрирующих звеньев, или с наклоном +20
интегрирующих звеньев, или с наклоном +20 дБ/дек, если в системе имеется
дБ/дек, если в системе имеется  дифференцирующих звеньев (при
дифференцирующих звеньев (при  = 0 низкочастотная асимптота ЛАХ
параллельна оси абсцисс).
= 0 низкочастотная асимптота ЛАХ
параллельна оси абсцисс).
. При прохождении слева направо каждой из частот сопряжения
характеристика испытывает приращение наклона -20 дБ/дек (для инерционного
звена), -40 дБ/дек (для колебательного звена), +20 дБ/дек (для форсирующего
звена), +40 дБ/дек (для звена, обратного колебательному). Если сопрягающие
частоты нескольких звеньев одинаковы, то приращение наклона ЛАХ равно
суммарному приращению от всех звеньев. Если имеется хотя бы одна частота
сопряжения, меньшая единицы, то точка 20lgk при ω = 1 не будет лежать на результирующей ЛАХ.
. Ввести поправку к асимптотической ЛАХ при наличии колебательных
или обратных им звеньев.
Для контроля правильности построения ЛАХ и ЛФХ полезно помнить,
что наклон ЛАХ в области высоких частот (ω → ∞) равен 20 (m-n) дБ/дек,
где m - порядок числителя, n - порядок знаменателя передаточной функции
системы. Кроме того
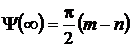 ;
; 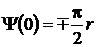 , (2.4.40)
, (2.4.40)
где знак минус берётся при наличии  интегрирующих, а плюс -
интегрирующих, а плюс -  дифференцирующих звеньев. Из анализа методики построения ЛАХ по
передаточной функции вытекает возможность обратного перехода, т. е.
восстановления передаточной функции минимально-фазовой системы по ЛАХ.
дифференцирующих звеньев. Из анализа методики построения ЛАХ по
передаточной функции вытекает возможность обратного перехода, т. е.
восстановления передаточной функции минимально-фазовой системы по ЛАХ.
При восстановлении передаточной функции минимально-фазовой системы
по ЛАХ записываем дробь, в числителе которой ставим общий коэффициент усиления 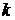 и далее делаем начинку дроби. По величине
наклона низкочастотного участка определяем количество интегрирующих или
дифференцирующих звеньев (формально отрицательному наклону соответствуют
интегрирующие звенья и, соответственно, множитель
и далее делаем начинку дроби. По величине
наклона низкочастотного участка определяем количество интегрирующих или
дифференцирующих звеньев (формально отрицательному наклону соответствуют
интегрирующие звенья и, соответственно, множитель 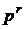 в знаменателе, положительному наклону -
множитель
в знаменателе, положительному наклону -
множитель 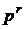 в числителе,
в числителе,  - кратность наклона 20-ти децибелам). В
случае нулевого наклона интегрирующие или дифференцирующие звенья отсутствуют.
Далее при движении слева направо по мере встречи частот сопряжения анализируем
приращение (изменение) наклона. Если приращение составляет +20 Дб/дек, то в
числитель записываем
- кратность наклона 20-ти децибелам). В
случае нулевого наклона интегрирующие или дифференцирующие звенья отсутствуют.
Далее при движении слева направо по мере встречи частот сопряжения анализируем
приращение (изменение) наклона. Если приращение составляет +20 Дб/дек, то в
числитель записываем  для форсирующего звена вида
для форсирующего звена вида  , если приращение составляет -20 Дб/дек,
то в знаменатель записываем
, если приращение составляет -20 Дб/дек,
то в знаменатель записываем  для инерционного звена вида
для инерционного звена вида 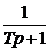 . В случае приращения наклона +40 Дб/дек в числитель записываем
два форсирующих звена
. В случае приращения наклона +40 Дб/дек в числитель записываем
два форсирующих звена 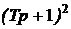 , в случае приращения наклона -20 Дб/дек в
знаменатель записываем
, в случае приращения наклона -20 Дб/дек в
знаменатель записываем 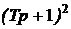 для двух инерционных звена вида
для двух инерционных звена вида  . Если на ЛАХ показана поправка на
коэффициент затухания
. Если на ЛАХ показана поправка на
коэффициент затухания 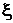 , то вместо двух форсирующих или
инерционных звеньев записываем обратное колебательному или колебательное звено
(множитель
, то вместо двух форсирующих или
инерционных звеньев записываем обратное колебательному или колебательное звено
(множитель  в числителе или в знаменателе). Если
кратность наклона 3 и более, то записываем соответствующее количество звеньев с
одинаковыми частотами сопряжения. Для определения коэффициента усиления находим
точку пересечения продолжения низкочастотного участок ЛАХ с вертикальной прямой
с абсциссой
в числителе или в знаменателе). Если
кратность наклона 3 и более, то записываем соответствующее количество звеньев с
одинаковыми частотами сопряжения. Для определения коэффициента усиления находим
точку пересечения продолжения низкочастотного участок ЛАХ с вертикальной прямой
с абсциссой 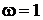 и по ординате этой точки
и по ординате этой точки 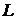 определяем
определяем 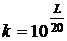 .
.
В случае минимально-фазовой системы в двучленах и трехчленах,
упомянутых выше, берем знаки “+”. Если бы имелись не минимально-фазовые звенья,
то нужно было бы взять знак “-“. При этом ЛАХ осталась бы прежней, а ЛФХ была
бы другой. Поэтому в случае минимально-фазовой системы восстановление
однозначно и нет необходимости контролировать АФХ.
Пример 2.4.4. Восстановить передаточную функцию минимально-фазовой
системы по ЛАХ рис.2.4.15.
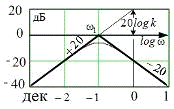
Рис.2.4.15. ЛАХ минимально-фазовой системы
В соответствие с приведенными соображениями передаточная
функция минимально-фазовой системы будет равна
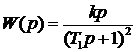 .
.
По RLC-цепи задания 1 записать частотную передаточную
функцию и аналитические выражения частотных характеристик.
. Построить амплитудно-фазовую характеристику (АФХ).
. Построить амплитудную и фазовую частотные характеристики.
. Построить вещественную и мнимую частотные характеристики.
. Построить логарифмические характеристики (ЛАХ и ЛФХ).
Определить к какому типу корректирующих звеньев относится данное звено
(интегрирующее, дифференцирующее, интегро-дифференцирующее). Каких частот этот
фильтр.
. По АФХ построить обратную частотную характеристику.
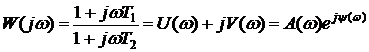
- частотная передаточная функция в параметрической форме
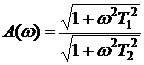
амплитудная частотная характеристика
|
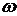 , крад/с0714,3250040000 , крад/с0714,3250040000
|
|
|
|
|
|
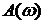 10,7350,3890,286 10,7350,3890,286
|
|
|
|
|
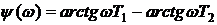
фазовая частотная характеристика
|
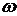 , крад/с0714,3250040000 , крад/с0714,3250040000
|
|
|
|
|
|
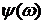 , град0-29,055-29,055-2,553 , град0-29,055-29,055-2,553
|
|
|
|
|

вещественная частотная характеристика
|
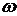 , крад/с0714,3250040000 , крад/с0714,3250040000
|
|
|
|
|
|
 10,6430,340,286 10,6430,340,286
|
|
|
|
|