Моделирование процессов конвективного обмена
Содержание
Введение
. Конвективный теплообмен в
однородной среде
.1 Основные понятия и
определения
.2 Физические свойства
жидкости
.3 Постановка задачи
конвективного теплообмена
.4 Гидродинамический и
тепловой пограничные слои
.5 Турбулентный перенос теплоты
и количества движения
. Моделирование процессов
конвективного обмена
.1 Моделирование процессов
конвективного обмена
.2 Однородные разностные
схемы для уравнения теплопроводности
.3 Третья краевая задача
.4 Схема для уравнения с
переменными коэффициентами
. Разработка программы
.1 Описание программы.
Исходные данные для расчета
.2 Описание переменных
программы
.3 Описание алгоритма
программы
.4 Демонстрация работы
программы
Заключение
Список использованных
источников
Приложение
Введение
Значительное число задач физики и техники приводит к линейным и
нелинейным дифференциальным уравнениям в частных производных (уравнениям
математической физики). Универсальным и чрезвычайно эффективным методом решения
задач математической физики является метод конечных разностей или метод сеток.
Он позволяет сводить приближенное решение уравнений в частных производных к
решению систем алгебраических уравнений.
Тема дипломного проекта: «Моделирование процессов конвективного обмена».
Цели и задачи дипломного проекта:
Изучить теорию конвективного обмена в однородной среде;
Изучить теорию моделирования процессов конвективного обмена;
Разработать программу на языке программирования Паскаль.
Дипломный проект состоит из трех глав.
В первой главе рассматривается теория конвективного теплообмена в
однородной среде. Приводятся общие понятия и определения.
Во второй главе приводится теория моделирования процессов конвективного
обмена. Рассматриваются общие сведения моделировании процессов конвективного
обмена. Описывается математическая модель.
В третье главе приводится описание разработанной программы. Разработанная
программа подробно описывается с рассмотрением ее алгоритма и переменных.
Ключевым понятием теории разностных схем является устойчивость. Поэтому
большое внимание уделяется изучению устойчивости разностных схем. Найдены
эффективные достаточные условия и получены априорные оценки, выражающие
устойчивость разностных схем. Достаточные условия устойчивости позволяют
формулировать общий принцип регуляризации схем для получения разностных схем
заданного качества.
В дипломной работе излагается теория однородных разностных схем для
стационарных и нестационарных одномерных задач теплопроводности с разрывными
коэффициентами, а также для одномерного уравнения колебаний. Характерной чертой
излагаемой теории в этой главе является то, что она позволяет не только дать
обоснование имеющихся разностных схем (доказать их устойчивость, сходимость,
получить оценку порядка точности и т. д.), но и позволяет сформулировать общие
принципы построения разностных схем заданного качества для решения различных
классов задач математической физики.
Разностные схемы трактуются как операторные или операторно-разностные
уравнения с линейными операторами, зависящими от параметра h (аналога шага сетки) и заданными на
абстрактном линейном нормированном пространстве любого числа измерений.
1.
Конвективный теплообмен в однородной среде
1.1 Основные
понятия и определения
Понятие конвективного теплообмена охватывает процесс теплообмена при
движении жидкости или газа. При этом перенос теплоты осуществляется
одновременно конвекцией и теплопроводностью. Под конвекцией теплоты понимают
перенос теплоты при перемещении макрочастиц жидкости или газа в пространстве из
области с одной: температурой в область с другой.
Конвекция возможна только в текучей среде, здесь перенос теплоты
неразрывно связан с переносом самой среды.
Если
в единицу времени через единицу контрольной поверхности нормально к ней
проходит масса жидкости  , кг/(м.кв.∙с), где
, кг/(м.кв.∙с), где 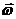 - скорость,
- скорость, 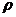 -
плотность жидкости, то вместе с ней переносится энтальпия, Дж/(м.кв.∙с):
-
плотность жидкости, то вместе с ней переносится энтальпия, Дж/(м.кв.∙с):
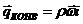 (1)
(1)
Конвекция
теплоты всегда сопровождается теплопроводностью, так как при движении жидкости
или газа неизбежно происходит соприкосновение отдельных частиц, имеющих
различные температуры. В результате конвективный теплообмен описывают
уравнением
 (2)
(2)
Здесь
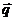 является локальным (местным) значением плотности
теплового потока за счет конвективного теплообмена. Первый член правой части
уравнения (2) описывает перенос теплоты теплопроводностью, второй - конвекцией.
является локальным (местным) значением плотности
теплового потока за счет конвективного теплообмена. Первый член правой части
уравнения (2) описывает перенос теплоты теплопроводностью, второй - конвекцией.
Конвективный
теплообмен между потоками жидкости или газа и поверхностью соприкасающегося с
ним тела называется конвективной теплоотдачей или теплоотдачей.
Очень
часто в инженерных расчетах определяют теплоотдачу; при этом знание
конвективного теплообмена внутри жидкой среды может представить косвенный
интерес, поскольку перенос теплоты внутри жидкости отражается и на теплоотдаче.
При
расчетах теплоотдачи используют закон Ньютона-Рихмана:
 (3)
(3)
Согласно
закону Ньютона-Рихмана тепловой поток  (Вт), от
жидкости к элементу поверхности соприкасающегося тела dF (или от dF к
жидкости) прямо пропорционален dF и разности температур A
(Вт), от
жидкости к элементу поверхности соприкасающегося тела dF (или от dF к
жидкости) прямо пропорционален dF и разности температур A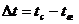 , где
, где  -
температура поверхности тела,
-
температура поверхности тела, 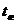 -
температура окружающей жидкой или газообразной среды.
-
температура окружающей жидкой или газообразной среды.
Разность
температур 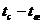 называют температурным напором.
называют температурным напором.
Коэффициент
пропорциональности 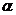 , входящий в уравнение (3), называется коэффициентом
теплоотдачи. Он учитывает конкретные условия процесса теплоотдачи, влияющие на
его интенсивность.
, входящий в уравнение (3), называется коэффициентом
теплоотдачи. Он учитывает конкретные условия процесса теплоотдачи, влияющие на
его интенсивность.
Согласно
уравнению (3)
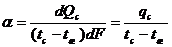 (4)
(4)
Это
тождество следует рассматривать как определение коэффициента теплоотдачи,
который измеряется в Вт/(м.кв.∙К).
Таким
образом, коэффициент теплоотдачи есть плотность теплового потока 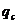 на границе жидкости (газа) и соприкасающегося тела,
отнесенная к разности температур поверхности этого тела и окружающей среды.
на границе жидкости (газа) и соприкасающегося тела,
отнесенная к разности температур поверхности этого тела и окружающей среды.
В
общем случае коэффициент теплоотдачи переменен по поверхности F. Если 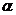 и
и 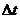 не
изменяются по F, то закон Ньютона-Рихмана может быть записан (5).
не
изменяются по F, то закон Ньютона-Рихмана может быть записан (5).
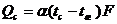 (5)
(5)
Коэффициент
теплоотдачи зависит от большого количества факторов. В общем случае 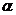 является функцией формы и размеров тела, режима
движения, скорости и температуры жидкости, физических параметров жидкости и
других величин. По-разному протекает процесс теплоотдачи в зависимости от
природы возникновения движения жидкости.
является функцией формы и размеров тела, режима
движения, скорости и температуры жидкости, физических параметров жидкости и
других величин. По-разному протекает процесс теплоотдачи в зависимости от
природы возникновения движения жидкости.
Чтобы
привести жидкость в движение, к ней необходимо приложить силу. Силы,
действующие на какой-либо элемент жидкости, можно разделить на массивы (или
объемные) и поверхностные.
Массовыми
называют силы, приложенные ко всем частицам жидкости и обусловленные внешними
силовыми полями (например, гравитационным или электрическим). Поверхностные
силы возникают вследствие действия окружающей жидкости или твердых тел; они
приложены к поверхности контрольного объема жидкости. Такими силами являются
силы внешнего давления и силы трения.
Различают
свободную и вынужденную конвекцию. В первом случае движение в рассматриваемом
объеме жидкости возникает за счет неоднородности в нем массовых сил. Если
жидкость с неоднородным распределением температуры, и, как следствие, с
неоднородным распределением плотности, находится в поле земного тяготения,
может возникнуть свободное гравитационное движение. В дальнейшем в основном
будет рассматриваться гравитационная свободная конвекция, вызванная
неоднородностью температурного поля.
Вынужденное
движение рассматриваемого объема жидкости происходит под действием внешних
поверхностных сил, приложенных на его границах за счет предварительно
сообщенной кинетической энергии (например, за счет работы насоса, вентилятора,
ветра). Как вынужденное рассматривается и течение изучаемого объема жидкости
под действием однородного в нем поля массовых сил. Иллюстрацией последнего
может являться течение изотермической пленки жидкости по стенке под действием
сил тяжести.
1.2
Физические свойства жидкости
В
зависимости от физических свойств жидкостей (газов) процесс теплообмена может
протекать различно и своеобразно. Особенно большое влияние оказывают
коэффициент теплопроводности 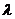 ,
удельная теплоемкость
,
удельная теплоемкость  , плотность
, плотность 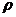 ,
коэффициент температуропроводности
,
коэффициент температуропроводности 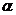 , уже
использовавшиеся при рассмотрении теплопроводности, и коэффициент вязкости
, уже
использовавшиеся при рассмотрении теплопроводности, и коэффициент вязкости  . Для каждого вещества эти величины имеют определенные
значения и являются функцией параметров состояния (температуры и давления,
прежде всего температуры). Особенно существенные изменения физических свойств
могут иметь место в околокритической области термодинамических состояний и в
области очень низких температур.
. Для каждого вещества эти величины имеют определенные
значения и являются функцией параметров состояния (температуры и давления,
прежде всего температуры). Особенно существенные изменения физических свойств
могут иметь место в околокритической области термодинамических состояний и в
области очень низких температур.
В
дипломной работе теплообмен в околокритической области будет рассмотрен особо.
При
теоретическом анализе конвективного теплообмена для простоты и наглядности
выводов в основном будем полагать, что физические свойства жидкости (газа)
постоянны в исследуемом интервале температур.
Все
реальные жидкости обладают вязкостью; между частицами или слоями, движущимися с
различными скоростями, всегда возникает сила внутреннего трения,
противодействующая движению. Согласно закону Ньютона эта касательная сила s. Па
(отнесенная к единице поверхности), которая действует в любой точке потока в
плоскости, ориентированной по течению, пропорциональна изменению скорости в
направлении нормали к этой плоскости:
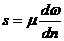 (6)
(6)
Коэффициент
 называется динамическим коэффициентом вязкости или
просто коэффициентом вязкости; его единица измерения Н∙с/м.кв. При
называется динамическим коэффициентом вязкости или
просто коэффициентом вязкости; его единица измерения Н∙с/м.кв. При  численно
численно 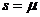 .
.
В
уравнении гидродинамики и теплопередачи часто входит отношение вязкости  к плотности
к плотности 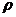 ,
называемое кинематическим коэффициентом вязкости и обозначаемое буквой
,
называемое кинематическим коэффициентом вязкости и обозначаемое буквой 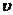 , м.кв./с (7).
, м.кв./с (7).
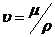 .(7)
.(7)
Коэффициенты
 и
и 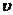 являются
физическими параметрами. Они существенно зависят от температуры.
являются
физическими параметрами. Они существенно зависят от температуры.
У
капельных жидкостей вязкость почти не зависит от давления, но значительно
уменьшается при повышении температуры. Типичный характер функции  для капельных жидкостей представлен на рисунке 1.
для капельных жидкостей представлен на рисунке 1.
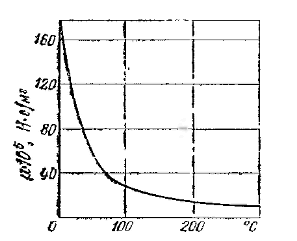
Рисунок 1 - Зависимость динамического коэффициента вязкости воды от
температуры
У
газов  увеличивается при повышении температуры (рис. 2). При
увеличении давления коэффициент вязкости газов также увеличивается, но слабо.
увеличивается при повышении температуры (рис. 2). При
увеличении давления коэффициент вязкости газов также увеличивается, но слабо.

Рисунок 2 Зависимость динамического и кинематического коэффициента
вязкости воздуха от температуры при давлении p=760 мм.рт.ст.
Кинематическая
вязкость капельных жидкостей уменьшается при повышении температуры почти в
такой же степени, как и  , так как плотность
, так как плотность 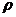 слабо
зависит от температуры. Напротив, у газов, плотность которых при повышении
температуры сильно уменьшается, кинематическая вязкость при увеличении
температуры быстро повышается. При течении жидкости или газа, обладающих
вязкостью, наличие внутреннего трения приводит к процессу диссипации
(рассеяния) энергии. Существо процесса диссипации состоит в том, что часть
кинетической энергии движущейся жидкости необратимо переходит в теплоту и
вызывает нагревание жидкости. Если вязкость жидкости или ее скорость невелики,
то нагревание будет незначительным.
слабо
зависит от температуры. Напротив, у газов, плотность которых при повышении
температуры сильно уменьшается, кинематическая вязкость при увеличении
температуры быстро повышается. При течении жидкости или газа, обладающих
вязкостью, наличие внутреннего трения приводит к процессу диссипации
(рассеяния) энергии. Существо процесса диссипации состоит в том, что часть
кинетической энергии движущейся жидкости необратимо переходит в теплоту и
вызывает нагревание жидкости. Если вязкость жидкости или ее скорость невелики,
то нагревание будет незначительным.
В
дальнейшем в основном будут рассматриваться процессы, для которых выделяемая
теплота трения незначительна и ею можно пренебречь.
На
теплоотдачу оказывает влияние сжимаемость жидкостей. Изотермической
сжимаемостью или коэффициентом сжатия тела при t=const называют
величину
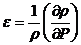 , (8)
, (8)
Представляющую
собой относительное изменение плотности вещества при изменении давления.
Для
капельных жидкостей изотермическая сжимаемость чрезвычайно мала. Так, например,
для воды 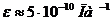 , т. е. повышение давления на 1 бар вызывает
относительное изменение плотности на 1/20000. То же самое имеет место и для
других капельных жидкостей, что позволяет пренебречь для них изотермической
сжимаемостью.
, т. е. повышение давления на 1 бар вызывает
относительное изменение плотности на 1/20000. То же самое имеет место и для
других капельных жидкостей, что позволяет пренебречь для них изотермической
сжимаемостью.
Для
воздуха в нормальном состоянии 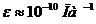 . Таким
образом, сжимаемость воздуха в 20000 раз больше сжимаемости воды. Аналогичное
соотношение имеет место и для других газов.
. Таким
образом, сжимаемость воздуха в 20000 раз больше сжимаемости воды. Аналогичное
соотношение имеет место и для других газов.
Однако
главным является не способность газа сжиматься, а то, насколько он в
действительности сжимается в рассматриваемом течении. Для значительного сжатия
газа необходимо значительное изменение давления. Если при движении газа
возникают разности давления, небольшие по сравнению с его абсолютным давлением,
то изменения объема получаются малыми, и такие потоки газа в первом приближении
можно считать несжимаемыми.
Значительные
изменения давления возникают при больших скоростях течения. При этом нужно учитывать
теплоту трения и сжимаемость газа. В результате теплоотдача при больших
скоростях имеет ряд особенностей, не учет которых может привести к существенным
ошибкам.
В
дальнейшем в основном будет рассматриваться теплоотдача несжимаемой жидкости.
При этом слово «жидкость» будет употребляться как собирательное понятие и для
жидкостей, и для газов. Теплоотдача сжимаемого газа будет рассмотрена отдельно.
Между
сжимаемыми и несжимаемыми течениями газа нет резкой границы. Обычно считают,
что если скорость газа меньше четвертой части скорости звука, то к газам
допустимо применять законы движения и теплоотдачи, полученные для несжимаемой
жидкости.
Помимо
изотермической сжимаемости для конвективного теплообмена большое значение имеет
тепловое расширение жидкости. Последнее характеризуется температурным
коэффициентом объемного расширения, определяемым уравнением (p=const).
 (9)
(9)
Согласно
определению температурный коэффициент объемного расширения  , представляет собой относительное изменение объема
при изменении температуры на один градус (при постоянном давлении) .
, представляет собой относительное изменение объема
при изменении температуры на один градус (при постоянном давлении) .
Для
жидкостей температурный коэффициент объемного расширения сравнительно мал
(исключение составляет область вблизи термодинамической критической точки). Для
некоторых жидкостей, например для воды при t<4°С, коэффициент  может иметь отрицательное значение.
может иметь отрицательное значение.
Для
идеального газа температурный коэффициент объемного расширения есть величина,
обратная абсолютной температуре газа (10).
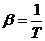 .(10)
.(10)
В
неравномерно нагретой жидкости вследствие теплового расширения возникает
неоднородное поле плотности, что в конечном итоге может привести к свободному
движению.
1.3
Постановка задачи конвективного теплообмена
Из уравнения (2) следует, что плотность теплового потока в любой точке
жидкости для каждого момента времени однозначно определяется, если известны
поля температур, удельной энтальпии и скорости.
Связь
между температурой и энтальпией может быть установлена следующим образом. Для
реальной жидкости 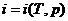 и согласно понятию о полном дифференциале (11).
и согласно понятию о полном дифференциале (11).
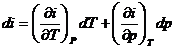 .(11)
.(11)
Отсюда
(12):
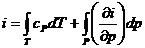 .(12)
.(12)
Из
дифференциальных уравнений термодинамики и из определения температурного
коэффициента объемного расширения следует, что (13).
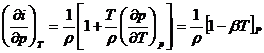 .(13)
.(13)
Приведенные
здесь уравнения позволяют установить связь между полем температур и полем
энтальпии. Чтобы аналитически найти поля температур (энтальпии) и скоростей и
определить 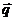 , необходимо располагать соответствующими уравнениями.
, необходимо располагать соответствующими уравнениями.
Выведем
дифференциальное уравнение, описывающее температурное поле в движущейся
жидкости. При выводе будем полагать, что жидкость однородна н изотропна, ее
физические параметры постоянны, энергия деформации мала по сравнению с
изменением внутренней энергии.
Выделим
в потоке жидкости неподвижный относительно координатной системы элементарный
параллелепипед (рис. 3) с ребрами dx, dy и dz.

Рисунок 3 - К выводу дифференциального уравнения энергии
Через грани параллелепипеда теплота переносится теплопроводностью и
конвекцией; в общем случае в рассматриваемом объеме может выделяться теплота
внутренними источниками за счет энергии, внешней по отношению к рассматриваемой
жидкости.
Для уравнения энергии, соответствующего принятым здесь условиям, было
получено уравнение (14).
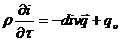 ,(14)
,(14)
где
(15):
 .(15)
.(15)
Согласно
уравнению (2) проекции плотности теплового потока 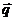 на координатные оси Ox, Oy, Oz
равны (16).
на координатные оси Ox, Oy, Oz
равны (16).
 (16)
(16)
Подставляя
значения 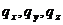 в уравнение, можно получить (17):
в уравнение, можно получить (17):
 (17)
(17)
Для
несжимаемых жидкостей  (18).
(18).
 .(18)
.(18)
Тогда
(19).
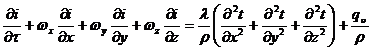 (19)
(19)
Или,
если 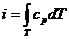 , (20)
, (20)
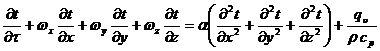 (20)
(20)
Последнее
уравнение, как и уравнение (9), является искомым уравнением энергии,
описывающим распределение температур внутри движущейся жидкости.
Многочлен,
стоящий в левой части уравнения (10), представляет собой полную производную от
температуры по времени. Действительно, если 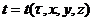 , то на
основании понятия о полной производной имеем (21).
, то на
основании понятия о полной производной имеем (21).
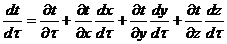 ,(21)
,(21)
Где
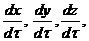
Имеют
смысл составляющих скорости 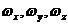 .
.
Здесь
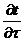 характеризует изменение температуры во времени в
какой-либо точке жидкости, т.е. является локальным изменением t; член
характеризует изменение температуры во времени в
какой-либо точке жидкости, т.е. является локальным изменением t; член
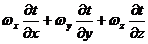
характеризует
изменение температуры при переходе точки к точке, т.е. является конвективным
изменением t.
Применяя
обозначение
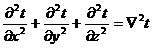 ,
,
Уравнение
энергии можно записать в форме
 .
.
Если
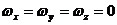 , уравнение энергии переходит в уравнение
теплопроводности.
, уравнение энергии переходит в уравнение
теплопроводности.
При
стационарных процессах конвективного теплообмена 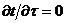 .
Уравнение (4-10) еще более упрощается, если температура изменяется только по
одной или двум координатам. В случае стационарного одномерного температурного
поля все производные по
.
Уравнение (4-10) еще более упрощается, если температура изменяется только по
одной или двум координатам. В случае стационарного одномерного температурного
поля все производные по 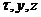 равны нулю.
равны нулю.
Как
следует из уравнения (4-10), температурное поле в движущейся жидкости зависит
от составляющих скорости 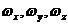 . Чтобы сделать систему уравнений замкнутой,
необходимо добавить уравнения, которые бы описывали изменение скорости во
времени и пространстве. Такими уравнениями являются дифференциальные уравнения
движения.
. Чтобы сделать систему уравнений замкнутой,
необходимо добавить уравнения, которые бы описывали изменение скорости во
времени и пространстве. Такими уравнениями являются дифференциальные уравнения
движения.
Уравнения
движения. Вывод дифференциального уравнения движения вязкой жидкости требует
громоздких математических выкладок. В связи с этим будет дан упрощенный вывод
этого уравнения для случая одномерного течения несжимаемой жидкости. Этот вывод
не является строгим, его основное достоинство заключается в наглядности. Для
трехмерного движения уравнение будет приведено без вывода. Уравнения движения
подробно рассматриваются в курсах гидродинамики и монографиях по теплопередаче.
Выделим
в потоке вязкой жидкости элементарный объем с размерами ребер dx, dy и dz (рис.
4).

Рисунок 4 - К выводу дифференциального уравнения движения жидкости
Скорость в потоке изменяется только в направлении оси у, закон изменения
скорости произволен.
Вывод уравнения движения основан на втором закона Ньютона; сила равна
массе, умноженной на ускорение.
Силы,
действующие на рассматриваемый элемент жидкости, можно разделить на массовые
(или объемные) и поверхностные. Массовые силы характеризуют вектором  (м.кв./с), значение которого равно отношению силы,
действующей на данную частицу, к массе этой частицы.
(м.кв./с), значение которого равно отношению силы,
действующей на данную частицу, к массе этой частицы.
Если
учитывается только сила тяжести, то 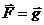 , где
, где 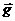 - ускорение свободного падения. В дипломном проекте в
дальнейшем учитывается только сила тяжести. Значение поверхностных сил равно
отношению силы, действующей на элемент поверхности, к величине площади этого
элемента. К поверхностным силам относятся силы трения и силы давления.
- ускорение свободного падения. В дипломном проекте в
дальнейшем учитывается только сила тяжести. Значение поверхностных сил равно
отношению силы, действующей на элемент поверхности, к величине площади этого
элемента. К поверхностным силам относятся силы трения и силы давления.
Таким
образом, на рассматриваемый элемент жидкости действуют три силы; сила тяжести,
равнодействующая сил давления и равнодействующая сил трения.
Найдем
проекции этих сил на ось Ох.
Силы
тяжести  приложена в центре тяжести элемента. Ее проекция на
ось Ох равна произведению проекции ускорения свободного падения
приложена в центре тяжести элемента. Ее проекция на
ось Ох равна произведению проекции ускорения свободного падения 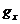 на массу элемента:
на массу элемента:
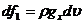 .
.
Равнодействующая
сила давления 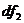 определяется следующим образом. Если на верхней грани
элемента давление жидкости равно p, то на площадку dydz действует сила pdydz.
определяется следующим образом. Если на верхней грани
элемента давление жидкости равно p, то на площадку dydz действует сила pdydz.
На
нижней грани давление с точностью до второго члена разложения в ряд Тейлора
равно  , и на эту грань действует сила
, и на эту грань действует сила  . Здесь знак минус указывает на то, что эта сила
действует против направления движения жидкости. Равнодействующая сил давления
равна их алгебраической сумме:
. Здесь знак минус указывает на то, что эта сила
действует против направления движения жидкости. Равнодействующая сил давления
равна их алгебраической сумме:
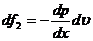
Равнодействующая
сил трения 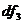 определяется из следующих соображений. Так как
скорость изменяется только в направлении оси Оу, то сила трения возникает на
боковых гранях элемента жидкости (рис. 4-4). Около левой грани скорость
движения частиц жидкости меньше, чем в самом элементе, поэтому здесь в сечении
у сила трения направлена против движения и равна sdxdz. Около правой грани,
наоборот, скорость движения частиц жидкости больше, чем в самом элементе,
поэтому здесь в сечении y+dy сила трения направлена в сторону движения.
Равнодействующая этих сил равна алгебраической сумме:
определяется из следующих соображений. Так как
скорость изменяется только в направлении оси Оу, то сила трения возникает на
боковых гранях элемента жидкости (рис. 4-4). Около левой грани скорость
движения частиц жидкости меньше, чем в самом элементе, поэтому здесь в сечении
у сила трения направлена против движения и равна sdxdz. Около правой грани,
наоборот, скорость движения частиц жидкости больше, чем в самом элементе,
поэтому здесь в сечении y+dy сила трения направлена в сторону движения.
Равнодействующая этих сил равна алгебраической сумме:
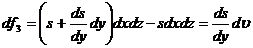 .
.
Подставляя
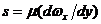 , получаем
, получаем
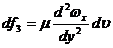 .
.
Суммируя
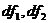 и
и 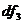 получаем
проекция на ось Ox равнодействующей всех сил, приложенных к объему:
получаем
проекция на ось Ox равнодействующей всех сил, приложенных к объему:
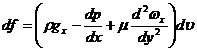 .
.
Согласно
второму закону механики эта равнодействующая равна произведению массы элемента
на его ускорение  и учитывает силы инерции:
и учитывает силы инерции:
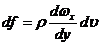 .
.
Приравнивая
правые части уравнений производя сокращения, окончательно имеем уравнение
движения вдоль оси Оx:
 .
.
Описание
движения жидкости усложняется, если скорость изменяется по трем направлениям. В
общем случае трехмерного движения несжимаемой жидкости с постоянными
физическими параметрами скоростное поле описывается тремя уравнениями движения,
каждое соответственно в проекциях сил на оси Ox, Oy и Oz:
Для
оси Ох: 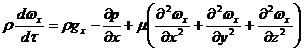
Для
оси Оy: 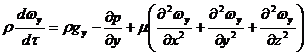
Для
оси Оz: 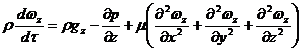
Уравнения
называют уравнениями Навье-Стокса. Все слагаемые уравнений имеют размерность
силы, отнесенной к единице объема.
В
общем случае составляющие скорости 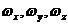 изменяются
во времени и в пространстве. Член, стоящий в левой части уравнений.
представляет собой полную производную от скорости по времени.
изменяются
во времени и в пространстве. Член, стоящий в левой части уравнений.
представляет собой полную производную от скорости по времени.
На
основании понятия о полной производной имеем:
Для
оси Ох: 
Для
оси Оy: 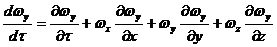
Для
оси Оz: 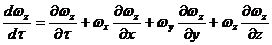
Производные
 ,
,  и
и 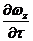 характеризуют изменение скорости по времени в
какой-либо точке жидкости, т. е характеризуют локальное изменение скорости;
остальные три члена, стоящие в правых частях уравнений, характеризуют изменение
скорости при переходе от точки к точке. Используя векторную форму записи,
уравнения можно написать в виде:
характеризуют изменение скорости по времени в
какой-либо точке жидкости, т. е характеризуют локальное изменение скорости;
остальные три члена, стоящие в правых частях уравнений, характеризуют изменение
скорости при переходе от точки к точке. Используя векторную форму записи,
уравнения можно написать в виде:
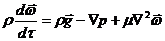
Уравнение
движении получено без учета зависимости физических параметров жидкости от
температуры. В частности, не учтена зависимость плотности от температуры В то
же время свободное движение жидкости определяется разностью плотностей холодных
и нагретых частиц жидкости
Ограничимся
приближенным учетом переменности плотности. Используем для этого температурный
коэффициент объемного расширения  . Будем
полагать, что в заданном интервале температур
. Будем
полагать, что в заданном интервале температур  является
постоянной величиной, не зависящей от температуры. Это условие лучше
выполняется для газов и хуже для капельных жидкостей.
является
постоянной величиной, не зависящей от температуры. Это условие лучше
выполняется для газов и хуже для капельных жидкостей.
)
граничных условий, характеризующих особенности протекания процесса иа границах
жидкой среды.
В
последних должны быть заданы граничные значения зависимых (искомых) переменных
или их производных. Например, для любого момента времени задаются распределение
температур или тепловых потоков по поверхности тела (в простейшем случае 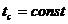 или
или 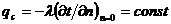 ,
распределение температур и скоростей жидкости на входе в канал или на большом
удалении от рассматриваемой поверхности теплообмена, значения скорости иа
стенке и т. д. Очевидно, в зависимости от вида задания граничных и других
условий результаты решения (интегрирования), представляемые в виде формул или
числовых значений, могут бить различны.
,
распределение температур и скоростей жидкости на входе в канал или на большом
удалении от рассматриваемой поверхности теплообмена, значения скорости иа
стенке и т. д. Очевидно, в зависимости от вида задания граничных и других
условий результаты решения (интегрирования), представляемые в виде формул или
числовых значений, могут бить различны.
Система
дифференциальных уравнений в совокупности с условиями однозначности
представляет собой математическую формулировку краевой задачи.
Задание
распределений 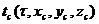 и
и 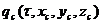 , где
, где  - координаты поверхности тела, часто затруднительно,
так как
- координаты поверхности тела, часто затруднительно,
так как  и
и 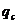 в общем
случае зависят от процессов теплообмена в стенке и по другую ее сторону. Строго
говоря, в этом случае тепловые граничные условия нельзя назначить заранее, так
как они являются сложной функцией совокупности всех отдельных процессов
теплообмена. Необходимо к системе дифференциальных уравнений рассматриваемого
процесса конвективного теплообмена присоединить дифференциальные уравнения,
описывающие процесс теплопроводности в стенке и процесс конвективного
теплообмена по другую ее сторону, и задать условия сопряжения.
в общем
случае зависят от процессов теплообмена в стенке и по другую ее сторону. Строго
говоря, в этом случае тепловые граничные условия нельзя назначить заранее, так
как они являются сложной функцией совокупности всех отдельных процессов
теплообмена. Необходимо к системе дифференциальных уравнений рассматриваемого
процесса конвективного теплообмена присоединить дифференциальные уравнения,
описывающие процесс теплопроводности в стенке и процесс конвективного
теплообмена по другую ее сторону, и задать условия сопряжения.
Для
непрерывных полей условия сопряжения могут быть заданы в виде равенства
температур на поверхности соприкосновения сред, а в случае отсутствия на
непроницаемой границе раздела тепловыделения за счет внутренних источников - в
виде равенства тепловых потоков, описываемых законом Фурье.
Для
сопряженной задачи дифференциальные уравнения и условия однозначности,
описывающие процессы теплообмена в смежных средах, и условия сопряжения можно
трактовать как граничные условия. Конечно, в этом случае граничные условия
будут очень сложны. Решения задач конвективного теплообмена большей частью
получают с помощью наперед заданных граничных условий.
Физический
анализ процессов конвективного теплообмена показывает, что в ряде случаев
математическая формулировка задачи может быть упрощена без внесения
существенных погрешностей. Например, математическая формулировка может быть
упрощена при использовании понятия пограничного слоя, рассматриваемого в
следующем параграфе. В результате могут быть получены математически точные
решения.
Сложность
процессов конвективного теплообмена заставляет при его изучении особенно широко
использовать методы экспериментального исследования. В результате эксперимента
получают синтезированные сведения о процессе, влияние отдельных факторов не
всегда легко выделить. Эти трудности помогает преодолевать теория подобия.
Основой теории подобия является математическая формулировка краевой задачи.
В
ряде случаев для исследования процесса конвективного теплообмена используется
его аналогия с процессами другой физической природы. Аналогия устанавливается
на основе математического описания этих процессов.
Внедрение
электронной вычислительной техники привело к более широкому использованию
численных методов расчета. Многие задачи, не поддающиеся точному решению, могут
быть рассчитаны с помощью ЭЦВМ. И в этом случае исходной для расчета является
математическая формулировка задачи в виде дифференциальных уравнении и условий
однозначности.
1.4
Гидродинамический и тепловой пограничные слои
Для инженерной практики особый интерес представляет теплообмен между
жидкостью и омываемым ею телом. Рассмотрим особенности течения и переноса
теплоты и пристенном слое жидкости.
Условия «прилипания». В настоящее время в гидродинамике вязкой жидкости
получила признание гипотеза о том, что частицы жидкости, непосредственно
прилегающие к твердому телу, адсорбируются последним, как бы прилипают к его
поверхности, т.е. их скорость равна скорости тела (а если тело неподвижно, то
нулю).
Этот слои «прилипшей» жидкости нужно рассматривать как бесконечно тонкий
слой. Гипотеза о равенстве нулю скоростей жидкости на стенке нашла косвенное
подтверждение в хорошем согласии с опытом результатов многочисленных
теоретических работ, в основу которых она была положена.
Равенство нулю скорости жидкости на стенке выполняется до тех пор, пока
газ можно считать сплошной средой. По мере увеличения разрежения ослабляется
взаимодействие газа со стенкой и разреженный газ вблизи стенки начинает
проскальзывать.
Степень
разрежения потока характеризуют значением параметра Кнудсена 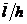 , представляющего собой отношение средней длины
свободною пробега молекул газа
, представляющего собой отношение средней длины
свободною пробега молекул газа 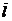 к
характерному размеру твердого тела
к
характерному размеру твердого тела 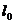 (например,
диаметру трубы или проволоки).
(например,
диаметру трубы или проволоки).
Если
примерно 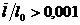 , то газ уже нельзя рассматривать как сплошную среду,
для которой выполняется условие прилипания.
, то газ уже нельзя рассматривать как сплошную среду,
для которой выполняется условие прилипания.
При
значениях параметра Кнудсена, примерно больших 10, газ должен рассматриваться
как свободный молекулярный поток. Его взаимодействие с твердым телом
описывается на основе законов кинетической теории газов.
При
значениях параметра Кнудсена, заключенных между 0,001 и 10, разреженный газ не
может рассматриваться ни как полностью сплошная, ни как полностью
свободномолекулярная среда. Для этой области чисел Кнудсена разрабатываются
свои методы расчета течения и теплообмена.
Мы
будем рассматривать в основном сплошные среды и исходить из равенства нулю
скорости исчезающие тонкого слоя жидкости, непосредственно прилегающего к
поверхности твердого тела.
Уравнение
теплоотдачи. Так как у поверхности твердого тела имеется тонкий слой
неподвижной жидкости, из уравнения следует, что плотность теплового потока на
стенке (теплоотдача) может быть определена по уравнению Фурье
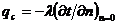 ,
,
где
 - нормаль к поверхности тела.
- нормаль к поверхности тела.
Таким
образом, если известно температурное поле 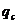 , то
можно вычислить, не обращаясь к закону Ньютона-Рихмана:
, то
можно вычислить, не обращаясь к закону Ньютона-Рихмана:
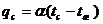 .
.
При
необходимости по известному температурному полю можно определить и коэффициент
теплоотдачи. Из уравнений следует, что

Будем
называть это уравнение уравнением теплоотдачи.
Из
условия равенства нулю относительной скорости жидкости на поверхности тела
следуют и другие важные для расчетной практики выводы, облегчающие нахождение
поля температур, и, следовательно, определение 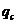 и
и 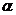 .
.
Гидродинамический
пограничный слой. Рассмотрим продольное обтекание плоской поверхности тела
безграничным потоком жидкости. Скорость и температура набегающего потока
постоянны и равны соответственно  и
и 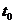 . При соприкосновении частиц жидкости с поверхностью
тела они «прилипают» к ней. В результате в области около пластины вследствие
действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах
которого скорость изменяется от нуля па поверхности тела до скорости
невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости получил
название гидродинамического пограничного слоя. Теория гидродинамического
пограничного слоя впервые дана Л. Прандтлем (1904 г.).
. При соприкосновении частиц жидкости с поверхностью
тела они «прилипают» к ней. В результате в области около пластины вследствие
действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах
которого скорость изменяется от нуля па поверхности тела до скорости
невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости получил
название гидродинамического пограничного слоя. Теория гидродинамического
пограничного слоя впервые дана Л. Прандтлем (1904 г.).
Чем
больше расстояние х от передней кромки пластины, тем толще пограничный слой,
так как влияние вязкости по мере движения жидкости вдоль тела все дальше
проникает в иевозмущенный поток. Эта особенность пограничного слоя
иллюстрируется на рисунке 6, на котором представлены распределения скорости при
различных значениях х.
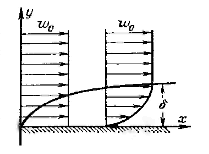
Рисунок 6 - Изменение скорости в гидродинамическом пограничном слое
Для
течения жидкости внутри пограничного слоя справедливо условие 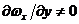 , вне пограничного слоя и на его внешней границе:
, вне пограничного слоя и на его внешней границе:
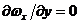 и
и 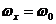 .
.
Понятия
«толщина пограничного слоя» и «внешняя граница пограничного слоя» довольно
условны, так как резкого перехода от пограничного слоя к течению вне слоя нет.
Скорость в пограничном слое по мере увеличения у асимптотически стремится к  .
.
Поэтому
под толщиной пограничного слоя 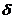 подразумевается
такое расстояние от стенки, на котором скорость будет отличаться от скорости
потока вдали от тела на определенную заранее заданную малую величину
подразумевается
такое расстояние от стенки, на котором скорость будет отличаться от скорости
потока вдали от тела на определенную заранее заданную малую величину 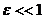 (например на 1%): при
(например на 1%): при  .
.
Таким
образом, при омывании тела ноток жидкости как бы разделяется на две части: на
пограничный слой и на внешний поток. Во внешнем потоке преобладают силы
инерции, вязкостные силы здесь не проявляются. Напротив, в пограничном слое
силы вязкости и инерционные силы соизмеримы.
1.5
Турбулентный перенос теплоты и количества движения
Турбулентное течение существенно отличается от ламинарного. На рисунке 7
показана осциллограмма колебаний скорости в определенной неподвижной точке
турбулентного потока, имеющего неизменную среднюю скорость течения.

Рисунок
7 - Изменение скорости 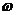 и температуры t в неподвижной
точке турбулентного потока
и температуры t в неподвижной
точке турбулентного потока
Мгновенная скорость пульсирует около некоторого среднего во времени
значения. Помимо показанного на графике рисунка 7 изменения абсолютной величины
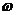 происходит еще и изменение
направления мгновенной скорости. Отклонение мгновенной скорости
происходит еще и изменение
направления мгновенной скорости. Отклонение мгновенной скорости 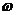 от средней во времени
от средней во времени 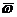 называют пульсациями скорости или
пульсационными скоростями
называют пульсациями скорости или
пульсационными скоростями 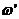 . При этом
. При этом 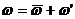 . Таким образом» турбулентное движение состоит как бы из
регулярного течения, описываемого осредненными значениями скоростей, и из
наложенного на него хаотического пульсационного течения.
. Таким образом» турбулентное движение состоит как бы из
регулярного течения, описываемого осредненными значениями скоростей, и из
наложенного на него хаотического пульсационного течения.
При
пульсациях скорости происходит перенос механической энергии. Если в потоке
имеет место разность температур, то пульсации скорости приводят и к переносу
теплоты, вследствие чего возникают пульсации температуры (рис. 7). Температура
в определенной неподвижной точке турбулентного потока колеблется около
некоторого среднего во времени значения  .
Пульсация температуры
.
Пульсация температуры 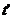 связана с
связана с  и
и  уравнением
уравнением 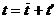 .
.
Таким
образом, турбулентное течение, строго говоря, является нестационарным
процессом, однако если осредненные во времени скорости и температуры 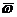 и
и  не
изменяются, то такое движение и связанный с ним перенос теплоты можно
рассматривать как стационарные (квазистационарные) процессы. При этом интервал
времени осреднения должен быть достаточно большим по сравнению с периодом
пульсации, но в то же время достаточно малым по сравнению с каким-либо
характерным для осредненного движения интервалом времени, чтобы учесть
возможные изменения средних скоростей и температур во времени. Будем в
дальнейшем полагать, что средние значения актуальных величин w, t получены как
среднеинтегральные.
не
изменяются, то такое движение и связанный с ним перенос теплоты можно
рассматривать как стационарные (квазистационарные) процессы. При этом интервал
времени осреднения должен быть достаточно большим по сравнению с периодом
пульсации, но в то же время достаточно малым по сравнению с каким-либо
характерным для осредненного движения интервалом времени, чтобы учесть
возможные изменения средних скоростей и температур во времени. Будем в
дальнейшем полагать, что средние значения актуальных величин w, t получены как
среднеинтегральные.
В
общем случае пульсации скорости и температуры приводят к пульсациям давления и
физических свойств.
Полагают,
что дифференциальные уравнения конвективного теплообмена справедливы для
отдельных струек пульсационного движения. Эти уравнения можно записать в
осредненных значениях скорости и температуры, если произвести замену 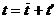 ,
, 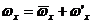 ,
, 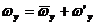 и т. д. Произведя некоторые преобразования и выдвинув
дополнительные гипотезы, можно получить систему дифференциальных уравнений,
описывающих в первом приближении осредненное турбулентное течение и теплообмен.
В достаточно строгой постановке этот вопрос до конца не разрешен.
и т. д. Произведя некоторые преобразования и выдвинув
дополнительные гипотезы, можно получить систему дифференциальных уравнений,
описывающих в первом приближении осредненное турбулентное течение и теплообмен.
В достаточно строгой постановке этот вопрос до конца не разрешен.
Запишем
ряд соотношений, необходимых для решения простейших задач.
Пусть
в некоторый момент времени 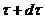 скорость
в фиксированной точке (малой области) турбулентного потока имеет компоненты
скорость
в фиксированной точке (малой области) турбулентного потока имеет компоненты 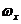 и
и 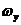 (рис.
8).
(рис.
8).
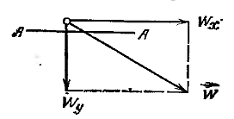
Рисунок 8 - Мгновенное значение скорости в плоском турбулентном потоке
Температура
жидкости в этой точке равна t. Условную контрольную поверхность АА расположим
близко к рассматриваемой точке и параллельно плоскости xz. За их через единицу
поверхности АА проходит масса 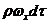 (кг/м.кв.).
При этом, в частности, в направлении оси Оу переносится количество движения
относительно оси Ох, равное
(кг/м.кв.).
При этом, в частности, в направлении оси Оу переносится количество движения
относительно оси Ох, равное 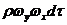 (кг/м.кв.)
и соответственно энтальпия
(кг/м.кв.)
и соответственно энтальпия 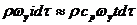 (полагаем,
что
(полагаем,
что 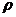 и
и  постоянны).
постоянны).
В
следующие моменты времени компоненты скорости могут быть другими.
Среднеинтегральное значение энтальпии 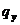 (Дж/(м.кв.∙с),
переносимое в направлении оси Оу за единицу времени через единицу контрольной
поверхности, будет равно:
(Дж/(м.кв.∙с),
переносимое в направлении оси Оу за единицу времени через единицу контрольной
поверхности, будет равно:
 2. Моделирование процессов конвективного обмена
2. Моделирование процессов конвективного обмена
2.1 Моделирование
процессов конвективного обмена
При моделировании изучение процесса в образце заменяется исследованием
этого же процесса на модели. Очевидно, процесс в модели должен быть осуществлен
так, чтобы результаты его изучения можно было перенести на образец. Условия
моделирования, т. е. условия, которым должна удовлетворять модель и протекающий
в ней процесс, дает теория подобия. Если процесс в модели будет подобен
процессу в образце, то результаты исследования на модели могут быть применены к
образцу.
Моделирование по существу включает в себя две самостоятельные задачи.
Во-первых, в модели необходимо осуществить процесс, подобный процессу,
происходящему в образце, и, во-вторых, выполнить на модели все требуемые
измерения и наблюдения. Мы рассматриваем первую задачу.
Чтобы процессы в модели и образце были подобны, необходимо осуществить
сформулированные ранее условия подобия.
Первое условие подобия говорит, что моделировать следует качественно
одинаковые процессы, т. е. процессы, имеющие одинаковую физическую природу и
описываемые одинаковыми дифференциальными уравнениями.
Второе условие подобия требует, чтобы условия однозначности подобных
процессов (в образце и модели) были одинаковы во всем, кроме числовых значений
постоянных, содержащихся в этих условиях.
Условия однозначности для стационарных процессов состоят:
) из геометрических условии, характеризующих форму и размеры тела, в
котором протекает процесс;
) из физических условий, характеризующих физические свойства
рассматриваемой среды;
) из граничных условий, характеризующих особенности протекания процесса
на границах жидкости.
Таким
образом, необходимо осуществить геометрическое подобие образца и модели. Вес
размеры образца и модели, существенные для процесса конвективного теплообмена,
должны быть связаны между собой соотношением  ,т.е.
модель должна быть построена как точная копия образца, уменьшенная в
,т.е.
модель должна быть построена как точная копия образца, уменьшенная в  раз. Конечно, копироваться должна не внешняя форма
образца, и внутренняя конфигурации каналов, по которым движутся гоазы или
жидкости.
раз. Конечно, копироваться должна не внешняя форма
образца, и внутренняя конфигурации каналов, по которым движутся гоазы или
жидкости.
Обычно
геометрическое подобие осуществить нетрудно. Следует только иметь в виду, что
изменение геометрических размеров не должно привести к качественному изменению
процесса в модели и, следовательно, к нарушению норного условии подобия.
Например, газ нельзя считать сплошной, средой и применять для исследования его
течении и теплообмена используемые нами дифференциальные уравнения
конвективного теплообмена, если параметр Кнудсена 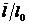 достаточно велик. При течении газа в трубе за
характерный размер
достаточно велик. При течении газа в трубе за
характерный размер 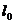 может быть принят диаметр d. Если средняя длина
свободного пробега молекул
может быть принят диаметр d. Если средняя длина
свободного пробега молекул 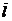 будет
примерно больше 0,001d, то такое течение газа по своим свойствам отклоняется
от течения сплошной среды.
будет
примерно больше 0,001d, то такое течение газа по своим свойствам отклоняется
от течения сплошной среды.
Если
физические параметры постоянны, как это было принято ранее при выводе
дифференциальных уравнений конвективного теплообмена, то выполнение подобия
физических условий особых трудностей не представляет. Однородные физические
параметры в модели и образце должны быть также связаны соответствующий
масштабом преобразования 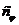 . При этом, если физические свойства жидкости в
образце и модели одни и те же,
. При этом, если физические свойства жидкости в
образце и модели одни и те же, 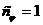 .
.
Сложнее
обстоит дело, сели физические параметры переменны и эта переменность
проявляется в исследуемом процессе. Этот вопрос будет рассмотрен несколько
позже.
При
моделировании необходимо также осуществить подобие процессов на границах
исследуемой жидкости. Чаще всего это условие ограничивается требованием подобия
условии входа жидкости в образец и модель (чтобы обеспечить подобное
распределение скоростей па входе) и требованием подобия температурных полей на
входе в аппарате и на поверхности тел. участвующих в теплообмене. Подобия
условий входа жидкости можно достичь путем устройства входного участка модели
геометрически подобный входному участку образца. Если температура жидкости На
входе в образец не' меняется по сечению канала, условие подобия температурных
полей на входе выдержать нетрудно. Для этого достаточно, чтобы в канале,
подводящем жидкость или газ к модели, не было теплообмена.
Если
же температурное поле на входе имеет сложный характер, то осуществить в модели
такое распределение температур труднее. Реализация подобия температурных полей
на поверхности теплообмена часто также представляет определенные трудности. В
атом случае вопрос о точном осуществлении граничных условий становится
предметом особых забот экспериментатора.
Третье
условие подобия требует, чтобы одноименные критерии подобных процессов имели
одинаковые значения. При этом определяемые одноименные безразмерные переменные
подобных процессов также будут иметь одинаковые значения.
Конвективная
теплоотдача существенно зависит от характера движения жидкости или газа. При
вынужденном движении картин течения в первую очередь зависит от числа
Рейнольдса. Поэтому при моделировании
2.2
Однородные разностные схемы для уравнения теплопроводности
Рассмотрим первую краевую задачу для уравнения теплопроводности: ищется
непрерывное в прямоугольнике DT = (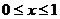 ,
, 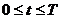 ) решение уравнения
) решение уравнения
 =
=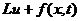 ,
, 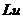 =
=
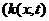
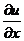 ),
),
удовлетворяющее начальному условию
 ,
, 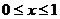 ,
,
и краевым условиям
 ,
,  ,
, 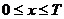 .
.
Коэффициент 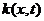 ограничен снизу и сверху
ограничен снизу и сверху
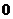
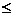

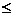
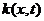
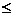
 ,
, 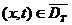 ,
,
где  ,
,  - постоянные, и удовлетворяет условию Липшица по t, которое
мы запишем в виде
- постоянные, и удовлетворяет условию Липшица по t, которое
мы запишем в виде
 ,
,
где  ,
, 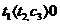 - постоянная.
- постоянная.
Предполагается, что задача имеет единственное решение, обладающее нужными
по ходу изложения производными.
Построим в  сетку. Пусть
сетку. Пусть
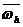 ={
={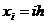 ,
, 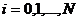 ,
,  } - равномерная сетка с шагом
} - равномерная сетка с шагом 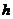 на отрезке
на отрезке 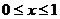 ;
;

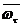 ={
={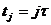 ,
, 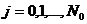 ,
, 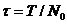 } - сетка с шагом
} - сетка с шагом 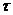 на отрезке
на отрезке 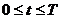 ;
;
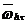 =
= 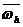 ×
×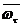 =
=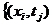 ,
, 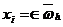 ,
, 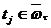
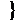 - сетка в пространстве
- сетка в пространстве 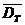
 =
=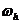 ×
×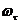 =
= 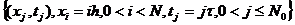 .
.
Для получения однородных консервативных разностных схем воспользуемся интегро-интерполяционным
методом. Рассмотрим уравнение (1) при t =  =
=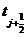 и напишем для него уравнение баланса на отрезке
и напишем для него уравнение баланса на отрезке 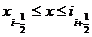 :
:
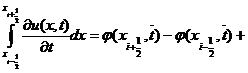
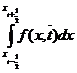 ,
,
где 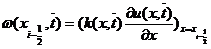 .
.
Аппроксимируем входящие в слагаемые
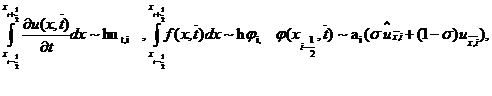
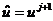 ,
,

Где 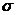 - параметр,
- параметр, 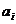 выражается через значения функции
выражается через значения функции 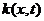 при
при  .
.
Подставим эти выражения, заменим 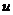 на у, знак аппроксимации - знаком
равенства. В результате получим следующую однородную консервативную разностную
схему (обозначим у =
на у, знак аппроксимации - знаком
равенства. В результате получим следующую однородную консервативную разностную
схему (обозначим у = ):
):
 Λ
Λ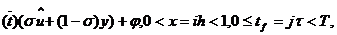
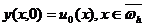 ,
,
 ,
, 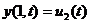 ,
,  ,
,
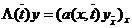 .
.
Начальное условие и краевые условия первого рода выполняются на сетке
точно.
Коэффициент 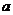 и правая часть
и правая часть  вычисляются при помощи шаблонных
функционалов:
вычисляются при помощи шаблонных
функционалов:
 , и
, и 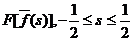
по следующим формулам
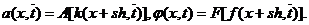
Шаблонные функционалы заданы на классах кусочно-непрерывных функций  . Так как
. Так как 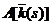 - неубывающий однородный функционал
первой степени и
- неубывающий однородный функционал
первой степени и  , то из условий следует
, то из условий следует
 ,
,
 .
.
Семейство однородных схем определяется заданием A, F и параметра 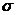 , от которого зависят устойчивость и
точность (по t) схемы.
, от которого зависят устойчивость и
точность (по t) схемы.
Если  , то
, то  и схема переходит в схему с весами для уравнения с
постоянным коэффициентом теплопроводности.
и схема переходит в схему с весами для уравнения с
постоянным коэффициентом теплопроводности.
Интегро-интерполяционный метод позволяет получить и ряд других схем. Так,
например, пользуясь уравнением баланса в прямоугольнике
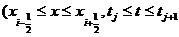
легко получить схему
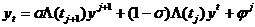 .
.
Для вычисления  могут быть использованы и другие формулы, например,
могут быть использованы и другие формулы, например,
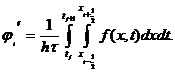
Мы ограничимся здесь изучением только схем. При практическом применении
схем для вычисления 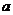 и
и  можно рекомендовать простейшие формулы:
можно рекомендовать простейшие формулы:


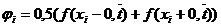
Приведем схему к «счетному виду», т. е. к виду, удобному для вычислений.
Для этого разрешим уравнение относительно  :
:
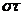 Λ
Λ
 .Λy+
.Λy+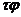 .
.
Запишем это уравнение в развернутом виде
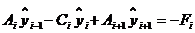 ,
, 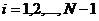 ,
,

Для определения 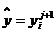 на новом слое получаем разностное уравнение второго порядка
(или трехточечное разностное уравнение) с краевыми условиями
на новом слое получаем разностное уравнение второго порядка
(или трехточечное разностное уравнение) с краевыми условиями
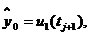
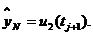
Для вычисления правой части уравнения можно пользоваться рекуррентной
формулой
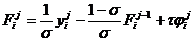 .
.
Объем вычислений при этом уменьшается.
Решение задачи может быть найдено методом прогонки при 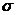 > 0, так как условия устойчивости
прогонки выполнены.
> 0, так как условия устойчивости
прогонки выполнены.

При 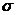 = 0 получаем явную схему
= 0 получаем явную схему
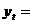 Λ
Λ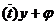
или
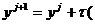 Λ
Λ
При 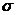 =1 - схему с опережением или чисто неявную схему
=1 - схему с опережением или чисто неявную схему
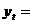 Λ
Λ 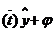 .
.
При 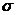 = 0,5 получаем симметричную схему.
= 0,5 получаем симметричную схему.
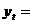 0,5 Λ
0,5 Λ .
.
2.3 Третья
краевая задача
Рассмотрим краевую задачу:
 ,
, 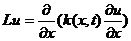 ,
,  ,
,
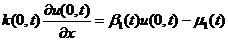 ,
, 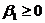 ,
,
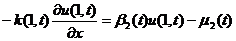 ,
, 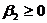
Ранее было получено разностное условие третьего рода для стационарного
уравнения 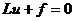 . Формально переход от стационарного к нестационарному
уравнению можно рассматривать как замену
. Формально переход от стационарного к нестационарному
уравнению можно рассматривать как замену 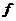 на
на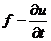 . Применяя этот прием при выводе
разностных условий, аппроксимирующих краевые условия третьего рода, приходим к
следующей разностной краевой задаче:
. Применяя этот прием при выводе
разностных условий, аппроксимирующих краевые условия третьего рода, приходим к
следующей разностной краевой задаче:
 ,
,  ,
, 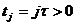 ,
,
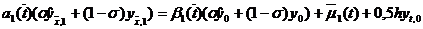 ,
,
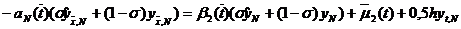 .
.
Здесь
 ,
,  ,
,  .
.
Приведенная выше схема имеет точность 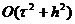 при
при  ,
,  при
при 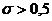 . Запишем эту разностную схему в
виде, пригодном для применения метода прогонки:
. Запишем эту разностную схему в
виде, пригодном для применения метода прогонки:
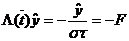 ,
,  ,
,  ,
,
Где
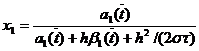 ,
, 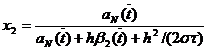 ,
,
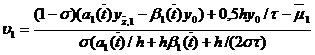 ,
,
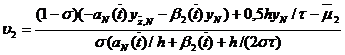 ,
,
 .
.
Прогонка устойчива, если  , так как
, так как 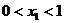 ,
,  .
.
2.4 Схема для
уравнения с переменными коэффициентами
Напишем схему переменных направлений для уравнения теплопроводности с
переменными коэффициентами
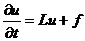 ,
, 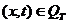 ,
,  ,
,  ,
,
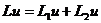 ,
, 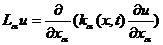 ,
, 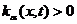 .
.
Напомним, что в случае одномерного уравнения теплопроводности неявная
схема на каждом слое приводит к разностной краевой задаче вида
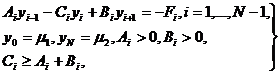 ,
,
которая решается стандартным методом прогонки с затратой числа 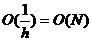 действий, пропорционального числу
действий, пропорционального числу  узлов сетки
узлов сетки
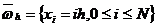 .
.
Обратимся к двумерной задаче в прямоугольнике. Сетку 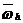 можно представить, как совокупность
узлов, расположенных на строках
можно представить, как совокупность
узлов, расположенных на строках 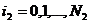 или как совокупность узлов, расположенных на столбцах
или как совокупность узлов, расположенных на столбцах 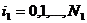 . Всего имеется
. Всего имеется 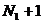 столбцов и
столбцов и 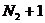 строк. Число узлов в каждой строке
равно
строк. Число узлов в каждой строке
равно 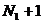 , а в каждом столбце имеется
, а в каждом столбце имеется 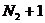 узлов.
узлов.
Если на каждой строке (или столбце) решать задачу вида методом прогонки
при фиксированном 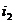 (или
(или 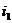 ), то для отыскания решения на всех строках (или столбцах),
т. е. во всех узлах сетки, понадобится число
), то для отыскания решения на всех строках (или столбцах),
т. е. во всех узлах сетки, понадобится число 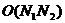 арифметических действий,
пропорциональное числу узлов двумерной сетки. Основная идея большинства
экономичных методов состоит в сведении перехода со слоя на слой к
последовательному решению одномерных задач вида (67) вдоль строк и вдоль
столбцов.
арифметических действий,
пропорциональное числу узлов двумерной сетки. Основная идея большинства
экономичных методов состоит в сведении перехода со слоя на слой к
последовательному решению одномерных задач вида (67) вдоль строк и вдоль
столбцов.
Весьма четко эту алгоритмическую идею выражает неявная схема переменных
направлений (продольно-поперечная схема), предложенная Писменом, Рекфордом и
Дугласом в 1955 году. Наряду с основными значениями искомой сеточной функции 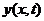 , т. е. с
, т. е. с 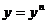 , и
, и 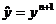 вводится промежуточное значение
вводится промежуточное значение 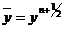 , которое можно формально
рассматривать как значение
, которое можно формально
рассматривать как значение  при
при 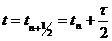 . Переход от слоя
. Переход от слоя  к слою
к слою 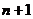 совершается в два этапа с шагами
совершается в два этапа с шагами 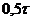 :
:
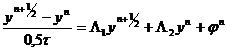 ,
,
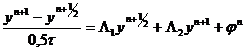 .
.
Эти уравнения пишутся во всех внутренних узлах 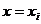 сетки
сетки 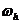 и для всех
и для всех 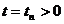 . Первая схема неявна по направлению
. Первая схема неявна по направлению 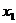 и явна по
и явна по 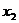 , вторая схема явна по
, вторая схема явна по 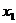 и неявна по
и неявна по 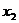 . К уравнениям надо добавить
начальные условия
. К уравнениям надо добавить
начальные условия
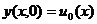 ,
, 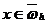
и разностные краевые условия, например, в виде
 при
при 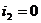 и
и 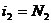 ,
,
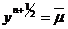 при
при 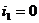 ,
,  ,
,
где
 .
.
В формулах меняется лишь формула для 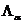 :
:
 ,
, 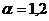 ,
, 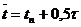 ,
,
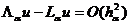 .
.
Для исследования устойчивости схемы проведем исключение промежуточного
значения 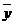 . Вычитая из уравнение, находим
. Вычитая из уравнение, находим
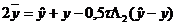 ,
, 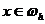 .
.
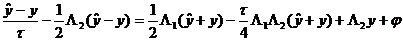 .
.
Учитывая, что 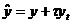 , преобразуем к каноническому виду:
, преобразуем к каноническому виду:
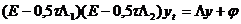 .
.
Из предыдущих рассуждений ясно, что формула должна выполняться и при 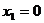 ,
, 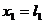 (иначе значение
(иначе значение 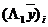 не определено при
не определено при 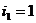 и
и  ). Так как
). Так как 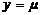 ,
, 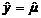 при
при 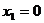 ,
, 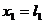 , то из формулы следует
, то из формулы следует
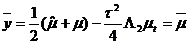
при 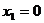 ,
, 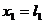 , что совпадает с краевым условием. Тем самым доказано, что
решение задачи удовлетворяет уравнению при дополнительных условиях:
, что совпадает с краевым условием. Тем самым доказано, что
решение задачи удовлетворяет уравнению при дополнительных условиях:
 ,
, 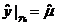 ,
, 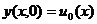 .
.
С другой стороны, решение задачи является также решением задачи (68) -
(73). В самом деле, введем 
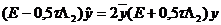
и подставим это выражение в уравнение. После несложных преобразований
получим уравнение. Тем самым доказана эквивалентность задач. Она имеет место
при согласованном задании граничных значений  . Исследование схемы можно заменить
исследованием полученной схемы «в целых шагах».
. Исследование схемы можно заменить
исследованием полученной схемы «в целых шагах».
Все рассуждения, показывающие эквивалентность схем, в данном случае
сохраняют силу. Схема имеет на решении 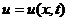 аппроксимацию
аппроксимацию  , если, кроме условий
, если, кроме условий
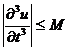 ,
, 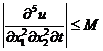 ,
, 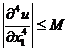 ,
,  ,
,
выполнены очевидные требования гладкости  no
no  . Отличие от случая постоянных
коэффициентов обнаруживается при изучении устойчивости схемы. Операторы
. Отличие от случая постоянных
коэффициентов обнаруживается при изучении устойчивости схемы. Операторы  ,
,  положительные и самосопряженные, но
не перестановочные. Поэтому положительность
положительные и самосопряженные, но
не перестановочные. Поэтому положительность 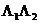 ниоткуда не следует. Вместо
ниоткуда не следует. Вместо 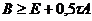 , удается доказать, что
, удается доказать, что
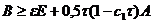
где  зависит от максимума производных
зависит от максимума производных  ,
,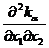 ,
, 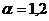 . Для решения задачи (76), (77) с
однородными краевыми условиями при достаточно малом
. Для решения задачи (76), (77) с
однородными краевыми условиями при достаточно малом 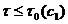 , где
, где 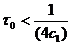 , справедлива оценка
, справедлива оценка
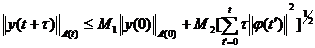 ,
,
 ,
,
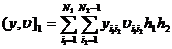 ,
, 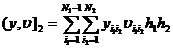
Из уравнения, очевидно, следует сходимость схемы со скоростью  . Заметим, что требование достаточной
малости шага по времени
. Заметим, что требование достаточной
малости шага по времени 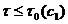 , при котором верна оценка, является весьма жестким, так как
в случае сильно меняющихся по
, при котором верна оценка, является весьма жестким, так как
в случае сильно меняющихся по 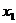 и
и 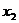 коэффициентов
коэффициентов  величина
величина  может оказаться столь малой, что
условие
может оказаться столь малой, что
условие 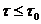 не выполняется при практически
допустимых значениях
не выполняется при практически
допустимых значениях  , обеспечивающих требуемую точность решения задачи.
, обеспечивающих требуемую точность решения задачи.
Оказывается, однако, что требование малости  связано с методом исследования
устойчивости. Ниже будет показано, что схема в случае не зависящих от t
коэффициентов
связано с методом исследования
устойчивости. Ниже будет показано, что схема в случае не зависящих от t
коэффициентов 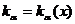 абсолютно устойчива (при любых
абсолютно устойчива (при любых  > 0 и
> 0 и 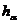 > 0) в другой норме. Если
> 0) в другой норме. Если  зависят от t, то этим свойством
абсолютной устойчивости обладает несколько измененная схема:
зависят от t, то этим свойством
абсолютной устойчивости обладает несколько измененная схема:
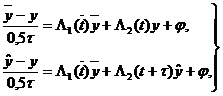
при однородных краевых условиях:
 ,
, 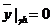 ,
, 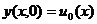 .
.
Рассмотрим операторно-разностный аналог задачи:
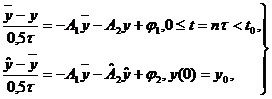 ,
,
где  ,
,  ,
, 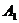 и
и 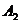 - линейные операторы, заданные на H. Пусть (,) и
- линейные операторы, заданные на H. Пусть (,) и  - скалярное произведение и норма в Н.
Будем предполагать, что
- скалярное произведение и норма в Н.
Будем предполагать, что 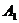 и
и 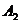 неотрицательные (несамосопряженные, вообще говоря)
операторы.
неотрицательные (несамосопряженные, вообще говоря)
операторы.
Лемма 1. Если 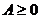 - линейный оператор в Н, то
- линейный оператор в Н, то
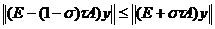 при
при 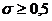 .
.
Действительно,
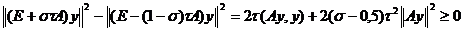
при 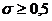 , откуда и следует.
, откуда и следует.
Перепишем уравнение в виде:
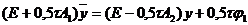 ,
,
 .
.
Воспользуемся неравенством треугольника и леммой 1:
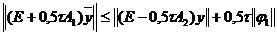 ,
,
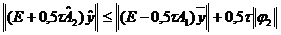 .
.
Отсюда находим
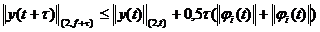 ,
,
где 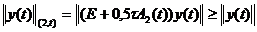 при
при 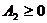 .
.
Суммирование по  дает
дает
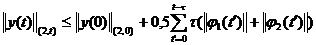 .
.
Нетрудно убедиться в том, что априорная оценка сохраняет силу, если норму
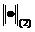 заменить нормой
заменить нормой 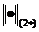 ,
,
где  .
.
Тем самым теорема доказана.
Теорема 3. Схема абсолютно устойчива (при любых 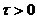 ,
, 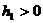 ,
, 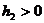 ) и для нее верна оценка
) и для нее верна оценка 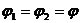 , в которой норма
, в которой норма 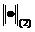 дается указанной формулой и
дается указанной формулой и  .
.
Однако априорная оценка сама по себе не позволяет доказать сходимость
схемы со скоростью  . Отметим, что оценка верна и в том случае, когда
. Отметим, что оценка верна и в том случае, когда 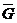 есть ступенчатая область (со
сторонами, параллельными осям координат).
есть ступенчатая область (со
сторонами, параллельными осям координат).
3. Разработка
программы
конвективный теплообмен
жидкость
3.1 Описание
программы. Исходные данные для расчета
В дипломной работе разработана программа «Расчет стационарно-двумерного
температурного поля при течении в трубе».
В
качестве примера численного решения задачи конвективного теплообмена при
заданном поле скоростей рассмотрим задачу расчета двумерного температурного
поля несжимаемой жидкости 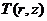 , протекающей в трубе радиусом
, протекающей в трубе радиусом  и длиной
и длиной 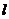 (рис.
9).
(рис.
9).
Температура
жидкости на входе в трубу постоянна по поперечному сечению и равна 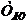 . На внутренней поверхности трубы задано либо
распределение по длине температуры стенки
. На внутренней поверхности трубы задано либо
распределение по длине температуры стенки 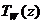 , либо
плотности теплового потока
, либо
плотности теплового потока 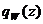 . Течение
считается гидродинамически стабилизированным, т. е. поперечная составляющая
скорости
. Течение
считается гидродинамически стабилизированным, т. е. поперечная составляющая
скорости 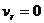 , а продольная
, а продольная 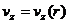 не
изменяется по длине трубы.
не
изменяется по длине трубы.
Предполагается,
что теплофизические свойства жидкости не зависят от температуры и что
диссипация энергии за счет вязкого трения и работа сил давления пренебрежимо
малы.
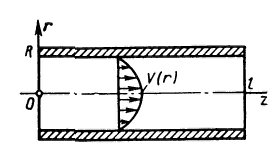
Рисунок 9 - Схема конвективного обмена
Исходными данными для программы являются:
Радиус трубы - 200 ед.
Длина трубы - 700 ед.
Объемная теплоемкость - 0.5
Объемная теплопроводность - 0.9
Температура жидкости в воде - 40° С
Средняя скорость - 3 ед./с
Число узлов сетки по оси R - 200
Число узлов сетки по оси Z -
700
Число сечений по оси Z, в которых печатается распределение температуры -
700
Все числовые поля исходных данных заданы в программе.
3.2 Описание
переменных программы
В таблицу 1 сведены переменные программы и их описание
Таблица 1 - Описание переменных
|
Имя переменной в программе
|
Описание переменной
|
Тип переменной в программе
|
|
DR
|
Радиус трубы
|
Real
|
|
DZ
|
Длина трубы
|
Real
|
|
CR
|
Объемная теплоемкость
|
Real
|
|
AL
|
Объемная теплопроводность
|
Real
|
|
U0
|
Температура жидкости в воде
|
Real
|
|
VC
|
Средняя скорость
|
Real
|
|
NR
|
Число узлов сетки по оси R
|
Integer
|
|
NZ
|
Число узлов сетки по оси Z
|
Integer
|
|
MV
|
Число сечений по оси Z, в
которых печатается распределение температуры
|
Integer
|
|
ZV(MV)
|
Координаты сечений вывода
результатов
|
Массив из элементов типа
Real
|
|
IPR
|
Признак граничного условия
на стенке (1 - температура, 2 - тепловой поток)
|
Integer
|
|
ALF(NZ)
|
Распределение коэффициентов
теплоотдачи по длине трубы
|
Массив из элементов типа
Real
|
3.3 Описание алгоритма программы

Рисунок 9 - Блок-схема алгоритма программы
3.4 Демонстрация работы программы
На рисунке 10 представлен результат работы программы для признака
граничного условия на стенке - температура.
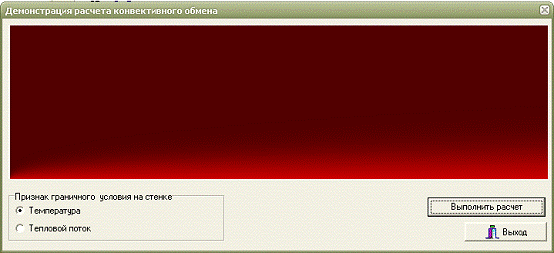
Рисунок 10 - Результат работы программы для признака граничного условия
на стенке - температура
На рисунке 11 представлен результат работы программы для признака
граничного условия на стенке - тепловой поток.
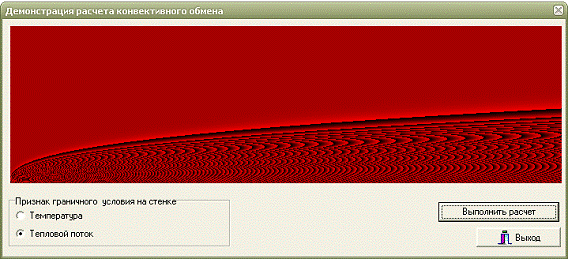
Рисунок 11 - Результат работы программы для признака граничного условия
на стенке - тепловой поток
Заключение
В связи с тем, что в процессах конвективного обмена важную роль играет
конвективный перенос, эти процессы должны в значительной мере зависеть от
характера движения жидкости, то есть от значения и направления скорости среды,
от распределения скоростей в потоке, от режима движения жидкости (ламинарное
течение либо турбулентное). При больших (сверхзвуковых) скоростях движения газа
на процессы конвективного обмена начинает влиять распределение давления в
потоке.
Наиболее интересным с точки зрения технических приложений случаем
конвективного обмена является конвективная теплоотдача, то есть процесс,
протекающий на границе раздела двух фаз (твердой и жидкой, твердой и
газообразной, жидкой и газообразной). При этом задача расчета состоит в
нахождении плотности теплового потока на границе раздела фаз, то есть величины,
показывающей, какое количество тепла получает или отдает единица поверхности
раздела фаз за единицу времени. Помимо указанных выше факторов, влияющих на
процесс конвективного обмена, плотность теплового потока зависит также от формы
и размеров тела, от степени шероховатости поверхности, а также от температур
поверхности и теплоотдающей или тепловоспринимающей среды.
Основной и наиболее трудной проблемой в расчётах процессов конвективной
теплоотдачи является нахождение коэффициента теплоотдачи. Современные методы
описания процесса конвективной теплоотдачи, основанные на теории пограничного
слоя, позволяют получить теоретические (точные или приближённые) решения для
некоторых достаточно простых ситуаций. В большинстве же встречающихся на
практике случаев коэффициент теплоотдачи определяют экспериментальным путём.
При этом как результаты теоретических решений, так и экспериментальные данные
обрабатываются методами подобия теории и представляются обычно в следующем
безразмерном виде.
В ходе дипломной работы решены следующие задачи:
изучена теория конвективного обмена в однородной среде;
изучена теория моделирования процессов конвективного обмена;
разработана программа на языке программирования Паскаль в среде
разработки Borland Delphi 7.0 для расчета стационарно-двумерного температурного
поля при течении в трубе.
Список
использованных источников
1 Самарский, А.А. Теория разностных схем: Москва: ”Наука”,
1989.- 616 с.
Дульнев, Г.Н. Применение ЭВМ для решения задач теплообмена :
Учебное пособие для теплофизических и теплоэнергетических специальных вузов /
Г.Н. Дульнев, В.Г. Парфенов, А.В. Сигалов. М.: Высш.шк., 1990. - 207с: ил. ISBN
5-06-000116-4
Самарский, А.А. Введение в теория разностных схем: Москва:
”Наука”, 1971.- 552 с.
Самарский, А.А. Устойчивость разностных схем / А.А.
Самарский, А.А. Гулин. - Москва: ”Наука”,1973.- 532 с.
Самарский, А.А. Лекции по теории разностных схем: Москва: ВЦ
АН СССР,1969.- 436 с.
Тихонов, А.Н., Самарский А.А. Уравнения математической физики
/ А.Н. Тихонов, А.А. Самарский. - Москва: ”Наука”,197.- 624 с.
Годунов, С.К., Рябенький В.С. Разностные схемы (введение в
теорию) / С.К. Годунов, , В.С. Рябенький. - Москва: ”Наука”,1977.- 586 с.
Болгарский А.В., Мухачев Г.А., Щукин В.К. Термодинамика и
теплопередача. Учебник для вузов. М. Высшая школа, 1975.
Михайлова М.М. Сборник задач и примеров расчета по
теплопередаче. Москва, 1963.
Саркисов Г.И. Справочник к курсовым и расчетно-графическим
работам по курсу "Теплопередача". Учебное пособие. Москва, 1981.
Варгафтик Н.Б. Справочник по теплофизическим свойствам газов
и жидкостей. Москва, Наука, 1972.
Эккерт Э.Р., Дрейк Р.М., Теория тепло- и массообмена, пер. с
англ., М. - Л., 1961
Гухман А. А., Применение теории подобия к исследованию
процессов тепло- и массообмена (Процессы переноса в движущейся среде), М., 1967
Исаченко В. П., Осипова В. А., Сукомел А. С., Теплопередача,
М., 1969.
Бахвалов Н. С., Численные методы / Н. С. Бахвалов, Н. П.
Жидков, Г. Н. Кобельков. - М.: БИНОМ., 2003. - 632 с.
Вержбицкий В. М., Численные методы. Математический анализ и
обыкновенные дифференциальные уравнения / В.М. Вержбицкий. - М.: Высш.шк.,
2001. - 383 с.
Турчак Л.И., Основы численных методов. / Л.И. Турчак - М.:
Наука, 1987.
Приложение
Unit1;, Messages, SysUtils, Variants, Classes, Graphics,
Controls, Forms,, ExtCtrls, StdCtrls, Buttons;= class(TForm): TImage;: TButton;:
TRadioGroup;: TBitBtn;Button1Click(Sender: TObject);
{ Private declarations }
{ Public declarations };: TForm1;
{$R *.dfm}MAX=1000;=Array[1..MAX] of Real;SYSTRD (Var
X,A,B,C,F:Mas; N:Integer);,K,I:Integer;,S:Real;:Mas;:Integer;{ошибка}:=0;N<3 Then:=1;;;:=N-1;:=B[1];[1]:=-A[1]/T;[1]:=-F[1]/T;i:=2
to M
do:=I-1;:=C[i];:=B[i]+T*X[k];[i]:=-A[i]/S;[i]:=-(F[i]+T*G[k])/S;;:=C[N];[N]:=-(T*G[M]+F[N])/(B[N]+T*X[M]);k:=1
to M do:=N-K;[i]:=X[i]*X[i+1]+G[i];
End;;
{ Зависимости от координат скорости }
Function V(R:Real):Real;:=2.0*(1.0-R*R);;
{ Зависимости от координат температуры стенки }
Function TW(Z:Real):Real;
Begin:=100;;
{ Зависимости от координат плотности теплового потока }
Function QW(Z:Real):Real;:=500;;TForm1.Button1Click(Sender:
TObject);,DZ,CR,AL,U0,VC:Real;,NZ,MV:Integer;,N:Integer;,ZV:Mas;:Integer;:Real;:Real;,R:Real;,B,C:Mas;,M:Integer;:Mas;:Real;:Real;:Mas;:Integer;
{
DR,DZ - радиус и длина трубы,AL - объемная теплоемкость и
теплопроводность- температура жидкости в воде- среняя скорость,NZ - число узлов
сетки- число сечений по оси Z, в которых печатается распределение
температуры(MV) - координаты сечений вывода результатов- признак граничного
условия на стенке (1-температура, 2-тепловой поток)(NZ)-распределение
коэффициентов теплоотдачи по длине трубы
}:=200;:=700.0;:=0.5;:=0.9;:=80.0;:=3.0;:=Round(DR);:=Round(DZ);:=Round(DZ);:=RG.ItemIndex+1;
{ Координаты сечений вывода результатов }N:=1 to MV do ZV[N]:=N*DZ/MV;
{ Задание температуры во входном сечении }
For N:=1 to NR do U[N]:=U0;
{ Вычисление постоянных коэффициентов для прогонок }
NR1:=NR-1;:=DR/NR1;:=DZ/(NZ-1);:=CR*VC*HR*HR/AL/HZ;
{ Точка на оси трубы }[1]:=1.0;[1]:=-1.0-F/4*V(0.0);[1]:=0.0;
{ Внутренние точки }
For N:=2 to NR1
do:=(N-1)*HR;[N]:=(R+HR/2)/R;[N]:=(R-HR/2)/R;[N]:=-A[N]-C[N]-F*V(R/DR);
End;
{ Точка на стенке }[NR]:=0;
B[NR]:=-1;[NR]:=0;(IPR=2) Then C[NR]:=1.0;
L:=1;
{ Цикл по сечеиням вдоль оси трубы }
For M:=2 to NZ do
{ Вычисление коэффициентов D[N] для прогонки }
{ Точка на оси трубы }[1]:=F*V(0)/4*U[1];
{ Внутренни точки }N:=2 to NR1 do:=(N-1)*HR;[N]:=F*V(R/DR)*U[N];
End;
{ Точка на стенке }:=(M-1)*HZ;
if IPR=1 Then D[NR]:=TW(Z/DZ);IPR=2 Then
D[NR]:=QW(Z/DZ)*HR/AL;
{ Решение системы уравнений }(U,A,B,C,D,NR);
{ Расчет локального коэффициент теплоотдачи }
{ Средняя температура в сечении (TC) }
TC:=0;N:=2 to NR
do:=(N-1)*HR;:=TC+U[N]*R*V(R/DR)+U[N-1]*(R-HR)*V((R-HR)/DR);;:=TC*HR/DR/DR;
{ Коэффициент теплоотдачи }[M]:=AL*(U[NR]-U[NR1])/HR/(U[NR]-TC);
{Вывод температур на печать}(Z>=ZV[L]) Then
Begin:=L+1;
// Write(Z:10:3,TC:10:3);
// Writeln;
// For N:=1 to NR do Write(U[N]:10:3);N:=1 to NR do
pic.canvas.Pixels[M,N]:=round(U[N]*2) mod 255;;;
// Writeln;
// Writeln;
// Writeln;
{ Печать локальных коэффициентов теплоотдачи }M:=2 to NZ do
Begin:=ALF[M]*2*DR/AL;:=(M-1)*HZ;
// Write(Z:10:3,ALF[M]:10:3,F:10:3);
End;;.