Теорія механізмів і машин
Міністерство освіти i науки,
молоді та спорту України
Національний університет
кораблебудування
імені адмірала Макарова
Ю.М. КІПРЄЄВ
КОНСПЕКТ ЛЕКЦІЙ
З ТЕОРІЇ МЕХАНІЗМІВ І МАШИН
Затверджено на засіданні кафедри
механіки і конструювання машин
Протокол №1 від30 серпня 2010 р.
Миколаїв, 2010
ББК 34.42
К-42
УДК 531.8
Кіпрєєв Ю.М. Конспект лекцій з теорії механізмів та машин:
Навчальний посібник. - Миколаїв: НУК, 2010. - 69c.
Викладено питання проектування схем і кінематичного
дослідження плоских важільних механізмів, планетарних та диференціальних
механізмів, динамічного дослідження машинних агрегатів. Посібник призначено для
студентів машинобудівних, електротехнічних та інших спеціальностей, які
вивчають курси прикладної механіки, технічної механіки та теорії механізмів і
машин.
ВВЕДЕННЯ
З історії розвитку механіки.
Механіка є одною з найдавніших наук, виникнення якої було
обумовлено практичними проблемами суспільства.
Розвиток механіки тісно зв’язаний із розвитком землеробства,
ростом міст, будовою крупних споруд, розвиток ремесел та мореплавства. Відомі
випадки застосування простих механічних пристроїв. Наприклад, під час побудови
єгипетських пірамід використовувались важелі, блоки, нахилені поверхні тощо.
Але в ті часи ще не існувало розподілу науки за галузями
знань і тому механіка була складовою частиною єдиної науки о природі і
суспільстві. Виділення окремих наук із загального природознавства розпочалась
після Аристотеля (384 - 322 рр. до н.е. ).
Засновником механіки як науки був знаменитий вчений древності
Архімед (287 - 212 рр. до н.е. ) він дав точне розв’язання задачі про рівновагу
сил, що прикладені до важеля, сформулював закон про гідростатичний тиск рідини
на тіло, що в неї заглиблено (занурено).
Швидкий та успішний розвиток механіки як науки розпочався
лише з епохи Відродження, коли було створено умови для розвитку науки і
техніки, в суспільстві з’явилась неухильна потреба в найскорішому розв’язанні
складних проблем його існування.
З епохою Відродження починається наступний етап розвитку
механіки, який потребує досліджень законів руху тіл. У ці часи створюються
основи динаміки - науки про загальні закони руху матеріальних тіл.
Яскравим представником епохи Відродження був геніальний
італійський художник, фізик і інженер Леонардо да Вінчі (1451 - 1519).
Інший
геніальний італійський вченій Галілео Галілей (1564 - 1642) створив основи
динаміки, виконав перші дослідження міцності консольних стрижнів. Англієць Ісаак Ньютон (1643 - 1727 ) у
систематичному вигляді виклав основні закони так званої класичної механіки. У
ті ж самі часи інший знаменитий англієць Роберт Гук (1635 - 1703 ), який був не
тільки талановитим винахідником (відомі його конструкції повітряного насосу,
пружинного приводу годинників, шарніра Гука, який використовується у конструкції
вала Кардана, тощо) і експериментатором, але не менш відомим вченим. Він
висловив добре відомий закон пружності, який на його честь названо законом
Гука. З цього закону розпочалася історія розвитку механіки пружного тіла, -
опору матеріалів. Ще до відкриття І. Ньютоном в 1681 році закону всесвітнього
тяжіння він провів серію експериментів у 1671 році, після проведення яких
висловив головну думку цього закону. Після довгих суперечок І. Ньютон був
змушений зробити примітку у книзі “Принципіа“: “Зворотний закон тяжіння має
місто в усіх небесних рухах, і він був незалежно відкритий моїми
співвітчизниками Реном, Гуком і Галеєм“. Але окремо відмітити Гука він не
хотів.
Розвиток науки у Російський імперії, до якого належала
частина України, розпочався за ініціативою Петра 1 у 1725 році після заснування
Російської Академії наук. Великий вплив на розвиток механіки оказали праці
видатного російського вченого М.В. Ломоносова (1711 - 1765), а також
швейцарського вченого Леонарда Ейлера (1707 - 1783), який біля 30 років
працював у Росії.
Велику роль у розвитку технічної механіки відіграють труди
вітчизняних вчених XIX і XX віків: М.В Остроградського (1801 - 1861), П.Л
Чебишова (1821 - 1891), Л.В. Асура (1878 - 1920), І.В. Мещерського (1859 -
1935), О.М. Крилова тощо. Видатний радянський вчений І.І. Артоболевський (1905
- 1977) є засновником теорії машин і механізмів. Праці видатного українського
вченого С.П. Тимошенко стали класичними у теоріях пружності, механіки твердого
тіла, опору матеріалів тощо.
Роль теорії механізмів та машин у процесі виробництва рухомих
конструкцій. У одноборстві з природою людина навчилася долати водяні перешкоди
і використовувати багатства рік, морів і океанів. Першим засобом пересування по
воді стала колода чи їх зв’язка (пліт), яки цілком підкорялися течії. Потім за
допомогою шматка дерева в руці людина навчилася прискорювати хід і керувати
цією колодою чи плотом. Пізніше, закріпивши рухливо на кормі і по бортах
подібні пристрої, подовживши їх рукоятки, люди створили найпростіші важільні
механізми - весла і поворотні рули. Їхня конструкція добре знайома по річкових
і морських прогулянках на гребних та моторних човнах, яхтах.
Прагнучи зробити судно більш морехіднім, міцним і
комфортабельним, люди перешли від створення простих човнів, виготовлених з
одного дерева, і плотів до збірних судів. Спочатку для оброблення дерев на
дошки застосовувалися клини, а для їхньої доставки до місць будівлі - ковзанки
і коловороти. Поступово ці найпростіші технологічні пристосування
видозмінювалися, праця ставала більш продуктивною. Але в цілому, у процесі
свого розвитку корпусна частина судна не перетерпіла принципових змін, у
корпусних роботах до середини XX століття переважала ручна праця. Дешевина
експлуатації водяних шляхів дозволяла водяному транспорту успішно конкурувати з
наземними видами транспорту. Але бурхливий розвиток техніки, що почався
наприкінці XIX - початку XX століття, призвів до росту швидкостей, виникненню
авіації.
Судна з традиційною формою корпуса і вертикальним способом
завантаження, досягши до п'ятидесятих років нашого століття порівняно великих
швидкостей ходу, втрачали 40-60 % часу свого рейса на
завантаження-розвантаження і ставали менш вигідними порівняно з іншими видами
транспорту. Це призвело до необхідності будівництва судів так названого
”відкритого” типу, що зажадали більш продуктивних вантажних механізмів і
пристроїв. Ці судна практично не мають просторів під палубами - ”кишень” через
велику площу розкриття трюмів. Дерев'яні люкові закриття були замінені
надійними, міцними, водонепроникними металевими з механічним приводом.
Для прискорення вантажних операцій за останні 45-55 років
були спроектовані і побудовані судна з укрупненням вантажних місць (пакетовози
і контейнеровози) і судна з горизонтальним способом завантаження і розвантаження.
На цих судах почали використовуватись різні спеціальні механізми, а при
проектуванні судів з горизонтальним способом розвантаження довелося навіть
відмовитися від традиційної форми корпуса і зробити його рознімним. На судні
такого типу (рис.1) вантажі можуть переміщуватися з однієї палуби на іншу по
пандусах 1, що опускаються, чи за допомогою гідравлічних підйомників 4. Для
розвантаження і завантаження частина корми чи носа (апарель) 2 піднімається, а
на пірс опускається спеціальний настил 3, по якому відбувається перевезення
вантажів. Такі конструктивні зміни корпуса і набору судна зажадали розробки
складних вантажопідйомних механізмів і пристроїв.

Рис.1.
Дослідження Світового океану зажадало створення спеціальних
глибоководних апаратів. Ці апарати обладнані найрізноманітнішими механізмами і
пристроями, виготовленими на рівні сучасних вимог. За допомогою таких апаратів
можна доставити зразки ґрунтів і вивчати життя глибоководних мешканців на
недосяжних раніше глибинах. Крім того, з їхньою допомогою удалося знайти і
підняти з дна Середземного моря водневу бомбу біля берегів Іспанії, загублену
американським льотчиком; знайти залишки затонулого атомного підвідного човна
США “Трешер” тощо. У 2001 році за допомогою сучасної техніки було проведено
унікальну операцію по підйому російського атомного човна ”Курск”, який загинув
у Баренцовому морі внаслідок вибуху на його борті.
Енергетична криза і порушення екологічної рівноваги призвели
до необхідності пошуку “чистих” видів енергії. Вже зараз відроджуються
вітрильні судна, створюються типи судів і пристроїв, що використовують енергію
вітру, підводних течій і сонця. Їхня експлуатація зажадає розробки нових
механізмів і пристроїв, що полегшують працю людини і дозволяють цим судам
успішно конкурувати зі звичайними видами транспорту.
Прогрес у науці і техніці не обійшов стороною і технологію
суднобудування. Велика частка ручної праці в корпусному і зварювальному
виробництві раніше гальмувала темпи будівлі судів. На сучасних суднобудівних
підприємствах вже рідко можна бачити робітників, вручну за допомогою
традиційного молота виконуючих виправлення сталевих листів, припасування частин
корпуса. У корпусно обробних цехах їх заміняють керованими цифровою
обчислювальною машиною правлячими вальцями, гільйотинами, гідравлічними пресами
і нагрівальними печами. На величезних рихтованих плитах автоматично формуються
викрутки для гребних валів, штевні й інші профільні деталі.
У зварювальному виробництві стали усе ширше застосовуватися автомати
і напівавтомати, а використання нових матеріалів призвело до корінної зміни
технології зварювального виробництва. У деяких випадках зварювання виробляється
за допомогою спеціальних маніпуляторів.
Короткий огляд досягнень сучасного суднобудування дозволяє
зробити висновок про необхідність ознайомлення майбутніх
інженерів-кораблебудівників з основами теорії машин і механізмів. Надалі ці
знання допоможуть у розв’язку складних комплексних проблем створення нових
досконалих судів, пристроїв і апаратів.
Проектування, виготовлення та правильна експлуатація машинних
агрегатів, які являють собою комплекси взаємно зв’язаних машин і механізмів,
передбачають знання фізичних процесів, що протікають у них, принципів
конструювання й методів розрахунку машин, механізмів та їх деталей. З цією
метою вивчається прикладна механіка, що містить питання дослідження руху і
напруженого стану реальних технічних об’єктів - механізмів, машин,
робототехнічних систем тощо.
Знання та розуміння задач прикладної механіки вимагаються від
усіх спеціалістів, які беруть участь у розробці будь-якої нової машини,
незалежно від їх фахової належності. І, навпаки, незнання особливостей роботи
створюваних об’єктів або нехтування ними призводить проектувальників до значних
помилок і прорахунків, що може мати непоправні наслідки при подальшій
експлуатації машинних агрегатів.
Особливості взаємодії складових частин машинних агрегатів
повинні враховуватися вже на первісній стадії проектувального розрахунку. Ці
особливості можна умовно поділити на такі етапи:
1. Вибір кінематичних схем машин і механізмів, які дозволяють
здійснити потрібний рух веденої ланки при заданому законі руху ведучої.
. Синтез кінематичних схем, тобто визначення основних
розмірів ланок і координат нерухомих шарнірів і напрямних.
. Кінематичне дослідження спроектованих схем механізмів і
визначення всіх характеристик їх руху.
. Вибір фізичних характеристик ланок, зокрема, форми й
розміру перерізу ланки, марки матеріалу, визначення маси, моменту інерції та
координат центра ваги ланки.
. Силове дослідження кінематичних схем механізмів, за
допомогою якого обчислюються навантаження, що діють на ланки. З умов міцності
уточнюються розміри і конструктивні відтворення ланок і кінематичних пар.
Згідно з уточненими характеристиками ланок повторюється їхній силовий
розрахунок, а також розрахунок на міцність. В результаті попереднього
проектування складаються конструктивні схеми машин і механізмів, що мають
потрібну міцність, яка відповідає заданим умовам робочих процесів.
. Завершальним етапом проектувального розрахунку є динамічне
дослідження машинного агрегату, протягом якого уточнюється закон руху ведучої
ланки, остаточно вибирається тип електроприводу і забезпечуються умови роботи
відповідно до потрібного закону руху.
Після виконання всіх наведених розрахунків і опрацювань
провадиться конструювання, тобто подальша детальна розробка всіх вузлів у
машині, яка дає змогу втілити принципову схему в реальну конструкцію.
1. Структурна класифікація механізмів
1.1 Загальні поняття і визначення
Наукою, що вивчає види кінематичних схем, кінематику і
динаміку машинних агрегатів у зв’язку з їхнім аналізом і синтезом, є теорія
механізмів і машин (ТММ).
Дослідження або проектування будь-якої конструкції, що
рухається, розпочинається із складання її кінематичної схеми. Така рухома
конструкція у механіці зветься механізмом.
Головним об’єктом дослідження у ТММ є кінематична схема -
умовне зображення механізму, на якому у спрощеному вигляді вказані елементи, що
впливають на його кінематичні характеристики. Структурна схема рухомої
конструкції, на відміну від кінематичної схеми, виконується довільно без
дотримання масштабу. Таке зображення дає уявлення тільки за склад конструкції.
Пристрої, що ведуть до збільшення продуктивності праці,
частково і цілком заміняють людину в її трудових і фізіологічних функціях,
називаються машинами (наприклад, ДВЗ - двигун внутрішнього згоряння, ГТД -
газотурбінний двигун, парові турбіни, електродвигуни, генератор струму,
компресор, помпа, тощо).
Механізм - це система штучно створених тіл (твердих, рідких і
газоподібних), яку призначено для перетворення руху одних тіл у потрібний рух
інших тіл (лебідка, вантажопідйомний кран, механізми гідравлічних приводів,
обробляючих верстатів, шпилі, брашпилі тощо). Головну увагу у ТММ приділяють
механізмам, які складаються з твердих тіл.
Таким чином, роль механізму, на відміну від машини, зводиться
лише до передачі руху і потоку енергії. У той же час механізм має ту ж
структуру, що і машина, і в цьому відношенні між ними немає ніякого розходження.
Механізм можна вважати машиною, якщо він в умовах руху переборює зовнішні
опори, зв’язані безпосередньо з процесом виробництва чи транспорту. При роботі
вхолосту машину можна розглядати як механізм у чистому вигляді.
Машина і механізми об’єднуються у машинні агрегати. Машинний
агрегат - це комплекс взаємопов’язаних машин, механізмів, пристроїв, виконавчих
органів тощо, призначений для виконання певних функцій.
Структурною одиницею будь-якої рухомої конструкції є ланка.
Ланкою називають одну або групу деталей, жорстко з’єднаних між собою. Ланки
бувають рухомими (поршень, шестірня, вал тощо) і нерухомими (станина,
фундамент, циліндрова втулка тощо). Нерухомі ланки складаються з ряду жорстко
зв’язаних тіл і називаються стійками. Будь-який механізм має тільки одну
нерухому і декілька рухомих ланок.
Вхідною вважають ланку, закон руху якої заданий і
перетворюється механізмом у потрібний закон інших ланок. Вона може співпадати
або не співпадати з провідною ланкою, якою зветься ланка, що за допомогою
рушійних навантажень надає рух усьому механізму. Веденою ланкою називають
ланку, що здійснює рух, для виконання якого призначений механізм. Решту ланок
механізму називають проміжними.
Ланки бувають прості і складні. Якщо ланка входить не більш,
ніж у два рухомих з’єднання з іншими ланками (рис. 1.1,а, б), то вона є
простою, в інших випадках (рис. 1.1, в) ланка зветься складною.

Рис. 1.1. Прості (а, б) та складні (в) ланки механізмів
На схемах ланки позначають арабськими цифрами, кінематичні
пари - великими латинськими літерами. Нерухому ланку, яка входить до складу
механізму, називають стояком або стійкою. На кінематичних схемах нерухомі ланки
позначають штрихуванням. Рухому ланку, яка здійснює повний оберт, називають
корбою. Ланки, які здійснюють коливний, плоскопаралельний і
зворотно-поступальний рухи, відповідно називають коромислом, гонком і
поковзнем. Рухому ланку, яка є напрямною для поковзня, називають кулісою.
Поковзень, що рухається по кулісі, називають каменем куліси.
.2 Класифікація кінематичних пар
Кожен механізм складається з ланок. З’єднання двох дотичних
ланок, яке дозволяє їхній відносний рух, називається кінематичною парою
(рис.1.2).
Між двома ланками може існувати тільки одне рухоме з’єднання
або кінематична пара, незважаючи на те, що ці ланки можуть мати контакт в
декількох місцях. Слід також відмітити, що в разі стикання в одному місці
декількох ланок, вони створюють поміж собою загальну кількість пар, що на
одиницю менша кількості ланок, яки збігаються у цьому місці.
Поверхні, лінії, або точки, якими одна ланка торкається
іншої, називають елементами кінематичних пар.
Кінематичні пари класифікують за чотирма ознаками.
1. За числом зв’язків, тобто обмежень, які кінематична пара
накладає на відносний рух ланок. За цією ознакою пари поділяються на п’ять
класів. Клас кінематичної пари визначають за числом зв’язків  , де
, де  -
кількість ступенів вільності у відносному русі ланок, які утворюють пару.
-
кількість ступенів вільності у відносному русі ланок, які утворюють пару.
. За видом елементів контакту ланок у парі вони розділяються на
вищі і нижчі. До вищих належать пари, у яких ланки дотикаються по поверхні
(рис.1.2, б, в, ж), нижчими - ланки, у яких елементами контакту є точки або
лінії (рис.1.2, г, д, є, з, і).

Рис. 1.2. Приклади різноманітних видів кінематичних пар:
а - незалежне або вільне тверде тіло (куля) з шістьма
ступенями вільності; б - кінематична пара І класу «куля - площина»; в -
кінематична пара ІІ класу «циліндр - площина»; г - кінематична пара ІІІ класу
«плоске тіло - площина»; д - кінематична пара ІІІ класу, сферичний шарнір; є -
кінематична пара ІV класу,
контакт ланок по циліндричної поверхні; ж - кінематична пара ІV класу у контакті зубчастих коліс; з
- поступальна кінематична пара V класу; і - обертальна кінематична пара V класу
3. За характером відносного руху ланок пари можуть бути
плоскими (рис.1.2, г, ж, з, і) і просторовими (рис.1.2, б, в, д, є).
. За умовами підтримки контакту ланок у парі вони
розділяються на відкриті (рис.1.2, б, в, г) і замкнені (рис.1.2, д, є, ж, з,
і). У відкритих ланках потрібне силове замикання контакту, в замкнених цей
контакт забезпечується геометричне замикання, тобто за допомогою особливостей
форми контактуючих поверхонь.
Системи ланок, які з’єднані між собою кінематичними парами,
називають кінематичними ланцюгами.
.3 Ступінь рухомості механізму
Механізмом називають кінематичний ланцюг з нерухомою ланкою,
у якому при заданому русі одної чи декількох ланок щодо будь-якого з них всі
інші ланки роблять однозначно обумовлені рухи.
Кількість узагальнених координат, що цілком характеризують
положення, а отже, і рух тіла чи механізму, прийнято називати числом ступенів
вільності (ступенем рухомості) тіла чи механізму.
Характер руху механізму визначається розмірами ланок,
послідовністю їх з`єднання, конструкцією кінематичних пар. Кількість ступенів
свободи або ступінь рухомості механізму визначається за структурною формулою
Сомова-Малишева
 ,
(1.1)
,
(1.1)
де  - кількість рухомих ланок механізму;
- кількість рухомих ланок механізму; 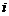 - номер класу кінематичної пари;
- номер класу кінематичної пари;  - кількість кінематичних пар, належать до класу за
номером
- кількість кінематичних пар, належать до класу за
номером 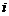 .
.
Більша частина кінематичних схем механізмів має деяку кількість  загальних, або співпадаючих умов зв’язку, тому
підрахування ступеню рухомості повинно виконуватися за умовою їх віднімання з
усіх коефіцієнтів наведеної залежності. Загальну структурну формулу з
урахуванням загальних зв’язків вивів у 1943 році В.В. Добровольский
загальних, або співпадаючих умов зв’язку, тому
підрахування ступеню рухомості повинно виконуватися за умовою їх віднімання з
усіх коефіцієнтів наведеної залежності. Загальну структурну формулу з
урахуванням загальних зв’язків вивів у 1943 році В.В. Добровольский
 .
(1.2)
.
(1.2)
Для плоских механізмів кількість співпадаючих умов зв’язку дорівнює
трьом ( ), тому ступінь рухомості визначається за формулою
П.Л.Чебишова
), тому ступінь рухомості визначається за формулою
П.Л.Чебишова
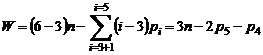 .
(1.3)
.
(1.3)
де  - кількість рухомих ланок;
- кількість рухомих ланок;  і
і  -
кількість кінематичних пар, відповідно IV і V класів.
-
кількість кінематичних пар, відповідно IV і V класів.
1.4 Види механізмів
Ступінь рухомості відповідає кількості узагальнених
(незалежних) координат, які повністю характеризують будь-яке положення
механізму. Найбільш розповсюджені в техніці механізми мають один ступінь
рухомості. Найпростішим з механізмів є дволанковий (рис.1.3). Дволанковий
механізм (рис.1.3,а) з обертальною парою (шарніром) застосовується як головний
механізм у роторних машинах і приладах: турбінах усіх видів, електродвигунах і
електрогенераторах, відцентрових насосах і вентиляторах, турбокомпресорах,
гіроскопах тощо.
Дволанковий механізм із поступальною парою (рис.1.3,б)
зустрічається в парових насосах, дизель-компресорах, у пристроях поступального
переміщення супортів.

а б
Рис. 1.3. Дволанкові механізми із обертальною (а) та
поступальною (б) кінематичними парами
У більшості механізмів ланки роблять обертальний,
зворотно-обертальний або зворотно-поступальний рух. Якщо всі точки ланок
механізму рухаються у паралельних плоскостях, то механізм буде плоским, у всіх
інших випадках - просторовим. Усі плоскі механізми можна розділити на механізми
з нижчими і з вищими парами. У плоских механізмах, яки називаються важільними
механізмами, ланки з’єднуються тільки нижчими парами, а в механізмах з вищими
парами існує хоча б одна вища пара.
Триланкові механізми представлені групами клинових (рис.1.4)
і гвинтових (рис.1.5) механізмів, що застосовуються в різного роду пресах,
затисках, пристроях подачі деталей тощо.

Рис. 1.4. Клиновий механізм

Рис. 1.5. Гвинтовий механізм
Чотириланкові важільні механізми показані на рис.1.6 і 1.7.
Шарнірні чотириланковики широко застосовують, коли потрібно
здійснити безперервне обертання або зворотно-обертальний рух відомої ланки. Ці
механізми зустрічаються в пресах і кувальних машинах, поперечно-стругальних і
довбальних верстатах, механізмах люкових закриттів, гідравлічних підйомниках
апарелів і пандусів, приладах і ін.
Шарнірні чотириланкові механізми (рис. 1.6) утворюються на базі
кінематичного ланцюга з чотирьох ланок (рис. 1.6,а), послідовно з’єднаних
обертальними парами п’ятого класу. Ці механізми, у залежності від дотримання
умови прокручування ланок, поділені на три групи. Умова прокручування, яка має
назву правила Грасгофа, може бути записана у вигляді нерівності  , де
, де  -
довжина самої короткої ланки механізму;
-
довжина самої короткої ланки механізму;  -
довжина його самої довгої ланки. Розміри шарнірного чотирикутника (рис. 1.6,а):
-
довжина його самої довгої ланки. Розміри шарнірного чотирикутника (рис. 1.6,а):
 ;
;  ;
;
 ;
;  .
З урахуванням правила Грасгофа:
.
З урахуванням правила Грасгофа:
– механізм буде корбово-коромисловим, якщо його розміри
задовольняють умови прокручування ланок і за стійку прийнята ланка, розташована
поруч із самою короткою (рис. 1.6,б);
– механізм буде двокорбовим при недотриманні правила і
за стійку прийнята сама коротша ланка (рис. 1.6,в);
– механізм буде двохкоромисловим при недотриманні
правила або, коли сама коротша ланка є гонком (рис. 1.6,г).


А б


В г
Рис. 1.6. Найпростіші шарнірні чотириланковики
а - простий замкнений кінематичний ланцюг з чотирьох ланок
(шарнірний чотириланковик); б - корбово-коромисловий механізм; в - двокорбовий
механізм; г - двохкоромисловий механізм
В усіх важільних механізмах ланку, яка робить повний оборот
навколо нерухомої осі і утворює
обертальні пари з іншими ланками, називають корбою (рис. 1.6,б,в). Ланку 3, яка гойдається
навколо нерухомої осі, називають коромислом (рис. 1.6,б). Ланку 3, яка утворює
поступальну пару зі стойкою, називають поковзнем (рис. 1.7,а), а ланка 2, що утворює
кінематичні обертальні пари тільки з рухомими ланками - гонком (рис. 1.6, рис. 1.7,а). У кулісних механізмах (рис. 1.7,б) кулісою називають рухому ланку
3, що утворить поступальну пару з іншою рухомою ланкою - каменем 2 куліси.
Ланку 3, яка гойдається навколо нерухомої осі і утворює поступальну пару з
іншою ланкою 2, називають хитним поковзнем (рис. 1.7,в).

Рис. 1.7. Важільні механізми з поступальними парами
а - корбово-поковзневий механізм; б - кулісний механізм; в -
механізм з хитним поковзнем; г - кулісний механізм з каменем і поковзнем
Крім представлених чотириланкових важільних механізмів широко
застосовуються важільні механізми з більшим числом ланок.
Механізми з вищими парами (рис. 1.8), у залежності від призначення і
умов роботи, можна поділити на види, з яких найбільше поширення одержали
кулачкові механізми, фрикційні, зубчасті і черв’ячні передачі.
Кулачкові механізми (рис. 1.8,а) служать для відтворення
необхідного закону руху відомої ланки-штовхача. Вища пара у них утворюється
кулачком 1 і штовхачем 2. Форма вхідної ланки визначає закон руху вихідної
ланки - штовхача 2. Завдяки простоті
проектування і задля зменшення кількості ланок ці механізми одержали широке
поширення у всіляких машинах і приладах, де потрібно автоматично робити
погоджені рухи виконавчих ланок: у металообробних верстатах, теплових двигунах,
зварювальних маніпуляторах, у лічильно-розв’язувальних пристроях тощо.
Зубчасті (рис. 1.8,в), черв’ячні (рис. 1.8,г) та фрикційні
механізми (рис. 1.8,а) служать, головним чином, для передачі обертального руху
між двома якими-небудь осями зі зміною кутової швидкості веденого вала. У
зубчастих механізмах передача руху здійснюється за допомогою сил тиску у зоні
контакту між елементами рухомих ланок - зубів (рис. 1.8,в).

Рис. 1.8. Триланкові механізми з вищими парами
а - фрикційна передача; б - кулачковий механізм; в - зубчаста
передача; г - черв’ячна передача ; д - мальтійський механізм
Зубчасті і черв’ячні механізми застосовується в шпилях,
брашпилях, вантажних лебідках і піднімальних пристроях, кранах, механізмах
передач двигунів, верстатів тощо. Важче назвати машину або прилад, де б їх не
було. Фрикційні механізми здійснюють передачу обертального руху між ланками, що
входять у вищу пару, за допомогою тертя і часто використовуються в
безступінчастих передачах і варіаторах, що дозволяють плавно змінювати не
тільки кутову швидкість веденої ланки, але і напрямок обертання.
Крім перелічених механізмів, у суднових машинах і в різного
виду технологічному устаткуванні застосовуються передачі з гнучкими зв’язками -
штуртросові, пасові, ланцюгові, а також хвильові зубчасті редуктори, що містять
гнучкі зубчасті колеса, храпові механізми тощо. На рис. 1.8, д зображено модель
мальтійського механізму, який застосовується у верстатах і приладах.
.5 Надлишкові (пасивні) зв’язки і зайві ступені
вільності
Крім зв’язків, що активно впливають на характер руху
механізмів, у них можуть зустрітися умови зв'язку і ступені вільності, що не
роблять ніякого впливу на рух ланок механізму в цілому. Вилучення з механізмів
ланок і кінематичних пар, яким ці ступені вільності і умови зв’язку належать,
може бути зроблене без зміни загального характеру руху механізму в цілому. Такі
зв’язки називаються надлишковими або пасивними зв’язками, а ступені вільності
-зайвими ступенями вільності.
Іноді зайвий зв`язок свідомо впроваджують до складу механізму для
підвищення його жорсткості або для усунення невизначеності руху ланок в деяких
положеннях. Включення до складу механізму таких ланок повинно відбуватися з
виконанням додаткових умов. Наприклад, ланка 4 входить до складу шарнірного
механізму при виконанні додаткових умов  і
і
 (рис.1.9, б). Дійсно, ступінь рухомості механізму з
ланкою 4 згідно розрахунку
(рис.1.9, б). Дійсно, ступінь рухомості механізму з
ланкою 4 згідно розрахунку  дорівнює
нулю. Цей результат відповідає дійсності тільки відносно статично визначеної
ферми (рис.1.9,а), яку побудовано без утримання згаданих умов. Але при
виконанні додаткових умов
дорівнює
нулю. Цей результат відповідає дійсності тільки відносно статично визначеної
ферми (рис.1.9,а), яку побудовано без утримання згаданих умов. Але при
виконанні додаткових умов  і
і  ланка
4 тільки дублює зв’язки ланки 2 і не створює перешкод руху інших ланок, тобто
накладає на рух механізму умови зв’язку, що є надлишковими. З приводу цього при
теоретичному дослідження вона повинна бути відкинута. Тільки вилучивши з
механізму надлишкову ланку з двома кінематичними парами, отримаємо шарнірний
паралелограм (рис. 1.9,в) з одним ступенем вільності,
ланка
4 тільки дублює зв’язки ланки 2 і не створює перешкод руху інших ланок, тобто
накладає на рух механізму умови зв’язку, що є надлишковими. З приводу цього при
теоретичному дослідження вона повинна бути відкинута. Тільки вилучивши з
механізму надлишкову ланку з двома кінематичними парами, отримаємо шарнірний
паралелограм (рис. 1.9,в) з одним ступенем вільності,  .
.

Рис. 1.9. Багатоланкові шарнірні конструкції
а - статично визначена ферма; б - шарнірний паралелограм з
пасивними зв’язками; в - шарнірний паралелограм
Для плоского кулачкового механізму, (рис. 1.10,а), якщо вважати, що
ролик 3 жорстко зв'язаний зі коромислом 2, то ступінь рухомості  .
.
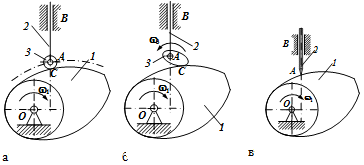
Рис. 1.10. Кулачковий механізм із зайвим ступенем рухомості (а), з двома
ступенями (б) і з теоретичним профілем
Але, якщо вважати ролик вільно обертовим, то формальний розрахунок
приведе до наступного результату  ,
тобто ролик вносить зайвий ступінь вільності і фактично при підрахунку ступеня
рухомості механізму цей обертальний рух прийматися в увагу не повинен. Цей
ступінь може бути реалізованим тільки у випадках, коли його форма не буде
ідеальною круглою, або вісь обертальної пари не співпадатиме з центром кола
(рис. 1.10,б).
,
тобто ролик вносить зайвий ступінь вільності і фактично при підрахунку ступеня
рухомості механізму цей обертальний рух прийматися в увагу не повинен. Цей
ступінь може бути реалізованим тільки у випадках, коли його форма не буде
ідеальною круглою, або вісь обертальної пари не співпадатиме з центром кола
(рис. 1.10,б).
При теоретичному дослідженні механізмів з зайвими ступенями вільності
робочий профіль замінюється на теоретичний (рис. 1.10,в), який співпадає з
траєкторією зворотного руху ролика 3 навколо нерухомого робочого профілю
(вказано штрихпунктиром на рис. 1.10,а).
1.6 Структурна класифікація плоских механізмів
Існують різні види класифікації, наприклад:
. Структурно-конструктивна, у якій механізми поєднуються за
ознаками їхнього конструктивного оформлення.
. За функціональним призначенням механізмів, наприклад,
механізми поперечно-стругальних верстатів, пресів і т.д.
. Структурна, в основу якої покладені особливості побудови
механізмів.
У теорії механізмів і машин замість конструктивних креслень
використовуються умовні зображення - кінематичні схеми, незалежні від функціональних
особливостей механізмів, тому структурна класифікація покладена в основу
утворення механізмів. Вона вперше була розроблена і запропонована російським
вченим Л.В. Ассуром у 1914 році для класифікації важільних механізмів.
За цією класифікацією найпростіший однорухомий механізм, що
складається з двох ланок - стояка і рухомої ланки, названо механізмом першого
класу (рис.1.3). У таких механізмах немає ведених ланок, тому немає передачі і
перетворення руху. Це механізми роторних приладів і машин (гіроскопів,
електродвигунів і генераторів, турбін, насосів, вентиляторів і ін.).
Механізм першого класу застосовується як початковий механізм для
створення будь-якого більш складного механізму. Кількість початкових механізмів
у складі кінематичного ланцюга дорівнює кількості ступенів вільності механізму.
Основний принцип утворення механізмів за Ассуром виходить з того, що ступінь
рухомості кінематичного ланцюга не змінюється від приєднання або видалення від
нього іншого ланцюга з нульовою рухомістю. Цей ланцюг названо структурною
групою, або групою Ассуру. Умова нульової рухомості групи ланок Ассуру
визначається структурною формулою П.Л. Чебишова 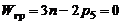 .
.
З умови забезпечення нульової рухомості  випливає,
що число ланок, що входять у групу, повинне бути парним, тому що
випливає,
що число ланок, що входять у групу, повинне бути парним, тому що  , інакше число пар V класу буде дробовим.
, інакше число пар V класу буде дробовим.
Структурні групи поділяються на класи, види і порядки. Від числа ланок,
що входять у групу і розподілу кінематичних пар у її складі, залежить її клас
(див. табл.1.2).
Таблиця 1.2. Склад структурних груп за класом
|
Клас групи
|
Число рухомих ланок
|
Розподіл
кінематичних пар
|
|
|
Загалом
|
Зайняті
|
Вільні
|
|
II
|
2
|
3
|
1
|
2
|
|
III
|
4
|
6
|
3
|
3
|
|
IV
|
4
|
6
|
4
|
2
|
Найпростіша структурна група, яка складається з двох ланок і
трьох кінематичних пар, відноситься до груп другого класу (рис. 1.11).


Рис. 1.11. Групи Ассуру другого класу різних видів: а)
першого, б) другого, в) третього, г) четвертого, д) п’ятого
Ці структурні групи приєднуються до основного механізму, або
до стояка , двома вільними парами, одна пара з’єднує ланки між собою у групі. У
залежності від класу кінематичних пар і їх розподілу на вільні та зайняті,
структурні групи другого класу розділяються на п’ять видів (рис. 1.11).
Для груп з класом вище другого клас структурної групи
визначається за найвищим класом замкнутого контуру, який входить до її складу.
Клас замкнутого контуру визначається за числом кінематичних
пар, які його утворюють. Наприклад, до складу груп третього класу входять
ланки, що створюють три кінематичні пари з іншими ланками (рис 1.2,а, б, в, г).
У групах четвертого класу створений внутрішній замкнутий
контур з чотирьох ланок (рис. 1.12,д).
Порядок структурної групи визначається за кількістю вільних
кінематичних пар, котрими група приєднається до механізму.
Структурні групи третього класу строгого поділу на види не
мають. Незалежно від виду кінематичних пар у групах на рис. 1.2, а, б, в, г, всі вони є структурними групами третього класу, третього порядку.

Рис. 1.12. Групи Ассуру третього (а, б, в, г) та четвертого (д) класів
За кількістю вільних кінематичних пар структурна група (рис.
1.12, д) є групою четвертого класу другого порядку.
Процес приєднання структурних груп до початкового механізму і
стояка називається структурним синтезом механізмів. Синтез механізмів ставить
метою проектування механізму попередньо обраної структури по відомих динамічних
і кінематичних умовах.
Склад механізму і послідовність приєднання до початкового механізму
структурних груп визначають у вигляді формули будови механізму. У формулі
будови римської цифрою позначається клас початкового або початкових механізмів
(якщо ступінь рухомості більш одиниці). Арабськими цифрами позначають номери
класів структурних груп, яки входять до механізму. Склад початкового механізму
і структурних груп вказується відповідно у дужках нижнього індексу. Наприклад,
для створення шарнірного чотириланковика до механізму першого класу
приєднується структурна група другого класу першого виду. Формула будови має
вигляд  і проілюстрована на рис. 1.13.
і проілюстрована на рис. 1.13.

Рис. 1.13. Структурний синтез шарнірного чотириланковика
Якщо до шарнірного чотириланковика додати структурну групу другого
класу другого виду, то одержимо новий механізм, вихідна ланка якого рухається
зворотно-поступально (рис. 1.14). Його формула будови має вже інший вигляд,  .
.

Рис. 1.14. Структурний синтез механізму з поступальної вихідною ланкою
Кожний важільний механізм має номер класу, який дорівнює найбільшому
номеру структурної групи з його складу. У кожному з двох розглянутих прикладів механізм
має другий клас. Наступний рисунок дає уяву про утворення механізму третього
класу (рис. 1.15) за формулою будови  .
.

Рис. 1.15. Структурний синтез механізму третього класу
Механізми III, IV і інших вищих класів застосовуються рідше механізмів
II класу, у підйомних пристроях апарелів, маніпуляторах підводних апаратів,
спеціальних зварювальних пристроях, ливарних печах тощо.
Необхідність у визначенні класу механізмів пояснюється перш за все тим,
належність механізму до того чи іншого клас визначає методи його кінематичного
і силового досліджень. Тому перед проведенням відповідних досліджень наданого
механізму визначається його клас. З цією метою виконується структурний аналіз. На
відміну від структурного синтезу аналіз виконується у зворотному напрямку.
Структурну класифікацію важільних механізмів можна також застосовувати
при класифікації плоских механізмів із вищими кінематичними парами. З цією
метою у них вищі пари попередньо замінюються відповідними ланцюгами з парами V
класу.
1.7 Заміна вищих кінематичних пар
механізм
кінематичний динамічний
Для перенесення структурної класифікації важільних механізмів
(ланки яких з’єднуються тільки нижчими парами) на механізми з вищими парами
вдаються до заміни вищих пар нижчими. Для спрощення кінематичного і динамічного
дослідження плоских механізмів у багатьох випадках доцільно замінити механізм
із вищими парами IV класу еквівалентним механізмом з нижчими парами V класу.
При подібній заміні кінематичний ланцюг з нижчими парами повинен бути
структурно і кінематичне еквівалентний заміненій парі IV класу.
Умовою структурної еквівалентності є те, що умовний кінематичний
ланцюг, що її замінює, повинен накладати на відносний рух ланок стільки умов зв’язку,
скільки накладає вища пара IV класу. Кожна кінематична пара IV класу в плоскому
механізмі накладає на відносний рух ланок одну умову зв’язку. Отже, і
кінематичний ланцюг, що її замінює, складається з p5 пар V класу і n рухомих
ланок і повинен накладати одну умову зв’язку, тобто  . Звідси випливає, що співвідношення між числом пар V
класу і числом ланок у заміненому ланцюзі, буде відповідати залежності
. Звідси випливає, що співвідношення між числом пар V
класу і числом ланок у заміненому ланцюзі, буде відповідати залежності
 .
(1.4)
.
(1.4)
Найменше число пар, яке відповідає цій умові, дорівнює двом при n = 1,
отже найпростішою заміною вищої пари є ланка з двома парами V класу.
Умовою кінематичної еквівалентності буде збереження кінематичних
характеристик відносного руху ланок (рис. 1.10). Для здійснення такої заміни
вищої пари варто нагадати відому з диференціальної геометрії наступну
властивість контактуючих кривих: коло кривини в точці дотику кривої і сама
крива еквівалентні до похідних другого порядку включно.
Виходячи з обох умов, в центрах кривини контактуючих кривих O1 і O2
слід розмістити кінематичні пари V класу, з’єднавши їх між собою фіктивною
ланкою 3 (рис. 1.16,а). Механізм (рис. 1.16,б),
до складу якого входить ця фіктивна ланка, є миттєвим механізмом. Він має
змінні розміри ланок, яки залежать від положення ланок механізму з вищою парою.

Рис. 1.16. Заміна вищих кінематичних пар
Розглянемо приклади побудови миттєвих механізмів, яки замінюють різни
типи кулачкових механізмів (рис. 1.17).

Рис.1.17. Заміна кулачкових механізмів миттєвими важільними механізмами
а - перетворення механізму з тарілчастим штовхачем на синусний
механізм; б - перетворення механізму із зворотно-поступовим штовхачем на
корбово-поковзневий; в - перетворення механізму з роликовим коромислом на
шарнірний чотириланковик
У випадку (рис.1.17, а), коли профіль одного з елементів вищої пари IV
класу буде прямою лінією (центр кривини його буде нескінченно віддалений)
фіктивна ланка, що заміняє вищу пару, повинна входити в одну обертальну С і в
одну поступальну А пари. Поковзень 3, який є фіктивною ланкою, можна сумістить
із обертальною парою С (рис. 1.17,а). А якщо одна контактуючих поверхонь
згорнулася до точки А (рис. 1.17,б), тоді ця точка буде центром кривини і в неї
необхідно розмістити відповідний центр обертальної пари А (рис. 1.17,б).
1.8 Структурний аналіз плоских механізмів
Структурний аналіз плоских механізмів виконується у наступній
послідовності.
1. Для наданої кінематичної схеми визначається загальна кількість
ланок  і кількість рухомих ланок
і кількість рухомих ланок  .
.
. Досліджуються з’єднання між ланками і визначається кількість
кінематичних пар п’ятого  і четвертого
і четвертого  класів.
класів.
. Розраховується ступінь рухомості механізму за формулою
Чебишова  .
.
. При наявності ланок, що створюють пасивні зв’язки або
надлишкові (зайві) ступені вільності, вказати їх і вилучити зі складу механізму
при структурному аналізі.
. Вищі кінематичні пари, якщо вони є, замінюються умовними
ланками з відповідними нижчими парами.
. Підраховується дійсний ступінь вільності миттєвого механізму,
який побудовано на підставі зауважень у п. 4 і 5.
. Якщо умовами задачі не позначена початкова ланка, слід
призначити її (або їх при ступені рухомості більше однієї).
. З кінематичної схеми механізму послідовно відділяються
структурні групи. Цей процес починається з вилучення зі складу механізму
крайній по відношенню до початкової ланки структурної групи.
. Після кожного відділення структурної групи перевіряється за
формулою Чебишова ступінь рухомості залишкового механізму. Він не повинен
змінюватись.
. Останнім залишається початковий механізм.
. Визначаються класи всіх структурних груп і записується формула
будови механізму.
. За складом формули будови визначається клас механізму.
Задачі 41-60. Виконати структурний аналіз для заданого
важільного механізму (табл. 1.3). Початкова ланка вказана на схемі стрілкою.
Довести правильність відділення груп ланок. Визначити клас, вид и порядок
структурних груп.
Написати формулу
будови, за якою визначити клас механізму.
2.
КІНЕМАТИЧНЕ ДОСЛІДЖЕННЯ МЕХАНІЗМІВ
.1 Задачі і методи кінематичного дослідження
Метою кінематичного дослідження є вивчення руху ланок
механізму від діючих на них сил. При цьому приймаються наступні допущення:
) ланки абсолютно тверді,
) зазори в кінематичних парах відсутні.
При кінематичному дослідженні визначаються:
– положення механізму в різні моменти часу;
– траєкторії окремих точок ланок;
– лінійні швидкості та прискорення точок механізму,
кутові швидкості і прискорення ланок;
– передаточні відношення.
Вихідними даними для визначення перерахованих характеристик
механізму є: кінематична схема і розміри всіх ланок механізму, закони руху
ведучих ланок.
Дослідження виконується в тій же послідовності, як і
утворення структурної схеми, тобто спочатку виконується аналіз руху ведучих
ланок, потім приєднаних до них ланок і т.д. Завершується дослідження аналізом
руху останніх приєднаних ланок. Звичайно досліджується повний цикл руху,
протягом якого ланки механізму послідовно проходять усі положення.
При кінематичному дослідженні механізмів використовуються
аналітичні, графічні, графоаналітичні й експериментальні методи. Метод
дослідження вибирається в залежності від структури механізму і необхідної
точності розрахунку.
Аналітичні методи дозволяють проводити дослідження кінематики
механізмів з будь-яким ступенем точності, але є досить громіздкими і
трудомісткими. Найчастіше розрахунки складних кінематичних схем виконують на ЕОМ.
У тих випадках, коли не потрібно високий ступінь точності, перевага віддається
графічним і графоаналітичним методам.
До графічних методів відноситься метод кінематичних діаграм.
Він використовується для наближеної побудови графічних залежностей переміщень,
швидкостей і прискорень від часу, одержуваних графічним диференціюванням чи
інтегруванням відомого закону руху чи точки ланки механізму. Недоліком цього
методу є низька точність результатів дослідження, особливо при графічному
диференціюванні.
Серед графоаналітичних методів найбільш відомий метод
миттєвих центрів і метод планів. Застосування першого з цих методів часто буває
утруднене тим, що миттєві центри швидкостей і прискорень виявляються поза
кресленням і тому цей метод не одержав широкого поширення. Найбільш доступним і
простим методом є метод планів, широко застосовуваний при кінематичному аналізі
механізмів з нижчими кінематичними парами V класу.
Експериментальними методами звичайно проводять перевірку
результатів аналітичних розрахунків і зроблених допущень при створенні
розрахункової схеми. У деяких випадках експериментально визначається закон руху
однієї з ланок механізму (наприклад, штовхача кулачкового механізму), а всі
інші кінематичні характеристики визначаються графічними чи графоаналітичними
методами. Експериментальні методи найчастіше використовуються для дослідження
складних кінематичних схем тоді, коли застосування інших видів дослідження
утруднено через складність розрахунків чи громіздкості побудов.
.2 Метод планів
Цей метод дозволяє визначити величини і напрямки швидкостей і
прискорень досліджуваних точок, а також кутові швидкості і прискорення ланок
механізму. Метод заснований на відомих теоремах теоретичної механіки, згідно
яким плоский рух точки твердого тіла (ланки) можна представити як складне, що
складається з переносного і відносного рухів.
Для кожної двоповідкової структурної групи чи окремої ланки
можна скласти два векторних рівняння, що зв'язують швидкість досліджуваної
точки з відомими швидкостями двох інших точок. Потім, щоб визначити швидкість
точки, ці рівняння потрібно спільно вирішувати графічно побудовою планів
швидкостей. Аналогічно вирішується задача визначення прискорень точки.
Планом швидкостей (прискорень) механізму називається фігура,
утворена векторами швидкостей (прискорень) точок ланок при заданому положенні
механізму.
При побудові планів варто пам’ятати, що ланка в складі
структурної групи може робити наступні види плоского руху:
а) поступальний рух твердого тіла, характеризується тим, що
будь-яка пряма, проведена в ланці, залишається при русі рівнобіжної самої собі
(рис. II,а). У результаті всі її точки описують однакові траєкторії, тобто
переміщаються зі швидкостями і прискореннями, рівними між собою в будь-який
момент і однаково спрямованими. Прикладом ланки, яка здійснює поступальний рух,
може служити поршень;

б) обертальний рух твердого тіла (наприклад, кривошипа)
характеризує тіла описує дугу окружності з центром, що збігається з віссю
обертання (рис. II, б). Отже, обертальний рух тіла навколо нерухомої вісі
цілком визначається рухом однієї довільної його точки. Окружна швидкість
будь-якої точки пропорційна відстані до вісі обертання і її вектор спрямований
перпендикулярно радіусу обертання;
Абсолютна швидкість будь-якої точки ланки дорівнює
геометричній сумі поступальної швидкості разом з довільно обраним полюсом і
обертальною швидкістю цієї точки навколо полюса (рис.12):

де 
 перпендикулярна AB; ω - кутова швидкість.
перпендикулярна AB; ω - кутова швидкість.

Рис
12.
.2.1 Побудова планів положень механізмів
У більшості випадків у важільних механізмах обертальний рух інших ланок
чи навпаки. Наприклад, зворотно-поступальний рух поршнів двигуна внутрішнього
згоряння, що переміщаються під дією
газів у циліндрах, перетвориться в обертальний рух колінчастого вала. У
той же час рух колінчастого вала поршневого компресора, що обертається
електродвигуном, може перетворитися в поступальний рух поршнів, що нагнітають
повітря в циліндрах компресора. В обох випадках кінематичні схеми механізмів
можуть мати однакову структуру незалежно від призначення. При цьому ланка, що
робить обертальний рух, має практично постійну кутову швидкість і може
повертатися на повний оборот, тобто є кривошипом. Такий закон руху кривошипа
характерний для багатьох важільних механізмів з обертовою ведучою ланкою
незалежно від їхнього призначення. Тому як ведучу ланку зручно в цих випадках
вважати кривошип. Ведучою ланкою називають ланку, закон руху якої вважається
відомим при кінематичному дослідження механізму. Узагалі ж ведучою є така
ланка, якої повідомляється рух, який перетворюється в необхідні рухи відомих
ланок.
Кінематичне дослідження механізму доцільно починати з побудови плану
механізму. Він являє собою зображення ряду послідовних положень механізму, що
відповідають повному циклу руху. План механізму малюється в масштабі, який
характеризується масштабним коефіцієнтом 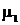 ,
який надалі будемо називати масштабом.
,
який надалі будемо називати масштабом.
Масштабом довжин називається відношення дійсних величин відстаней між
точками ланок механізму, виражених у метрах, до величин їхніх зображень на
кресленні  , де l - дійсний розмір, м;
, де l - дійсний розмір, м; 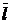 - масштабний розмір, мм.
- масштабний розмір, мм.
Між масштабами, яки використовуються в машинобудівному кресленні, і
масштабами довжин, прийнятими для зображення планів механізмів, існують
наступні співвідношення, що представлені в табличній формі (табл.. 1.2).
Таблиця 1.2.
|
Машинобудівний
масштаб
|
1:1
|
1:2
|
1:2,5
|
1:4
|
1:5
|
2:1
|
2,5:1
|
4:1
|
|
 , м/мм0,0010,0020,00250,0040,0050,00050,00040,00025 , м/мм0,0010,0020,00250,0040,0050,00050,00040,00025
|
|
|
|
|
|
|
|
|
Послідовність побудови плану механізму така. Спочатку наносять
положення нерухомої ланки чи окремих її точок у масштабі  (для кулісного механізму поперечно-стругального
верстата, показаного на рис.13, на схему наносять точки О1 і О2 ), потім на цій
схемі зображують положення ведучої ланки і тільки після цього знаходять
положення груп Ассура (у порядку їхнього приєднання). Для розглянутого
механізму повинні бути задані чи визначені розрахунком розміри
(для кулісного механізму поперечно-стругального
верстата, показаного на рис.13, на схему наносять точки О1 і О2 ), потім на цій
схемі зображують положення ведучої ланки і тільки після цього знаходять
положення груп Ассура (у порядку їхнього приєднання). Для розглянутого
механізму повинні бути задані чи визначені розрахунком розміри  і кут j повороту
кривошипа. За початок відліку положень механізму можна прийняти будь-як
положення кривошипа, але зручніше брати такі положення механізму і кривошипа,
що відповідають одному з крайніх положень відомої ланки (у розглянутому
прикладі - крайніми положеннями точки С ). Звичайно при кінематичному аналізі
розділяють кут робочого ходу
і кут j повороту
кривошипа. За початок відліку положень механізму можна прийняти будь-як
положення кривошипа, але зручніше брати такі положення механізму і кривошипа,
що відповідають одному з крайніх положень відомої ланки (у розглянутому
прикладі - крайніми положеннями точки С ). Звичайно при кінематичному аналізі
розділяють кут робочого ходу  (тобто
кут, що відповідає положенням механізму, у яких відома ланка 5 робить корисну
роботу) на кілька рівних частин, і окремо кут холостого ходу (
(тобто
кут, що відповідає положенням механізму, у яких відома ланка 5 робить корисну
роботу) на кілька рівних частин, і окремо кут холостого ходу ( ) - теж на деяке число рівних частин. У розглянутому
прикладі ці кути розділені на шість частин. Положення всіх інших точок
визначається за допомогою зарубок циркулем. Іноді потрібно досліджувати режими
роботи механізмів при нерівномірному русі ведучої ланки чи механізмів, що не
мають у своєму складі обертової ведучої ланки - кривошипа. До такої групи
механізмів відносяться механізми люкових закриттів, гідравлічні приводи
кермових пристроїв, різні спускно-піднімальні пристрої і т.д. Як приклад на
мал.14 зображений механізм спускно-підйомного пристрою, у якому ведучою ланкою
є повзун I (поршень 1 гідроциліндра 2 на конструктивній схемі рис.14,а).
) - теж на деяке число рівних частин. У розглянутому
прикладі ці кути розділені на шість частин. Положення всіх інших точок
визначається за допомогою зарубок циркулем. Іноді потрібно досліджувати режими
роботи механізмів при нерівномірному русі ведучої ланки чи механізмів, що не
мають у своєму складі обертової ведучої ланки - кривошипа. До такої групи
механізмів відносяться механізми люкових закриттів, гідравлічні приводи
кермових пристроїв, різні спускно-піднімальні пристрої і т.д. Як приклад на
мал.14 зображений механізм спускно-підйомного пристрою, у якому ведучою ланкою
є повзун I (поршень 1 гідроциліндра 2 на конструктивній схемі рис.14,а).

Рис.13

а б
Рис.14
У подібних випадках доцільно траєкторію точки А ведучої ланки
механізму (у нашому прикладі А0Ак ) розділити на частині, що відповідають
рівним проміжкам часу. Для всіх цих положень ведучої ланки будуються відповідні
плани механізмів.
Подальше кінематичне дослідження в будь-якому випадку
послідовно ведеться для всіх положень механізму з урахуванням конкретного
закону руху ведучої ланки.
.2.2 Побудова планів швидкостей і пришвидшень
Швидкості окремих точок механізмів з ведучою ланкою - кривошипом
знаходять у тій же послідовності, у якій утворений механізм по Ассуру. Як
приклад побудуємо плани швидкостей і пришвидшень для чотириланкового
кривошипно-коромислового механізму, кінематична схема якого в масштабі  представлена на рис.15,а. Вважаємо, що кривошип
обертається рівномірно w1 = const.
представлена на рис.15,а. Вважаємо, що кривошип
обертається рівномірно w1 = const.
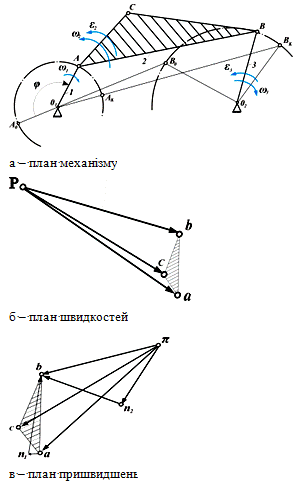
Рис.15
Спочатку необхідно визначити величину лінійної швидкості  пальця кривошипа
пальця кривошипа 
Швидкість  перпендикулярна кривошипу O1A і спрямована у бік його
обертання. Побудова плану швидкостей починаємо з полюса p, від якого
відкладаємо масштабне значення швидкості точки А. Масштаб плану швидкостей
дорівнює
перпендикулярна кривошипу O1A і спрямована у бік його
обертання. Побудова плану швидкостей починаємо з полюса p, від якого
відкладаємо масштабне значення швидкості точки А. Масштаб плану швидкостей
дорівнює
При виборі масштабу швидкостей величину відрізка pа вибираємо не менш
50 мм. Чим більше величина, тим точніше результати побудов.
Відклавши на плані швидкостей відрізок pa, що відповідає в масштабі  швидкості
швидкості  ,
перейдемо до визначення швидкості точки В, що належить ланкам 2 і 3. На
підставі відомої з курсу теоретичної механіки теореми про плоско паралельний
рух можна представити рух точки В шатуна 2, що складається з двох рухів -
поступального разом із точкою А зі швидкістю
,
перейдемо до визначення швидкості точки В, що належить ланкам 2 і 3. На
підставі відомої з курсу теоретичної механіки теореми про плоско паралельний
рух можна представити рух точки В шатуна 2, що складається з двох рухів -
поступального разом із точкою А зі швидкістю  й
обертального навколо точки B тобто
й
обертального навколо точки B тобто 
Точка В належить шатунові і коромислу 3, що качається навколо
нерухомого центра О2, траєкторія точки В - окружність радіуса 02В; VB^02B. Швидкість VBA^АВ , тому що пряма АВ в абсолютно твердій ланці 2 не
деформується й обертальна швидкість VBA точки В повинна бути перпендикулярна
радіусу обертання АВ.
Як у рівнянні (2.1), так і в наступних векторних рівняннях підкреслення
вектора однією рискою буде означати, що відомо тільки лінію дії, двома - модуль
вектора і лінія дії.
Отримане векторне рівняння можна вирішити графічно. Для цього на плані
швидкостей із точки а проводимо промінь, перпендикулярний прямої АВ на плані
механізму до перетинання в точці В з лінією дії швидкості VB, проведеної з
полюса p (під прямим кутом до прямої ВО2 ). На плані швидкостей відрізок pb
зображує швидкість точки В:  ,
a відрізок ab - обертальну швидкість VBA,
,
a відрізок ab - обертальну швидкість VBA, 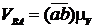 .
.
Для визначення швидкості точки С не будемо вирішувати спільно векторні
рівняння, що визначають швидкість цієї точки стосовно полюсів А і B, а
скористаємося відомою з курсу теоретичної механіки теоремою подоби: відрізки
прямих ліній, що з'єднують точки ланки на схемі механізму, і відрізки, що
з'єднують на плані швидкостей (пришвидшень ) кінці векторів абсолютних
швидкостей (пришвидшень ) тих же точок, утворять подібно розташовані фігури.
Отже, 
Для визначення швидкості точки С на стороні ab плану швидкостей
побудуємо Dabc~DABC з
таким же напрямком обходу сторін. Для цього зменшимо сторону DАВС до розмірів Dаbс і
повернемо в площині креслення DAВС до
сполучення однойменних вершин: А з а, В з b, С з c. Абсолютна швидкість точки  .
.
Величини кутових швидкостей ланок 2 і 3 знаходимо за
формулами:

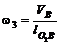 .
.
Легко знаходяться також і напрямки кутових швидкостей ланок.
Наприклад, якщо умовно перенести вектор швидкості VBA у точку В ланки 2, тоді
побачимо, що точка В відносно точки А рухається проти годинникової стрілки.
Отже, обертання шатуна спрямоване проти годинникової стрілки. Аналогічним
чином, розглянувши рух точки В стосовно нерухомого центра обертання, помітимо,
що обертання ланки 3 спрямоване по годинній стрілці.
Розрахунок і побудова плану пришвидчень починається з визначення
пришвидчень точки А. У зв’язку з тим, що обертання кривошипа відбувається з
постійною кутовою швидкістю, прискорення точки А складається тільки з
нормального пришвидчення , спрямованого від точки А до центра обертання O1.
Величина цього пришвидчення 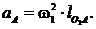
Прийнявши відрізок pa за
зображуване пришвидчення точки А, можна визначити масштаб плану пришвидчень 
Для визначення пришвидчення точки В можна скористатися тим, що ця точка
одночасно належить шатунові 2 і коромислу 3. Для точки В у системі ланки 2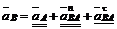 .
.
Для точки В у системі ланки 3 
У векторних рівностях (2.2) і (2.3) дотичні пришвидчення  і
і  відомі
лише по лініям дії, величину їх знаходимо в результаті побудови плану
пришвидчень .
відомі
лише по лініям дії, величину їх знаходимо в результаті побудови плану
пришвидчень .
Нормальні пришвидчення можна знайти по формулах:


Ці пришвидчення спрямовані від точки В відповідно до центрів обертання
А и O2 , тобто  ÷÷BA,
÷÷BA,  ÷÷BO2.
÷÷BO2.
Масштабні значення нормальних пришвидчень на планах пришвидчень будуть
представлені відрізками  і
і 
З полюса p відкладається в напрямку дії пришвидчення 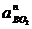 відрізок pn2, а з
точки а - у напрямку
відрізок pn2, а з
точки а - у напрямку 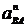 - відрізок аn1. З точок n1 і n2, у напрямках дії
дотичних пришвидчень
- відрізок аn1. З точок n1 і n2, у напрямках дії
дотичних пришвидчень  і
і  ,
тобто перпендикулярно відповідним відрізкам an1 і pn2, проводимо лінії до їхнього перетину в точці b.
Відрізок pb буде зображувати на плані пришвидчень
масштабне значення пришвидчення точки В. Отже,
,
тобто перпендикулярно відповідним відрізкам an1 і pn2, проводимо лінії до їхнього перетину в точці b.
Відрізок pb буде зображувати на плані пришвидчень
масштабне значення пришвидчення точки В. Отже, 
Значення дотичних пришвидчень знаходяться по аналогічних формулах:
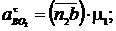
Для визначення пришвидчення точки С потрібно скористатися раніше
сформульованою властивістю подоби і побудувати на стороні ab трикутник abс,
подібний до трикутника AВС і подібно до нього розташований. Значення
пришвидчення точки С 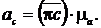
Кутові пришвидчення ланок 2 і 3:


Для визначення напрямку e2 необхідно
тангенціальне пришвидчення 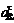 уявно
перенести в точку В і спостерігати, у якому напрямку щодо точки А відбувається
пришвидчення . Аналогічно за допомогою вектора
уявно
перенести в точку В і спостерігати, у якому напрямку щодо точки А відбувається
пришвидчення . Аналогічно за допомогою вектора  визначається
напрямок кутового пришвидчення e3. На
рис.15,а ці напрямки показані стрілками.
визначається
напрямок кутового пришвидчення e3. На
рис.15,а ці напрямки показані стрілками.
На закінчення можна сформулювати основні властивості планів швидкостей
(пришвидчень ) для плоских важільних механізмів з ведучою ланкою --кривошипом:
. Вектори абсолютних швидкостей (пришвидчень ) точок механізму завжди
спрямовані від полюса.
. Вектори відносних швидкостей (повних відносних пришвидчень ) точок
однієї ланки з'єднують кінці векторів абсолютних швидкостей (пришвидчень ) цих
точок.
. Вектори відносних швидкостей (повних відносних пришвидчень ) точок
однієї ланки утворять фігури, подібно розташовані однойменним фігурам на плані
механізму. У розглянутому прикладі трикутники abc на планах швидкостей і
пришвидчень подібні трикутнику AВС на плані механізму.
2.3 Кінематичний аналіз кулачкового механізму
Усі перераховані вище методи кінематичного аналізу можуть
бути застосовані і для дослідження кулачкових механізмів. Результати
кінематичного аналізу дозволяють визначити, чи відповідає прийнята схема
механізму, форма і співвідношення розмірів його ланок поставленій задачі
відтворення необхідного закону руху відомої ланки (штовхача чи коромисла). Крім
того, дані про співвідношення швидкостей різних точок дозволяють визначити
характер передачі сил у механізмі, а значення пришвидчень дають можливість
підрахувати виникаючі в окремих ланках сили інерції і врахувати їх при
визначенні реакцій у кінематичних парах і навантажень на ту чи іншу ланку. Якщо
профіль кулачка обкреслений спеціальними лініями (дугами окружностей, прямими і
т.п.), то в кожному досліджуваному положенні може бути побудований замінюючий
важільний механізм, що досліджується методом планів чи аналітичним методом. Як
приклад розглянемо кінематичний аналіз планів кулачкового механізму з плоским
штовхачем і круглою кулачковою шайбою (рис.16,а).

Рис.16
За відомими правилами побудований (рис.16,б) замінюючий важільний
механізм (точка А - центр окружності кулачка, lAC = R, lOA = r). По відомій
кутовій швидкості w1 = const визначаємо швидкість точки A замінюючого механізму. Швидкість  тому що ланка 2 робить поступальний рух. Вибравши
масштаб побудови планів швидкостей mV,
відкладаємо відрізок pa=pc2 , що зображує в цьому масштабі швидкості точок А і
С2 . Для визначення швидкості штовхача 3 скористаємося теоремою про складний
рух, що зв'язує швидкості ланок, що утворять поступальну пару С
тому що ланка 2 робить поступальний рух. Вибравши
масштаб побудови планів швидкостей mV,
відкладаємо відрізок pa=pc2 , що зображує в цьому масштабі швидкості точок А і
С2 . Для визначення швидкості штовхача 3 скористаємося теоремою про складний
рух, що зв'язує швидкості ланок, що утворять поступальну пару С  де
де  ^OA;
^OA;  ççBK;
ççBK;
 ççKC.
ççKC.
Відповідно до відомого напрямку швидкостей  і
і  будуємо
план швидкостей (рис.16,в). Через точку С2 проводиться горизонтальна пряма -
лінія дії
будуємо
план швидкостей (рис.16,в). Через точку С2 проводиться горизонтальна пряма -
лінія дії  , а через полюс р - вертикальна - лінія дії
, а через полюс р - вертикальна - лінія дії  . Точка перетинання C3 дає можливість визначити
значення цих швидкостей:
. Точка перетинання C3 дає можливість визначити
значення цих швидкостей: 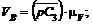

Аналогічним образом будується план пришвидчень (рис.16,г).
Тут

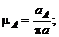


Якщо профіль кулачкової шайби описаний довільною кривою, тоді
кінематичний аналіз механізму зручніше робити за допомогою методу кінематичних
діаграм. Розглянемо метод на прикладі аналізу поза центрового кулачкового
механізму з роликовим штовхачем, який
рухається поступально. Розміри ланок механізму відомі (його схема представлена
на рис.17,а), швидкість кулачка w1 = const.
Для побудови графіка переміщення штовхача S=S(t) необхідно спочатку
побудувати плани положень механізму, потім розмітити шлях центра ролика в
абсолютному русі. При побудові планів положень механізму зручно використовувати
метод інверсії чи зверненого руху. У цьому випадку для різних положень механізму
досить лише один раз зобразити кулачок. Усім ланкам механізму уявно
повідомляється рух навколо осі обертання кулачка з кутовою швидкістю  . При цьому кулачок стає нерухомим, а штовхальник зі
стійкою буде робити довкола нього поворот з кутовою швидкістю
. При цьому кулачок стає нерухомим, а штовхальник зі
стійкою буде робити довкола нього поворот з кутовою швидкістю  , одночасно зміщуючись в направляючих стійкі
відповідно до профілю кулачка. Таким чином, характер відносного руху не
порушується. Для ілюстрації необхідних побудов обмежимося вісьма положеннями.
, одночасно зміщуючись в направляючих стійкі
відповідно до профілю кулачка. Таким чином, характер відносного руху не
порушується. Для ілюстрації необхідних побудов обмежимося вісьма положеннями.
Вочевидь, що траєкторією центра ролика в зверненому русі буде
теоретичний профіль, эквідистантний заданому дійсному. Під эквідистантністю
кривих розуміється рівновіддаленість їх на ту саму величину по нормалі (у
розглянутому випадку такою відстанню є радіус ролика). При аналізі кулачкових
механізмів спочатку будують теоретичний профіль по заданому робочому профілю, а
при проектуванні спочатку визначають необхідний теоретичний профіль, а потім -
дійсний.
Кінематичний аналіз виконують у наступній послідовності (рис.17):
) по дійсному профілю будують теоретичний;
) з центра О описують коло радіусом е і поділяють його на n (у даному
випадку n = 8) рівних частин. Точки розподілу нумеруються відповідно до
напрямку зверненого руху;
) через точки 0, I, 2,..., 7, 8 проводять дотичні до кола e і
відзначають точки їхнього перетину з теоретичним профілем. Ці дотичні являють
собою лінії руху штовхача відносно напрямних у зверненому русі навколо профілю
кулачка;
) проводять осі координат S і j, де
S - переміщення штовхача в направляючих, j -
кут повороту кулачка. У зверненому русі цим переміщенням відповідають відрізки
1-l’, 2-2',... ,6-6' кут повороту j =w1t. Значення в обраних масштабах mS і mj
відкладаються в системі координат S - j
(рис.17,б).

а
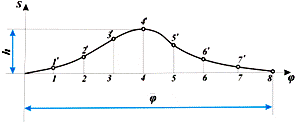
б
Рис. 17
Діаграми швидкостей і пришвидчень штовхача одержують послідовним
диференціюванням діаграми переміщень S(j), що
виконується в наступному порядку (рис.18).
. Зробивши поділ осі абсцис j на декілька
рівних частин, на кожній з ділянок криву переміщень S(j) заміняємо відрізками хорд (січних) Оа , аb , bс , cd
і т.д.(рис.18,а).
. На нижньому графіку аналогів швидкостей ліворуч (рис.18,б) від осі
ординат 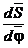 вибираємо полюс Р на відстані h1. Аналогами
швидкостей і пришвидчень називаються похідні
вибираємо полюс Р на відстані h1. Аналогами
швидкостей і пришвидчень називаються похідні 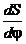 і
і
 котрі при рівномірному обертанні ведучої ланки
зв'язані з дійсними значеннями швидкостей і пришвидчень наступними
залежностями:
котрі при рівномірному обертанні ведучої ланки
зв'язані з дійсними значеннями швидкостей і пришвидчень наступними
залежностями: 

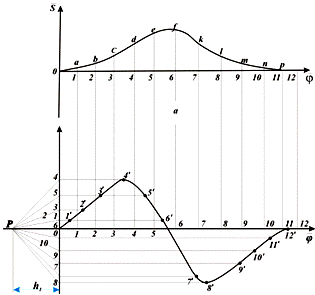
Рис.18
Використання аналогів дозволяє виключити кутову швидкість з
розрахунків і отримані графіки застосовувати для аналізу механізмів з різними
значеннями швидкостей, але з однаковим профілем кулачка.
3. З полюса Р проводимо промені I, 2, 3, 4..., рівнобіжні січним Оa,
ab, bс, cd, і т.д. до перетинання з віссю ординат  .
.
. З точок перетинання проводимо горизонтальні лінії, рівнобіжні осі j до перетинання з вертикальними прямими, проведеними
із середини відрізків D - 0-I, 1-2, 2-3, і т.д.
- 0-I, 1-2, 2-3, і т.д.
. З’єднавши точки їхнього перетинання 1’, 2', 3’, 4'... плавної кривої,
одержуємо шуканий графік функції 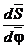 =
=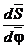 (j).
(j).
. Справжні значення аналогів швидкості 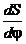 можна
знайти, помноживши креслярські значення
можна
знайти, помноживши креслярські значення 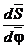 на
масштаб, що обчислюється за формулою
на
масштаб, що обчислюється за формулою 
У цій формулі величини mS у м/мм, mj у I/мм і h2 у мм.
. Для побудови графіка аналогів пришвидчень  =
= (j) досить
зробити графічне диференціювання графіка функції
(j) досить
зробити графічне диференціювання графіка функції  =
= (j).
Послідовність операцій така ж, як і при диференціюванні графіка
(j).
Послідовність операцій така ж, як і при диференціюванні графіка  . Масштаб аналогів пришвидчень визначається за
формулою
. Масштаб аналогів пришвидчень визначається за
формулою 
2.4 Кінематика передач
.4.1 Основні кінематичні співвідношення
У багатьох суднових машинах і пристроях широко застосовуються
механізми для відтворення обертального руху з постійним передатним відношенням
між двома осями, по-різному розташованими в просторі. Серед них можна назвати
шпилі і брашпилі, різні типи лебідок, пристрою люкових закриттів, шлюпбалки,
піднімальні крани, механізми підйому й опускання апарелей тощо.
Механізми, що служать для відтворення обертального руху,
називаються механізмами передачі обертального чи руху скорочено механізмами
передачі.
Найпростішим механізмом є триланковий механізм, до складу
якого належать дві рухомих ланки та стійка, що входять у дві обертальні й одну
вищу пари..
Якщо передатне відношення, що повинне здійснюватися
механізмом передачі, дуже велике чи дуже мало, то конструктивно зручно між
ведучою і відомою осями мати проміжні осі з відповідними ланками, що
обертаються навколо них. Таким чином, передача обертання з ведучого на відомий
вал здійснюється східчасто, послідовною зміною передаточного відношення.
Складний механізм передачі можна розділити на окремі ступіні, кожна з який
являє собою дві ланки, що утворять між собою вищу пару й осі, що мають, вхідні
в нижчі пари.
У залежності від числа ступіней розрізняють одно - і
багатоступінчасті передачі, найчастіше дво - і триступінчасті.
.4.2 Кінематичні співвідношення в одноступінчатих механізмах
передач
Осі ланок передачі можуть бути:
а) паралельними, б) пересічними, в) перехресними.
Відношення кутової швидкості однієї ланки w1 до кутової швидкості іншої ланки w2 у механізмі з одним ступенем рухомості називається
пере даточним відношенням іпозначається буквою u з
цифровими індексами, що відповідають номерам розглянутих ланок (рис.19), 

Рис. 19
Тут знак (-) свідчить про те, що кутові швидкості w1 і w2 мають
різні напрямки. Точка Р0 - миттєвий центр обертання у відносному русі ланок 1 і
2. Тому що u12 = const, отже, O2P0 = r2 = const, O1P0 = r1 = const, тоді 
Звідси випливає висновок про те, що передача з паралельними
осями при сталому передатному відношенні може бути завжди здійснена круглими
циліндричними колесами.

Рис. 20
Для передачі з пересічними осями зі сталим передатним відношенням 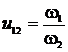 при обертанні конусів 1 і 2 навколо осей O1 і O2
окружності S1 другу. Тоді для точки М, що лежить на миттєвій осі обертання OP,
можна записати (рис.20)
при обертанні конусів 1 і 2 навколо осей O1 і O2
окружності S1 другу. Тоді для точки М, що лежить на миттєвій осі обертання OP,
можна записати (рис.20)  де r1 і r2 - радіуси окружностей S1 і S2.
де r1 і r2 - радіуси окружностей S1 і S2.
Таким чином, з (2.4) і (2.5) випливає
і S2 перекочуються без ковзання друг по, що  .
.
З останнього вираження випливає, що передача обертання зі
сталим передатним відношенням між пересічними осями може бути завжди здійснена
круглими конічними колісьми.

Рис. 21
Аналогічну формулу можна одержати, розглянувши передачу з
перехресними осями (рис.21). У цьому випадку d1 і d2 - кути, утворені осями O1 і
O2 з миттєвою віссю обертання і ковзання ОР.
Точка Р лежить на лінії найкоротшої відстані O1O2 між осями O1 і O2.
Тому що відношення  стале, то кути d1 і d2 також будуть сталими, і в усіх положеннях миттєва
вісь обертання і ковзання буде займати те саме положення, а аксоїди у
відносному рухи цих ланок завжди будуть стикатися своїми утворюючими по
загальної прямої ОР. Такими аксоїдами є лінійчаті гіперболоїди обертання з
осями O1 і O2. Таким чином, передача обертання між перехресними осями зі сталим
передаточним відношенням може бути здійснена гіперболоїдними колісьми.
стале, то кути d1 і d2 також будуть сталими, і в усіх положеннях миттєва
вісь обертання і ковзання буде займати те саме положення, а аксоїди у
відносному рухи цих ланок завжди будуть стикатися своїми утворюючими по
загальної прямої ОР. Такими аксоїдами є лінійчаті гіперболоїди обертання з
осями O1 і O2. Таким чином, передача обертання між перехресними осями зі сталим
передаточним відношенням може бути здійснена гіперболоїдними колісьми.
Передачі можуть мати також нестале передаточне відношення. У
цьому випадку вони будуть складатися з не круглих, наприклад, еліптичних
центроїд.
2.4.3 Класифікація передач
Крім уже розібраної класифікації по розташуванню осей варто
помітити, що обертання від одного вала до іншого може передаватися як
безпосередньо, так і через гнучкий зв’язок. До механізмів з безпосереднім
контактом відносяться дуже розповсюджені передачі зачепленням і фрикційні
передачі, а до механізмів із гнучким зв’язком - ремінні, ланцюгові, тросові й
ін.
.4.4 Зубчасті передачі
У зубчастій передачі ланки, що сполучаються з вищими парами,
містять зуби і називаються зубчастими колесами.
При обертанні одного з коліс його зуби входять у зачеплення з
зубами другого парного колеса і змушують його обертатися. При цьому зуби
відомого колеса передачі можуть розташовуватися як по зовнішньої, так і по
внутрішній його поверхні, і відповідно до цього зачеплення буде зовнішнім або
внутрішнім.
Коли зуби розташовані на циліндричних поверхнях, а утворюючі
зубів рівнобіжні осям цих циліндрів, то передача називається циліндричною
прямозубою.
Якщо зуби розташовані на поверхнях під деяким кутом до
утворюючого циліндра, то передача з такими колесами називається циліндричної
косозубою.
Циліндричні косозубі передачі складніше прямозубих у
виготовленні і мають потребу в пристрої для сприйняття осьових навантажень, але
мають більшу плавність зачеплення і здатні витримати великі окружні
навантаження, чим прямозубі.
Циліндричні передачі відносяться до плоских механізмів. Сюди
ж можна віднести зубчасті передачі з некруглими колесами і рейкові зачеплення,
у яких центр одного з коліс, що знаходяться в зачепленні, вилучений у
нескінченність. У результаті цього його обід перетворюється у зубчасту рейку.
До просторових зубчастих передач відносяться конічні,
черв’ячні тощо.
Для забезпечення нормальної роботи механізму зубчасті
передачі повинні задовольняти наступним вимогам:
– простота профілю за умови дотримання заданих
кінематичних співвідношень;
– найбільша міцність зубів при мінімальному зносі. При
цьому тиск на опори валів повинен залишатися сталим по величині і напрямку при
передачі крутячого сталого моменту;
– технологічність;
– довговічність;
– безшумність ходу;
– легкість операцій при ремонті і взаємозамінності.
Найважливішою вимогою, пропонованим до передач зачепленням, є
збереження сталості передаточного числа.
У теорії зачеплення доводиться: для забезпечення сталості
передаточного числа в будь-який момент роботи передачі необхідно так побудувати
робочі профілі зубів, щоб загальна нормаль до них у будь-якій точці дотику
проходила через нерухому точку Р (полюс зачеплення), що лежить на лінії центрів
і поділяє її у відношенні, зворотно пропорційнім відношенню кутових швидкостей.
У цьому полягає основна теорема зачеплення. Найбільше часто застосовуються зуби
з евольвентними профілями, що задовольняють перерахованим умовам.

Рис.22
Евольвента I (рис.22) являє собою траєкторію точки Р прямої
МN, що перекочується без ковзання по нерухомій окружності. Окружність, по якій
котиться пряма, називається основній, а пряма - виробляючою прямої. Точка
контакту М прямої з окружністю буде миттєвим центром обертання. Тому що
виробляюча пряма MN перекочується по основній окружності без ковзання, то
відрізок МР цієї прямої дорівнює дузі MM0 окружності.
Звідси 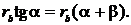
Отже,
 (2.6)
(2.6)
де a - визначає положення точки на евольвенті; b - евольвентна функція, або інволюта.
Радіус-вектор r евольвенти можна
визначити з прямокутного трикутника OMР
 (2.7)
(2.7)
Формули (2.6) і (2.7) параметрически визначають евольвенту в
полярних ординатах.
.4.5 Основні геометричні співвідношення. На рис.23 показане
циліндричне колесо з прямими зубами. Число зубів колеса - z. Профілі зубів зовні
обмежені дугами окружності вершин діаметром da. Западини з боку тіла колеса
обмежені дугами окружності западин діаметром df.
Розміри елементів колеса відкладають від ділильної окружності
діаметром d, що поділяє висоту зуба h на висоту hа голівки і висоту hf ніжки.
Висотою зуба h називають радіальна відстань між окружностями
вершин і западин


Рис.23
Відстань між однойменними точками двох сусідніх профілів r, обмірювана по дузі ділильної окружності, називається
окружним кроком зубчастого колеса 
Отже, задавши величиною r і числом
зубів z, можна визначити діаметр ділильної окружності 
Але, подібне співвідношення незручне для розрахунку через ірраціональне
число p у знаменнику. Тому в теорію зубчастих передач
уведена величина  , названа окружним модулем зубів колеса (зачеплення).
Величини модулів зачеплення виражаються в міліметрах і стандартизовані за ГОСТ
9563-60. З уведенням модуля діаметр ділильної окружності можна визначати більш
зручним співвідношенням
, названа окружним модулем зубів колеса (зачеплення).
Величини модулів зачеплення виражаються в міліметрах і стандартизовані за ГОСТ
9563-60. З уведенням модуля діаметр ділильної окружності можна визначати більш
зручним співвідношенням 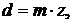
звідкіля зрозумілий фізичний зміст модуля 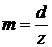 , як величини, що визначає частку діаметра ділильної
окружності, що приходиться на один зуб колеса. Тому іноді модуль називають
діаметральним кроком.
, як величини, що визначає частку діаметра ділильної
окружності, що приходиться на один зуб колеса. Тому іноді модуль називають
діаметральним кроком.
Модуль представляє найважливішу характеристику зубчастої передачі. У
двох коліс, що знаходяться в зачепленні, (рис.23) повинні бути однаковими крок,
а отже, і модуль. При зачепленні двох коліс їх окружності з радіусами r1 і r2
котяться друг по другу без ковзання і називаються початковими окружностями.
Поняття початкових окружностей, що є центроїдами відносного руху коліс, є
кінематичним поняттям і може відноситися до конкретного зачеплення, тоді як
поняття про ділильну окружність індивідуальне поняття для кожного колеса. Два
колеса, по різному входячи в зачеплення, можуть мати різні початкове
окружності, тоді як їхні ділильні окружності будуть величинами незмінними. В
окремому випадку ці окружності будуть збігатися. Кут a між нормаллю N1N2 до поверхонь зубів у точці контакту
Р и дотичної до окружностей у цій точці називається кутом зачеплення, а точка P
- полюсом зачеплення.
Зубчасте колесо, у якому a = 20°,
товщини зубів S і западини e (рис. 23) однакові, називається нормальним. Для
нормального зубчастого колеса характерні наступні геометричні співвідношення: d
= mz; ha = т; f= 1,25т; d0 = т (z + 2); df = m(z - 2,5 ), а ділильні і
початкові окружності збігаються.
Передаточне відношення нормального зачеплення

3.
Динамічний аналіз механізмів
Основними задачами динамічного аналізу механізмів є: силовий
розрахунок, дослідження енергетичних характеристик механізмів, дослідження
їхнього руху під дією заданих сил, регулювання ходу механізмів і
зрівноважування мас, що рухаються.
.1 Цілі силового дослідження механізмів
При проектуванні нових і аналізі існуючих механізмів силовий
розрахунок має важливе значення. Силовим розрахунком механізмів передбачається
визначення сил інерції, що діють на ланки, реакцій, що виникають у кінематичних
парах, невідомих зовнішніх сил (моментів), необхідних для підтримки необхідного
закону руху ведучого ланки. Усе це необхідно для наступного розрахунку на
міцність і знос ланок і кінематичних пар механізму, визначення потужності
привода і т.д.
Наближене рішення перерахованих задач звичайно виробляється
при наступних допущеннях:
– ланки механізму абсолютно тверді;
– у кінематичних парах відсутні зазори;
– маси і моменти інерції всіх ланок відомі;
– сили тертя в порівнянні з всіма іншими діючими на
ланки силами малі і можуть не враховуватися.
Невідомі сили при розрахунку механізму можна визначити
аналітично і графічно з рівнянь статики, застосувавши до ланок, що рухаються,
принцип Даламбера, тобто вважаючи їх урівноваженими за рахунок сил і моментів
сил інерції. Такий метод розрахунку одержав назву кінетостатичного.
.2
Сили, що діють на ланки механізму
При роботі механізму на його ланки діють рушійні сили, сили
опору і сили ваги ланок. Під дією цих сил виникають реакції зв’язків, що діють
на елементи кінематичних пар. При русі ланок із прискореннями в рівняння
статики сили інерції вводяться відповідно до принципу Даламбера.
Рушійними силами називаються сили, що прискорюють механізм, і
роблять позитивну роботу.
Сили опору переборюються механізмом, що затрачає на це
енергію, інакше кажучи, робота цих сил негативна. Сили опору розділяють на сили
корисного і шкідливого опору.
Сили корисного опору - це ті сили, для подолання яких
призначений механізм (опір оброблюваного матеріалу у верстатах, рідких чи
газових середовищ у компресорах, насосах, кермових пристроях і т.д.). До сил
шкідливого опору відносять сили тертя в кінематичних парах, сили опору
середовища, у якій працюють ланки й ін. Однак у деяких видах механізмів
(фрикційних, клиноремінних, штуртросних передачах) сили тертя можуть бути і
рушійними силами.
Сили ваги ланок прикладені в центрах їх мас. За повний цикл
руху механізму їх робота дорівнює нулю.
Під силами інерції розуміють динамічні реакції тіл на
пришвидчення , що повідомляється ззовні. Ці сили прикладені у відповідності з
другим законом Ньютона до тіла, що прискорює, але в кінетостатичних розрахунках
вони умовно переносяться на розглянуті ланки. У цьому складається фіктивність
сил інерції, використовуваних для розрахунків за допомогою рівнянь рівноваги.
У загальному випадку систему сил інерції однієї ланки можна привести до
головного вектора сил інерції  прикладеному
в центрі мас Si ланки (рис.24), і до головного моменту сил інерції
прикладеному
в центрі мас Si ланки (рис.24), і до головного моменту сил інерції  Знак
(-) у цих вираженнях указує, що напрямки сили
Знак
(-) у цих вираженнях указує, що напрямки сили  і
моменту
і
моменту  протилежні напрямкам пришвидчень
протилежні напрямкам пришвидчень  і
і  .
.
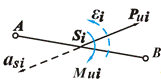
Рис 24.
Силові впливи на ланки механізму можуть мати різний характер. Так, при
точковому контакті силовий вплив виражається у виді зосередженої сили.
Тиск газів на поршень являє собою розподілену по робочій поверхні
поршня навантаження, а сили ваги - навантаження, розподілену по всій довжині
ланки. Надалі, унаслідок допущення про абсолютну твердість ланок, розподілені
навантаження замінені зосередженими силами. Однак у багатьох випадках силовий
вплив, що розподіляється, зводиться до рівнодіючої пари сил або моменту,
наприклад, до рушійного моментам Mдв у електродвигуна, турбіни, до моменту
опору Mо гребного гвинта, компресора і т.д.
Реакції зв’язків є результатом основного взаємодіючи ланок. У
вищих кінематичних парах IV класу реакція спрямована по нормалі в точці
контакту (рис.25,а).
 а
а  б
б  в
в
Рис.25
В обертальній парі, що зв’язує ланки i і j (рис.25,б), тиск
із боку i -тої ланки по циліндричній поверхні розподілений по визначеному
закону, що залежить від ступеня припрацьованности поверхні, пружних
властивостей, матеріалу, змащення й ін. При відсутності сил тертя рівнодіюча
Rij проходить через центр O шарніра. Її величина і напрямок невідомі і повинні
бути визначені з кінетостатичного розрахунку.
У поступальній парі, що зв’язує нерухому ланку O (стійку) з
рухомою k (рис.25,в), виникає реакція Rok з боку стійки, нормальна до
направляючих (без обліку сил тертя), але величина її і точка прикладення
невідомі.
Таким чином, у нижчих парах при наявності плоскої системи
сил, що діють на ланки механізму, для визначення реакцій необхідно скласти два
рівняння, що збігається з числом умов зв’язків, яки накладаються кінематичною
парою на рух плоского механізму
Якщо в розрахункову систему входить n ланок, то для них можна скласти
3n рівнянь рівноваги. При з’єднанні ланок кінематичними парами 5-го класу число
невідомих параметрів, що визначають тиски в кінематичних парах, буде
дорівнювати 2р5. Кожну із сил можна визначити в тому випадку, якщо число рівнянь
рівноваги дорівнює числу невідомих компонентів сил, тобто якщо 3n = 2p5. Таким
чином, умова статичної визначності груп ланок  збігається
з умовою, якої задовольняють структурні групи Асура.
збігається
з умовою, якої задовольняють структурні групи Асура.
Використовуючи цей збіг, повний кінетостатичний розрахунок механізму
можна замінити кінетостатичним розрахунком окремих груп Асура, на які може бути
розкладений механізм.
3.3 Кінетостатичний розрахунок плоских важільних
механізмів
Вихідними даними для силового розрахунку є:
– кінематична схема механізму і розміри всіх
ланок;
– закон руху ведучого ланки;
– маси і моменти інерції ланок;
– зовнішні сили і моменти, що діють на ланки.
Для визначення невідомих силових факторів при
кінетостатичному розрахунку складаються рівняння рівноваги, котрі розв’язуються
щодо не відомих як графічно, шляхом побудови планів сил, так і аналітичним
шляхом.

Рис.26
Як приклад розглянемо розрахунок чотириланкового
кривошипно-повзунного механізму висадочного преса, представленого на рис.26,а.
До складу механізму входить структурна група II класу, що складає з повзуна 3 і
шатуна 2, і механізм I класу, що складає з кривошипа 1 і стійки 0.
Для ілюстрації правильності напрямку інерційних навантажень,
обумовлених по формулах (3.1.) і (3.2.), на рис.26,б показаний план пришвидчень
.
Силове дослідження починається з розрахунку структурної групи 2-3
(рис.26,в). Для цього вона звільняється від зв’язків і замість них у шарнірі А
та звільненій поступальній парі B прикладаються реакції R12 і R03. Тому що
величина і напрямок реакції R12 невідомі, то її розкладаємо на нормальну  і тангенціальну
і тангенціальну 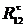 складові.
За умовою центр мас збігається із шарніром 6 (рис.26,а) і усі відомі зовнішні
інерційні навантаження, що діють на 3 ланку, проходять через точку В. Завдяки
цьому через цю точку проходить і лінія дії реакції R03 перпендикулярно
переміщенню повзуна.
складові.
За умовою центр мас збігається із шарніром 6 (рис.26,а) і усі відомі зовнішні
інерційні навантаження, що діють на 3 ланку, проходять через точку В. Завдяки
цьому через цю точку проходить і лінія дії реакції R03 перпендикулярно
переміщенню повзуна.
Складаємо
рівняння рівноваги для ланки 2 у вигляді рівняння моментів щодо точки В. При
цьому моменти сил  і R54, що проходять через центр шарніра 8, дорівнюють нулю. У такий спосіб:
і R54, що проходять через центр шарніра 8, дорівнюють нулю. У такий спосіб:  Звідси випливає
Звідси випливає

Складаємо векторне рівняння рівноваги для групи 2-3

Для скорочення подальших побудов у цьому рівнянні спочатку складаються
відомі сили, що діють на ланку 3, потім випливають відомі і невідомі
навантаження, що діють на 2 ланку, і закінчується побудова невідомою реакцією  .
.
Побудова плану сил (замкнутого багатокутника сил) для групи 2-3
ведеться в наступній послідовності: вибравши масштаб побудови mp, Н/мм. Від довільної точки а відкладаємо сумарний вектор
( ), відомий по величині і напрямку. Далі з кінця цього
вектора відкладаємо величину
), відомий по величині і напрямку. Далі з кінця цього
вектора відкладаємо величину 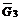 в
напрямку дії сили ваги, потім випливає сила
в
напрямку дії сили ваги, потім випливає сила  і
так до сили
і
так до сили  . Через кінець з вектора
. Через кінець з вектора  , паралельно осі АB ланки 2, проводимо лінію дії
, паралельно осі АB ланки 2, проводимо лінію дії  . Тому що багатокутник сил повинний замкнутися в точці
а вектором
. Тому що багатокутник сил повинний замкнутися в точці
а вектором  , то через цю точку проводимо в напрямку ba лінію її
дії. Відрізки сb і ba у масштабі mp визначають
величини невідомих сил
, то через цю точку проводимо в напрямку ba лінію її
дії. Відрізки сb і ba у масштабі mp визначають
величини невідомих сил  і
і  .
Для визначення реакції
.
Для визначення реакції  =
= 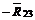 ,
що діє з боку ланки 3 на ланку 2 у шарнірі В, складемо векторне рівняння
рівноваги ланки 2.
,
що діє з боку ланки 3 на ланку 2 у шарнірі В, складемо векторне рівняння
рівноваги ланки 2. 
Складові цього рівняння, за винятком останнього R32, записані в тій же
послідовності B (див. підкреслені частини рівнянь), що й у рівнянні (3.3).
Отже, для визначення величини і напрямку  можна
скористатися тим же планом сил, з'єднавши кінець вектора
можна
скористатися тим же планом сил, з'єднавши кінець вектора  - точку b з початком вектора
- точку b з початком вектора  - точкою k . Відрізок bk у масштабі mp визначає величину сили
- точкою k . Відрізок bk у масштабі mp визначає величину сили  .
.
До кривошипа I первинного механізму (рис.26.г) прикладена
реакція  = -
= - , відомий за умовою головний момент сил інерції
, відомий за умовою головний момент сил інерції  ,
сила ваги ланки G1, і невідомі зовнішній рушійний момент Mдв,
прикладений з боку привода до даного механізму, і невідома реакція R01
впливу стійки 0 на ланку I.
,
сила ваги ланки G1, і невідомі зовнішній рушійний момент Mдв,
прикладений з боку привода до даного механізму, і невідома реакція R01
впливу стійки 0 на ланку I.
Векторне рівняння рівноваги ланки I має вид  відкіля значення невідомої сили
відкіля значення невідомої сили  знаходиться шляхом побудови плану сил (рис.26,г) по
цьому рівнянню.
знаходиться шляхом побудови плану сил (рис.26,г) по
цьому рівнянню.
Рівняння моментів сил, прикладених до ланки I щодо точки O

дає можливість знайти зовнішній момент Mдв. У такий спосіб можна
виконати кінетостатичний розрахунок для ряду послідовних положень механізму за
повний цикл його руху і побудувати графіки сил, що діють у механізмі.
3.4
Дослідження руху механізму
Раніше в розрахунках покладалося, що закон руху ведучої ланки
відомий. У дійсності кінематичні параметри механізмів є функцією зовнішніх сил
і інерційних характеристик його рухливих ланок.
Для визначення закону руху механізму необхідно скласти
рівняння руху механізму і вирішити його щодо шуканого кінематичного параметра.
Для механізму з одним ступенем вільності розв’язання цієї
задачі значно спрощується, якщо всі зовнішні сили і моменти сил, прокладені до
ланок механізму, замінити зведеною силою (моментом), прикладеної до ланки
приведення, а маси і моменти інерції рухливих ланок замінити динамічно
еквівалентною зведеною масою (моментом інерції) ланки приведення. Така умовна
заміна сил і мас дозволяє при рішенні динамічних задач замість дослідження
механізму досліджувати закон руху ланки приведення. У якості останнього
звичайно вибирається ведуче ланка.
.4.1 Зведення сил і моментів
Точка прикладення зведеної сили  називається
точкою зведення, а ланка, якій належить ця точка - ланкою зведення. Ланка і
точка зведення, а також напрямок
називається
точкою зведення, а ланка, якій належить ця точка - ланкою зведення. Ланка і
точка зведення, а також напрямок  можуть
бути обрані довільно. У більшості випадків
можуть
бути обрані довільно. У більшості випадків  приводиться
до точки ведучого ланки механізму і направляється по дотичній до траєкторія
точки зведення.
приводиться
до точки ведучого ланки механізму і направляється по дотичній до траєкторія
точки зведення.
Зведеною силою  називається така умовна сила, елементарна робота якої
на можливому переміщенні точки зведення дорівнює сумі елементарних робіт
зведених сил на відповідних переміщеннях точок прикладання цих сил. Дійсні
переміщення завжди є можливими.
називається така умовна сила, елементарна робота якої
на можливому переміщенні точки зведення дорівнює сумі елементарних робіт
зведених сил на відповідних переміщеннях точок прикладання цих сил. Дійсні
переміщення завжди є можливими.
Зведеним моментом сил 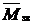 називається
момент зведеної сили.
називається
момент зведеної сили.
Для механізмів з одним ступенем волі принцип можливих переміщень
приводиться до рівності потужності зведеної сили (або зведеного моменту) сумі
потужностей сил, що приводяться, і моментів, прикладених до ланок механізму:


відкіля


Тут VA - швидкість точки прикладання A;
wзв -
кутова швидкість ланки зведення.
Кут між Рзв і VA звичайно дорівнює нулю, тому 
З формул (3.5) і (3.6) видно, що Рзв і Мзв залежать не тільки від
значень сил, що приводяться, і моментів сил, але і від відносин швидкостей. У
механізмах з одним ступенем волі відносини швидкостей не залежать від швидкості
руху і можуть бути сталими чи залежати тільки від положень ланок механізму.
.4.2 Зведення мас і моментів інерції
Зведеною масою тзв називається така умовна маса, що зв’язана з ланкою
зведення ОA (рис.27,а) і рухаючи зі швидкістю точки зведення A, має кінетичну
енергію, рівної кінетичної енергії механізму: 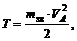 відкіля
відкіля
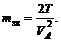
Зведеним моментом інерції Iзв (рис.27,б,в) називається умовний момент
інерції обертового ланки зведення, що має кінетичну енергію, яка дорівнює
кінетичної енергії механізму  відкіля
відкіля

Кінетична енергія механізму дорівнює сумі кінетичних енергій усіх його
рухомих ланок  Тут при поступальному русі ланки -
Тут при поступальному русі ланки -  при обертанні ланки навколо нерухомої осі -
при обертанні ланки навколо нерухомої осі -  і при плоско паралельному русі ланки -
і при плоско паралельному русі ланки - 


Рис.27
На основі аналізу розглянутих прикладів можна зробити висновок, що в
загальному випадку значення зведеного моменту інерції (зведеної маси)
повторюються в кожнім циклі і залежать від положення ланки зведення, але не
залежать від її кутової швидкості і часу. Для механізмів зі сталими
передаточними відношеннями 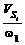 і
і
 (зубчасті передачі, роторні машини й ін.) зведений
момент інерції теж сталий.
(зубчасті передачі, роторні машини й ін.) зведений
момент інерції теж сталий.
.4.3 Рівняння руху механізму. Таке рівняння можна визначити,
застосувавши до механізму основне рівняння динаміки: зміна кінетичної енергії
механізму за деякий проміжок часу дорівнює сумі робіт усіх прикладених до
системи сил і моментів на відповідних переміщеннях:
DT =
Aдв- Aо, (3.6)
де DT - зміна кінетичної енергії за деякий
проміжок часу; Aдв, Aо - робота рушійних сил і сил опору за той самий час.
Знак (-) у формулі враховує, що на подолання сил опору механізмом
витрачається робота.
Скорочуючи проміжок часу до нескінченно малого, рівняння руху механізму
можна записати в диференціальній формі
Т = d(Aдв- Aо). (3.7)
Якщо механізм
замінений ланкою зведення, усі характеристики якої визначені по вищенаведених
залежностях, тоді:


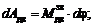

де  і
і 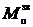 -
відповідно зведені моменти рушійних сил і сил опору.
-
відповідно зведені моменти рушійних сил і сил опору.
Таким чином, рівняння
руху (3.7) можна представити в наступному виді:

На практиці дуже розповсюджений
випадок, коли зовнішні сили залежать тільки від положення механізму, тобто  тоді
тоді
 (3.8)
(3.8)
Інтегруючи рівняння
(3.8), одержимо

де  і
і  -
значення зведеного моменту інерції і кутової швидкості, що відповідають
початковому положенню ланки зведення j10.
-
значення зведеного моменту інерції і кутової швидкості, що відповідають
початковому положенню ланки зведення j10.
Отже,

тобто кутова
швидкість також є функцією положення механізму. У залежності від характеру
зміни кутової швидкості рух механізму від пуску до зупинки можна розбити на три
стадії:
перша - розбіг або пуск; друга - усталений рух і третя -
зупинка (рис.28).

Рис.28
При пуску (розбігу) механізму кутова швидкість ведучого ланки
наростає від нуля до швидкості сталого руху, при зупинці - навпаки, падає від
швидкості сталого руху до нуля.
При усталеному режимі роботи механізму кутова швидкість ведучого ланки
в багатьох механізмах міняється періодично (циклічно), тобто повторюючи через
рівні проміжки часу, що відповідають циклу роботи механізму. Таким чином, на
початку і кінці кожного циклу швидкість дорівнює w1(t)= w1(t + t) де t - час
циклу. Отже, зміна кінетичної енергії за цикл t:  ,
тому що
,
тому що 
З рівняння руху  видно, що при усталеному русі механізму вся робота
рушійних сил затрачається на подолання сил опору, тобто
видно, що при усталеному русі механізму вся робота
рушійних сил затрачається на подолання сил опору, тобто  . Аналогічним образом можна показати, що при пуску
. Аналогічним образом можна показати, що при пуску  протягом часу зупинці
протягом часу зупинці 
Час розбігу механізму можна скоротити шляхом відключення роботи сил
корисного опору на період пуску (пуск у холосту). Час зупинки звичайно
скорочують шляхом гальмування, тобто збільшенням роботи сил шкідливих опорів.
3.5 Регулювання руху механізму
Для більшості технологічних машин, багатьох суднових машин і
механізмів, таких як електрогенератори, насоси і компресори, прилади й ін.,
найбільш характерним режимом роботи є сталий режим.
Тому що зведені сили і моменти, приведений момент інерції
періодично змінюються в залежності від кута повороту j1 ведучого ланки, те цей
режим роботи, незважаючи на рівність кутових швидкостей на початку і кінці
циклу руху, характеризується нерівномірним обертанням ведучого ланки, про що
свідчить формула (3.7).
Нерівномірність руху механізму прийнято оцінювати
коефіцієнтом нерівномірності руху ведучого ланки:

де  - середня кутова швидкість за період циклу;- частота
обертання ведучого ланки, про/хв. Циклу відповідає кут j = 2p (рис.29).
- середня кутова швидкість за період циклу;- частота
обертання ведучого ланки, про/хв. Циклу відповідає кут j = 2p (рис.29).

Рис.29
Нерівномірність руху впливає на роботу машин і механізмів, точність і
якість технологічних процесів, величину додаткових динамічних навантажень і
т.д. Оскільки коливання швидкості, обумовлені періодичною дією сил, цілком
усувати не можна, те потрібно хоча б по можливості скоротити їхній розмах.
Іншими словами, величину коефіцієнта нерівномірності d необхідно знизити до прийнятно малих значень,
визначених практикою експлуатації.
У залежності від призначення, структури й умов роботи механізмів
застосовуються .наступні способи регулювання їхнього руху:
. З аналітичної формули (3.9) випливає, що зниження коливань кутової
швидкості можна домогтися за рахунок збільшення Iзв. Це досягається або за
рахунок підвищення моментів інерції ланок, зв’язаних з ланкою зведення сталим
передаточним відношенням, або за допомогою установки на валу ланки зведення
додаткової маси, виконуваної у виді махового колеса - маховика.
. Регулювання кутової швидкості ведучого ланки з метою автоматичної
стабілізації її в межах заданого d при
випадковому (неперіодичному) зміні роботи сил корисних чи опорів рушійних сил.
Цей вид регулювання найчастіше застосовують у машинах роторного типу (турбіни,
потужні електрогенератори та електродвигуни) і приладах, до яких показуються
підвищені вимоги по плавності ходу.
Список
літератури
1. Артоболевский И.И. Теория механизмов и машин. М., ”Наука”, 1975. - 639с.
2. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по
теории механизмов и машин. М., ”Наука”, 1975. - 256с.
3. Теория механизмов. Под редакцией В.А. Гавриленко.
Учебное пособие для втузов. - М., ”Высшая
школа”, 1973. -
511с.
4. Теория механизмов и машин: Учеб. для втузов/К.В.
Фролов, С.А. Попов, А.К. Мусатов, и др.; Под редакцией К.В. Фролова. - М., ”Высшая школа”, 1987. - 496с.
. Кореняко О.С. Теорія механізмів и машин. - К., Вища шк.., 1987. - 206с.
6. Кипреев Ю.Н. Конспект лекций по кинематике и динамике
судовых механизмов. - Николаев: НКИ, 1981. - 48с.
7. Попов А.П., Кипреев Ю.Н., Руденко В.Г. Проектирование
и кинематическое исследование механизмов с применением ЭВМ. - Николаев: НКИ,
1992. - 89с.
. Руденко В.Г. Методические указания к выполнению
курсового проекта по теории механизмов и машин. - Николаев: НКИ, 1983. - 58с.
9. Смірнов В.М., Пелевін Л.Є., Гаркавенко О.М.
Механіка механізмів.- К., КНУБА, 2001. - 154с.
. Кіпрєєв Ю.М. Комплексні задачі з прикладної
механіки: Навчальний посібник. - Миколаїв: УДМТУ, 2001. - 120с.