Динамический расчет массивной плоской рамы
1.
Техническое задание
Дана массивная стальная плоская рама с установленным на ней
электродвигателем весом Q=15 кН (рисунок 1). Поперечные сечения всех стержней
рамы одинаковы и выполнены в виде составного сечения из двух швеллеров.
Вследствие вращения неуравновешенного ротора электродвигателя со скоростью
n=214 об/мин возникает центробежная сила величиной Р=2,1 кН, которая вызывает
колебания рамы.

Рисунок 1 - Исследуемая плоская рама
Требуется:
1) подобрать номер швеллера из условия статической прочности;
2) используя упрощенную расчетную схему с двумя
степенями свободы, определить собственные частоты колебаний ω1 и ω2, формы колебаний,
пренебрегая массой стержней рамы;
) рассчитать спектр собственных колебаний рамы по
уточненной схеме, приближенно учитывающей массу стержней рамы;
) рассматривая стационарный режим колебаний,
определить амплитуду установившихся колебаний массы электродвигателя и
рассчитать траекторию движения центра масс электродвигателя;
) построить эпюру амплитудных значений изгибающих
моментов, возникающих в раме от действия заданной вибрационной нагрузки при
стационарном режиме колебаний;
) вычислить максимальные динамические напряжения в
сечениях рамы (с учетом собственного веса двигателя) и сравнить их с расчетным
сопротивлением материала;
) сравнить значения максимальных динамических
напряжений со значениями, полученными из статического расчета и сделать
заключение о прочности рамы.
Расчетное сопротивление стали изгибу принять равным Ru= 210 МПа, модуль
упругости стали Е = 200 ГПа, длина L=2,3 м.
2.
Определение спектра собственных колебаний по упрощенной схеме
2.1
Выбор номера швеллера
Расчет спектра собственных колебаний рамы можно выполнить,
если известна изгибная жесткость стержней, из которых состоит данная рама. В
свою очередь, изгибная жесткость зависит от размеров поперечного сечения
стержней (в данном случае оно представляет собой два швеллера, повернутые друг
к другу длинными сторонами). Для нахождения оптимальных параметров сечения проведем
статический расчет исходной рамы на прочность от действия суммарной силы Q + P.
На основании знаний, полученных из курса «Сопротивление
материалов», построим эпюру изгибающих моментов.

Рисунок 2 - Эпюра изгибающих моментов
Значение максимального изгибающего момента: 
 . Условие статической прочности:
. Условие статической прочности:

 (3.1)
(3.1)
где σmax - максимальное
нормальное напряжение в поперечном сечении, Mmax - максимальный
изгибающий момент, W - момент сопротивления сечения, Rи - сопротивление изгибу.
Тогда искомый момент сопротивления сечения:

Поскольку поперечное сечение состоит из двух швеллеров, то:

Выбираем из ГОСТ 8240-97 швеллер №16аП со следующими параметрами:
площадь поперечного сечения F=19,5 см2,
погонная масса 
 , момент сопротивления Wшв=103 см3, момент инерции Ixш=827 см4.
, момент сопротивления Wшв=103 см3, момент инерции Ixш=827 см4.
Изгибная жесткость сечения:


Масса двигателя:


2.2
Вычисление параметров собственных колебаний
Построим эпюры изгибающих моментов от единичных сил,
приложенных к массе э/д.

Рисунок 3 - Единичные эпюры
Вычислим коэффициенты матрицы податливости при помощи
построенных эпюр по следующей формуле:

 (3.2)
(3.2)
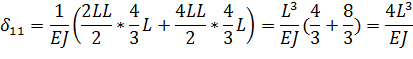


Если принять 
 и m0=m, то матрица относительных податливостей и
матрица относительных масс соответственно примут вид:
и m0=m, то матрица относительных податливостей и
матрица относительных масс соответственно примут вид:

 и
и 

Общий вид частотного уравнения:

 (3.3)
(3.3)
где 
 и
и 
 . Его корни:
. Его корни:

 (3.4)
(3.4)
в данном случае составят λ1=12,099 и λ2=1,901. Собственные частоты:

 (3.5)
(3.5)
примут значения ω1=6,64 с-1 и ω2=16,752 с-1.
Из уравнений

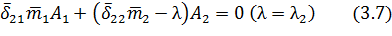
при 
 (заданы при построении эпюр) получим остальные компоненты
векторов главных форм колебаний:
(заданы при построении эпюр) получим остальные компоненты
векторов главных форм колебаний:
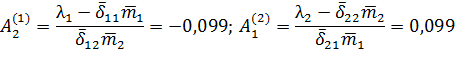
Сами векторы: A(1)=(1 -0,099)T A(2)=(0,099 1)T.

Рисунок 4 - Направления главных форм колебаний
Проверка подтверждает их ортогональность:
 .
.
3.
Расчет спектра собственных колебаний по уточненной схеме
Для начала сосредоточим массы стержней в их средних и крайних
точках, причем средней точке каждого стержня придадим половину его массы, а
крайним - по ¼ этой величины. Обозначим эти массы
согласно рисунку 5.

Рисунок 5 - Расположение и обозначение сосредоточенных масс
Подсчитаем величину каждой массы mi и занесем значения в таблицу 1.
Таблица 1 - Значения сосредоточенных масс
|
Номер массы
|
Величина, кг
|
|
1
|
1529+8,798=1537,798
|
|
2
|
17,595
|
|
3
|
8,798*2+17,595=35,19
|
|
4
|
17,595
|
8,798+17,595=26,393
|
|
6
|
35,19
|
|
7
|
35,19
|
|
8
|
17,595
|
|
9
|
17,595
|
|
∑
|
1740,141
|
Выполним проверку. Как видно из рисунка 5, суммарная длина
всех стержней рамы составляет 6L. Тогда масса всей рамы вместе с электродвигателем составит

 ,
,
что согласуется с таблицей 1.
Пронумеруем динамические степени свободы системы с
сосредоточенными массам, и, учитывая наложенные связи, направим соответствующим
образом оси обобщенных координат (см. рисунок 6).

Рисунок 6 - Направления осей обобщенных координат
Матрица масс для такой системы (при данной нумерации
сосредоточенных масс и динамических степеней свободы) будет иметь вид:

Построим эпюры изгибающих моментов от единичных сил,
приложенных к соответствующим сосредоточенным массам по направлениям обобщенных
координат (рисунки 7, 8, 9).

Рисунок 7 - Единичные эпюры 
 ,
, 
 ,
, 


Рисунок 8 - Единичные эпюры 
 ,
, 


Рисунок 9 - Единичные эпюры 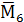
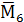 ,
, 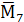
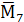
Коэффициенты податливости системы δij определим на ЭВМ.
Проконтролируем результаты расчетов сравнением некоторых di,j, вычисленных вручную и на ЭВМ, а также используя свойство
взаимности коэффициентов di,j = dj,i.
Например, в результате ручного расчета получено значение коэффициента d11 = d0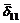 = 3,999×10-6 м/Н. Расчет на ЭВМ дает значение
коэффициента 4×10-6
м/Н. Разница объясняется учетом влияния продольных деформаций стержней в
машинном расчете, а также погрешностями округления. Ниже в таблице 1 приведены
значения коэффициентов в ручном и машинном расчетах (необходимо делать анализ
размерностей).
= 3,999×10-6 м/Н. Расчет на ЭВМ дает значение
коэффициента 4×10-6
м/Н. Разница объясняется учетом влияния продольных деформаций стержней в
машинном расчете, а также погрешностями округления. Ниже в таблице 1 приведены
значения коэффициентов в ручном и машинном расчетах (необходимо делать анализ
размерностей).
Таблица 1
|
Ручной расчет
|
Расчет на ЭВМ
|
|
d11
|
3,999×10-6
|
4×10-6
|
|
d22
|
0,665×10-6
|
0,666×10-6
|
|
d21
|
-0,331×10-6
|
-0,333×10-6
|
получим следующий вид матрицы относительной податливости 
 (обозначена ниже как D1):
(обозначена ниже как D1):
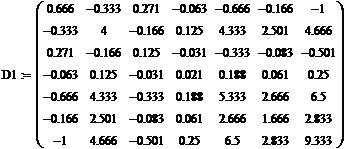
Матрицу C определим выражением

 (4.1),
(4.1),
где 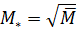
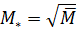 , и вычислим ее собственные числа λ. Первые три собственных числа: λ1=3,317*105, λ2=4,747*104, λ3=3,353*103. Частоты собственных колебаний найдем так:
, и вычислим ее собственные числа λ. Первые три собственных числа: λ1=3,317*105, λ2=4,747*104, λ3=3,353*103. Частоты собственных колебаний найдем так:

 (4.2).
(4.2).
Результаты расчетов: ω1=6,272 с-1, ω2=16,58 с-1, ω3=62,383 с-1.
Первые две частоты незначительно отличаются от найденных в п. 3.2 в меньшую
сторону вследствие учета масс стержней.
Собственные формы колебаний определим по формуле

 (4.3),
(4.3),
где Bi - собственные векторы матрицы С. В данном случае
собственные формы примут вид:



С помощью данных векторов построим первые три формы
собственных колебаний рамы (рисунок 10).

Рисунок 10 - Первые три формы собственных колебаний рамы
4.
Определение амплитуды установившихся колебаний. Расчет траектории движения
центра масс двигателя
Исходные данные: скорость вращения ротора n=214 об/мин, амплитуда
возмущающей нагрузки P=2100 Н. В случае равномерного вращения (φ=Θt) нагрузку можно разложить на составляющие Pi (i - номер обобщенной
координаты, в направлении которой прикладывается составляющая):

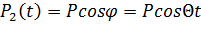
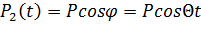 ,
,

Рисунок 11 - Разложение нагрузки Р
Поскольку система линейна, можно использовать принцип
суперпозиции: рассчитать отдельно на силы P1(t) и P2(t), а затем сложить
результаты. Сформируем векторы амплитуд гармонической нагрузки
косинусоидального (Pc) и синусоидального (Ps) характера:
Константа Р в данных векторах занимает место, соответствующее
той обобщенной координате, по направлению которой приложена гармоническая
нагрузка. Например, нагрузка P2(t), имеющая косинусоидальный характер, приложена в направлении
обобщенной координаты q2, поэтому амплитуду Р этой нагрузки размещаем на
месте второго компонента вектора Рc.
 ,
,  .
.
Амплитуды Ac и As установившихся колебаний от воздействия
косинусоидальной и синусоидальной нагрузки определяются из векторных уравнений:

 ,
, 
 , (5.2)
, (5.2)
в которых 
 - матрица относительных податливостей,
- матрица относительных податливостей, 
 - матрица относительных масс (в данном случае численно совпадает
с М), Е - единичная матрица, q -
круговая частота нагрузки, Аs и Ас
- искомые векторы амплитуд колебаний соответственно от синусоидальной и
косинусоидальной составляющих нагрузки. Размерность всех векторов и матриц
совпадает с числом степеней свободы механической системы.
- матрица относительных масс (в данном случае численно совпадает
с М), Е - единичная матрица, q -
круговая частота нагрузки, Аs и Ас
- искомые векторы амплитуд колебаний соответственно от синусоидальной и
косинусоидальной составляющих нагрузки. Размерность всех векторов и матриц
совпадает с числом степеней свободы механической системы.
Параметр l определим по формуле:

 (5.3)
(5.3)
Получим λ=2,599*104.
Выразим из уравнений 5.2 амплитуды Ac и As:
Результаты вычислений (в м):

 .
.
Вектор амплитуд А от суммарного действия составляющих P1(t) и P2(t):

 (5.5)
(5.5)
Для данной задачи он равен (в м):

Вектор узловых перемещений по направлениям обобщенных
координат:

 (5.6)
(5.6)
Траекторию движения центра масс электродвигателя рассчитаем
без учета его эксцентриситета относительно оси вращения ротора, т.е. фактически
рассчитывается динамическое перемещение оси вращения. Результаты построений
представлены на рисунке 12. Из построенного графика видим, что траектория
представляет собой эллипс.

Рисунок 12 - Траектория движения центра масс электродвигателя (в
м)
5.
Построение эпюры изгибающих моментов в амплитудном состоянии
Для построения динамической эпюры изгибающих моментов
необходимо найти значения сил инерции в амплитудном состоянии по направлениям обобщенных
координат q1, q2,…, q7. Векторы сил инерции Фs, Фс,
возникающих соответственно от синусоидальной и косинусоидальной составляющих
гармонической нагрузки, определим из уравнений:

 ,
, 
 (6.1)
(6.1)
Решение данных уравнений:

 ,
, 
 (6.2)
(6.2)
Результаты вычислений (в Н):

Амплитудные значения изгибающих моментов определяют из расчета
рамы на суммарное действие вычисленных сил инерции и амплитудных значений
составляющих гармонической нагрузки. Эпюру моментов целесообразно построить,
используя единичные эпюры моментов 
 :
:

 ,
, 
 ,
,
в которых Фsi - i-й компонент вектора Фs, Мps - эпюра статических моментов от действия
амплитуды «синусоидальной» силы P1(t), n - число степеней свободы системы. Обозначения во втором
уравнении имеют аналогичный смысл. Очевидно, 
 ,
, 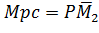
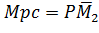 .
.
Для представления эпюр в численном виде на раме необходимо
отметить ряд сечений. Количество сечений ns должно быть таким, чтобы
любая единичная или грузовая эпюра однозначно представлялась соответствующим
числовым вектором. Если в жестком узле соединяются три стержня, то
рассматривают три сечения, примыкающие к узлу. Данную раму я счел
целесообразным рассечь 11-ю сечениями (ns=11) (рисунок 13).

Рисунок 13 - Расположение и нумерация сечений
Необходимо также назначить правило знаков, поскольку обычно
на эпюрах моментов в рамах знаки не ставятся. Например, в рассматриваемой задаче
за положительные ординаты приняты следующие: на горизонтальном стержне -
отложенные сверху, на вертикальном стержне - справа. В таблице 2 приведены
значения ординат единичных и грузовых эпюр в намеченных сечениях.
Таблица 2 - Значения единичных моментов 
 , а также Mps и Mpc в сечениях рамы
, а также Mps и Mpc в сечениях рамы
Сечения 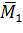
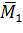 , м
, м
 , м
, м
 , м
, м
 , м
, м
 , м
, м
 , м
, м
 , мMpc,
, мMpc,
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
2
|
1,15
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2,415
|
|
3
|
2,3
|
0
|
1,15
|
0
|
0
|
0
|
0
|
0
|
4,83
|
|
4
|
2,3
|
0
|
1,15
|
0
|
-2,3
|
0
|
-4,6
|
0
|
4,83
|
|
5
|
1,15
|
0,575
|
-0,575
|
-3,45
|
-1,15
|
-4,6
|
-4,83
|
2,415
|
|
6
|
0
|
-4,6
|
0
|
0
|
-4,6
|
-2,3
|
-4,6
|
-9,66
|
0
|
|
7
|
0
|
0
|
0
|
0
|
2,3
|
0
|
4,6
|
0
|
0
|
|
8
|
0
|
0
|
0
|
0
|
0
|
0
|
2,3
|
0
|
0
|
|
9
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
10
|
0
|
-2,3
|
0
|
0
|
-2,3
|
-2,3
|
-2,3
|
-4,83
|
0
|
|
11
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Значения векторов Ms и Mc (в Н*м):



Рисунок 14 - Амплитудные эпюры моментов от составляющих
вибрационной нагрузки P1(t) и P2(t)
Эпюра динамических моментов изменяется во времени по формуле


Максимальные по модулю значения динамических моментов определяются
выражением:

 , i=1,2…ns
, i=1,2…ns
и в данном случае составят (в Нм):
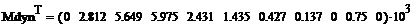
Итак, максимальный изгибающий момент в раме, обусловленный
действием гармонической нагрузки, в условиях стационарных колебаний:


Он возникает в сечении 4 (узел с сосредоточенной массой m3).
Максимальные динамические напряжения в узле:

Кроме динамической нагрузки, учтем силу тяжести
электродвигателя Q=15 кН в виде вектора
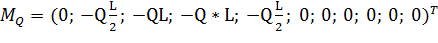
 ,
,
Тогда суммарный изгибающий момент составит 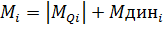
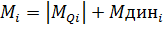 . Своего максимального значения он, также как и Мдин,
достигнет в 4-м сечении: Mmax=40,475
кН*м.
. Своего максимального значения он, также как и Мдин,
достигнет в 4-м сечении: Mmax=40,475
кН*м.
Максимальные суммарные напряжения:

 .
.
Аналогично при неработающем электродвигателе:
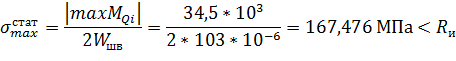
Различие между последними величинами составляет 17,3%.
Список
литературы
1.
Бусыгин, В.Г. Динамический расчет массивной плоской рамы: Методические указания
по выполнению курсового проекта по дисциплине «Аналитическая динамика и теория
колебаний» / Алт. гос. техн. ун-т им. И.И. Ползунова. - Барнаул: Изд-во АлтГТУ,
2004. - 32 с.
.
Строительная механика. Динамика и устойчивость сооружений / Под ред. А.Ф.
Смирнова. - М.: Стройиздат, 1984. - 416 с.
Приложение
спектр колебание рама амплитудный
Файл пакета MathCAD
. Расчеты для главы 4
 - начало нумерации строк и столбцов с 1 (по
умолчанию с нуля)
- начало нумерации строк и столбцов с 1 (по
умолчанию с нуля)
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 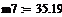 ,
,  - значения сосредоточенных масс, кг
- значения сосредоточенных масс, кг
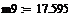
 - длина пролета, м
- длина пролета, м
 - изгибная жесткость сечения, Н*м2
- изгибная жесткость сечения, Н*м2

 - переменные-счетчики
- переменные-счетчики

- матрица масс 
 (в данном случае)
(в данном случае)
 - матрица
- матрица 

 - коэффициент пропорциональности между матрицами D и
- коэффициент пропорциональности между матрицами D и 
 , м/Н
, м/Н

- матрица относительных податливостей 

 - матрица С*
- матрица С*
 - собственные числа матрицы С*
- собственные числа матрицы С*

 - собственные частоты колебаний, 1/с
- собственные частоты колебаний, 1/с

 - собственные векторы матрицы С*
- собственные векторы матрицы С*
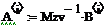 - векторы главных форм колебаний
- векторы главных форм колебаний



 - вектор значений изгибающих моментов в
выбранных сечениях от суммарного действия статических и динамических (при
амплитудных значениях) сил, Н*м
- вектор значений изгибающих моментов в
выбранных сечениях от суммарного действия статических и динамических (при
амплитудных значениях) сил, Н*м
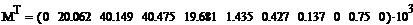
 - максимальное значение напряжения от суммарного
действия статических и динамических сил, Па
- максимальное значение напряжения от суммарного
действия статических и динамических сил, Па

 - максимальное значение напряжения при
неработающем э/д, Па
- максимальное значение напряжения при
неработающем э/д, Па
