Введение
1. Исходные данные
2. Постановка краевой задачи
3. Расчёт выходной распределенной величины
4. Расчёт интегральной передаточной функции
5. Построение логарифмической амплитудно-частотной
характеристики
Заключение
Список используемых источников
Введение
Существуют среды, которые не могут быть
математически описаны в пространстве сосредоточенных параметров (например,
электромагнитное поле, электростатическое поле, течение потока, температура и
т.д.).
Системой с распределенными параметрами
(СРП) называется система, в которой практически все сигналы (в первую очередь -
входной и выходной) являются функциями пространственных координат и времени.
Математически СРП описываются
дифференциальными уравнениями в частных производных. Также для этого вводятся
функции Грина, континуальная и интегральная передаточные функции.
Система с сосредоточенными параметрами
(ССП) является частным случаем СРП и вводится для упрощения и решения задач на
первом этапе. В большинстве случаев такого упрощения оказывается достаточно для
получения адекватных результатов, но в ряде задач распределение параметров в
пространстве оказывает существенное воздействие на результаты. В этом случае
применяется аппарат теории СРП.
Целью данной работы является моделирование
на микро и макроуровне. При моделировании на микроуровне необходимо построить
математическую модель колебания круглой мембраны. На макроуровне исследуется
гидравлическая система. При разработке и исследовании модели макроуровня
необходимо выполнить: синтез моделей в графической и матричный формах, в виде
системы обыкновенных дифференциальных уравнениях, а также анализ полученной
математической модели в статическом и динамическом режиме.
1.
Исходные данные
1) Уравнение колебания мембраны:

) Начальные условия:
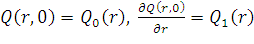
) Граничные условия:
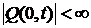
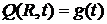
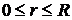 ;
; 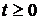 ; a > 0
; a > 0
) Стандартизирующая функция:
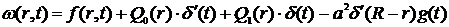
) Функция Грина:
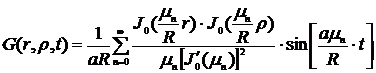
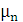 - положительные корни уравнения
- положительные корни уравнения 
) Континуальная передаточная функция:

2.
Постановка краевой задачи
Уравнение (1) представляет собой
одномерное уравнение гиперболического типа, имеющую вторую производную по
времени t. Данная мембрана имеет радиус R=2 метра и толщину 0,001 метра.
Материал мембраны - резина, модуль Юнга E=0.7 кг/мм2, поверхностная
плотность ρ=1,8 кг/м2.
Проведём идентификацию всех величин входящих в уравнение (1). В момент времени
t=0 к поверхности мембраны приложена равномерно распределенная гармоническая
сила плотностью  .
.
Дифференциальное уравнение имеет вид:

Где Q (r,t) - выходная распределённая
величина, представляющая собой ортогональную деформацию мембраны, м;(r,t) -
входное распределённое воздействие на мембраны, м/c2,граничные
условия: 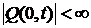 ,
,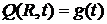 ,
, 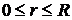 ,
, 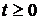 , a > 0.
, a > 0.
Для уравнения (1) формулируются следующие
условия:
начальные условия: 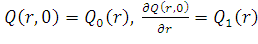
Стандартизирующая функция, компенсирующая
влияние начальных и граничных условий для данной одномерной задачи имеет вид
(2).
Функция Грина, являющаяся решением краевой
задачи при начальных и граничных условиях и входном воздействии в виде δ-функции имеет вид (3).
Континуальная передаточная функция,
являющаяся преобразованием Лапласа функции Грина имеет вид (4).
Для решения краевой задачи примем
следующие условия:
входное воздействие:
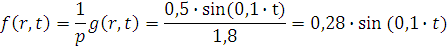
начальные условия, описывающие положение и
скорость мембраны в начальный момент времени:
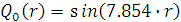 ,
, 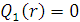 ;
;
Представим на рисунке 1 изображение
мембраны в начальный момент времени:
Рисунок 1 - Изображение мембраны в начальный
момент времени
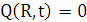
Волновая скорость мембраны:
 м/с,
м/с,
где Т - сила натяжения струны, Н;
рл - линейная плотность, примем
1,8 кг/м
С учётом входного воздействия, принятых
начальных и граничных условий стандартизирующая функция принимает вид:
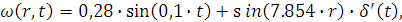
где
δ' (t) - импульсная
переменная функции.
3.
Расчёт выходной распределенной величины
Идентификация исходного уравнения
позволяет перейти к расчету распределенной выходной величины, являющейся
функцией как пространственной, так и временной координаты и рассчитываемой как
пространственно-временная композиция от произведения функции Грина на
стандартизирующую функцию:

Выходная величина Q (x,t) находится как
сумма двух составляющих:
(x,t) =Q1 (x,t) + Q2
(x,t)
гдеQ1 (x,t) и Q2
(x,t) - первая и вторая составляющие выходной величины и находятся как:
В данном случае примем радиус мембраны и
время соответственно R=2 м и t=1 c. Вычислим интеграл, связывающий выход
объекта при заданном начальном состоянии с выходными воздействиями:
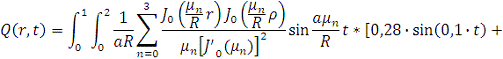

Причем 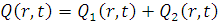


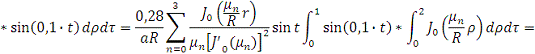

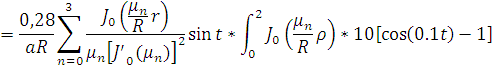
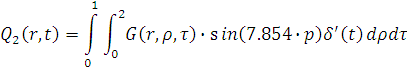
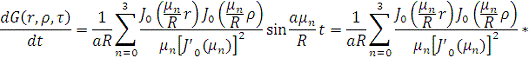
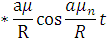

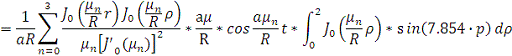
Определим значения 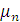 как
корни уравнения:
как
корни уравнения:
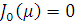
Построим функцию Бесселя

Рисунок 2 - Функция Бесселя.
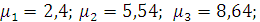
Представим функцию Грина в виде суммы
слагаемых:
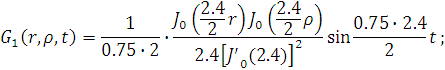
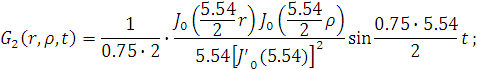
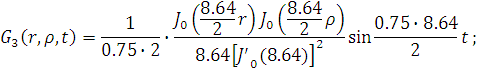
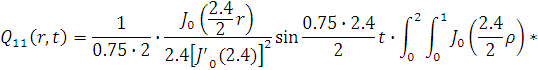
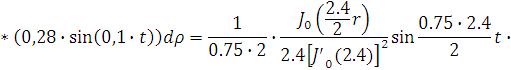
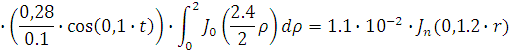

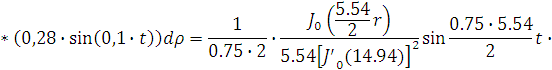
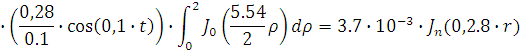

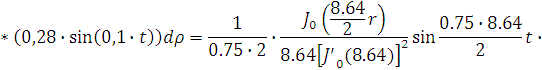
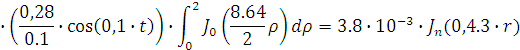
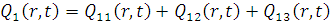

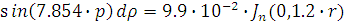
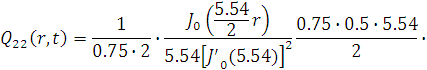

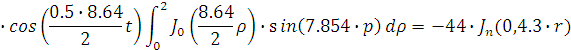

В результате получим уравнение выходной
функции состояния объекта с распределенными параметрами:
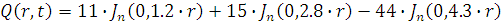
Построим функцию колебания мембраны для
t=1с и t=50с:
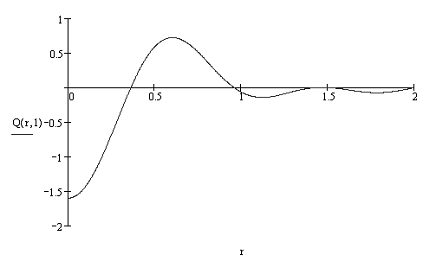
Рисунок 3. - График выходной величины Q
(x,t) при t=1 c
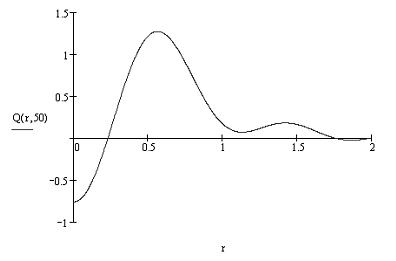
Рисунок 4. - График выходной величины Q
(x,y,t) при t=50 c
4.
Расчёт интегральной передаточной функции
По заданному дифференциальному уравнению
объекта получим выражение для передаточной функции в распределённых параметрах.
Континуальная передаточная функция имеет
вид:

Стандартизирующая функция имеет вид:
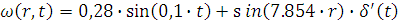
Преобразование по Лапласу
стандартизирующей функции:
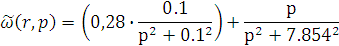
Вынесем за скобку входное воздействие,
преобразованное по Лапласу:
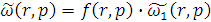

Рассчитаем интегральную передаточную
функцию как пространственную композицию от произведения континуальной функции 

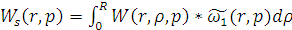
Причем 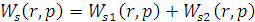
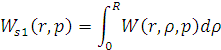
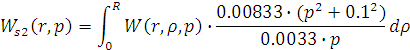

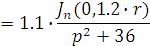

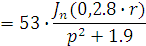
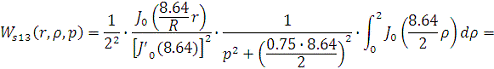
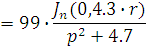
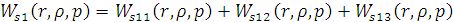
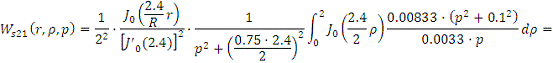

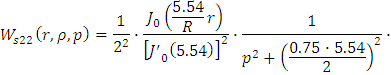
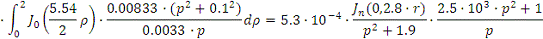
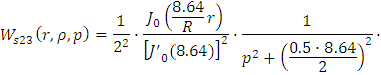
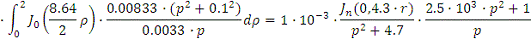
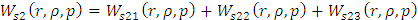
Следовательно получим:
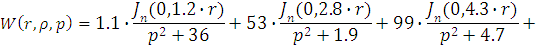
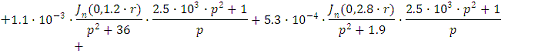

Примем 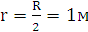 и
и 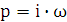 , и
получим выражение для частотной передаточной функции:
, и
получим выражение для частотной передаточной функции: