Численные методы

Содержание работы

Введение

1. Понятие определенного интеграла, его геометрический смысл, основные свойства

2. Численные методы вычисления определенных интегралов

2.1 Формула прямоугольников

2.2 Формула трапеций

2.3 Формула парабол

3. Формула Чебушева

4. Решение задач аналитическим способом

5. Применение пакета Mathcad для вычисления интегралов, проверка результатов вычислений с помощью Mathcad

Выводы

Заключение

Список литературы

Введение

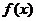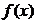Цель данной курсовой работы - изучение методов приближённого интегрирования. Для некоторых подынтегральных функций  интеграл можно вычислить аналитически или найти в справочниках. Однако в общем случае первообразная  может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами подынтегральные функции не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов. Наиболее общеупотребительными приближенными методами вычисления одномерных определенных интегралов являются, так называемые, "классические" методы численного интегрирования: метод прямоугольников, метод трапеций, метод парабол (основанные на суммировании элементарных площадей, на которые разбивается вся площадь под функцией 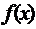). Хотя эти методы обычно предпочтительней в случае малых размерностей, они практически не годятся для вычисления многомерных интегралов, для их вычисления используются другие методы.

1. Понятие определенного интеграла, его геометрический смысл, основные свойства

Понятие определенного интеграла

Пусть функция  определена на отрезке 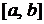, 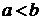. Выполним следующие операции:

)        разобьем отрезок  точками 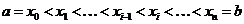 на n частичных отрезков ;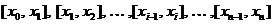

)        в каждом из частичных отрезков ,  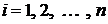выберем произвольную точку  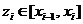и вычислим значение функции в этой точке

3)      найдем произведения

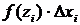
где 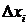 - длина частичного отрезка , ;

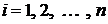4)      составим сумму

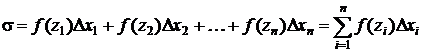                            (1)

которая называется интегральной суммой функции y = f(x) на отрезке [а, b]. С геометрической точки зрения интегральная сумма 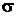 представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки 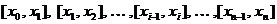, а высоты равны  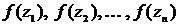соответственно (рис. 1).

Обозначим через 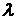 длину наибольшего частичного отрезка ;

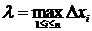)        найдем предел интегральной суммы, когда .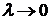

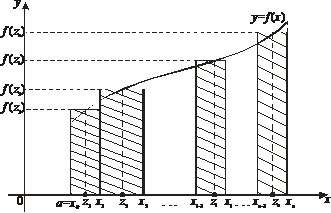
Рис. 1

Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка  на частичные отрезки, ни от выбора точек 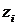 в них, то этот предел называется определенным интегралом от функции  на отрезке  и обозначается

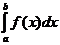
Таким образом

.

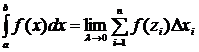В этом случае функция 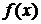 называется интегрируемой на . Числа а и b называются соответственно нижним и верхним пределами интегрирования, 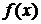 - подынтегральной функцией, 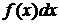 - подынтегральным выражением,  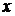- переменной интегрирования; отрезок  называется промежутком интегрирования.

Теорема: если функция  непрерывна на отрезке , то она интегрируема на этом отрезке.

Геометрический смысл определенного интеграла

Пусть на отрезке  задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу - осью Ох, слева и справа - прямыми x = a и x = b (рис. 2).

Рис. 2

Определенный интеграл 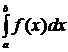 от неотрицательной функции  с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа - отрезками прямых  и , снизу - отрезком  оси Ох.

Основные свойства определенного интеграла

1.   Значение определенного интеграла не зависит от обозначения переменной интегрирования

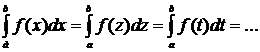
2.   Определенный интеграл с одинаковыми пределами интегрирования равен нулю

3.      Если , то, по определению, полагаем

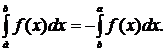
4.   Постоянный множитель можно выносить за знак определенного интеграла:

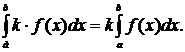
5.   Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

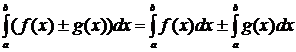
.        Если функция 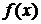 интегрируема на  и , то

7.      (теорема о среднем). Если функция  непрерывна на отрезке , то на этом отрезке существует точка , такая, что

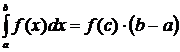
2. Численные методы вычисления определенных интегралов

.1 Формула прямоугольников

Рассмотрим первый вид приближённого вычисления:

требуется вычислить определённый интеграл

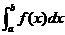
Пусть на отрезке [a,b] задана непрерывная функция y=f(x). Разделим отрезок [a,b], аналогично как в формуле трапеций: точками a=x0,x1,x2,…,xn=b на n равных частей длины Δх, где Δх=(b-a)/n.

Обозначим через y0,y1,y2,…,yn-1,yn значение функции f(x) в точках x0, x1, x2…,xn, то есть, если записать в наглядной формуле:

Y0=f(x0), y1=f(x1), y2=f(x2)…yn,=f(xn).

В данном способе подынтегральную функцию заменяем функцией, которая имеет ступенчатый вид (на рис. выделена).

Составим суммы y0Δx+ y1Δx1+ y2Δx2…+yn-1Δx; Y1Δx+ y2Δx+…+ynΔx

Каждое слагаемое этих сумм выражает площадь, полученных прямоугольников с основанием Δх, которое является шириной прямоугольника, и длиной выраженной через yi: Sпр=a*b=yiΔx.

Каждая из этих сумм является интегральной суммой для f(x) на отрезке [a,b], и равна площади ступенчатых фигур, а значит приближённо выражает интеграл. Вынесем Δx=(b-a)/n из каждой суммы, получим:

f(x)dx≈Δx(y0+y1+…+yn-1);

f(x)dx≈Δx(y1+y2+…+yn).

Выразив x, получим окончательно:

f(x)dx≈((b-a)/n)(y0+y1+…+yn-1);(1)

f(x)dx≈((b-a)/n)(y1+y2+…+yn);(1*)

Ошибка, совершаемая при вычислении интегралов по формуле прямоугольников, будет тем меньше, чем больше число n (то есть чем меньше шаг деления

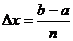
Для вычисления погрешности этого метода используется формула:

=

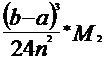
где 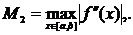 Результат полученный по формуле (1) заведомо даёт большую площадь прямоугольника, так же по формуле (1*) даёт заведомо меньшую площадь, для получения среднего результата используется формула средних прямоугольников

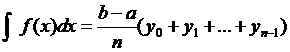 (1**)

2.2 Формула трапеций

Возьмём определённый интеграл

∫f(x)dx

где f(x)- непрерывная подынтегральная функция, которую мы для наглядности будем предполагать положительной. При вычислении интеграла с помощью формулы трапеций подынтегральная функция f заменяется функцией, график которой представляет собой ломанную линию (на рисунке 2 красным цветом), звенья которой соединяют концы ординат yi-1 и yi (i=1,2,…,n).

определенный интеграл mathcad вычисление

Тогда площадь криволинейной трапеции, ограниченной линиями x=a, x=b, y=0, y=f(x), а значит (следуя из геометрического смысла), и значение нужного нам интеграла, приблизительно равна сумме площадей обычных трапеций с основаниями yi-1 и yi и высотой h=(b-a)/n, так как (если более привычно выражать для нас) h это Δx,a Δx=(b-a)/n при делении отрезка на n равных отрезков при помощи точек x0=a<x1<…<xn=b. Прямые x=xk разбивают криволинейную трапецию на n полосок. Принимая каждую из этих полосок за обыкновенную трапецию, получаем, что площадь криволинейной трапеции приблизительно равна сумме обыкновенных трапеций.

Площадь крайней полоски слева, как помниться из школьного курса геометрии, равна произведению полусуммы основания на высоту.

S=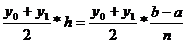

Итак, запишем сказанное выше в математическом виде

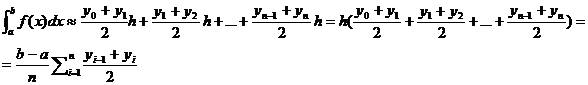
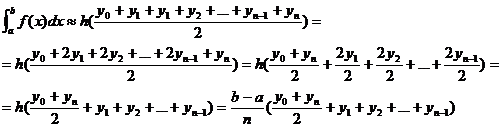 (2)

Формула (2) и есть формула трапеций

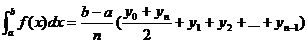
Для определения погрешности интеграла вычисленного с помощью формулы трапеций используется формула

где

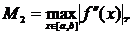
2.3 Формула парабол

Существует два подхода к формуле парабол (Симпсона). В одном используется парабола в другом нет.

А) с использованием параболы.

Разделим отрезок [a;b] на чётное число равных частей n=2m. Площадь криволинейной трапеции, соответствующей первым двум отрезкам [x0,x1], [x1,x2] и ограниченной заданной кривой y=f(x), заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через три точки M0[x0,y0], M1[x1,y1], M2[x2,y2] и имеющей ось, параллельную оси Oy (рис). Такую криволинейную трапецию будем называть параболической трапецией.

Уравнение параболы с осью, параллельной оси Oy, имеет вид:

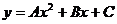
Коэффициенты A, B и C однозначно определяются из условия, что парабола проходит через три заданные точки. Аналогичные параболы строятся и для других пар отрезков. Сумма параболических трапеций и даст приближённое значение интеграла. Сначала вычислим площадь одной параболической трапеции. Для этого докажем лемму.

Лемма: если криволинейная трапеция ограничена параболой 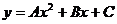, осью Ox и двумя ординатами, расстояние между которыми равно 2h, то её площадь равна

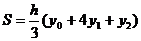 (3)

где y0 и y2- крайние ординаты, а y1- ордината кривой в середине отрезка.

Доказательство

Расположим вспомогательную систему координат так, как показано на рис. Коэффициент в уравнение параболы 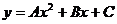 определяются из следующих уравнений:

Если x0=-h, то

Если x1=0, то 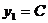 (4)

Если x2=-h, то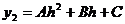

Считая коэффициенты A. B, C известными определим площадь параболической трапеции с помощью определённого интеграла:

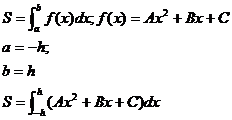
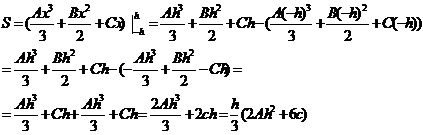
из равенства (4) следует, что

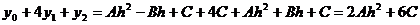
следовательно: 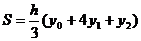 ч.т.д. пользуясь формулой (3), можно написать приближённые равенства, учитывая, что

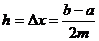
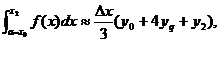
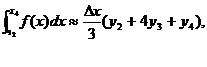
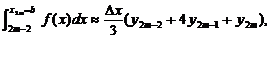
складывая левые и правые части, получим слева искомый интеграл, справа его приближённое значение

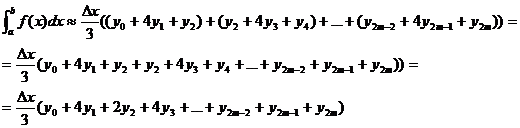
или

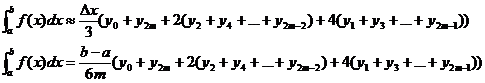 (5)

Это и есть формула Симпсона. Здесь число точек деления произвольно, но чем это число больше, тем точнее сумма в правой части равенства даёт значение интеграла. Формула Симпсона даёт самое точное значение интеграла (из классических формул приближённого интегрирования), погрешность для этого метода находится по формуле:

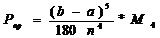
где

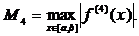
Б) Без использования парабол

В тех случаях, когда линия y=f(x) между x=a и x=b мало изогнута, интеграл 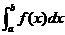 приближенно выражается достаточно простой формулой.

Будем считать f(x) положительной и искать площадь криволинейной трапеции aABb. Для этого разделим отрезок [a;b] точкой  пополам и в точке c(c,f(c))проведём касательную к линии y=f(x). После этого разделим [a,b] точками p и g на 3 равные части и проведём через них прямые x=p и x=q. P и Q - точки пересечения прямых с касательной. Соединив AP и BQ, получим 3 прямолинейные трапеции aAPp, pPQq, qQBb. Сумма площадей этих трапеций равна будет примерно равна площади криволинейной трапеции aABb:

Обозначим: Aa, Pp, qQ, bB - основания трапеций;

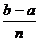- высота трапеций, в данном случае число n строго задано n=3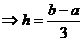

Получаем

(6)

Обозначим, что: aA=f(a)=ya, bB=f(b)=yb. Отрезки pP и qQ не являются ординатами точек линии y=f(x), так как P и Q лежат на касательной. Но нам нужна сумма этих отрезков, которая выражается через среднюю линию трапеции и равна полусумме её оснований, откуда . Значит 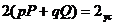. Формула (6) принимает вид:

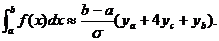(7)

Эта формула называется малой формулой Симпсона.

Малая формула Симпсона пригодна, когда график подынтегральной функции мало изогнут, например для случая, изображённого на рисунке, применять малую формулу уже нельзя, так как она даёт значение 0 на [a,b]. Но если отрезок [a,b] разбить на части [a,c] и [c,b] и к каждому из них применить формулу (7), то получится приемлемый результат.

Эта идея лежит в основе вывода «большой» формулы Симпсона.

Для вычисления интеграла 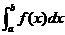 выберем какое-либо чётное число и разложим [a,b] на n равных частей точками 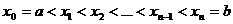. Интеграл представим в виде суммы

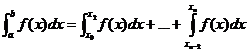
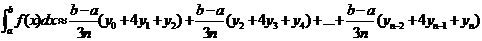
Раскроем скобки

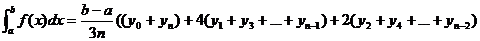
Это и есть «большая формула Симпсона». Её точность, также как и у всех формул рассмотренных выше, тем выше, чем больше n. Эта формула совпадает с формулой (5), выведенной с помощью парабол. Для оценки погрешности формулы Симпсона используется формула

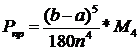
Качество этой формулы лучше, чем формулы трапеции и прямоугольников, так как при одном и том же n она даёт большую точность.

3. Формула Чебушева

В технических вычислениях часто применяется формула Чебышева для приближенного интегрирования.

Пусть снова требуется вычислить

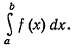
Заменим подынтегральную функцию интерполяционным многочленом Лагранжа Р (х), взяв на отрезке [а, b] некоторые n значений функции

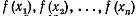
где  какие угодно точки отрезка [а, b]:

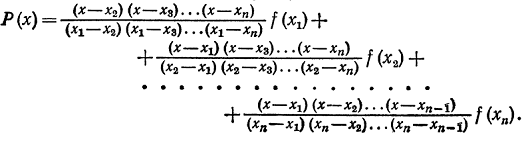
Получим следующую приближенную формулу интегрирования:

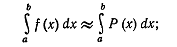
после некоторых вычислений она примет вид

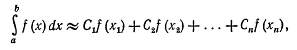
где коэффициенты Ci вычисляются по формулам

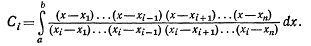
Формула (8) громоздка и неудобна для вычислений, так как коэффициенты С выражаются сложными дробями.

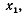
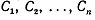Чебышев поставил обратную задачу: задать не абсциссы , а коэффициенты  и определить абсциссы

Коэффициенты Ci- задаются так, чтобы формула (8) была возможно проще для вычислений. Очевидно, что это будет тогда, когда все коэффициенты Ci равны между собой: .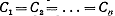

Если обозначить общее значение коэффициентов  через Cn то формула (8) примет вид

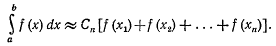
Формула (9) представляет вообще приближенное равенство, но если f(x) есть многочлен степени не выше n - 1, то равенство будет точным. Это обстоятельство и позволяет определить вели- чины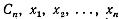

Чтобы получить формулу, удобную для любого промежутка интегрирования, преобразуем отрезок интегрирования [а, b] в отрезок [-1, 1]. Для этого положим  ; тогда при t = - 1 будет х = а, при t=1 будет х = b.

Следовательно

,

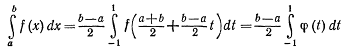где через ф (t) обозначена функция от t, стоящая под знаком интеграла. Таким образом, задача интегрирования данной функции

f(x) на отрезке [а, b] всегда может быть сведена к интегрированию некоторой другой функции ф(х) на отрезке [-1, 1].

Итак, задача свелась к тому, чтобы в формуле

подобрать числа 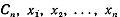 так, чтобы эта формула была точной для всякой функции f(x) вида

Заметим, что

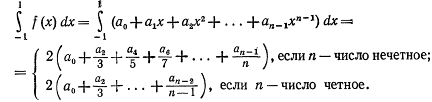
С другой стороны, сумма, стоящая в правой части равенства (10), на основании (11) будет равна

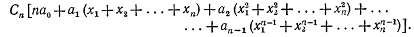
Приравнивая выражения (11) и (12), получим равенство, которое должно быть справедливо при любых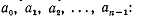

Приравняем коэффициенты при  в левой и правой частях равенства

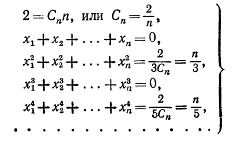
Из последних n - 1 уравнений находим абсциссы  Эти решения найдены Чебышевым для различных значений n.

Ниже приводятся найденные им решения в случаях, когда число n промежуточных точек равно 3, 4, 5, 6, 7, 9

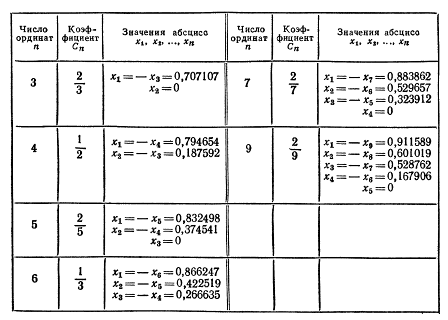
Таким образом, приближенное вычисление интеграла на отрезке [ - 1,1] производится по следующей формуле Чебышева

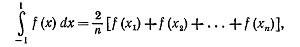
где n -какое-либо из чисел 3, 4, 5, 6, 7 или 9, a  -числа, приведенные в таблице. В качестве n нельзя брать число 8 или числа, превосходящие 9; в этом случае система уравнений (13) дает мнимые корни. Когда заданный интеграл имеет пределы интегрирования а и b, формула Чебышева принимает вид

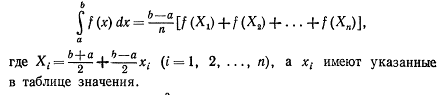
Отметим, что теория приближенного вычисления интегралов получила дальнейшее развитие в работах академика А. Н. Крылова (1863-1945).

4. Решение задач аналитическим способом

Формула Ньютона-Лейбница.

Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции 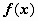, то

Доказательство.

Мы установили, что функция - первообразная непрерывной f(x). Так как F(x) - тоже первообразная, то Ф(x) = F(x) + C. Положим в этом равенстве x = a.

Так как

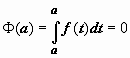
то

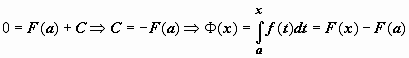
В равенстве переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x , верхний предел x обозначим b. Окончательно

Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом

(здесь читается как "подстановка от a до b"), поэтому формулу Ньютона-Лейбница обычно записывают так

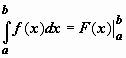
Пример применения формулы Ньютона-Лейбница

Формула интегрирования по частям для определённого интеграла.

Если u(x), v(x) - непрерывно дифференцируемые функции, то

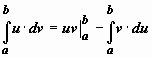
Доказательство.

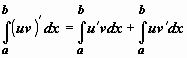
Функция в левом интеграле имеет первообразную uv, по формуле Ньютона-Лейбница

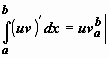
Следовательно

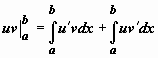
откуда и следует доказываемое равенство.

Пример

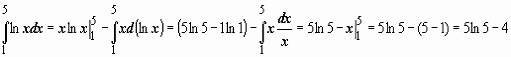
Замена переменной в определённом интеграле.

Теорема. Пусть функция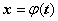

определена, непрерывно дифференцируема и монотонна на отрезке ,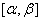

,

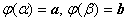функция 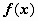непрерывна на отрезке [a, b].

Тогда

Доказательство.

Пусть F(x) - первообразная для функции f(x), т.е. 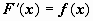, тогда 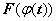- первообразная для функции .

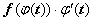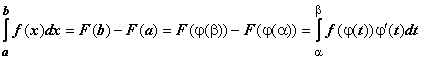
что и требовалось доказать.

При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.

Пример

.

5. Применение пакета Mathcad для вычисления интегралов, проверка результатов вычислений с помощью Mathcad

Аналитическое вычисление определенного интеграла.

Для вычисления определенного интеграла следует использовать специальный оператор Definite Integral панели Calculus (клавиши Shift+7).

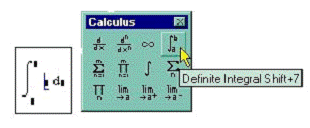
Оператор содержит четыре маркера, которые заполняются в полном соответствии с принятой в математике формой. В отличие от неопределенного интеграла, определенный может быть вычислен как аналитически, так и численно. Сначала нужно вычислить определенный интеграл аналитически и если это не удается - численно.

Чтобы вычислить определенный интеграл аналитически, необходимо заполнить все маркеры соответствующего оператора, а затем ввести оператор символьного вывода «→» . В случае аналитического интегрирования пределы могут быть как числовыми, так и буквенными.

Можно даже использовать символ бесконечности (Ctrl+Shift+z).

Численное вычисление определенного интеграла.

Численное интегрирование в Mathcad - это куда более тонкая операция, чем интегрирование аналитическое. Зачастую, чтобы получить правильный ответ, нужно верно задать точность, выбрать наиболее эффективный алгоритм, проанализировать поведение функции и, при наличии точек разрыва, представить интеграл в виде суммы интегралов. Неплохо также иметь общее представление об алгоритмах численного интегрирования, чтобы понимать, в каких случаях они могут быть использованы, а в каких нет.

Если возникло желание использовать численный метод при интегрировании, то прежде всего нужно присвоить всем параметрам, входящим в интегрируемую функцию, конкретные значения. Пределы интегрирования, естественно, также должны быть числами. В качестве оператора вывода следует использовать оператор численного вывода «=».

В систему Mathcad разработчиками было встроено несколько численных методов интегрирования: метод трапеций, метод средних прямоугольников, метод Симпсона и др. Каждый из методов подходит для определенной группы функций или типа интеграла.

Чтобы произвести смену численного метода, нужно щелкнуть правой мышью по оператору интегрирования и откроется его контекстное меню. Оно содержит список вариантов возможных алгоритмов интегрированияSelect (Автоматический выбор).

Метод интегрирования выбирается системой автоматически. Лучше, если по умолчанию будет отмечен именно этот пункт.(Ромберга)

Весьма эффективный метод, применяемый для вычисления интегралов от функций, не имеющих особенностей. Является основным методом в Mathcad.(Адаптивный)

Метод, предназначенный для вычисления интегралов от функций, быстро изменяющихся на промежутке. При этом ширина интервала разбиения не постоянна, как в случае метода Ромберга, а изменяется в зависимости от скорости изменения функции. В большинстве случаев данный алгоритм дает более точный результат, чем метод Ромберга. Поэтому этот метод используется по умолчанию. Адаптивный метод дает возможность интегрировать функции с разрывами, чего не может метод Ромберга.

Если при интегрировании возникла проблема вычисления интеграла методом по умолчанию, следует сменить алгоритм и попытаться вычислить этот интеграл другим методом.

Выводы

Очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное.

Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же очень важно то, какой будет взят шаг интегрирования.

Хотя численные методы и не дают очень точного значения интеграла, но они очень важны, так как не всегда можно решить задачу интегрирования аналитическим способом.

Для проверки вычислений или вычисления определенных интегралов можно использовать пакет Mathcad, но для точности его вычислений также надо знать какой метод интегрирования лучше использовать.

Заключение

В завершении работы, хочется отметить ряд особенностей применения рассмотренных выше методов. Каждый способ приближённого решения определённого интеграла имеет свои преимущества и недостатки, в зависимости от поставленной задачи следует использовать конкретные методы. Если необходимо быстро получить решение, но нет необходимости в большой точности ответа, следует воспользоваться одним из методов прямоугольника. Если же необходимо получить наиболее точный результат, идеально подходит метод Симпсона. Метод трапеций даёт ответ более точный, чем метод прямоугольников, но методу Симпсона он сильно уступает, этот метод можно назвать «золотой серединой» между двумя другими. Можно повысить точность вычисления увеличивая шаг интегрирования.

Так же очень важны аналитические способы нахождения определенного интеграла, но они не всегда выполнимы, т.к. не всегда можно найти первообразную функции.

Пакет Mathcad дает точные результаты. Его можно использовать, как для проверки результатов, так и для вычисления интегралов.

Наилучший способ вычисления определенных интегралов выделить нельзя. И лучше всего для каждого отдельного случая подобрать свой метод решения.

Список литературы

1.   Волков Е. А. Численные методы.М., Высшая школа, 1990.

2.      Гусак А.А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. - Мн., 1998. - 544 с. (1 т.), 448 с. (2 т.).

.        Гусак А.А. Математический анализ и дифференциальные уравнения. - Мн.: ТетраСистемс, 1998. - 416 с.

.        Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. I. - М.: Наука, 1982. - 616 с.

Интеграл - Пресс, 2004.

5.   Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: Учебник для вузов Под ред. проф. Н.Ш. Кремера. - М.: ЮНИТИ, 2002. - 471 с.

6.      Пискунов Н. С. Дифференциальное и интегральное исчисление. М.,

7.   Шипачев В. С. Высшая математика. М., Высшая школа, 1990.

8.   Яблонский А.И., Кузнецов А.В., Шилкина Е.И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С.А. Самаля. - Мн.: Выш. шк., 2000. - 351 с.

9.   Иванов А. А. Математика. Пособие по лабораторным работам в Mathcad’e. Изд. Академии, 2004.

10.    Давыдова Т. В. И др. Математика: Методические рекомендации и задания по курсовым работам. Смоленск. ВУ ВПВО, 2005г.59с.