Стандартная и рациональная схемы статистического моделирования
Содержание
Введение
.
Аналитическое решение
. Стандартная
схема статистического моделирования
.
Рациональная схема статистического моделирования
Заключение
Список
использованных источников
Приложения
Введение
Требуется определить математическое ожидание выходного сигнала X
неустойчивого апериодического звена в заданный момент времени Т. Модель звена:
где
g = G( t ), X(0) = A.
Данная
модель звена содержит случайные параметры с равномерным законом распределения в
заданных интервалах.
Допустимая
абсолютная погрешность результата: εдоп. =
0,01.
Задачу
решить тремя способами:
· Используя стандартную схему статического моделирования;
· Используя рациональную схему статистического моделирования с
применением метода расслоенной выборки;
· Аналитически.
Результаты аналитического решения использовать для проверки результатов
статистического моделирования и для обоснования построения рациональной схемы
моделирования.
При использовании рациональной схемы статистического моделирования
обеспечить снижение требуемого количества опытов по сравнению со стандартной
схемой не менее чем в 10 раз.
Исходные данные (вариант 2-2):
G =
1 ÷ 1.4,
a = 0.6
÷ 0.8,
T =
1.3,
A = 1,
k =
1.2.
1.
Аналитическое решение
статистический
моделирование математический апериодический
Решим дифференциальное уравнение вида[1]:
(1)
где
g = G(t),
X(0) = A.
Сначала
найдем решение соответствующего однородного дифференциального уравнения:
Подставим полученное решение однородного дифференциального уравнения в
(1):
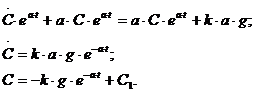
Найдем
С1 из условия X(0) = A:
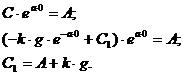
В
результате имеем:
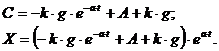
Решение
исходного дифференциального уравнения (1) имеет вид:
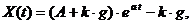(2)
где
g - случайный параметр, распределенный по равномерному
закону в интервале [1;1.4],
a -
случайный параметр, распределенный по равномерному закону в интервале
[0.6;0.8],
Для Т=1.3 с учетом статистической независимости k и g
определим искомую характеристику:
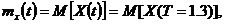
где
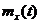- искомое математическое ожидание.
С
учетом (1) находим :
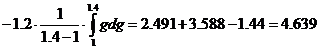
Таким
образом,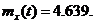 
Определим дисперсию :
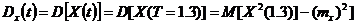, (3)
где
- дисперсия выходного сигнала.
Введем
обозначение: 
и найдем 
:
(4)
Рассчитаем
слагаемые, входящие в (4):
;
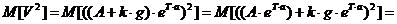
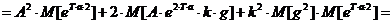
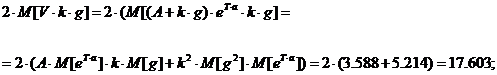
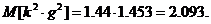
Таким
образом, 
21.77.
Подставив полученные значения в (3), определим дисперсию выходного
сигнала:
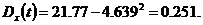
С
учетом известной дисперсии оценим необходимое количество опытов с погрешностью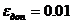 
:
,
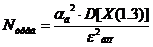где
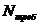- необходимое количество опытов.
Значение
параметра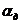 
зависит от доверительной вероятности 
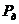. Примем Pд=0,997 и aд=3. Подставив значения параметров в (5), получим:
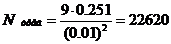опытов.
Все
перечисленные расчеты производились в математическом пакете MathCAD
[2], приводятся в Приложении А.
2. Стандартная схема статистического моделирования
Если трудоемкость эксперимента имеет существенное значение, применяются
итерационные алгоритмы получения оценок [3]. Идея итерационных алгоритмов
состоит в том, что определение точности и требуемого количества опытов
проводится в ходе эксперимента на основе получаемых оценок искомых параметров.
Блок-схема типового итерационного алгоритма приведена на рисунке 1.
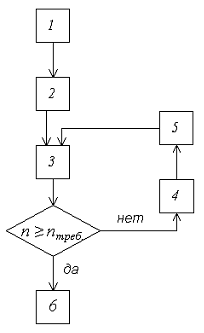
. Проведение начальной серии опытов объемом n и накопление сумм
,
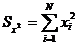где
- реализация случайной величины x в
отдельных опытах.
. Вычисление
оценок математического ожидания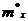 
и
дисперсии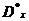 
:
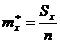, (6)
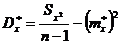. (7)
3. Получение оценки требуемого количества опытов:
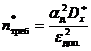. (8)
. Проведение
дополнительной серии опытов объемом 
и
накопление сумм:
, 
.
5. Уточнение оценок математического ожидания m*x и дисперсии D*x:
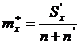, (9)
. (10)
Провели
начальную серию опытов n = 200. Накопили суммы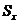 
и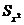 
: 
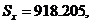
Вычислили оценки математического ожидания и дисперсии
по (6) и (7): 
Получили оценку требуемого количества опытов 
по (8): 
Так как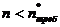 
, то провели дополнительную серию опытов 
Для того, чтобы не проводилось лишнее число опытов
искусственно уменьшили n’ в 2
раза. Таким образом, 
опытов. Вновь накопили суммы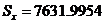 
, 
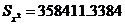и
уточнили оценки математического ожидания и дисперсии по (9) и (10):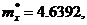 
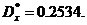Тогда оценка требуемого количества опытов получилась:
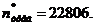Значение n = 16260+200=16460 опытов.
После
данной итерации 16460<22806, следовательно, продолжили выполнение
итерационного алгоритма. Получили следующие результаты:
.
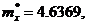
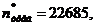
Проверили
выполнение условия 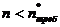. Данное условие не выполнилось, так как
22806>22685, следовательно, алгоритм завершил работу.
Окончательные
результаты :
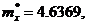
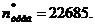
Дифференциальное
уравнение (1) решается численным интегрированием методом Эйлера первого порядка
[4] с шагом 0.001. Программа, реализующая итерационный алгоритм, написана в
среде Borland Delphi 7 [5]. Текст программы
представлен в Приложении Б.
Проблема
метода связана с тем, что результаты проводимых серий опытов складываются
случайным образом и при конечных n возможны следующие негативные эффекты:
· Выборочный закон распределения может существенно отличаться
от нормального. Чаще всего оценки требуемого количества опытов оказываются
завышенными.
· Разброс составляющих выборку реализаций случайной величины
может оказаться существенно меньше истинного ее разброса.
· Оценки требуемого количества опытов оказываются резко
заниженными, а результаты моделирования - неточными. Во избежание подобных
ситуаций рекомендуется выбирать объем начальной серии опытов не менее 100-500.
· В выборке могут оказаться реализации случайной величины,
значительно отличающиеся от ее среднего значения, в непропорционально большом
количестве (возможны завышенные оценки требуемого количества опытов для
получения точных результатов моделирования).
3. Рациональная схема статистического моделирования
Требуемое число опытов для решения поставленной задачи с заданной
точностью можно уменьшить, если воспользоваться одним из методов снижения
трудоемкости статического моделирования. В качестве такого метода рассмотрим
метод расслоенной выборки [3].
В соответствии с данным методом область G возможных значений случайного вектора разбивается на K=10 непересекающихся областей Gk:
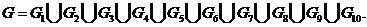
Метод
предполагает проведение статического моделирования для каждой из областей Gk с использованием для вектора случайных параметров плотностей
распределения вероятностей
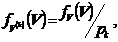
где
pk - вероятность попадания случайного вектора V в
область Gk
.
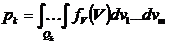В
нашем случае pk = 0.1.
Блок-схема итерационного алгоритма метода расслоенной выборки приведена
на рисунке 2.
Рисунок 2 - Блок-схема итерационного алгоритма метода
расслоенной выборки.
.Если для области Gk выполним Nk
опытов, получим оценку математического ожидания искомого показателя для данной
области:
. (11)
Результирующая
оценка 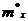должна рассматриваться как случайная дискретная
величина, значения которой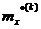 
наблюдаются
с вероятностями pk . Тогда результирующая оценка определяется
усреднением:
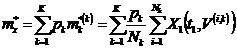. (12)
.Определим
дисперсию оценки (9), имея в виду, что все N1+ N2+ N3+…+ N10
слагаемые - независимые случайные величины:
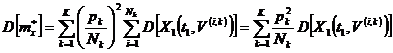. (13)
Дисперсия
случайной величины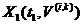 
может быть оценена следующим образом:
(14)
3.
Введя в рассмотрение доли от общего количества опытов, соответствующие областям
Gk,
,
на
основе (10) получим соотношение для определения количества опытов, необходимого
для получения результата с погрешностью не выше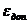 
:
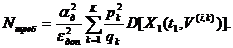(15)
При
удачном разбиении области G и удачном выборе соотношения количества опытов для
отдельных областей Gk дисперсия
оценки (13) может быть существенно снижена. Оптимальные значения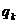 
должны быть пропорциональны произведениям 
Провели
начальную серию опытов N=200. После проведения данной серии опытов были
получены следующие результаты:
· Оценка математического ожидания для каждой из 10 областей на
основании (11):
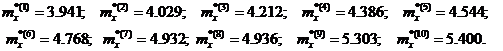
· Результирующая оценка математического ожидания по (12):
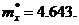
· Дисперсия для каждой из 10 областей по (14):
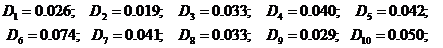
· Дисперсия оценки математического ожидания по (13):
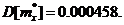
· Требуемое количество опытов, рассчитанное по (15):
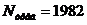опытов.
Алгоритм
повторялся до тех пор, пока не выполнилось условие 
. Данное условие выполнилось после третьей итерации
алгоритма.
После
второй итерации получили:
· N = 1982 опытов.
· Оценка математического ожидания для каждой из 10 областей:
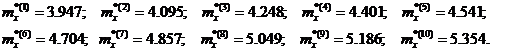
· Результирующая оценка математического ожидания:
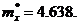
· Дисперсия для каждой из 10 областей:
(
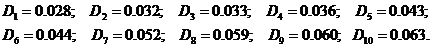
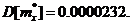· Требуемое количество опытов:
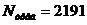опытов.
После
третьей итерации алгоритма:
· N = 2191 опытов.
· Оценка математического ожидания для каждой из 10 областей:
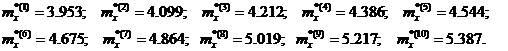
· Результирующая оценка математического ожидания:
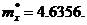
· Дисперсия для каждой из 10 областей:
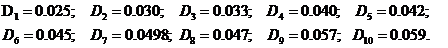
· Дисперсия оценки математического ожидания:
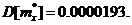
· Требуемое количество опытов:
опытов.
Дифференциальное
уравнение (1) решается численным интегрированием методом Эйлера первого порядка
[4] с шагом 0.001. Программа, реализующая данный метод снижения трудоемкости,
написана на языке Delphi 7 [5].
Таким
образом, использование метода расслоенной выборки позволило обеспечить снижение
требуемого количества опытов по сравнению со стандартной схемой в 
раз.
Заключение
По
заданию работы требовалось определить математическое ожидание выходного сигнала
X апериодического звена в момент времени T
тремя методами. В результате решения данной задачи тремя способами были
получены следующие результаты:
§ Используя стандартную схему статистического
моделирования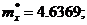 
§ Используя метод расслоенной выборки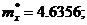 
§ Аналитически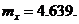 
Использование метода расслоенной выборки обеспечило снижение требуемого
количества опытов по сравнению со стандартной схемой в 10.85 раз.
Список использованных источников
1. Бертмант
А.Ф. Краткий курс математического анализа. - М.: Наука, 1965.
. Кирьянов
Д. Самоучитель MathCAD 11.- СПБ.:
Бхв-Петербург, 2003.
. Емельянов
В.Ю. Методы моделирования стохастических систем управления. - СПб.: БГТУ, 2004.
. Потапов
М. К. Алгебра и анализ элементарных функций. - М.: Наука, 1980.
. Бобровский
С. DELPHI 7. Учебный курс.- СПБ.: Питер, 2003.
Приложения
Приложение А
Аналитические расчеты, произведенные в математическом пакете MathCAD.
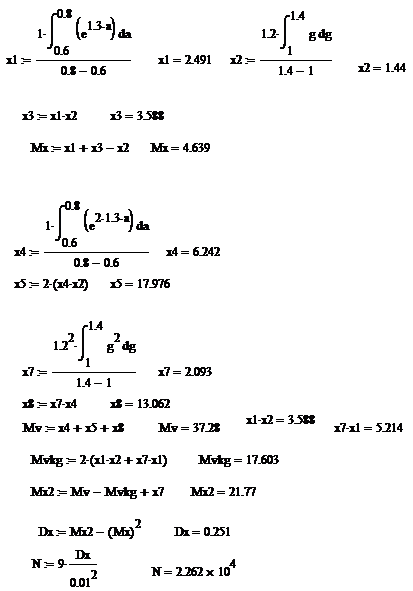
Приложение
Б
Программная
реализация стандартной схемы статистического моделирования
unit Standart;, Messages, SysUtils, Variants, Classes,
Graphics, Controls, Forms,, StdCtrls, Buttons;= class(TForm): TMemo;: TEdit;:
TMemo;: TButton;: TBitBtn;Button1Click(Sender: TObject);
{ Private declarations }
{ Public declarations };=9;=0.001;=0.01;=1300;=0.5;:
TForm1;
{$R *.dfm}TForm1.Button1Click(Sender:
TObject);,Sx2,mx,Dx,G,a,x,Sx2n,Sxn,mxn,Dxn:real;,j,ll:integer;,nn,n,n1,n2:longint;:boolean;:=0;:=0;;:=200;.Lines.Clear;.Lines.Clear;i:=1
to nn do:=random*0.4+1;:=random*0.2+0.6;:=1;j:=1 to kk do x:=x+a*x*h+g*1.2*a*h;:=Sx+x;:=Sx2+sqr(x);;:=Sx/nn;:=Sx2/(nn-1)-sqr(mx);:=round(alfa*Dx/sqr(eps));.Lines.Add('Mx='+FloatToStr(mx));.Lines.Add('Dx='+FloatToStr(Dx));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('nn='+FloatToStr(nn));:=0;:=true;nn<ntreb
do:=ntreb-nn;.text:=floattostr(n1);(n1>8500) then n1:=n1 div 2beginn1<7
then n1:=n1*2;end;i:=nn to n1+nn do:=random*0.4+1;:=random*0.2+0.6;:=1;j:=1 to
kk do x:=(a*x+g*1.2*a)*h+x;:=Sx+x;:=Sx2+sqr(x);;.Lines.Add('n1='+FloatToStr(n1));:=(Sx)/(n1+nn);:=(Sx2)/(n1+nn-1)-sqr(mx);.Lines.Add('Sxn='+FloatToStr(Sx));.Lines.Add('Sx2n='+FloatToStr(Sx2));.Lines.Add('mx='+FloatToStr(mx));.Lines.Add('Dx='+FloatToStr(Dx));:=n1+nn;:=round(alfa*Dx/sqr(eps));.Lines.Add('nn='+FloatToStr(nn));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('************************');
end.
Приложение
В
Программная
реализация метода расслоенной выборки
unit Viborka;, Messages, SysUtils, Variants, Classes,
Graphics, Controls, Forms,, Buttons, StdCtrls;= class(TForm): TMemo;: TMemo;:
TMemo;: TMemo;: TMemo;: TMemo;: TMemo;: TButton;: TBitBtn;: TEdit;: TEdit;:
TEdit;: TStaticText;: TStaticText;: TStaticText;: TStaticText;: TStaticText;:
TStaticText;: TStaticText;: TStaticText;: TStaticText;: TStaticText;: TMemo;:
TMemo;: TMemo;: TMemo;: TMemo;: TStaticText;: TStaticText;:
TStaticText;Button1Click(Sender: TObject);
{ Private declarations }
{ Public declarations };: TForm1;Okno2;
{$R *.dfm}TForm1.Button1Click(Sender:
TObject);=0.001;=0.01;=9;=10;=0.1;=1300;=1.3;:array [1..10] of longint;:array
[1..10] of
real;,n:real;,j,jj,jj1:integer;:boolean;,Mx,Mxcp,Sx,Sx2,x,qk2,qk,g,a,Disp,treal,xn:real;;:=200;:=0;:=true;:=0;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;.Lines.Clear;n<ntreb
do begin:=0;:=0;:=0;:=0;:=0;i:=1 to k do begin:=0;:=0;f then
Nk[i]:=9[i]:=round(ntreb*Pk*sqrt(Dk[i])/qk2);j:=1 to Nk[i] do
begin:=random*0.4+1;:=random*Pk*0.2+0.6+Pk*(i-1)*0.2;:=1;jj:=1 to kk do begin
x:=(a*x+g*a*1.2)*h+x;;:=Sx+x;:=Sx2+sqr(x);;:=Sx/Nk[i];[i]:=Sx2/Nk[i]-sqr(Sx/Nk[i]);:=Dx+(Pk*Pk)*Dk[i]/Nk[i];:=Mxcp+Pk*Sx/Nk[i];i
of
: begin
//Memo1.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('***********');;
: begin //Memo2.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('***********');end;
: begin
//Memo3.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('***********');end;
: begin//
Memo4.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;
: begin
//Memo5.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;
: begin
//Memo6.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;
: begin
//Memo7.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;
: begin
//Memo8.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;
: begin
//Memo9.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;
: begin
//Memo10.Lines.Clear;.Lines.Add('Mx='+FloatToStr(Mx));.Lines.Add('Dx='+FloatToStr(Dk[i]));.Lines.Add('n='+FloatToStr(n));.Lines.Add('ntreb='+FloatToStr(ntreb));.Lines.Add('Disp='+FloatToStr(Disp));.Lines.Add('Nk='+FloatToStr(Nk[i]));.Lines.Add('Sx='+FloatToStr(Sx));.Lines.Add('Sx2='+FloatToStr(Sx2));.Lines.Add('***********');end;;
//
Form2.Visible:=true;:=Pk*sqrt(Dk[i])+qk;:=Disp+Dk[i]*qk/(Pk*sqrt(Dk[i]));;:=qk;.Lines.Add('Mxcp='+floattostr(Mxcp));.Lines.Add('Dxcp='+floattostr(Dx));.Lines.Add('***********');.Text:=floattostr(Mxcp);.Text:=floattostr(Dx);:=ntreb;:=round(alfa*Disp*sqr(Pk)/sqr(eps));.Lines.Add('n='+floattostr(n));.Lines.Add('ntreb='+floattostr(ntreb));.Lines.Add('***********');.text:=floattostr(ntreb);:=false;.