Теорема Лагранжа
Введение
Понятие производной является одним
из важнейших в курсе математического анализа. Многие задачи, как самой
математики, так и естествознания и техники приводят к этому понятию. Всюду где
есть неравномерно меняющиеся величины, скорость их изменения выражается
производной.
Опыт показывает, что относительно не
трудно научить учащихся формулировать определение производной, вычислять
производную, находить производную функцию в точке, пользуясь основными
правилами дифференцирования и применять ее в тех случаях, когда учащимся
известен заранее алгоритм решения. Гораздо труднее добиться того, чтобы
учащиеся научились самостоятельно видеть производную в различных ее частных
проявлениях (в физике, химии, биологии и т.д.). Ведь очень многие понятия
естественных наук не только не могут быть количественно охарактеризованы без
понятия производной, но даже не могут быть без нее определены. Важно также,
чтобы учащиеся усвоили так называемый механический смысл производной. Данная
курсовая работа помогает направить усвоение темы «Производная» таким образом,
чтобы учащиеся смогли самостоятельно применять знания, полученные при изучении
данной темы при изучении других предметов.
Таким образом, в данной работе
значительное место уделяется задачам, способствующим усвоению основных понятий
математического анализа и его свойств, совершенствованию знаний учащихся,
развитию их творческого мышления. Эти задачи учитель может использовать при
изучении нового материала, для домашних заданий учащихся, для самостоятельных и
контрольных работ, для факультативных занятий, работы математических кружков и
т.д.
Основная цель данной работы -
изучить научно-методическую литературу и адаптировать наиболее интересный
материал к процессу обучения учащихся.
Объектом исследования выступает
теорема Лагранжа в школьном курсе математики, а предметом исследования является
методика обучения учащихся выбранной теме исследования.
Задачами работы являются:
проведение
реферативно-исследовательского анализа теоретических основ изучения производной
в школьном курсе математики;
выделение основного материала по
теме исследования курсовой работы;
адаптация данного материала для
усвоения учащимися основных приемов решения задач.
1. Производная
Понятие производной возникло еще в
17 в. Формирование понятия производной исторически связано с двумя задачами:
задачей проведения касательной к кривой и задачей нахождения скорости движения.
Французский математик и юрист П.
Ферма (1601-1665) не позднее чем в 1629 г. Предложил способы отыскания
наибольшего и наименьшего значения функций и проведения касательных к
произвольным кривым, которые по существу основывались на применении
производных. Другой французский философ и математик Р. Декарт (1596-1650)
разработал к 1637 г. Метод координат и основы аналитической геометрии. Научная
переписка между ними помогла выработать общее понятие касательной, понимаемой
как предельное положение секущей.
Работы Р. Декарта и П. Ферма
способствовали открытию интегрального исчисления и его постепенному
обоснованию.
В 1666 году английский ученый И.
Ньютон (1643-1727) и независимо от него несколько позднее немецкий математик Г.
Лейбниц (1646-1716) разработали теорию производных, получившую название
дифференциального исчисления. И. Ньютон, исходя из вопросов механики,
представлял аргумент функции как время, функцию времени называл флюентой (т.е.
текущей величиной), а ее производную рассматривал как скорость течения (т.е.
изменения) функции и называл флюксией.
Еще раньше понятие производной
встречалось в работах итальянского математика Тартальи (около 1500-1557 гг.) -
здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при
котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.
Галилея о движении активно развивалась кинематическая концепция производной.
Различные изложения стали встречаться в работах у Декарта, французского
математика Роберваля, английского ученого Л. Грегори.
Вопрос о взаимосвязи между
непрерывностью функции и существованием ее производной сыграл важную роль в
проблеме строгого обоснования математического анализа. Дело в том, что в
течение 17, 18 и первой половины 19 века ученые - математики считали, что любая
непрерывная функция имеет производную. Это утверждение основывалось на том, что
непрерывную кривую представляли как траекторию движения тела, а производная -
это скорость движения, тогда естественно считать, что всякое движение
совершается с некоторой скоростью. Немецкий математик К. Вейерштрасс
(1815-1897) в 1875 г. Построил пример непрерывной функции, не имеющей производной
ни в одной точке. Геометрически это значит, что кривая непрерывна, но ни в
одной точке не имеет касательной. Пример К. Вейерштрасса показывает, что
интуиция в некоторых случаях не подводит. Можно различными способами построить
непрерывные функции на некотором промежутке, но не имеющие производной ни в
одной точке [3].
В середине 18 в. Л.
Эйлер стал пользоваться греческой буквой 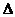 для обозначения
приращений переменной величины, т.е.
для обозначения
приращений переменной величины, т.е. 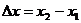 ,
, 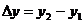 и
т.д. Это обозначение используется и сегодня.
и
т.д. Это обозначение используется и сегодня.
Обозначение 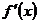 для
производной функции
для
производной функции 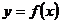 было
введено Ж. Лагранжем (1736-1813).
было
введено Ж. Лагранжем (1736-1813).
Г. Лейбниц обозначил ту
же производную через 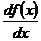 ,
или
,
или 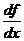 ,
или
,
или 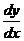 .
.
Термин «производная»
является буквенным переводом на русский французского слова derivce. О. Коши, используя начальную букву этого термина, обозначал
производную символом 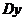 или
или
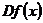 .
.
Терминология И. Ньютона
(флюенты, флюксии) и его символы производной утратили свое значение [3].
Понятие производной является
математическим аналогом понятия мгновенной скорости движения и характеризует
мгновенную скорость изменения функции в данной точке.
Определение. Пусть
функция 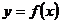 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки 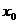 . Производной функции
. Производной функции 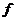 в
точке
в
точке 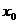 называется
предел отношения приращения функции в этой точке к приращению аргумента при
стремлении к нулю приращения аргумента, если этот предел существует.
называется
предел отношения приращения функции в этой точке к приращению аргумента при
стремлении к нулю приращения аргумента, если этот предел существует.
Обозначается производная
функции в точке как 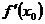 или
или
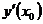 .
Таким образом, по определению:
.
Таким образом, по определению:
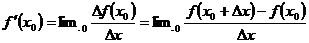 .
.
Иначе данное определение
можно сформулировать так.
Производной функции 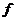 в
точке
в
точке 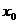 называется
предел разностного отношения функции в этой точке для приращения
называется
предел разностного отношения функции в этой точке для приращения 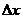 к
нулю, если этот предел существует.
к
нулю, если этот предел существует.
Определение. Функция
имеющая производную в точке 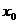 называется
дифференцируемой в этой точке [3].
называется
дифференцируемой в этой точке [3].
2. Теорема Лагранжа и ее
следствия
Тема «Производная и ее
приложения» занимает значительное место в школьном курсе математики. Однако
почти не рассматривается применение теоремы Лагранжа и ее следствий при решении
задач элементарной математики. Однако значение теоремы Лагранжа в
математическом анализе трудно переоценить. Если применять эту теорему без
доказательства, то из нее могут быть получены многие факты, применяемые обычно
в школьном курсе без доказательства [4].
Основные задачи решаемые
с помощью теоремы Лагранжа, это задачи на доказательство тождеств, неравенств,
вывод формул тригонометрии, разложение алгебраических выражений на множители,
решение уравнений, неравенств, систем уравнений, уравнений с параметрами и т.п.
При этом можно указать общие методы решения, некоторые частные приемы и
обозначить круг задач, которые решаются тем или иным методом [2].
Приведем формулировку
теоремы Лагранжа и следствий из нее в той форме, в какой они излагаются в
учебном пособии: Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. [1].
Теорема Лагранжа. Пусть
функция f непрерывна на отрезке 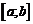 и дифференцируема во
внутренних точках этого отрезка. Тогда существует внутренняя точка с этого
отрезка, такая, что
и дифференцируема во
внутренних точках этого отрезка. Тогда существует внутренняя точка с этого
отрезка, такая, что 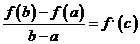 .
.
Следствие 1 (условие
постоянства). Если функция f
непрерывна на отрезке 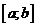 ,
а ее производная равна нулю внутри этого отрезка, то функция f постоянна на
,
а ее производная равна нулю внутри этого отрезка, то функция f постоянна на 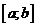 .
.
Следствие 2. Если
функции 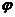 и
и
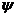 непрерывны
на отрезке
непрерывны
на отрезке 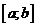 и
имеют одинаковые производные внутри этого отрезка, то они отличаются лишь
постоянным слагаемым.
и
имеют одинаковые производные внутри этого отрезка, то они отличаются лишь
постоянным слагаемым.
Условие монотонности
функции также является следствием теоремы Лагранжа. В школьном учебнике оно
устанавливается отдельно в виде теоремы [2].
Следствие 3
(условие монотонности). Если функция f
непрерывна на промежутке I
и ее производная положительна (соответственно отрицательна) во внутренних
точках этого промежутка, то функция f
возрастает (соответственно убывает) на I
[1].
3. Применение теоремы
Лагранжа и ее следствий при решении задач
Разберем несколько
примеров на прямое применение теоремы. Теорему Лагранжа можно использовать при
решении неравенств и уравнений, при нахождении числа корней некоторого уравнения.
В процессе решения таких
задач рассматривается функция 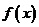 на
отрезке
на
отрезке 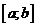 ,
удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула
,
удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула
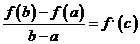 ,
,
где 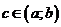 и
оценивается
и
оценивается 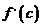 .
.
Пример 1. Доказать,
что 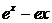 при
при
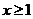 .
.
Решение. Неравенство
справедливо при х= 1. Рассмотрим функцию 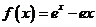 . Тогда для любого числа
b> 1 для данной функции на отрезке
. Тогда для любого числа
b> 1 для данной функции на отрезке 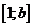 выполняются
условия теоремы Лагранжа и, следовательно, существует внутренняя точка с этого
отрезка, такая, что
выполняются
условия теоремы Лагранжа и, следовательно, существует внутренняя точка с этого
отрезка, такая, что 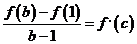 т.е.
т.е.
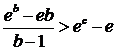 .
Так как с > 1, то
.
Так как с > 1, то 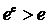 и,
следовательно,
и,
следовательно, 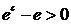 .
Тогда
.
Тогда 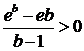 ,
а значит
,
а значит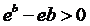 ,
т.е.
,
т.е. 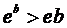 для
любого b > 1. Таким образом, доказано, что
для
любого b > 1. Таким образом, доказано, что 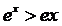 при
при
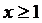 .
.
Можно заметить, что
неравенство 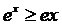 верно
при любом действительном х. В частности, при х=с+1 получим
верно
при любом действительном х. В частности, при х=с+1 получим 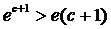 ,
т.е.
,
т.е.
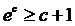 ,
,
где с - любое
действительное число.
Пример 2.
Доказать, что 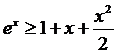 при
при
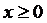 .
.
Решение. Пусть b - любое положительное число. Рассмотрим функцию 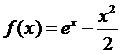 на
отрезке
на
отрезке 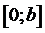 .
По теореме Лагранжа имеем
.
По теореме Лагранжа имеем 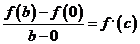 ,
, 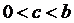 т.е.
т.е. 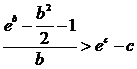 .
А так как при любом с
.
А так как при любом с 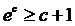 (доказано
в примере 1), то
(доказано
в примере 1), то 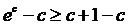 ,
т.е.
,
т.е. 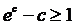 и,
следовательно
и,
следовательно 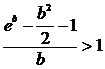 .
Отсюда получим, что
.
Отсюда получим, что 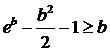 ,
а значит,
,
а значит, 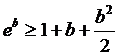 для
любого b > 0. Таким образом,
для
любого b > 0. Таким образом, 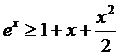 при
при 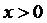 ,
а учитывая, что при
,
а учитывая, что при 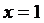 неравенство
также справедливо, получаем, что
неравенство
также справедливо, получаем, что 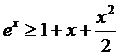 при
при 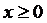 .
.
Пример 3.
Доказать, что 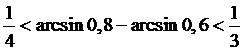 .
.
Решение. Функция 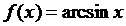 на
отрезка [0,6; 0,8] непрерывна и дифференцируема,
на
отрезка [0,6; 0,8] непрерывна и дифференцируема, 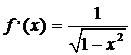 .
Следовательно, для функции
.
Следовательно, для функции 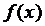 на данном отрезке
выполняются условия теоремы Лагранжа и
на данном отрезке
выполняются условия теоремы Лагранжа и 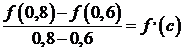 , где
, где 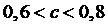 .
.
Имеем 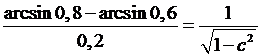 Оценим
число
Оценим
число 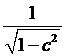 .
Так как
.
Так как 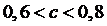 ,
то
,
то 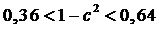 и
и
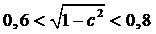 ,
следовательно,
,
следовательно, 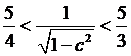 .
Тогда
.
Тогда 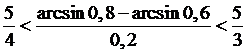 ,
и окончательно
,
и окончательно 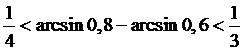 .
.
Пример 4.
Доказать, что для любых действительных значений х1 и х2 выполняется
неравенство 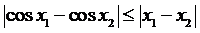 .
.
Решение. Если 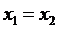 ,
то
,
то 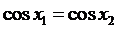 и
и
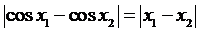 .
Если
.
Если 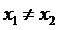 ,
то для функции
,
то для функции 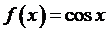 на отрезке
на отрезке 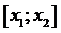 в
случае
в
случае 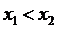 ,
или на отрезке
,
или на отрезке 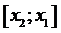 в
случае
в
случае 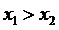 выполняются
условия теоремы Лагранжа, следовательно, найдется внутренняя точка с отрезка,
такая, что
выполняются
условия теоремы Лагранжа, следовательно, найдется внутренняя точка с отрезка,
такая, что 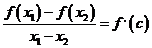 ,
т.е.
,
т.е.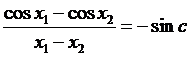 .
Тогда
.
Тогда 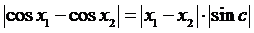 ,
а учитывая, что
,
а учитывая, что 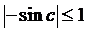 ,
получим
,
получим 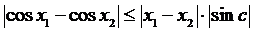 .
.
Пример 5. Доказать,
что на промежутке 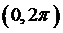 имеется
не более двух различных действительных корней уравнения
имеется
не более двух различных действительных корней уравнения 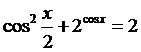 .
.
Решение. Предположим,
что уравнение имеет не менее трех различных действительных корней х1,
х2, х3, принадлежащих промежутку 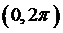 ,
и пусть х1 <х2 < х3. Тогда они являются
нулями функции
,
и пусть х1 <х2 < х3. Тогда они являются
нулями функции 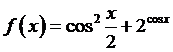 т.е.
т.е.
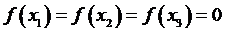 .
На каждом из отрезков
.
На каждом из отрезков 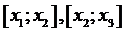 для
функции
для
функции 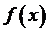 выполняются
условия теоремы. Лагранжа, следовательно, существуют числа с1 и с2
из интервалов (х1; х2), (х2; х3)
соответственно, такие, что
выполняются
условия теоремы. Лагранжа, следовательно, существуют числа с1 и с2
из интервалов (х1; х2), (х2; х3)
соответственно, такие, что 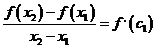 ,
, 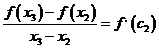 .
А так как
.
А так как 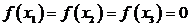 ,
то
,
то 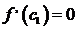 и
и
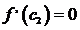 ,
причем
,
причем 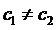 .
Найдем производную
.
Найдем производную 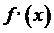 :
:
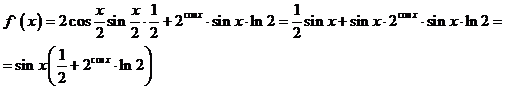
Так как 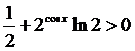 для
любых х, то уравнение
для
любых х, то уравнение 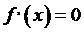 имеет
единственный корень
имеет
единственный корень 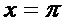 ,
принадлежащий промежутку
,
принадлежащий промежутку 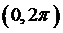 .
Пришли к противоречию, ведь с1, и с2
.
Пришли к противоречию, ведь с1, и с2 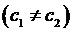 должны
быть корнями уравнения
должны
быть корнями уравнения 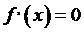 .
Тем самым доказано, что уравнение
.
Тем самым доказано, что уравнение 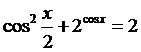 имеет на промежутке
имеет на промежутке 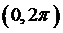 не
более двух различных действительных корней.
не
более двух различных действительных корней.
Пример 6. Решить
уравнение 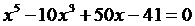
Решение. Легко заметить,
что число х1 = 1 является корнем данного уравнения. Предположим, что
существует еще хотя бы один действительный корень х2, отличный от х1
Числа х1 и х2 являются нулями функции 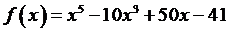 и,
следовательно,
и,
следовательно, 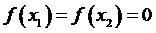 .
Применим теoрему Лагранжа к функции
.
Применим теoрему Лагранжа к функции 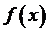 на отрезке
на отрезке 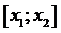 ,
если х1 < х2, или на отрезке
,
если х1 < х2, или на отрезке 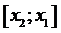 ,
если х1 > х2. Согласно ей, найдется такая внутренняя
точка с этого отрезка, что будет выполняться
,
если х1 > х2. Согласно ей, найдется такая внутренняя
точка с этого отрезка, что будет выполняться 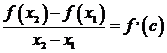 . Учитывая что
. Учитывая что 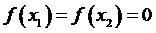 получим
получим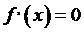 ,
т.е. число с - корень уравнения
,
т.е. число с - корень уравнения 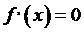 . Но производная
. Но производная 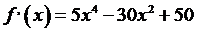 положительна
для любых х, а значит, уравнение
положительна
для любых х, а значит, уравнение 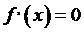 не имеет корней. Полученное противоречие доказывает, что найденный
корень х1 = 1 является единственным.
не имеет корней. Полученное противоречие доказывает, что найденный
корень х1 = 1 является единственным.
Пример 7.
Определить число критических точек функции
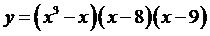 .
.
Решение. Так как степень
многочлена 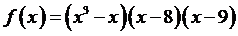 равна
5, то его производная
равна
5, то его производная 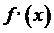 является
многочленом четвертой степени и имеет не более четырех действительных корней.
Применим теорему Лагранжа к функции
является
многочленом четвертой степени и имеет не более четырех действительных корней.
Применим теорему Лагранжа к функции 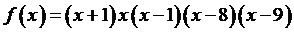 на отрезках [-1; 0],
[0; 1], [1; 8], [8; 9], и при этом учтем, что
на отрезках [-1; 0],
[0; 1], [1; 8], [8; 9], и при этом учтем, что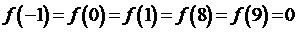 .
.
На каждом таком отрезке
найдутся внутренние точки х1, х2, х3, х4
соответственно, такие, что
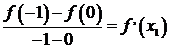 ,
, 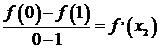 ,
, 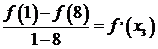 ,
,
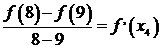 ,
,
Т.е. 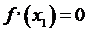 ,
, 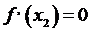 ,
, 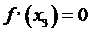 ,
, 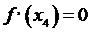 .
.
А учитывая, что 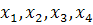
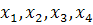 корни многочлена
корни многочлена 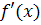
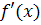 четвертой степени, дeлаем вывод, что других корней, отличных от полученных, нет и,
следовательно, функция
четвертой степени, дeлаем вывод, что других корней, отличных от полученных, нет и,
следовательно, функция 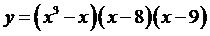 имеет четыре критические точки.
имеет четыре критические точки.
при доказательстве
тождеств, в частности при выводе формул элементарной математики;
при упрощении выражений;
при разложении
алгебраических выражений на множители.
При решении таких задач
на некотором промежутке рассматривается либо одна функция 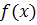
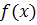 , такая, что ее
производная
, такая, что ее
производная 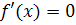
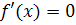 и, следовательно, функция
постоянна, т.е. имеет вид
и, следовательно, функция
постоянна, т.е. имеет вид 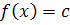
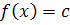 , либо две функции
, либо две функции 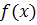
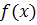 , и
, и 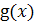
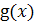 , такие, что
, такие, что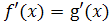
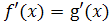 , и делается вывод, что
, и делается вывод, что 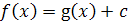
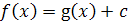 , где с - постоянная.
Эту постоянную находят, положив х равным некоторому значению
, где с - постоянная.
Эту постоянную находят, положив х равным некоторому значению 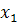
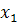 .
.
Пример 8. Не
пользуясь основным тригонометрическим тождеством, вывести формулу 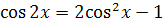
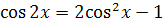 .
.
Решение. Функция 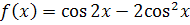
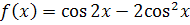 непрерывна на всей числoвой прямой. Найдем производную этой функции
непрерывна на всей числoвой прямой. Найдем производную этой функции
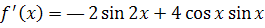
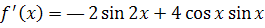 .
.
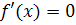
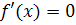 для любого
действительного значения х, следовательно, на основании условия постоянства
функции можно сделать вывод, что функция
для любого
действительного значения х, следовательно, на основании условия постоянства
функции можно сделать вывод, что функция 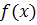
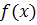 постоянна, т.е.
постоянна, т.е. 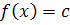
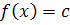 . Для определения
постоянной положим
. Для определения
постоянной положим 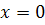
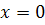 и
получим
и
получим 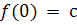
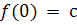 , т.е.
, т.е. 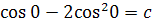
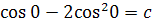 . Таким образом,
. Таким образом, 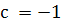
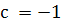 и, значит,
и, значит, 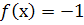
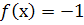 , откуда и получим
, откуда и получим 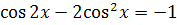
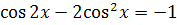 , или
, или 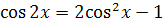
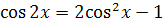 .
.
Пример 9. Доказать
тождество
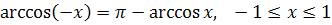
Решение. Функция 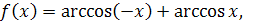
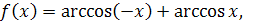 непрерывна на отрезке
непрерывна на отрезке 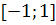
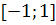 , и ее
производная
, и ее
производная 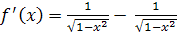
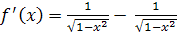 на
на 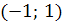
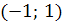 равна нулю.
Следовательно,
равна нулю.
Следовательно, 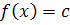
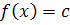 . При
. При 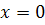
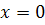 получим
получим 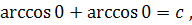
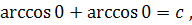 т.е.
т.е. 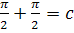
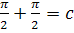 . Таким образом,
постоянная
. Таким образом,
постоянная 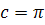
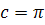 , значит,
, значит, 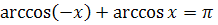
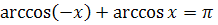 , следовательно,
, следовательно, 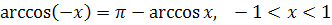 .
.
При 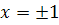
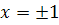 имеем
имеем 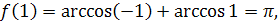
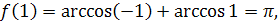 .
.
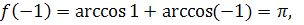
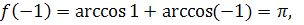 Таким образом, доказано,
что
Таким образом, доказано,
что 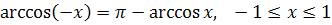
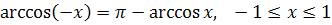
Пример 10. Доказать,
что
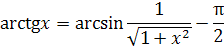
Решение. Рассмотрим две
непрерывные на промежутке 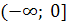
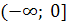 функции
функции 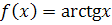
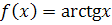 и
и 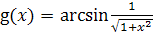
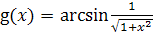 . Они непрерывны на
любом отрезке
. Они непрерывны на
любом отрезке 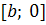
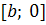 . Найдем производные
этих функций.
. Найдем производные
этих функций.
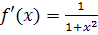
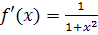 ,
, 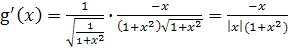
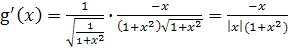 .
.
Так как при 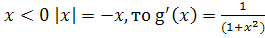
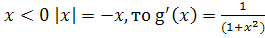 , и тогда
, и тогда
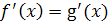
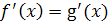 внутри отрезка
внутри отрезка 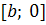
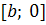 . На основании следствия
2 имеем
. На основании следствия
2 имеем 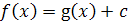
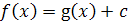 , где с - постоянная.
Для определения с положим, например,
, где с - постоянная.
Для определения с положим, например, 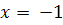
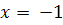 , что дает
, что дает 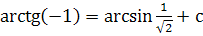
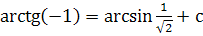 , т.е.
, т.е. 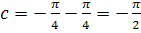
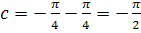 Итак, получим, что
Итак, получим, что 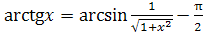
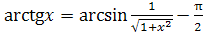 при х<0.
при х<0.
Пример 11. Доказать
тождество
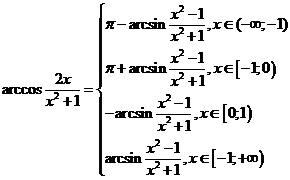
Решение. Заметим, что 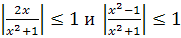
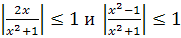 , для любого
действительного х, и функции
, для любого
действительного х, и функции 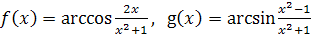
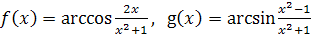 непрерывны на
непрерывны на
всей числовой прямой.
Имеем 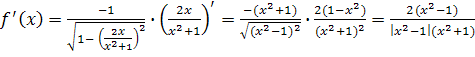
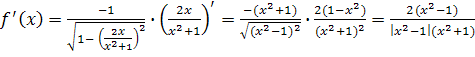 ,
,
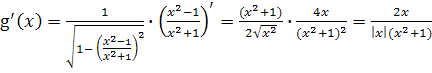
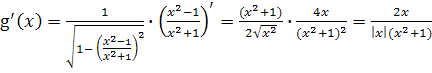
. Рассмотрим
функцию 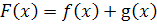
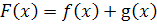 ,
, 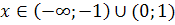
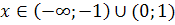 .
.
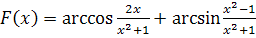
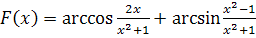 ,
,
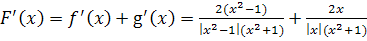
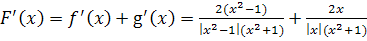 .
.
Если 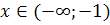
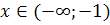 , то
, то 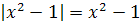
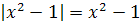 ,
, 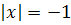
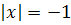 и
и 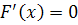
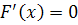 . Если
. Если 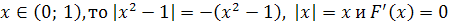
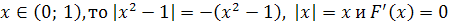 . На основании условия
постоянства функции
. На основании условия
постоянства функции 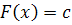
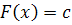 , или
, или 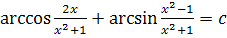
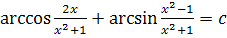 . На каждом из
рассматриваемых промежутков определим с, положив,
. На каждом из
рассматриваемых промежутков определим с, положив, 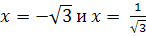
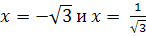 .
.
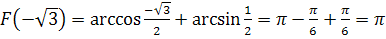
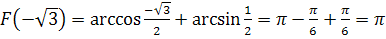 , следовательно,
, следовательно, 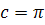
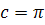 .
.
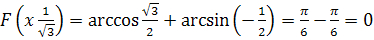
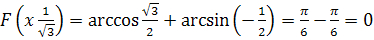 , следовательно,
, следовательно, 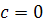
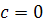 . Имеем:
. Имеем: 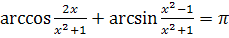
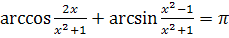 при
при 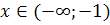
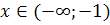 ,
, 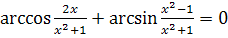
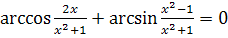 при
при 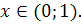
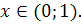
. Рассмотрим
функцию 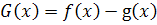
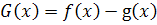 ,
, 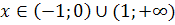
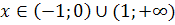 .
.
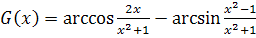
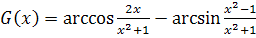 ,
,
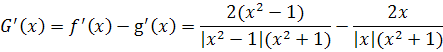
Если 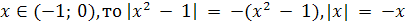
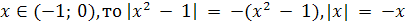 и
и 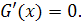
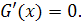
Если 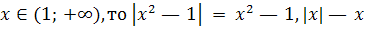
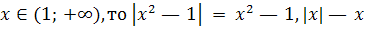 и
и
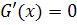
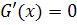 . Тогда на указанных
промежутках функция
. Тогда на указанных
промежутках функция 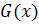
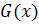 постоянна, т.е.
постоянна, т.е. 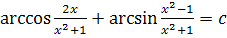
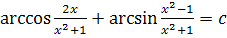 .
.
Положив, 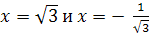
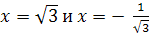 . получим
. получим
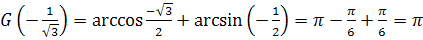
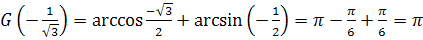 , следовательно,
, следовательно, 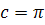
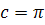 ;
; 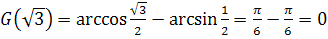
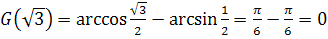 тогда
тогда 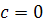
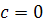 .
.
Имеем: 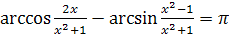
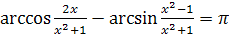 при
при 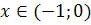
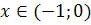 ,
,
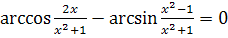
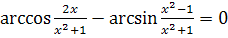 при
при 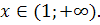
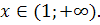
. Вычислим значения 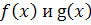
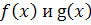 при
при 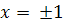
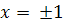 и
и 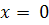
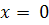 .
.
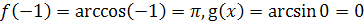
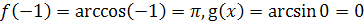 ; следовательно, при
; следовательно, при 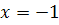
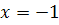
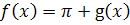
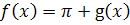 , т.е.
, т.е. 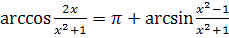
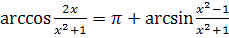 .
. 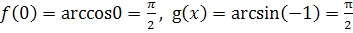
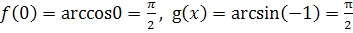 , следовательно, при
, следовательно, при 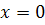
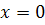
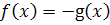
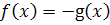 т.е.
т.е. 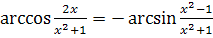
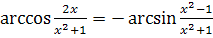 .
. 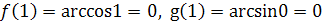
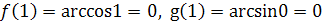 , следовательно, при
, следовательно, при 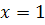
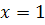
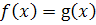
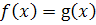 , т.е.
, т.е. 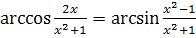
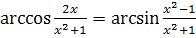 .
.
Таким образом, исходное
тождество доказано для всех действительных х.
Пример 12. Разложить
на множители выражение
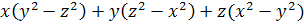
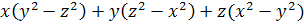 .
.
Решение. На данное
выражение будем смотреть как на функцию от переменной х: 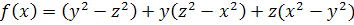
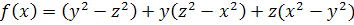 .
.
Найдем 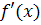
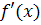 .
.
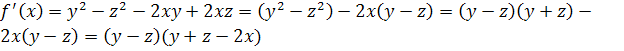
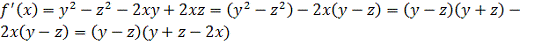
Будем считать, что 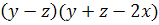
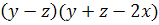 есть производная
некоторой другой функции
есть производная
некоторой другой функции 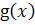
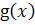 , при этом множитель
, при этом множитель 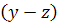
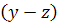 будем рассматривать как
постоянную, вынесенную при дифференцировании за знак производной, т.е.
будем рассматривать как
постоянную, вынесенную при дифференцировании за знак производной, т.е. 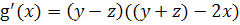
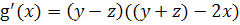 . В качестве функции
. В качестве функции 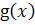
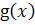 можно взять
можно взять 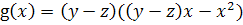
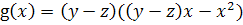 .
.
Так как функции 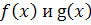
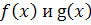 непрерывны и
дифференцируемы на всей числовой прямой и
непрерывны и
дифференцируемы на всей числовой прямой и 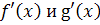
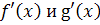 , то по второму
следствию
, то по второму
следствию 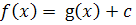
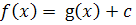 , где с не зависит от x, но возможно зависит от у и z.
Имеем
, где с не зависит от x, но возможно зависит от у и z.
Имеем
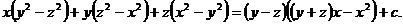
Найдем с, полагая в этом
равенстве, например, х = 0. Получим 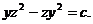 Тогда
Тогда 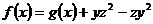 ,
т.е.
,
т.е.
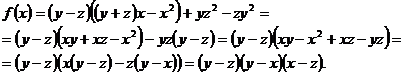
Итак,
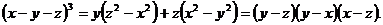
Пример 13. Упростить
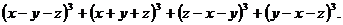
Решение. Будем считать х
переменной и рассмотрим функцию
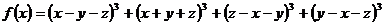
которая непрерывна и
дифференцируема для любого х.
Найдем 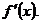
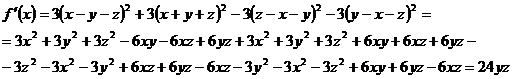
Будем считать, что 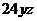 также
является производной другой функции
также
является производной другой функции 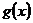 , т.е.
, т.е. 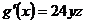 .
Возьмем
.
Возьмем 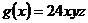 .
Функции
.
Функции 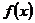 и
и
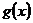 удовлетворяют
условию второго следствия, поэтому
удовлетворяют
условию второго следствия, поэтому 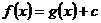 , где с не зависит от х,
но, возможно, зависит от у и
, где с не зависит от х,
но, возможно, зависит от у и 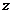 . Имеем
. Имеем
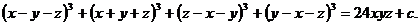
Положим х = 0 и найдем
с.
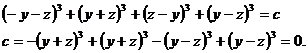
Тогда 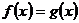 ,
а значит,
,
а значит,
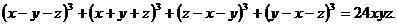
Условие монотонности
функции можно использовать:
при доказательстве
неравенств с переменной;
при доказательстве
числовых неравенств;
при исследовании вопроса
о количестве корней уравнения;
в некоторых случаях при
решении уравнений, уравнений с параметрами, систем уравнений.
Решение задач с
использованием условия монотонности основано на связи между возрастанием или
убыванием функции и знаком ее производной на некотором промежутке. При этом,
сравнивая различные значения аргумента из этого промежутка рассматриваемой
монотонной функции, делается вывод о соответствующих значениях данной функции.
лагранж теорема
уравнение неравенство
Заключение
На протяжении четырех веков
человечество применяет дифференциальное исчисление для решения задач и это не
случайно. Ведь благодаря методам дифференцирования решение приобретает
стройность, четкость и закономерность. Из приведенных примеров в курсовой
работе видно, что дифференцирование должно изучаться в школьном курсе
математике так как, овладевая данным математическим аппаратом, учащиеся могут
эффективно использовать его при решении многих задач по математике и физике.
Кроме того, язык производной позволяет строго формулировать многие законы
природы, решать задачи, которые невозможно решить элементарными методами.
В результате разработки данной
курсовой работы были реализованы следующие задачи:
проведение
реферативно-исследовательского анализа теоретических основ изучения производной
в школьном курсе математики;
выделение основного материала по
теме исследования курсовой работы;
адаптация данного материала для
усвоения учащимися основных приемов решения задач.
Список источников
1. Виленкин, Н.Я. Алгебра и математический анализ для 10 класса [Текст]: учеб. пособие / Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд
- М.: Просвещение, 1992. - 359 с.
. Островерхая, Л.Д. Применение теоремы Лагранжа и ее следствий
при решении задач [Текст]: Л.Д. Островерхая // Научно - теоретический и методический журнал «Математика в школе»,
2001, №9
3. Алгебра и начало анализа: Учеб. Пособие для 10-го кл.
общеобразоват. шк. с углубленным изучением математики [Текст]: / К.О Ананченко,
Коваленко В.С., Воробьев Н.Т. и др. - Мн.: Народная асвета, 1996. - 575 с.