Решение типовых задач теории оптимизации

Решение типовых задач теории оптимизации

Введение

Каждый человек время от времени оказывается в ситуации, когда достижение некоторого результата может быть осуществлено не единственным способом. В таких случаях приходится отыскивать наилучший способ. Однако в различных ситуациях наилучшими могут быть совершенно разные решения. Все зависит от выбранного или заданного критерия.

На практике оказывается, что в большинстве случаев понятие "наилучший" может быть выражено количественными критериями - минимум затрат, минимум времени, максимум прибыли и т.д. Поэтому возможна постановка математических задач отыскания оптимального (optimum - наилучший) результата, так как принципиальных различий в отыскании наименьшего или наибольшего значения нет. Задачи на отыскание оптимального решения называются задачами оптимизации. Оптимальный результат, как правило, находится не сразу, а в результате процесса, называемого процессом оптимизации. Применяемые в процессе оптимизации методы получили название методов оптимизации. Чтобы решить практическую задачу надо перевести ее на математический язык, то есть составить ее математическую модель.

Одним из наиболее общих подходов к решению задачи поиска экстремума (локального максимума или минимума) функции при наличии связующих ограничений на ее переменные (или, как еще говорят, задачи условной оптимизации) является метод Лагранжа. Данный метод используется в задачах 1, 6, 7, 8 данной курсовой работы.

Задача 1. Решить задачу выпуклого программирования

Составим функцию Лагранжа:

Теперь запишем условия равенства нулю частных производных функции, условие дополняющей нежёсткости и, т.к. ищется минимум функции, условие неотрицательности всех .

1)      Рассмотрим случай :

→

Получаем нулевые , нулевой Лагранжиан  решение отсутствует

)        Рассмотрим случай:

2.1) Пусть :

→→

→ т. Min, т. к. выполняется условие  и . Так как мы решаем задачу выпуклого программирования, то точка минимума является единственной и глобальной и рассматривать остальные случаи не имеет смысла. И все же:

.2) Пусть :

→→

→→

→

- не может быть точкой минимума

.3) Пусть :

→→

→

→ - не может быть точкой минимума

.4) Пусть :

→→

→→

→→

- не может быть точкой минимума.

Таким образом точка (25/7, -48/7) является точкой глобального минимума функции .

Задача 2. Решить задачу линейного программирования графическим методом. Во всех вариантах

Т.к. в условии следующей задачи первоначальная крайняя точка , логично будет использовать в качестве базисных переменных x₃, x₄, x₅ и выделить именно их, решая систему методом Гаусса. Запишем систему в матричном виде и решим, наконец, ее:

Построим график для новой системы уравнений и нанесем линию уровня:

Для получения координат точки максимума исследуемой функции линию положения нужно передвигать вправо (т.к. функция прямо пропорциональна x₁) и вниз (т.к. функция обратно пропорциональна x₂) до крайнего положения.

Точка максимума находится на пересечении двух прямых, задаваемых уравнениями:

Таким образом, точка M(1, 1/2) является точкой максимума данной функции.

Задача 3. Решить задачу № 2 симплекс-методом, используя  в качестве первоначальной крайней точки

Т.к. мы будем искать максимум функции, а симплекс метод применяется для поиска минимума функции, домножим целевую функцию на минус единицу, таким образом обратив ее минимумы и максимумы.

;

Ищем среди коэффициентов p_i (коэффициентов целевой функции) p_i<0, берем соответствующий этому элементу столбец (кроме столбца свободных членов). Для выбора опорного элемента необходимо найти, какой из них удовлетворит условию минимума отношения свободного члена к данному элементу: , причем

После выбора опорного элемента совершаем пересчет таблицы:

опорный элемент заменяем на единицу, деленную на опорный элемент;

опорную строку делим на опорный элемент;

опорный столбец делим на опорный элемент и умножаем на минус единицу;

остальные элементы считаем по "правилу определителя" (при этом беря со знаком "+" произведение, содержащее опорный элемент) и делим на опорный элемент

совершаем эти итерации до тех пор, пока в нижней строке все элементы (кроме свободного члена) не станут положительными.

Таким образом, мы получили сходный ответ с полученным во второй задаче: точка с координатами x₁=1, x₂=1/2, x₃=2/3, x₄=-1/6, x₅=1,

.

.

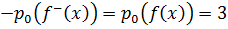Задача 4. Решить простейшую задачу классического вариационного исчисления

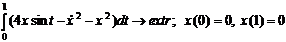
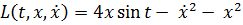
Воспользуемся уравнением Эйлера-Лагранжа для решения простейшей задачи:

.

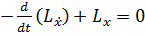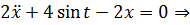
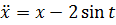Предположим, что:

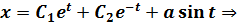Подставим в исходное уравнение:

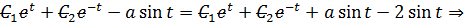
Применим краевые условия для нахождения констант:

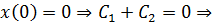
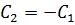
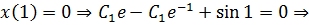
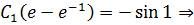
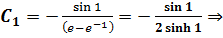
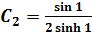
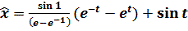 - экстремаль

Исследуем экстремаль на предмет доставления функции максимума/минимума:

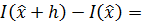
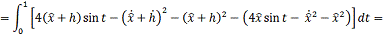
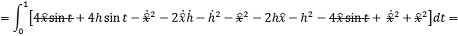
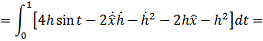
Проинтегрируем по частям: , где:

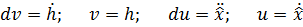
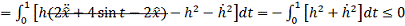
- точка 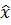 является точкой максимума.

Задача 5. Решить задачу Больца

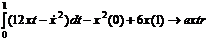
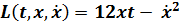 - Интегрант

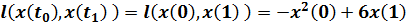 - Терминант

Воспользуемся уравнением Эйлера-Лагранжа для решения задачи Больца:

.

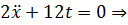
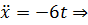
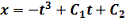 - экстремаль

Воспользуемся условиями трансверсальности:

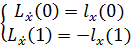
Посчитаем каждый элемент:

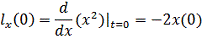
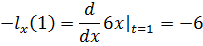
Тогда условия трансверсальности запишутся:

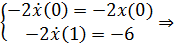
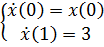
Мы будем использовать эти уравнения как краевые условия для нахождения констант .

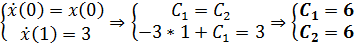
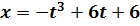
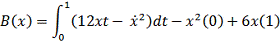
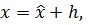
Исследуем экстремаль на предмет доставления функции максимума/минимума:  (Запишем, сразу группируя интегральную и неинтегральную части)

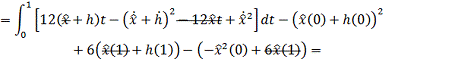
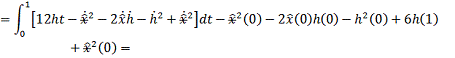
Проинтегрируем по частям: 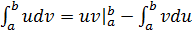, где:

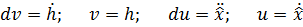
А также воспользуемся условием:  и  в подстановке 0 и 1 (для подсчета значения элемента ):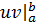

,

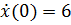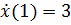
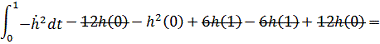
 - отрицательный результат - следовательно 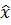 является точкой максимума.

Задача 6. Решить изопериметрическую задачу

;  ,

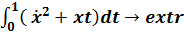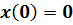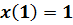
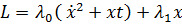
Воспользуемся уравнением Эйлера-Лагранжа для решения изопериметрической задачи:

.

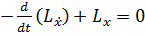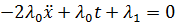
1) 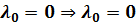 - нет решений (Лагранжиан не м. б. равен нулю)

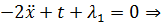
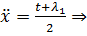
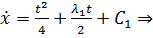
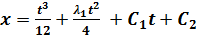
Воспользуемся краевыми условиями для нахождения констант:

,

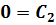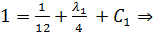
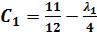
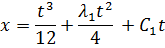
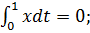 - Воспользуемся уравнением для нахождения :

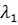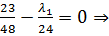
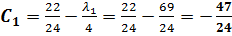
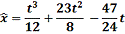
Исследуем экстремаль на предмет доставления функции максимума/минимума:

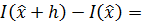
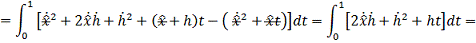
Проинтегрируем по частям: 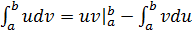, где:

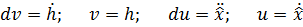
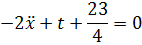
Так как 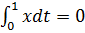,  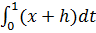тоже должна быть равна нулю, следовательно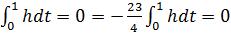

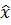 -  точка минимума.

Задача 7. Решить задачу с подвижными концами

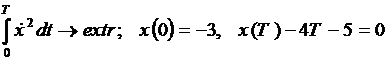
Выпишем, как положено, функцию Лагранжа:

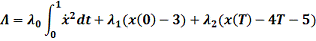
Воспользуемся уравнением Эйлера-Лагранжа для решения задачи с подвижными концами:

.

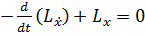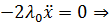
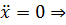
Воспользуемся условиями трансверсальности:

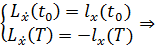
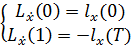
Посчитаем каждый элемент:

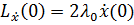
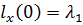
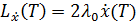
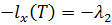
Тогда условия трансверсальности запишутся:

Запишем условие стационарности:

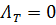
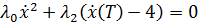
Пусть  Тогда  также равны нулю - нет решений.

Пусть 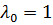, тогда:

Если , найдем константы, используя краевые условия:

,

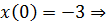
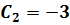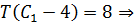
В уравнение стационарности также подставим 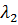, используя уравнение, написанное выше:

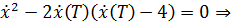
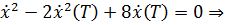
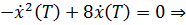
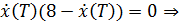
Рассмотрим 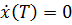, тогд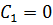а  а 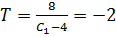 - что является недопустимым значением

Рассмотрим 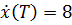, тогда  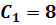и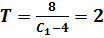

Итак, мы получили:

,

;,

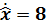
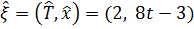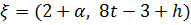Исследуем экстремаль  на предмет доставления функции максимума/минимума:

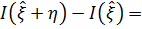
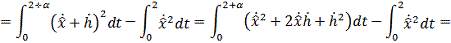
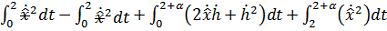
Воспользуемся 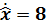 и h(0)=0 (в силу наложенного ограничения на левый конец).

Также, стоит выразить значение 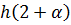 из уравнения 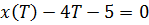, помня, что 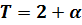, а

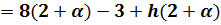
Итак:

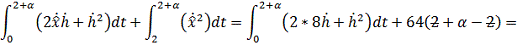
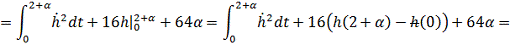
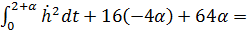
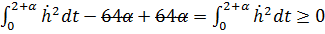
- следовательно найденная точка является точкой минимума.

Задача 8. Решить задачу Лагранжа

; , ,

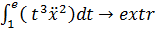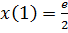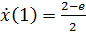
Используем замену переменных 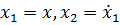, тогда условие запишется:

; , ,

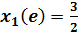Запишем функцию Лагранжа:

1)      Воспользуемся уравнением Эйлера-Лагранжа для решения задачи с Лагранжа. Оно запишется отдельно относительно x₁ и x₂ и образует, таким образом, систему уравнений:

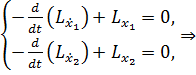
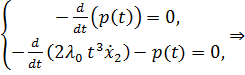
2)      Воспользуемся условиями трансверсальности:

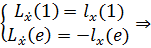
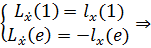
 - уравнения, записанные относительно x₁

 - уравнения, записанные относительно x₂

,

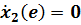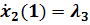
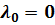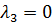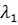Положим . Тогда из уравнений, записанных выше, получим  из третьего уравнения условий трансверсальности, а также равенство нулю функции p(t) из второго уравнения Эйлера-Лагранжа, а как следствие и равенство нулю  и 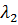 (1 и 2 уравнения условий трансверсальности соответственно). Таким образом, этот вариант нам не подходит, так как для нахождения решения Лагранжиан не может быть нулевым.

Тогда, пусть :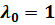

Из уравнения

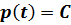
Из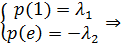

Из 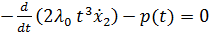 получим:

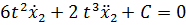, сделаем замену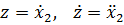

Решим однородное уравнение:

,

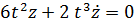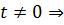
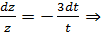
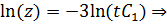
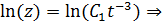
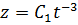
Теперь решим неоднородное:

Пусть 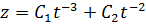. Подставим:

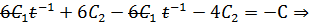
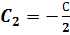
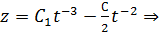
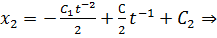
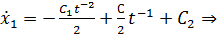
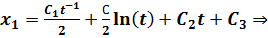
Используем краевые условия для нахождения констант:

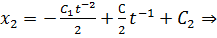
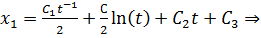
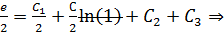
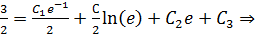
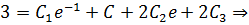
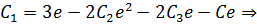
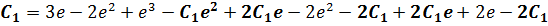
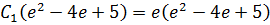
Таким образом, очевидно:

,

,

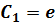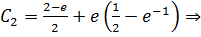
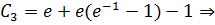
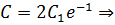
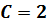
Получаем:

, ,

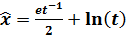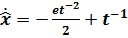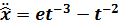
Исследуем экстремаль функции 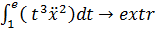 на предмет доставления ей максимума/минимума:

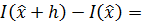
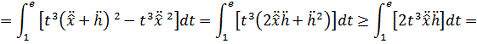
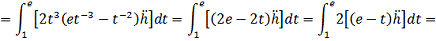
Интегрируем по частям:

.

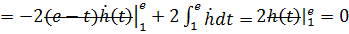Таким образом, разница оказалась больше равна нулю. Это значит, что точка 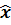 является точкой минимума.

Заключение

лагранж вариационный исчисление изопериметрический

В курсовой работе получены решения семи типовых задач теории оптимизации: двух конечномерных (задачи выпуклого программирования и линейного программирования) и пяти задач вариационного исчисления (простейшей задачи вариационного исчисления, задачи Больца, изопериметрической задачи, задачи с подвижными концами и задачи Лагранжа)

В результате работы над настоящей курсовой работой были достигнуты следующие цели:

1.      расширен объем и углублены теоретические знания по дисциплине "Методы оптимизации";

.        закреплены практические навыки решения задач теории оптимизации;

.        получены навыки применения метода множителей Лагранжа как основного метода решения задач оптимизации с ограничениями, как конечномерных, так и бесконечномерных;

.        получен навык подготовки и оформления научно-технической документации.

Список использованных источников

1. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. Москва : Наука, 1979.

. Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. Москва : Наука, 1984.

. Галеев Э.М., Тихомиров В.М. Оптимизация: теория, примеры, задачи. Москва.: Эдиториал УРСС, 2000.

. Галеев Э.М. Оптимизация: теория, примеры, задачи. Москва : УРСС, 2002.

. Магарил-Ильяев Г.Г., Тихомиров В.М. Выпуклый анализ и его приложения. Москва.: Эдиториал УРСС, 2000.

. Шатина А.В. Методы оптимизации. Практические занятия. М.: МИРЭА, 2012,

. Методы оптимизации. 4-ый курс. Контрольные задания для студентов факультета Кибернетики. М.: МИРЭА, 2010.