Прямые методы решения линейных систем. Метод квадратного корня
Введение
Три четверти прикладных математических задач в
конечном итоге сводятся к решению систем алгебраических и трансцендентных
уравнений, причем подавляющее большинство из них - линейные алгебраические
системы, имеющие единственное решение.
Современная вычислительная математика обладает
большим арсеналом методов, а математическое обеспечение ЭВМ - многими пакетами
прикладных программ, позволяющих решать различные линейные системы. Казалось
бы, этого достаточно, но на практике при решении линейных систем возникает
множество разных проблем.
Поэтому ввиду большой важности и практической
значимости задача решения линейных систем до сих пор привлекает внимание
математиков. Создано большое количество разных методов решения этой задачи и
сопутствующих ей задач (вычисление определителей, обратных матриц). Среди этих
методов можно выделить две большие группы: прямые (или точные) и итерационные
методы [4].
Прямые методы приводят к точному решению системы
(если не учитывать вычислительные погрешности округлений), причем за конечное
число шагов. К ним относятся методы Гаусса, LU-разложение, квадратного корня,
методы прогонки, вращений и т.п. [2,4].
Итерационные методы позволяют получить
приближенное решение системы с заданной точностью, используя идею
последовательных приближений. К ним относятся методы простой итерации, Зейделя,
релаксации, установления, спуска и т. п.[2,4].
Каждый из существующих методов решения линейных
систем имеет свою сферу применения, где он является наиболее эффективным.
Эффективность же названных численных методов зависит в основном от свойств
матрицы системы (порядка, симметричности, меры обусловленности, заполненности).
Целью данной курсовой работы является:
обзор литературы по прямым методам решения
линейных систем;
реализация метода квадратного корня средствами
системы программирования Turbo Pascal.
Курсовая работа содержит две главы. Первая глава
посвящена таким прямым методам решения линейных систем, как метод Гаусса,
LU-разложение, метод прогонки для решения линейных систем с трехдиагональными
матрицами коэффициентов и метод вращений для решения линейных систем. Во второй
главе отдельно рассматривается метод квадратного корня для решения линейных
систем, а именно: приведены теоретические основы метода, а также произведена
его реализация в системе программирования Turbo Pascal.
Глава 1. Прямые методы решения
линейных систем
.1 Постановка задачи
К решению систем линейных уравнений сводятся
многочисленные практические задачи. В данной курсовой работе изучается вопрос о
численном решении систем вида [4]:
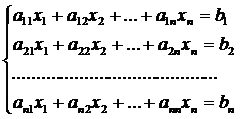 (1.1.1)
(1.1.1)
Совокупность коэффициентов (aij), неизвестных
(хi) и свободных членов (bi) этой системы запишем в виде матриц [4]:
=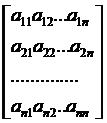 , x=
, x=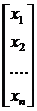 ,
b=
,
b= (1.1.2)
(1.1.2)
Помимо введенной матрицы А мы введем еще и
расширенную матрицу системы, получающуюся из матрицы А добавлением столбца
правых частей:
 (1.1.3)
(1.1.3)
Матрица системы А и столбец правых частей b
считаются заданными, а столбец x ищется, при этом определитель матрицы не
должен равняться 0.
1.2 Метод Гаусса
Данный метод является наиболее простым и
популярным способом решения линейных систем вида (1.1.1). Он основан на
последовательном исключении неизвестных [5].
Итак, пусть дана система (1.1.1). Для удобства
можно представить её в виде (1.1.3). На первом этапе разделим все коэффициенты
первой строки, а также свободный член на первый коэффициент. Таким образом
перед х1 в первой строке получится единица. Теперь наша задача - исключить
переменную х1 из остальных строк, другими словами сделать коэффициенты перед х1
нулевыми. Для этого заменяем все уравнения, начиная со второго, уравнениями,
полученными сложением каждого из них с первым, умноженным на -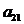 ,
-
,
-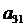 ,…,
-
,…,
- .
Таким образом, получаем [2]:
.
Таким образом, получаем [2]:
 (1.2.1)
(1.2.1)
В общем виде формулы для данного этапа выглядят
следующим образом [2]:
 ,
,
 , (i,j=2…n)
, (i,j=2…n)
На втором этапе проделаем то же самое, только
первую строку в расчет не берем. Делим все элементы второй строки на 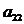 ,
а затем исключаем переменную х2 из оставшихся строк путем опять же замены всех
уравнений, начиная с третьего, уравнениями, полученными сложением каждого из
них со вторым, умноженным на -
,
а затем исключаем переменную х2 из оставшихся строк путем опять же замены всех
уравнений, начиная с третьего, уравнениями, полученными сложением каждого из
них со вторым, умноженным на -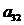 , -
, -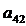 ,…,
-
,…,
- .
Таким образом, получаем [2]:
.
Таким образом, получаем [2]:
 (1.2.2)
(1.2.2)
Формулы в общем виде[2]:
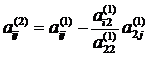
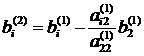 , (i,j=3…n)
, (i,j=3…n)
Этот процесс продолжается до тех пор, пока
матрица не будет приведена к виду [2]:
 (1.2.3)
(1.2.3)
Коэффициенты данной системы получены по формулам
[2]:

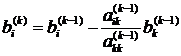 , (i, j=k+1…n,
k=1…n-1)
, (i, j=k+1…n,
k=1…n-1)
Все рассмотренные выше этапы называются прямым
ходом метода Гаусса. Далее идет обратный ход: значения х вычисляются снизу
вверх по формуле [2]:
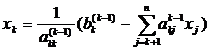 , (k=n,n-1,…,1)
, (k=n,n-1,…,1)
1.3 LU-разложение матриц
Данный метод напрямую связан с методом Гаусса. В
предыдущем пункте решение линейной системы сводилось к тому, что матрицу
(1.1.3) путем элементарных преобразований сводили к верхней треугольной матрице
(1.2.3). Заметим, что, умножая исходную матрицу на матрицу (1.2.3), получится
нижняя треугольная матрица с единицами на главной диагонали [5]. Учитывая эту
взаимосвязь, можно подойти к решению линейной системы иначе, то есть, разложив
исходную матрицу в произведение двух треугольных матриц А=LU [5, 7]:

 (1.3.1)
(1.3.1)
То есть систему Ax=b можно переписать в виде:
LUx=b (1.3.2)
Введем вектор вспомогательных переменных  и
(1.3.2) перепишем в виде [2, 7]:
и
(1.3.2) перепишем в виде [2, 7]:
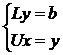 (1.3.3)
(1.3.3)
Очевидно, чтобы найти х, нужно сначала найти у.
Для этого запишем первое уравнение (1.2.3) в развернутом виде:
 (1.3.4)
(1.3.4)
Найти у можно сверху вниз по формуле [7]:
 при i=1,2,…,n.
(1.3.5)
при i=1,2,…,n.
(1.3.5)
Аналогично для второго уравнения (1.3.3):
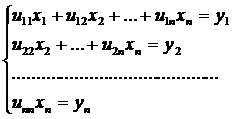 (1.3.6)
(1.3.6)
Найти у можно снизу вверх по формуле [7]:
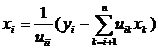 при i=n,n-1,…,1
(1.3.7)
при i=n,n-1,…,1
(1.3.7)
1.4 Метод прогонки решения систем с
трехдиагональными матрицами коэффициентов
Данный метод удобно применять для так называемых
ленточных трёхдиагональных матриц вида [10]:
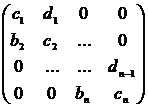 *
*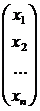 =
=
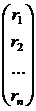 (1.4.1)
(1.4.1)
Каждое уравнение такой системы связывает три
«соседних» неизвестных [2, 10]:
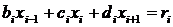 , где i=1…n; b1=0;
dn=0. (1.4.2)
, где i=1…n; b1=0;
dn=0. (1.4.2)
Предположим, что существуют такие наборы чисел 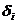 и
и
 (i=1…n),
при которых [10]
(i=1…n),
при которых [10]
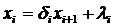 (1.4.3)
(1.4.3)
Уменьшим индекс на единицу, подставим полученное
в (1.4.2) и выразим хi [2,10] :
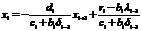 (1.4.4)
(1.4.4)
Сравнив (1.4.3) и (1.4.4), получаем, что [10]:
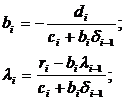 (1.4.5)
(1.4.5)
при i=1…n - прямая прогонка,
при i=n…1 - обратная прогонка.
Эти коэффициенты называются прогоночными. Найдя
их по формулам (1.4.5), можно найти хi из формулы (1.4.3).
1.5 Метод вращений решения линейных
систем
Цель данного метода - привести систему (1.1.1) к
треугольному виду (как в методе Гаусса).
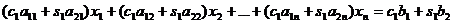 (1.5.1)
(1.5.1)

На введенные параметры накладываются 2 условия
[8]:
условие обнуления (исключения х1 из второго
уравнения)
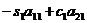 =0 (1.5.2)
=0 (1.5.2)
условие нормировки. За 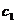 и
и
 можно
принять соответственно
можно
принять соответственно
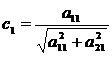 ,
,  (1.5.3)
(1.5.3)
Отсюда система (1.1.1) принимает вид [8]:
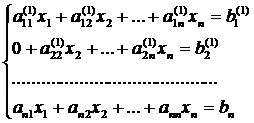 (1.5.4)
(1.5.4)
Где 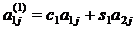 (j=1…n)
(j=1…n)

 (j=2…n)
(j=2…n) 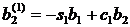
Далее первое уравнение системы (1.5.4)
заменяется новым, полученным сложением результатов умножения первого и третьего
уравнений на [8]:
 и
и 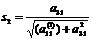
А третье уравнение системы (1.5.4) заменим
полученным сложением результатов умножения тех же уравнений, умноженных на - и
и 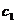 .
Таким образом, получаем систему [8]:
.
Таким образом, получаем систему [8]:
 (1.5.5)
(1.5.5)
где 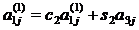 (j=1…n)
(j=1…n)
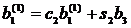
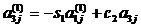 (j=2…n)
(j=2…n) 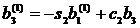
Проделав такие преобразования n-1 раз мы обнулим
коэффициенты при х1 в первом столбце, кроме первой строчки. Затем проделаем
аналогичные преобразования с остальными столбцами и в конечном итоге получим
треугольную матрицу. После этого можно будет найти неизвестные. Это делается
точно так же как в обратном методе Гаусса.
Глава 2. Метод квадратного корня для
решения линейных систем
.1 Краткая характеристика метода
Метод квадратного корня применяется в том
случае, когда матрица А симметричная, то есть:
= aji (i, j = 1, 2, …, n).
Кроме того, матрица должна быть невырожденной,
то есть её определитель не должен равняться нулю (det(A)¹0).
Таким образом, система будет иметь единственное решение.
Метод квадратного корня дает большой выигрыш во
времени по сравнению с другими методами (например, методом Гаусса), так как,
во-первых, существенно уменьшает число умножений и делений (почти в два раза
для больших n), во-вторых, позволяет накапливать сумму произведений без записи
промежуточных результатов.
Всего метод квадратных корней требует [2,3] 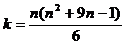 операций
умножения и деления (примерно в два раза меньше, чем метод Гаусса), а также n
операций извлечения корня.
операций
умножения и деления (примерно в два раза меньше, чем метод Гаусса), а также n
операций извлечения корня.
2.2 Постановка задачи
К решению систем линейных уравнений сводятся
многочисленные практические задачи. Запишем еще раз систему (1.1.1) n линейных
алгебраических уравнений с n неизвестными [4]:
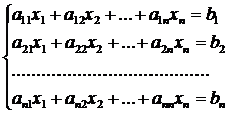
Совокупность коэффициентов (aij), неизвестных
(хi) и свободных членов (bi) этой системы запишем в виде матриц (1.1.2) [4]:
=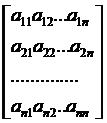 , X=
, X=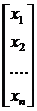 ,
B=
,
B=
Используя понятие матрицы , систему уравнений
(1.1.1) можно записать в матричном виде:
=b (2.2.1)
Таким образом, задача состоит в том, чтобы
вычислить столбец неизвестных, используя метод квадратного корня.
2.3 Теоретическая основа метода
квадратного корня для решения линейных систем
Пусть дана симметричная система линейных
уравнений в матричном виде (2.2.1): Ах=b
К ee решению может быть применена идея
разложения матрицы А в произведение двух матриц специального вида. Основанием для
этого служит следующая теорема [3]:
Теорема. Какова бы ни была матрица А с отличными
от нуля главными минорами:
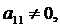
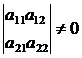 ,
… ,
,
… , 
ее всегда можно разложить в произведение двух
треугольных матриц:=BC,
где В - левая треугольная матрица:
В=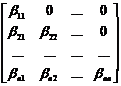
С - правая треугольная матрица:
С=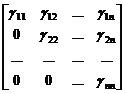
Так как данная матрица (2.2.1) симметрична, то
она раскладывается на произведение двух взаимно транспонированных треугольных
матриц[1,2,3]:
А = Т¢ Т, (2.3.1)


Найдем элементы tij матрицы Т. Для этого
перемножим T и T’ между собой и приравняем полученное к исходной матрице [2]:
t211 = a11 , t11 t12 =a12 , … , t11
t1n = a1n ,+ t222= a22 , … , t12 t1n + t22 t2n= a2n ,
…………………………………………………………………..n + t22n +…+ t2nn =
ann
Получим следующие формулы для определения tij
[3]:
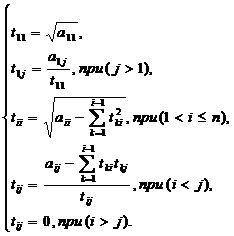 (2.3.2)
(2.3.2)
Далее, решение системы сводится к решению двух
треугольных систем. Действительно, равенство (2.2.1) равносильно двум
равенствам:
’y=b и Tx=y. (2.3.3)
Запишем в развернутом виде системы (2.3.3)
[1,3]:
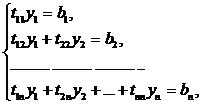 (2.3.4)
(2.3.4)
 (2.3.5)
(2.3.5)
И из этих систем (2.3.4) и (2.3.5)
последовательно находим [1,2,3]:
 ,
, 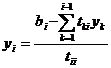 ,
при (i>1) (2.3.6)
,
при (i>1) (2.3.6)
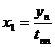 ,
, 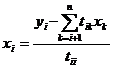 ,
при (i<n). (2.3.7)
,
при (i<n). (2.3.7)
2.4 Реализация метода квадратного
корня для решения линейных систем. Тестирование программы
В данном пункте описано тестирование программы,
посвященной методу квадратного корня решения линейных систем. Код программы
составлен на языке Pascal и находится в приложении.
Для того, чтобы удостовериться, что программа
работает правильно, решим конкретный пример вручную, а затем сравним полученный
результат с результатом программы.
Задача 1.Пусть дана система линейных уравнений:
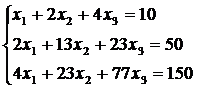
Этой системе соответствуют: матрица
коэффициентов А и столбец свободных членов b:
А=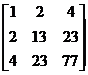 b=
b=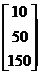
В коде программы прописано, что пользователь
может ввести матрицу размерности не более, чем 10×10,
но, вводя коэффициенты, необходимо помнить о том, что матрица должна быть
симметричной. В противном случае программа сработает неправильно.
Найдем элементы матрицы Т. Это действие
оформлено в коде программы в качестве процедуры PROCEDURE Tij, которая
вычисляет коэффициенты матрицы Т из разложения (2.3.1) по формулам (2.3.2).
Таким
образом,
получим:
t211 = 1  t11
= 1, t12 =2
t11
= 1, t12 =2  t12 = 2,t13 = 4
t12 = 2,t13 = 4  t13
= 4,+ t222= 13
t13
= 4,+ t222= 13  t22 = 3,t13 + t22
t23= 23
t22 = 3,t13 + t22
t23= 23  t23
=5,+ t223 +t233 = 77
t23
=5,+ t223 +t233 = 77  t33 =6
t33 =6
Таким образом, матрица А раскладывается в
произведение матриц T’ и Т (2.3.1):
Решим систему T’y=b. В коде программы данному
действию соответствует процедура PROCEDURE Yi , которая описывает процесс
вычисления вспомогательного столбца у по формулам (2.3.6) из нижней треугольной
матрицы (2.3.4).

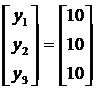
Решим систему Тх=у. Данное действие представлено
в коде программы в виде процедуры PROCEDURE Хi, которая считает искомый столбец
х по формулам (2.3.7) из верхней треугольной матрицы (2.3.5). По завершении
этого этапа программа выводит на экран значения х1…xn, а также выполняется
проверка правильности найденного решения. Суть её состоит в том, что полученные
значения х подставляются в исходную матрицу и высчитывается значение столбца
свободных членов b. Если оно совпадает с исходным, то решение найдено верно.
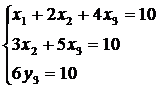
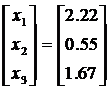
Результаты, которые вывела на экран программа
при вводе тех же самых значений элементов матрицы А и столбца b, совпадают с
результатами, полученными в данном пункте и находятся на рис.1.
Программа отлажена и готова к работе.
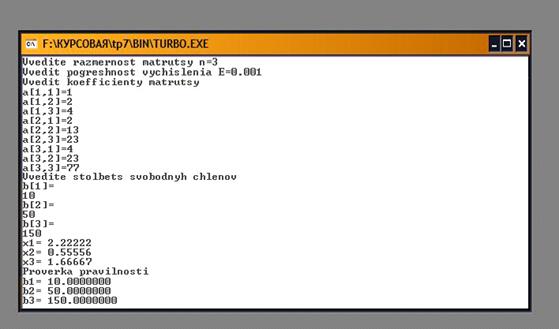
Рис. 1 - Реализация задачи
Задача 2. Протестируем эту же программу для
других значений. Зададим очень маленькое значение Е. Входные данные, а также
результат, полученный в ходе программы отражен на рисунке 2. По полученным
результатам можно сделать вывод: значение Е не влияет на результат. И это не
случайно. Ведь метод квадратного корня относится к группе точных методов.
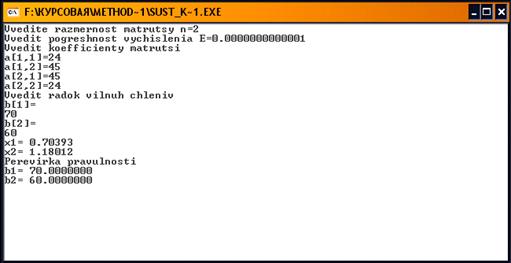
Рис. 2
Заключение
В данной работе были рассмотрены прямые методы
решения линейных систем: метод Гаусса, метод LU-разложения, метод прогонки,
метод вращений и метод квадратного корня. К основным результатам курсовой
работы можно отнести:
обзор литературы, связанной с прямыми методами
решения линейных систем.
Реализация метода квадратного корня средствами
системы программирования Turbo Pascal.
Более подробно был проанализирован один из
методов решения систем линейных алгебраических уравнений: метод квадратных
корней. Метод был предложен для решения системы Ax=b, где матрица A -
симметрическая.
Также в данной системе были проанализированы
разного рода матрицы, и их влияние на точность полученного решения. Основываясь
на полученных выводах, можно контролировать в каких конкретно моментах удобно
решать систему линейных алгебраических уравнений методом квадратных, а когда
лучше использовать другой метод.
Список используемой литературы
1. Бахвалов
Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 2001.
2. Вержбицкий
В.М. Основы численных методов. М.: Высшая школа. 2002.
. Крылов
В.И. и др. Вычислительные методы, т.I. М.: Наука, 1976.
. Трубников
С.В Численные методы. Часть 1: Теория погрешностей. Решение алгебраических и
трансцендентных уравнений и систем: Учебное пособие для студентов вузов. -
Брянск: Изд-во БГУ, 2005.
. Фаддеев
Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М., Л.: изд-во
физ.-мат. лит-ры, 1963.
. Лапчик
М.П., рагулина М.И., Хернер Е.К. Численные методы.- М.: Наука, 2007.
. Заварыкин
В.М., Житомирский Г.В. Численные методы.- М.: Просвещение 1990.
. Березин
И.С., Жидков Н.П. Методы вычислений, том 1. М.: Наука, 1966.
. Березин
И.С., Жидков Н.П. Методы вычислений, том 2. М.: Наука, 1966.
. Воеводин
В.В., Кузнецов Ю.А., Матрицы и вычисления.- М.: Наука, 2007.
. Программирование
в среде Turbo Pascal 7.0: А. М. Епанешников, В. А. Епанешников - Москва,
Диалог-МИФИ, 2004 г.- 368 с.
Приложение
линейный система матрица программа
Листинг программы, реализующей метод
квадратного корня для решения линейных систем
Program KvadrKoren;crt;= record
d: real;
y: real;
end;= array [1..10] of complex; {массив
для
задания
вектор-столбцов
}= array [1..10, 1..10] of complex; {массив
для
задания
матриц}
Y, X, B: Vector;{вектор-столбцы:
вспомогательный, искомый и свободных членов}, T: Massiv;{матрицы: исходная и
матрица из разложения (2.3.1)}, j, n: integer; {индексы}, s, f: complex;
{вспомогательные переменные}: array [1..10] of real; {вспомогательный
вектор-столбец}: real; {погрешность}SUM (a,b: complex; var c: complex);
{процедуры SUM-KOR - это заранее описанные математические операции, .d
:=a.d+b.d; используемые в программе}
c.y:=a.y+b.y;;RAZ (a,b: complex; var
c: complex);.d :=a.d-b.d;.y:=a.y-b.y;;UMN (a,b: complex; var c: complex);.d
:=a.d*b.d - a.y*b.y;.y:=a.d*b.y + a.y*b.d;;DIL (a,b: complex; var c:
complex);.d :=(a.d*b.d + a.y*b.y)/(b.d*b.d + b.y*b.y);.y:= (b.d*a.y -
a.d*b.y)/(b.d*b.d + b.y*b.y);;KOR (a: complex; var c: complex);r, f: real;:=
sqrt (a.d*a.d + a.y*a.y);.d :=sqrt(r)*sqrt((a.d/r+1)/2);.y:=
sqrt(r)*sqrt((1-a.d/r)/2)
END;Tij; {нахождение матрицы Т из разложения
(2.3.1) по формулам (2.3.2)}
var k, i, j: integer;
BEGIN(A[1,1], T[1,1]); {нахождение 1 элемента по
1 формуле из (2.3.2)}i:= 1 to n do {нахождение элементов1 строки и главной
диагонали по 3 формуле из (2.3.2)}
for j:=1 to n do(i=j) and
(i<>j) then
begin.d:= 0;{вспомогательные переменные}
s.y:=
0;
for
k:=1 to
i-1 do
begin(T[k, i], T[k, i], p);(s, p,
s);;(A[i, j], s, p);(p, T[i, j]); i<j then
{нахождение оставшихся элементов}
begin.d:= 0;.y:= 0;k:= 1 to i-1 do(T[k,
i], T[k, i], p);(s, p, s);;(A[i, j], s, p);
DIL(p, T[i, j], T[i, j]);
endi>j then {так как матрица Т - верхняя
треугольная, то все элементы под главной диагональю - нулевые}[i, j].d := 0;
T[i, j].y := 0;;;
PROCEDURE Yi {нахождение столбца у по формулам
(2.3.6) из k, i: integer; из нижней треугольной системы (2.3.4)}
BEGIN(b[1], T[1, 1], y[1]);{находим
у1}
for i:= 2 to n do{находим все остальные у}.d:=
0;{вспомогательные переменные}
s.y:= 0;k:= 1 to i-1 do(T[k, i],
y[k], p);(s, p, s);;(b[i], s, p);(p, T[i, i], y[i]);;
END;Xi {нахождение искомого вектор-столбца х k,
i: integer; по формулам (2.3.7) из верхней треугольной матрицы (2.3.5)}(y[n],
T[n,n], x[n]); {нахождение хn}i:= n-1 downto 1 do {нахождение остальных х} .d:=
0;{вспомогательные переменные}
s.y:= 0;k:= i+1 to n do(T[i,k],
x[k], p);(s, p, s);;(y[i], s, p);(p, T[i, i], x[i]);;
END;PROVERKA;{подставляем полученные значения в
исходную i, j: integer; систему и считаем столбец свободных членов заново. Эти
значения заносим во вспомогательный вектор- i:=1 to n do столбец свободных
членов z. Сравниваем этот столбец с исходным столбцом b. Если они совпали,
[i]:= 0; то система решена правильно. }
for j:=1 to n do[i]:=z[i] +
a[i,j].d*x[j].d;(‘b’, i, ’=’, z[i]:7:7);;;; {очистить
экран}(‘vvedite
razmernost matritsy n=’);
readln(n); {ввод размерности матрицы}
write(‘vvedite pogreshnost
vychislenia e=’);(e); {ввод погрешности}(‘vvedite
koefficienty matritsy’);
for i:=1 to n do{ввод коэффициентов матрицы}
for j:=1 to n do(‘a[’, I, ‘,’, j,
‘]=’);(a[i,j].d);;(‘vvedite stolbets svobodnyh chlenov’);
for i:=1 to n do {ввод столбца свободных членов}
begin(‘b[’, i, ‘]=’);(b[i].d);;
Tij; {нахождение матрицы Т}; {нахождение
вектор-столбца y}; {нахождение решения x}i:=1 to n do(‘proverka
pravilnosty’);{процедура проверки};;.