Исследование математической модели прицепа, движущегося по неровной дороге
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ
РЕСПУБЛИКИ
БЕЛАРУСЬ
ГОМЕЛЬСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ИМЕНИ П.О. СУХОГО
Кафедра
”Информационные технологии ”
Курсовая
работа
по
курсу
"Информатика"
на
тему:
"Исследование
математической модели прицепа, движущегося по неровной дороге"
Выполнил: ст. группы
ТМ-22
Лапицкий Е.Е.
Руководитель:
Самовендюк Н.В.
Гомель
2012г.
Содержание
Введение
.
Теория
колебаний
.1
Затухающие колебания
.2
Вынужденные колебания при наличии сопротивления
.3
Установление колебаний
.
Математическое моделирование
.1
Понятие модели
.2
Математические модели и их свойства
.3
Классификация математических моделей
.
Решение дифференциальных уравнений второго порядка
.1
Линейные однородные дифференциальные уравнения
.2
Линейные неоднородные дифференциальные уравнения
.
Численное интегрирование дифференциальных уравнений
.1
Метод Рунге-Кутта
.
Краткая характеристика системы MathCAD
.
Алгоритмический анализ задачи
.1
Постановка задачи
.2
Таблица исходных данных
.3
Математическое описание модели
.4
Графическая схема алгоритма исследования
.
Описание компьютерного документа и результатов исследования
.1
Описание
компьютерного документа
.2
Результаты
исследования
Заключение
Литература
Приложение
Введение
В настоящее время в механике, физике и технике
все больше внимания уделяется изучению теории колебаний.
Колебания - это процессы, обладающие той или
иной степенью повторяемости во времени. Колебания свойственны всем явлениям
природы. При эксплуатации сооружений и машин современные ученые сталкиваются с
такой проблемой как вибрация. Вибрация машин особенно опасна при наступлении
резонанса, т.е. при совпадении собственной частоты колебания системы с частотой
вынуждающей силы. Колебания системы ведут к старению деталей, усталости и
образованию концентраторов напряжений, которые могут стать причиной аварии.
При изучении колебаний применяют различные
математические модели, описывающие колебания механической системы. Для изучения
математической модели широко используют компьютер. Одной из систем, позволяющих
проводить научные исследования над моделью, является система MathCAD. Система
MathCAD позволяет выполнять математические расчеты, как в численном, так и в
символьном виде. Система MathCAD относится к классу интегрированных математических
систем для научно-технических расчетов, к этому же классу можно отнести такие
системы как MathLAB, Maple V, Mathematica 3 и многие другие.
Применительно к исследованию математической
модели прицепа, движущегося по неровной дороге, использование системы MathCAD
ускоряет процесс построения графиков, нахождения функции перемещения и т.п.,
что дает возможность творческой личности сделать свой труд более
производительным. С использованием системы MathCAD можно проследить, как
меняется процесс колебаний, при изменении начальных параметров системы или
возмущающей силы.
Рассматривая математические модели и методы
изучения колебания системы, необходимо, чтобы формальные математические методы
не заслоняли физическое содержание колебательного процесса.
1.Теория колебаний
.1 Затухающие колебания
Рассмотрим, как влияет на свободные колебания
сопротивление среды, считая, что сила сопротивления пропорциональна первой
степени скорости: R= µv (знак минус указывает, что сила R направлена
противоположно v). Пусть на точку при её движении действует восстанавливающая
сила F и сила сопротивления R.Тогда Fx =-cx, Rx =-µvx и дифференциальное
уравнение движения будет иметь вид [3,10,14]:
Деля обе части уравнения на m, получим :
где обозначено:
При этом легко проверить, что величины k и b
имеют
одинаковые
размерности (1/сек); это позволяет сравнивать их друг с другом.
Уравнение (1) представляет собою
дифференциальное уравнение свободных колебаний при сопротивлении,
пропорциональном скорости. Его решение ищут в виде x=ent. Подставляя это
значение x в уравнение (1), получим характеристическое уравнение n2 +2bn+k2=0,
корни которого будут:
n1,2=-b±√b2-k2 (3)
Рассмотрим случай, когда k>b т.е. когда
сопротивление по
сравнению
с восстанавливающей силой мало. Введя обозначение
k1=√k2-b2 (4)
получим из (3), что n1,2=-b±ik1,т.е. что корни
характеристического
уравнения
являются комплексными. Тогда общее решение уравнения (1) будет иметь вид,
отличающийся от уравнения свободных колебаний, т.е. имеет вид [10]:
x=e-bt (C1sink 1t+ C2cosk 1t) (5)
Или же в другом виде:
=ae-bt sin(k 1t+α)
(6)
Входящие сюда величины a и α
являются
постоянными интегрирования и определяются по начальным условиям.
Колебания, происходящие по закону (6) называются
затухающими, так как благодаря наличию множителя e-bt величина x с течением
времени убывает, стремясь к нулю, аналогичная ситуация происходит со скоростью
и ускорением материальной точки [3,10,14].
.2 Вынужденные колебания при наличии
сопротивления
Рассмотрим движение точки, на которую
действуют: восстанавливающая сила F, сила сопротивления R, пропорциональная
скорости и возмущающая сила Q, определяемая формулой [10]:
Qx=Q0sin pt (7)
Дифференциальное уравнение этого движения имеет
вид:
Q0/m =P0 (8)
после преобразования получаем:
Уравнение (9) является дифференциальным
уравнением вынужденных колебаний точки при наличии сопротивления
[1,3,10,14].Его общее решение, как известно, имеет вид x=x1+ x2, где x1-общее
решение уравнения без правой части, а x2-какое-нибудь частное решение полного
уравнения (9). Будем искать x2 в виде:
x2=A sin (pt-β)
Где А и β - постоянные,
которые надо подобрать так, чтобы равенство (9) обратилось в тождество.
Вычисляя производные, получим:
Подставляя эти значения производных и величины
x2 в левую часть уравнения (9) и обозначая для краткости pt-β=ψ
(или
pt+β=ψ),будем
иметь:
A(-p2+k2)sin ψ+2bpAcos ψ=P0(cos β sin
ψ+ sin β cos ψ)
Чтобы это равенство выполнялось при любом ψ,
т.е.
в любой момент времени, коэффициенты при sin ψ
и cos
ψ в
левой и правой части должны порознь равны друг другу; следовательно:
(-p2+k2)=P0cos β,
2bpA=P0sin β
Из полученных уравнений (ими также пользуются
для однозначного определения величины β)
находим, возводя их сначала почленно в квадрат и складывая, а затем деля
почленно друг на друга:
A= P0/√(k2-p2)2+4 b2 p2, tg β=2bp/k2-p2
(10)
Так как x=x1+ x2,а значение x1 (при k>b )
дается равенством (6), то
окончательно
найдем решение уравнения (9) в виде:
x= ae-bt sin(k 1t+α)+Asin(pt
- β)
(11)
Где a и α- постоянные
интегрирования, определяемые по начальным условиям, а значения A и β
даются
формулами (10) и от начальных условий не зависят.
.3 Установление
колебаний
Одна из возможных картин установления колебаний,
происходящих по закону (11) и начинающихся из состояния покоя показана на
рисунке 1в.При других начальных условиях и соотношениях между частотами p и k 1
характер колебаний в интервале времени 0<t< t y может оказаться
совершенно другим [4]. Однако во всех случаях по истечении времени установления
собственные колебания практически затухнут и точка будет совершать колебания по
закону
x= Asin(pt - β) (12)
Эти колебания и называются вынужденными
[3,10].Они представляют собой незатухающие колебания с амплитудой A,
определяемые равенством (10) и частотой p, равной частоте возмущающей силы.
Величина β характеризует
сдвиг фазы вынужденных колебаний по отношению к фазе возмущаающей силы.

Рис1.
а-график затухающих колебаний
б-график свободных колебаний
в-график вынужденных колебаний
2. Математическое
моделирование
.1 Понятие
модели
Под математическим моделированием
понимается процесс замещения объекта исследования некоторой его моделью и
проведение исследований на модели с целью получения необходимой информации об
объекте. Мы создаем модель для исследования интересующей нас стороны
физического объекта. Модель-это физический или абстрактный образ объекта,
удобный для проведения исследований и позволяющий адекватно отображать
интересующие исследователя физические свойства и характеристики объекта [5,9].
Различают предметное и абстрактное моделирование.При предметном моделировании
строят физическую модель, которая соответствующим образом отображает основные
физические свойства и характеристики моделируемого объекта. Если физическая
природа модели и объекта совпадают, то модели называются физическими. При
абстрактном моделировании строится абстрактная модель. Наиболее мощным
средством построения абстрактных моделей является математическое моделирование.
Оно позволяет посредством известных математических функций, символов и
зависимостей описать функционирование технического объекта во внешней среде.
Под математической моделью понимается совокупность математических объектов и отношений
между ними, адекватно отображающих физические свойства объекта. Математическое
моделирование - это процесс формирования модели и использования ее для анализа
и синтеза.
2.2 Математические модели и их свойства
При проектировании различных технических
объектов используют множество видов математических моделей В общем случае
уравнения математической модели связывают физические величины, которые
характеризуют состояние объекта. Такими величинами являются: скорости и силы -
в механических системах; расходы и давления - в гидравлических и пневматических
системах; температуры и тепловые потоки - в тепловых системах и т.п.
Параметры, характеризующие состояние
технического объекта в процессе его функционирования, называют фазовыми
переменными (фазовыми координатами) [13]. Вектор фазовых переменных задает
точку в пространстве, называемом фазовым пространством. Фазовое пространство, в
отличие от геометрического, многомерное. Его размерность определяется
количеством используемых фазовых координат.
Математические модели технических
объектов,используемые при проектировании, предназначены так же и для анализа
процессов функционирования объектов и оценки их выходных параметров. Они должны
отображать физические свойства объектов, существенные для решения конкретных
задач проектирования. При этом математическая модель должна быть как можно
проще, но в то же время обеспечивать адекватное описание анализируемого
процесса.
Аналитическая модель представляет собой явные
зависимости искомых переменных от заданных величин (обычно зависимости выходных
параметров объекта от внутренних и внешних параметров). Такие модели получают
на основе физических законов, либо в результате прямого интегрирования исходных
дифференциальных уравнений, используя табличные интегралы. К ним относятся
также регрессионные модели, получаемые на основе результатов эксперимента.
Графическая (схемная) модель представляется в
виде графиков, эквивалентных схем, динамических моделей, диаграмм и т. п. Для
использования графических моделей должно существовать правило однозначного
соответствия условных изображений элементов графической и компонентов
инвариантной математических моделей.
Структурные модели отображают только структуру
объектов и используются при решении задач структурного синтеза. Параметрами структурных
моделей являются признаки функциональных или конструктивных элементов, из
которых состоит технический объект и по которым один вариант структуры объекта
отличается от другого. Эти параметры называют морфологическими переменными.
Структурные модели имеют форму таблиц, матриц и графов. Наиболее перспективно
применение древовидных графов типа дерева. Они позволяют аккумулировать
накопленный опыт, используя описания всех существующих аналогов, известных из
патентной литературы, и гипотетических объектов.
Функциональные модели описывают процессы
функционирования технических объектов и имеют форму систем уравнений.
Теоретические модели получают на основе описания
физических процессов функционирования объекта, а экспериментальные - на основе
изучения поведения объекта во внешней среде, рассматривая его как
кибернетический "черный ящик". Эксперименты при этом могут быть
физические (на техническом объекте или его физической модели) или
вычислительные (на теоретической математической модели).
При построении теоретических моделей используют
физический и формальный подходы.
Физический подход сводится к непосредственному
применению физических законов для описания объектов. Формальный подход
использует общие математические принципы и применяется при построении как теоретических,
так и экспериментальных моделей.
Линейные модели содержат только линейные функции
фазовых переменных и их производных. Характеристики многих элементов реальных
технических объектов нелинейные. Математические модели таких объектов включают
нелинейные функции фазовых переменных или их производных и относятся к
нелинейным.
2.3 Классификация
математических моделей
Математические модели классифицируются :
)по форме представления:
инвариантные (представляют собой систему
уравнений вне связи с
методом
решения)
алгоритмические (модели связаны с выбранным
численным методом решения и его реализацией в виде алгоритма)
аналитические (отображаются явными зависимостями
переменных)
графические (схемные);
)по характеру отображаемых свойств:
функциональные (описывают процессы
функционирования объектов)
структурные (отображают только структуру и
используются при решении задач структурного синтеза);
) по степени абстрагирования:
модели микро-уровня с распределенными
параметрами
модели макро-уровня с сосредоточенными
параметрами
модели мега-уровня(в зависимости от параметра
динамической системы могут быть либо микро-, либо макро-уровневые модели);
) по способу получения:
теоретически
экспериментальные;
)по учету физических свойств:
динамические
статические
непрерывные
дискретные
линейные
нелинейные;
) по способности прогнозировать результаты:
детерминированные
вероятностные.
Модель считается адекватной, если отражает
исследуемые свойства с приемлемой точностью, которая оценивается степенью
совпадения предсказанного в процессе эксперимента на модели значений выходных
параметров с истинными значениями.
3. Решение дифференциальных уравнений второго
порядка
.1 Линейные
однородные дифференциальные уравнения
Имеем ЛОДУ второго порядка в виде:
где p и q постоянные [7,8].
Для нахождения общего решения уравнения (13)
достаточно найти два его частных решения, образующих фундаментальную систему.
Будем искать частные решения уравнения (13) в
виде
где k-некоторое число (предложено Л. Эйлером).
Дифференцируя эту функцию два раза и подставляя выражения для
в уравнение (13), получим:
Уравнение (14) называется характеристическим
уравнением (13).
При решении характеристического уравнения (14)
возможны три случая:
случай 1. корни k1 и k2 действительные и
различные. Следовательно, общее решение уравнения (13) имеет вид:лучай 2. Корни
k 1 и k 2 характеристического уравнения (13) действительные и различные.
Следовательно, в этом случае общее решение ЛОДУ имеет вид:
лучай 3. Корни k 1 и k 2 уравнения (13)
комплексные :
В этом случае общее решение ЛОДУ имеет вид:
.3.2 Линейные неоднородные дифференциальные
уравнения
Введем следующие сокращения ЛНДУ - линейное
неоднородное дифференциальное уравнение.
Рассмотрим решение ЛНДУ второго порядка с
постоянными коэффициентами, т.е. уравнение
где p и q - некоторые числа [8].
Общее решение уравнения (15) представляет собой
сумму yо.о. соответствующего однородного уравнения и частного решения yч.н. неоднородного
уравнения. Частное решение уравнения (15) может быть найдено методом вариации
произвольных постоянных.
Для уравнения с постоянными коэффициентами
существует более простой способ нахождения yч.н., если правая часть уравнения
(15) имеет так называемый " специальный вид "лучай 1.Правая часть
имеет вид
Тогда уравнение (15) запишется в виде:
В этом случае частное решение yч.н ищем в виде:
где r-число, равное кратности α
как
корня характеристического уравнения.
Случай 2.Правая часть имеет вид
Где α
и β
- действительные
числа.Уравнение (15) запишется в виде:
Можно показать, что в этом случае частное
решение yч.н уравнения (16) следует искать в виде [8]:
Где M(x) и N(x)-многочлены степени l с
неопределенными
коэффициентами, l-наивысшая степень многочленов
P(x) и Q(x), т.е.
=max(n,m).
4. Численное интегрирование дифференциальных
уравнений
.1 Метод Рунге-Кутта.
Метод Рунге-Кутта-один из наиболее
употребительных методов повышенной точности [2].
Пусть требуется найти численное решения (1),
удовлетворяющее условию (2).Предположим, что в точке x известно y(x); пусть
h>0. Обозначим Δy(x)=y(x+h)-y(x), где
y(x+h) надо вычислить. Представим разность Δy(x) в
виде суммы "поправок" kj с коэффициентами pj:
Δy=p1k1+ p2k2+…+ prkr
(17)
Где k1=hf(x,y)
k2=hf(x+ α2h,y+ β21 k1)
………………………….
kr=hf(x+ αrh,y+ βr1 k1+ βr2 +…+
βrr-1 kr-1)
Коэффициенты pj, αj, βji получаются
при сравнении разложения Δy и ki по
степеням h
В случае r=4, получим ф-лы (18):
k1=hf(x,y),=hf(x+h/2,y+k1/2),
(18)=hf(x+h/2,y+k2/2),=hf(x+h,y+k3)
Δy=(1/6)*(k1+2*k2+2*k3+k4)
(19)
При x=x0 с помощью формул (17-19) находим y1=y0+
Δy0.
Аналогично получаем последующие приближения:
y(i+1)=yi+ Δyi (i=1,2,3,…)
(20)
где
Δyi=(1/6)*(k1(i)+2*k2(i)+2*k3(i)+k4(i)),
(21)(i)=hf(xi,yi);(i)=hf(xi+h/2,yi+ k1(i)/2);(i)= hf(xi+h/2,yi+ k2(i)/2);
(22)(i)= hf(xi+h/2,yi+ k3(i)/2);
Для уравнения
Верна следующая оценка погрешности метода
Рунге-Кутта:
где M и N-постоянные,такие, что в области
|x-xo|<a, |y-yo|<b
выполняются неравенства
Метод Рунге-Кутта применим также к системам
дифференциальных уравнений первого порядка. Пусть дана система двух уравнений
С начальными условиями:
Определяя параллельно числа λn
и μn
по формулам
λn=(1/6)*
(k1+2*k2+2*k3+k4)
μn=(1/6)* (l1+2*l
2+2*l3+l4)
где
=hf(xn,yn,zn);=hf(xn+h/2,yn+k1/2,zn+l1/2);=
hf(xn+h/2,yn+k2/2,zn+l2/2); =hf(xn+h,yn+k3,zn+l3);
=hg(xn,yn,zn);=hg(xn+h/2,yn+k1/2,zn+l1/2);=hg(xn+h/2,yn+k2/2,zn+l2/2);=hg(xn+h,yn+k3,zn+l3);
находят
(n+1)=yn+ λn,
z(n+1)=zn+ μn. (29)
Метод Рунге-Кутта применяется также при решении
обыкновенных дифференциальных уравнений высших порядков.
5. Краткая характеристика системы MathCAD
Система MathCAD разработана фирмой MathSoft
(США) и является одной из самых мощных и эффективных систем математического
направления.Она обладает прекрасной графикой и визуализацией на всех этапах
ваычислений, включая ввод, имеет образцовый интерфейс.Ввод данных с помощью
помощью палитр математических знаков. Удачный отбор операторов и функций. В то
же время, она обладает рядом недостатков и неудобств [9]:
Ограниченные средства символьной математики.
Примитивные средства программирования. Повышенные требования к аппаратным
ресурсам. Дороговизна электронных книг и библиотек. Отсутствие русифицированных
версий последних.
Система MathCAD относится к классу
интегрированных математических программных систем для научно-технических
расчетов, к этому же классу можно отнести такие системы как , Maple
V,Mathematica2 и 3 и т.д. MathCAD чрезвычайно
прост
использовании и легок в обучении.
Большинство действий, необходимых для управления
являются индуктивно прозрачными, и на освоение основных ее возможностей
человеку, работавшему ранее в среде Windows, требуется 2-3 часа. Помимо
привычных численных расчетов MathCAD способен делать символьные преобразования.
MathCAD обладает множеством функций, запишем основные из них: вычислительные
функции, графические функции, программирование, сервисные функции.
Графические возможности системы применяются для
визуализации результатов вычислений и включают построение двумерных графиков в
различных системах координат, создание графиков поверхностей, карт линий
уровня, трехмерных гистограмм, точечных графиков и графиков, векторных полей.
Система позволяет продемонстрировать процесс движения или изменения каких-либо
результатов в виде анимационного клипа. Возможно также внесения графических
файлов определенного формата из других систем в документ MathCAD.
Система позволяет создать программы,
представляющие собой выражения, состоящие из программных конструкций, подобных
конструкциям языков программирования. Программные выражения позволяют успешно
решать в системе те задачи, которые невозможно вычислить с помощью имеющихся
встроенных функций.
Общение пользователя с системой MathCAD
происходит на некотором промежуточном математически ориентированном языке
визуального программирования -входном языке. Математические записи вэтом языке
вводятся просто выводом шаблонов соответствующих операторов и функций. Этот
язык настолько приближен к обычному математическому языку описания
вычислительных задач, что практически не требует их программирования. Нужно
лишь точное описание алгоритма решения задачи [9,12].
Операторы - это специальные символы, указывающие
на выполнение тех или иных операций. Подоперационный материал может быт
представлен константами или переменными - объектами с именами, хранящими данные
определенного типа и значения. Наиболее известны арифметические операторы,
например сложения +, вычитания -, умножения *,деления /, вычисления квадратного
корня и т.д.
Функция - объект входного языка, имеющий имя и
параметры, указываемые в круглых скобках. Имя функции отождествляется с
соответствующей математической функций - например sin(x) - это функция
вычисления синуса аргумента x. Отличительной чертой функции является возврат
значения (результата вычисления функции) в ответ на обращение к ней.
Операторы и функции используются для создания
математических выражений - формул, которые могут вычисляться в численном или
символьном виде. И если к вычислениям по формулам, представленным в
соответствующем виде, мы привыкли, то возможность их аналитического
преобразования - важная новая черта систем MathCAD под Windows.
.1 Постановка задачи
Прицеп массой m движется по неровной дороге с
постоянной скоростью v (Рис. 2). Считать, что точка крепления прицепа к
автомобилю (точка О) не имеет вертикальных перемещений. При решении считать,
что жесткость шин весьма велика по сравнению с жесткостью рессор c. Профиль
неровностей дороги можно описать уравнением h=h0(1-cos(2πx/l1)).
Момент
инерции системы относительно точки О равен Jo. Счиатать, что в рессорах
возникает вязкое трение с коэффициентом трения α Массой
колес прицепа по сравнению с массой m можно пренебречь. При решении задачи
прицеп можно представить схемой, как показано на (рис2б.), причем h значительно
меньше l (т.е. поворот на угол φ приводит
только к вертикальному смещению точки А).
Требуется определить: использованием системы
MathCAD рассчитать значение функций перемещения, скорости и ускорения прицепа
под воздействием начальных значений перемещения и скорости без учета
возмущающей силы неровностей дороги.Построить графики этих функций.
Рассчиать значение функций перемещения, скорости
и ускорения прицепа без воздействия начальных значений перемещения и скорости с
учетом возмущающей силы неровностей дороги. Построить графики этих функций.
Исследовать влияние массы прицепа на
максимальную амплитуду колебаний. Провести не менее 6-10 опытов, полученные
результаты представить в виде графиков.
Вычислить аналитические аппроксимирующие функции
по результатам исследований предыдущего пункта. Построить графически исходную и
аппроксимирующую зависимости
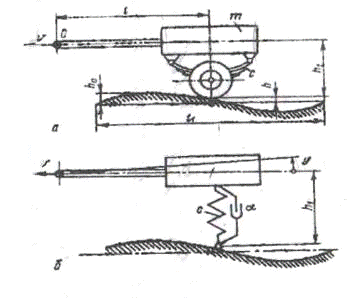
Рис2.
6.2 Таблица исходных данных
перемещение скорость модель
колебание
|
Параметр
|
Имя
в задаче
|
Значение
|
Размерность
|
|
Масса
прицепа
|
m
|
500
|
кГ
|
|
Скорость
прицепа
|
v
|
12.5
|
м/c
|
|
Расстояние
от точки крепления до прицепа
|
L
|
1.71
|
м
|
|
Длина
цикла перегиба дороги
|
L1
|
10
|
м
|
|
Момент
инерции прицепа относительно точки О
|
J0
|
400
|
кГ*м2
|
|
Коэффициент
вязкого сопротивления
|
α
|
30
|
Н*с/м
|
|
Жесткость
рессор
|
c
|
6000
|
Н/м
|
|
Амплитуда
возмущающей силы
|
h0
|
0.023
|
Н
|
6.3 Математическое описание модели
Уравнение Лагранжа 2-го рода является одним из
универсальных уравнений теоретической механики и позволяет находить закон
движения тела, кроме того оно учитывает все активные силы действующие на
систему будь то сила или момент сил [1,3,6,10,14].
Для решения данной задачи воспользуемся
уравнением Лагранжа второго рода. Кинетическая и потенциальная энергия, а также
диссипативная функция Релея соответственно равны:
T = mv2 /2+ J0φ2/2;
П = с(Lφ-h)2/2;
R = α(Lφ-h)2/2;
Обобщенная сила Q будет равна: Q = -dП/dφ
-R/d φ;
Возмущающая сила неровности дороги описывается
следующим законом: h(t)=h0(1-cos(2πvt/L1)).
Уравнение Лагранжа второго рода имеет вид:
Где q-обобщенная координата, в данной задаче в
качестве обобщенной координаты мы выбираем угол поворота прицепа φ,
что
позволит нам однозначно определить местоположение прицепа в пространстве.
В нашей задаче уравнение иммет вид:
Найдем компоненты уравнения Лагранжа:
dT/dφ =0,т.к. кинетическая
энергия T не зависит от угла поворота φ
dT/dφ = J0φ
d(dT/dφ)dt = J0φ, т.к.
φ
зависит
от времени t.
-dП/dφ =-2с(Lφ-h(t))L/2
= -cL(Lφ-h(t));
dR/dφ = -2α(Lφ-h(t))L/2 =
-αL(Lφ-h(t));
Уравнение (31) примет вид:
J0φ+ αL(Lφ-h(t))+cL(Lφ-h(t)) =
0;
В развернутом виде получим:
В первом случае не учитываем возмущающую силу
неровности дороги h(t).Решаем уравнение (32) с учетом начальных параметров
(задача Коши) и получаем зависимость φ(t)
и φ(t).
Перемещение прицепа находим как [1,4,10,14]:
A=Lsin(φ(t)) (33)
где L -расстояние от прицепа до точки О.
Скорость прицепа V = ω(t)L
(34)
Угловое ускорение ε(t) определяем
из уравнения (32):
Т.к. h(t) для первого опыта равно нулю, тогда
ур-е (35) примет вид:
Тангенциальное ускорение прицепа [1,3,4,10,14]:
At:= ε(t)L (36)
Нормальное ускорение прицепа равно
[1,3,4,10,14]:
An:= (ω(t))2L (37)
Полное усорение прицепа [1,3,4,10,14] :
Аp:= √An2+At2 (38)
учетом возмущающей силы имеем тот же алгоритм,
но теперь h(t)=0Решаем уравнение (32) с учетом начальных параметров (задача
Коши) и получаем зависимость φ(t)
и φ(t).
Перемещение прицепа находим как A=Lsin(φ(t)),
где L -расстояние от прицепа до точки О.Угловая скорость прицепа ω(t)
= φ(t), определена из уравнения (32).
Скорость прицепа V = ω(t)L
Угловое ускорение ε(t) определяем
из уравнения (32):
Т.к. h(t) для первого опыта равно нулю, тогда
ур-е (35) примет вид:
Тангенциальное ускорение прицепа:
At:= ε(t)L (36)
Нормальное ускорение прицепа равно:
An:= (ω(t))2L (37)
Полное ускорение прицепа Аp:= √An2+At2
(38)
7. Описание компьютерного документа и
результатов исследования
.1 Описание компьютерного документа
В результате исследования была построена математическая
модель прицепа, движущегося по неровной дороге.Движение прицепа было
рассмотрено для двух вариантов:
-с учетом начальных значений угла поворота и
угловой скорости,без учета возмущающей силы неровности дороги;
-без учета начальных значений угла поворота и
угловой скорости под действием возмущающей силы неровности дороги).
Приложение пункт №1:
В пункте №1 проводим исследование движения
прицепа по неровной дороге с учетом начальных значений угла поворота и угловой
скорости и без учета возмущающей силы неровности дороги.
По имеющемуся уравнению движения прицепа (32) с
учетом начальных значений угла поворота и угловой скорости, но без учета
возмущающей силы неровности дороги, при помощью метода Рунге-Кутта получаем
матрицу решений, из которой находим зависимость угла поворота от времени и
зависимость угловой скорости прицепа от времени. После этого получаем
зависимость перемещения от времени по аналитической формуле (33).
Далее находим зависимость скорости прицепа от
времени по формуле (34).После этого по аналитическим формулам получаем
зависимость тангенциального ускорения прицепа и нормального ускорения прицепа
ф-лы (36-37).Ниже записали полное ускорение прицепа по формуле (38).
Приложение пункт №2:
В пункте №2 проводится исследование движения
прицепа по неровной дороге без учета начальных значений угла поворота и угловой
скорости под действием возмущающей силы неровности дороги.
По имеющемуся уравнению движения прицепа (32)
без учета начальных значений угла поворота и угловой скорости, но с учетом возмущающей
силы неровности дороги, методом Рунге-Кутта находим матрицу решений, из которой
мы получаем зависимость угла поворота от времени и зависимость угловой скорости
прицепа от времени. После этого была находим зависимость перемещения от времени
по аналитической формуле (33).
Далее записываем зависимость скорости прицепа от
времени по формуле (34) .После этого по аналитическим формулам находим
зависимость тангенциального ускорения прицепа и нормального ускорения прицепа
ф-лы (36-37). Ниже получили полное ускорение прицепа по формуле (38).
Приложение пункт №3:
В пункте №3 проводится исследование влияние
массы прицепа на максимальную амплитуду колебаний (Исследование проводится по
пункту №1).Для этого последовательно изменияется масса прицепа m=250-2500кГ.
Решаем дифференциальное уравнение (32), после чего находим максимальную
амплитуду колебаний для соответствующей массы. Проводим 10 исследований , в
результате получает значения результатов: изменение массы и изменение
максимальной амплитуды.По полученным результатам строим график зависимости
максимальной амплитуды колебания от массы прицепа (Пункт 3).
Приложение пункт №4
В пункте 4 проводится вычисление аналитической
аппроксимирующей функции по результатам исследований пункта№3.На графике
представлено построение аппроксимирующей функции (график синего цвета) и
функции по результатам исследований (график красных точек).
Для наглядности описания курсового проекта
создаем презентацию в Microsoft Power Point, которая содержит исходные значения
параметров, основные формулы и изображения графиков по результатам
исследований.
7.2 Результаты исследования
Задачей исследования было нахождение функций
перемещения, скорости и ускорения прицепа, а также проведение исследований
влияния массы прицепа на максимальную амплитуду колебаний.
Результатом проведенного исследования явилось
следующее:
.Аналитическим методом были выведены функции
перемещения, скорости, тангенциального и нормального ускорения, а также полного
ускорения прицепа.
.Аналитически были обоснованы различия графиков
перемещений при затухающих колебаниях и вынужденных.
.С использованием системы MathCAD были
рассчитаны значения функций перемещения, скорости и ускорения прицепа под
воздействием начальных значений перемещения и скорости без учета возмущающей силы
неровности дороги.
.По пункту 3 получили следующие выводы:
a) Амплитуда колебаний с течением времени
стремится к нулю.
б) Скорость прицепа с течением времени стремится
к нулю.
в)Тангенциальное ускорение стремится к нулю и в
вертикальной плоскости принимает знакопеременные значения.
г)Нормальное ускорение прицепа стремтися к нулю
и в вертикальной плоскости имеет только положительные значение.
д)Полное ускорение прицепа стремится к нулю.
.По пункту 4 получили вывод, что при наличии сил
сопротивления с учетом начальных значений и при отсутствии возмущающей силы
движение прицепа является устойчивым и приемлимым режимом при эксплуатации,
т.к. устраняются разрушающие колебания системы.
. С использованием системы MathCAD были
рассчитаны значения функций перемещения, скорости и ускорения прицепа без
воздействия начальных значений перемещения и скорости с учетом возмущающей силы
неровности дороги.
.По пункту 6 получили следующие выводы:
а) мплитуда с течением времени к нулю не
стремится.
б)Скорость прицепа с течением времени к нулю не
стремится.
в)Тангенциальное ускорение не стремится к нулю и
в вертикальной плоскости принимает знакопеременные значения.
г)Нормальное ускорение прицепа не стремтися к
нулю и в вертикальной плоскости имеет только положительные значение.
д)Полное ускорение прицепа к нулю не стремится.
е)Перемещение, скорость и ускорение прицепа
имеют время установления, которое при заданных параметрах равняятся 30 сек.
ж)После времени установления колебаний
амплитуда, скорость и ускорение имеют периодический характер.
з)Амплитуда, скорость и ускорение принимают
максимальные значеия в первые секунды движения.
и)
.По пункту 7 получили вывод , что при наличии
сил сопротивления без учета начальных значений и при наличии возмущающей силы
движение прицепа является периодическим. Степень его пригодности к эксплуатации
зависит от механических характеристик деталей
(выносливость , надежность и т.д.)
. С использованием системы MathCAD были
проведены исследования влияния массы прицепа на максимальную амплитуду колебания.
.При затухающих колебаниях с увеличением массы
прицепа максимальная амплитуда колебания увеличивается.Это обьясняется силами
инерции: при увеличении массы сила инерции увеличивается и она больше
воздействует на рессоры прицепа, растягивая их.
Заключение
Применение математического пакета MathCAD
значительно облегчило процесс исследования математической модели прицепа . По
проведенному исследованию видно, что теоретические выкладки и результаты,
полученные в среде MathCAD совпадают.
Использование системы MathCAD позволило быстрее
посторить графики, найти функции перемещения и т.д. Это дает возможность
инженеру сделать свой труд более производительным.
В дальнейшем, процесс исследований будет
проходить ещё быстрее. Скорость обработки и доступ к различного рода информации
повысятся на порядок. Решающая роль в решении задач, по-прежнему, будет
принадлежать творческой личности, от количества которых и зависит процветание
нашей Родины.
Литература
.
Гусак А.А.Элементы методов вычислений-2-изд.,Мн.:
Изд-во
БГУ,1982.-166с.,илл.
.
Добронравов В.В., Никитин Н.Н., Дворников А.А. Курс теоретической механики.М.:Высш.
Шк.1968.
.
Зисман Г.А., Тодес О.М. Курс общей физики. Т1. М.: Наука, 1974.-336с., илл.
.
Крылов В.И., Бобков В.В., Монастырский П.И. Вычислительные методы.Т.1,2.
М.:Наука, 1976.
.
Мандельштам Л.И. Лекции по колебаниям. М.: АН СССР, 1955.-504с.
.
Пискунов Н.С.Дифференциальное и интегральное исчисления. Т
2.М.:Наука,1978.-576с.,илл.
.
Письменный Д.Т. Конспект лекций по высшей математике.Ч2. М.: Рольф,2000.-256с.,
илл.
.
Рычков В., Дьяконов В., Новиков В. Компьютер для студента. Самоучитель-Спб:Питер,2001.-592с.:
илл.
.
Тарг С.М.Краткий курс теоретической механики.М. :Наука, 1970. - 480с. , илл.
.
Токочаков В.И. Практическое пособие по теме "Решение систем алгебраических
и дифференциальных уравнений в среде MathCAD Windows".М/ук 2453
Гомель,ГГТУ,2000
Трохова
Т.А. Основные приемы работы в системе MathCAD,
версии
6.0.М/ук 2286.Гомель, ГГТУ, 1998
.
Шабловский О.Н.Учебное пособие по курсу "Теоретическая механика".
Избранные лекции по теории колебаний и волн в механике сплошных сред. М/ук
2094,ГПИ им.П.О.Сухого 1996. - 85с.
.
Яблонский А.А. Курс теоретической механики. Ч2.Динамика М. : Высш. шк.,
1984.-423с.,илл.