Синтез комбінаційної схеми в обмеженому базисі
Міністерство
освіти і науки, молоді та спорту України
Вінницький
національний технічний університет
Інститут
інформаційних технологій та комп’ютерної інженерії
Кафедра
ОТ
Пояснювальна
записка
з
дисципліни "Організація функціонування ЕОМ"
Синтез
комбінаційної схеми в обмеженому базисі
Керівник
курсової роботи
к.т.н., доц.
Біліченко Н.О.
Розробив
студент гр. 1КІ-10
Гнатюк А.В.
Вінниця
ВНТУ 2011
Анотація
У цій курсовій роботі ми детально
познайомимся з двійковою арифметикою, яка є невід`ємною частиною обчислювальної
техніки. Тобто, ми розглянемо закони диз’юнкції, кон’юнкції та інші? які
пов’язані з булевою алгеброю.
Зміст
Вступ
. Основи двійкової арифметики.
Порозрядні логічні операції (Булівські операції)
.1 Суттєві та несуттєві змінні
.2 Еквівалентні формули та
закони
.3 Бульові функції та
комбінаційні схеми
. Розрахунок таблиці істинності
.1 Мінімізація методом
послідовного виключення логічних змінних
.2 Мінімізація методом
мінімізуючих карт Карно
.3 Зведення до базису
.4 Синтез комбінаційної схеми
.5 Часові діаграми
Висновок
Список посилань
Вступ
Вся інформація в пам'яті цифрового
комп'ютера зберігається в двійковій формі, тобто у вигляді послідовностей нулів
та одиниць. Причина цього полягає в особливостях фізичної реалізації, при якій
електронні елементи цифрового комп'ютера можуть перебувати в одному з двох
стійких станів: висока напруга - низька напруга, або є струм - немає струму
тощо. Усе це реалізується в комп’ютерній схемотехніці за допомогою законів
булевої алгебри які надалі будуть розглянути.
. Основи двійкової арифметики.
Порозрядні логічні операції (Булеві операції)
Множину {0, 1} позначимо літерою B.
Множину всіх можливих послідовностей з 0 і 1 - Bn. Такі послідовності за
традицією будемо називати наборами або векторами довжини n. Очевидно, Bn
містить 2n елементів. Значення 0 і 1 називаються протилежними одне до одного.
Означення. Всюди визначена функція з
Bn у B називається n-місною функцією алгебри логіки або n-місною бульовою
функцією.
Послідовність змінних (x1, x2, …,
xn) із значеннями у B позначимо  . Бульова функція
f(
. Бульова функція
f( )
задається у вигляді таблиці, або графіка зі стандартним розташуванням наборів:
)
задається у вигляді таблиці, або графіка зі стандартним розташуванням наборів:

Зауважимо, що в стандартному
розташуванні набори можна розглядати як двійкові записи послідовних чисел від 0
до 2n-1. Функцію, задану зі стандартним розташуванням наборів, можна ототожнити
з набором довжини 2n. Наприклад, двомісну функцію, задану таблицею можна
ототожнити з вектором (1011).

Далі іноді будемо позначати n-місну
функцію f( ) як f(n)(
) як f(n)( ),
підкреслюючи кількість змінних, від яких вона залежить.
),
підкреслюючи кількість змінних, від яких вона залежить.
Очевидно, що множина всіх можливих
наборів довжини 2n, тобто множина n-місних бульових функцій, складається з 22n
елементів. При n=0 це 2, при n=1 - 4, при n=2 - 16, при n=3 - 256 тощо.
Нуль-місними функціями є сталі 0 і
1.
Одномісні функції подано у наступній
таблиці разом з виразами, якими ці функції позначаються:
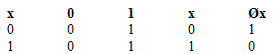
Функції 0 і 1 називаються тотожними
нулем і одиницею, функція x - тотожною, Øx - запереченням.
Замість виразу Øx вживається
ще вираз  .
Ці вирази читаються як "не x".
.
Ці вирази читаються як "не x".
Подамо також деякі з 16 двомісних
функцій разом із їх позначеннями:

Функція, позначена виразом xÙy,
називається
кон'юнкцією і позначається ще як x&y, x×y
або
xy. Усі ці вирази читаються як "x і y".
Функція, позначена виразом xÚy,
називається
диз'юнкцією. Вираз читається як "x або y".
Функція, позначена виразом x®y,
називається імплікацією і позначається ще як xÉy.
Ці
вирази читаються як "x імплікує y" або "з x випливає y".
Функція, позначена виразом x"y,
називається еквівалентністю і позначається ще як x~y або xºy.
Ці
вирази читаються як "x еквівалентно y", що в даному випадку
збігається з "x дорівнює y".
Функція, позначена виразом xÅy,
називається
додаванням за модулем 2 або "виключним або". Зауважимо, що її
значення є протилежними до значень еквівалентності.
Функція, позначена виразом x|y,
називається штрихом Шеффера і має значення, протилежні значенням кон'юнкції. Її
вираз читається як "не x або не y".
Функція, позначена виразом x¯y,
називається
стрілкою Пірса і має значення, протилежні значенням диз'юнкції. Її вираз
читається як "не x і не y".
Зауважимо, що інфіксні позначення
наведених функцій вигляду x f y, де f - відповідний знак, склалися історично.
Їх так само можна позначати й у вигляді f(x, y), наприклад, Ù(x,
y).
З тримісних функцій наведемо лише
так звану функцію голосування m(x, y, z), графік якої має такий вигляд:

Її назва зумовлена тим, що її
значення на кожному наборі збігається з більшістю значень змінних у цьому
наборі.
Множину всіх n-місних функцій
позначимо P(n), а множину всіх функцій, тобто об'єднання P(n) по всіх n - P2.
Перейдемо до означення таких понять,
як алгебра бульових функцій і алгебра формул.
Алгебри бульових функцій, як і всі
інші алгебри, визначаються своїми носіями та сигнатурами операцій. Носіями в
алгебрах бульових функцій є множини функцій. Сигнатуру складає операція
суперпозиції, або підстановки.
Означення. Нехай є n-місна функція
f(n)( )
і n функцій g1(y1,1, y1,2, …, y1,m1), g2(y2,1, y2,2, …, y2,m2), …, gn(yn,1,
yn,2, …, yn,mn), залежні від змінних з деякої їх множини Y={y1, y2, …, yk}.
Суперпозицією, або підстановкою функцій g1, g2, …, gn у функцію f(n)
називається функція h(m)(y1, y2, …, ym), кожне значення якої h(a1, a2, …, am)
визначається як
)
і n функцій g1(y1,1, y1,2, …, y1,m1), g2(y2,1, y2,2, …, y2,m2), …, gn(yn,1,
yn,2, …, yn,mn), залежні від змінних з деякої їх множини Y={y1, y2, …, yk}.
Суперпозицією, або підстановкою функцій g1, g2, …, gn у функцію f(n)
називається функція h(m)(y1, y2, …, ym), кожне значення якої h(a1, a2, …, am)
визначається як
f(n)(g1(a1,1, a1,2, …, a1,m1),
g2(a2,1, a2,2, …, a2,m2), …, gn(an,1, an,2, …, an,mn)).
Суперпозиція
ще
позначається
як
S(f(n); g1(y1,1, y1,2, …, y1,m1), g2(y2,1, y2,2, …, y2,m2),…, gn(yn,1, yn,2, …,
yn,mn)).
Приклади.
1. h1(x, y, z)=S(Ù; xÚy,
y®z) задається наступною таблицею:

2. h2(x, y)=S(Ù; xÚy, y®x)
задається
таблицею:

Нехай є множина бульових функцій F.
Утворюючи з них та їх суперпозицій усі можливі суперпозиції, ми одержимо
множину функцій, яку позначимо [F]. Отже, маємо алгебру ([F]; S), породжену
множиною функцій F. Інша множина функцій F1 буде породжувати, взагалі кажучи,
іншу алгебру ([F1]; S). Наприклад, алгебри ([{(0111), (0001)}]; S) і ([{(10),
(0001)}]; S).
Розглянемо тепер поняття алгебри
формул (термів, або виразів). Нехай є множина функцій F. Кожній n-місній
функції з F поставимо у взаємно однозначну відповідність символ, що її позначає
(функціональний символ) f(n). Нехай X - зліченна множина змінних (точніше, їх
імен).
Означення.
. Якщо f(n) - функціональний символ,
а T1, T2, …, Tn є формулами, то f(n)( T1, T2, …, Tn) є формулою.
. Інших формул немає.
Це означення задає множину формул із
функціональними символами з множини F, які одержуються за допомогою
підстановок, тобто суперпозицій. Таким чином, ми маємо алгебру формул,
породжену множиною функціональних символів F. Інша множина функціональних
символів буде породжувати й іншу алгебру формул.
Зв'язки між алгебрами функцій і
алгебрами формул встановлюють наступні два означення.
Означення. Значенням формули T на
наборі значень змінних з множини X є:
) значення змінної x, якщо T є
змінною x;
) f(n)(a1, a2, …, an), якщо
T=f(n)(T1, T2, …, Tn), а формули T1, T2, …, Tn мають на цьому наборі значення
відповідно a1, a2, …, an.
Означення. n-місна бульова функція
f(n) задається формулою T, якщо всі змінні у формулі T є змінними з множини X,
і при будь-якому наборі значень (a1, a2, …, an) цих змінних x1, x2, …, xn
значення формули дорівнює значенню f(n)(a1, a2, …, an).
Звідси випливає інше означення
суперпозиції функцій.
Означення. n-місна бульова функція
f(n) є суперпозицією функцій f1, f2, …, fn, якщо її можна задати формулою, усі
функціональні символи якої є серед символів функцій f1, f2, …, fn.
З наведених прикладів 1 і 2 видно,
що функція h1(x, y, z) задається формулою Ù(Ú(x,
y), ®(y, z)), або в інфіксному записі (xÚy)Ù(y®z).
Аналогічно
функція h2(x, y) задається формулою Ù(Ú(x,
y), ®(y, x)), або (xÚy)Ù(y®x).
Як
бачимо, обидві функції задаються формулами з тими самими функціональними
символами Ù, Ú, ®, тобто
є суперпозиціями цих функцій.
Наостанок наведемо узгодження, які
склалися в математиці й дозволяють у формулах з функціональними символами Ø,
Ù, Ú, ®, Å, ",
|, ¯ записувати не всі необхідні дужки.
1.1 Суттєві та несуттєві змінні
Розглянемо поняття суттєвої
залежності функції від її змінних. Почнемо з прикладів: значення функції h2(x,
y) з прикладу 2 на кожному з наборів збігаються зі значеннями x. Отже, зміна
значення y не впливає на значення функції, тобто вона фактично не залежить від
y. В той час як зміна значення x веде до зміни значення h2. Уточнимо ці
міркування наступними означеннями.
Означення. Змінна xi функції
f(n)(x1, x2, …, xi, …, xn) називається суттєвою, якщо існує хоча б одна пара
наборів значень змінних
(a1, a2, …, ai-1, 0, ai+1, …, an) і
(a1, a2, …, ai-1, 1, ai+1, …, an),
така,
що
f(n)(a1, a2, …, ai-1, 0, ai+1, …, an) ¹
f(n)(a1, a2, …, ai-1, 1, ai+1, …, an).
Змінна xi називається несуттєвою у
противному разі, тобто коли за всіх можливих пар наборів значень
(a1, a2, …, ai-1, 0, ai+1, …, an) і
(a1, a2, …, ai-1, 1, ai+1, …, an)
мають
місце
рівності:
(n)(a1, a2, …, ai-1, 0, ai+1, …, an)
= f(n)(a1, a2, …, ai-1, 1, ai+1, …, an).
Наприклад,
неважко
переконатися,
що
всі
змінні
функції
h1 з прикладу
1 є суттєвими.
Функція
h2 має суттєву
змінну
x і несуттєву
y. Функція двох
змінних,
задана
як
вектор
(1111), не
має
суттєвих
змінних.
1.2 Еквівалентні формули та закони
Одна й та сама бульова функція
задається, взагалі кажучи, багатьма різними формулами. Наприклад, неважко
переконатися, що формули x®y і ØxÚy обидві
задають функцію (1101). Таким чином, можна говорити про еквівалентність цих
двох формул.
Означення. Нехай **** Формули F1 і
F2 називаються еквівалентними, якщо
1.3 Бульові функції та комбінаційні схеми
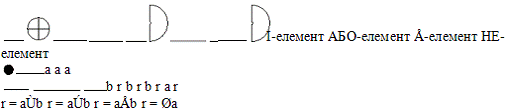
Розглянемо реалізацію бульових
функцій у вигляді комбінаційних схем. Найпростішими з них є логічні елементи,
відповідні бульовим функціям: кон'юнкції Ù, диз'юнкції
Ú,
додавання
за модулем 2 Å та
заперечення Ø. Вони
позначаються й зображаються таким чином:
Входи перших трьох елементів
вважаються симетричними згідно законів комутативності, яким задовольняють
кон'юнкція, диз'юнкція та додавання за модулем 2.
З наведених логічних елементів
будуються складніші схеми, які в загальному випадку мають n входів і m виходів
і реалізують набір з m функцій від n аргументів.
. Розрахунок таблиці
істинності
Вислів - твердження, по відношенню
до якого має сенс стверджувати істинне воно чи хибне.
Вислови бувають складні чи прості. Прості
вислови - логічні змінні. Складні - логічні функції від логічних змінних. Логічні
функції називають також бульовими або перемикаючими.
Функціонування цифрових
обчислювальних пристроїв комбінаційного типу, які мають n входів та m виходів,
у загальному випадку може бути описано системою функцій виду :
 ,де
значення функції 3333yi визначають значення вихідних сигналів, а
набори аргументів (x1,x2,…,xn) відповідають
вхідним сигналам. Як функції, так і аргументи можуть приймати тільки кінцеве
число значень (як правило xj,yjÎ{0,1}).
Саме такі функції отримали назву перемикаючих (нульових, двозначних, логічних).
,де
значення функції 3333yi визначають значення вихідних сигналів, а
набори аргументів (x1,x2,…,xn) відповідають
вхідним сигналам. Як функції, так і аргументи можуть приймати тільки кінцеве
число значень (як правило xj,yjÎ{0,1}).
Саме такі функції отримали назву перемикаючих (нульових, двозначних, логічних).
Перемикаючі функції частіше всього
задають за допомогою таблиць, що називаються таблицями істинності, шляхом
перечислення їх значень на всіх наборах значень аргументів. З метою спрощення
таблиць істинності набори аргументів нумерують. Номер х набору аргументів
дорівнює двійковому числу, яке відповідає цьому набору, тобто
 .
.
Якщо функція залежить від n
аргументів, то число різних наборів дорівнює 2n, оскільки кожен
набір має свій номер, а загальне число номерів дорівнює кількості різних
двійкових n-розрядних чисел. Дві
функції відрізняються одна від одної, якщо вони приймають різні значення хоча б
на одному наборі аргументів. Число різних функцій від n аргументів дорівнює 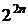 ,так
як для задання функцій
,так
як для задання функцій
 необхідно
вказати набір з 2n констант
необхідно
вказати набір з 2n констант  ,
,
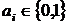 ,
а число 2n-розрядних наборів дорівнює
,
а число 2n-розрядних наборів дорівнює  .
В таблиці істинності значення функції на деяких наборах можуть бути не
визначені, тобто можуть приймати як значення 0, так і значення 1. Серед функцій
n змінних завжди можна вказати функції, аналогічні по властивостям функціям
двох змінних. До таких функцій, наприклад, відносяться константи 0 і 1; змінні
x1,x2,…,xn; кон’юнкція, що приймає одиничне
значення тільки на одному наборі аргументів; диз’юнкція, що приймає нульове
значення тільки на одному наборі аргументів; сума по модулю 2; рівнозначність;
функції Пірса і Шеффера та ін. Логічну
функцію можна вважати повністю заданою, якщо задано її значення на всіх
можливих поєднаннях значень змінних, що називається набором.
Розрахуємо
таблицю істинності для заданих функцій F1, F2, F3:
.
В таблиці істинності значення функції на деяких наборах можуть бути не
визначені, тобто можуть приймати як значення 0, так і значення 1. Серед функцій
n змінних завжди можна вказати функції, аналогічні по властивостям функціям
двох змінних. До таких функцій, наприклад, відносяться константи 0 і 1; змінні
x1,x2,…,xn; кон’юнкція, що приймає одиничне
значення тільки на одному наборі аргументів; диз’юнкція, що приймає нульове
значення тільки на одному наборі аргументів; сума по модулю 2; рівнозначність;
функції Пірса і Шеффера та ін. Логічну
функцію можна вважати повністю заданою, якщо задано її значення на всіх
можливих поєднаннях значень змінних, що називається набором.
Розрахуємо
таблицю істинності для заданих функцій F1, F2, F3:

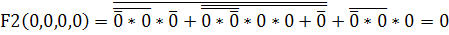











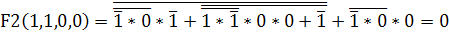

















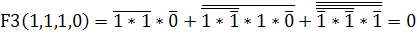

Таблиця 1 - таблиця істинност
|
№
|
A
|
B
|
C
|
D
|
F1
|
F2
|
F3
|
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
|
2
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
|
3
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
4
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
|
5
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
|
6
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
|
7
|
0
|
1
|
1
|
1
|
1
|
1
|
|
8
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
|
9
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
|
10
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
|
11
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
|
12
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
|
13
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
14
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
|
15
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2.1 Мінімізація
методом послідовного виключення логічних змінних
Мінімальною формою представлення
перемикаючої функції називають таку форму, яка не дозволяє більше ніяких
спрощень. Процес спрощення функції з метою отримання найменшої форми називають
мінімізацією. Мінімізувати функцію треба для того, щоб спростити їх реалізацію
на практиці. Мінімізація
функції методом винятку логічних змінних шляхом спрощення форми по законам
алгебри логіки. Основні
закони алгебри логіки.
1. Переставний
закон:
 (1)
(1)
2. Сполучний:
 (3)
(3)
 (4)
(4)
3. Розподільний:
 (5)
(5)
 (6)
(6)
4. Заперечення
(правило де Моргана):
 (7)
(7)
 (8)
(8)
5. Константи:
 (9)
(9)
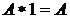 (10)
(10)
 (11)
(11)
 (12)
(12)
6. Доповнення:
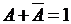 (13)
(13)
 (14)
(14)
7. Поглинання:
 (15)
(15)
8. Склеювання:
 (16)
(16)
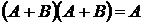 (17)
(17)
9. Подвійного повторювання:
 (18)
(18)
 (19)
(19)
10. Подвійного заперечення:
 (20)
(20)
 (21)
(21)
 (22)
(22)
Мінімізуємо дані функції методом
послідовного виключення логічних змінних, використавши основні закони та
тотожності алгебри логіки.
F1=1


2.2 Мінімізація методом мінімізуючих карт Карно
Карти Карно - це графічне
представлення таблиці істинності. Карти Карно налічують стільки клітинок,
скільки рядків є в таблиці істинності.
Основу мінімізації за допомогою карт
Карно складають такі положення:
1) Дві одиниці, які знаходяться
в сусідніх клітинках карти можуть бути замінені однією кон’юнкцією, яка містить
на одну змінну менше.
2) Якщо сусідніми є дві пари
одиниць, то така група змінюється на кон’юнкцію, яка містить на дві змінних
менше, відповідно якщо сусідніми є 2n
одиниць, то така група може бути замінена кон’юнкцією, яка містить на n
змінних менше.
) Сусідніми є клітинки
розміщенні поряд по горизонталі і вертикалі, а також клітинки, які знаходяться
на протилежних границях карти Карно.
) Поєднувати можна тільки 2n
одиниць за принципом квадрату, прямокутнику або тору.
На основі теоретичних відомостей
мінімізуємо функції F1, F2, F3 графічним методом.

Рисунок 2.1 ─ Карта Карно для
функції F1

Рисунок 2.1 ─ Карта Карно для
функції F2

Рисунок 4.1 ─ Карта Карно для
функції F1

2.3 Зведення до базису
Функіонально повною системою, або
базисом перемикаючих функцій називають систему перемикаючих функцій F(xl,x2,...,xn),
за допомогою якої може бути представлена будь-яка функція алгебри логіки.
Функціонально повними системами є базиси: І, АБО, НЕ (базис 1); І, НЕ (базис
2); АБО, НЕ (базис 3); І-НЕ або базис Шефера (базис 4); АБО-НЕ або базис Пірса
(базис 5) та І-АБО-НЕ (базис 6). Універсальним називають такий базис, за
допомогою якого можна реалізувати всі три основні бульові операції І, АБО та
НЕ.
Приведення перемикаючих функції до
обмеженого універсального базису І-НЕ проводиться в такій послідовності:
.Задана функція мінімізується в
базисі І, АБО, НЕ.
.Над отриманим виразом перемикаючої
функції ставиться подвійне заперечення.
.При перетворенні перемикаючої
функції використовують формули (7,8,20).
На основі теоретичних відомостей, закону
подвійного заперечення і закону де-Моргана приведемо дані функції до обмеженого
базису І-НЕ.

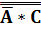 +
+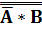 +
+ +
+ +
+ =
=

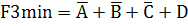 =
=
2.4 Синтез комбінаційної схеми
Логічна схема, яку можна повністю
описати таблицею істиності і бульовими виразами називається комбінаційною
схемою.
Комбінаційна схема - це така схема,
в якій значення вхідних даних в даний момент часу повністю визначає значення х
змінних.
Для синтеза комбінаційної схеми ми
користуємося логічним елементом і входами А і В (де А і В = або х1, або х2, або
х3, або х4) і інвертором на виході.
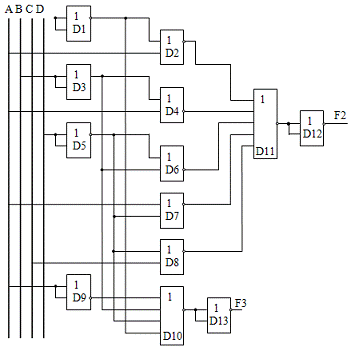
Рисунок 2.1 - Комбінаційна схема для
функцій F1,
F2, F3
2.5 Часові діаграми
Часова діаграма представляє собою
часову організацію найбільш важливих подій, що виникають в цифровій схемі, якою
керує генератор тактових сигналів(таймер). Опорний сигнал
часової діаграми виробляється генератором тактових сигналів, в якості яких
завжди застосовується кварцовий генератор. Тактові
і часові сигнали, а також дані, що представляються, являються в дійсності
імпульсами, високі і низькі рівні яких відповідають передачі 1 та 0, на часовій
діаграмі суцільною горизонтальною лінією позначаються ті з них, які в даний
момент часу є активними. Ці лінії забезпечують достатньо наочну інтерпретацію
сигналів. Сигнали високого рівня з’являються на виході схеми тоді, коли обидва
вхідні сигнали будуть відповідати високому рівню. В
загальному випадку для часової діаграми сигналами низького рівня відповідають
напруги від 0.3В до 0.8В, а сигналам високого рівня - напруга в 4.3В.
На
рисунку 2.2 зображена часова діаграма до комбінаційної схеми, яка зображена на
рисунку 2.1.

Рисунок 2.2 - Часова діаграма для
функцій F1, F2,
F3
Висновок
Отже,
як ми бачимо двійкова арифметика -
це основа будь якої ЕОМ. У даній темі курсової роботи ми розглянули все, що
стосується двійкової арифметики і булевих функцій та законів.
Список посилань
1. Виленкин Н.Я.
Популярная комбинаторика.-М.: Наука, 2000.─ 263c.
2. Гильберт Д., Бернайс П.
Основания математики. Логические исчисления и формализация арифметики.-М.:
Наука, 1982.─ 546c.
. Глушков В.М., Цейтлин
Г.Е., Ющенко Е.Л. Алгебра. Языки. Программирование.-К.: Наукова думка, 1988. ─
846c.
. Ершов Ю.Л., Палютин
Е.А., Математическая логика.-М.:Наука, 1979. ─ 246c.
. Карри Х.Б. Основания
математической логики.-М.: Мир, 1969. ─
456c.
. Клини С.К.
Математическая логика.- М.: Мир, 1973. ─ 744c.
. Колмогоров А.Н. Фомин
С.В. Элементы теории функций и функционального анализа.-М.: Наука, 1981. ─
166c.
. Кузнецов О.П.,
Адельсон-Вельский Г.М. Дискретная математика для инженера.-М.:Энергоатомиздат,
1988. ─
214c.