Розв’язання алгебраїчних рівнянь. Методи простих ітерацій та Ньютона
ЗМІСТ
ВСТУП
РОЗДІЛ
1. ВИДИ РІВНЯНЬ ТА МЕТОДИ ЇХ РОЗВ’ЯЗАНЬ
.1
Загальні поняття та визначення
.2
Чисельні методи уточнення коренів
.3
Постановка задачі
РОЗДІЛ
2. РОЗВ’ЯЗКИ МЕТОДІВ ПРОСТИХ ІТЕРАЦІЙ ТА НЬЮТОНА
.1
Рішення нелінійного рівняння методом простих ітерацій
.2
Рішення нелінійного рівняння методом Ньютона (дотичних)
.3
Використання програмних засобів
.4
Алгоритми розв’язку задач
РОЗДІЛ
3. ПРАКТИЧНЕ ЗАСТОСУВАННЯ МЕТОДІВ
.1
Програми мовою С++
.2
Тестування програм
ВИСНОВКИ
ЛІТЕРАТУРА
ВСТУП
При рішенні систем нелінійних і
трансцендентних рівнянь дуже складно знайти точне рішення. Задача пошуку кореня
системи рівняння може вважатися практично вирішеною, якщо ми зуміємо визначити
корінь з потрібним ступенем точності і вказати межі можливої погрішності.
У наш час рішення систем нелінійних
рівнянь досить актуальна тема, адже її можна застосовувати на практиці для
рішення кола задач. Прикладом цього є задачі, які виникають у геодезії.
Геодезія - це наука про методи визначення фігури і розмірів Землі, зображення
земної поверхні на планах і картах і точних вимірювань на місцевості,
пов’язаних з розв’язанням різних наукових і практичних завдань. Вона тісно
пов’язана з математикою, фізикою, радіоелектронікою, геофізикою, астрономією,
картографією, географією, геоморфологією, геоінформатикою.
Практична цінність чисельного методу
в значній мірі визначається швидкістю та ефективністю отримання розв’язку.
Вибір необхідного алгоритму для розв’язку рівнянь залежить від характеру
задачі, яка розглядається.
Наступна частина роботи буде
присвячена розробці програм для методів простих ітерацій та Ньютона.
1. ВИДИ РІВНЯНЬ ТА МЕТОДИ ЇХ
РОЗВ’ЯЗАНЬ
.1 Загальні поняття та визначення
Рівняння виду φ(х)=g(x)
або f(x)=0 називаються нелінійними рівняннями. Всі нелінійні рівняння можна
поділити на алгебричні та трансцендентні.
Нелінійні рівняння :
алгебраїчні (з раціональними
функціями, з ірраціональними функціями);
трансцендентні (логарифмічні,
показникові, тригонометричні, обернено тригонометричні функції ).
Функція називається алгебраїчною,
якщо для отримання значення функції на заданій множині х потрібно здійснити
арифметичні операції та піднесення в степінь з раціональним або ірраціональним
показником. Рівняння, яке містить алгебраїчні функції називають нелінійними
алгебраїчними рівняннями.
До трансцендентних функцій відносять
всі неалгебраїчні функції:
показникові ах ;
логарифмічні loga x, ln x;
тригонометричні sin x, cos x, tg x,
ctg x;
обернено тригонометричні arcsin x,
arccos x, arctg x, arcctg x та ін..
Нелінійні рівняння, які містять
трансцендентні функції називаються нелінійними трансцендентними рівняннями.
Процес розв’язання нелінійних
рівнянь виду φ(х)=g(x)
або f(x)=0 розбивається на два етапи:
відокремлення коренів;
уточнення коренів.
Перший етап іноді може виконуватися
вручну, другий же виконується за допомогою спеціальних методів уточнення
коренів та програм.
1.2 Чисельні методи уточнення
коренів
Розглянемо детальніше другий етап
наближеного розв’язання нелінійних рівнянь - уточнення коренів. Для уточнення
коренів нелінійного рівняння з заданою похибкою ε
на
деякому відрізку [a,b] на
практиці використовують такі методи:
половинного ділення;
хорд (метод пропорційних частин);
дотичних (метод Ньютона);
січних;
комбінований (метод хорд та
дотичних);
метод Ейткена - Стефенсона;
ітерацій і ін..
Всі ці методи є ітераційними, тобто
побудовані на алгоритмах, в яких одна з їх частин повторюється багаторазово,
при чому кількість повторень залежить від початкових даних (від заданої
користувачем похибки, від відрізка дослідження та інше).
При використанні ітераційних методів
виникає проблема збіжності чисельного методу. Вона (збіжність) означає
близькість одержаного після проведення ітерації розв’язку до істинного
розв’язку. Збіжність ітераційного процесу: якщо в результаті проведення
ітерацій одержуємо деяку послідовність х1, х2, … , хn (не важливо, це скалярні
чи векторні величини), та якщо ця послідовність збігається до точного розв’язку
х = а, тобто існує границя цієї послідовності  ,
то метод є збіжним.
,
то метод є збіжним.
1. Метод половинного ділення
Метод, як правило використовується
для грубого знаходження кореня рівняння. При підвищенні точності (тобто при
зменшенні e) значно зростає об’єм
обчислювальної роботи. Крім того, простота реалізації методу зменшує число
допоміжних операцій і частково компенсує затрати машинного часу через повільну
збіжність.
. Метод хорд
Цей метод забезпечує швидку
збіжність, ніж метод половинного ділення. Ідея методу полягає в тому, що на
достатньо малому проміжку [a,b] функція f(x) змінюється лінійно і тому дуга
кривої f(x) замінюється хордою, яка її стягує. Метод хорд має лінійну збіжність
- похибка на наступній ітерації пропорційна (лінійно) похибці на попередній
ітерації.
. Метод Ньютона (Ньютона - Рафсона,
метод дотичних)
Метод послідовних наближень розробив
Ньютон, він дуже широко використовується при побудові ітераційних алгоритмів.
Цей метод відомий своєю швидкою збіжністю (квадратичною збіжністю). Метод
Ньютона ефективний для розв’язування тих рівнянь, для яких значення модуля і
похідної | f’(x)| біля кореня достатньо велике , тобто графік функції f(x) в
околі даного кореня має велику крутизну. Основні труднощі в методі Ньютона
полягають у виборі початкового наближення х0, такого, що знаходилось би
всередині інтервалу шуканого нуля х.
. Метод січних
Оскільки крок методу січних вимагає
лишень одного обчислення функції, цей метод можна оцінити як більш швидкий в
порівнянні з методом Ньютона.
Схема алгоритму для цього методу
така ж, як і для методу Ньютона (дещо інший вигляд має ітераційна формула).
. Комбінований метод хорд та
дотичних
Метод хорд та дотичних дають
наближення кореня з різних сторін (менше і більше від істинного значення). Тому
доцільно використовувати обидва способи одночасно, завдяки чому уточнене
значення кореня одержується швидше. Можливі чотири випадки поведінки функції на
відрізку [а, b] в залежності від знаків похідної. В комбінованому методі краще
застосувати метод Ньютона і метод хорд з врахуванням обчислень Ньютона.
. Метод простої ітерації
Для застосування цього методу
рівняння f(x) = 0 представляється у вигляді
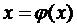 (1.1).
(1.1).
Виберемо за початкове
наближення кореня значення 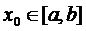 і підставимо в праву частину
рівняння (1.1). Одержимо деяке число
і підставимо в праву частину
рівняння (1.1). Одержимо деяке число
 (1.2).
(1.2).
Підставляючи в праву частину
рівності (1.2) замість х0 значення х1 одержимо нове число

Повторний процес буде мати
наступну послідовність
 .
.
. Метод Ейткена - Стефенсона
Прискорену збіжність при
складних рівняннях f(x) = 0 має метод Ейткена - Стефенсена. Рівняння в цьому
випадку зводять до вигляду 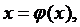 тоді обчислюється перше наближення
для хn = x0. Процес повторюється до тих пір, доки не буде досягнута бажана
(потрібна) точність
тоді обчислюється перше наближення
для хn = x0. Процес повторюється до тих пір, доки не буде досягнута бажана
(потрібна) точність  .
.
1.3
Постановка задачі
Метою даної роботи є розробка
програм для розв’язання алгебраїчних рівнянь двома методами, а саме, методами
простих ітерацій та Ньютона. Програма створюється для рівнянь, які вирішуються
чисельним методом і перевірка яких може здійснюватися аналітично.
Дані програми повинні
виводити результат знайдених коренів, при введені користувачем х та точності
розрахунку.
Для перевірки результатів
аналітичним способом використаємо Mathcad, ця програма побудує графік для
нашого рівняння.
Для написання програм
скористаємося мовою програмування С++.
При дослідженні програм
використаємо рівняння
(x) =2sin (3x) - x,
за допомогою якого порівняємо
дані методи і на основі цього зробимо певні висновки.
2. РОЗВ’ЯЗКИ МЕТОДІВ ПРОСТИХ
ІТЕРАЦІЙ ТА НЬЮТОНА
На основі літературних відомостей
розглянемо детальніше задані методи.
2.1 Рішення нелінійного рівняння
методом простих ітерацій
Метод простої ітерації застосовують
для розв’язання задач про нерухому точку.
Для застосування цього методу
рівняння f(x) = 0 представляється у вигляді
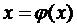 (2.1.1)
(2.1.1)
Виберемо за початкове
наближення кореня значення 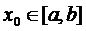 і підставимо в праву частину
рівняння (2.1.1). Одержимо деяке число
і підставимо в праву частину
рівняння (2.1.1). Одержимо деяке число
 (2.1.2)
(2.1.2)
Підставляючи в праву частину
рівності (2.1.2) замість х0 значення х1 одержимо нове число

Повторний процес буде мати
наступну послідовність
 .
.
Якщо ця послідовнясть збіжна, то
границя цієї послідовності 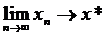 - корінь рівняння
f(x) = 0 і може бути обчислений з будь-якою точністю.
- корінь рівняння
f(x) = 0 і може бути обчислений з будь-якою точністю.
Геометрично метод ітерації можна
пояснити наступним чином. Побудуємо на площині хоу графіки функцій у = х і  .
Відштовхуючись від деякої точки
.
Відштовхуючись від деякої точки  будуємо ламану
лінію А0В1А1В2… («сходинки»), вершини яких обов’язково паралельні осі х і у ,
вершини А0А1А2 лежать на кривій
будуємо ламану
лінію А0В1А1В2… («сходинки»), вершини яких обов’язково паралельні осі х і у ,
вершини А0А1А2 лежать на кривій 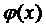 , а вершини В1В2…-
на прямій у = х.
, а вершини В1В2…-
на прямій у = х.
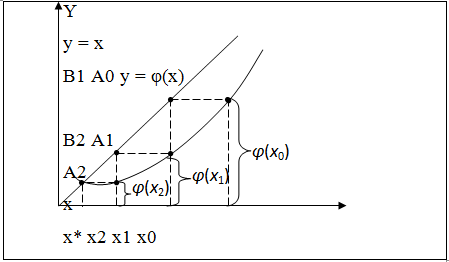
Рис. 2.1 - Абсциси точок А1А2; В1В2…
- преставляють собою відповідно послідовне наближення кореня х*.
Теорема. Про збіжність методу
ітерації.
Якщо для всіх  виконується
нерівність
виконується
нерівність

то на проміжку [a, b]
рівняння  має єдиний
корінь і процес ітерації
має єдиний
корінь і процес ітерації 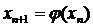 збігається
до цього кореня незалежно від вибору початкового наближення
збігається
до цього кореня незалежно від вибору початкового наближення 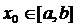 .
.
Приклад.
Методом ітерації знайти
додатній корінь рівняння
х3 - 5х + 1 = 0
на відрізку [0; 0,5], ще два
корені на відрізку [-3; -2], [2, 3].
Корінь знаходиться на
відрізку [0; 0,5].
Дане рівняння зведемо до
вигляду
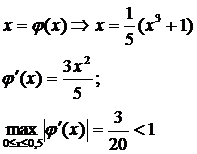
процес ітерацій збіжний.
Візьмемо за перше наближення
х0 = 0,25 - середину відрізка [0; 0,5]. Обчислення будемо вести за формулою
 .
.
Результати розв’язку наведені в
таблиці 2.1.
Таблиця 2.1
|
n
|
xn
|
xn+1
|
|
0
|
0,25
|
0,20313
|
|
1
|
0,20313
|
0,20168
|
|
2
|
0,20168
|
0,20164
|
|
3
|
0,20164
|
0,20164
|
При знаходженні двох інших коренів
методом ітерацій вже не можна скористатись формулою
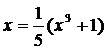 ,
,
оскільки
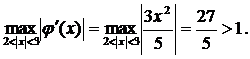
В цьому випадку рівняння потрібно
представити у вигляді, наприклад, 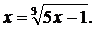 Тоді
на відрізках [-3; -2], [2, 3] умова
Тоді
на відрізках [-3; -2], [2, 3] умова  буде
виконуватись.
буде
виконуватись.
Таким чином при практичному
знаходженні кореня за методом ітерації при переході від рівняння f(x) = 0 до
(2.1.1) необхідно зобразити 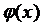 так, щоб похідна
так, щоб похідна 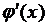 за
абсолютною величиною була якомога менша одиниці.
за
абсолютною величиною була якомога менша одиниці.
Для зведення рівняння f(x) = 0 до
вигляду (2.1.1) може бути застосований загальний метод, котрий забезпечує
виконання нерівності (2.1.3).
Нехай
 (2.1.4)
(2.1.4)
при 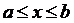 ,
де m1 - найменше значення похідної
,
де m1 - найменше значення похідної 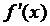 ,
,
 ;
;
М1 - найбільше значення похідної на
відрізку [a, b], 
Якщо похідна 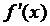 -
від’ємна, то замість рівняння f(x) = 0 розглянемо рівняння - f(x) = 0.
-
від’ємна, то замість рівняння f(x) = 0 розглянемо рівняння - f(x) = 0.
Замінимо це рівняння f(x) = 0
еквівалентним йому рівнянням  і виберемо сталу λ
так,
щоб забезпечити виконання умови (2.1.3)
і виберемо сталу λ
так,
щоб забезпечити виконання умови (2.1.3)
) 
Розкриваємо нерівність 
Візьмемо праву нерівність  ,
з неї випливає, що
,
з неї випливає, що 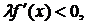 тобто
тобто  оскільки
оскільки
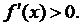
З лівої нерівності  випливає,
що
випливає,
що 
Отже, значення коефіцієнта λ
знаходиться
в межах 

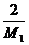 <
<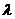 <0
<0 як правило за λ приймають
значення
як правило за λ приймають
значення  де
М1 - максимальне значення похідної
де
М1 - максимальне значення похідної 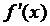 на
проміжку [a, b].
на
проміжку [a, b].
Відповідно, ітераційна формула буде
мати вигляд
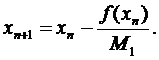
) Якщо  то
можна довести, що
то
можна довести, що
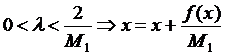 . (2.1.5)
. (2.1.5)
І відповідний ітераційний процес має
вигляд
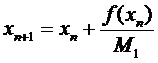 (2.1.6)
(2.1.6)
Ітераційний процес полягає в
послідовному уточненні початкового наближення. Кожен такий процес називається
ітерацією. У результаті отримують послідовність x0, x1, ..., хn. Якщо ці
значення із зростанням n наближаються до істинного значення, то ітераційний
процес сходиться.
2.2 Рішення нелінійного рівняння
методом Ньютона (дотичних)
Якщо для рівняння F (х) = 0 відоме
«зручне» початкове наближення, то замість методу простої ітерації можна
застосувати метод Ньютона.
Метод послідовних наближень розробив
Ньютон, він дуже широко використовується при побудові ітераційних алгоритмів.
Цей метод відомий своєю швидкою збіжністю (квадратичною збіжністю).
Нехай корінь рівняння f(x) = 0
відокремлений на відрізку [а, b], причому f’(x) і f’’ (x) неперервні і
зберігають сталі знаки на всьому відрізку [а, b].
Нехай корінь рівняння f(x) = 0
відокремлений на відрізку [а, b], причому f’(x) і f’’ (x) неперервні і
зберігають сталі знаки на всьому відрізку [а, b]. Геометричний зміст методу
Ньютона полягає в тому, що дуга кривої у = f(x) замінюється дотичною до цієї
кривої.
Візьмемо деяку точку x0 відрізка [а,
b] і проведемо в точці [x0, f(x0)] дотичну до цього графіку.
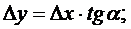




Рис. 2.2 - Метод Ньютона
Її рівняння має вигляд
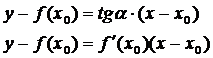
беремо за перше наближення кореня
абсцису точки перетину дотичної з віссю ОХ, одержимо, що

 (2.2.1).
(2.2.1).
Наступне наближення знаходимо
відповідно за формулою
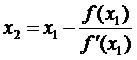
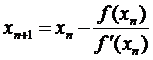 (2.2.2).
(2.2.2).
Відмітимо, що початкове
наближення х0 доцільно вибирати так, щоб
(x0) ·f’’(x0) > 0 (2.2.3).
В протилежному випадку
збіжність методу Ньютона не гарантується.
Частіше всього x0 = а і x0 =
b, в залежності від того, для якої із цих точок виконується умова (2.2.3).
Метод Ньютона ефективний для
розв’язування тих рівнянь, для яких значення модуля і похідної | f’(x)| біля
кореня достатньо велике , тобто графік функції f(x) в околі даного кореня має
велику крутизну.
Достатня умова збіжності
методу вимагає, щоб на відрізку [а, b]:
) функція F (х) була
визначена і двічі диференційована;
) похідні F'(х), F''(х)
зберігали знак.
Зі сказаного випливає, що на
кожній ітерації обсяг обчислень в методі Ньютона великий, оскільки доводиться
знаходити значення не тільки функції F (х), але і її похідної. Однак швидкість
збіжності методу дотичних тут значно вища, ніж в інших методах.
Труднощі в застосуванні цього
методу полягають у виборі початкового наближення, тому іноді вибирають змішаний
алгоритм - на початку використовують завжди метод, що сходиться (наприклад,
метод половинного поділу), а потім метод Ньютона.
2.3
Використання програмних засобів
Для досягнення даної мети ми
використаємо програму розроблену мовою С++, для розв’язку даного рівняння. C++
- компільована статично типізована мова програмування загального призначення.
Ми обрали саме цю мову оскільки вона поєднує властивості як високорівневих, так
і низькорівневих мов. Область застосування цієї мови включає створення
операційних систем, різноманітних прикладних програм, драйверів пристроїв,
додатків для вбудованих систем, високопродуктивних серверів, а також
розважальних доданків.
Для перевірки знайдених
результатів, ми скористаємося програмою Mathcad. Mathcad - система комп’ютерної
алгебри з класу систем автоматизованого проектування, орієнтована на підготовку
інтерактивних документів з обчисленнями і візуальним супроводом. Отож, наш
приклад буде вирішено і аналітичним способом.
2.4
Алгоритми розв’язку задач
Для вирішення поставленої
задачі, необхідно розробити алгоритм дій. Для обох методів можна обрати
спільний алгоритм:
за допомогою функції return
ввести функцію;
обрати тип даних та ввести
змінні;
вивести на екран рядок для
введення користувачами даних;
вивести на екран результати.
Можна скористатися наступними
алгоритмами:
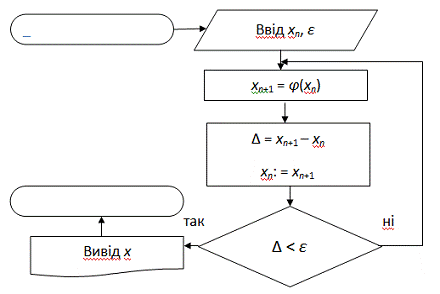
Рис. 2.3 - Метод ітерацій

Рис. 2.4 - Метод Ньютона
Для роботи програми використаємо
наступні дані:
#include <cmath> - бібліотека
використана в програмі, оскільки вона відповідає за виведення тригонометричних
функцій, використання модуля,
#include <iomanip> -
бібліотека для використання setw(),
#include <iostream> - ця
бібліотека використана, оскільки вона відповідає за ввід і вивід даних (подібно
до stdio.h в Сі), в даній програмі вона використовується для об’єктів cout,
cin;- початкове значення;- точність обчислення;- вивід на екран;- повертає
значення, переважно з користувацьких функцій, як параметри функціонального
запиту;- тип даних з плаваючою крапкою;- цикл, який повторює дії, поки не
виконається задана умова, тобто поки не набуде істинного значення.
3. ПРАКТИЧНЕ ЗАСТОСУВАННЯ МЕТОДІВ
.1 Програми мовою С++
Наведена програма (рис.3.1)
розроблена для розв’язання алгебраїчних рівнянь методом простих ітерацій із
застосуванням конкретного рівняння.
#include <cmath>
#include <iomanip>
#include <iostream>namespace
std;f(double x)
{2*sin(3*x) - x;
}
g(double x)
{x + 0.5*f(x);
{x;eps;<<"Введіть
початкове значення : ";cin>>x;<<"Введіть точність
обчисленння : ";cin>>eps;(double iter = 1; eps < fabs(f(x)); iter
= iter + 1)
{("cls");
//*Ітерацій може бути дуже багато,
тому пропоную
//використовувати не
//цілі, а дабл як лічильник, хоча,
якщо рішення не знайшли
//за 10-100 ітерацій, то рішення для
даного коефіцієнту
//при f(x) в g(x) не має і не слід
його змінювати<<"Iteration : "<<setprecision(0)<<iter<<endl;<<"x
= "<<x <<endl;<<"g(x) =
"<<g(x)<<endl;<<"f(x) =
"<<f(x)<<endl;= g(x);
}("pause");0;
}
Наступна програма розроблена для
розв’язку алгебраїчних рівнянь методом Ньютона(методом дотичних).
#include <cmath>
#include <iomanip>
#include <iostream>namespace
std;f(double x)
{2*sin(3*x) - x;
}df(double x)
{6*cos(3*x)-1;
}g(double x)
{x - f(x)/df(x);
}main()
{x;eps;<<"Введіть
початкове значення : ";cin>>x;<<"Введіть точність
обчислень : ";cin>>eps;(double iter = 1; eps < fabs(f(x)); iter =
iter + 1)
{("cls");
//*Ітерацій може бути дуже багато,
тому пропоную використовувати
//не цілі, а дабл як лічильник, хоча
якщо
//рішення не знайшли за 10-100
ітерацій то рішення для даного коефіцієнту
//при f(x) в g(x) не має і
непотрібно його змінювати<<"Iteration :
"<<iter<<endl;(df(x) == 0);<<"x = "<<x
<<endl;<<"g(x) = "<<g(x)
<<endl;<<"df(x)=
"<<df(x)<<endl;<<"f(x) = "<<f(x)
<<endl;= g(x);
}("pause");0;
}
3.2 Тестування програм
Для перевірки розв’язків програми в
Mathcad-і було побудовано графік заданої функції, результати рис. 3.1.
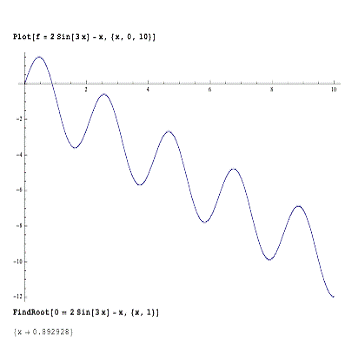
Рис. 3.1 - Графік функції F(x) =2sin
(3x) - x
Результати виконані програмою
написані в таблиці 3.1.
Для перевірки ми використали
довільні допустимі дані.
Таблиця 3.1
|
Введіть початкове значення
|
1
|
|
Введіть точність обчислень
|
0.01
|
|
Метод простих ітерацій
|
Метод Ньютона
|
|
Кількість виконаних ітерацій
|
|
300
|
2
|
|
Значення х
|
|
0.5
|
0.896576
|
|
Значення g(x)
|
|
0.9
|
0.892936
|
|
|
|
ВИСНОВКИ
рівняння ітерація
програма тестування
При виконанні даної роботи були
розглянуті теоретично і практично основні характеристики методів простих
ітерацій та Ньютона.
Метою нашого дослідження було
створення програм для методів простих ітерацій та Ньютона та порівняння
результатів їх обчислень.
Проаналізувавши отримані результати,
можна сказати, що розв’язки рівнянь, які близькі до розв’язків аналітичним
способом залежать від вибору початкового значення х та введеної точності.
Порівнявши отримані розв’язки двома
методами, виявилося, що метод простих ітерацій здійснює більшу кількість
ітерацій (300), а метод Ньютона видає результат за декілька кроків за допомогою
двох ітерацій (дані результати для заданого рівняння). Хоча метод простих
ітерацій простіше в реалізації, в результаті він видає наближені розв’язки, а
метод Ньютона більш точні.
Дані методи сходяться за невелику
кількість ітерацій, якщо початкове наближення взято близько до точного
розв’язання. При віддаленні початкового наближення від точного рішення,
швидкість збіжності і число ітерацій методів відрізняються на порядки, метод
Ньютона сходиться за набагато менший час і число ітерацій. При дуже сильному
віддаленні від початкового рішення застосування методу простої ітерації
недоцільно через дуже великі обчислювальні витрати.
Метод Ньютона виявився більш
ефективним, ніж метод простих ітерацій по всіх розглянутих параметрах.
ЛІТЕРАТУРА
1. Демидович
Б.П., Марон И.А. «Основы вычислительной математики», - М.: Наука, 1970. - 664
с.
2. Демидович
Б.П., Марон И.А., Шувалова Е.З. «Численные методы анализа», - М.: Мир, 1967
. Мак
- Кракен Д., Дрон У. «Численные методы и программирование на фортране», - М.:
Мир, 1977. - 584 с.
. Программирование
и математическое моделирование. Методические указания. Часть 1./ Тихомиров
А.Е., Снежко Е.М., Еременко А.Н. и др., Издательство ДГУ, 1993.
. Бугрім
Є.Д., Боцьва Н.П.: «Методичні рекомендації до вивчення курсу «Основи мови
програмування Сі»», - Д: ДДУ,1999.
. posibnyky.vntu.edu.ua/met/lek4.htm
. www.100balov.com/.../NEL_RIWN.doc