Анализ алгоритмов цифровой обработки сигналов. Исследование корректирующих способностей циклических кодов

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1. ИССЛЕДОВАНИЕ АЛГОРИТМОВ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

1.1 Исследование свойств дискретной свертки

1.2 Исследование работы цифрового фильтра без помехи

1.3 Исследование работы цифрового фильтра при наличии помехи

2. КОДОПРЕОБРАЗОВАТЕЛИ ЦИКЛИЧЕСКИХ КОДОВ И ИССЛЕДОВАНИЕ ИХ КОРРЕКТИРУЮЩИХ СПОСОБНОСТЕЙ

2.1 Анализ работы кодирующего устройства циклического кода

2.3 Анализ корректирующих способностей заданного циклического кода

2.4 Анализ помехоустойчивости заданного циклического кода

3. ИССЛЕДОВАНИЕ КОРРЕКТИРУЮЩИХ СПОСОБНОСТЕЙ КОДОВ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА

3.1 Исследование характеристик кода

3.2 Синтезирование кодирующего и декодирующего устройства кода

3.3 Исследование корректирующих способностей помехоустойчивого кода

3.4 Исследование кода, позволяющего исправить двукратные ошибки

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

ПРИЛОЖЕНИЕ А. МОДЕЛЬ КОДА (15, 7) С ПРОВЕРКОЙ НА ЧЕТНОСТЬ, ИСПРАВЛЯЮЩЕГО ДВУКРАТНЫЕ ОШИБКИ

ПРИЛОЖЕНИЕ Б. МОДЕЛЬ ДИСКРЕТНОЙ СВЕРТКИ СИГНАЛА

ВВЕДЕНИЕ

цифровой сигнал циклический код

Цифровой фильтр - в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового, аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов.

Цифровые фильтры на сегодняшний день применяются практически везде, где требуется обработка сигналов, в частности в спектральном анализе, обработке изображений, обработке видео, обработке речи и звука и многих других приложениях.

Преимуществами цифровых фильтров перед аналоговыми являются:

·        Высокая точность (точность аналоговых фильтров ограничена допусками на элементы).

·        Стабильность (в отличие от аналогового фильтра передаточная функция не зависит от дрейфа характеристик элементов).

·        Гибкость настройки, лёгкость изменения.

·        Компактность - аналоговый фильтр на очень низкую частоту (доли герца, например) потребовал бы чрезвычайно громоздких конденсаторов или индуктивностей.

Недостатками цифровых фильтров по сравнению с аналоговыми являются:

·        Трудность работы с высокочастотными сигналами. Полоса частот ограничена частотой Найквиста, равной половине частоты дискретизации сигнала. Поэтому для высокочастотных сигналов применяют аналоговые фильтры, либо, если на высоких частотах нет полезного сигнала, сначала подавляют высокочастотные составляющие с помощью аналогового фильтра, затем обрабатывают сигнал цифровым фильтром.

·        Трудность работы в реальном времени - вычисления должны быть завершены в течение периода дискретизации.

·        Для большой точности и высокой скорости обработки сигналов требуется не только мощный процессор, но и дополнительное, возможно дорогостоящее, аппаратное обеспечение в виде высокоточных и быстрых ЦАП и АЦП.

Для повышения эффективности СЭС широко используются помехоустойчивые коды. Применение корректирующих кодов позволяет повысить верность передачи сообщений или при заданной верности повысить энергетическую эффективность системы. Это особенно важно для систем с малой энергетикой, например, систем спутниковой связи.

1. ИССЛЕДОВАНИЕ АЛГОРИТМОВ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

Из теории аналоговых фильтров известно, что сигнал Sv(t) на выходе фильтра выражается в виде свертки

где h(t) - импульсная характеристика фильтра (напоминаем - отклик фильтра на дельта-функцию ); S(t-τ) - входной сигнал.

При реализации цифровых фильтров используется дискретная свертка

где h(kT) - дискретные значения (цифровые) импульсной характеристики фильтра; S[(n-k)T]- дискретные (цифровые) значения задержанного на k тактов входного сигнала.

Для вычисления дискретной свертки можно использовать дискретное преобразование Фурье (ДПФ). Для этого необходимо выполнить следующие действия:

. Вычислить ДПФ входного сигнала:

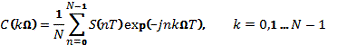
где Ω=2π/NT - основная частота преобразования, exp(-jΩT) = exp(-j2π/N) - отсчеты дискретной экспоненты, которая называется поворачивающим множителем, С(kΩ)=C(k) - коэффициенты ряда Фурье, число коэффициентов ряда равно числу отсчетов (N) дискретного сигнала.

. Вычислить ДПФ дискретной импульсной характеристики

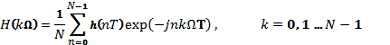
3. Перемножить коэффициенты полученных ДПФ

4. Вычислить обратное ДПФ от G(kΩ)

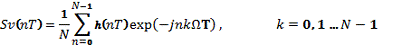
1.1. Исследование свойств дискретной свертки

Сигнал S(nT) периодический [1, 4, 2, 3] с периодом N=4 (рис. 1).

Рис. 1

Импульсная характеристика h(nT) периодическая [0, 1, 0, 0] с периодом N=4 (рис. 2).

Рис. 2

Определим круговую свертку в соответствии с выражением (1) (рис. 3).

Рис. 3

1.2. Исследование работы цифрового фильтра без помехи

Цифровой фильтр (ЦФ) представляет собой цифровое устройство или алгоритм обработки сигнала, реализованный программно на ЭВМ. Математически работа цифрового фильтра описывается уравнением в конечных разностях

где a_m и b_k  - коэффициенты, определяемые задачами обработки сигнала.

В теории цифровой обработки синтезирован фильтр, минимизирующий среднеквадратичное отклонение. Структурная схема фильтра приведена на рис. 4.

Рис. 4

К, D - коэффициенты усиления, определяемые параметрами аддитивной смеси.

Алгоритм работы фильтра программно реализуется в соответствие с выражением

где

Для оценки качества фильтра используют среднеквадратическое отклонение, которое определяется по формуле

Пусть сигнал Sign(t) - прямоугольный импульс (рис. 5)

Рис. 5

Его дискретное представление изображено на рис. 6.

Рис. 6

Интервал дискретизации Т=1.

Отклик фильтра на заданный сигнал представлен на рис. 7.

Рис. 7

Для данного случая СКО равно σ = 5.4*10^-3.

Исследуем работу цифрового фильтра, если на входе произвольный сигнал, представленный на рис. 8.

Рис. 8

Дискретное представление сигнала изображено на рис. 9.

Рис. 9

Интервал дискретизации T = 1.

Для данного случая СКО равно σ = 4.2*10^-3

1.3. Исследование работы цифрового фильтра при наличии помехи

Пусть сигнал - произвольной формы (рис. 10).

Рис. 10

Помеха - случайный процесс с нулевым средним, изменяемой мощностью и изменяемой полосой частот.

Окно изменений:

Aml = 0.72     Fhum = 10

Помеха представлена на рис. 11.

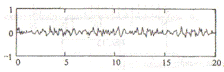
Рис. 11

Аддитивная смесь сигнала и помехи представлена на рис. 12.

Рис. 12

Произведем дискретизацию аддитивной смеси с интервалом T = 1(рис. 13).

Рис. 13

Отклик цифрового фильтра на аддитивную смесь представлен на рис. 14.

Рис. 14

Сплошной линией изображен исходный сигнал.

2. КОДОПРЕОБРАЗОВАТЕЛИ ЦИКЛИЧЕСКИХ КОДОВ И ИССЛЕДОВАНИЕ ИХ КОРРЕКТИРУЮЩИХ СПОСОБНОСТЕЙ

2.1 Анализ работы кодирующего устройства циклического кода

Выберем заданный порождающий полином

В результате получим проверочную матрицу:

Структура кодирующего устройства определяется порождающим полиномом. Так, максимальная степень полинома определяет количество ячеек сдвига, количество x в полиноме определяет количество сумматоров по модулю два. Сумматоры размещаются: один на входе, остальные после ячеек, номер которых совпадает со степенями x в порождающем полиноме.

Классическая схема кодирующего устройства представлена на рис. 1.

Рис.15

В качестве примера ниже приведены уравнения состояния ячеек кодирующего устройства, синтезированного по полиному x³ + x + 1

1 яч.=вх3`;

яч.=вх3`1`;

яч.=2`.

.2 Анализ работы декодирующего устройства циклического кода

В основе декодирующего устройства лежит многотактный кодовый фильтр, порядок синтеза которого рассмотрен в п.1 с одним лишь отличием: МКФ должен делить n-разрядную кодогрумму. Классическая схема декодирующего устройства приведена на рис.16.

Рис.16. Функциональная схема декодирующего устройства

В качестве примера ниже записаны уравнения состояния ячеек для многотактного кодового фильтра, построенного по полиному x³ + x + 1

1 яч.=вх3`;

яч.=вх3`1`;

яч.=2`.

2.3 Анализ корректирующих способностей заданного циклического кода

Для определения позиции ошибочного символа воспользуется свойством циклического кода - цикличность. Это значит, что необходимо прокручивать символы синдрома в многократном кодовом фильтре до тех пор, пока не образуется синдром 0001. Номер такта циклической перестановки, на которой получен синрдом 0001 соответствует номеру искаженной позиции.

2.4 Анализ помехоустойчивости заданного циклического кода

Введено значение дисперсии шума: 0.1, 0.2, 0.25, 0.3, 0.35, 0.5, 0.6, 0.7, 0.8, 1, 10. Таким образом получено 11 значений отношения сигнал/шум.

В процессе фиксации значений Р_ош наблюдал физический процесс увеличения мощности шума, процесс появления и исправления ошибок по приведенным ниже эпюрам.

Окно значений: σ2:=0.4

Разрешенная кодограмма h2:=6.25

Рис. 17

Гауссовский шум

Рис. 18

Сигнал плюс гауссовский шум (аддитивная смесь) на входе решающего устройства схема с однократным отчетом и порогом 0.5.

Рис. 19

Выход с решающего устройства схемы однократного отчета с порогом 0.5. Вход декодера. На рис.6 зафиксирована кодограмма с ошибками.

Рис. 20

Вектор ошибки Korekt^T =

Выход декодера (рис.21)

Рис. 21

Построены графики зависимости ошибки приема одиночного символа до и после декодера от отношения сигнал/шум и графики зависимости ошибки приема кодограммы до и после декодера от отношения сигнал/шум вида:

h:= 1, 1.1 .. 10³

Рис. 22

3. ИССЛЕДОВАНИЕ КОРРЕКТИРУЮЩИХ СПОСОБНОСТЕЙ КОДОВ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА

3.1 Исследование характеристик кода

Поставим задачу - наименьшим количеством тестов определить больного в больничном отделении.

Количество больных - 7 человек. Пронумеруем их - 1, 2, 3 7. Разобьем их на 3 группы: первая - 1, 4, 5, 7; вторая - 2, 4, 6, 7; третья - 3, 4, 5, 6. Проведенный тест дал отрицательный результат в 1-й и 3-й группе. Нетрудно видеть, что это больной под номером 5. Если тест даст отрицательный результат в 3 группах - это соответствует 7. Напоминаем, что двоичное представление 7 - 111, 5 - 101. Под 1 подразумевается отрицательный тест, под 0 - положительный. В теории кодирования контрольное двоичное число будет называться синдромом кода. Эта идея положена в коды с проверкой на четность.

Информационные символы делятся на пересекающиеся группы и к каждой группе приписывается проверочный символ так, чтобы в каждой группе было четное число единиц.

Для автоматизации процесса формирования контрольных групп используют теорию линейных метрических пространств в виде матриц с линейно независимыми строками. Так порождающая матрица G_kxr строится приписыванием к единичной матрице размером kxk справа матрицы проверочных символов размером kxρ,строки которой имеют максимальное количество 1. Проверочная матрица H_nxρ строится транспонированием порождающей. Пример: код (7,4)

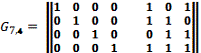
                 a₄    a₃   a₂   a₁           b₃  b₂   b₁

        c₃   c₂     c₁

Используя эти матрицы, можно записать уравнения кодирования:

и проверки:

3.2 Синтезирование кодирующего и декодирующего устройства кода

Кодирующее устройство.

Полученное уравнение кодирования показывает, что для получения кодограммы необходимо иметь два регистра сдвига и состоящий из сумматоров по модулю 2 алгоритмический блок.

Для заданных уравнений кодирования структурная схема изображена на рис. 22.

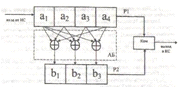
Рис.22. Структурная схема КУ кода (7,4) с проверкой на четность

Для заданных уравнений декодирования (п. 1.1.) структурная схема представлена на рис.23.

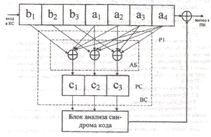
Рис. 23. Структурная схема декодирующего устройства для кода (7,4)

3.3 Исследование корректирующих способностей помехоустойчивого кода

Для увеличения корректирующих способностей кода необходимо использовать большее количество проверочных разрядов. Для исправления двукратных ошибок параметры кода должны быть (15, 7). При этом проверочная матрица должна быть увеличена в размере. Так для исправления однократных ошибок проверочная матрица  Н1 имеет вид:

Данная матрица построена с использованием примитивных элементов поля кода GF(2⁴) по основанию полинома х⁴+х+1. Дополнительные строки к матрице H1 допишем как кубы столбцов в метрике поля GF(2⁴). Поэтому проверочная матрица Н2 примет вид:

Для обеспечения режима исправления однократных и двукратных ошибок заранее просчитываются всевозможные варианты синдромов и записываются их десятичные соответствия искаженным позициям кода. Это можно представить в виде матрицы

Так десятичное представление синдрома 113 соответствует ошибкам на 1-й и 15-й позициях, синдром 20 соответствует одной ошибке на 14-й позиции, синдром 0 - нет ошибок.

3.4 Исследование кода, позволяющего исправить двукратные ошибки

Задана разрешенную кодограмму кода (в качестве таковой можно выбрать любую строку матрицы Н2):=(l 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ) .

Для того, чтобы найти синдром необходимо кодограмму умножить на проверочную матрицу Н2. Получим восьмиразрядное двоичное слово, которое необходимо перевести в десятичное. Умножение произведем с использованием ЭВМ^T=(0 0 0 0 0 0 0 0 0 0).

Его десятичное представление=0.

Следовательно, в кодограмме ошибок нет.

Введемм одну ошибку на произвольно выбранной позиции.:=(l 1 1 0 1 1 1 1 1 1 1 1 1 1 1 ) .

Получим синдром^T=(0 1 1 1 0 1 0 0 0).

Его десятичное представление=23.

С использованием таблицы LL убедимся, что синдром соответствует № позиции, на которой произошла ошибка.

Введем  две ошибки на произвольных позициях разрешенной кодограммы:=(l 1 1 0 1 1 1 0 1 1 1 1 1 1 1 )

Получим синдром^T=(0 10 1 1 1 0 0 1)

Его десятичное представление=157

С использованием таблицы LL убедимся, что синдром соответствует № позиций, на которых произошли ошибки.

Введем три ошибки. Проведем аналогичные операции декодирования:=(. О 1 1 1 1 1 0 1 1 1 0 1 1 1)

Получим синдром^T=(0 1 1 1 0 1 1 0 0 )

Его десятичное представление=55

С использованием таблицы LL убедимся, что синдром не соответствует № позиций, на которых произошли ошибки. Однако наличие ошибок подтверждено.

Моделируем двоичный канал связи с помехой. Схема принятия решения - однократный отсчет. Предусмотрена возможность изменять отношение сигнал/шум. ЭВМ статистически определяет вероятность ошибки символа в зависимости от отношения сигнал/шум. Результат статистического исследования представить в виде графика Р_ош(h²).

Следующим этапом исследования является включение после схемы однократного отсчета декодера, исправляющего одно и двукратные ошибки. Результатом исследования является зависимость вероятности ошибки принятия решения по кодограмме от отношения сигнал/шум.

Зададим разрешенную кодограмму, как любую строчку проверочной матрицы:=(l 1 1 1 0 1 0 1 1 0 0 1 0 0 0)

На сигнальном уровне эта кодограмма имеет вид, представленный на рис.

Рис.24

В канале связи действует флуктуационная помеха, мощность которой можно менять

σ2:=0.1.

Следовательно, можно менять и отношение сигнал/шум

h2=100.

Гауссовский шум (рис. 25)

Рис. 25

Сигнал плюс гауссовский шум (аддитивная смесь) на входе решающего устройства схемы с однократным отсчетом и порогом 0.5 (рис. 26).

Рис.26

На выходе решающего устройства с порогом 0.5 и последующей коррекцией ошибок декодером сигнал выглядит следующим образом (рис. 27).

Рис. 27

Из рис.2 7 видно, что ошибки скорректированы, вид сигнала повторяет рис.

Обработку аддитивной смеси проведем | с использованием декодера, способного обнаруживать одно- и двукратные ошибки. Для определения вероятности ошибки параллельно с предыдущим пунктом вычисляем вероятность ошибки после декодера.

Вероятность ошибки после декодера

PohKod=0

Работа декодера поясняется эпюрой, приведенной ниже. Одновременноотображается вектор ошибки.

Вектор ошибки VektorOh^T

Построим график зависимости вероятности ошибки приема одиночного символа после декодера от отношения сигнал/шум на входе. График будет иметь вид, представленный на рис. 28.

Рис.2 8

ЗАКЛЮЧЕНИЕ

В ходе выполнения курсовой работы были получены следующие результаты:

1.Исследованы алгоритмы цифровой обработки сигналов в условиях как наличия и отсутствия помех. В ходе работы была спроектирована модель дискретной свертки в среде Mathcad 14.

.Исследованы кодопреобразователи циклических кодов и исследованы их корректирующие способности.

.Исследованы корректирующие способности кодов БЧХ. В ходе работы была спроектирована модель кода (15, 7) с проверкой на четность, исправляющего двукратные ошибки.

СПИСОК ЛИТЕРАТУРЫ

1.       Цифровые фильтры. Анализ и проектирование. Антонью А. Радио и связь - 318 с.

. [#"598827.files/image049.gif">

На примере определим позиции ошибок в кодограмме. Так если ошибки произошли на позициях 2 и 7, то результат вычисления синдрома соответствует SindD=l. В треугольной матрице этот синдром находится соответственно во 2-й строке 7-го столбца.

Для проведения исследования корректирующих способностей помехоустойчивого кода (15,7) необходимо многократно проводить подобные вычисления для различных значений мощности шума. Кроме того, для исправления ошибочной кодограммы необходимо определять программно позиции ошибок и формировать вектор ошибок. Данная операция представлена в части кода, приведенного ниже.

С целью более точного построения графиков помехоустойчивости необходимо произвести многократный расчет вероятностей ошибки Posh и Poh, а затем найти их среднее значение. Данную процедуру можно также осуществить в виде цикла подпрограммы.

ПРИЛОЖЕНИЕ Б. МОДЕЛЬ ДИСКРЕТНОЙ СВЕРТКИ СИГНАЛА

Из теории аналоговых фильтров известно, что сигнал Sv(t) на выходе фильтра выражается в виде свертки

где h(t) - импульсная характеристика фильтра (напоминаем - отклик фильтра на дельта-функцию ); S(t-τ) - входной сигнал.

Для реализации цифровых фильтров используется дискретная свертка

где h(kT) - дискретные значения (цифровые) импульсной характеристики фильтра; S[(n-k)T]- дискретные (цифровые) значения задержанного на k тактов входного сигнала.

Запишем период сигнала N. Далее запишем непосредственно сигнал Sl_n, фильтр hl_n и выражение для их свертки. Элемент кода представлен ниже.

Поскольку свертка двух функций осуществляется на двух периодах сигнала, то введено дополнительное обозначение сигнала и фильтра S2_nnn и h2_nnn, расширенных до длины nnn = 16, достаточной для визуального отображения. Обратите внимание на выражение, вычисляющее свертку Sv_nn, где индекс при S2 меняется в пределах от 1 до 7.

Для вычисления дискретной свертки сигнала на выходе фильтра можно использовать дискретное преобразование Фурье (ДПФ)

где Ω=2π/NT - основная частота преобразования, exp(-jΩT) = exp(-j2π/N) - отсчеты дискретной экспоненты, которая называется поворачивающим множителем, С(kΩ)=C(k) - коэффициенты ряда Фурье, число коэффициентов ряда равно числу отсчетов (N) дискретного сигнала.