Методы моделирования
курсовая РАБОТА
«Методы
моделирования»
Содержание
Введение
. Метод конечных элементов и метод
конечных разностей
. Метод конечных объёмов
. Метод подвижных клеточных
автоматов
. Метод молекулярной динамики
. Метод дискретного элемента
. Метод компонентных цепей
. Метод узловых потенциалов
. Метод переменных состояния
Заключение
Литература
Введение
Компьютерная модель (англ. computer model), или
численная модель (англ. computational model) - компьютерная программа,
работающая на отдельном компьютере, суперкомпьютере или множестве
взаимодействующих компьютеров (вычислительных узлов), реализующая абстрактную
модель некоторой системы. Компьютерные модели стали обычным инструментом
математического моделирования и применяются в физике, астрофизике, механике,
химии, биологии, экономике, социологии, метеорологии, других науках и
прикладных задачах в различных областях радиоэлектроники, машиностроения,
автомобилестроения и проч. Компьютерные модели используются для получения новых
знаний о моделируемом объекте или для приближенной оценки поведения систем,
слишком сложных для аналитического исследования.
Компьютерное моделирование является одним из
эффективных методов изучения сложных систем. Компьютерные модели проще и
удобнее исследовать в силу их возможности проводить т. н. вычислительные
эксперименты, в тех случаях, когда реальные эксперименты затруднены из-за
финансовых или физических препятствий или могут дать непредсказуемый результат.
Логичность и формализованность компьютерных моделей позволяет выявить основные
факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса
объектов), в частности, исследовать отклик моделируемой физической системы на
изменения ее параметров и начальных условий.
Построение компьютерной модели базируется на
абстрагировании от конкретной природы явлений или изучаемого объекта-оригинала
и состоит из двух этапов - сначала создание качественной, а затем и
количественной модели. Компьютерное же моделирование заключается в проведении
серии вычислительных экспериментов на компьютере, целью которых является
анализ, интерпретация и сопоставление результатов моделирования с реальным
поведением изучаемого объекта и, при необходимости, последующее уточнение
модели и т. д.
К основным этапам компьютерного моделирования
относятся:
постановка задачи, определение объекта
моделирования;
разработка концептуальной модели, выявление
основных элементов системы и элементарных актов взаимодействия;
формализация, то есть переход к математической
модели; создание алгоритма и написание программы;
планирование и проведение компьютерных
экспериментов;
анализ и интерпретация результатов.
Различают аналитическое и имитационное
моделирование. При аналитическом моделировании изучаются математические
(абстрактные) модели реального объекта в виде алгебраических, дифференциальных
и других уравнений, а также предусматривающих осуществление однозначной
вычислительной процедуры, приводящей к их точному решению. При имитационном
моделировании исследуются математические модели в виде алгоритмов,
воспроизводящего функционирование исследуемой системы путем последовательного
выполнения большого количества элементарных операций.
Компьютерное моделирование применяют для
широкого круга задач, таких как:
анализ распространения загрязняющих веществ в
атмосфере
проектирование шумовых барьеров для борьбы с
шумовым загрязнением
конструирование транспортных средств
полетные имитаторы для тренировки пилотов
прогнозирование погоды
эмуляция работы других электронных устройств
прогнозирование цен на финансовых рынках
исследование поведения зданий, конструкций и
деталей под механической нагрузкой
прогнозирование прочности конструкций и
механизмов их разрушения
проектирование производственных процессов,
например химических
стратегическое управление организацией
исследование поведения гидравлических систем:
нефтепроводов, водопровода
моделирование роботов и автоматических
манипуляторов
моделирование сценарных вариантов развития
городов
моделирование транспортных систем
имитация краш-тестов
Различные сферы применения компьютерных моделей
предъявляют разные требования к надежности получаемых с их помощью результатов.
Для моделирования зданий и деталей самолетов требуется высокая точность и
степень достоверности, тогда как модели эволюции городов и социально-экономических
систем используются для получения приближенных или качественных результатов
1. Метод конечных элементов и метод конечных
разностей
Метод конечных элементов является численным
методом решения дифференциальных уравнений, встречающихся в физике и технике.
Основная идея метода конечных элементов состоит
в том, что любую непрерывную величину, такую, как температура, давление и
перемещение, можно аппроксимировать дискретной моделью, которая строится на
множестве кусочно-непрерывных функций определенных на конечном числе
подобластей. Кусочно-непрерывные функции определяются с помощью значений
непрерывной величины в конечном числе точек рассматриваемой области. В общем
случае непрерывная величина заранее неизвестна и нужно определить значения этой
величины в некоторых внутренних точках области. Дискретную модель, однако,
очень легко «построить, если сначала предположить, что числовые значения этой
величины в каждой внутренней точке области известны. После этого можно перейти
к общему случаю. Итак, при построении дискретной модели непрерывной величины
поступают следующим образом:
В рассматриваемой области фиксируется конечное
число точек. Эти точки называются узловыми точками или просто узлами.
Значение непрерывной величины в каждой узловой
точке считается переменной, которая должна быть определена. Область определения
непрерывной величины разбивается на конечное число подобластей, называемых
элементами. Эти элементы имеют общие узловые точки и в совокупности
аппроксимируют форму области. Непрерывная величина аппроксимируется на каждом
элементе полиномом, который определяется с помощью узловых значений этой
величины. Для каждого элемента определяется свой полином, но полиномы
подбираются таким образом, чтобы сохранялась непрерывность величины вдоль
границ элемента.
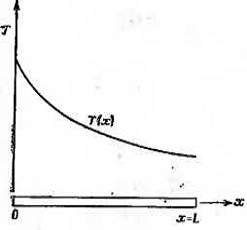

Основная концепция метода конечных элементов
может быть наглядно проиллюстрирована на одномерном примере заданного
распределения температуры в стержне, показанном на рис. 1.1. Рассматривается
непрерывная величина Т(х), область определения-отрезок- OL вдоль оси х.
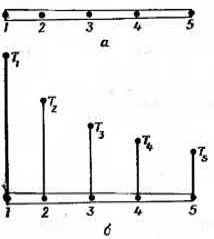
Фиксированы и пронумерованы пять точек на оси х (рис. 1.2 а). Это узловые
точки; совсем не обязательно располагать их на равном расстоянии друг от друга.
Очевидно, можно ввести в рассмотрение более пяти точек, но этих пяти вполне
достаточно, чтобы проиллюстрировать основную идею метода. Значения Т(x) В
данном случае известны в каждой узловой точке. Эти фиксированные значения
представлены графически на рис. 1.2 б и обозначены. В соответствии с номерами
узловых точек через T1 + T2 + … + T5 Разбиение области на элементы может быть
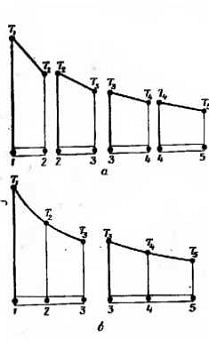
проведено двумя различными способами. Можно, например, ограничить каждый
элемент двумя соседними узловыми точками, образовав четыре элемента (рис. 1.4 а),
или разбить область на два элемента, каждый из которых содержат три узла (рис.
1.3 6). Соответствующий элементу полном определяется по значениям Т(x) в
узловых точках элемента. В случае разбиения области на четыре элемента, когда
на каждый элемент приходится по два узла, функция элемента будет линейна по х
(две точки однозначно определяют прямую лилию). Окончательная аппроксимация
Т(x) будет состоять из четырех кусочно-линейных функций, каждая из которых
определена на отдельном элементе (рис. 1.4 с). Другой способ разбиения области
на два элемента с тремя узловыми точками приводит к представлению функции
элемента в виде полинома второй степени. В этом случае окончательной
аппроксимацией Т(х) будет совокупность двух кусочно-непрерывных квадратичных
функций. Отметим, что это приближение будет именно кусочно-непрерывным, так как
углы наклона графиков обеих этих функций могут иметь разные значения в третьем
узле.
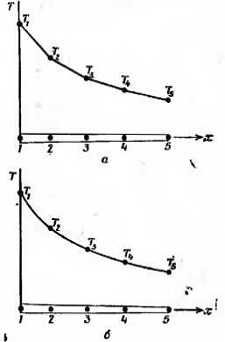
В общем случае распределение температуры
неизвестно и мы хотим определить значения этой величины в некоторых точках.
Методика построения дискретной модели остается точно такой же, как описано
выше, но с добавлением одного дополнительного шага. Снова определяются
множество узлов и значения температуры в этих узлах Т1,Т2,Т3 …, которые теперь
являются переменными так как они заранее неизвестны. Область разбивается на
элементы, на каждом из которых определяется соответствующая функция элемента.
Узловые значения Т(х) должны быть теперь «отрегулированы» таким образом, чтобы
обеспечивалось «наилучшее» приближение к истинному распределению температуры.
Это «регулирование» осуществляется путем минимизации некоторой величины,
связанной с физической сущностью задачи. Если рассматривается задача
распространения тепла, то минимизируется функционал, связанный с соответствующим
дифференциальным уравнением. Процесс минимизации сводится к решению систем
линейных алгебраических уравнений относительно узловых значений Т(х).

При построении дискретной модели непрерывной
величины, определенной в двух или трехмерной области, основная концепция метода
конечных элементов используется аналогично. В двумерном случае элементы
описываются функциями от х, у, при этом чаще всего рассматриваются элементы в
форме треугольника или четырехугольника. Функции элементов изображаются теперь
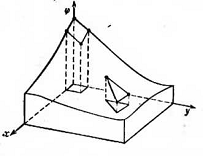
плоскими (рис. 1.5) или Криволинейными (рис. 1.6) поверхностями. Функция
элемента будет представляться плоскостью, если для данного элемента взято
минимальное число узловых точек, которое для треугольного элемента равняется
трем, а для четырехугольного - четырем.
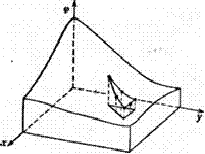
Если используемое число узлов больше
минимального то - функция элемента будет соответствовать криволинейная
поверхность. Кроме того, избыточное число узлов позволяет рассматривать
элементы с криволинейными границами. Окончательной аппроксимацией двумерной
непрерывной величины 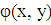 будет служить
совокупность кусочно-непрерывных поверхностей, каждая из которых определяется
на отдельном элементе с помощью значений
будет служить
совокупность кусочно-непрерывных поверхностей, каждая из которых определяется
на отдельном элементе с помощью значений 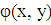 в
соответствующих узловых точках. Важным аспектом метода конечных элементов
является возможность выделить из набора элементов типичный элемент при
определении функции элемента. Это позволяет определять функцию элемента
независимо от относительного положения элемента в общей связной модели и от
других функций элементов. Задание функции элемента через произвольное множество
узловых значений и координат позволяет использовать функции элемента для
аппроксимации геометрии области.
в
соответствующих узловых точках. Важным аспектом метода конечных элементов
является возможность выделить из набора элементов типичный элемент при
определении функции элемента. Это позволяет определять функцию элемента
независимо от относительного положения элемента в общей связной модели и от
других функций элементов. Задание функции элемента через произвольное множество
узловых значений и координат позволяет использовать функции элемента для
аппроксимации геометрии области.

Преимущества и недостатки
В настоящее время область применения метода
конечных элементов очень обширна и охватывает все физические задачи, которые
могут быть описаны дифференциальными уравнениями. Наиболее важными
преимуществами метода конечных элементов, благодаря которым он широко
используется, являются следующие:
Свойства материалов смежных элементов не должны
быть обязательно одинаковыми. Это позволяет применять метод к телам, составленным
из нескольких материалов.
Криволинейная область может быть
аппроксимирована с помощью прямолинейных элементов или описана точно с помощью
криволинейных элементов. Таким образом, методом можно пользоваться не только
для областей с «хорошей» формой границы.
Размеры элементов могут быть переменными. Это
позволяет укрупнить или измельчить сеть разбиения области на элементы, если в
этом есть необходимость.
С помощью метода конечных элементов не
представляет труда рассмотрение граничных условий с разрывной поверхностной
нагрузкой, а также смешанных граничных условий.
Указанные выше преимущества метода конечных
элементов могут быть использованы при составлении достаточно общей программы
для решения частных задач определенного класса. Например, с помощью программы
для асимметрической задачи о распространении тепла можно решать любую частную
задачу этого типа. Факторами, препятствующими расширению круга задач, решаемых
методом конечных элементов, являются ограниченность машинной памяти и высокая
стоимость вычислительных работ.
Главный недостаток метода конечных элементов
заключается в необходимости составления вычислительных программ и применения
вычислительной техники. Вычисления, которые требуется проводить при
использовании метода конечных элементов, слишком громоздки для ручного счета
даже в случае решения очень простых задач. Для решения сложных задач необходимо
использовать быстродействующую ЭВМ, обладающую большой памятью.настоящее время
имеются технологические возможности для создания достаточно мощных ЭВМ.
Метод конечных разностей является старейшим
методом решения краевых задач.
Применение метода конечных разностей позволяет
свести дифференциальную краевую задачу к системе нелинейных в общем случае
алгебраических уравнений относительно неизвестных узловых значений функций.
Основная идея метода конечных разностей (метода
сеток) для приближенного численного решения краевой задачи для двумерного
дифференциального уравнения в частных производных состоит в том, что
) на плоскости в области А, в которой ищется
решение, строится сеточная область As (рис.1.7), состоящая из одинаковых ячеек
размером s ( s - шаг сетки) и являющаяся приближением данной области А;
) заданное дифференциальное уравнение в частных
производных заменяется в узлах сетки As соответствующим конечно-разностным
уравнением;
) с учетом граничных условий устанавливаются
значения искомого решения в граничных узлах области Аs.
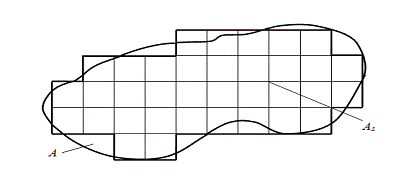
Рис. 1.7. Построение сеточной области
Решая полученную систему конечно-разностных
алгебраических уравнений, получим значения искомой функции в узлах сетки Аs,
т.е. приближенное численное решение краевой задачи. Выбор сеточной области Аs
зависит от конкретной задачи, но всегда надо стремиться к тому, чтобы контур
сеточной области Аs наилучшим образом аппроксимировал контур области А.
Рассмотрим уравнение Лапласа
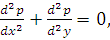 (1)
(1)
где p (x, y) - искомая функция, x, y -
прямоугольные координаты плоской области и получим соответствующее ему
конечно-разностное уравнение.
Заменим частные производные 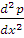 и
и
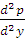 в
уравнении (1) конечно-разностными отношениями:
в
уравнении (1) конечно-разностными отношениями:
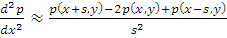 (2)
(2)
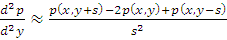 (3)
(3)
Тогда решая уравнение (1) относительно 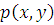 ,
получим:
,
получим:
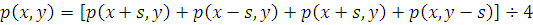 , (4)
, (4)
Задав значения функции 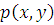 в
граничных узлах контура сеточной области Аs в соответствии с граничными
условиями и решая полученную систему уравнений (4) для каждого узла сетки,
получим численное решение краевой задачи (1) в заданной области А.
в
граничных узлах контура сеточной области Аs в соответствии с граничными
условиями и решая полученную систему уравнений (4) для каждого узла сетки,
получим численное решение краевой задачи (1) в заданной области А.
Ясно, что число уравнений вида (4) равно
количеству узлов сеточной области Аs, и чем больше узлов (т.е. чем мельче
сетка), тем меньше погрешность вычислений. Однако надо помнить, что с
уменьшением шага s возрастает размерность системы уравнений и следовательно,
время решения. Поэтому сначала рекомендуется выполнить пробные вычисления с
достаточно крупным шагом s , оценить полученную погрешность вычислений, и лишь
затем перейти к более мелкой сетке во всей области или в какой-то ее части.
Сравнение метода конечных разностей и метода
конечных элементов
Оба метода относятся к классу сеточных методов
приближенного решения краевых задач. С точки зрения теоритических оценок
точности методы обладают примерно равными возможностями. В зависимости от формы
области, краевых условий, коэффициентов исходного уравнения оба метода имеют
погрешности аппроксимации от первого до четвертого порядка относительно шага. В
силе этого они успешно используются для разработки программных комплексов
автоматизированного проектирования технических объектов.
Методы конечных элементов и конечных разностей
имеют ряд существенных отличий. Прежде всего, методы различны в том, что в
методе конечных разностей аппроксимируется производные искомых функций, а метод
конечных элементов - само решение, т.е. зависимость искомых функций от
пространственных координат и времени. Методы сильно отличаются и в способе
построения сеток. В методе конечных разностей строятся, как правило, регулярные
сетки, особенности геометрии области учитываются только в около граничных
узлах. В связи с этим метод конечных разностей чаще применяется для анализа
задач с прямолинейными границами областей определения функций. К числу
традиционных задач, решаемых на основе метода конечных разностей, относятся
исследования течений жидкостей и газов в трубах, каналах с учетом теплообменных
процессов и ряд других. В методе конечных элементов разбиение на элементы
производится с учетом геометрических особенностей области, процесс разбиения
начинается от границы с целью наилучшей аппроксимации её геометрии. Затем
разбивают на элементы внутренние области, причем алгоритм разбиения строится
так чтобы элементы удовлетворяли некоторым ограничениям, например стороны
треугольников не слишком отличались по длине и т.д. Поэтому метод конечных
элементов наиболее часто используется для решения задач с произвольной областью
определения функций, таких, как расчет на прочность деталей и узлов
строительных конструкций, авиационных и космических аппаратов, тепловой расчет
двигателей и т.д.
. Метод конечных объёмов
алгоритм программа моделирование
Отправной точкой метода конечных объёмов (МКО)
является интегральная формулировка законов сохранения массы, импульса, энергии
и др. Балансовые соотношения записываются для небольшого контрольного объема;
их дискретный аналог получается суммированием по всем граням выделенного объема
потоков массы, импульса и т.д., вычисленных по каким - либо квадратурным
формулам. Поскольку интегральная формулировка законов сохранения не накладывает
ограничений на форму контрольного объема, МКО пригоден для дискретизации
уравнений гидрогазодинамики как на структурированных, так и на
неструктурированных сетках с различной формой ячеек, что, в принципе, полностью
решает проблему сложной геометрии расчетной области.
Следует заметить, однако, что использование
неструктурированных сеток является довольно сложным в алгоритмическом
отношении, трудоемким при реализации и ресурсоемким при проведении расчетов, в
особенности при решении трехмерных задач. Это связано как с многообразием
возможных форм ячеек расчетной сетки, так и с необходимостью применения более
сложных методов для решения системы алгебраических уравнений, не имеющей
определенной структуры. Практика последних лет показывает, что развитые
разработки вычислительных средств, базирующихся на использовании
неструктурированных сеток, по силам лишь достаточно крупным компаниям, имеющим
соответствующие людские и финансовые ресурсы. Гораздо более экономичным
оказывается использование блочно-структурированных сеток, предполагающее
разбиение области течения на несколько подобластей (блоков) относительно
простой формы, в каждой из которых строится своя расчетная сетка. В целом такая
составная сетка не является структурированной, однако внутри каждого блока
сохраняется обычная индексная нумерация узлов, что позволяет использовать
эффективные алгоритмы, разработанные для структурированных сеток. Фактически,
для перехода от одноблочной сетки к многоблочной необходимо лишь организовать
стыковку блоков, т.е. обмен данными между соприкасающимися подобластями для
учета их взаимного влияния. Заметим также, что разбиение задачи на отдельные
относительно независимые блоки естественным образом вписывается в концепцию
параллельных вычислений на кластерных системах с обработкой отдельных блоков на
разных процессорах (компьютерах). Все это делает использование
блочно-структурированных сеток в сочетании с МКО сравнительно простым, но
чрезвычайно эффективным средством расширения геометрии решаемых задач, что
исключительно важно для небольших университетских групп, разрабатывающих
собственные программы в области гидрогазодинамики.
Отмеченные выше достоинства МКО послужили
основанием к тому, что в начале 1990-х гг. именно этот подход с ориентацией на
использование блочно-структурированных сеток был выбран авторами в качестве
основы для разработки собственного пакета программ широкого профиля для задач
гидрогазодинамики и конвективного теплообмена.
Математическое описание:
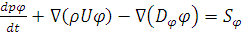 (5)
(5)
где: 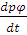 -
изменение некоторой физической величины
-
изменение некоторой физической величины 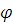
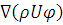 - конвективное
слагаемое в абстрактном законе сохранения физической величины
- конвективное
слагаемое в абстрактном законе сохранения физической величины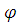
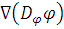 - диффузное
слагаемое в абстрактном законе сохранения физической величины
- диффузное
слагаемое в абстрактном законе сохранения физической величины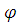
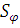 - источниковое
слагаемое в абстрактном законе сохранения физической величины
- источниковое
слагаемое в абстрактном законе сохранения физической величины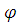
. Метод подвижных клеточных автоматов
Метод подвижных клеточных автоматов (MCA, от
англ. movable cellular automata) - это метод вычислительной механики
деформируемого твердого тела, основанный на дискретном подходе. Он объединяет
преимущества метода классических клеточных автоматов и метода дискретных
элементов. Важным преимуществом метода клеточных автоматов является возможность
моделирования разрушения материала, включая генерацию повреждений,
распространение трещин, фрагментацию и перемешивание вещества. Моделирование
именно этих процессов вызывает наибольшие трудности в методах механики сплошных
сред (метод конечных элементов, метод конечных разностей и др.), что является
причиной разработки новых концепций, например, таких как перидинамика.
Известно, что метод дискретных элементов весьма эффективно описывает поведение
гранулированных сред. Особенности расчета сил взаимодействия между подвижными
клеточными автоматами позволяют описывать в рамках единого подхода поведение
как гранулированных, так и сплошных сред. Так, при стремлении характерного
размера автомата к нулю формализм метода клеточных автоматов позволяет перейти
к классическим соотношениям механики сплошной среды.
В рамках метода клеточных автоматов объект моделирования
описывается как набор взаимодействующих элементов/автоматов. Динамика множества
автоматов определяется силами их взаимодействия и правилами для изменения их
состояния. Эволюция этой системы в пространстве и во времени определяется
уравнениями движения. Силы взаимодействия и правила для связанных элементов
определяются функциями отклика автомата. Эти функции задаются для каждого
автомата. В течение движения автомата следующие новые параметры клеточного
автомата рассчитываются: - радиус-вектор автомата; - скорость автомата;
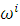 - угловая скорость
автомата;
- угловая скорость
автомата;
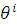 - вектор поворота
автомата; - масса автомата; - момент инерции автомата.
- вектор поворота
автомата; - масса автомата; - момент инерции автомата.
Ввод нового типа состояния требует нового
параметра используемого в качестве критерия переключения в состояние связанные.
Это определяется как параметр перекрытия автоматов hij.
И так, связь клеточных автоматов характеризуется
величиной их перекрытия.
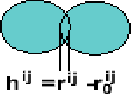 <E:\wiki\?¤?°???»:MCA_sh1.gi>
<E:\wiki\?¤?°???»:MCA_sh1.gi> <E:\wiki\?¤?°???»:MCA_sh2.gi>
<E:\wiki\?¤?°???»:MCA_sh2.gi>
Рис 3.1 Начальная структура
формируется установкой свойств особой связи между каждой парой соседних
элементов.
По сравнению с методом классических клеточных
автоматами в методе MCA не только единичный автомат но и также связи автоматов
могут переключаться. В соответствии с концепцией бистабильных автоматов
вводится два состояния пары (взаимосвязь):
|
связанные
|
оба
автомата принадлежат одному сплошному телу
|
|
несвязанные
|
каждый
автомат принадлежит разным телам или фрагментам поврежденного материала
|
Итак, изменение состояния связи пары
определяется относительным движением автоматов, и среда формируемая такими
парами может быть названа бистабильной средой.
Уравнения движения клеточных автоматов
Эволюция клеточных автоматов среды описывается
следующими уравнениями трансляционного движения:
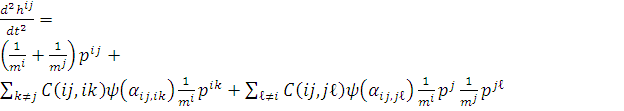 (6)
(6)

Рис 3.2 Учет сил, действующих между автоматами
ij со стороны их соседей.
Здесь mi это масса автомата i, pij это
центральная сила действующая между автоматами i и j, C(ij, ik) это особый
коэффициент ассоциированный с переносом параметра h из пары ij к ik, ψ(αij,
ik) это угол между направлениями ij и ik.
Вращательные движения также могут быть учтены с
точностью ограниченной размером клеточного автомата. Уравнения вращательного движения
могут быть записаны следующим образом:
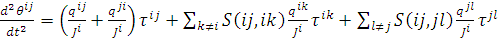 (7)
(7)
Здесь Θij
угол относительного поворота (это параметр переключения подобно hij
трансляционного движения), qij(ji) это расстояние от центра автомата i(j) до
точки контакта с автоматом j(i) (угловой момент), τij
это парное тангенциальное взаимодействие, S(ij, ik(jl)) это особый коэффициент
ассоциированный с параметром переноса Θ
от одной пары к другой (это похоже на C(ij, ik(jl)) из уравнений
трансляционного движения). Следует отметить, что уравнения полностью аналогичны
уравнениям движения для много-частичной среды. Определение деформации пары
автоматов
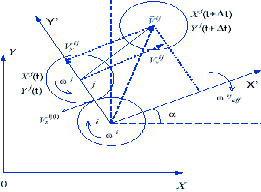
Рис 3.3 Вращение тела как целого не приводит к
деформации между автоматами
Смещение пары автоматов Безразмерный параметр
деформации для смещения i j пары автоматов записывается как:
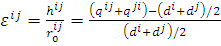 (8)
(8)
В этом случае:
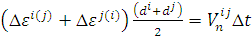 (9)
(9)
где Δt
временной шаг, Vnij - зависимая скорость. Вращение пары автоматов может быть
посчитано аналогично с связью последнего смешения.
Необратимая деформация в методе клеточных
автоматов
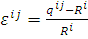 (10)
(10)
Параметр εij
используется как мера деформации автомата i взаимодействующего с автоматом j.
Где qij - расстояние от центра автомата i до точки его контакта с автоматом j;
Ri=di/2 (di - размер автомата i).
Например, титановый образец при циклическом
нагружении (растяжение-сжатие). Диаграмма деформирования показана на следующем
рисунке:
|
схема
нагружения
|
Диаграмма
деформирования
|
|

|
|
(Точки
- экспериментальные данные)
|
Преимущества метода клеточных автоматов
Благодаря подвижности каждого автомата метод
клеточных автоматов позволяет напрямую учитывать такие события как:
перемешивание масс
эффект проникновения
химические реакции
интенсивные деформации
фазовые превращения
накопление повреждений
фрагментация и трещины
генерация и развитие повреждений
Используя различные граничные условия разных
типов (жесткие, упругие, вязко-упругие, т.д.) можно имитировать различные
свойства окружающей среды, содержащей моделируемую систему. Можно моделировать
различные режимы механического нагружения (растяжение, сжатие, сдвиг, т.д.) с
помощью настроек дополнительных состояний на границах.
. Метод молекулярной динамики
Метод молекулярной динамики (метод МД) - метод,
в котором временная эволюция системы взаимодействующих атомов или частиц
отслеживается интегрированием их уравнений движения
Метод классической (полноатомной) молекулярной
динамики позволяет с использованием современных ЭВМ рассматривать системы,
состоящие из нескольких миллионов атомов на временах порядка нескольких
пикосекунд. Применение других подходов (тяжело-атомные, крупно-зернистые
модели) позволяет увеличить шаг интегрирования и тем самым увеличить доступное
для наблюдения время до порядка микросекунд. Для решения таких задач все чаще
требуются большие вычислительные мощности, которыми обладают суперкомпьютеры.
Основные положения метода
Для описания движения атомов или частиц
применяется классическая механика. Закон движения частиц находят при помощи
аналитической механики.
Силы межатомного взаимодействия можно
представить в форме классических потенциальных сил (как градиент потенциальной
энергии системы).
Точное знание траекторий движения частиц системы
на больших промежутках времени не является необходимым для получения
результатов макроскопического (термодинамического) характера.
Наборы конфигураций, получаемые в ходе расчетов
методом молекулярной динамики, распределены в соответствии с некоторой
статистической функцией распределения, например отвечающей микроканоническому
распределению.
Ограничения применимости метода
Метод молекулярной динамики применим, если длина
волны Де Бройля атома (или частицы) много меньше, чем межатомное расстояние.
Также классическая молекулярная динамика не
применима для моделирования систем, состоящих из легких атомов, таких как гелий
или водород. Кроме того, при низких температурах квантовые эффекты становятся
определяющими и для рассмотрения таких систем необходимо использовать
квантовохимические методы. Необходимо, чтобы времена на которых рассматривается
поведение системы были больше, чем время релаксации исследуемых физических
величин.
Применение
Метод молекулярной динамики, изначально
разработанный в теоретической физике, получил большое распространение в химии
и, начиная с 1970х годов, в биохимии и биофизике. Он играет важную роль в
определении структуры белка и уточнении его свойств (см. также кристаллография,
ЯМР). Взаимодействие между объектами может быть описано силовым полем
(классическая молекулярная динамика), квантовохимической моделью или смешанной
теорией, содержащей элементы двух предыдущих (QM/MM (quantum mechanics/molecular
mechanics, QMMM (англ.)).
Наиболее популярными пакетами программного
обеспечения для моделирования динамики биологических молекул являются: AMBER,
CHARMM (и коммерческая версия CHARMm), GROMACS, GROMOS,Lammps и NAMD.
. Метод дискретного элемента
Метод дискретного элемента (DEM, от англ.
Discrete element method) - это семейство численных методов предназначенных для
расчёта движения большого количества частиц, таких как молекулы, песчинки,
гравий, галька и прочих гранулированных сред. Метод был первоначально применён
Cundall в 1971 для решения задач механики горных пород. Williams, Hocking и
Mustoe детализировали теоретические основа метода. В 1985 они показали, что DEM
может быть рассмотрен как обобщение метода конечных элементов (МКЭ, FEM). В
книге Numerical Modeling in Rock Mechanics, by Pande, G., Beer, G. and
Williams, J.R. описано применение этого метода для решения геомеханических
задач. Теоретические основы метода и возможности его применения неоднократно
рассматривалось на 1-й, 2-й и 3-й Международной Конференции по Методам
Дискретного Элемента. Williams, и Bicanic (см. ниже) опубликовали ряд
журнальных статей описывающих современные тенденции в области DEM. В книге The
Combined Finite-Discrete Element Method, Munjiza детально описано комбинирование
Метода Конечного Элемента и Метода Дискретного Элемента.
Этот метод иногда называют молекулярной
динамикой (MD), даже когда частицы не являются молекулами. Однако, в
противоположность молекулярной динамике, этот метод может быть использован для
моделирования частиц с не сферичной поверхностью. Методы дискретного элемента
очень требовательны к вычислительным ресурсам ЭВМ. Это ограничивает размер
модели или количество используемых частиц. Прогресс в области вычислительной
техники позволяет частично снять это ограничение за счет использования
параллельной обработки данных. Альтернативой обработки всех частиц отдельно
является обработка данных как сплошной среды. Например, если гранульный поток
подобен газу или жидкости, можно использовать вычислительную гидродинамику.
Основные принципы метода
Моделирование МДЭ начинается c помещения всех
частиц в конкретное положение и придания им начальной скорости. Затем силы,
воздействующие на каждую частицу, рассчитываются, исходя из начальных данных и
соответствующих физических законов.
Следующие силы могут иметь влияние в
макроскопических моделях:
трение, когда две частицы касаются друг друга;
отскакивание, когда две частицы сталкиваются;
гравитация (сила притяжения между частицами
из-за их массы), которая имеет отношение только при астрономическом
моделировании;
На молекулярном уровне, мы можем рассматривать
Силу Кулона, электростатическое притяжение или отталкивание частиц, несущих
электрический заряд;
Отталкивание Паули, когда два атома находятся
вблизи друг от друга;
Силу Ван дер Ваальса.
Все эти силы складываются, чтобы найти
результирующую силу, воздействующую на каждую частицу. Чтобы рассчитать
изменение в положении и скорости каждой частицы в течение определенного
временного шага из законов Ньютона, используется метод интеграции. После этого
новое положение используется для расчёта сил в течение следующего шага, и этот
цикл программы повторяется до тех пор, пока моделирование не закончится.
Типичные методы интеграции используемые в методе
дискретного элемента:
алгоритм Верлета,
скорость Верлета,
метод прыжка.
Дальнодействующие силы
Когда во внимание принимаются дальнодействующие
силы (гравитация, сила Кулона), взаимодействия каждой пары частиц необходимо
рассчитывать. Число взаимодействий, а следовательно, ресурсоёмкость расчёта,
возрастает с увеличением количества частиц квадратично, что не приемлемо для
моделей с большим числом частиц. Возможный путь решить эту проблему -
объединить некоторые частицы, которые находятся на расстоянии от
рассматриваемой частицы, в одну псевдочастицу. Рассмотрим, например,
взаимодействие между звездой и отдаленной галактикой: ошибка, возникающая из-за
объединения массы всех звезд в удалённой галактике в одну точку, незначительна.
Для того, чтобы определить, какие частицы могут быть объединены в одну
псевдочастицу, используются так называемые древесные алгоритмы. Эти алгоритмы
распределяют все частицы в виде дерева, квадрадерева в случае двухмерной модели
и октадерева в случае трехмерной модели.
Модели в молекулярной динамике делят пространство,
в котором происходит моделируемый процесс, на ячейки. Частицы, уходящие через
одну сторону ячейки просто вставляются с другой стороны (периодические
граничные условия); так же происходит и с силами. Силы перестают приниматься в
расчёт после так называемой дистанции отсечения (обычно половина длины ячейки),
так что на частицу не воздействует зеркальное расположение той же частицы на
другой стороне ячейки. Таким образом, можно увеличивать количество частиц
простым копированием ячеек.
Применение
Фундаментальным предположением метода является
то, что материал состоит из отдельных, дискретных частиц. Эти частицы могут
иметь различные поверхности и свойства. Примеры:
жидкости и растворы, например сахар или белок;
сыпучие вещества в элеваторе, такие как крупа;
гранулированный материал, такой как песок;
порошки, такие как тонер.
Типичные отрасли промышленности использующие
DEM:
Горнодобывающая
Фармацевтическая
Нефтегазовая
Сельскохозяйственная
Химическая
. Метод компонентных цепей
Метод компонентных цепей - это метод,
предназначенный для моделирования физически неоднородных устройств и систем,
исходная информация о которых задана в виде модели структуры. Основной
структурной сущностью метода компонентных цепей является многополюсный
компонент с произвольным числом связей, которым инцидентны переменные связей.
Математическая модель компонента - это уравнение
либо система уравнений (линейных, нелинейных, обыкновенных дифференциальных
1-го порядка) относительно его переменных связей и внутренних переменных. Совокупность
компонентов, связи которых, именуемые ветвями компонентных цепей, объединены в
общих точках, именуемых узлами, определяется как компонентная цепь Ск = {К, S,
N}, где К - множество компонентов; S - множество связей компонентов из К; N -
множество узлов цепи.
В соответствии с типом переменных, действующих
на связи, определены два основных типа связей:
связи энергетического типа S%, которым
соответствует пара топологических координат и пара дуальных переменных 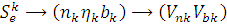 ,
где nk - номер узла k-й связи; bk - номер ветви, nk - знак, задающий ориентацию
связи,
,
где nk - номер узла k-й связи; bk - номер ветви, nk - знак, задающий ориентацию
связи, 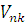 ,
,
 -
переменные связи потенциального и потокового типа;
-
переменные связи потенциального и потокового типа;
связи информационного типа S'k, которым
соответствует одна топологическая координата и одна переменная связи, имеющая
произвольный физический смысл 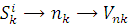 .
.
Принципиальное отличие переменных потенциального
и потокового типа состоит в том, что для последних при формировании
математической модели компонентных цепей в нее автоматически включаются
уравнения узловых топологических законов сохранения. Таким образом,
математическая модель компонентных цепей имеет вид
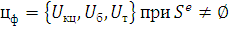 (10)
(10)
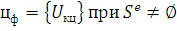 (11)
(11)
где 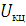 -
совокупность уравнений моделей компонентов, входящих в компонентные цепи;
-
совокупность уравнений моделей компонентов, входящих в компонентные цепи; 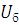 -
уравнения базового узла;
-
уравнения базового узла; 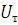 - уравнения
узловых топологических законов сохранения для переменных потокового типа,
записанные для всех узлов за исключением базового;
- уравнения
узловых топологических законов сохранения для переменных потокового типа,
записанные для всех узлов за исключением базового; 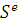 -
множество связей энергетического типа.
-
множество связей энергетического типа.
Согласно числу переменных, действующих на
связях, выделяются связи скалярного и векторного типа. На связи скалярного типа
могут действовать лишь по одной потенциальной и потоковой переменной, т.е. по
одной разнотипной переменной. К скалярным связям относятся связи
энергетического и информационного типов. Связи векторного типа может быть
инцидентно более двух переменных одного типа. Связи векторного типа являются
объединением скалярных. Методом компонентных цепей предусматривается
автоматическое формирование моделей компонентных цепей во временной и в
частотной (для линейных непрерывных схем) областях. При моделировании во
временной области
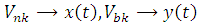
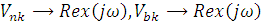
где  -
комплексная частота, а мнимые составляющие реализуются посредством внутренних
переменных. В результате алгебраизации и линеаризации дифференциальных и
нелинейных уравнений модель компонентных цепей принимает вид системы линейных
алгебраических уравнений относительно переменных связей компонентных цепей и
вспомогательных переменных:
-
комплексная частота, а мнимые составляющие реализуются посредством внутренних
переменных. В результате алгебраизации и линеаризации дифференциальных и
нелинейных уравнений модель компонентных цепей принимает вид системы линейных
алгебраических уравнений относительно переменных связей компонентных цепей и
вспомогательных переменных:
ФV = W,
где Ф - квадратная матрица коэффициентов; W -
вектор-столбец правых частей; V - вектор-столбец решения компонентных цепей,
включающий векторы потенциальных, потоковых и внутренних переменных
компонентных цепей.
7. Метод узловых потенциалов
Метод узловых потенциалов - метод расчета
электрических цепей путём записи системы линейных алгебраических уравнений, в
которой неизвестными являются потенциалы в узлах цепи. В результате применения
метода определяются потенциалы во всех узлах цепи, а также, при необходимости,
токи во всех ветвях.
Очень часто необходимым этапом при решении самых
разных задач электроники является расчет электрической цепи. Под этим термином
понимается процесс получения полной информации о напряжениях во всех узлах и о
токах во всех ветвях заданной электрической цепи. Для расчета линейной цепи
достаточно записать необходимое число уравнений, которые базируются на правилах
Кирхгофа и законе Ома, а затем решить полученную систему.
Однако на практике записать систему уравнений
просто из вида схемы удается только для очень простых схем. Если в схеме более
десятка элементов или она содержит участки типа мостов, то для записи системы
уравнений уже требуются специальные методики. К таким методикам относятся метод
узловых потенциалов и метод контурных токов.
Метод узловых потенциалов не привносит ничего
нового к правилам Кирхгофа и закону Ома. Данный метод лишь формализует их
использование настолько, чтобы их можно было применить к любой, сколь угодно
сложной цепи. Иными словами, метод даёт ответ на вопрос «как использовать
законы для расчета данной цепи?».
Если в цепи, состоящей из У узлов и Р рёбер
известны все характеристики звеньев (полные сопротивления R, величины
источников ЭДС E и тока J), то возможно вычислить токи Ii во всех рёбрах и
потенциалы φi во всех узлах.
Поскольку электрический потенциал определён с точностью до произвольного
постоянного слагаемого, то потенциал в одном из узлов (назовём его базовым
узлом) можно принять равным нулю, а потенциалы в остальных узлах определять
относительно базового узла. Таким образом, при расчёте цепи имеем У+Р-1
неизвестных переменных: У-1 узловых потенциалов и Р токов в рёбрах.
Не все из указанных переменных независимы.
Например, исходя из закона Ома для участка цепи, токи в звеньях полностью
определяются потенциалами в узлах:
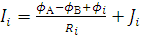 (12)
(12)
С другой стороны, токи в рёбрах однозначно
определяют распределение потенциала в узлах относительно базового узла:
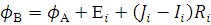 (13)
(13)
Таким образом, минимальное число независимых
переменных в уравнениях цепи равно либо числу звеньев, либо числу узлов минус
1, в зависимости от того, какое из этих чисел меньше.
При расчёте цепей чаще всего используются
уравнения, записываемые исходя из законов Кирхгофа. Система состоит из У-1
уравнений по 1-му закону Кирхгофа (для всех узлов, кроме базового) и К уравнений
по 2-му закону Кирхгофа для каждого независимого контура. Независимыми
переменными в уравнениях Кирхгофа являются токи звеньев. Поскольку согласно
формуле Эйлера для плоского графа число узлов, рёбер и независимых контуров
связаны соотношением 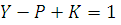 или
или 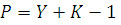 то
число уравнений Кирхгофа равно числу переменных, и система разрешима. Однако
число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа
уравнений является метод узловых потенциалов. Переменными в системе уравнений
являются У-1 узловых потенциалов. Уравнения записываются для всех узлов, кроме
базового. Уравнения для контуров в системе отсутствуют.
то
число уравнений Кирхгофа равно числу переменных, и система разрешима. Однако
число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа
уравнений является метод узловых потенциалов. Переменными в системе уравнений
являются У-1 узловых потенциалов. Уравнения записываются для всех узлов, кроме
базового. Уравнения для контуров в системе отсутствуют.
Перед началом расчёта выбирается один из узлов
(базовый узел), потенциал которого считается равным нулю. Затем узлы
нумеруются, после чего составляется система уравнений.
Уравнения составляются для каждого узла, кроме
базового. Слева от знака равенства записывается:
потенциал рассматриваемого узла, умноженный на
сумму проводимостей ветвей, примыкающих к нему;
минус потенциалы узлов, примыкающих к данному,
умноженные на проводимости ветвей, соединяющих их с данным узлом.
Справа от знака равенства записывается:
сумма всех источников токов, примыкающих к
данному узлу;
сумма произведений всех ЭДС, примыкающих к
данному узлу, на проводимость соответствующего звена.
Если источник направлен в сторону
рассматриваемого узла, то он записывается со знаком «+», в противном случае -
со знаком «−».
. Метод переменных состояния
Метод переменных состояния (называемый иначе
методом пространственных состояния) представляет собой упорядоченный способ
нахождения состояния системы в функции времени, использующий матричный метод
решения системы дифференциальных уравнений первого порядка, записанных в форме
Коши (в нормальной форме). Применительно к электрическим цепям под переменными
состояниями понимают величины, определяющие энергетическое состояние цепи, т.е.
токи через индуктивные элементы и напряжения на конденсаторах. Значения этих
величин полагаем известными к началу процесса. Переменные состояния в
обобщенном смысле назовем х. Так как это некоторые функции времени, то их можно
обозначить x(t).
Метод переменных состояния основывается на двух
уравнениях, записываемых в матричной форме.
Структура первого уравнения определяется тем,
что оно связывает матрицу первых производных по времени переменных состояния x¢(t)
с матрицами самих переменных состояний x и внешних воздействий u, в качестве
которых рассматриваются ЭДС и токи источников.
Второе уравнение по своей структуре является
алгебраическим и связывает матрицу выходных величин y с матрицами переменных
состояния x и внешних воздействий u.
Определяя переменные состояния, отметим
следующие их свойства:
В качестве переменных состояния в
электрических цепях следует выбрать токи 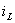 в индуктивностях и напряжения
в индуктивностях и напряжения 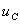 на
емкостях, причем не во всех индуктивностях и не на всех емкостях, а только для
независимых, т.е. таких, которые определяют общий порядок системы
дифференциальных уравнений цепи.
на
емкостях, причем не во всех индуктивностях и не на всех емкостях, а только для
независимых, т.е. таких, которые определяют общий порядок системы
дифференциальных уравнений цепи.
Дифференциальные уравнения цепи
относительно переменных состояния записываются в канонической форме, т.е.
представляются решенными относительно первых производных переменных состояния
по времени.
Отметим, что только при выборе в
качестве переменных состояния токов 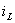 в независимых индуктивностях и
напряжений
в независимых индуктивностях и
напряжений 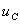 на
независимых емкостях первое уравнение метода переменных состояния будет иметь
указанную выше структуру.
на
независимых емкостях первое уравнение метода переменных состояния будет иметь
указанную выше структуру.
Если в качестве переменных состояния
выбрать токи 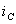 в ветвях с
емкостями или токи
в ветвях с
емкостями или токи  в ветвях с
сопротивлениями, а также напряжения
в ветвях с
сопротивлениями, а также напряжения 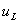 на индуктивностях или напряжения
на индуктивностях или напряжения 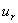 на
сопротивлениях, то первое уравнение метода переменных состояния также можно
представить в канонической форме, т.е. решенным относительно первых производных
по времени этих величин. Однако, структура их правых частей не будет
соответствовать данному выше определению, так как в них будет еще входить
матрица первых производных от внешних воздействий u¢. Число
переменных состояния равно порядку системы дифференциальных уравнений
исследуемой электрической цепи. Выбор в качестве переменных состояния токов
на
сопротивлениях, то первое уравнение метода переменных состояния также можно
представить в канонической форме, т.е. решенным относительно первых производных
по времени этих величин. Однако, структура их правых частей не будет
соответствовать данному выше определению, так как в них будет еще входить
матрица первых производных от внешних воздействий u¢. Число
переменных состояния равно порядку системы дифференциальных уравнений
исследуемой электрической цепи. Выбор в качестве переменных состояния токов 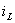 и
напряжений
и
напряжений 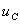 удобен еще
и потому, что именно эти величины согласно законам коммутации в момент коммутации
не изменяются скачком, т.е. одинаковы для моментов времени t=0+ и t=0-.
Переменные состояния
удобен еще
и потому, что именно эти величины согласно законам коммутации в момент коммутации
не изменяются скачком, т.е. одинаковы для моментов времени t=0+ и t=0-.
Переменные состояния 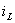 и
и 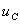 потому так
и называются, что в каждый момент времени задают энергетическое состояние
электрической цепи, так как последнее определяется суммой выражений
потому так
и называются, что в каждый момент времени задают энергетическое состояние
электрической цепи, так как последнее определяется суммой выражений 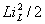 и
и  .
Представление уравнений в канонической форме очень удобно при их решении на
аналоговых вычислительных машинах и для программирования при их решении на
цифровых вычислительных машинах. Поэтому такое представление имеет очень важное
значение при решении этих уравнений с помощью средств современной
вычислительной техники. Пусть в системе n переменных состояния, m выходных
величин и р источников воздействия. Тогда матрицу-столбец переменных состояния
в n-мерном пространстве состояний, матрицу-столбец выходных величин,
матрицу-столбец источников воздействий обозначим соответственно
.
Представление уравнений в канонической форме очень удобно при их решении на
аналоговых вычислительных машинах и для программирования при их решении на
цифровых вычислительных машинах. Поэтому такое представление имеет очень важное
значение при решении этих уравнений с помощью средств современной
вычислительной техники. Пусть в системе n переменных состояния, m выходных
величин и р источников воздействия. Тогда матрицу-столбец переменных состояния
в n-мерном пространстве состояний, матрицу-столбец выходных величин,
матрицу-столбец источников воздействий обозначим соответственно
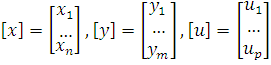 (14)
(14)
Для электрических цепей можно
составить матричные уравнения вида:
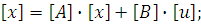 (15)
(15)
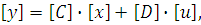 (16)
(16)
где [A], [B], [C], [D] - некоторые матрицы,
определяемые структурой цепи и значениями ее параметров. Причем [A] - всегда
квадратная матрица порядка n.
(15) - система n дифференциальных уравнений
первого порядка (в общем случае взаимосвязанных), называемая уравнением
переменных состояния в нормальной форме. Вспомогательные переменные х , х ...х
- переменные состояния, а [x] - вектор переменных состояния.(16) - выходное
уравнение.
Преимущества
Решение таких систем широко известно в математике
как в численном, так и в аналитическом виде.
Уравнения легко решаются на ЭВМ.
Как правило, число уравнений в системе (15)
оказывается меньше, чем число уравнений, составленных МУП.
Метод может быть обобщен для решения нелинейных
систем
Заключение
Польза от компьютерного моделирования по
сравнению с натурным экспериментом:
это дешевле
это быстрее.
В некоторых процессах, где натурный эксперимент
опасен для жизни и здоровья людей, вычислительный эксперимент является
единственно возможным (термоядерный синтез, освоение космического пространства,
проектирование и исследование химических и других производств).
Для проверки адекватности математической модели
и реального объекта, процесса или системы результаты исследований на ЭВМ
сравниваются с результатами эксперимента на опытном натурном образце.
Результаты проверки используются для корректировки математической модели или
решается вопрос о применимости построенной математической модели к
проектированию либо исследованию заданных объектов, процессов или систем. В
задачах проектирования или исследования поведения реальных объектов, процессов
или систем чаще всего используются математические модели типа ДНА
(детерминированная, непрерывная, аналитическая). Методы решения математических
задач можно разделить на 2 группы:
точные методы решения задач (ответ получается в
виде формул);
численные методы решения задач (формулы нет, но
можно построить много арифметических операций, которые приведут к решению).
Численные методы разрабатываются вычислительной
математикой и особенно актуальны при применении ЭВМ. Ни те, ни другие методы
обычно не дают точного решения, однако это не значит, что разум бессилен а, это
всего лишь означает, что надо установить требуемую степень точности и решать
проблему с заданной точностью.
Литература
1. Сегерлинд Л. «Применение
метода конечных элементов» Перевод с английского Шестакова А.А. Москва 1979
. http://ru.wikipedia.org/wiki/Метод_классической_молекулярной_динамики
. Е.М. Смирнов, Д.К. Зайцев
«Метод конечных объемов в приложении к задачам гидрогазодинамики и теплообмена
в областях сложной геометрии» Научно технические ведомости 2’ 2004
. http://ru.wikipedia.org/wiki/Метод_подвижных_клеточных_автоматов
. http://ru.wikipedia.org/wiki/Метод_классической_молекулярной_динамики
. http://ru.wikipedia.org/wiki/Метод_дискретного_элемента
. В.М. Дмитриев, Т.Н.
Зайченко, Ю.А. Шурыгин «Применение метода компонентных цепей для компьютерного
моделирования электронных компонентов, узлов и систем» Электроника и связь.
Тематический выпуск «Электроника и нанотехнологии», ч.1, 2009
. http://ru.wikipedia.org/wiki/Метод_узловых_потенциалов
. Зевеке Г.В. «Основы теории
цепей». Учебник для вузов. М., «Энергия», 1975г.
. Бессонов Л.А.
«Теоретические основы электротехники. Электрические цепи». М.: Гардарики,
2000г.