Исследование поведения модели системы дифференциальных уравнений

Исследование поведения модели системы дифференциальных уравнений

Введение

Математическая модель - это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования - исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование - это еще и метод познания окружающего мира, дающий возможность управлять им.

Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, «что было бы, если бы...» Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.

1). Основные этапы математического моделирования

а) Построение модели. На этом этапе задается некоторый «нематематический» объект - явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.

б) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.

в) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

г) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.

д) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

). Исходные данные

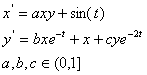
3). Основная теория

Для моделирования данной нам системы дифференциальных уравнений мы будем использовать метод Эйлера.

Метод Эйлера - наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.

Пусть дана задача Коши для уравнения первого порядка

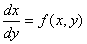
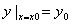
где функция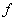 определена на некоторой области . Решение разыскивается на интервале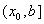. На этом интервале введем узлы

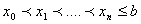
Приближенное решение в узлах , которое обозначим через 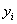 определяется по формуле

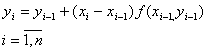
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

4). Задание и план работы

. Изучение и проработка теоретического материала.

. Разработка алгоритмов и компьютерной программы.

а) программа должна строить графики функций по входным данным;

б) исследовать поведение математической модели по графикам в зависимости от выбранных коэффициентов;

. Примеры реализации программы.

Компьютерная реализация

С помощью метода Эйлера, я реализовал программу, которая по введенным начальным данным строит графики, по которым можно исследовать данную систему дифференциальных уравнений (рис. 1).

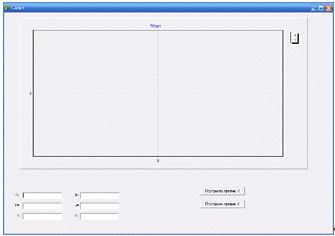
Рисунок 1 - основной интерфейс программы.

Так как программа позволяет сразу строить два графика, то это позволяет удобно исследовать поведение графиков в зависимости от заданных параметров.

Далее мы будем рассматривать серию скриншотов, которые будут иллюстрировать сделанные мною выводу по поводу поведения модели.

На графиках красной линией идет график функции Х, а синей Y.

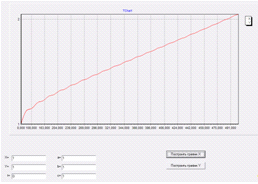
Так как в функции Х мы можем наблюдать функцию sin(t), а мы делаем шаг именно по t, то мы сможем увидеть, что начало графика имеет «волнообразную» (синусоидальную) структуру, и начинает стремиться к прямой линии с увеличением параметра t. Это мы получаем за счет зависимости от функции Y ,которая в свою очередь имеет в теле функции экспоненту.

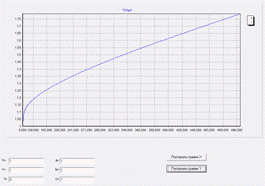
Построив график Y с теми же начальными параметрами, мы увидим, что график сначала резко увеличивается (за счет параметра t , который вначале цикла равен 0 и затем медленно увеличивается ,что экспонента близка к 1), а затем выходит на отрезок стабильности, т.е. стабильно растет.

Далее, я начну изменять параметры a, b ,c для того чтобы проследить за изменением характера нашей модели.

Самый интересный график по функции Х, как мне кажется, мы можем получить, прировняв коэффициент a к 0.1 т.е. устремляя его к минимуму. Он будет зависеть только от одного параметра t, который будет увеличиваться пошагово. Поэтому мы получим своеобразную, показанную на графике синусоидальную кривую.

График же зависимости Y не претерпел сильных изменений, его структура не изменилась, а изменилась только скорость его роста.

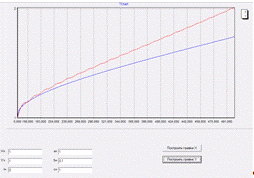
При данных параметрах график Х ведет себя так же, как и в первом случае. График Y имеет чуть меньше скорости в росте по сравнению с первым графиком и чуть большую скорость, чем во втором случае, т.е. в первом случае к 490 он уже достигал значения 1.75 , а во втором случае достигал лишь 1.55. В данном примере он находиться чуть ниже, чем 1.75.

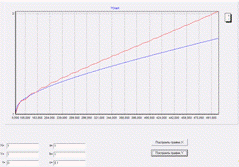
Этот случай тоже ничем примечательным не отличает. График Х ведет себя стабильно - синусоидальные периодические колебания под углом. У графика Y изменяется только скорость роста. Будем надеяться, что когда я начну уменьшать по два параметра сразу, то нас ждут более интересные графики.

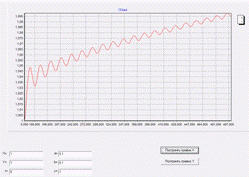
Уменьшив параметры a и b, мы получаем точно такой же график, который мы получили и в начале, что является следствием того, что график функции X не сильно зависит от параметра b.

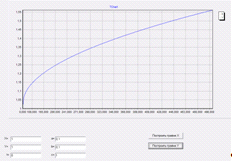
График Y как всегда не может нам показать ничего интересного кроме незначительного изменения скорости роста.

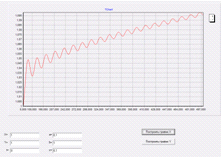
График X при единственном единичном параметре b. График если и изменился, то себя выдал не сильно. Поэтому мы можем сделать заключение, что параметр c влияет на него тоже слабо.

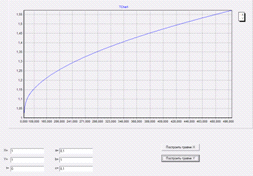
График Y все также остается, зависим от изменений, которые претерпевают параметры b и c, вследствие чего скорость его, то увеличивается, то уменьшается.

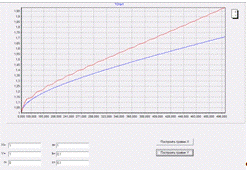
График X по-прежнему стремиться стать неколеблющейся прямой. График Y набирает скорость роста.

Далее я попробую, уменьшите все параметры сразу и посмотреть, что произойдет.

Ожидается, что график X будет в виде косой синусоидальной увеличивающейся, а Y будет увеличиваться.

График X оправдал мои ожидания.

График Y растет, но чуть медленнее из-за уменьшенных значений параметров b и c ,а с уменьшением параметра a он растет быстрее.

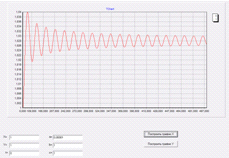
Устремляя параметр a, мы можем увидеть изменения угла в графике X.

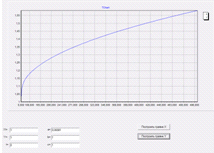
Как можно заметить из этих двух графиков, функция Y зависит так же от параметра a, который регулирует скорость возрастания. Чем меньше a тем больше скорость роста.

Далее я решил поэкспериментировать с начальными данными, а точнее с начальными значениями X,Y и t.

Так как я теперь знаю зависимость наших графиков X и Y то могу спокойно предполагать и поведение.

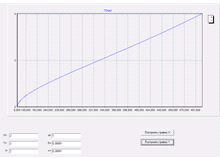
Как мы видим все идет стабильно.

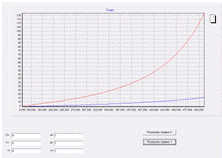
И вот свершилось. График X дал резкое увеличение, в то время когда график Y все, также не спеша растет.

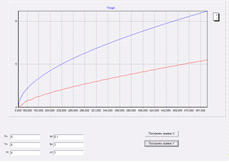
Уменьшив параметр a, мы увидим то, что и ожидали - график X стал заметно притормаживать, в то время как график Y растет.

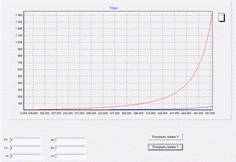
Продолжая развлекаться с начальными условиями, мы приходим к тому, что при одинаковых начальных условиях график функции X намного быстрее растет, чем график функции Y.

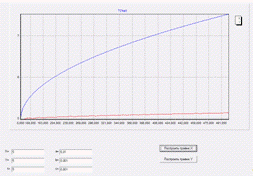
Хотя в то же время график функции X очень зависим от своего параметра a , вследствие чего при низком значении оного мы получим, что график Y будет обгонять X.

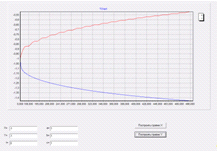
При отрицательных начальных значениях график Y уменьшается, а график X неотступно растет.

Заключение

Написав программу, которая позволяет изучать графики представленной системы дифференциальных уравнений, я провел тщательный анализ оной и сделал для себя следующие выводы:

1)   График X очень сильно зависит от параметра a;

2)   График Y зависит, но не очень сильно от параметров b и c, а скорость его роста зависит от параметра a;

)     График X растет намного быстрее по сравнению с графиком Y, но если уменьшить параметр a, то X затормозиться и Y его перегонит;

)     При отрицательных начальных значениях график Y уменьшается, в то время как график X растет.

Список литературы

математическое моделирование дифференциальное уравнение

1.В.В. Фаронов «Delphi. Программирование на языке высокого уровня»

.Б.Ф. Кирьянов «Математическое моделирование»

Приложение

Программа реализована в среде Delphi 7.

unit Laba;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, StdCtrls, ExtCtrls, TeeProcs, TeEngine, Chart, Series, TeeFunci;= class(TForm): TEdit;: TEdit;: TEdit;: TEdit;: TEdit;: TEdit;: TLabel;: TLabel;: TLabel;: TLabel;: TLabel;: TLabel;: TButton;: TLabel;: TLabel;: TLabel;: TChart;: TLineSeries;: TButton;: TLineSeries;: TAddTeeFunction;Button1Click(Sender: TObject);Button2Click(Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm1;

{$R *.dfm}f1(a:real;x:real;y10:real;y20:real):real;:=a*y10*y20+sin(x);;f2(b:real;x:real;c:real;y10:real;y20:real):real;:=(b*y10*exp(-x))+y10+(c*y20*exp(-2*x));TForm1.Button1Click(Sender: TObject);,x,a,b,c:real;:array[0..1000] of real;:array[0..1000] of real;:integer;.Repaint;[0]:=StrToFloat(Trim(Edit1.Text));[0]:=StrToFloat(Trim(Edit2.Text));:=StrToFloat(Trim(Edit3.Text));:=StrToFloat(Trim(Edit4.Text));:=StrToFloat(Trim(Edit5.Text));:=StrToFloat(Trim(Edit6.Text));:=0.001;i:=0 to 500 do:=x+h*i;[i+1]:=y1[i]+h*f1(a,x,y1[i],y2[i]);[i+1]:=y2[i]+h*f2(b,x,c,y1[i],y2[i]);.Series1.AddXY(x,y1[i],FloatToStrF(i,ffFixed,10,3),clRed);;;TForm1.Button2Click(Sender: TObject);,x,a,b,c:real;:array[0..1000] of real;:array[0..1000] of real;:integer;.Repaint;[0]:=StrToFloat(Trim(Edit1.Text));[0]:=StrToFloat(Trim(Edit2.Text));:=StrToFloat(Trim(Edit3.Text));:=StrToFloat(Trim(Edit4.Text));:=StrToFloat(Trim(Edit5.Text));:=StrToFloat(Trim(Edit6.Text));:=0.001;i:=0 to 500 do:=x+h*i;[i+1]:=y1[i]+h*f1(a,x,y1[i],y2[i]);[i+1]:=y2[i]+h*f2(b,x,c,y1[i],y2[i]);.Series2.AddXY(x,y2[i],FloatToStrF(i,ffFixed,10,3),clBlue);;;.