Коэффициенты: m =6, n = 3
Задача
1.
Получен кредит в размере 6 млн. руб. под 3 % ежемесячно.
Какая сумма должна быть возвращена через 9 месяцев при простом проценте? Какая
должна быть процентная ставка при сложном проценте, чтобы за это же время
возвращаемая сумма была та же, что и при простом проценте?
Решение:
Формула простых процентов:
= P · (1 + i · n) = 6 · (1 + 0,03 · 9) = 7,62 млн. руб.
Формула сложных процентов: Sn = P · (1+i) n, отсюда определим i:
0,027 или 2,7%.
Задача
2.
Заемщик должен одному кредитору три различные суммы: 6 тыс.
руб. с выплатой через 3 месяца, 3 тыс. руб. с выплатой через 4 месяца, 9 тыс.
руб. через 6 месяцев. Через какой срок заемщик может погасить весь долг сразу,
если кредиты брались под простую годовую ставку 16%?
Решение:
А1 = 
20 689,7 руб.
А2 =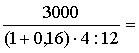 
7 758,6руб.
А3 = 
15 517,2руб.
А = 20 689,7 + 7 758,6 + 15 517,2 = 43 965,5 руб.
А =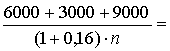 
43 965,5 руб.
Определим срок n:
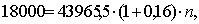
= 0,35 или 0,35 · 360 
127 дней или 4 месяца.
Задача
3.
Фирме требуется накопить 700 тыс. руб. для покупки
оборудования через 2 года. Для этого в конце каждого полугодия на счет в банке
собираются делать взнос. Какова должна быть величина этого взноса, если банк
начисляет проценты ежеквартально по ставке сложных процентов 13% годовых? Найти
современную стоимость этой ренты.
Решение:
Величина платежа равна:
руб.
Современная стоимость этой ренты:
руб.
Задача
4.
Некто хочет вложить определенную сумму в финансовую операцию
на срок 8 месяцев. Он рассматривает следующие варианты:
а) положить в банк под простые 23% годовых; б) положить в
банк под сложные 23% годовых с начислением в конце каждых двух месяцев; в)
купить облигацию по курсу 86% с тем же сроком погашения.
Какой из вариантов выбрать?
Решение:
Вариант А:
Вариант Б:
Вариант В:
Доходность к погашению равна:
.
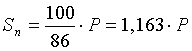Отсюда вывод, что предпочтительнее вариант В.
Задача
5.
Банк учел вексель по простой учетной ставке d = 3% годовых за 106 дней
до срока выплаты и, кроме того, удержал комиссионные в размере 0,6% от
номинала. Оценить доходность этой операции в виде годовой ставки: а) простых,
б) сложных процентов.
Решение:
а) По формуле простых процентов:
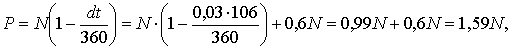
отсюда доходность равна:
-0,37, или - 37%.
б) По формуле сложных процентов:
отсюда доходность равна:
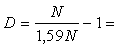- 0,37, или - 37%.
процентная ставка рента сумма
Список
использованной литературы
1.
Капитоненко В.В. Финансовая математика и ее приложения. М., 2009.
.
Кочович Е. Финансовая математика. М., 2004.
.
Малыхин В.И. Финансовая математика. М., 2009.