Расчет вероятности катастрофы и надежности системы энергоснабжения самолета
Департамент
по авиации
Министерства
транспорта и коммуникации Республики Беларусь
Минский
государственный высший авиационный колледж
Кафедра
ЕНД
Контрольная
работа
по
дисциплине: Теория вероятностей и математическая статистика
Специальность:
«Техническая эксплуатация авиационного оборудования (приборное и
электросветотехническое оборудование)»
студента группы
ЗПВ107
Рыжко Дмитрия
Александровича
Минск-2012
г.
Содержание
.
Сравнительный анализ вероятностей катастрофы летательного аппарата
.1
Постановка задачи задания 1
.2
Решение. Математическая часть
.3
Расчетная часть
.
Определение надежности элементов системы энергоснабжения самолета
.1
Постановка задачи задания 2
.2
Решение. Математическая часть
.3
Расчетная часть
Список
использованной литературы
вероятность катастрофа отказ система
надежность
Задание 1. Сравнительный анализ вероятностей
катастрофы летательного аппарата
.1 Задача
Летательный аппарат (ЛА) состоит из:двигателей с
вероятностью отказа P1 , P2 , …, Pm ; дублирующих систем энергоснабжения с
вероятностью отказа
P1э , P2э , …, ;вспомогательных
подсистем с вероятностью отказа PС
;вспомогательных
подсистем с вероятностью отказа PС
каждая.
Катастрофа наступает, если выходят
из строя:
любые (r+1) и более двигателей;
все системы энергоснабжения;
хотя бы одна из N вспомогательных
подсистем.
В случае отказа любого r из m
двигателей катастрофа наступает с вероятностью PD .
Определить вероятность катастрофы ЛА
и сравнить ее с вероятностью катастрофы ЛА без дублирующих систем (один
двигатель с вероятностью катастрофы P1, одна система энергоснабжения с
вероятностью отказа P1э и N вспомогательных подсистем с вероятностью отказа PС
каждая), предполагая, что все упомянутые выше системы и подсистемы ЛА
функционируют независимо друг от друга.
В обоих случаях сравнить вероятности
катастроф, связанных с отказом:
двигателей;
систем энергоснабжения;
вспомогательных подсистем.
Дано
|
m
|
r
|
n
|
N
|
P1
|
P2
|
P3
|
P4
|
PD
|
P1э
|
P2э
|
P3э
|
PС
|
|
4
|
3
|
3
|
2∙103
|
5∙10-4
|
4·10-4
|
6·10-4
|
2∙10-4
|
0,3
|
2∙10-4
|
6·10-3
|
4∙10-4
|
4∙10-9
|
Решение:
Математическая часть
Введем обозначения событий:, D2, D3, D4 - отказ
1-го, 2-го, 3-го и 4-го двигателей соответственно;, B2, B3 - отказ 1-й, 2-й и
3-й системы энергоснабжения соответственно;
Ci - отказ i-й вспомогательной
подсистемы, i = 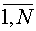 ;
;
ЕК - катастрофа;
ЕKD, ЕKЭ, ЕKC - катастрофы, связанные с отказом
двигателей, систем энергоснабжения и вспомогательных подсистем соответственно.
Вероятность катастрофы ЛА с дублирующими
системами
 . (1.1)
. (1.1)
Перейдем к противоположным событиям
и будем иметь:
 . (1.2)
. (1.2)
Вследствие соотношения
двойственности из равенства (1.2) получим:
 . (1.3)
. (1.3)
Тогда
вероятность катастрофы будет определяться по формуле:
 . (1.4)
. (1.4)
Вследствие независимости событий  из
равенства (1.4) получим:
из
равенства (1.4) получим:

Рассмотрим структуру событий ЕKD, ЕKЭ, ЕKC и
найдем их вероятности катастроф, связанных с отказом:
двигателей ЕKD;
систем энергоснабжения ЕKЭ;
вспомогательных подсистем ЕKC .
Рассмотрим структуру событий ЕKD и найдем P(ЕKD)
= PKD .
Так как событие ЕKD - это событие, состоящее в
том, что катастрофа произошла из-за отказа двигателей, а по условию задачи
катастрофа, связанная с отказом двигателей, наступает, если выходят из строя
любые (r + 1) и более двигателей из m двигателей, а в случае отказа любого r из
m двигателей катастрофа наступает с вероятностью PD .
Значит,
 .
.
Так как в нашем случае число
двигателей m = 4, а r = 3; то
r + 1 = 3 + 1 = 4.
Следовательно,
 ,
,
где ЕKD3 - событие, состоящее в том,
что катастрофа произошла из-за отказа любого r = 3 из m = 4 двигателей;
ЕKD≥4 - событие, состоящее в
том, что катастрофа произошла в
связи с выходом из строя любых (r+1)
= 4 и более двигателей, а в нашем случае ЕKD≥4 = ЕKD4 - это событие,
состоящее в том, что катастрофа произошла из-за отказа всех четырех двигателей.
Из этого следует, что
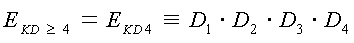 . (1.6)
. (1.6)
В свою очередь, катастрофа, связанная с отказом
r = 3 двигателей (при работающих остальных), не обязательно влечет за собой
катастрофу (а с вероятностью PD), значит,
 , (1.7)
, (1.7)
тогда
 .
.
Так как события ЕKD3 и ЕKD ≥ 4
несовместны, то
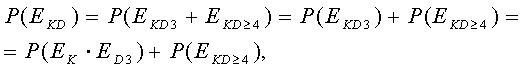
а для нашего случая, учитывая выражение (1.6),
получим:
С другой стороны, катастрофа, связанная с
отказом r = 3 двигателей (при работающих остальных) из четырех имеющихся у ЛА
по условию задачи, есть следующее событие:

 (1.8)
(1.8)
то есть работает только 4-й, либо 3-й, либо 2-й,
либо 1-й двигатель из четырех имеющихся у ЛА.
Доказать, что события EKD3 и ЕKD ≥ 4
несовместны, можно следующим образом:
Согласно равенствам (1.7) и (1.6) имеем:
в соответствии с выражением (1.8) находим далее:

Используя тот факт, что 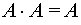 и
и  , получим:
, получим:

Но если произведение двух событий равно
невозможному событию (пустому множеству), то такие события являются
несовместными.
______________________
Примечание -  и
и  -
прерванное и продолженное преобразование текущего выражения.
-
прерванное и продолженное преобразование текущего выражения.
По определению условной вероятности
имеем:
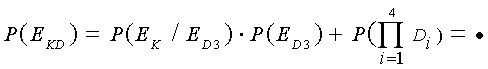
а вследствие независимости событий  далее
находим:
далее
находим:

Используя равенство (1.7) и
несовместимость  его
слагаемых, получим:
его
слагаемых, получим:

Вследствие независимости всех
событий  и так как
и так как  , будем
далее иметь:
, будем
далее иметь:

Так как P (Di) = Pi , i = 1,4 и P (EK / ED3) =
PD , то
Если выполняется условие
 (1.9)
(1.9)
для всех 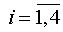 и учитывая,
что значение вероятности случайного события меньше единицы, то
и учитывая,
что значение вероятности случайного события меньше единицы, то
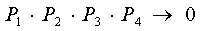 ,
,
а также значит, что
 .
.
Тогда имеем
(1.1(1.10)
Подставив значения, данные из условия задания,
получим:
(1.11)
Рассмотрим структуру событий ЕКЭ и найдем Р(ЕКЭ)
= РКЭ .
ЕКЭ ≡ В1 · В2 · В3 - катастрофа, связанная
с отказом всех трех систем энергоснабжения (n = 3 по условию задачи).
.12)
Подставив значения, данные из условия задания,
получим
|
P(EKЭ)
≡ P(B1 ∙ B2 ∙ B3) = P(B1) ∙ P(B2) ∙ P(B3) = P1Э
∙ P2Э ∙ P3Э = = 2 ∙ 10-4 ∙ 6 ∙ 10-3 ∙ 4 ∙
10-4 = 48 ∙ 10-11
|
(1.13)
|
Рассмотрим структуру событий ЕКС и найдем Р(ЕКС)
= РКС . Событие ЕКС наступает, если отказывает хотя бы одна из вспомогательных
подсистем. Значит,
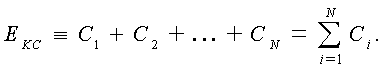
По закону двойственности

Так как события  независимы,
получим:
независимы,
получим:
Поскольку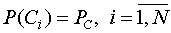 , получим:
, получим:

Тогда

Если выполняется условие:

то
(1.14)
Подставив значения, данные из условия задания,
получим:
 (1.15)
(1.15)
Расчетная часть
Переходим к числовым расчетам. Вычислим
вероятность катастрофы по выведенной нами формуле (1.5). Так как в нашем случае
выполняется условие (1.9), то

Если выполняется условие  и
и  и
и  , то будем
далее иметь
, то будем
далее иметь
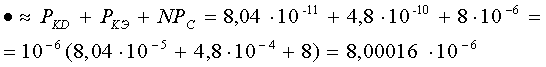
Видно, что PKD ≤ PKЭ ≤PKC,
так как  ≤
≤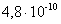 ≤
≤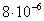 .
.
Из этого следует, что вероятность
катастрофы, связанной с отказом вспомогательных подсистем, является
определяющей.
.2 Вероятность катастрофы ЛА без
дублирующих систем
Вероятность катастрофы ЛА без
дублирующих систем (один двигатель с вероятностью катастрофы  , одна
система энергоснабжения с вероятностью отказа
, одна
система энергоснабжения с вероятностью отказа  и N вспомогательных подсистем с
вероятностью отказа
и N вспомогательных подсистем с
вероятностью отказа  каждая) с
учетом, что все упомянутые выше системы и подсистемы ЛА функционируют
независимо друг от друга, будет определяться по формуле:
каждая) с
учетом, что все упомянутые выше системы и подсистемы ЛА функционируют
независимо друг от друга, будет определяться по формуле:
 (1.16)
(1.16)
где  - вероятность катастрофы ЛА без
дублирующих систем;
- вероятность катастрофы ЛА без
дублирующих систем;
 - вероятность катастрофы, связанной
с отказом двигателя, системы энергоснабжения соответственно в случае без
дублирующих систем.
- вероятность катастрофы, связанной
с отказом двигателя, системы энергоснабжения соответственно в случае без
дублирующих систем.
Исходя из исходных данных будем
иметь:
P’KD = P1 = 5∙10-4 ; P’KЭ = P’1Э = 2∙10-4,
а как уже подсчитано ранее, PKC = 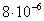 , то,
подставив эти значения в формулу (1.16), получим:
, то,
подставив эти значения в формулу (1.16), получим:
P’(EK)=P’KD+P’KЭ+PKC=P1+P1Э+NPc=5∙10-4+2∙10-4+8
∙10-6=
-4(5+2+8∙10-2)=7,08∙10-4
Так как
 ≫
≫ ,
,
то из этого следует, что вероятность катастрофы,
связанной с отказом двигателя и систем энергоснабжения, является определяющей.
И, наконец, сравним вероятности  и
и  :
:
 ’(EK)/P(EK)= 7,08∙10-4/8.00016∙10-6=88(раз)
’(EK)/P(EK)= 7,08∙10-4/8.00016∙10-6=88(раз)
Вывод
Наиболее вероятной является катастрофа,
связанная с отказом одной из вспомогательных подсистем, а отсутствие дублирующих
систем увеличивает вероятность катастрофы в 88 раз, при этом определяющим
фактором становится отказ двигателя или системы энергоснабжения.
. Определение надежности элементов системы
энергоснабжения самолета
.1 Задача
Испытываются m элементов системы
энергоснабжения самолета, которые работают независимо один от другого.
Длительность времени безотказной работы элементов распределена по
показательному закону с функциями распределения  для каждого из m элементов.
для каждого из m элементов.
Определить вероятность того, что в
интервале (0; 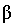 ) часов
откажут:
) часов
откажут:
только один элемент;
только два элемента;
все m элементов;
ни один из m элементов не откажет.
2.2 Типовой пример решения задачи
Дано:
|
Номер
варианта
|
m
|

|
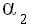
|

|
β
|
|
18
|
3
|
0,37
|
0,47
|
0,17
|
5
|
Решение
Математическая часть
Введем обозначения:
 - события, состоящие в том, что
отказал только один элемент, только два, все три элемента, ни один элемент не
отказал;
- события, состоящие в том, что
отказал только один элемент, только два, все три элемента, ни один элемент не
отказал;
Тогда
 - вероятности безотказной работы
1-го, 2-го, 3-го элемента в заданном интервале (0; 5) соответственно.
- вероятности безотказной работы
1-го, 2-го, 3-го элемента в заданном интервале (0; 5) соответственно.
Так как время безотказной работы
элемента определяется его функцией надежности, которая равна

вероятность безотказной работы i-го
элемента будет

Таким образом, вероятность
безотказной работы 1-го элемента в заданном интервале (0; 5) будет
=e-0,37∙5=e-1,85=0,1572
Вероятность отказа 1-го элемента в
заданном интервале (0; 5) будет
p1=1-q1=1-0,1572=0,8428
_________________________
Примечание - Значения функции у = е-х взяты из
приложения Б.
Вероятность безотказной работы 2-го элемента в
заданном интервале (0; 5) будет
q2=e-0,47∙5=0,09537
Вероятность отказа 2-го элемента в заданном
интервале (0; 5) будет
=1-q2=1-0,09537=0,90463
Вероятность безотказной работы 3-го элемента в
заданном интервале (0; 5) будет
=e-0,17∙5=e-0,85=0,4274
Вероятность отказа 3-го элемента в заданном
интервале (0; 5) будет
=1-q3=1-0,4274= 0,5726
Расчетная часть
Переходим к расчету искомых вероятностей,
которые находятся следующим образом:
Вероятность отказа только одного элемента в
заданном интервале (0; 5) будет
(A1)=p1 ∙ q2 ∙ q3 + p2 ∙ q1 ∙
q3 + p3 ∙ q1 ∙ q2 = 0,8428 ∙ 0,09537 ∙ 0,4274 + 0,90463
∙ 0,1572 ∙ 0,4274 + 0,5726 ∙ 0,1572 ∙ 0,09537 =
0,103717
вероятность отказа только двух элементов в
заданном интервале (0; 5) будет(A2)= p1p2 q3 +p1p3q2 +p2p3q1 = 0,8428 ∙
0,90463 ∙ 0,4274 + 0,8428 ∙ ∙0,5726 ∙ 0,09537 + 0,90463
∙ 0,5726 ∙ 0,1572 = 0,45311
вероятность отказа всех трех элементов в
заданном интервале (0; 5) будет
(A3)=p1p2p3= 0,8428 ∙ 0,90463 ∙
0,5726 = 0,43656
вероятность безотказной работы всех трех
элементов во время испытаний в заданном интервале (0; 5) будет
(A4)=q1∙q2∙q3 = 0,4274 ∙
0,09537 ∙ 0,1572 = 0,0064
Вывод
При заданных данных во время испытаний в
заданном интервале (0; 5) наиболее вероятным является отказ только двух
элементов, а наименее вероятным - отказ всех трех элементов, так как
P(A1) = 0,103717 < P(A3) = 0,43656 < P(A2)
= 0,45311
Вероятность же того, что все три элемента
безотказно отработают во время испытаний в заданном интервале (0; 5) является
небольшой, а именно P(A4) = 0,0064 ≈ 0,006
Список используемой литературы
Н.
Нарольская «Методическое руководство по выполнению курсовой работы»
«Минск-2010».
Л.С.
Барковская «Теория вероятностей : практикум»/ Л.В. Станишевская, Ю.Н
Черторицкий - Минск: БГЭУ, 2004.
А.П.
Рябушко «Индивидуальные задания по высшей математике» Часть4 Минск «Высшая
школа».
1.