Прикладная математика

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ

Институт управления и предпринимательства в социальной сфере

Кафедра прикладной математики

Курсовая работа

по дисциплине "Прикладная математика"

Исполнитель:

Студентка Филиппова А.

Руководитель курсовой работы:

Курочкин АП

Москва

Оглавление

1. Линейная производственная задача

. Двойственная задача

. Задача о "расшивке узких мест производства"

. Транспортная задача линейного программирования

. Динамическое программирование. Распределение капитальных вложений

. Анализ доходности и риска финансовых операций

. Матричная игра как модель конкуренции и сотрудничества

1. Линейная производственная задача

Исходные данные:

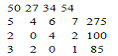
Фирма "Вуаля" может выпускать четыре вида продукции:

Х₁-столы

Х₂-кровати

Х₃-шкафы

Х₄-стулья

Используя для этого три вида материалов

т - пластика

т - фанеры

т - бамбука

Требуется такой план выпуска изделий при котором фирма уложится в имеющиеся ресурсы и при котором суммарная прибыль от реализации изготовленных по плану изделий будет максимальной.

Математическая модель задачи

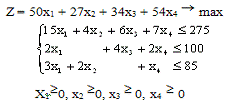
Для ее решения систему неравенств при помощи дополнительных неизвестных х₅, х₆, х₇ заменим системой линейных алгебраических уравнений

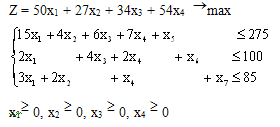
где дополнительные переменные имеют смысл остатков соответствующих ресурсов, а именно

х₅ - остаток ресурса 1-го вида,

х₆ - остаток ресурса 2-го вида,

х₇ - остаток ресурса 3-го вида.

Решаем полученную задачу симплексным методом (методом направленного перебора базисных допустимых решений):

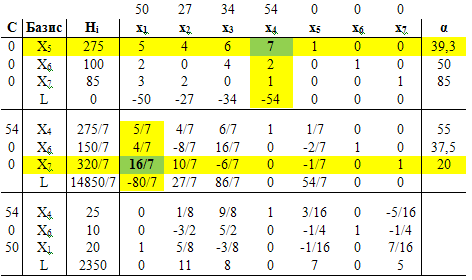
Как видно из последней симплексной таблицы, оптимальная производственная программа имеет вид:

х₁ = 20, х₂ = 0, х₃ = 0, х₄ = 25,

а максимальная прибыль равна: Z_max = 2350

При этом 1-й и 3-й ресурсы будут исчерпаны полностью (х₅=0, х₇=0), а 2-й ресурс будет иметь остаток х₆ = 10 единиц.

При выполнении производственной программы 2-й и 3-ий ресурсы используются полностью, то есть образуют "узкие места производства".

2. Формулировка двойственной линейной задачи и её решение двойственным симплексным методом

Задача линейного оптимального планирования - исходная в своей паре симметричных двойственных задач. Вообще же другая задача в двойственной паре строится так:.

1 каждому неравенству-ограничению исходной задачи ставим в соответствие переменную двойственной задачи (у), принимающую неотрицательные значения;

2 транспонируем матрицу коэффициентов при неизвестных;

3 правые части ограничений заменяем коэффициентами целевой функции;

4 меняем направление неравенств;

5 коэффициенты целевой функции заменяем правыми частями ограничений;

6 то максимизации целевой функции переходим к минимизации.

Обе задачи выглядят так

Симплексная таблица N 3

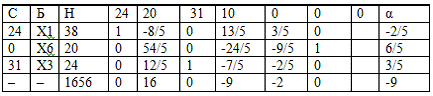
Исходная задача: x1= 38;x2= 0;x3=24;x4=0;x5=0;x6=20;x7= 0;

Двойственная задача: y1=2; y2=0; y3=9 Заметим, что данное решение содержалось в последней строке последней симплексной таблицы исходной задачи. Экстремумы целевых функций исходной и двойственной задач равны 1656.Решение одной из пары двойственных задач можно найти, зная только ответ к другой задаче и пользуясь 2-й теоремой двойственности: если i-е ограничение одной из пары двойственных задач на компонентах оптимального решения есть строгое неравенство, то оптимальное значение i-й переменной другой задачи равно 0, или, что то же самое - если оптимальное значение j-й переменной одной задачи строго положительно, то j-е ограничение другой из пары двойственных задач на компонентах оптимального решения есть равенство.

Экономический смысл полученных результатов.

Смысл двойственных оценок ресурсов у1=2, у2=0, у3=9 показывает, что добавление одной единицы 1-го (2-го;3-го) ресурса обеспечит прирост прибыли на 2 (0, 9) денежных единиц

 

. Задача о "расшивке узких мест производства"

При выполнении оптимальной производственной программ второй и третий ресурсы используются полностью, то есть образуют "узкие места производства". Будем заказывать их дополнительно. T = (t₁, t₂, t₃) - вектор дополнительных объёмов ресурсов.

Итак, необходимо составить план "расшивки узких мест" производства, то есть указать, сколько единиц каждого из дефицитных видов ресурсов должно быть приобретено, чтобы суммарный прирост прибыли был максимальным при условии, что для расчетов используются найденные двойственные оценки ресурсов.

Так как мы используем найденные оценки ресурсов, то должно выполняться условие:

 + Q^-1T ³ 0

Задача состоит в том, чтобы найти вектор Т(t₁;0;t₂), максимизирующий суммарный прирост прибыли W = 7t₁ + 5t₃ при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы).

Обращённый базис Q, соответствующий оптимальной производственной программе, содержатся в последней симплексной таблице в первой, второй, третьей строках восьмого, девятого и десятого столбцов:

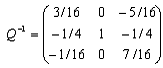
Подставив соответствующие значения, получим требуемую математическую модель:

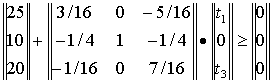
предполагая, что дополнительно можно надеяться получить не более 1/3 первоначального объёма ресурса каждого вида, то есть

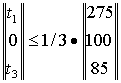
причём по смыслу задачи t₂ ³ 0, t₃ ³ 0. Перепишем неравенства в другом виде. Получим:

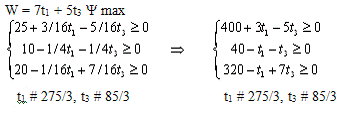
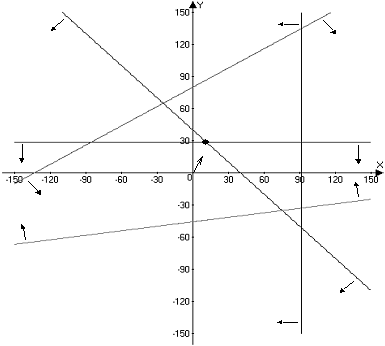
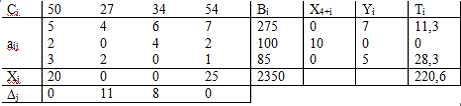
По графику видно, что решение данной задачи находится в точке А(11,3;28,3). Таким образом, программа "Расшивки узких мест производства" имеет вид: t₁=11,3, t₂=0, t₃=28,3 и прирост прибыли составит W = 7*11,3 + 5*28,3 = 220,6

Сводная таблица результатов:

. Транспортная задача линейного программирования

Транспортная задача формулируется следующим образом. Однородный продукт, сосредоточенный в m пунктах производства (хранения) в количествах A=(а1, а2,..., аm) единиц, необходимо распределить между n пунктами потребления, которым необходимо соответственно B=(b1, b2,..., bn) единиц. Стоимость перевозки единицы продукта из i-го пункта отправления в j-ый пункт назначения равна C=|сij| и известна для всех маршрутов. Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.

 матрица транспортных издержек

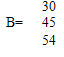 -- вектор объёма ресурсов

A= (24; 20; 31; 40) -- вектор объёма потребления

В нашей задаче 4 потребителя и 3 поставщика, причём суммарный объем поставок равный 129 превышает суммарный объем потребления равный 115. Поэтому для решения задачи ведём дополнительно ещё одного потребителя, с потреблением равным 14.

Имеем:

-тарифная стоимость перевозки 1 единицы груза;

Ĉij-фактическая стоимость перевозки 1 единицы груза;

Dij-условие оптимальности;

рi-платежи за единицу груза в пункте отправления;

pj- платежи за единицу груза в пункте назначения

 + qj = Cij

Для заполненных (базисных)клеток : Ĉij=Cij

Для пустых: Xij=0

опорная=24*1+6*2+14*1+31*3+40*1=183(общая сумма затрат)

Проверка на оптимальность

Т.к. не все Dij £ 0, то мы еще не нашли оптимальное решение.

Далее выбираем пустую клетку таблицы с максимальной переплатой Dij³0.

В ней будет вершина цикла, а остальные должны быть в занятых клетках. Строим следующую таблицу.

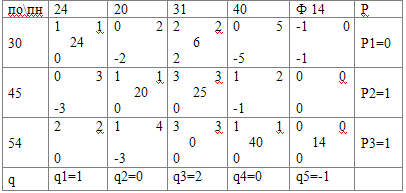
Итак, выполняется условие оптимальности: Dij £ 0, и мы получили оптимальный план затрат.

_оптим.= 24*1+6*2+20*1+25*3+40*1=171

LD=183-171=12

5. Динамическое программирование. Распределение капитальных вложений

Динамическое программирование - это вычислительный метод для решения задач управления определённой структуры. Данная задача с n переменными представляется как много шаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной.

Рассмотрим нелинейную задачу распределения ресурсов между предприятиями отрасли. Предположим, что указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через f_j(x_j) прирост мощности или прибыли на j-том предприятии, если оно получит x_j рублей капвложений. Требуется найти такое распределение (х₁, х₂, ..., х_n) капвложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли

Z=f₁(x₁)+f₂(x₂)+...+f_n(x_n)

при ограничении по общей сумме капвложений

х₁ + х₂ +...+х_n = b

причём будем считать, что все переменные x_j принимают только целые значения x_j =1,2,...

Функции f_j(x_j) мы считаем заданными, заметив, что их определение -довольно трудоёмкая экономическая задача.

Воспользуемся методом динамического программирования для решения этой задачи.

Введём параметр состояния и определим функцию состояния. За параметр состояния x примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния F_k(x) определим как максимальную прибыль на первых k предприятиях, если они вместе получат x рублей. Параметр x может меняться от 0 до b. Если из x рублей k-ое предприятие получит Х_к рублей, то каково бы ни было это значение, остальные x-Х_к рублей естественно распределить между предприятиями от 10-го до (к-1)-го предприятия, чтобы была получен максимальная прибыль F_k-1(x-x_k). Тогда прибыль k предприятий будет равна f_k(x_k) + F_k-1(x-x_k). Надо выбрать такое значение x_k между 0 и x, чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению:

линейный задача программирование матричный

F_k(x) = max {f_k(x_k) + F_k-1(x-x_k)}

£ X £ x

для k=2,3,....,n .Если же k=1 ,то

F₁(x)=f₁(x).

Рассмотрим конкретный пример. Пусть производственное объединение состоит из 4-х предприятий (k=4).Общая сумма капвложений равна 700 тыс. рублей (b=700) , выделяемые предприятиям суммы кратны 100 тыс. рублей.

Значения функций f_j(x_j) приведены в табл. 1.

Прежде всего заполняем табл.3. Значения f₂(x₂) складываем со значениями F₁(x-x₂)=f₁(x-x₂) и на каждой побочной диагонали находим наибольшее число, которое помечаем звёздочкой. Заполняем табл .3.

Продолжая процесс табулируем функции F₃(x), x₃(x) и т.д. В табл.6 заполняем только одну диагональ для значения x=700.

Таблица 1.

Xj	0	100	200	300	400	500	600	700
f1(xj)	0	75	90	100	108	113	115	117
f2(xj)	0	85	100	111	118	124	129	132
f3(xj)	0	42	58	71	80	89	95	100
f4(xj)	0	28	45	66	78	90	102	113

Таблица 2.

	x-х2	0	100	200	300	400	500	600	700
х2		0	75	90	100	108	113	115	117
0	0	0	75	90	100	108	113	115	117
100	85	85*	160*	175	185	193	198	200	---
200	100	100	175*	190*	200	208	213	---	---
300	111	111	186	201*	211*	219*	---	---	---
400	118	118	193	208	218	---	---	---	---
500	124	124	199	214	---	---	---	---	---
600	129	129	204	---	---	---	---	---	---
700	132	132	---	---	---	---	---	---	---

Таблица 3.

x	0	100	200	300	400	500	600	700
F2(x)	0	85	160	175	190	201	211	219
x2(x)	0	100	100	200	200	300	300	300

Таблица 4.

	x-x3	0	100	200	300	400	500	600	700
x3		0	85	160	175	190	201	211	219
0	0	0	85*	160*	175	190	201	211	219
100	42	42	127	202*	117	232	243	253	---
200	58	58	143	218*	233*	248*	259	---	---
300	71	71	156	231	246	261*	---	---
400	80	80	165	240	255	---	---	---	---
500	89	89	174	249	---	---	---	---	---
600	95	95	180	---	---	---	---	---	---
700	100	100	---	---	---	---	---	---	---

Таблица 5.

x	0	100	200	300	400	500	600	700
F3(x)	0	85	160	202	218	233	248	261
x3(x)	0	0	0	100	200	200	200	300

Таблица 6.

	x-x4	0	100	200	300	400	500	600	700
x4		0	85	160	202	218	233	248	261
0	0	0	85	160	202	218	233	248	261
100	28	28						276
200	45	45					278
300	66	66				284*
400	78	78			280
500	90	90		250
600	102	102	187
700	113	113

Наибольшее число диагонали в табл.6 :

Z_max = 284 тыс. рублей

X4* = 3003*+X2*+X1*=700-300=400

В табл.5:

где сумма равна 400

Х3* = 200

Х1*+Х2*=400-200=200

В табл.3.

где сумма равна 200

Х2*=100

Х1*=100

Оптимальная программа: 1) Х1*=100; Х2*=100;

Х3*=200 ; Х4*=300_max(X1*;... X4*)=284

6. Анализ доходности и риска финансовых операций

 

Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками. Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию). Существует несколько разных способов оценки операции с точки зрения ее доходности и риска. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.

Средний ожидаемый доход: Ǭ = Σq_ip_i

Среднее квадратическое отклонение r=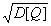

Дисперсия: D[Q] = M[Q²]- Ǭ²

Даны четыре операции Q1, Q2, Q3, Q4. Найдём средние ожидаемые доходы и риски ri операций. Нанесём точки (Ǭ_i, r_i) на плоскость, найдём операции, оптимальные по Парето. С помощью взвешивающей формулы φ(Q)=2Q-r найдём лучшую и худшую операции.

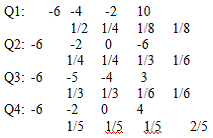
Нанесем средние ожидаемые доходы и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):

 

Получили 4 точки. Чем правее точка (Ǭ, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (Ǭ’, r') доминирует точку (Ǭ, r) если Ǭ'³ Ǭ и r’£ r. В нашем случае 2-я операция доминирует 1-ю и 3-ю, 4-я доминирует 1-ю. Но 2-я и 4-я операции между собой не сравнимы.

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (Ǭ, r) дает одно число, по которому и определяют лучшую операцию. Воспользуемся формулой φ(Q)=2Q-r . Тогда получаем:

 

φ(Q1)= 2*(-3)-5,1 = -11,1; φ(Q2)= 2*(-3)-2,64=-8,64; φ(Q3)= 2*(-3,83)-3,13=-10,79;

φ(Q4)= -3,79

 

Видно, что 4-я операция - лучшая, а 1-я - худшая.

7. Матричная игра как модель конкуренции и сотрудничества

Первый и Второй игроки играют в матричную игру с матрицей А = (a_ij). Стратегия первого есть P, а стратегия второго - Q.

В нашем случае имеем:

Седловой точки нет, что легко видеть:

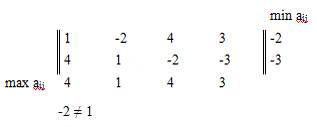
Для начала необходимо свести нашу игру (2*4) к игре 2*2. Для этого необходимо графическое решение.

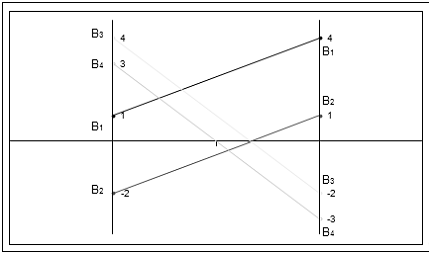
Отсюда видно, что данная матричная игра сводится к следующему варианту:

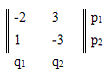
Имеем

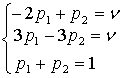
Понятно, что p₁ = 1 - p₂. Отсюда

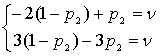
+ 2p₂ + p₂ = 3 - 3p₂ - 3p₂

+ 3p₂ = 3 - 6p₂

p₂ = 5 => p₂ = 5/9, p₁ = 4/9

Аналогично с q₁ и q₂. Получаем q₁ = 2/3, q₂ = 1/3

Пару оптимальных стратегий для каждого из игроков:

P* = (4/9, 5/9)* = (2/3, 1/3)

Рассчитаем цену игры υ, получаем:

υ = -2 * 4/9 + 1 * 1/5 = -8/9 + 5/9 = -3/9 = -1/3

Цена игры есть математическое ожидание случайной величины W(P,Q), а, учитывая, что выигрыш одного есть проигрыш другого, имеем:

υ = m₁ = m₂

Рассчитаем риски игры r для Первого и Второго игроков:

= δ = √D, D(x) = M(x²) - M²(x)₁ = 4 * 4/9 + 5/9 - (-1/3)2 = 16/9 + 5/9 - 1/9 = 20/9

δ₁ = √20/9 = 2√5/3 . 1,5

r₁ = δ₁ = 1,5

D₂ = 9 * 4/5 + 9 * 5/9 -1/9 = 4 + 5 - 1/9 = 80/9

δ ₂ = √80/9 = 4√5/3 . 3

r ₂ = δ₂ = 3

Рассчитаем среднюю дисперсию и риск:

 = 4 * 4/9 * 2/3 + 5/9*2/3 + 9 * 4/9 * 1/3 + 9 * 5/9 * 1/3 - (-1/3)2 = 32/27 + +10/27 + 36/27 + 45/27 - 1/9 = 120/27 = 40/9

δ = √40/9 = 2√10/3 . 2,1

R = δ = 2,1