Обработка экспериментальных данных методами математической статистики
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ
АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное
образовательное учреждение
Высшего
и профессионального образования
«МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
пищевых
производств»
Зачётная
работа по теме
«Обработка
экспериментальных данных
методами
математической статистики»
Вариант
№
Работу выполнил:
студент группы
10-ТПМ-14
Работу проверил:
Галушкина Ю.И.
Москва
2012
Обработать эти данные методом математической
статистики
|
X
|
Y
|
X
|
Y
|
X
|
Y
|
X
|
Y
|
|
75
|
|
65
|
|
63
|
|
65
|
|
|
68
|
|
78
|
|
69
|
|
61
|
|
|
65
|
|
66
|
|
59
|
|
63
|
|
|
80
|
|
64
|
|
71
|
|
76
|
|
|
71
|
|
70
|
|
55
|
|
74
|
|
|
61
|
|
67
|
|
64
|
|
52
|
|
|
77
|
|
66
|
|
58
|
|
61
|
|
|
69
|
|
67
|
|
70
|
|
63
|
|
|
64
|
|
71
|
|
83
|
|
49
|
|
|
68
|
|
62
|
|
56
|
|
71
|
|
|
52
|
|
70
|
|
68
|
|
77
|
|
|
59
|
|
55
|
|
71
|
|
73
|
|
|
63
|
|
69
|
|
76
|
|
74
|
|
|
56
|
|
59
|
|
77
|
|
70
|
|
|
62
|
|
67
|
|
73
|
|
65
|
|
Задача 1. Обработка
одномерной выборки признака Х методами математического статистического анализа
1. n
=;
xнм =;
xнб
=;
hx
=
Вариационный ряд
. Число интервалов 
Тогда длина интервала 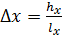 =
=
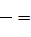
Статистический ряд
|
№
|
Интервалы
xi
 xi+1 xi+1
|
Середины
x̅i
|
Частота mi
|
Относительная
частота pi*=
|
Кумулятивная
частота F*n
(x)
|
|
1
|
49-54
|
51,5
|
3
|
0,05
|
0,05
|
|
2
|
54-59
|
56,5
|
8
|
0,133
|
0,183
|
|
3
|
59-64
|
61,5
|
12
|
0,2
|
0,383
|
|
4
|
64-69
|
66,5
|
15
|
0,25
|
0,633
|
|
5
|
69-74
|
71,5
|
13
|
0,217
|
0,85
|
|
6
|
74-79
|
76,5
|
7
|
0,117
|
0,967
|
|
7
|
79-84
|
81,5
|
2
|
0,033
|
1
|
|
8
|
|
|
|
|
|
|
Σ
|
|
|
|
|
|



3. Оценки числовых характеристик.
|
№
|
Интервалы
xi - xi+1
|
Середина
͡xi
|
pi*
|
F*n
(x)
|
͡xi
 pi* pi*
|
͡xi
- x̅i
|
(͡xi
- x̅i)2 pi* pi*
|
(͡xi
- x̅i)3 pi* pi*
|
(͡xi
- x̅i)4 pi* pi*
|
|
1
|
49-54
|
51,5
|
0,05
|
0,05
|
2,575
|
-14,67
|
10,7604
|
-157,8557
|
2315,7435
|
|
2
|
54-59
|
56,5
|
0,133
|
0,183
|
7,515
|
-9,67
|
12,4367
|
-120,2627
|
1162,9406
|
|
3
|
59-64
|
61,5
|
0,2
|
0,383
|
12,300
|
-4,67
|
4,3618
|
-20,3695
|
95,1256
|
|
4
|
64-69
|
66,5
|
0,25
|
0,633
|
16,625
|
0,33
|
0,0272
|
0,0090
|
0,0030
|
|
5
|
69-74
|
71,5
|
0,217
|
0,85
|
15,516
|
5,33
|
6,1647
|
32,8580
|
175,1332
|
|
6
|
74-79
|
76,5
|
0,117
|
0,967
|
8,951
|
10,33
|
12,4849
|
128,9694
|
1332,2544
|
|
7
|
79-84
|
81,5
|
0,033
|
1
|
2,690
|
15,33
|
7,7553
|
118,8887
|
1822,5630
|
|
8
|
|
|
|
|
|
|
|
|
|
|
Σ
|
|
|
|
|
66,170
|
|
53,9911
|
-17,7629
|
6903,7634
|
x̅
= Σi
͡xi pi*
= 66,170
Mo=64 +5 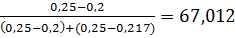
Me =
S2 =
Σ
(͡xi - x̅i)2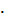 pi*
= 53,9911
pi*
= 53,9911
S=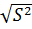 =
=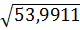 =
7,3479
=
7,3479
V= 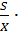 100% =
100% = 100%=11,1046%
100%=11,1046%
A= =
=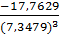 =-0,0448=
=-0,0448= 3=
3= 3= -0,6317
3= -0,6317
Поправки Шеппарда
S2 =
Σ
(͡xi - x̅i)2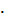 pi*
-
pi*
-  53,9911-2,0833=51,9078
53,9911-2,0833=51,9078
Sx=7,2047
V= 100% = 10,8882%
100% = 10,8882%
A= =-0,0475
=-0,0475
E= 3=-0,4727
3=-0,4727
Выводы: 1. x̅
, Mo , Me
- принадлежат одному интервалу;
. Интервал (x̅
- 3S; x̅
+3S) () содержит выборку;
3. А= длинная часть лежит от
центра;
. Е=, распределение имеет в
окрестности центра более вершину.
Для сравнения гистограммы и кривой
нормального распределения заполним следующую таблицу:
|
№
|
Интервалы
|
Середины
x̅i
|
pi*
|
Нормированные середины
|
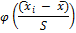
|

|
|
1
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
Σ
|
|
|
|
|
|
|
Здесь нормированные середины:
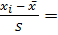 ,
, 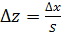 =
=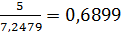

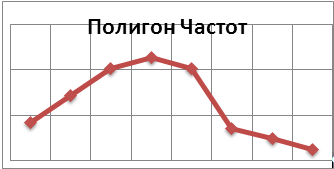
На графике представлена гистограмма
статистического ряда, а также подобная теоретическая кривая нормального
распределения. Можно видеть, что теоретическая кривая отличается от
эмпирического распределения
. Выдвигаем гипотезу о том, что выборка
извлечена из нормальной генеральной совокупности, где за неизвестные параметры
распределения α и σ
принимаются соответственно их числовые оценки x̅
= и S=, и проверим эту гипотезу с помощью критерия Колмогорова-Смирнова
(К-С) и критерия Пирсона, с уровнем значимости α=0,1;
0,05.
Проверка гипотезы с помощью критерия
Колмогорова-Смирнова.
Функция K(λ)=1-
α=1-0,1=0,9λ1=1,23;
K(λ)=1-
α=1-0,05=0,95λ2=1,36;
Dкр=
 Dкр=
Dкр= =0,1587
=0,1587
Dкр=
 Dкр=
Dкр= =0,1754
=0,1754
Таблица для расчёта Dэм
|
№
|
Середины
интервалов ͡xi
|
Кумулятивн-ая
частота F*n
(x)
|
Нормирован-ные середины 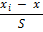
|

|
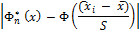
|
|
1
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
8
|
|
|
|
|
|
Dэм=0,1219
Вывод т.е. Dэм
Dкр,
следовательно, выдвинутая гипотеза о нормальном распределении с уровнем
значимости α=0,1 и с уровнем
значимости α=0,05.
Проверка гипотезы с помощью критерия
Пирсона
χ2кр=7,8
при α=0,1;
χ2кр=9,5
при α=0,05;
k=7-2-1=4
Таблица для расчёта χ2эм
|
№
|
Интервалы
xi
 xi+1 xi+1
|
Частота
mi
|
pi =P(xi<X<xi+1)
|
npi
|
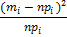
|
|
1
|
|
|
0,0399
|
|
|
|
2
|
|
|
0,177
|
|
|
|
3
|
|
|
0,2186
|
|
|
|
4
|
|
|
0,2696
|
|
|
|
5
|
|
|
0,206
|
|
|
|
6
|
|
|
0,1022
|
|
|
|
7
|
|
|
0,0328
|
|
|
|
8
|
|
|
|
|
|
|
Σ
|
|
|
|
|
|
p1
= P(49<x
<54) = Ф(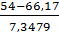 )-Ф(
)-Ф(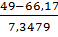 )=Ф(-1,65)-Ф(-2,34)=0,0495-0,0096=0,0399
)=Ф(-1,65)-Ф(-2,34)=0,0495-0,0096=0,0399
p2
= P(54<x
<59) = Ф(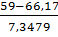 )-Ф(
)-Ф(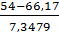 )=Ф(-0,98)-Ф(-1,65)=0,1635-0,0465=0,177
)=Ф(-0,98)-Ф(-1,65)=0,1635-0,0465=0,177
p3
= P(59<x
<64) = Ф( )-Ф(
)-Ф(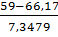 )=Ф(-0,3)-Ф(-0,98)=0,3821-0,1635=0,2186
)=Ф(-0,3)-Ф(-0,98)=0,3821-0,1635=0,2186
p4
= P(64<x
<69) = Ф(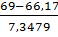 )-Ф(
)-Ф( )=Ф(0,39)-Ф(-0,3)=0,6517-0,3821=0,2696
)=Ф(0,39)-Ф(-0,3)=0,6517-0,3821=0,2696
p5
= P(69<x
<74) = Ф( )-Ф(
)-Ф(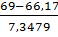 )=Ф(1,07)-Ф(0,39)=0,8577-0,6517=0,206
)=Ф(1,07)-Ф(0,39)=0,8577-0,6517=0,206
p6
= P(74<x
<79) = Ф( )-Ф(
)-Ф( )=Ф(1,75)-Ф(1,07)=0,9599-0,8577=0,1022
)=Ф(1,75)-Ф(1,07)=0,9599-0,8577=0,1022
p7
= P(79<x
<84) = Ф( )-Ф(
)-Ф( )=Ф(2,43)-Ф(1,75)=0,9927-0,9599=0,0328
)=Ф(2,43)-Ф(1,75)=0,9927-0,9599=0,0328
χ2эм=1,1367
Вывод. т.е.
χ2эм
χ2кр,
и при α=0,1
, и
при α=0,05
выдвигаемая
гипотеза с уровнем значимости α=0,1 и
с уровнем значимости α=0,05.
5. Считая, что выборка извлечена из нормальной
генеральной совокупности, построим доверительные интервалы, накрывающее
неизвестное математическое ожидание с доверительными вероятностями 0,9; 0,95;
0,99. Строим доверительные интервалы
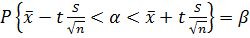 ,
,
для 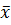 =66,17; S=7,3479;
=66,17; S=7,3479; =7,746
=7,746
|
№
|
β
|
α
|
t
|
Левая граница
|
Правая граница
|
Длина интервала
|
0,9
|
0,1
|
1,67
|
64,5859
|
66,75
|
2,1641
|
|
2
|
0,95
|
0,05
|
2,00
|
64,2728
|
68,0672
|
3,7944
|
|
3
|
0,99
|
0,01
|
2,66
|
63,6467
|
68,6933
|
5,0466
|
 0,9;
0,9;
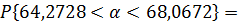 0,95;
0,95;
 0,99
0,99
С увеличением доверительно вероятности
последовательно 0,9; 0,95; 0,99 ширина доверительного интервала увеличивается
соответственно
Задача 2. Обработка
одномерной выборки признака Y
методами
статистического анализа
1. n
=;
yнм =;
yнб
=;
hy=.
Вариационный ряд
2. Число интервалов ly=lx-1= ,увеличим
размах варьирования, отодвинув yнб
до.
статистический пирсон регрессия корреляция
Тогда длина интервала 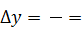
Статистический ряд
|
№
|
Интервалы
yj
 yj+1 yj+1
|
Середины ͡yj
|
Частота
mj
|
Относительная
частота pj*=
|
͡yj
 pj* pj*
|
͡yj
-͞͞
y
|
(͡yj
-͞͞y)2 pj* pj*
|
|
1
|
71-77
|
74
|
7
|
0,117
|
8,633
|
-15,000
|
26,250
|
|
2
|
77-83
|
80
|
8
|
0,133
|
10,667
|
-9,000
|
10,800
|
|
3
|
83-89
|
86
|
12
|
0,200
|
17,200
|
-3,000
|
1,800
|
|
4
|
89-95
|
92
|
19
|
0,317
|
29,133
|
3,000
|
2,850
|
|
5
|
95-101
|
98
|
9
|
0,150
|
14,700
|
9,000
|
12,150
|
|
6
|
101-107
|
104
|
5
|
0,083
|
8,667
|
15,000
|
18,750
|
|
7
|
|
|
|
|
|
|
|
|
Σ
|
|
|
60
|
1,000
|
89,000
|
|
72,600
|
͞͞͞y=
Σi ͡yi
pi* =89,00
Sy2 =
Σ
(͡yi - ͞͞͞yi)2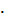 pi*
=72,600
pi*
=72,600
Sy= =8,5206
=8,5206
Задача 3. Обработка двумерной выборки (X,Y) методами
корреляционного и регрессионного анализов
. Корреляционное поле

По расположению точек на корреляционном поле
можно сделать вывод о наличии положительной корреляционной зависимости.
. Корреляционная таблица
|
|
xi-xi+1
|
49-54
|
54-59
|
59-64
|
64-69
|
69-74
|
74-79
|
79-84
|
|
mj
|
|
yj-yj+1
|
͡xi
͡yj
|
51,5
|
56,5
|
61,5
|
66,5
|
71,5
|
76,5
|
81,5
|
|
|
|
71-77
|
74
|
|
1
|
1
|
1
|
4
|
|
|
|
7
|
|
77-83
|
80
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
|
8
|
|
83-89
|
86
|
1
|
1
|
1
|
5
|
3
|
1
|
|
|
12
|
|
89-95
|
92
|
1
|
3
|
5
|
4
|
3
|
2
|
1
|
|
19
|
|
95-101
|
88
|
|
|
3
|
3
|
2
|
1
|
|
|
9
|
|
101-107
|
104
|
|
1
|
1
|
1
|
|
2
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
mi
|
3
|
8
|
12
|
15
|
13
|
7
|
2
|
|
60
|
По заполненным клеточкам корреляционной таблицы,
делаем вывод о наличии положительной зависимости между случайными величинами X
и
Y.
3. Вычисление выборочного коэффициента
корреляции.
x̅=66,17 Sx=7,3479
͞͞͞y=
89,00 Sy= 8,5206
Для вычисления выборочного
корреляционного момента Kxy используем формулу 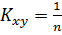 Σ Σ (͡xi-
͞x)
Σ Σ (͡xi-
͞x)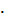 (͡yj
-͞yj)
(͡yj
-͞yj)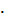 mij
и заполним следующую расчётную таблицу:
mij
и заполним следующую расчётную таблицу:
Kxy= =
=
rxy=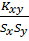 =
=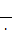 =
=
По шкале Чеддока делаем вывод:
корреляционная зависимость между случайными величинами X
и
Y
4. Проверка гипотезы значимости
Выдвигаем гипотезу о независимости случайных
величин и проверим эту гипотезу с помощью критерия
Пирсона, выбрав уровень значимости α=0,1;
К= (ly-1)
(lx-1)
= 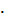 =
=
χ2кр=
Таблица для расчета χ2эм
χ2эм=
Так как χ2эм
χ2кр,
то гипотеза о независимости случайных величин с заданным уровнем значимости α=0,1.
Регрессионный анализ
1. Фиксируем ͡xi
и
найдем соответствующие средние арифметические
͡yj=
Построим диаграмму рассеивания, нанося на
плоскость XY точки с
координатами (͡xi
;
͞͞͞yi)

Фиксируем ͡yj
и
найдем соответствующие средние арифметические
͡xi=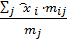 .
.
Построим диаграмму рассеивания, нанося на
плоскость XY точки с
координатами ( ͞͞͞xj
; ͡yj)

. Составим линейную эмпирическую регрессию:
y(x)=a0+a1x;
x(y)=b0+b1y.
Коэффициенты регрессии a0;
a1
и b0;
b1оценим
с помощью метода наименьших квадратов.
y(x)=a0+a1x
Нормальная система метода наименьших квадратов

Расчётная таблица
|
№
|
͡xi
|
͞͞͞yi
|
͡xi
2
|
͡xi ͞͞͞yi ͞͞͞yi
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
6
|
|
|
|
|
|
7
|
|
|
|
|
|
8
|
|
|
|
|
|
Σ
|
|
|
|
|
 a0=;
a1=
a0=;
a1=
y(x)=
+x
x(y)=b0+b1y
Нормальная система метода наименьших квадратов
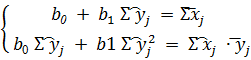
Расчётная таблица
|
№
|
͡yj
|
͞xj
|
͡yj
2
|
͡yj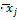
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
6
|
|
|
|
|
|
7
|
|
|
|
|
|
Σ
|
|
|
|
|
 b0
= ; b1
=
b0
= ; b1
=
x(y)=
+y
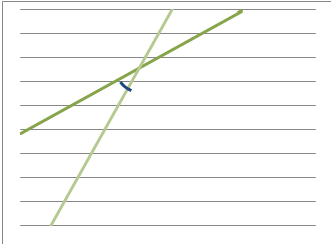
По графику линий регрессий x(y)
и y(x)
делаем вывод о наличии положительной корреляционной зависимости.
. Проверим адекватность линейной регрессии
y(x)=
+x
Для этого составим с помощью метода наименьших
квадратов полулогарифмическую модель эмпирической регрессии:
y(x)=a0+a1lg
x.
Нормальная система метода наименьших квадратов
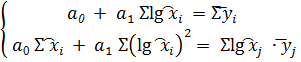
Расчётная таблица
|
№
|
͡xi
|
lg ͡xi
|
(lg ͡xi)2
|
͞͞͞yi
|
͞͞͞yi lg ͡xi
lg ͡xi
|
|
1
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
Σ
|
|
|
|
|
|
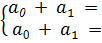 a0
=; a1
=
a0
=; a1
=
y(x)=
+lgx
Составим таблицу
|
№
|
yi
|
xi
|
y(x)=
|
|
|
|
y(xi)
|

|
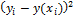
|
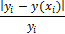
|
|
1
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
Σ
|
|
|
|
|
|
|
Делаем выводы
|
Модель
функции
|
Остаточная
дисперсия 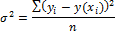
|
Средняя
ошибка аппроксимации 
|
|
y(x)=
|

|
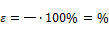
|
|
y(x)=
|

|
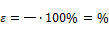
|
Наиболее адекватная модель эмпирической
регрессии
y(x)=
+lgx
4. Найдем выборочные корреляционные отношения
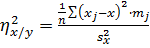
͞x =;
 ()2;
n =
()2;
n =
|
№
|
͞xj
|
mj
|

|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
Σ
|
|
|
|
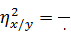 =
=
͞͞͞y
=; Sy2
= ()2 =; n =
|
№
|
͞͞͞yi
|
mi
|
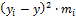
|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
|
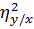 =
=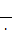 =
=
r2xy=()2 =;
 - =
- =
 -
=
-
=
Разность 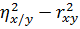 свидетельствует о линейной регрессии.
свидетельствует о линейной регрессии.
Разность 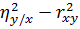 свидетельствует о линейной регрессии.
свидетельствует о линейной регрессии.