Анализ электромеханической следящей системы с учетом уточненной модели электродвигателя

Анализ электромеханической следящей системы с учетом уточненной модели электродвигателя

Введение

электромеханический следящий передаточный

Целью данного курсового проекта является проведение анализа электромеханической следящей системы с учетом уточненной модели электродвигателя. Необходимо написать уравнения, передаточные функции элементов, составить структурную схему, определить передаточные функции разомкнутой, замкнутой систем и передаточную функцию по ошибке. Также нужно построить частотные характеристики АЧХ, ФЧХ, ЛАЧХ, ЛФЧХ разомкнутой системы и исследовать систему на устойчивость.

Курсовой проект выполнен в рамках заключительной работы по изучению дисциплины ОТУ.

Анализ следящей системы

Данный анализ следящей системы служит примером для выполнения задания, варианты которого приведены в пункте 2.

Следящая система на рисунке 1 представляет собой простейшую следящую систему, задачей которой является обеспечить равенство входной и выходной величин. Подобная система используется, например, для управления положением антенны радиолокационной станции. Входной (задающей) величиной служит угол поворота Пз движка задающего потенциометра, который связан с органом управления, например с рукояткой, на пульте управления радиолокационной станции. Выходной (регулируемой) величиной является угловое положение Пт объекта управления (антенны радиолокационной станции).

САУ работает следующим образом. Чувствительный элемент состоит из задающего (Пз) и принимающего (Пт) потенциометров. Принимающий потенциометр жестко связан с валом объекта управления ОУ (конструктивно он установлен в редукторе). При наличии разности угловых положений движков задающего и принимающего потенциометров с чувствительного элемента ЧЭ на электромагнитный усилитель ЭМУ поступает разность напряжений DU. Разность D U будем называть рассогласованием. Усилитель служит для обеспечения требуемой мощности сигнала. Напряжение U с ЭМУ подается на электродвигатель постоянного тока Д, вал которого через редуктор Р связан с ОУ. ОУ будет поворачиваться до тех пор, пока рассогласование не примет нулевое значение. При достижении объектом управления заданного угла, т.е. Пт = Пз, рассогласование будет равно нулю, следовательно, DU =U=0 и двигатель остановится. Таким образом, объект управления стремится принять положение, согласованное с положением рукоятки управления. Связь элементов системы между собой отраженна на рисунке 2. Значения параметров элементов системы приведены в таблице 1.

Рисунок 1 - Следящая система

Рисунок 2 - Блок схема следящей системы

Таблица 1 - Исходные данные

Передаточные функции звеньев и САУ. Структурная схема

Уравнения элементов системы имеет вид:

Электромагнитный усилитель:

Из уравнения элемента

Tу + U(t) = kу ∆U(t),

∆U(t) = Uз(t) - UТ(t),

получаем передаточную функцию

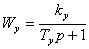
Электродвигатель:

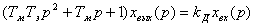
получим передаточную функцию

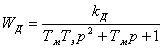
Редуктор:

передаточная функция

Задающий и принимающий потенциометры:

,

,

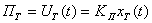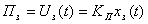Передаточные функции

Структурная схема будет выглядеть следующим образом:

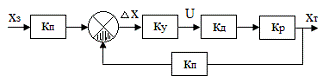
Рисунок 3 - Структурная схема

Проведем преобразования структурной схемы. Перенесем элемент сравнения с правой стороны задающего потенциометра (Пз) в левую, добавив (по правилу) в цепь обратной связи звено с передаточной функцией 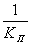 получим:

Рисунок 4 - Преобразованная схема

Объединим последовательно соединенные звенья в эквивалентное звено:

Рисунок 5 - Звено, эквивалентное структурной схеме

Передаточная функция разомкнутой системы рассчитывается по формуле:

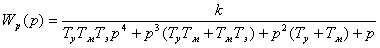
При условии, что k=k_уk_пk_дk_р

В общем виде:

, , , , , , .

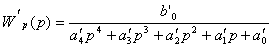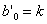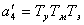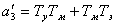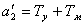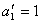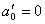Передаточная функция замкнутой системы:

, , , , ,

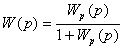
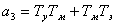Передаточная функция по ошибке:

Построение частотных функций

Аналитические выражения для частотных характеристик замкнутой системы получают из комплексной передаточной функции :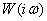

АЧХ - модуль комплексной передаточной функции: ,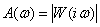

ФЧХ - аргумент комплексной передаточной функции: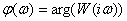

Комплексная передаточная функция разомкнутой системы в общем виде

,

Одним из возможных путей получения функций АЧХ и ФЧХ является следующий:

Обозначим:

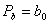- действительная часть числителя,

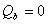- мнимая часть числителя,

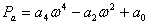- действительная часть знаменателя,

- мнимая часть знаменателя.

Тогда получим

Для того чтобы избавиться от мнимой единицы в знаменателе умножим выражение на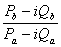

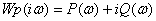
и получим

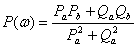
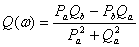
Амплитуда - модуль комплексной передаточной функции

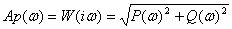
Фаза - аргумент комплексной передаточной функции

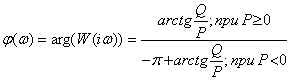
По полученным формулам рассчитаем P_a(ω), P_b(ω), Q_a(ω), Q_b(ω), P(ω), Q(ω), A(ω), 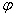(ω)при изменении ω от 1 до 16, занесем данные в таблицу 2 и построим зависимости A(ω) и 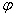(ω)(если фаза получается положительной, на графике откладываем 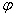 (ω) = -2π). Диапазон изменения частоты выбирается таким, чтобы показать все особенности частотных характеристик.

Расчетные данные для частотных характеристик:

Таблица 2 - Расчетные данные для частотных характеристик

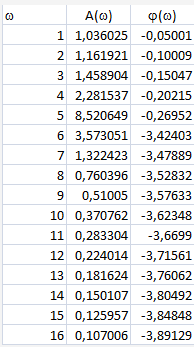
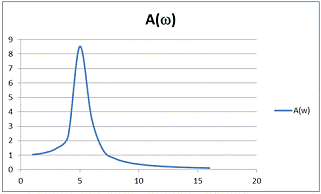
Рисунок 6 - АЧХ замкнутой системы

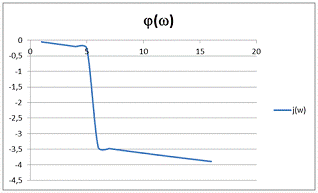
Рисунок 7 - ФЧХ замкнутой системы

Аналогично построим логарифмические частотные характеристики (ЛАЧХ и ЛФЧХ) разомкнутой системы. ЛАЧХ равна (преобразование выражений для L_p(ω) и 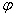_p(ω) и расчетные данные опущены для краткости изложения)

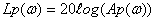
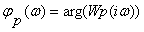
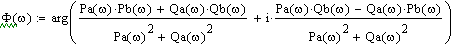
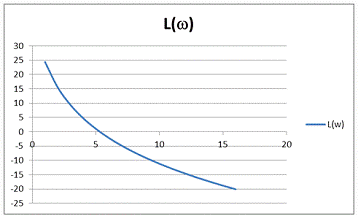
Рисунок 8 - ЛАЧХ для разомкнутой системы

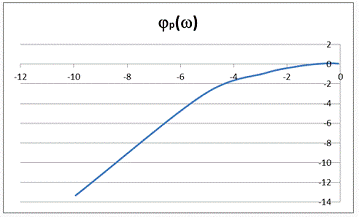
Рисунок 9 - ЛФЧХ для разомкнутой системы

Исследование системы на устойчивость

Критерий Гурвица

Составим определитель Гурвица в общем виде

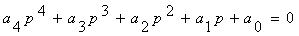
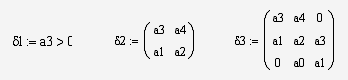
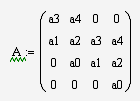
Подставим значения коэффициентов (см. передаточную функцию замкнутой системы), получим определители Гурвица

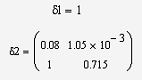
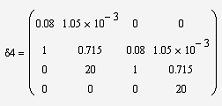
Вывод: так как не все определители Гурвица больше 0, то система не устойчива.

Критерий Михайлова

Годограф Михайлова - кривая, описываемая характеристическим вектором на комплексной плоскости. Характеристический вектор получим, подставив p=iω в характеристический полином (знаменатель передаточной функции замкнутой системы).

 ,

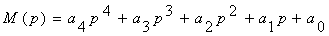
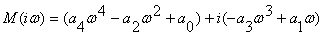
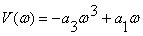
Система четвертого порядка

Изменяя частоту в диапазоне ω=0..60 с - 1 построим кривую Михайлова (рисунок 6)

Вывод: так как характеристический вектор описывает угол 4 π/2, т.е. последовательно проходит первый, второй, третий и четвертый квадранты (уходит в бесконечность в четвертом квадранте) и порядок системы равен четырем, то система устойчива.

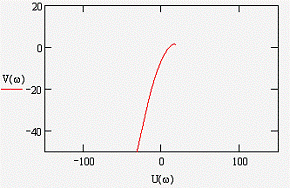
Рисунок 10 - Кривая Михайлова

Критерий Найквиста

Откладываем значение комплексной передаточной функции разомкнутой системы W_p(iω) на комплексной плоскости при изменении частоты ω=40..500 с - 1, получим амплитудно-фазовую характеристику (АФХ) разомкнутой системы.

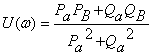
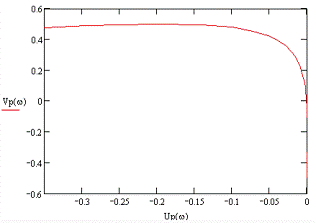
Рисунок 11 - АФХ разомкнутой системы

Вывод: система устойчива, т.к. кривая Найквиста охватывает точку с координатами (-1;0).

Определим запасы устойчивости графически по ЛЧХ разомкнутой системы (см. график «ЛЧХ разомкнутой системы»).

Запасы устойчивости: по фазе Фзап = 19.2⁰, по амплитуде Lзап = 12.5 дБ.

Можно найти запасы устойчивости без построения ЛЧХ разомкнутой системы, если есть выражения для функции Lp(ω) и Фp(ω).

Находим ωС и ωП из уравнений Lp(ωС) = 0 и Фp(ωП) = -π.

20 log (Ap(ωC)) = 0

Arg(Wp(iω)) = - π.

Решение этих двух уравнений: ωС = 21.2 с-1, ωП = 44.8 с-1

Тогда запасы устойчивости определяются из выражений

Lзап = -L(ωП) = 12.5 дБ;

Фзап = Ф(ωС)+ π = 0.335 рад = 19.2⁰.

Вывод: запас устойчивости по фазе недостаточен (рекомендуемые запасы устойчивости Lзап>6 дБ, Фзап>30⁰). Поэтому необходима коррекция динамических свойств системы (в примере это не производится).

Заключение

В результате работы, была достигнута цель курсового проекта, а именно был проведен анализ электромеханической следящей системы управления элементов, составлена структурная схема, построены частотные характеристики (АЧХ, ФЧХ) системы, ЛАЧХ разомкнутой системы, переходную характеристику.

Также система была исследована на устойчивость, определены коэффициенты ошибок, найдена установившаяся ошибка ∆x(t) при функции входного сигнала и определены показатели качества (время регулирования, перерегулирование, колебательность переходного процесса).

Список используемой литературы

.Теория автоматического управления и регулирования: учеб. пособие / Г. С. Аверьянов, В. Ю. Куденцов, А. Б. Яковлев ; ОмГТУ. - Омск : Изд-во ОмГТУ, 2005.

.Управление в технических системах: учеб. пособие / Г. С. Аверьянов, А. Г. Туровец, А. Б. Яковлев ; ОмГТУ. - Омск : Изд-во ОмГТУ, 2000.

.Теория автоматического управления: учеб. для вузов / В. Я. Ротач. - 2-е изд., перераб. и доп. - М. : Изд-во МЭИ, 2004.

.Практикум по теории автоматического управления: учеб. пособие для вузов по направлениям подгот. 550200, 651900 "Автоматизация и управление" / Л. Д. Певзнер. - М. : Высш. шк., 2006.

.Теория автоматического управления: метод. указания для самостоят. работы студентов днев. формы обучения / ОмГТУ ; Сост. Д. В. Ситников. - Омск : Изд-во ОмГТУ, 2003.