Акустические волны в среде с флуктуирующей плотностью
Введение
Аморфное состояние
формируется, как правило, из жидкого или парообразного в условиях сверхбыстрой
закалки, предотвращающей кристаллизацию. Отличительными особенностями такого
состояния являются отсутствие дальнего порядка в расположении атомов и неравновесность.
Структурный беспорядок аморфной фазы характеризуется флуктуациями величины
межатомных расстояний, а так же плотности вещества. Кроме того, в сплавах имеют
место флуктуации концентрации атомов различных компонентов (химический
беспорядок). В аморфном состоянии отсутствует точка плавления. При повышении
температуры аморфное вещество размягчается и переходит в жидкое состояние
постепенно. Эти особенности обусловлены отсутствием в аморфном состоянии так
называемого дальнего порядка- строгой периодической повторяемости в
пространстве одного и того же элемента структуры. В то же время у вещества в
аморфном состоянии существует согласованность в расположении соседних атомов-
так называемый ближний порядок, соблюдаемый в пределах первой координационной
сферы, и постепенно теряющийся при переходе ко второй и третей сферам, т.е.
соблюдающийся на расстояниях, сравнимых с размерами кристаллической ячейки. С
расстоянием согласованность уменьшается и через 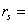 5-10
5-10 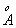 исчезает
[1].
исчезает
[1].
1. Акустические волны
Кристаллический и
ориентационный порядки сильно отличаются. Ориентация сохраняется на расстояниях
100-1000 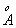 ,
когда кристаллический порядок разрушен. На рис. 1 условно изображена атомная
структура, в которой координаты атомов существенно стохастизуются уже при
расстояниях
,
когда кристаллический порядок разрушен. На рис. 1 условно изображена атомная
структура, в которой координаты атомов существенно стохастизуются уже при
расстояниях 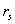 ,
а ориентация оси кристаллографической ячейки сохраняется примерно однородной на
гораздо больших расстояниях
,
а ориентация оси кристаллографической ячейки сохраняется примерно однородной на
гораздо больших расстояниях  . Такая модель (с
разными элементами стохастизованной кристаллической решетки, имеющими разные
корреляционные радиусы) существенно меняет представление о структуре аморфного
состояния.
. Такая модель (с
разными элементами стохастизованной кристаллической решетки, имеющими разные
корреляционные радиусы) существенно меняет представление о структуре аморфного
состояния.
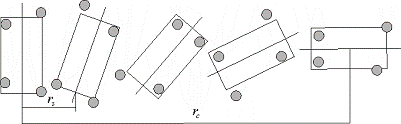
Рис. 1. Условное
изображение модели атомной структуры аморфного вещества, в которой различным
параметрам стохастизованной решетки соответствуют различные радиусы корреляций.
Расстояния между атомами (черными кружками) стохастизованы на расстояниях 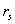 ,
средняя ориентация элементарной ячейки (прямоугольники) имеет гораздо больший
радиус корреляций
,
средняя ориентация элементарной ячейки (прямоугольники) имеет гораздо больший
радиус корреляций  .
.
Корреляционный радиус 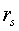 экспериментально
определяется методами хорошо развитыми для кристаллических материалов
(рентгеновская, электронная, нейтронная спектроскопии). Для определения
корреляционных радиусов порядка 100-1000
экспериментально
определяется методами хорошо развитыми для кристаллических материалов
(рентгеновская, электронная, нейтронная спектроскопии). Для определения
корреляционных радиусов порядка 100-1000 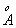 потребовалось
обоснование и развитие новых методов исследования. Теоретически было показано,
что корреляционные радиусы крупномасштабных композиционных и структурных
неоднородностей должны проявляться в виде характерных особенностей на законах
дисперсии и затухании всех элементарных возбуждений твердого тела: спиновых,
упругих [2, 3], плазменных, и электромагнитных волн [4].
потребовалось
обоснование и развитие новых методов исследования. Теоретически было показано,
что корреляционные радиусы крупномасштабных композиционных и структурных
неоднородностей должны проявляться в виде характерных особенностей на законах
дисперсии и затухании всех элементарных возбуждений твердого тела: спиновых,
упругих [2, 3], плазменных, и электромагнитных волн [4].
В данной работе
рассматриваются упругие волны, распространяющиеся в среде с флуктуирующей
плотностью. Решение задачи проводится методом, развитым в работе [2], однако
спектральные характеристики вычисляются в приближении Бурре.
2. Дисперсионное
соотношение для волн в неоднородной упругой среде
.1 Одномерный случай
Объемная плотность
лагранжиана для вектора упругого смещения 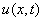 в сплошной одномерной
среде определяется выражением
в сплошной одномерной
среде определяется выражением
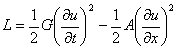 , (1)
, (1)
где первый и второй
член- плотность кинетической и потенциальной энергии, соответственно, G-
плотность вещества, A- константа взаимодействия. Уравнение движения имеет вид
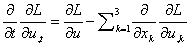 . (2)
. (2)
Для начала рассмотрим
случай, когда G и A постоянные величины, не зависящие от координаты.
 ,
,  ,
(3)
,
(3)
 . (4)
. (4)
Получили уравнение
колебаний в привычном виде.
Положим, что плотность
вещества меняется в зависимости от координаты 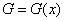 , а константа
взаимодействия остается постоянной.
, а константа
взаимодействия остается постоянной.
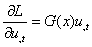 ,
,  ,
(5)
,
(5)
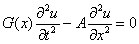 . (6)
. (6)
Удобно переписать 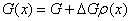 ,
где G- средняя плотность,
,
где G- средняя плотность, 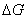 -
среднеквадратичная флуктуация плотности,
-
среднеквадратичная флуктуация плотности,  - безразмерная случайная
функция с математическим ожиданием, равным нулю
- безразмерная случайная
функция с математическим ожиданием, равным нулю 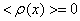 , и дисперсией
, и дисперсией 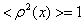 .
Угловые скобки означают усреднение по ансамблю реализаций случайных функций.
.
Угловые скобки означают усреднение по ансамблю реализаций случайных функций.
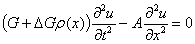 . (7)
. (7)
Положим, что константа
взаимодействия меняется в зависимости от координаты  ,
а плотность вещества остается постоянной. Сразу заменим
,
а плотность вещества остается постоянной. Сразу заменим 
 , (8)
, (8)
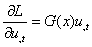 ,
, 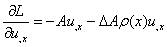 ,
(9)
,
(9)
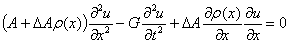 . (10)
. (10)
В большинстве реальных
материалов, преобладает неоднородность какого-то одного физического параметра.
Поэтому мы здесь не будем рассматривать случай одновременных флуктуаций A и G.
Рассмотрим уравнение
колебаний (7) с неоднородной плотностью G(x).
Выполним в (7)
преобразование Фурье
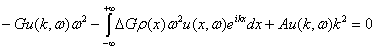 . (11)
. (11)
В (11) после
интегрирования по 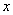 возникает
свертка.
возникает
свертка.
 , (12)
, (12)
где 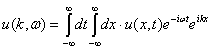 .
(13)
.
(13)
Введем обозначения
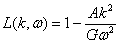 ,
, 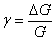 ,
(14)
,
(14)
тогда уравнение (12)
перепишется в виде
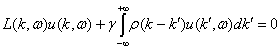 . (15)
. (15)
Если положить 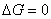 (
( ),
т.е. плотность среды однородная, то уравнение (15) принимает вид
),
т.е. плотность среды однородная, то уравнение (15) принимает вид
 . (16)
. (16)
Поскольку амплитуда 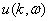 упругой
волны отлична от нуля, то уравнение (16) выполняется при
упругой
волны отлична от нуля, то уравнение (16) выполняется при 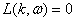 .
Решение этого дисперсионного уравнения дает линейный закон дисперсии волны
.
Решение этого дисперсионного уравнения дает линейный закон дисперсии волны
 , (17)
, (17)
где 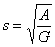 -
скорость звука,
-
скорость звука, 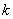 -
волновой вектор возбуждений.
-
волновой вектор возбуждений.
В случае неоднородной
плотности, закон дисперсии должен некоторым образом модифицироваться. Получим
эту модификацию на основе теории возмущений, считая параметр  .
.
Запишем формальное
решение уравнения (15)
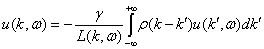 . (18)
. (18)
Подставим это решение в
подинтегральное выражение уравнения (15), получим
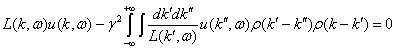 . (19)
. (19)
Учитывая, что
 , (20)
, (20)
усредним по случайным
реализациям
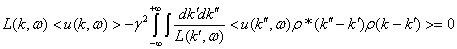 . (21)
. (21)
Приближенно расцепляем
коррелятор
 . (22)
. (22)
Для однородной случайной
функции справедливо 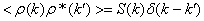 ,
или
,
или
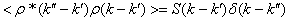 , (23)
, (23)
где 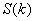 -
спектральная плотность корреляционной функции. Подставим (23) в (21)
-
спектральная плотность корреляционной функции. Подставим (23) в (21)
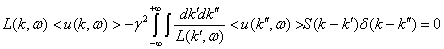 , (24)
, (24)
выполним интегрирование
по  ,
получим
,
получим
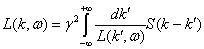 . (25)
. (25)
Таким образом получено
дисперсионное уравнение в приближении Бурре (25) для усредненной волны.
Дисперсионное
соотношение несет информацию о спектральной плотности 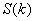 ,
т.е. о корреляционной функции
,
т.е. о корреляционной функции 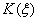 флуктуирующего в
пространстве параметра плотности среды.
флуктуирующего в
пространстве параметра плотности среды.
Для оценок выберем
экспоненциальную корреляционную функцию и связанною с ней преобразованием Фурье
спектральную плотность (см. приложение 1).
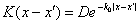 ;
; 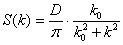 ,
(26)
,
(26)
где  -
характерное волновое число (2/
-
характерное волновое число (2/ характерный размер
неоднородности,
характерный размер
неоднородности, 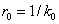 -
радиус корреляций случайной функции
-
радиус корреляций случайной функции  , описывающей
неоднородности); D- дисперсия
, описывающей
неоднородности); D- дисперсия  (в нашем случае D=1 по
определению).
(в нашем случае D=1 по
определению).
Подставим (26) и (14) в
(25), получаем
 . (27)
. (27)
Введем обозначения 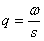 .
Тогда уравнение (27) примет вид
.
Тогда уравнение (27) примет вид
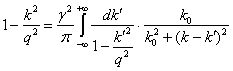 (28)
(28)
или
Из граничных условий 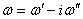 ,
где
,
где  -
действительные и положительные числа, а k- действительное волновое число,
определяемое размерами образца.
-
действительные и положительные числа, а k- действительное волновое число,
определяемое размерами образца.
Под интегралом будем
считать  -
действительным. В соответствии с выбранной формой преобразования Фурье имеем
-
действительным. В соответствии с выбранной формой преобразования Фурье имеем
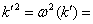
 . (30)
. (30)
С учетом (30) введем
обозначение
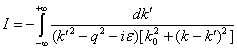 . (31)
. (31)
Этот интеграл вычислим
методом вычетов вводя комплексную переменную Z. Контур представлен на рис. 2. 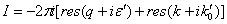 .
.
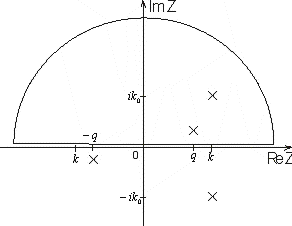
Рис. 2. Контур
интегрирования. Обход против часовой стрелки
Особые точки- полюсы
первого порядка. В результате имеем
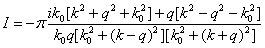 . (32)
. (32)
Подставив (32) в
уравнение (29), получим
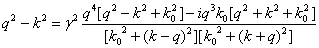 . (33)
. (33)
Решая это уравнение
получим модифицированный закон дисперсии и затухания волны в приближении Бурре.
Удобно работать с
безразмерными величинами. Введем обозначение 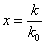 ,
, 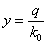 .
Тогда (33) принимает вид
.
Тогда (33) принимает вид
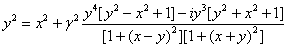 . (34)
. (34)
Как было указано выше, 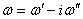
 ,
,
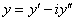 .
Тогда уравнение (34) от комплексной переменной
.
Тогда уравнение (34) от комплексной переменной 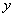 , можно представить в
виде системы двух уравнений
, можно представить в
виде системы двух уравнений
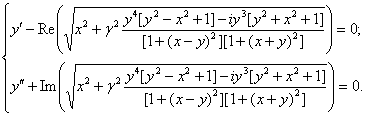 (35)
(35)
Получили нелинейную
систему уравнений, которую можно решать численно. Эта система была решена двумя
способами: с помощью вложенного в Maple 10 численного метода решения систем
уравнений и метода релаксации (см. приложение 2). Совпадение получилось до
шестого знака.
Если в правой части (33)
положить 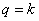 как
это делалось в работах [2], (разложение Релея-Шредингера), то имеем
как
это делалось в работах [2], (разложение Релея-Шредингера), то имеем
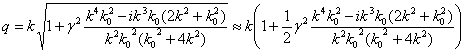 . (36)
. (36)
Таким образом, для
модифицированного закона дисперсии упругой волны получаем простое выражение,
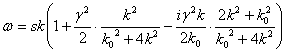 , (37)
, (37)
совпадающее с
соответствующим выражением в работе [2].
В безразмерных величинах
(36) принимает вид
 . (38)
. (38)
На рис. 3 приведены
кривые: сплошные- приближение Бурре (решение системы (35)), штриховые-
приближение Релея- Шредингера, точечная прямая- линейный закон дисперсии. Было
взято .
.
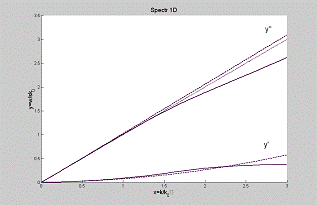
Рис. 3. Дисперсионные
соотношения. Сплошные кривые- приближение Бурре (решение системы (35)),
штриховые кривые- приближение Релея- Шредингера, точечная прямая соответствует
невозмущенному дисперсионному соотношению.  .
.
.2 Трехмерный случай
Уравнение колебаний для
трехмерного вектора упругого смещения в сплошной среде с флуктуирующей
плотностью имеет вид
 . (39)
. (39)
Выполним в (39)
преобразование Фурье
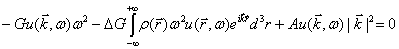 . (40)
. (40)
В (40) после
интегрирования по 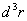 возникает
свертка.
возникает
свертка.
 , (41)
, (41)
где
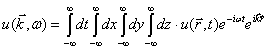 . (42)
. (42)
В обозначениях (14),
уравнение (41) примет вид
 . (43)
. (43)
Так же, как и в
одномерном случае модификацию закона дисперсии будем получать на основе теории
возмущений, считая параметр  .
.
Запишем формальное
решение уравнения (43)
 . (44)
. (44)
Подставляя это решение в
подинтегральное выражение уравнения (43), получим
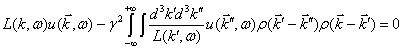 . (45)
. (45)
Учитывая, что
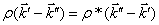 , (46)
, (46)
усредним (45) по
случайным реализациям
 . (47)
. (47)
Расцепив коррелятор и
выполнив интегрирование по 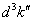 получим
получим
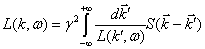 . (48)
. (48)
Для оценок выберем
экспоненциальную корреляционную функцию и связанною с ней преобразованием Фурье
спектральную плотность (см. приложение 1)
 ;
; 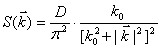 ,
(49)
,
(49)
Подставляя (49) и (14) в
(48), получаем
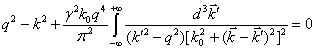 . (50)
. (50)
Выполнив интегрирование
в (50) по угловым переменным, используя сферическую систему координат, получим
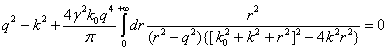 . (51)
. (51)
Так же как и в
одномерном случае 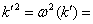
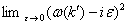 .
.
Введем обозначение
 . (52)
. (52)
Этот интеграл вычислим
методом вычетов. Контур представлен на рис. 3. 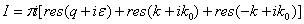 .
.
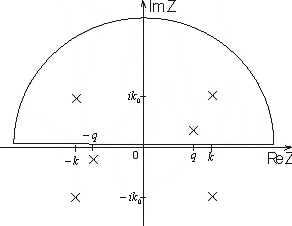
Рис. 4. Контур
интегрирования. Обход против часовой стрелки
Особые точки- полюсы
первого порядка. В результате имеем
 . (53)
. (53)
акустическая волна
флуктуирующая плотность
Подставив (53) в
уравнение (51), получим
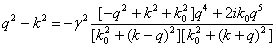 . (54)
. (54)
Решая это уравнение
получим модифицированный закон дисперсии и затухания волны в приближении Бурре.
Перепишем (54) в
безразмерных величинах.
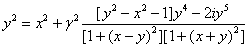 . (55)
. (55)
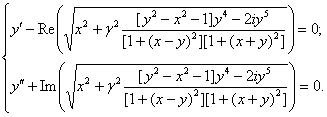 (56)
(56)
Получили нелинейную
систему уравнений, которую можно решать численно. Эта система была решена с
помощью вложенного в Maple 10 численного метода решения систем уравнений.
Если в правой части (54)
положить 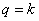 (разложение
Релея-Шредингера), то имеем
(разложение
Релея-Шредингера), то имеем
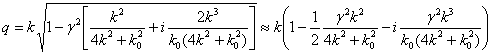 . (57)
. (57)
Таким образом, для
модифицированного закона дисперсии получаем простое выражение, совпадающее с
соответствующей формулой в [2].
 . (58)
. (58)
В безразмерных величинах
(57) принимает вид
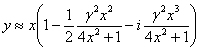 . (59)
. (59)
На рис.5 приведены
кривые: сплошные- приближение Буре (решение системы (56)), штриховые-
приближение Релея- Шредингера, точечная прямая- линейный закон дисперсии. Было
взято .
.
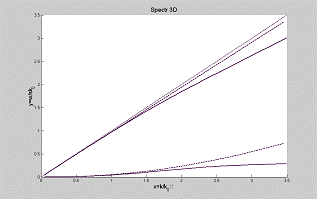
Рис. 5. Дисперсионные
соотношения. Сплошные кривые- приближение Бурре (решение системы (56)),
штриховые кривые- приближение Релея- Шредингера, точечная прямая соответствует
невозмущенному дисперсионному соотношению.  .
.
Заключение
Рассмотрим пределы
применимости полученных законов дисперсии. Приближение сплошной среды (39)
применимо при условии
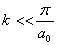 , (60)
, (60)
где 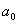 -
межатомное расстояние. Приближенное решение интегрального уравнения (43) было
получено при условии малости возмущений
-
межатомное расстояние. Приближенное решение интегрального уравнения (43) было
получено при условии малости возмущений
 . (61)
. (61)
Приближение
Релея-Шредингера накладывает условие связанное с требованием малости затухания.
В трехмерном случае, как это следует из выражения (57) имеем
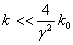 . (62)
. (62)
Численное решение в
приближении Бурре дало меньшее затухание в области 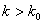 .
Значит это приближение применимо в более широкой области значений
.
Значит это приближение применимо в более широкой области значений 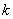 ,
определяемой только неравенствами (60) и (61).
,
определяемой только неравенствами (60) и (61).
Необходимо так же
отметить, что закон дисперсии в приближении Бурре имеет точку излома при
больших значениях волнового вектора k (см. рис. 3,5), чем в приближении
Релея-Шредингера. При обработке эксперимента с использованием этой
теоретической кривой могут получиться другие значения корреляционного радиуса.
Приложение 1
Корреляционные функции
Аморфный магнетик
является стохастической системой, параметры которой (намагниченность, константа
обмена и т.п.) есть случайные функции координат. Как известно, характеристики
случайной функции координат 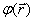 представляют собой
неслучайные функции- моменты различного порядка. Основные из них: момент
первого порядка- математическое ожидание
представляют собой
неслучайные функции- моменты различного порядка. Основные из них: момент
первого порядка- математическое ожидание 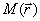 и центрированный момент
второго порядка- корреляционная функция
и центрированный момент
второго порядка- корреляционная функция 
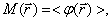
 (1.1)
(1.1)
где 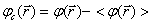 -
центрированная случайная функция.
-
центрированная случайная функция.
Параметры аморфного материала
описываются однородными случайными функциями, для которых корреляционные
функции зависят только от модуля разности координат 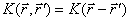 .
Здесь мы будем иметь дело только с однородными случайными функциями. В
пространстве волновых векторов
.
Здесь мы будем иметь дело только с однородными случайными функциями. В
пространстве волновых векторов 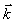 эквивалентном
корреляционной функции является связанная с ней преобразованием Фурье
спектральная плотность
эквивалентном
корреляционной функции является связанная с ней преобразованием Фурье
спектральная плотность 
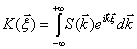 , (1.2)
, (1.2)
где 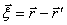 .
Спектральная плотность
.
Спектральная плотность 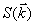 связана
с трансформантой Фурье
связана
с трансформантой Фурье  флуктуации
флуктуации
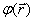 следующим
соотношением (мы будем обозначать трансформанты Фурье случайных функций теми же
буквами, что и сами функции):
следующим
соотношением (мы будем обозначать трансформанты Фурье случайных функций теми же
буквами, что и сами функции):
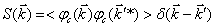 . (1.3)
. (1.3)
Корреляционная функция  (или
спектральная плотность
(или
спектральная плотность 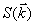 )
является основной характеристикой стохастичности в системе, ибо она описывает и
величину флуктуаций случайной функции (дисперсию
)
является основной характеристикой стохастичности в системе, ибо она описывает и
величину флуктуаций случайной функции (дисперсию 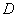 или среднеквадратичное
отклонение
или среднеквадратичное
отклонение 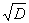 ),
и характерный пространственный размер флуктуаций (радиус корреляций
),
и характерный пространственный размер флуктуаций (радиус корреляций 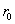 ).
Расчет и измерение корреляционной функции каждого флуктуирующего параметра (и
функции взаимной корреляции при флуктуации нескольких параметров) есть основная
задача при изучении любой стохастической системы.
).
Расчет и измерение корреляционной функции каждого флуктуирующего параметра (и
функции взаимной корреляции при флуктуации нескольких параметров) есть основная
задача при изучении любой стохастической системы.
В данной работе, для
оценок была выбрана экспоненциальная корреляционная функция и связанная с ней
преобразованием Фурье спектральная плотность. В одномерном случае функции имеют
вид
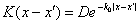 ;
; 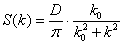 .
(1.4)
.
(1.4)
Их вид представлен на
рис. 6. В трехмерном случае
 ;
;  .
(1.5)
.
(1.5)
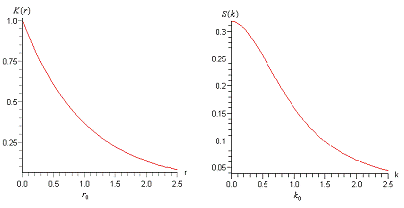
Рис. 6. Корреляционная
функция случайной функции  и
спектральная плотность
и
спектральная плотность 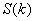 (1.4).
Одномерный случай
(1.4).
Одномерный случай
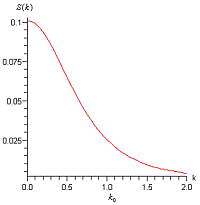
Рис. 7. Спектральная
плотность 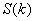 (1.5).
Трехмерный случай
(1.5).
Трехмерный случай
Приложение 2
Метод релаксации для
решения систем нелинейных уравнений
Дана система уравнений ,
или подробно
,
или подробно
 . (2.1)
. (2.1)
Начальное приближение 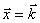 .
.
 . (2.2)
. (2.2)
Когда  ,
то
,
то 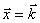 -
начальное приближение.
-
начальное приближение.
Когда 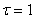 ,
то
,
то 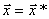 -
решение системы.
-
решение системы.
Перепишем систему (2.2)
через индексы
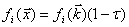 ,
,  .
(2.3)
.
(2.3)
Полагая что переменные 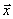 зависят
от
зависят
от 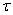 ,
,
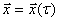 ,в
(2.3) возьмем производную по
,в
(2.3) возьмем производную по 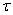 от левой и правой
части, получим
от левой и правой
части, получим
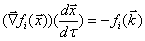 . (2.4)
. (2.4)
Обозначим
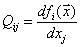
 .
(2.5)
.
(2.5)
Так как 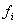 функция
от независимых переменных, то можно перейти к частным дифференциалам. Из
элементов (2.5) можно составить матрицу размерности n на n.
функция
от независимых переменных, то можно перейти к частным дифференциалам. Из
элементов (2.5) можно составить матрицу размерности n на n.
 . (2.6)
. (2.6)
В (2.4) явно распишем
скалярное произведение
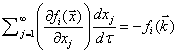 . (2.7)
. (2.7)
Подставив (2.6) в (2.7),
получим
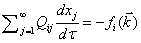 , (2.8)
, (2.8)
или
 . (2.9)
. (2.9)
Умножим левую и правую
часть в (2.9) на 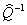 слева
слева
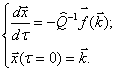 (2.10)
(2.10)
Требование 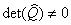 .
.
Система дифференциальных
уравнений (2.10) решается методом Рунге- Кутта четвертого порядка. Разностная
схема для уравнения
 , (2.11)
, (2.11)
имеет вид
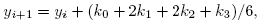 (2.12)
(2.12)
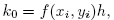 (2.13)
(2.13)
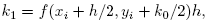 (2.14)
(2.14)
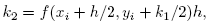 (2.15)
(2.15)
Литература
1. Займан Дж. Модели беспорядка. М.: “Мир”, 1982г.
. Игнатченко В. А., Исхаков Р. С. Стохастическая магнитная
структура и спиновые волны в аморфном ферромагнетике. Сб. Физика магнитных
материалов. Новосибирск: “Наука”, 1983. Стр. 3-30.
. Хандрих К., Кобе С. Аморфные ферро- и ферримагнетики. М.:
“Мир”, 1982г.
. Игнатченко В. А., Исхаков Р. С. Стохастические свойства
неоднородностей аморфных магнетиков. Сб. Магнитные свойства кристаллических и
аморфных сред. Новосибирск: “Наука”, 1989. Стр. 128-144.