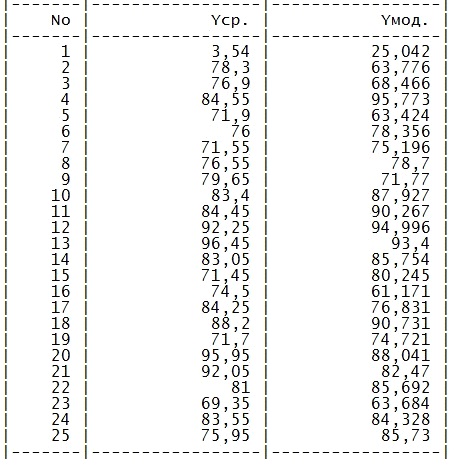Исследование типа технология-свойство на основе экспериментально-статистического подхода
Отчет №1
Регрессионный анализ
Тип задачи: технология-свойство.
Число технологических факторов: 4.
Равное число параллельных опытов в
экспериментальных точках = 2.
Число экспериментальных точек в плане = 16.
Число членов модели = 15.
Вид модели:
y= a0 + a1x1 + a2x2 + x3 + a4x4 +
a5x1x2 + x1x3 + a7x1x4 + a8x2x3 + x2x4 + a10x3x4 + a11x1^2 +
a12x2^2 + a13x3^2 + a14x4^2
Таблица. План эксперимента.

Внимание! Детерминант информационной матрицы
равен нулю.
План вырожден.
Таблица. Экспериментальные значения выходной
переменной.

Проверка однородности дисперсий
Табличное значение критерия Кохрена Gт
для уровня значимости q = 0,05
и числа степеней свободы f1 = 1, f2 = 16 равно
0,3894.
Расчетное значение критерия Кохрена Gр =
0,41234,р > Gт, дисперсии не однородны, некорректный анализ.
Дисперсия воспроизводимости = 0,077309, число
степеней свободы = 16.
Оценка значимости коэффициентов модели
Табличное значение критерия Стьюдента tт
для уровня значимости q = 0.1
и числа степеней свободы f = 16 равно 1,75.=
0,54606; ;tр = 55,548, tр > tт, значим= 0,47656; x1 ;tр = 9,6957, tр >
tт, значим= 0,57781; x2 ;tр = 11,756, tр > tт, значим= -0,34719; x3 ;tр =
7,0635, tр > tт, значим= -0,38469; x4 ;tр = 7,8265, tр > tт, значим=
0,15406; x1x2 ;tр = 3,1344, tр > tт, значим= -0,020937; x1x3 ; tр = 0,42597,
tр < tт, не значим= 0,081562; x1x4 ; tр = 1,6594, tр < tт, не значим=
0,0015625; x2x3 ; tр = 0,031789, tр < tт, не значим= 0,029062; x2x4 ; tр =
0,59128, tр < tт, не значим= 0,095313; x3x4 ;tр = 1,9391, tр > tт,
значим= 0,54606; x1^2 ;tр = 55,548, tр > tт, значим= 0,54606; x2^2 ;tр =
55,548, tр > tт, значим= 0,54606; x3^2 ;tр = 55,548, tр > tт, значим=
0,54606; x4^2 ;tр = 55,548, tр > tт, значим
Табличное значение критерия Фишера Fт для уровня
значимости q = 0.1 и чисел степеней свободы= 1,
f2 = 16 равно 3,0481.
Расчетное значение критерия Фишера Fр = 19,072.
Вывод: так как Fр > Fт, модель не
адекватна(используется дисперсия воспроизводимости).
Так как дисперсионная матрица не является
диагональной,
при отбрасывании незначимых коэффициентов
требуется заново рассчитать
значения параметров модели.
При этом, минимальный по модулю не диагональный
элемент
дисперсионной матрицы min El = 0,0000E+000.
Максимальный по модулю не диагональный элемент
дисперсионной матрицы max El = 1,2500E-003.
Модель:
= + 0,54606 + 0,47656x1 + 0,57781x2
0,34719x3 - 0,38469x4 + 0,15406x1x2
0,020937x1x3 + 0,081562x1x4 + 0,0015625x2x3
+ 0,029062x2x4 + 0,095313x3x4 + 0,54606x1^2
+ 0,54606x2^2 + 0,54606x3^2 + 0,54606x4^2
Детерминант информационной матрицы = 0.
Детерминант дисперсионной матрицы = 0.
Общее среднее = 2,7303.
Общая сумма = 29,323.
Общая дисперсия = 1,9548,
Число степеней свободы = 15.
Остаточная сумма = 1,4744.
Остаточная дисперсия = 1,4744,
число степеней свободы = 1.
Таблица. Средние и расчетные значения выходной
переменной.

Отчет №2
Регрессионный анализ
Тип задачи: технология-свойство.
Число технологических факторов: 4.
Равное число параллельных опытов в
экспериментальных точках = 2.
Число экспериментальных точек в плане = 16.
Число членов модели = 15.
Вид модели:
y= a0 + a1x1 + a2x2 + x3 + a4x4 +
a5x1x2 + x1x3 + a7x1x4 + a8x2x3 + x2x4 + a10x3x4 + a11x1^2 +
a12x2^2 + a13x3^2 + a14x4^2
Таблица. План эксперимента.

Внимание! Детерминант информационной матрицы
равен нулю.
План вырожден.
Таблица. Экспериментальные значения выходной
переменной.

Табличное значение критерия Кохрена Gт
для уровня значимости q = 0,05
и числа степеней свободы f1 = 1, f2 = 16 равно
0,3894.
Расчетное значение критерия Кохрена Gр =
0,21036,р < Gт, дисперсии однородны.
Дисперсия воспроизводимости = 87,718, число
степеней свободы = 16.
Оценка значимости коэффициентов модели
Табличное значение критерия Стьюдента tт
для уровня значимости q = 0.1
и числа степеней свободы f = 16 равно 1,75.=
16,174; ;tр = 48,844, tр > tт, значим= 0,20625; x1 ; tр = 0,12457, tр <
tт, не значим= -2,7313; x2 ; tр = 1,6496, tр < tт, не значим= 2,6562; x3 ;
tр = 1,6044, tр < tт, не значим= -3,9437; x4 ;tр = 2,382, tр > tт,
значим= 1,8438; x1x2 ; tр = 1,1136, tр < tт, не значим= 0,89375; x1x3 ; tр =
0,53982, tр < tт, не значим= 1,7187; x1x4 ; tр = 1,0381, tр < tт, не
значим= -0,03125; x2x3 ; tр = 0,018875, tр < tт, не значим= 1,4937; x2x4 ;
tр = 0,90221, tр < tт, не значим= -1,6688; x3x4 ; tр = 1,0079, tр < tт,
не значим= 16,174; x1^2 ;tр = 48,844, tр > tт, значим= 16,174; x2^2 ;tр =
48,844, tр > tт, значим= 16,174; x3^2 ;tр = 48,844, tр > tт, значим=
16,174; x4^2 ;tр = 48,844, tр > tт, значим
Табличное значение критерия Фишера Fт для уровня
значимости q = 0.1 и чисел степеней свободы= 1, f2 = 16 равно 3,0481.
Расчетное значение критерия Фишера Fр = 5,5191.
Вывод: так как Fр > Fт, модель не
адекватна(используется дисперсия воспроизводимости).
Так как дисперсионная матрица не является
диагональной, при отбрасывании незначимых коэффициентов требуется заново
рассчитать значения параметров модели.
При этом, минимальный по модулю не диагональный
элемент дисперсионной матрицы min El = 0,0000E+000.
Максимальный по модулю не диагональный элемент
дисперсионной матрицы max El = 1,2500E-003.
Модель:
= + 16,174 + 0,20625x1 - 2,7313x2
+ 2,6562x3 - 3,9437x4 + 1,8438x1x2
+ 0,89375x1x3 + 1,7187x1x4 - 0,03125x2x3
+ 1,4937x2x4 - 1,6688x3x4 + 16,174x1^2
+ 16,174x2^2 + 16,174x3^2 + 16,174x4^2
Детерминант информационной матрицы = 0.
Детерминант дисперсионной матрицы = 0.
Общее среднее = 80,869.
Общая сумма = 1837,1.
Общая дисперсия = 122,47,
Число степеней свободы = 15.
Остаточная сумма = 484,13.
Остаточная дисперсия = 484,13,
число степеней свободы = 1.
регрессионный анализ однородность
дисперсия
Таблица. Средние и расчетные значения выходной
переменной.

Отчет №3
Регрессионный анализ
Тип задачи: технология-свойство.
Число технологических факторов: 4.
Равное число параллельных опытов в
экспериментальных точках = 2.
Число экспериментальных точек в плане = 25.
Число членов модели = 15.
y= a0 + a1x1 + a2x2 +
a3x3 + a4x4 + a5x1x2 + x1x3 + a7x1x4
+ a8x2x3 + x2x4 + a10x3x4 + a11x1^2 + x2^2 + a13x3^2 + a14x4^2
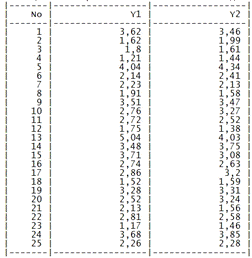
Таблица. План эксперимента.

Таблица. Экспериментальные значения выходной
переменной.
Проверка однородности дисперсий
Табличное значение критерия Кохрена Gт для
уровня значимости q = 0,05 и числа степеней свободы f1 = 1, f2 = 25 равно
0,2929.
Расчетное значение критерия Кохрена Gр =
0,28298,р < Gт, дисперсии однородны.
Дисперсия воспроизводимости = 0,072098, число
степеней свободы = 25.
Оценка значимости коэффициентов модели
Табличное значение критерия Стьюдента tт
для уровня значимости q = 0.1
и числа степеней свободы f = 25 равно 1,71.=
2,27; ;tр = 11,956, tр > tт, значим= 0,44062; x1 ;tр = 11,369, tр > tт,
значим= 0,41979; x2 ;tр = 10,832, tр > tт, значим= -0,30229; x3 ;tр =
7,7998, tр > tт, значим= -0,46062; x4 ;tр = 11,885, tр > tт, значим=
0,15406; x1x2 ;tр = 3,2457, tр > tт, значим= -0,020937; x1x3 ; tр = 0,4411,
tр < tт, не значим= 0,081562; x1x4 ;tр = 1,7183, tр > tт, значим=
0,0015625; x2x3 ; tр = 0,032918, tр < tт, не значим= 0,029062; x2x4 ; tр =
0,61227, tр < tт, не значим= 0,095313; x3x4 ;tр = 2,008, tр > tт, значим=
0,036094; x1^2 ; tр = 0,63887, tр < tт, не значим= 0,23484; x2^2 ;tр =
4,1568, tр > tт, значим= 0,030469; x3^2 ; tр = 0,5393, tр < tт, не
значим= 0,097969; x4^2 ;tр = 1,7341, tр > tт, значим
Табличное значение критерия Фишера Fт для уровня
значимости q = 0.1 и чисел степеней свободы= 10,
f2 = 25 равно 1,8658.
Расчетное значение критерия Фишера Fр = 7,0725.
Вывод: так как Fр > Fт, модель не
адекватна(используется дисперсия воспроизводимости).
Так как дисперсионная матрица не является
диагональной, при отбрасывании незначимых коэффициентов требуется заново
рассчитать значения параметров модели.
При этом, минимальный по модулю не диагональный
элемент
дисперсионной матрицы min El = 0,0000E+000.
Максимальный по модулю не диагональный элемент
дисперсионной матрицы max El = 1,2500E-001.
Модель:
= + 2,27 + 0,44062x1 + 0,41979x2
0,30229x3 - 0,46062x4 + 0,15406x1x2
0,020937x1x3 + 0,081562x1x4 + 0,0015625x2x3
+ 0,029062x2x4 + 0,095313x3x4 + 0,036094x1^2
+ 0,23484x2^2 + 0,030469x3^2 + 0,097969x4^2
Детерминант информационной матрицы = 5,7377E23.
Общее среднее = 2,6534.
Общая сумма = 40,793.
Общая дисперсия = 1,6997,
Число степеней свободы = 24.
Остаточная сумма = 5,0991.
Остаточная дисперсия = 0,50991,
число степеней свободы = 10.
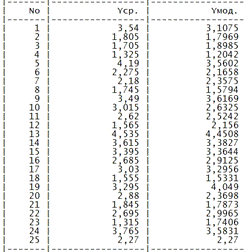
Таблица. Средние и расчетные значения выходной
переменной.
Отчет №4
Регрессионный анализ
Тип задачи: технология-свойство.
Число технологических факторов: 4.
Равное число параллельных опытов в
экспериментальных точках = 2.
Число экспериментальных точек в плане = 25.
Число членов модели = 15.
Вид модели:
y= a0 + a1x1 + a2x2 + x3 + a4x4 +
a5x1x2 + x1x3 + a7x1x4 + a8x2x3 + x2x4 + a10x3x4 + a11x1^2 +
a12x2^2 + a13x3^2 + a14x4^2
Таблица. План эксперимента.

Таблица. Экспериментальные значения выходной
переменной.

Проверка однородности дисперсий
Табличное значение критерия Кохрена Gт для
уровня значимости q = 0,05 и числа степеней свободы f1 = 1, f2 = 25 равно
0,2929.
Расчетное значение критерия Кохрена Gр =
0,14476,р < Gт, дисперсии однородны.
Дисперсия воспроизводимости = 81,58, число
степеней свободы = 25.
Оценка значимости коэффициентов модели
Табличное значение критерия Стьюдента tт для
уровня значимости q = 0.1 и числа степеней свободы f = 25 равно 1,71.= 75,95;
;tр = 11,892, tр > tт, значим= -4,1921; x1 ;tр = 3,2156, tр > tт, значим=
-4,5171; x2 ;tр = 3,4649, tр > tт, значим= -0,67958; x3 ; tр = 0,52128, tр
< tт, не значим= -6,4296; x4 ;tр = 4,9319, tр > tт, значим= -2,8569; x1x2
;tр = 1,7893, tр > tт, значим= -5,9506; x1x3 ;tр = 3,7269, tр > tт,
значим= -5,6444; x1x4 ;tр = 3,5351, tр > tт, значим= -7,9131; x2x3 ;tр =
4,956, tр > tт, значим= -6,2319; x2x4 ;tр = 3,903, tр > tт, значим=
-4,1881; x3x4 ;tр = 2,623, tр > tт, значим= 1,2395; x1^2 ; tр = 0,65221, tр
< tт, не значим= 0,63948; x2^2 ; tр = 0,33649, tр < tт, не значим=
1,3145; x3^2 ; tр = 0,69168, tр < tт, не значим= -1,2043; x4^2 ; tр =
0,63368, tр < tт, не значим
Табличное значение критерия Фишера Fт для уровня
значимости q = 0.1 и чисел степеней свободы f1 = 10, f2 = 25 равно 1,8658.
Расчетное значение критерия Фишера Fр = 4,9771.
Вывод: так как Fр > Fт, модель не
адекватна(используется дисперсия воспроизводимости).
Так как дисперсионная матрица не является
диагональной, при отбрасывании незначимых коэффициентов требуется заново
рассчитать значения параметров модели.
При этом, минимальный по модулю не диагональный
элемент дисперсионной матрицы min El = 0,0000E+000.
Максимальный по модулю не диагональный элемент
дисперсионной матрицы max El = 1,2500E-001.
Модель:
= + 75,95 - 4,1921x1 - 4,5171x2
0,67958x3 - 6,4296x4 - 2,8569x1x2
5,9506x1x3 - 5,6444x1x4 - 7,9131x2x3
6,2319x2x4 - 4,1881x3x4 + 1,2395x1^2
+ 0,63948x2^2 + 1,3145x3^2 - 1,2043x4^2
Детерминант информационной матрицы = 5,7377E23.
Детерминант дисперсионной матрицы = 1,7429E-24.
Общее среднее = 77,86.
Общая сумма = 14383.
Общая дисперсия = 599,31,
Число степеней свободы = 24.
Остаточная сумма = 4060,3.
Остаточная дисперсия = 406,03,
число степеней свободы = 10.
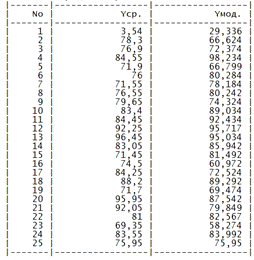
Таблица. Средние и расчетные значения выходной
переменной.
Отчет №5
Регрессионный анализ
Тип задачи: технология-свойство.
Число технологических факторов: 4.
Равное число параллельных опытов в
экспериментальных точках = 2.
Число экспериментальных точек в плане = 25.
Число членов модели = 15.
Вид модели:
y= a0 + a1x1 + a2x2 + x3 + a4x4 +
a5x1x2 + x1x3 + a7x1x4 + a8x2x3 + x2x4 + a10x3x4 + a11x1^2 +
a12x2^2 + a13x3^2 + a14x4^2
Таблица. План эксперимента.

Таблица. Экспериментальные значения выходной
переменной.
Проверка однородности дисперсий
Табличное значение критерия Кохрена Gт для
уровня значимости q = 0,05 и числа степеней свободы f1 = 1, f2 = 25 равно
0,2929.
Расчетное значение критерия Кохрена Gр =
0,35567,р > Gт, дисперсии не однородны, некорректный анализ.
Дисперсия воспроизводимости = 0,057362, число
степеней свободы = 25.
Табличное значение критерия Стьюдента tт для
уровня значимости q = 0.1 и числа степеней свободы f = 25 равно 1,71.= 2,2509;
;tр = 22,157, tр > tт, значим= 0,44066; x1 ;tр = 11,636, tр > tт, значим=
0,56339; x2 ;tр = 14,877, tр > tт, значим= -0,33362; x3 ;tр = 8,8097, tр
> tт, значим= -0,43751; x4 ;tр = 11,553, tр > tт, значим= 0,15406; x1x2
;tр = 3,6388, tр > tт, значим= -0,020937; x1x3 ; tр = 0,49452, tр < tт,
не значим= 0,081562; x1x4 ;tр = 1,9264, tр > tт, значим= 0,0015625; x2x3 ;
tр = 0,036905, tр < tт, не значим= 0,029062; x2x4 ; tр = 0,68643, tр <
tт, не значим= 0,095313; x3x4 ;tр = 2,2512, tр > tт, значим= 0,0050616; x1^2
; tр = 0,084519, tр < tт, не значим= 0,51271; x2^2 ;tр = 8,5614, tр > tт,
значим= 0,042573; x3^2 ; tр = 0,71089, tр < tт, не значим= -0,071211; x4^2 ;
tр = 1,1891, tр < tт, не значим
Табличное значение критерия Фишера Fт для уровня
значимости q = 0.1 и чисел степеней свободы= 10, f2 = 25 равно 1,8658.
Расчетное значение критерия Фишера Fр = 3,9502.
Вывод: так как Fр > Fт, модель не
адекватна(используется дисперсия воспроизводимости).
Так как дисперсионная матрица не является
диагональной, при отбрасывании незначимых коэффициентов требуется заново
рассчитать значения параметров модели.
При этом, минимальный по модулю не диагональный
элемент дисперсионной матрицы min El = 0,0000E+000.
Максимальный по модулю не диагональный элемент
дисперсионной матрицы max El = 4,9979E-002.
Модель:
= + 2,2509 + 0,44066x1 + 0,56339x2
0,33362x3 - 0,43751x4 + 0,15406x1x2
0,020937x1x3 + 0,081562x1x4 + 0,0015625x2x3
+ 0,029062x2x4 + 0,095313x3x4 + 0,0050616x1^2
+ 0,51271x2^2 + 0,042573x3^2 - 0,071211x4^2
Детерминант информационной матрицы = 8,992E21.
Детерминант дисперсионной матрицы = 1,1121E-22.
Общее среднее = 2,6422.
Общая сумма = 40,455.
Общая дисперсия = 1,6856,
Число степеней свободы = 24.
Остаточная сумма = 2,2659.
Остаточная дисперсия = 0,22659, число степеней
свободы = 10.
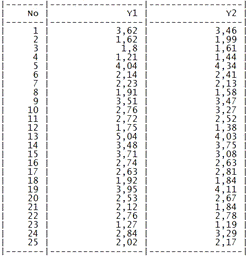
Таблица. Средние и расчетные значения выходной
переменной.
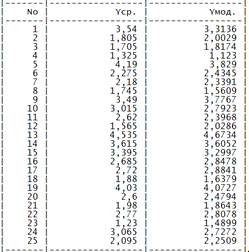
Отчет №6
Регрессионный анализ
Тип задачи: технология-свойство.
Число технологических факторов: 4.
Равное число параллельных опытов в экспериментальных
точках = 2.
Число экспериментальных точек в плане = 25.
Число членов модели = 15.
Вид модели:
y= a0 + a1x1 + a2x2 + x3 + a4x4 +
a5x1x2 + x1x3 + a7x1x4 + a8x2x3 + x2x4 + a10x3x4 + a11x1^2 +
a12x2^2 + a13x3^2 + a14x4^2
Таблица. План эксперимента.
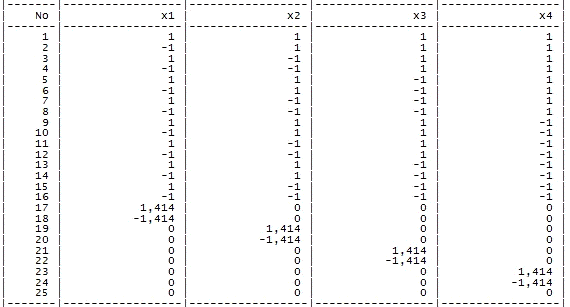
Таблица. Экспериментальные значения выходной
переменной.
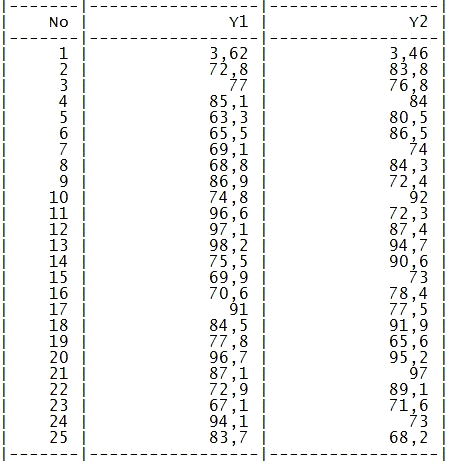
Проверка однородности дисперсий
Табличное значение критерия Кохрена Gт для
уровня значимости q = 0,05 и числа степеней свободы f1 = 1, f2 = 25 равно
0,2929.
Расчетное значение критерия Кохрена Gр =
0,14476,р < Gт, дисперсии однородны.
Дисперсия воспроизводимости = 81,58, число
степеней свободы = 25.
Оценка значимости коэффициентов модели
Табличное значение критерия Стьюдента tт для
уровня значимости q = 0.1 и числа степеней свободы f = 25 равно 1,71.= 85,73;
;tр = 22,377, tр > tт, значим= -4,9151; x1 ;tр = 3,4415, tр > tт, значим=
-4,7103; x2 ;tр = 3,2981, tр > tт, значим= -1,1393; x3 ; tр = 0,79777, tр
< tт, не значим= -7,2999; x4 ;tр = 5,1114, tр > tт, значим= -2,8569; x1x2
;tр = 1,7893, tр > tт, значим= -5,9506; x1x3 ;tр = 3,7269, tр > tт,
значим= -5,6444; x1x4 ;tр = 3,5351, tр > tт, значим= -7,9131; x2x3 ;tр =
4,956, tр > tт, значим= -6,2319; x2x4 ;tр = 3,903, tр > tт, значим=
-4,1881; x3x4 ;tр = 2,623, tр > tт, значим= -0,97472; x1^2 ; tр = 0,43159, tр
< tт, не значим= -2,1751; x2^2 ; tр = 0,96309, tр < tт, не значим=
-0,82468; x3^2 ; tр = 0,36515, tр < tт, не значим= -5,8637; x4^2 ;tр =
2,5963, tр > tт, значим
Табличное значение критерия Фишера Fт для уровня
значимости q = 0.1 и чисел степеней свободы f1 = 10, f2 = 25 равно 1,8658.
Расчетное значение критерия Фишера Fр = 4,2572.
Вывод: так как Fр > Fт, модель не
адекватна(используется дисперсия воспроизводимости).
Так как дисперсионная матрица не является
диагональной, при отбрасывании незначимых коэффициентов требуется заново
рассчитать значения параметров модели.
При этом, минимальный по модулю не диагональный
элемент дисперсионной матрицы min El = 0,0000E+000.
Максимальный по модулю не диагональный элемент
дисперсионной матрицы max El = 4,9979E-002.
Модель:
= + 85,73 - 4,9151x1 - 4,7103x2
1,1393x3 - 7,2999x4 - 2,8569x1x2
5,9506x1x3 - 5,6444x1x4 - 7,9131x2x3
6,2319x2x4 - 4,1881x3x4 - 0,97472x1^2
2,1751x2^2 - 0,82468x3^2 - 5,8637x4^2
Детерминант информационной матрицы = 8,992E21.
Детерминант дисперсионной матрицы = 1,1121E-22.
Общее среднее = 77,86.
Общая сумма = 14383.
Общая дисперсия = 599,31,
Число степеней свободы = 24.
Остаточная сумма = 3473.
Остаточная дисперсия = 347,3, число степеней
свободы = 10.
Таблица. Средние и расчетные значения выходной
переменной.