Теория множеств
Содержание
Введение
Глава
I. Понятие множества
Глава
II. Операции над множествами
Глава
III. Соответствия между множествами
Глава
IV. Счетные множества
Глава
V. Числовые множества
Заключение
Список
использованной литературы
Введение
Теория множеств - основа построения математики.
Путь к понятию “множество” проходил через развитие представлений о числе, более
глубокое понимание понятия бесконечности. Создатели теории множеств - чешский
математик С.Больцано и немецкий ученый Г.Кантор не только разработали новую
теорию, но и определили ее место как основополагающей в системе математических
знаний.
Множество - понятие неопределяемое, оно не может
быть введено через другие понятия.
Под множеством понимается некоторая совокупность
объектов, объединенных общим признаком и рассматриваемых как одно целое. Этот
общий признак называется характеристическим.
Теорию множеств Кантора считают “наивной”,
потому что ее исходные положения основываются не на строгих определениях и
аксиомах, а лишь на пояснениях. Вместе с тем, на практике она используется
активно.
Элементы множества могут иметь произвольную
природу, не обязательно числовую. Например:
множество людей, гуляющих в парке;
множество капель дождя;
множество массивов, используемых в программе для
ЭВМ;
множество натуральных чисел на отрезке [-1;4].
Множества обозначаются обычно заглавными
латинскими буквами: A, B, C - и так далее, а их элементы - строчными: a, b, c,
... .
Глава I. Понятие множества
Множество может быть задано через перечисление
его элементов. Например, запись
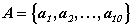
означает, что множество А состоит из
элементов  .
.
Во многих задачах выделяют некоторое
свойство F элементов x множества X такое, что каждый элемент либо обладает этим
свойством, либо нет. Приняты обозначения:
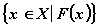 или
или 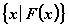 .
.
Например, запись
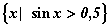
определяет множество таких значений
x, что  .
.
Принадлежность элемента а множеству
А задается обозначением
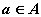 .
.
Отрицание этого факта обозначается
следующим образом:
 .
.
Вводится в рассмотрение также ПУСТОЕ
МНОЖЕСТВО, то есть не содержащее элементов. Оно обозначается  .
.
Множества А и В называются равными,
если каждый элемент множества А является элементом множества B и, обратно,
каждый элемент множества В является элементом множества А. Принято обозначение
А = В.
Множество А называется подмножеством
множества В, если каждый элемент множества А является элементом множества В. В
таком случае записывают:
А Í В.
Если А Í В, но А ¹ В, то А
называют собственным подмножеством множества В и обозначают
А Ì В.
Например, пусть 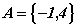 ;
; 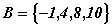 и
и 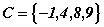 . В этом
случае А Ì В и
является его собственным подмножеством. Кроме того, А Ì C. Однако В
не принадлежит С. Это записывается в виде:
. В этом
случае А Ì В и
является его собственным подмножеством. Кроме того, А Ì C. Однако В
не принадлежит С. Это записывается в виде:
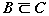 .
.
Очевидно, что, если А Í В и B Í A, то A=B.
Множества делятся на КОНЕЧНЫЕ и
БЕСКОНЕЧНЫЕ в зависимости от того, является ли число элементов, входящих в их
состав, конечным или же бесконечным. Например, множество участников
соревнования конечно, а множество точек, лежащих в круге, бесконечно.
Во многих математических науках чаще
всего изучаются ЧИСЛОВЫЕ множества, элементы которых - числа.
Глава II. Операции над множествами
Введем операции над множествами и
установим некоторую аналогию с операциями над другими математическими
объектами, например, высказываниями.
Операции над множествами и их
свойства во многом аналогичны алгебре высказываний. Это, как отмечалось,
отражает единство математической науки и, благодаря использованию метода
математического моделирования, позволяет находить ее связь с различными
областями знаний.
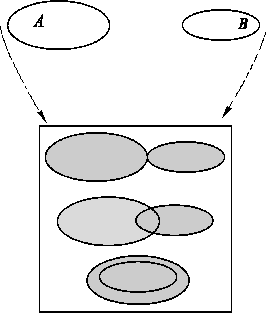
Рис. 1. Объединение множеств 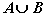 .
.
ОБЪЕДИНЕНИЕМ множеств A и B
называется множество 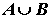 , содержащее
те и только те элементы, которые принадлежат хотя бы одному из множеств A или
B.
, содержащее
те и только те элементы, которые принадлежат хотя бы одному из множеств A или
B.
Схематично эта операция изображена
на рис. 1.
Она удовлетворяет коммутативному и
ассоциативному законам:

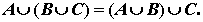
Очевидны соотношения:

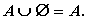
Множество E называется УНИВЕРСАЛЬНЫМ
для некоторой системы множеств, если каждое из них принадлежит этому множеству,
то есть является его подмножеством.
Можно считать поэтому, что

ПЕРЕСЕЧЕНИЕМ множеств A и B
называется множество  , содержащее
те и только те элементы, которые принадлежат и A, и B одновременно.
, содержащее
те и только те элементы, которые принадлежат и A, и B одновременно.
Схематично операция пересечения
множеств представима в виде (рис. 2).
Для этой операции также справедливы
коммутативный и ассоциативный законы:
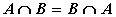 ;
;
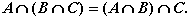
Множества A и B называются
НЕПЕРЕСЕКАЮЩИМИСЯ, если
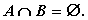
Операции объединения и пересечения
множеств подчиняются законам дистрибутивности:
 ;
;

Рис. 2. Пересечение множеств  .
.
РАЗНОСТЬЮ двух множеств A и B называется
множество A\B, состоящее из тех и только тех элементов, которые принадлежат A,
но не принадлежат B.

Рис. 3. Разность множеств 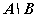 .
.
Эта операция изображена на рис. 3.
ДОПОЛНЕНИЕМ множества A до
универсального множества E называется разность E \ A и обозначается  (рис. 4).
(рис. 4).

Рис. 4. Дополнение множества А до
универсального множества Е:  .
.
праведливы соотношения:
1.  .
.
.  .
.
. 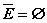 .
.
. 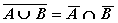 .
.
.  .
.
. 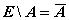 .
.
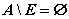 .
.
Будем обозначать через  количество
элементов множества A, если оно конечно.
количество
элементов множества A, если оно конечно.
Для конечных множеств A и B справедлива
формула:
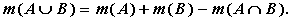 ( 1 )
( 1 )
Действительно, если множества A и B
не пересекаются, то  , поэтому
, поэтому  и
и 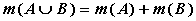 . Если же
множества A и B пересекаются, то количество элементов в объединении множеств
. Если же
множества A и B пересекаются, то количество элементов в объединении множеств 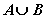 складывается
из числа элементов множеств A и B, но так как элементы, находящиеся в
пересечении множеств
складывается
из числа элементов множеств A и B, но так как элементы, находящиеся в
пересечении множеств  ,
учитываются дважды (рис. 5), то справедливо равенство (1). Конкретный пример
указан на рис. 5.
,
учитываются дважды (рис. 5), то справедливо равенство (1). Конкретный пример
указан на рис. 5.
Рис. 5. Общие элементы в объединении
конечных пересекающихся множеств.
Если множества конечны, то сравнение
числа их элементов может быть уподоблено сравнению натуральных чисел. Труднее
сравнить множества бесконечные. Чего больше: натуральных чисел или
действительных, точек отрезка или точек квадрата, построенного на нем?
Очевидно, что часть меньше целого. Но будет ли это “очевидное” сохраняться,
когда мы имеем дело с бесконечными множествами? Изучение феноменов бесконечного
породило принципиально новые оценки множеств.
Глава III. Соответствия между
множествами
Математика не всегда интересуется
природой элементов множеств, больший интерес представляет сравнение множеств.
Поэтому должна быть введена универсальная характеристика, которая могла бы их
описать. Этой характеристикой стала мощность множества.
МОЩНОСТЬЮ конечного множества
называется число его элементов.
Это определение кажется тривиальным.
Однако такой критерий для оценки бесконечных множеств вряд ли приемлем, так как
простой пересчет элементов множества для их последующего сравнения невозможен.
Г. Кантор нашел выход из
создавшегося положения, предложив установить связь между любыми множествами,
включая и конечные, через взаимно однозначное соответствие. Это явилось
принципиально новым взглядом на теорию множеств. Пусть, например, дан репертуар
оперных спектаклей театра, составленный на неделю. Представим его в виде
таблицы.
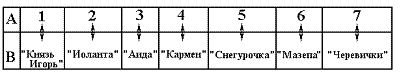
Тогда между множеством  и
множеством B={“Князь Игорь”, “Иоланта”, ..., “Черевички”} может быть
установлено соответствие, по которому каждому элементу множества А указывается
один определенный элемент множества В и обратно: каждому элементу множества В
ставится в соответствие также один определенный элемент множества A. Этот
способ позволяет без пересчета указать, что множества A и B содержат одинаковое
количество элементов. Именно эта идея и положена в основу сравнения бесконечных
множеств.
и
множеством B={“Князь Игорь”, “Иоланта”, ..., “Черевички”} может быть
установлено соответствие, по которому каждому элементу множества А указывается
один определенный элемент множества В и обратно: каждому элементу множества В
ставится в соответствие также один определенный элемент множества A. Этот
способ позволяет без пересчета указать, что множества A и B содержат одинаковое
количество элементов. Именно эта идея и положена в основу сравнения бесконечных
множеств.
Будем говорить, что между
множествами A и B установлено ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ, если каждому
элементу множества А поставлен в соответствие один элемент множества B, а
каждому элементу множества B - один элемент множества А.
Если между множествами A и B удается
установить взаимно однозначное соответствие, то говорят, что они ЭКВИВАЛЕНТНЫ,
или имеют ОДИНАКОВУЮ МОЩНОСТЬ.
Для таких множеств принята запись:

Мощность конечных множеств есть
численная характеристика, совпадающая с числом элементов множества; мощность
бесконечных множеств есть характеристика сравнительная, вытекающая из
возможности установить взаимно однозначное соответствие между парами различных
множеств.
Рассмотрим примеры.
. Пусть A - множество натуральных
чисел, а B - множество их квадратов.
Установим следующее взаимно
однозначное соответствие между этими множествами.

Это означает, что бесконечные
множества A и B эквивалентны и имеют одинаковую мощность. Интересно, что при
этом множество A эквивалентно своему подмножеству, так как квадраты натуральных
чисел - числа натуральные. Такая эквивалентность возможна потому, что оба
множества бесконечны.

Рис. 6. Установление взаимно
однозначного соответствия между равными сторонами равнобедренного треугольника.
. Пусть LM и NM - равные стороны
равнобедренного треугольника LMN (рис. 6).
Связав точки А и В равных сторон
треугольника отрезками прямых, параллельных основанию LN, получим взаимно
однозначное соответствие между точками множеств, определяемых отрезками LM и
NM. Эти множества эквивалентны и имеют одинаковую мощность.

Рис. 7.Установление взаимно
однозначного соответствия между неравными сторонами равнобедренного
треугольника.
3. Пусть теперь LN и МN - неравные
стороны треугольника LMN (рис. 7). Связав точки А и В на этих сторонах
отрезками прямых, параллельных стороне LM, получим, что и неравные между собой
стороны определяют множества точек одинаковой мощности. Дело в том, что стороны
LN и MN имеют разную длину, но каждая из них содержит бесконечное множество
точек, которых одинаково “много”.
Глава IV. Счетные множества
Множество назовем СЧЕТНЫМ, если оно
эквивалентно множеству натуральных чисел.
Таким образом, возможность
«пронумеровать» элементы множества определяет его счетность. Эта задача далеко
не всегда решается просто.
Отметим некоторые свойства счетных
множеств.
. Из всякого бесконечного множества
можно выделить счетное.
Действительно, если множество A
бесконечно, то счетное множество N можно построить следующим образом. Выделим в
качестве первого элемента множества N, например, элемент 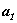 множества
A. Так как A бесконечно, то исключение из него одного элемента
множества
A. Так как A бесконечно, то исключение из него одного элемента  сохранит
его бесконечность. Далее отделим от оставшегося множества
сохранит
его бесконечность. Далее отделим от оставшегося множества 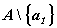 элемент
элемент  ,
присоединив его к множеству N, потом из бесконечного множества
,
присоединив его к множеству N, потом из бесконечного множества  отделим
элемент
отделим
элемент 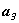 ,
присоединив к N, и так далее. Множество N примет вид:
,
присоединив к N, и так далее. Множество N примет вид: 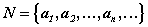 и будет
счетным.
и будет
счетным.
. Всякое бесконечное подмножество
счетного множества  тоже
счетно.
тоже
счетно.
Если множество A счетно, а B - его
бесконечное подмножество, то, последовательно перебирая элементы множества A,
мы будем встречать элементы множества B и, нумеруя их, получим бесконечное
счетное множество.
. Объединение любого конечного или
счетного множества счетных множеств есть счетное множество.
Для доказательства этого свойства
рассмотрим счетные множества:

Сформируем из этих множеств новое
множество

Оно образуется так, что вначале
располагается элемент 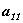 , затем идут
элементы, у которых сумма индексов равна 3, потом 4, и так далее. Такое
множество охватывает все элементы множеств
, затем идут
элементы, у которых сумма индексов равна 3, потом 4, и так далее. Такое
множество охватывает все элементы множеств  и само является счетным.
и само является счетным.
Рассматривая свойства счетных множеств,
мы стремились доказать счетность тех или иных бесконечных множеств. Однако все
ли бесконечные множества счетны? Чтобы обнаружить несчетные множества, пришлось
преодолеть немало трудностей. И Б. Больцано, и Г. Кантор, чувствуя, что идея
установления взаимно однозначного соответствия есть ключ к поиску мощности
бесконечных множеств, были близки к решению вопроса одновременно. Б. Больцано
первым пришел к способу оценки бесконечных множеств путем установления взаимно
однозначного соответствия, а Г. Кантор первым сумел найти несчетное множество.
ТЕОРЕМА. Отрезок 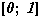 числовой
прямой содержит несчетное множество точек.
числовой
прямой содержит несчетное множество точек.
ДОКАЗАТЕЛЬСТВО.
Предположим противное: 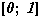 - счетное
множество точек. Пронумеруем их:
- счетное
множество точек. Пронумеруем их:

Любая ли точка этого отрезка
оказывается включенной в данную последовательность?
Для доказательства теоремы следует
найти такую точку на отрезке 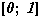 , которая не охватывается данной
последовательностью.
, которая не охватывается данной
последовательностью.
Для этого разделим отрезок на три
равные части (рис. 8). Получим отрезки:

Рис. 8. Построение точки, не
входящей в последовательность  .
.
Хотя бы на одном из них нет точки 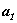 . Выделив
его, делим новый отрезок, являющийся подмножеством отрезка
. Выделив
его, делим новый отрезок, являющийся подмножеством отрезка 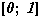 , снова на
три равные части и выделим ту, на которой нет точки
, снова на
три равные части и выделим ту, на которой нет точки  (на этой
“трети” не будет и точки
(на этой
“трети” не будет и точки 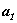 , и точки
, и точки  , как это
было установлено выше). Далее новый отрезок опять делим на три равные части и
выбираем ту из них, где нет точки а3 (как показано, точек
, как это
было установлено выше). Далее новый отрезок опять делим на три равные части и
выбираем ту из них, где нет точки а3 (как показано, точек 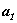 и
и  на ней
также не будет), и так далее. В результате на n-м шаге мы получаем отрезок
длины
на ней
также не будет), и так далее. В результате на n-м шаге мы получаем отрезок
длины 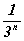 , на котором
нет точек
, на котором
нет точек 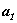 ,
, ,
,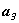 ,...,
,...,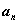 . Продолжая
бесконечно этот процесс, мы находим точку а, которая не включена в
последовательность
. Продолжая
бесконечно этот процесс, мы находим точку а, которая не включена в
последовательность
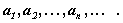
Действительно, а - общая точка этих
отрезков. Будучи точкой отрезка 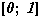 , она должна входить в указанную
последовательность, но это невозможно, потому что, какое бы n мы ни взяли,
точка аn не может принадлежать соответствующему отрезку, а точка а будет ему
принадлежать, следовательно, а отлична от всех аn, что и доказывает теорему.
, она должна входить в указанную
последовательность, но это невозможно, потому что, какое бы n мы ни взяли,
точка аn не может принадлежать соответствующему отрезку, а точка а будет ему
принадлежать, следовательно, а отлична от всех аn, что и доказывает теорему.
Мощность множеств, эквивалентных
отрезку 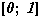 , назовем
МОЩНОСТЬЮ КОНТИНУУМА и обозначим буквой c.
, назовем
МОЩНОСТЬЮ КОНТИНУУМА и обозначим буквой c.
Укажем некоторые из этих множеств.
Рассмотрим отрезок  . Формула
. Формула
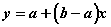 ,
, 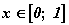
устанавливает взаимно однозначное
соответствие между множеством 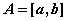 и множеством
и множеством 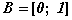 .
Следовательно,
.
Следовательно,  имеет
мощность континуума.
имеет
мощность континуума.
Кроме того, множества:
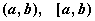 и
и 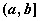 -
-
имеют ту же мощность континуума c,
так как отличаются от множества  конечным числом точек, что
сохраняет их мощность.
конечным числом точек, что
сохраняет их мощность.
Совершенно неожиданный результат
получил Г. Кантор, предполагая первоначально, что квадрат со стороной, равной
1, содержит “больше” точек, чем отрезок 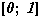 . Множества эти оказались
эквивалентными.
. Множества эти оказались
эквивалентными.

Рис. 9. Взаимно однозначное
соответствие между точками внутри квадрата и точками интервала 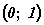 .
.
Сравнение множества натуральных
чисел, являющегося счетным, и несчетного множества точек отрезка 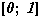 вызывает
вопрос: имеются ли множества промежуточной мощности? Иначе говоря, есть ли
бесконечное множество, в котором количество элементов “больше”, чем натуральных
чисел, и “меньше”, чем точек на отрезке
вызывает
вопрос: имеются ли множества промежуточной мощности? Иначе говоря, есть ли
бесконечное множество, в котором количество элементов “больше”, чем натуральных
чисел, и “меньше”, чем точек на отрезке 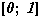 ? Это есть знаменитая проблема
КОНТИНУУМА, которая до сих пор волнует многих математиков. В начале
шестидесятых годов этого столетия было установлено, что существуют как системы
аксиом, в которых гипотеза континуума истинна, так и аксиоматические
построения, в которых она ложна.
? Это есть знаменитая проблема
КОНТИНУУМА, которая до сих пор волнует многих математиков. В начале
шестидесятых годов этого столетия было установлено, что существуют как системы
аксиом, в которых гипотеза континуума истинна, так и аксиоматические
построения, в которых она ложна.
В теории множеств доказаны следующие
интересные утверждения:
. Для любого множества A существует
множество большей мощности.
. Множества самой большой мощности
не существует.
. Множество всех подмножеств
множества A имеет мощность большую, чем мощность A.
. Множество всех подмножеств
счетного множества имеет мощность континуума.
Теория множеств полна проблем и
парадоксов, которые и в настоящее время вызывают интерес у исследователей. Вот,
например, парадокс Б. Рассела.
Пусть M - множество всех множеств, а
N - множество всех его подмножеств. Тогда мощность множества N всех подмножеств
должна быть больше мощности множества M (по утверждению 3). Но N - подмножество
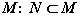 или N=M.
или N=M.
Глава V. Числовые множества
На всех этапах развития математики представления
о числе определяли уровень значимости математических знаний. Глубокое
проникновение в теорию числовых множеств сочеталось с мистическим и наивным
пониманием их свойств. Многие достижения теории чисел появлялись как дерзкие
догадки человеческой мысли.
Представление о числе существовало еще в далекой
древности, но лишь в XIX веке эти знания стали формироваться в строгую научную
теорию.
Еще пифагорийцы в VI–V веках до н.э. при
измерении геометрических величин столкнулись с недостаточностью рациональных
чисел при решении некоторых задач. По этой причине действия производились над
геометрическими величинами, а не над выражающими их числами. Первые попытки
введения иррациональных чисел были предприняты в VI веке до н.э. греческими
математиками Теэтетом и Евдоксом, позже – в “Началах” Евклида. Лишь спустя
полтора тысячелетия арабский математик и поэт Омар Хайям внес новый вклад в
понимание иррациональности. Чтобы освободить алгебру от геометрической формы,
требовалось создать общее представление о числах и действиях над ними, не
основанное на геометрии.
Понятие действительного числа появилось в
математике не сразу. Многие задачи теории действительных чисел имеют очень
давнюю историю. Проблемы, возникавшие при изучении различных числовых множеств,
появлялись спонтанно, обособленно, предопределяя порой решение смежных
вопросов. Но глубокое понимание этих проблем возникло, пожалуй, позже создания
самого математического анализа, основанного на теории действительных чисел.
Потребности счета предметов привели к появлению
множества натуральных чисел
 .
.
Далее практическая деятельность
расширила понятие числа. Возникли целые числа

и рациональные числа
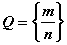 ,
,
где 
Будем считать, что дробь

несократима. Это позволит добиться
однозначности в записи рациональных чисел.
Введение рациональных чисел
оказалось еще недостаточным для решения некоторых задач. Например, диагональ
квадрата со стороной, равной 1, не может быть представлена рациональным числом.
Появились новые числа - иррациональные. Уже Аристотель пытался доказать, что  - число
иррациональное. Совокупность рациональных и иррациональных чисел образует
множество R действительных чисел. Их называют еще ВЕЩЕСТВЕННЫМИ ЧИСЛАМИ. В
математике рассматриваются различные способы введения действительных чисел. Мы
определим их как бесконечные десятичные дроби вида
- число
иррациональное. Совокупность рациональных и иррациональных чисел образует
множество R действительных чисел. Их называют еще ВЕЩЕСТВЕННЫМИ ЧИСЛАМИ. В
математике рассматриваются различные способы введения действительных чисел. Мы
определим их как бесконечные десятичные дроби вида
 ,
,
где  - некоторое целое неотрицательное
число,
- некоторое целое неотрицательное
число,  - цифры 0,
1, 2, ... , 9. Из двух знаков “±”
берется только один: для положительных чисел - знак “+”, для отрицательных
чисел - знак “-”. Знак “+” обычно опускают.
- цифры 0,
1, 2, ... , 9. Из двух знаков “±”
берется только один: для положительных чисел - знак “+”, для отрицательных
чисел - знак “-”. Знак “+” обычно опускают.
Рациональные числа представимы в
виде бесконечных десятичных периодических дробей, иррациональные - в виде
бесконечных непериодических десятичных дробей. Некоторые рациональные числа
являются конечными десятичными дробями, однако они могут быть заданы и в виде
бесконечных десятичных дробей с нулем в периоде или же в виде бесконечной
десятичной дроби с цифрой 9 в периоде. Например,
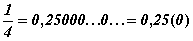
Или
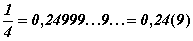 .
.
Действительные числа  и
и  называются
равными в одном из следующих случаев:
называются
равными в одном из следующих случаев:
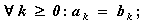
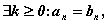


и 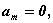

 (при
(при  равенство с индексом
равенство с индексом  следует
опустить).
следует
опустить).
В противном случае считают  .
.
Сравним неравные между собой числа.
Здесь возможны три случая.
. a и b - неотрицательны. При всегда
найдется такое натуральное n (или n=0), что
всегда
найдется такое натуральное n (или n=0), что  и
и 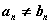 . Будем считать, что a > b, если an > bn и a < b, если an < bn.
. Будем считать, что a > b, если an > bn и a < b, если an < bn.
. a - неотрицательно, b - отрицательно.
Тогда будем считать a > b.
. a и b - отрицательны. Будем
считать, что a > b, если |a|<|b|, и a<b, если |a|>|b|.
Запись  означает,
что либо
означает,
что либо  , либо
, либо  .
.
Множество действительных чисел R
можно изобразить точками числовой прямой, на которой выбрано начало отсчета O,
масштаб и положительная ориентация: точке М, лежащей справа от точки О,
поставим в соответствие число c > 0, равное длине отрезка ОМ, точке Р,
расположенной слева от точки О, - число d < 0, где |d| - длина отрезка ОР, а
точке О - число 0. Примем без доказательства, что между точками прямой и
множеством действительных чисел существует взаимно однозначное соответствие.
Вот почему множество действительных чисел называют числовой прямой, а сами
числа - точками. Таким образом,  - множество всех действительных
чисел (числовая прямая).
- множество всех действительных
чисел (числовая прямая).
Напомним уже известную терминологию:
 - отрезок (сегмент) - множество всех
действительных чисел x, удовлетворяющих неравенству
- отрезок (сегмент) - множество всех
действительных чисел x, удовлетворяющих неравенству 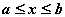 ;
;
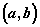 - интервал - множество всех
действительных значений x, удовлетворяющих неравенству
- интервал - множество всех
действительных значений x, удовлетворяющих неравенству 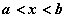 ;
;
 или
или  - полуинтервал (полусегмент) -
множество всех действительных чисел x, удовлетворяющих неравенству
- полуинтервал (полусегмент) -
множество всех действительных чисел x, удовлетворяющих неравенству  или
или  ;
;
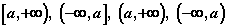 - полупрямые - множества
действительных чисел, удовлетворяющих, соответственно, неравенствам:
- полупрямые - множества
действительных чисел, удовлетворяющих, соответственно, неравенствам:
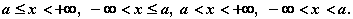
Отрезок, интервал, полуинтервал,
полупрямую и числовую прямую будем называть промежутками.
Рассматриваются также окрестность
точки c как любой интервал, содержащий точку с, и e-окрестность точки с (e > 0) - интервал 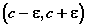 . e-окрестность может быть
задана в виде множества
. e-окрестность может быть
задана в виде множества 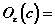
 .
.
Множество 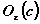 =
=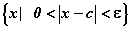 будем
называть проколотой e-окрестностью
точки с. Это есть интервал
будем
называть проколотой e-окрестностью
точки с. Это есть интервал 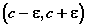 , из которого исключена точка с.
, из которого исключена точка с.
На множестве действительных чисел
вводятся основные операции - сложения и умножения, а также отношения между
действительными числами - отношения порядка, обладающие следующими свойствами.
Аксиомы сложения
1. Переместительный
закон сложения:
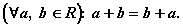
. Сочетательный закон сложения:
3. (свойство существования нуля в R).
(свойство существования нуля в R).
.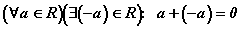 (существование противоположного
числа в R).
(существование противоположного
числа в R).
Аксиомы умножения
. Переместительный закон умножения:
множество
число действительное

6. Сочетательный закон умножения:
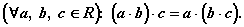
 (свойство
единицы при умножении).
(свойство
единицы при умножении).
. 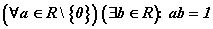 (существование обратного числа в
R).
(существование обратного числа в
R).
. Распределительный закон умножения
относительно сложения:
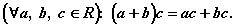
Аксиомы порядка
.  (ни для одного а не выполняется
соотношение a < a).
(ни для одного а не выполняется
соотношение a < a).
. Для любых двух различных
действительных чисел а, b выполняется одно и только одно из соотношений: a < b, b < a .
.  (если a < b и b < c, то a < c).
(если a < b и b < c, то a < c).
.  (если a < b, то для любого
действительного числа с имеем: a + c <
b + c).
(если a < b, то для любого
действительного числа с имеем: a + c <
b + c).
. 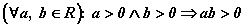 (если a > 0 и b > 0, то ab > 0).
(если a > 0 и b > 0, то ab > 0).
Аксиома полноты (непрерывности)
. Если непустые множества А и В
действительных чисел таковы, что для любых 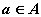 и
и  выполняется неравенство a < b, то найдется такое
действительное число с, что a <
с < b.
выполняется неравенство a < b, то найдется такое
действительное число с, что a <
с < b.
Аксиома полноты справедлива только в
R. Из данных аксиом можно вывести единственность нуля и единицы, существование
и единственность разности и частного. Отметим дополнительно свойства
неравенств, которые широко используются в различных преобразованиях.
. Если a < b, с < d , то a+c < b+d.
2. Если
a <
b, то
-a >
-b .
3. Если a > 0, b < 0, то ab < 0, а если a < 0, b < 0, то ab > 0.
. Если 0 < a < b, 0 < c < d, то 0 < ac < bd .
. Если a < b, c > 0, то ac < bc , а если a < b, c < 0, то bc < ac .
. Если 0 < a < b, то  .
.
0 < 1, -1 <
0.
. Для любых положительных чисел а и
b найдется такое натуральное число n, что na > b (аксиома Архимеда).
Обычно используются следующие
обозначения числовых множеств:
N - множество
натуральных чисел;
Z - множество целых
чисел;
Q - множество
рациональных чисел;
I - множество
иррациональных чисел;
R - множество
действительных чисел;
R+ - множество
действительных положительных чисел;
R_ - множество
действительных отрицательных чисел;
R0 - множество
действительных неотрицательных чисел;
С множество комплексных чисел (с
этим множеством нам предстоит в дальнейшем познакомиться).
Введем на множестве действительных
чисел понятие ограниченности, которое далее будет активно использоваться в
рассуждениях.
Будем называть множество  ОГРАНИЧЕННЫМ
СВЕРХУ (СНИЗУ), если существует такое действительное число М (m), что любой
элемент
ОГРАНИЧЕННЫМ
СВЕРХУ (СНИЗУ), если существует такое действительное число М (m), что любой
элемент  удовлетворяет
неравенству
удовлетворяет
неравенству 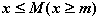 :
:

Число M называется ВЕРХНЕЙ ГРАНЬЮ
МНОЖЕСТВА A, а число m - НИЖНЕЙ ГРАНЬЮ этого множества.
Множество, ограниченное сверху и
снизу, называется ограниченным.
Множество N натуральных чисел
ограничено снизу, но не ограничено сверху. Множество целых чисел Z не
ограничено ни снизу, ни сверху.
Если рассмотреть множество площадей
произвольных треугольников, вписанных в круг диаметра D, то снизу оно
ограничено нулем, а сверху - площадью любого многоугольника, включающего в себя
круг (в частности, площадью описанного квадрата, равной D2).
Очевидно, что всякое ограниченное
сверху (снизу) множество имеет бесконечно много верхних (нижних) граней.
Возникает вопрос, есть ли наименьшая из всех верхних границ и наибольшая из
всех нижних?
Будем называть число 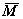 точной
верхней гранью ограниченного сверху множества А Ì R, если:
точной
верхней гранью ограниченного сверху множества А Ì R, если:
. 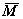 является одной из верхних граней
множества А;
является одной из верхних граней
множества А;
. 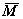 является наименьшей из верхних
граней множества А. Другими словами, действительное число
является наименьшей из верхних
граней множества А. Другими словами, действительное число 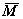 является
точной верхней гранью множества А Ì R, если:
является
точной верхней гранью множества А Ì R, если:
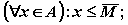
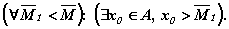
Принято обозначение
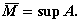
Аналогично вводятся: 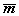 - точная
нижняя грань ограниченного снизу множества А и соответствующие обозначения
- точная
нижняя грань ограниченного снизу множества А и соответствующие обозначения
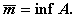
Точные грани множества могут ему как
принадлежать, так и не принадлежать.
ТЕОРЕМА. Ограниченное сверху (снизу)
непустое множество действительных чисел имеет точную верхнюю (нижнюю) грань.
Эту теорему мы примем без
доказательства. Например, если 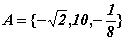 , то верхней границей можно считать
число 100, нижней -10, а
, то верхней границей можно считать
число 100, нижней -10, а 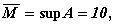
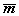
 . Если же
. Если же  , то
, то 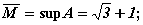
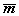
 . Во втором примере точные границы
данному множеству не принадлежат.
. Во втором примере точные границы
данному множеству не принадлежат.
На множестве действительных чисел
можно выделить два непересекающихся подмножества алгебраических и
трансцендентных чисел.
АЛГЕБРАИЧЕСКИМИ ЧИСЛАМИ называются
числа, которые являются корнями многочлена

коэффициенты которого - целые числа.
В высшей алгебре доказывается, что
множество комплексных корней многочлена 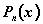 конечно и равно n (комплексные
числа являются обобщением действительных). Множество алгебраических чисел
счетно, оно включает в себя все рациональные числа (так как числа вида
конечно и равно n (комплексные
числа являются обобщением действительных). Множество алгебраических чисел
счетно, оно включает в себя все рациональные числа (так как числа вида
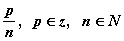
удовлетворяют уравнению

Доказано также, что существуют
алгебраические числа, не являющиеся радикалами из рациональных чисел. Этот
очень важный результат остановил бесплодные попытки найти решения уравнений
степени выше четвертой в радикалах.
Множество, являющееся разностью
множеств действительных и алгебраических чисел, называют множеством
ТРАНСЦЕНДЕНТНЫХ ЧИСЕЛ. Очевидно, каждое трансцендентное число не может быть
корнем многочлена с целыми коэффициентами. Вместе с тем, доказательство трансцендентности
каких-либо отдельных чисел вызывало огромные трудности. Лишь в 1882 году
профессор Кенигсбергского университета Ф. Линдеман сумел доказать
трансцендентность числа  , откуда
стала ясна невозможность решения задачи о квадратуре круга (построить с помощью
циркуля и линейки квадрат, имеющий площадь данного круга). Мы видим, что идеи
алгебры, анализа, геометрии взаимно проникают друг в друга.
, откуда
стала ясна невозможность решения задачи о квадратуре круга (построить с помощью
циркуля и линейки квадрат, имеющий площадь данного круга). Мы видим, что идеи
алгебры, анализа, геометрии взаимно проникают друг в друга.
Аксиоматическое введение
действительных чисел далеко не единственное. Эти числа могут быть введены путем
объединения множества рациональных и иррациональных чисел, или же как
бесконечные десятичные дроби, или с помощью сечений на множестве рациональных
чисел.
В современной математике понятие
множества является одним из основных. Универсальность этого понятия в том, что
под него можно подвести любую совокупность явлений, предметов и объектов
реального мира. Сами множества так же могут объединяться во множества.
Например, математики говорят о множестве фигур на плоскости, о множестве тел в
пространстве, но каждую фигуру, каждое тело они мыслят как множество точек.
Суть понятия “множество” вполне
передается словами: “совокупность”, “собрание”, “набор” и т.д. Однако, как
абстрактное математическое понятие “множество” неопределимо.
Несмотря на это, определить
какое-либо конкретное множество - задача не из трудных. Определить любое
конкретное множество - значит определить, какие предметы (явления, объекты)
принадлежат данному множеству, а какие не принадлежат. Иначе говоря, всякое
множество однозначно определяется своими элементами.
Для того чтобы некоторую
совокупность элементов можно было назвать множеством, необходимо, чтобы
выполнялись следующие условия:
Должно существовать правило,
позволяющее определить, принадлежит ли указанный элемент данной совокупности.
Должно существовать правило,
позволяющее отличать элементы друг от друга. (Это, в частности, означает, что
множество не может содержать двух одинаковых элементов).
Система аксиом теории множеств была создана для
решения задачи обоснования базовых положений современной математики. Таким
образом существующие разделы математики можно считать a priori
непротиворечивыми, поскольку все их доказанные высказывания логически могут
быть сведены к аксиомам. В этом отношении аксиоматика выполнила свое
предназначение.
Список использованной литературы
Варпаховский
Ф.Л., Солодовников А.С. Алгебра. Элементы теории множеств. Линейные уравнения и
неравенства. Матрицы и определители. - М.: Педагогика, 2004,- 160 с.
Завало
С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел. Часть I - Киев: Вища
школа, 1977. - 398 с.
Куликов
Л.А. Алгебра и теория чисел. - М.: Высшая школа, 1999. - 560 с.
Куратовский
К., Мостовский А. Теория множеств. - М.: 2000 - 400 с.
Ларин
А. А. Курс высшей математики. М.: 2001 - 632 с.
1.