Математика
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО
ХОЗЯЙСТВА и ГОСУДАРСТВЕННОЙ СЛУЖБЫ
при ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
СИБИРСКИЙ ИНСТИТУТ - ФИЛИАЛ РАНХиГС
ЦЕНТР ПЕРЕПОДГОТОВКИ СПЕЦИАЛИСТОВ
Кафедра Информатики и математики
Письменное контрольное задание
для студентов дистанционного обучения
Математика
Студент Кобус Ирина Юрьевна
Группа 11417
Дата 24.03.2012 г
Преподаватель Шеремет Михаил Сергеевич
Новосибирск 2012 г.
Найти участки возрастания и убывания функций,
классифицировать точки экстремума
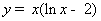
Функция
определена на промежутке .
.
Необходимое
условие существования точек экстремума для функции - это существование корней
уравнения: первая производная функции равна нулю, y'(x)=0.
Найдем
первую производную функции, решим уравнение y'(x)=0. Найдем
точки подозрительные на экстремум.

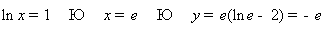
Точка
возможного экстремума A(e, -e).
Рассмотрим
знак производной на промежутках 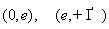
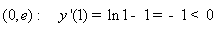 . Значит,
функция убывает на этом промежутке.
. Значит,
функция убывает на этом промежутке.
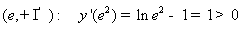 . Значит,
функция возрастает на этом промежутке.
. Значит,
функция возрастает на этом промежутке.
Точка
A(e, -e) - точка минимума.
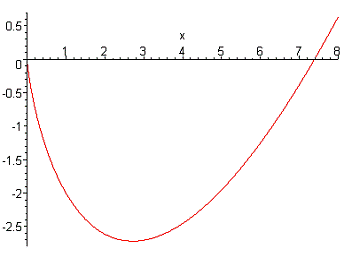
Найти
определенные интегралы
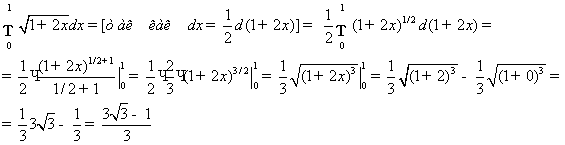
Выполнить
умножение матриц АВ-1С
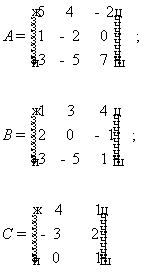
Найдем
матрицу B-1.
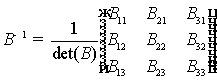
det(B) -
определитель матрицы B
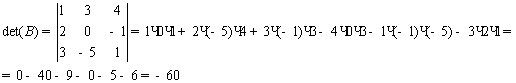
 ,
,
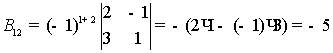 ,
,
 ,
,
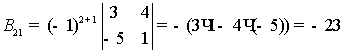 ,
,
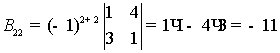 ,
,
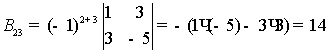 ,
,
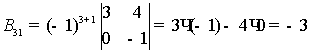 ,
,
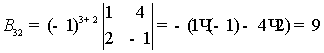 ,
,
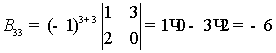
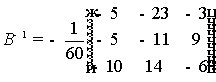


Теория
вероятности (события)
В
одной комнате находятся четыре девушки и семь юношей. Наудачу выбирают двух человек.
Найти вероятность того, что оба они окажутся юношами.
Всего
человек 4+7=11
Событие
A - два выбранных человека - юноши.
Найдем
вероятность p(A) по классическому определению вероятности, 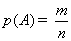 , где m - число способов выбора, благоприятных событию A, n -
число всеx способов выбора.
, где m - число способов выбора, благоприятных событию A, n -
число всеx способов выбора.
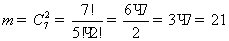 - число
способов выбора двух юношей из семи юношей.
- число
способов выбора двух юношей из семи юношей.
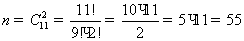 - число
способов выбора двух человек из 11-ти человек.
- число
способов выбора двух человек из 11-ти человек.

Теория
вероятности (случайные величины)
Вероятность того, что стрелок попадет в «десятку», равна 0,5. Составить
закон распределения числа попаданий в серии их четырех выстрелов. Построить
многоугольник распределения. Найти математическое ожидание и дисперсию
случайной величины.
Пусть
событие А - стрелок попадет в «десятку», тогда p(A) =
0,5, p( ) = 1 - p = 1 - 0,5 = 0,5 - вероятность того, что стрелок не
попадет в «десятку».
) = 1 - p = 1 - 0,5 = 0,5 - вероятность того, что стрелок не
попадет в «десятку».
Случайная
величина X может принимать значения 0,1,2,3,4 - число попаданий
из четырех выстрелов. Найдем вероятности p(X)
для каждого значения X - закон распределения случайной величины.
P0 = (X=0) = p( )
p(
)
p( ) p(
) p( )p(
)p( ) = 0,54 = 0,0625= P(X=1) = 4·p(
) = 0,54 = 0,0625= P(X=1) = 4·p( )p(
)p( )p(
)p( )p(A) = 4·0,54 = 0,25= P(X=2) = 6·p(
)p(A) = 4·0,54 = 0,25= P(X=2) = 6·p( )p(
)p( )p(A)
p(A) = 6·0,54 = 0,375= P(X=3) = 4·p(
)p(A)
p(A) = 6·0,54 = 0,375= P(X=3) = 4·p( )p(A)
p(A) p(A)=4· 0,54 = 0,25= P(X=4) = p(A)p(A) p(A) p(A)= 0,54 = 0,0625
)p(A)
p(A) p(A)=4· 0,54 = 0,25= P(X=4) = p(A)p(A) p(A) p(A)= 0,54 = 0,0625
Сумма
всех вероятностей P = 0,0625+0,25+0,375+0,25+0,0625 = 1. Значит закон
распределения случайной величины составлен верно.
|
Xi
|
0
|
1
|
2
|
3
|
4
|
|
Pi
|
0,0625
|
0,25
|
0,375
|
0,0625
|
Математическое ожидание
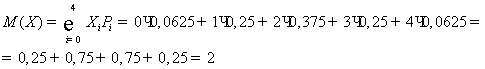
Дисперсия
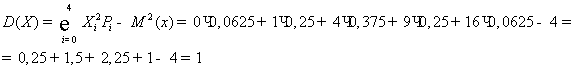
Математическая
статистика
1. В продовольственном магазине в течение месяца собрана информация
о числе посетителей в сутки (в тыс. человек):
|
0,98
|
1,06
|
1,12
|
1,11
|
0,68
|
1,04
|
0,94
|
0,94
|
0,61
|
1,02
|
|
0,97
|
1,04
|
0,96
|
1,16
|
1,17
|
0,71
|
0,58
|
1,03
|
0,65
|
1,28
|
|
1,04
|
0,98
|
0,71
|
0,7
|
1,27
|
1,09
|
1,03
|
0,93
|
1,16
|
1,2
|
Построить интервальную группировку данных по пяти интервалам равной длины
и соответствующую гистограмму. Найти среднее число посетителей и исправленную
дисперсию для выборки. Построить доверительные интервалы надежности 90% и 98%
для среднего числа посетителей.
Для построения интервальной группировки необходимо определить величину
частичных интервалов.
Найдем размах варьирования R. : R= Xmax - Xmin =
1,28-0,58=0,7.
Число интервалов равно v = 5, тогда длина частичного интервала
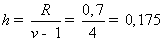
За
начало первого интервала рекомендуется брать величину
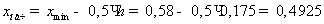
Конец
последнего интервала должен удовлетворять условию
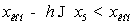
ni* - частоты
соответствующего интервала
Интервальная
группировка:
|
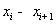 0,4925-0,66750,6675-0,84250,8425-1,01751,0175-1,19251,1925-1,3675 0,4925-0,66750,6675-0,84250,8425-1,01751,0175-1,19251,1925-1,3675
|
|
|
|
|
|
|
ni*
|
3
|
4
|
7
|
13
|
3
|
Выборочная
средняя 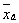 .
.
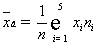 ,
,  - объем выборки
- объем выборки

Исправленная
дисперсия
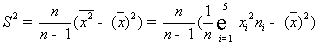
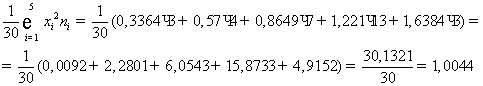

Доверительный
интервал для среднего числа посетителей - a надежности 90%, то есть с
доверительной вероятностью 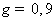
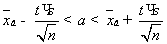 , где
, где 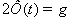
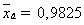 , n = 30,
, n = 30,
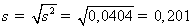
Ф(t) -
функция Лапласа, значения которой вычисляются по таблице.
Вычислим
значение t из таблицы значений функции Лапласа, если 2Ф(t) =
0,9.
Ф(t) =
0,45. Находим t = 1,64.
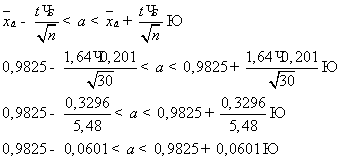
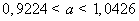 -
интервал для среднего числа посетителей - a надежности 90%.
-
интервал для среднего числа посетителей - a надежности 90%.
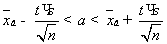 , где
, где 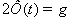
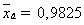 , n = 30,
, n = 30,
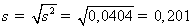
Ф(t) -
функция Лапласа, значения которой вычисляются по таблице.
Вычислим
значение t из таблицы значений функции Лапласа, если 2Ф(t) =
0,98.
Ф(t) =
0,49. Находим t = 2,32.
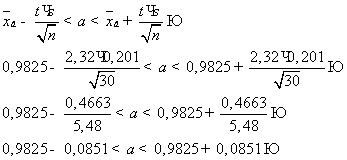
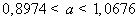 -
интервал для среднего числа посетителей - a надежности 98%.
-
интервал для среднего числа посетителей - a надежности 98%.
Решить задачу линейного программирования
|
10
|
|
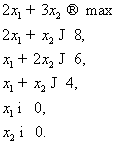
|
Решим задачу графически
Построим область на координатной плоскости, точки которой удовлетворяют
данным неравенствам.
Построим прямые по точкам, ограничивающие область.



экстремум матрица
вероятность линейный
Найдем точки пересечения прямых между собой и с осями координат.
Точка
пересечения прямых (1) и (2)  .
.
Точка
пересечения прямых (1) и (3) 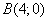 .
.
Точка
пересечения прямых (2) и (3)  .
.
Точка
пересечения прямой (2) с осью 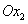
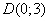 .
.
Область,
удовлетворяющая неравенствам - четырехугольник OBCD.
Так
как функция 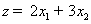 линейная, то для нахождения максимума функции найдем
значения функции
линейная, то для нахождения максимума функции найдем
значения функции 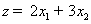 в точках O, B, C, D и выберем наибольшее значение.
в точках O, B, C, D и выберем наибольшее значение.

Значит,
 .
.