Векторное обоснование евклидовой геометрии-аксиоматика Вейля
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Калужский
государственный университет им. К.Э. Циолковского»
Дипломная
работа.
Тема:
Векторное обоснование евклидовой геометрии-аксиоматика Вейля
Выполнила: Студентка 5-го курса
Группы ФМ-51
Ильина Е.Е.
Научный руководитель:
доцент, к.ф-м.н. Савоськина И.И.
Калуга,2012г.
Содержание
Введение
Глава
I. Теоретические
основы аксиоматики Вейля
.
Биография Вейля
2. Варианты аксиоматики Вейля
.Аксиоматика Вейля
. Непротиворечивость и категоричность
аксиоматики Вейля
.Прямая
. Плоскость
. Аксиоматика Вейля и школьная геометрия
Глава
II. Задачи, решаемые
векторным способом
.
Основные задачи о прямых и плоскостях
2. Доказательства и решения задач
Заключение
Список
литературы
Введение
Одним из фундаментальных понятий современной
математики являются вектор и его обобщение - тензор. Эволюция понятия вектора
осуществлялась благодаря широкому использованию этого понятия в различных
областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия
ознаменовались широким развитием векторного исчисления и его приложений. Были
созданы векторная алгебра и векторный анализ, общая теория векторного
пространства. Эти теории были использованы при построении специальной и общей
теории относительности, которые играют исключительно важную роль в современной
физике.
Тема этой работы «Векторное обоснование
евклидовой геометрии». Тема достаточно актуальна в современном мире, это
объясняется тем, что в соответствии с требованиями новой программы по
математике понятие вектора стало одним из ведущих понятий школьного курса
математики.
Векторному способу решения задач в школьном
курсе геометрии уделяется достаточно мало времени. На уроках разбираются и
решаются лишь немногие задачи. Векторный способ решения задач достаточно
сложный, нельзя понять и уловить его смысл за пару занятий. Таким образом,
школьники не могут в полной мере овладеть таким способом решения задач. В
институтской программе также мало часов отводится на изучение данной темы.
Встречаясь с задачей, которую необходимо решать данным способом и учащийся, и
студент видят перед собой сложную, временами неразрешимую задачу. Для освоения
данного способа решения, необходимо изучить основы векторного способа решения
задач.
Традиционный путь построения геометрии, идущий
от Евклида и закрепленный Д. Гильбертом в его аксиоматики геометрии (1899 год),
заключается в следующем. Основными неопределяемыми понятиями геометрии служат
понятия точки, прямой, плоскости. Основными неопределяемыми отношениями между
ними являются: отношения принадлежности (например, точка лежит на прямой,
плоскость проходит через прямую и т.д.); понятие «между», являющееся отношением
трёх точек одной прямой и позволяющее определить отрезок, луч, угол и т.д;
отношение равенства (конгруэнтности), связывающее два отрезка или два угла.
Формулируются два десятка аксиом, связывающих между собой основные понятия и
отношения (и, по существу, дающих косвенное определение этих основных понятий и
отношений). Среди этих аксиом имеются такие хорошо известные, как «Через две
различные точки проходит единственная прямая», «Из трёх точек одной прямой лишь
одна лежит между двумя другими», а также аксиома параллельности и некоторые
другие. Все остальные понятия геометрии уже точно определяются, предложения
геометрии (отличные от аксиом) строго доказываются (то есть выводятся из аксиом
в соответствии с правилами логики.
Этот путь построения евклидовой геометрии
является самым известным, но отнюдь не единственно возможным.
В основе всех современных теорий евклидова
пространства лежит понятие числа. В этом состоит коренное отличие современных
теорий от классической теории Евклида-Гильберта, в которой число рождается в
рамках самой теории как отношение отрезков или мера длины.
В современных теориях система действительных
чисел либо непосредственно используется в определении структуры евклидова
пространства, либо является вспомогательной структурой для определения других
вспомогательных структур (векторного пространства, метрического пространства).
Более того, категоричность теории евклидова пространства позволяет
рассматривать его как арифметическое пространство 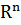 ,
в котором должным образом определены необходимые понятия и отношения.
,
в котором должным образом определены необходимые понятия и отношения.
Использование числа значительно упрощает
построение теории евклидова пространства, однако во многом лишает это
построение наглядности и того, конструктивного характера, который присущ теории
Евклида - Гильберта. В этом состоит существенный методический недостаток таких
теорий с точки зрения их использования для построения начал школьного курса
геометрии.
В 1918 году известным математиком Г.Вейлем было
предложено так называемое «векторное» обоснование евклидовой геометрии. В
качестве вспомогательной структуры он использует евклидово векторное
пространство, элементы которого играют роль операторов в пространстве точек.
Размерность векторного пространства определяет
размерность точеного пространства. Аксиоматика Вейля переводит теорию евклидова
(точечного) пространства на язык линейной алгебры.
Простота аксиоматики, её пригодность для
обоснования геометрии многомерных пространств, алгоритмизация теории на основе
линейной алгебры сделали аксиоматику Вейля наиболее употребительной в
современной геометрии и её приложениях. Использование векторных пространств
позволяют построит «в духе Вейля» аксиоматики неевклидовых пространств, придав
тем самым известное единообразие обоснованию различных геометрий.
В качестве основных неопределяемых понятий и отношений
геометрии в аксиоматике Вейля принимаются: вектор, точка, сумма векторов,
произведение вектора на действительное число, скалярное произведение векторов и
откладывание вектора от точки. Прямые, плоскости, равенство фигур и т.п.
определяются через эти первоначальные понятия и отношения.
Основной целью написания данной работы является,
ознакомление с векторным обоснованием евклидовой геометрии и рассмотрение
основных видов задач, решаемых векторным способом.
Исходя из данной цели, были поставлены следующие
задачи:
- ознакомиться с биографией Г. Вейля;
- изучить различные аксиоматики Вейля;
- выявить взаимосвязь школьного курса
геометрии и аксиоматики Вейля;
- рассмотреть основные виды задач,
решаемые векторным способом.
Глава I.
Теоретические основы аксиоматики Вейля
. Биография Вейля
Герман Клаус Хуго Вейль (9.11.1885 - 9.12.1955)
- немецкий математик и физик, член Национальной Академии Наук США, Американский
академик искусств и наук. В 1908 году окончил Гёттингенский университет, где
получил степень доктора философии. Учителем Вейля был Д.Гильберт. В 1908-1913 и
1930-1933 работал там же, в 1913-1930 профессор Цюрихского технологического
института, в 1933-1955- Принстонского института перспективных исследований
(США). Первые работы посвящены теории тригонометрических рядов, рядам по
ортогональным функциям и почти периодическим функциям, теории дифференциальных
и интегральных уравнений (в частности, создал спектральную теорию
дифференциальных операторов), а также теории функций комплексного переменного.
В последней он заложил основы тех её направлений, которые опираются на понятие
римановой поверхности. В теории чисел известны суммы Вейля, имеющие большое
значение в аддитивной теории чисел (особенно для работ И.М.Виноградова).
Одновременно с Э.Ж.Картаном исследовал теорию непрерывных групп, применение
которым нашел в дифференциальной геометрии, физике и теории относительности.
Одновременно с Я.А.Схоутеном обобщил понятие риманова пространства на случай
пространства аффинной и конформной связности. Ввёл понятие аффинной связности,
играющей важную роль в дифференциальной геометрии и физике. Поставил (1915)
проблему реализации в трёхмерном евклидовом пространстве регулярной метрики
положительной кривизны, заданной на сфере. С помощью методов групп теории получил
некоторые результаты, относящиеся к теории атомных спектров. Разработал (1924)
теорию представлений групп преобразований. Исследовал (1927) значение теории
групп для развития квантовой механики. В области философии математики он
примкнул к направлению интуиционизма. Ему принадлежит суждение о наступлении
нового кризиса в математике. Попытка Вейля разработать единую теорию поля
потерпела неудачу.
. Варианты аксиоматики Вейля
Известны разные варианты аксиоматики Вейля.
Рассмотрим один из них.
Пусть V
- n-мерное евклидово
векторное пространство и Е- непустое множество, элементы которого А,В,С,… будем
называть точками. Пусть на множестве Е задано отображение 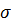 :
Е
:
Е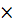 Е
Е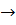 V.
V.
Обозначим вектор 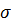 (A,B)=
(A,B)= и назовем его переносом, переводящим точку А в точку В.Потребуем что бы
отображение
и назовем его переносом, переводящим точку А в точку В.Потребуем что бы
отображение 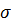 обладало
свойствами:
обладало
свойствами:
I.Для любой
фиксированной точки А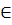 E
отображение
E
отображение  : E
: E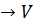 по закону:
по закону:
 (В)=
(В)=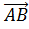 ,
,
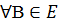 является
биекцией.
является
биекцией.
II. 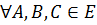 ,
, +
+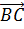 =
=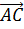
Тогда множество Е называется n-мерным
евклидовым пространством, а векторное пространство V
- его пространством переносов. Свойства I,II
отображения 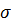 называются
аксиомами Вейля.
называются
аксиомами Вейля.
Отображение 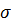 каждой
паре точек (А,В) ставит в соответствие вектор
каждой
паре точек (А,В) ставит в соответствие вектор  =
= из V. Если первую точку
А пары зафиксируем, а вторая точка В будет пробегать все множество Е, то
получим отображение
из V. Если первую точку
А пары зафиксируем, а вторая точка В будет пробегать все множество Е, то
получим отображение  : E
: E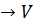 . Аксиома I требует чтобы
полученное отображение
. Аксиома I требует чтобы
полученное отображение  было биективным
отображением Е на V. Требование
аксиомы I можно истолковать
как требование биективности соответствия между точками В
было биективным
отображением Е на V. Требование
аксиомы I можно истолковать
как требование биективности соответствия между точками В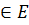 и радиус-векторами
и радиус-векторами 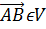 этих точек при
фиксированном начале А.
этих точек при
фиксированном начале А.
Требование аксиомы II
означает следующее. Если вектор  переводит точку А
в точку В
переводит точку А
в точку В 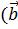 =
= ),
а вектор
),
а вектор 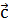 переводит
точку В в точку С (c=
переводит
точку В в точку С (c=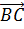 ),
то вектор
),
то вектор  +
+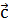 должен переводить точку в точку С (
должен переводить точку в точку С ( +
+ =
=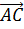 ).
).
Таким образом, в определении структуры евклидова
пространства по вейлю векторы играют роль операторов на множестве точек:  (A)=B
(A)=B
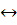
 =
= ,
аналогично роли чисел в определении структуры векторного пространства.
,
аналогично роли чисел в определении структуры векторного пространства.
Если в определении структуры евклидова
пространства не требовать евклидовости его пространства переносов (то есть не
вводить отображение g, обладающее
свойствами 9)-11), то мы получим определение n-мерного
аффинного пространства. Поэтому евклидово пространство можно рассматривать как
обогащенную структуру аффинного пространства: в пространстве переносов V
аффинного пространства вводится новое отношение - скалярное умножение или
положительно определенная квадратичная форма (называемая метрической формой
евклидова пространства). Это новое отношение позволяет определить в Е новые
понятия, о которых не может идти речь в аффинном пространстве: «расстояние
между точками» 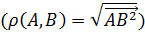 , «движение»
(преобразование пространства Е, сохраняющее расстояния) и др.
, «движение»
(преобразование пространства Е, сохраняющее расстояния) и др.
В аксиоматике Вейля основное отношение 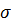 каждой
паре точек (А,В)
каждой
паре точек (А,В)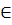 E
E сопоставляет вектор
сопоставляет вектор 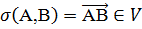 . В силу аксиомы I
каждой паре (
. В силу аксиомы I
каждой паре (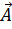 ,
, )
) сопоставляется единственная точка В=
сопоставляется единственная точка В=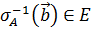 и, значит, возникает отображение
и, значит, возникает отображение  .
Это позволяет придать аксиоматике Вейля иной вид.
.
Это позволяет придать аксиоматике Вейля иной вид.
В качестве основного отношения задают
отображение 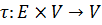 и обозначают
и обозначают 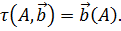 Операцию,
сопоставляющую точке А и вектору
Операцию,
сопоставляющую точке А и вектору 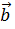 точку
точку
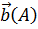 =В,
называют «откладыванием вектора
=В,
называют «откладыванием вектора  от точки А».
от точки А».
В этом случае аксиомы Вейля - свойства
отображения 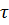 - формулируют
следующим образом:
- формулируют
следующим образом:
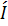 .
.  B,
B,
то есть существует и единственный вектор,
который переводит заданную точку А в любую заданную точку B.
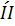 .
. 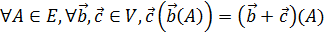 .
.
Существование отображения 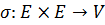 здесь
обеспечивается аксиомой
здесь
обеспечивается аксиомой 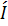 .
.
При таком подходе особо подчеркивается роль
векторов как операторов на множестве точек. Этот подход хорошо сочетается с
истолкованием вектора как параллельного переноса в школьном курсе геометрии.
Напротив, первый из указанных вариантов аксиоматики Вейля, в котором вектор
связывается с парой точек, более подходит к такому изложению школьного курса
геометрии, в котором вектор выступает как направленный отрезок или класс
эквивалентных направленных отрезков.
Таким образом, если заключительная часть
школьного курса геометрии строится на основе аксиоматики Вейля, то имеется
возможность выбрать тот из вариантов, который наиболее близок изложению
предыдущего материала.
. Аксиоматика Вейля
а)внутренний закон композиции (алгебраическая
операция) f: V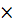 V
V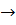 V,
который мs назовем сложение и
обозначим f (
V,
который мs назовем сложение и
обозначим f ( ,
, )=
)=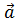 +
+
 ,
обладающий свойствами:
,
обладающий свойствами:
) +
+  )
+
)
+ =
=  +
+
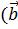 +
+
 )
для любых трёх векторов
)
для любых трёх векторов  ,
,  ,
,

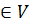 ;
;
)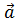 +
+  =
= +
+ для любых двух векторов
для любых двух векторов  ,
,  ;
;
) Существует такой вектор 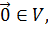 что
что
 =
=
 для
любого вектора
для
любого вектора 
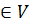 (вектор
(вектор
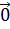 называется
нулевым вектором);
называется
нулевым вектором);
) Для любого вектора  найдется
такой вектор
найдется
такой вектор 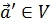 , что
, что  +
+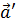 =
=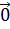 (вектор
(вектор 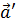 называется
вектором, противоположным вектору
называется
вектором, противоположным вектору 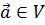 ,
и обозначается через -
,
и обозначается через - );
);
б)Внешний закон композиции (внешняя
алгебраическая операция),
h: R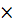 V
V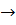 V,
который мы назовем умножение вектора на число и обозначим h(
V,
который мы назовем умножение вектора на число и обозначим h(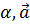 )=
)=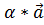 (
(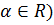 ,
обладающий свойствами:
,
обладающий свойствами:
) 1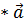 =
= для любого вектора
для любого вектора 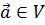 ;
;
) 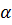 (
(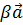 )
= (
)
= (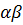 )
) для любого вектора
для любого вектора 
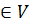 и
любых (действительных) чисел
и
любых (действительных) чисел 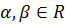
) (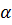 +
+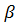 )
) =
= +
+ для любого вектора
для любого вектора 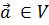 и любых
(действительных) чисел
и любых
(действительных) чисел 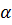 ,
, 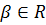 .
.
) 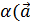 +
+
 )=
)=
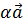 +
+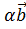 для любых двух векторов
для любых двух векторов  ,
,  и
любого действительного числа
и
любого действительного числа 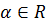 .
.
Свойства 1)-8) законов сложения и умножения на
число называются аксиомами векторного пространства. Векторное пространство
называется также линейным пространством.
Заметим, что в определении структуры векторного
пространства числа выступают в роли операторов, действующих в V
по закону: 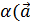 )=
)=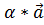 .
.
Векторы 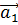 ,
,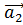 ,…,
,…, называются линейно независимыми, если равенство
называются линейно независимыми, если равенство
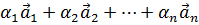 =
=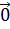 выполняется только в том случае, когда все числа
выполняется только в том случае, когда все числа 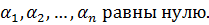 Если
же указанное равенство выполняется в том случае, когда некоторые из
Если
же указанное равенство выполняется в том случае, когда некоторые из  отличны
от нуля, то векторы
отличны
от нуля, то векторы 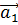 ,
,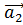 ,…,
,…, называются линейно независимыми.
называются линейно независимыми.
Векторное пространство V
называют n-мерным и пишут dimV=n,
если в V существуют n
линейно независимых векторов и всякие n+1
векторов из М линейно зависимы. Эти условия составляют аксиому размерности
векторного пространства V.
Если dimV=n,
то любые n линейно
независимых векторов 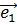 ,
,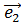 ,…,
,…,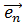 из V составляют базис
этого векторного пространства. Из аксиомы размерности следует, что всякий
вектор
из V составляют базис
этого векторного пространства. Из аксиомы размерности следует, что всякий
вектор 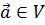 разлагается
и притом однозначно по векторам базиса:
разлагается
и притом однозначно по векторам базиса:  =
=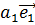 +
+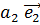 +…+
+…+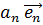 (
(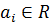 )/
Числа
)/
Числа 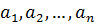 называются
координатами вектора
называются
координатами вектора  относительно
базиса
относительно
базиса 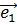 ,
,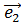 ,…,
,…,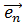 .
.
Евклидовым векторным пространством называется
векторное пространство V,
на котором определено отображение g:
V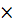 V
V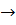 R,
которое мы назовем скалярным умножением векторов и обозначим g(
R,
которое мы назовем скалярным умножением векторов и обозначим g(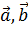 )=
)=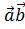 ,
обладающее свойствами:
,
обладающее свойствами:
)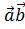 =
=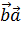 для любых двух векторов
для любых двух векторов  и
и 
)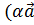 +
+  )
) =
=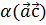 +
+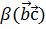 для любых трёх векторов
для любых трёх векторов  ,
,  ,
,
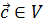 и
любых (действительных) чисел
и
любых (действительных) чисел 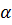 ,
, 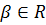 ;
;
)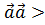 0 для любого
вектора
0 для любого
вектора 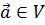 ,
,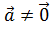 .
.
Число 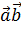 называют
скалярным произведением векторов
называют
скалярным произведением векторов 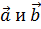 ,
а число
,
а число  -
скалярным квадратом вектора
-
скалярным квадратом вектора  и обозначают
и обозначают 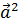 .
.
Аксиомы 1)-4) векторного пространства определяют
на множестве V структура абелевой
группы. Введение нового отношения (умножения вектора на число) придает абелевой
группе новые свойства: появляется возможность говорить о линейно зависимых и
линейно независимых векторах, о линейной оболочке системы векторов, о
размерности векторного пространства и др. Поэтому говорят, что векторное
пространство получено обогащением структуры абелевой группы. В свою очередь,
евклидово векторное пространство получено обогащением структуры векторного
пространства: в нем введено новое отношение- скалярное умножение, позволяющее
говорить о длине вектора 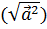 , об
ортогональности векторов (
, об
ортогональности векторов (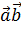 =0) и др.
=0) и др.
Отображение g:
V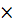 V
V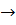 R,
обладающее свойствами 9)-11), является симметрической билинейной положительной
формой, определенной на векторном пространстве V.
Она определяет положительную квадратичную форму
R,
обладающее свойствами 9)-11), является симметрической билинейной положительной
формой, определенной на векторном пространстве V.
Она определяет положительную квадратичную форму 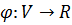 по
закону
по
закону 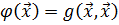 ,
для
,
для 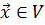 .
.
Обратно, по квадратичной форме 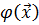 ,заданной
на V, можно
восстановить билинейную форму
,заданной
на V, можно
восстановить билинейную форму 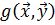 по формуле
по формуле
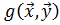 =
= (
(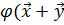 )-
)-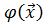 -
-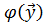 ).
).
Значит, векторное пространство М можно
превратить в евклидово векторное пространство, задав на М положительно
определенную (симметрическую) квадратичную форму.
4. Непротиворечивость и
категоричность аксиоматики Вейля
Для доказательства непротиворечивости системы
аксиом Вейля n- мерного евклидова
пространства нужно построить какую-нибудь её модель. Сначала построим модель
вспомогательной структуры n-мерного
евклидова векторного пространства.
Возьмем V= .
Сумму векторов, произведение вектора на число и скалярное произведение векторов
определим следующим образом: если
.
Сумму векторов, произведение вектора на число и скалярное произведение векторов
определим следующим образом: если
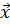 =
=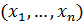 ,
,
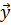 =
=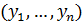 ,
то
,
то
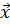 +
+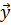 =(
=( ),
),
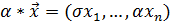 ,
,
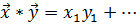 +
+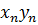 .
.
Тогда, очевидно, все аксиомы n-
мерного евклидова векторного пространства будут выполнятся и, значит, эта система
аксиом непротиворечива (если непротиворечива арифметика действительных чисел).
Теперь в качестве множества Е точек возьмем то
же множество  таким, каким оно
было до наделения его структурой векторного пространства: А=
таким, каким оно
было до наделения его структурой векторного пространства: А=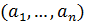 ,
B=
,
B=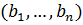 - точки множества E=
- точки множества E= .
Основное отношение - отображение
.
Основное отношение - отображение  определим
следующим образом:
определим
следующим образом: . Тогда легко
проверить, что аксиомы I,
II Вейля будут
выполнятся. Следовательно, система аксиом Вейля n-мерного
евклидова (а также и аффинного) пространства непротиворечива, если
непротиворечива арифметика. Построенная модель евклидова пространства
называется арифметической.
. Тогда легко
проверить, что аксиомы I,
II Вейля будут
выполнятся. Следовательно, система аксиом Вейля n-мерного
евклидова (а также и аффинного) пространства непротиворечива, если
непротиворечива арифметика. Построенная модель евклидова пространства
называется арифметической.
Зафиксировав какую-нибудь точку A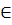 E
и воспользовавшись биективностью отображения
E
и воспользовавшись биективностью отображения  :E
:E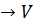 ,
можно отождествить пространства Е и V.
Но все n-мерные евклидовы
векторные пространства изоморфны. Следовательно, система аксиом Вейля n-мерного
евклидова пространства категоричная, то есть все её модели изоморфны. Поэтому
для изучения геометрии такого пространства можно использовать какую-нибудь одну
её модель, например арифметическую. Так часто и поступают, рассматривая
евклидово пространство как
,
можно отождествить пространства Е и V.
Но все n-мерные евклидовы
векторные пространства изоморфны. Следовательно, система аксиом Вейля n-мерного
евклидова пространства категоричная, то есть все её модели изоморфны. Поэтому
для изучения геометрии такого пространства можно использовать какую-нибудь одну
её модель, например арифметическую. Так часто и поступают, рассматривая
евклидово пространство как  .
.
Арифметическая модель n-мерного
евклидова пространства, в которой и векторы, и точки - кортежи действительных
чисел, наталкивает на мысль построить модель евклидова пространства в рамках
теории любого евклидова векторного пространства.
Именно пусть V
- n-мерное евклидово
векторное пространство. Положим E=V,
то есть точками будем называть векторы из V.
Пусть 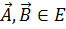 .
Отображение
.
Отображение  определим законом:
определим законом:
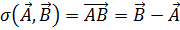 .
.
Тогда аксиомы Вейля будут выполнятся так же, как
в арифметической модели. Эту модель евклидова пространства назовем векторной.
5. Прямая
аксиоматика
вейль векторный геометрия
Пусть Е - трехмерное аффинное пространство и V
- его пространство переносов (dimV=3)/
Возьмем точку А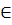 E
и вектор
E
и вектор 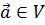 ,
,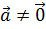 .
Прямой назовем множество точек: d=
.
Прямой назовем множество точек: d=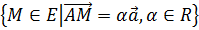 .
.
Вектор  называется
направляющим вектором прямой d.
Он может быть заменен любым ненулевым вектором, коллинеарным
называется
направляющим вектором прямой d.
Он может быть заменен любым ненулевым вектором, коллинеарным  :
:
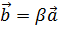 ,
,
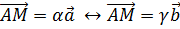 ,
где
,
где 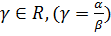 .
.
Точку А также можно заменить любой другой точкой
этой прямой. Действительно, возьмем какую-нибудь точку В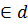 .
Тогда
.
Тогда 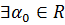 /
/
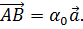 Рассмотрим
прямую
Рассмотрим
прямую 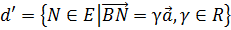 .
.
Для любой точки М 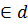 :
:
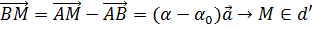 .
.
Обратно, для любой точки N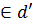 :
:
 .
.
Следовательно, 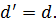
Множество всех векторов 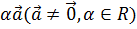 представляет
собой одномерное векторное пространство V
представляет
собой одномерное векторное пространство V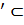 V.
Поэтому прямая d=
V.
Поэтому прямая d= одномерна. Сужение
одномерна. Сужение 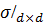 отображения
отображения 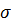 удовлетворяет
аксиомам I,II,
и поэтому прямая d является
одномерным аффинным пространством (в евклидовом пространстве - евклидовым) с
пространством переносов V
удовлетворяет
аксиомам I,II,
и поэтому прямая d является
одномерным аффинным пространством (в евклидовом пространстве - евклидовым) с
пространством переносов V .
.
В пространстве E
существуют точки, не лежащие на прямой d.
Действительно, если векторы  и
и  линейно
независимы, то точка N
линейно
независимы, то точка N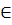 E
/
E
/ 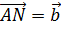 не
лежит на прямой d.
не
лежит на прямой d.
Теорема 1. Через любые две различные точки
проходит одна и только одна прямая.
Доказательство: Пусть A,B
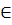 E,
A
E,
A . Прямая d=
. Прямая d=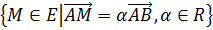 проходит через точки A
и B, ибо для
проходит через точки A
и B, ибо для 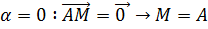 ,
для
,
для 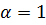 :
:
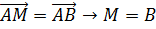 .
.
Пусть 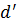 -
какая-нибудь прямая, проходящая через точки А и В. Тогда можно записать:
-
какая-нибудь прямая, проходящая через точки А и В. Тогда можно записать: 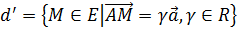 .
.
B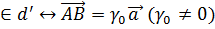 и
и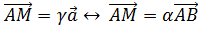 ,
где
,
где 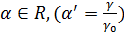 .
Значит,
.
Значит, 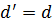 /
Теорема доказана.
/
Теорема доказана.
Прямую, проходящую через две различные точки А и
В, будем обозначать (АВ). Поэтому можно записать: (АВ)=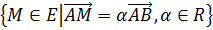 .
.
Прямая d
называется параллельной прямой l,
если их направляющие векторы линейно зависимы (коллинеарны). Отсюда следует,
что отношение параллельности (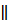 ) является
отношением эквивалентности на множестве D
всех прямых пространства Е. Элементы фактор - множества D/
) является
отношением эквивалентности на множестве D
всех прямых пространства Е. Элементы фактор - множества D/
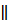 называют
связками параллельных прямых.
называют
связками параллельных прямых.
Точкой А и вектором 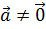 (определенным
с точностью до коллинеарного) определяется единственная прямая, проходящая
через А и имеющая
(определенным
с точностью до коллинеарного) определяется единственная прямая, проходящая
через А и имеющая  направляющим
вектором. Отсюда следует, что через данную точку проходит единственная прямая,
параллельная данной прямой.
направляющим
вектором. Отсюда следует, что через данную точку проходит единственная прямая,
параллельная данной прямой.
Теорема 2: Две параллельные прямые либо
совпадают, либо не имеют общих точек.
Доказательство: Пусть две прямые параллельны.
Тогда можно считать, что они имеют один и тот же направляющий вектор  .
Если эти прямые имеют общую точку А, то и та, и другая прямая есть множество
точек
.
Если эти прямые имеют общую точку А, то и та, и другая прямая есть множество
точек 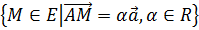 ,
то есть эти прямые совпадают.
,
то есть эти прямые совпадают.
Прямые d=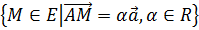 ,
и l=
,
и l= 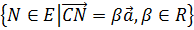 ,
где С
,
где С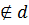 ,
параллельны и d
,
параллельны и d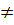 l. Они не имеют
общих точек, ибо если бы у них была общая точка, то по доказанному выше d
l. Они не имеют
общих точек, ибо если бы у них была общая точка, то по доказанному выше d l, чего нет.
l, чего нет.
6. Плоскость
Возьмем точку A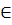 E и неколлинеарные
(линейно независимые) векторы
E и неколлинеарные
(линейно независимые) векторы 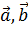
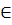 V.
Плоскостью назовем множество точек
V.
Плоскостью назовем множество точек 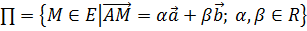 .
.
Линейная оболочка 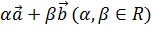 ,
натянутая на векторы
,
натянутая на векторы 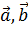 представляет собой
двумерное векторное пространство V
представляет собой
двумерное векторное пространство V .
.
Поэтому 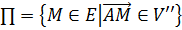 ,
и вместо векторов
,
и вместо векторов 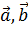 можно взять любой
другой базис векторного пространства V
можно взять любой
другой базис векторного пространства V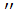 .
.
Сужение 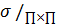 отображения
отображения
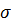 удовлетворяет
аксиомам I,II,
и поэтому плоскость
удовлетворяет
аксиомам I,II,
и поэтому плоскость  является двумерным
аффинным (в евклидовом - евклидовым) пространством с пространством переносов V
является двумерным
аффинным (в евклидовом - евклидовым) пространством с пространством переносов V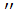 .
.
Точку А можно заменить любой другой точкой
плоскости  . Действительно
если В
. Действительно
если В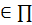 ,
то
,
то 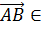 V
V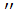 .
Так как
.
Так как 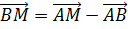 ,
то
,
то 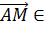 V
V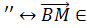 V
V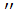 .
.
В пространстве Е существуют точки, не лежащие на
плоскости  . Действительно,
если векторы
. Действительно,
если векторы 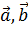 и
и  линейно
независимы, то точка N
линейно
независимы, то точка N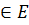 /
/ 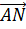 =
= не лежит на плоскости
не лежит на плоскости  .
.
Теорема 3: Через три точки, не принадлежащие
одной прямой проходит одна и только одна плоскость.
Доказательство: Пусть A,B,C
- точки, не лежащие на одной прямой. Тогда векторы  и
и
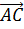 линейно
независимы. Плоскость
линейно
независимы. Плоскость 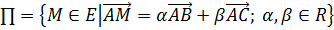 проходит через
точки A,B,C,
ибо для
проходит через
точки A,B,C,
ибо для 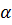 =
=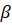 =0:
=0:
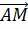 =
= ;
для
;
для 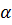 =1,
=1,
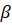 =0:
=0:
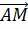 =
=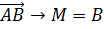 ;
для
;
для 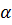 =0,
=0,
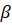 =1:
=1:
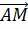 =
= .
.
Пусть 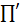 -
какая-нибудь плоскость, проходящая через точки A,B,C.
Тогда можно записать:
-
какая-нибудь плоскость, проходящая через точки A,B,C.
Тогда можно записать: =
=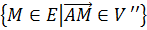 .
.
Так как B,C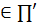 ,
то
,
то  ,
, и образуют базис этого двумерного пространства. Следовательно
и образуют базис этого двумерного пространства. Следовательно 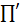 =
= .
.
Теорема 4: Если две различные плоскости имеют
общую точку, то их пересечение есть прямая.
Доказательство: Пусть  и
и
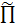 -
две различные плоскости. V
-
две различные плоскости. V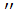 ,
,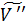 -
их пространства переносов, A
-
их пространства переносов, A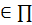 ,
A
,
A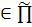 . Тогда можно
записать:
. Тогда можно
записать:  =
=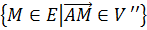 ,
,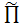 =
=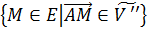 .
.
Так как 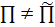 ,
то V
,
то V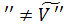 . Очевидно, что M
. Очевидно, что M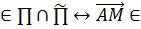 V
V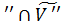 . Известно, что два
различных двумерных пространства трехмерного векторного пространства V
пересекаются по одномерному подпространству V
. Известно, что два
различных двумерных пространства трехмерного векторного пространства V
пересекаются по одномерному подпространству V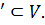 Следовательно,
Следовательно, =
= - прямая.
- прямая.
Плоскость  называется
параллельной плоскости
называется
параллельной плоскости 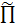 , если эти
плоскости имеют одно и тоже пространство переносов. Отсюда следует, что
отношение параллельности является отношением эквивалентности на множестве Р
всех плоскостей пространства E.
Элементы фактор - множества P/
, если эти
плоскости имеют одно и тоже пространство переносов. Отсюда следует, что
отношение параллельности является отношением эквивалентности на множестве Р
всех плоскостей пространства E.
Элементы фактор - множества P/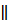 называются пучками параллельных плоскостей.
называются пучками параллельных плоскостей.
Можно доказать что две параллельные плоскости
либо совпадают, либо не имеют общих точек. Верно и обратное предложение.
Действительно, если 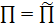 , то
, то 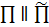 по
определению. Докажем, что
по
определению. Докажем, что 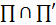 =
=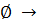 V
V .
.
Предположим, что V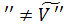 .
Пусть (
.
Пусть ( ,
, )-
базис векторного пространства V
)-
базис векторного пространства V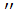 .
Тогда
.
Тогда 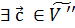 /
/
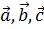 -
линейно независимы и, значит, составляют базис трехмерного векторного
пространства V. Если A
-
линейно независимы и, значит, составляют базис трехмерного векторного
пространства V. Если A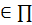 ,
B
,
B 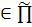 ,
то
,
то 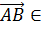 V
и
V
и 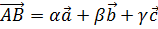 .
Тогда M
.
Тогда M

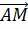 =
=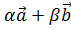 принадлежит
принадлежит  . Так как
. Так как 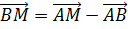 =-
=-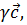 то
M
то
M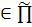 . Следовательно,
плоскости
. Следовательно,
плоскости 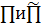 имеют общую точку M,
что противоречит условию. Поэтому V
имеют общую точку M,
что противоречит условию. Поэтому V и
и 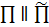 .
.
Доказанное необходимое и достаточное условие
параллельности двух плоскостей можно было бы принять за определение
параллельных плоскостей и доказать, в качестве признака, что две плоскости
параллельны тогда и только тогда, когда их пространства переносов совпадают.
Такой подход позволяет сделать несколько более наглядной сильно
алгебраизированную теорию.
Теорема 5: Прямая, проходящая через де различные
точки плоскости, лежит в этой плоскости.
Доказательство: Пусть дана плоскость  и
A, B
и
A, B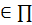 ,
A
,
A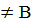 . Если V
. Если V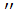 - пространство переносов плоскости
- пространство переносов плоскости  ,
то
,
то 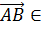 V
V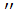 .
Тогда можно записать: (AB)=
.
Тогда можно записать: (AB)=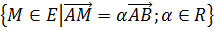 ,
,
 ,
где
,
где 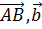 -
линейно независимые векторы из V
-
линейно независимые векторы из V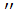 .
Точки плоскости
.
Точки плоскости  , для которых
, для которых 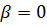 ,
,
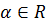 ,
составляют прямую (AB).
Следовательно, (AB)
,
составляют прямую (AB).
Следовательно, (AB)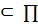 .
.
7. Аксиоматика Вейля и школьная
геометрия
Наиболее сильной стороной теории Вейля является
её алгебраизация. Это обеспечивает возможность в значительной мере
алгоритмизировать доказательства теорем, поэтому открывает «царский путь» в
изучение геометрии.
Однако при первоначальном изучении геометрии
(особенно, стереометрии) указанное достоинство теории Вейля оборачивается её
существенным недостатком: она не развивает пространственных представлений
учащихся, не развивает их геометрической интуиции. Этот недостаток можно
частично компенсировать возвращением к традиционным определениям и теоремам с
последующим их использованием для построения теории.
Пример: Прямая перпендикулярная к плоскости,
определяется «в духе Вейля» как такая прямая, пространство переносов которой
является ортогональным дополнением к пространству переносов плоскости. Вместо
этого можно принять традиционное определение, доказать обычный признак
перпендикулярности прямой и плоскости и воспользоваться им, например, для
доказательства теоремы о трех перпендикулярах.
Заметим, что именно так и сделано в школьном
учебнике под редакцией З.А. Скопеца «Геометрия 9-10», хотя использование
скалярного произведения позволяет доказать эту теорему, не опираясь на указанный
признак.
Сильная алгебраизация вейлевской теории
предъявляет повышенные требования к алгебраической и общелогической культуре
учащихся. Однако в процессе обучения нужный уровень не достигается не только к
началу систематического курса геометрии (6 класс), но и к началу изучения
стереометрии (9 класс). Пожалуй, это является наиболее серьезным препятствием
для внедрения векторного построения геометрии в школьное преподавание.
Принимая, кроме того, во внимание необходимость
значительной пропедевтики аналитических методов в геометрии, мы приходим к
выводу о возможности завершить школьное геометрическое образование
ознакомлением с обоснованием геометрии по Вейлю. Предварительное изучение
геометрии может в значительной мере исходить из интуитивно-наглядных представлений
о простейших свойствах пространства, фиксируемых в качестве аксиом.
Всеобщее среднее образование создает
благоприятные возможности для выведения общих, достаточно сложных и идейно
глубоких вопросов школьной математики в завершающий концентр. На этом пути, мы
надеемся, удастся совместить расширение и углубление школьной математики с её
доступностью.
Однако в нашей стране и за рубежом не
прекращается поиск такой аксиоматики евклидова пространства, на которой можно
было бы построить начала систематического курса геометрии в форме доступной,
для учащихся соответствующего возраста.
Отдавая должное векторному обоснованию геометрии
как «царскому пути» в геометрию, видный французский математик Г.Шоке в своей
книге пишет о том, что понятиями векторного пространства и скалярного
произведения «нельзя овладеть штурмом, без всякой подготовки, особенно в том
возрасте, когда у ученика ещё не совсем сформировалось понятие алгебраической
операции». Поэтому нужна новая аксиоматика, позволяющая «так одеть сам по себе совершенный,
но слишком абстрактный для ребенка логический каркас, чтобы он превратился в
нечто знакомое и приветливое».
В своей книге Г.Шоке наиболее четко
сформулировал требования к такой аксиоматике: «… Нам надо найти простую
аксиоматику с аксиомами, которые были бы сильными, то есть позволяющими очень
быстро вывести неочевидные теоремы, и интуитивно ясными, то есть
представляющими свойства окружающего нас пространства в форме, которая
допускает простую проверку».
Аксиоматика должна быть такой, «чтобы в этой
системе было удобно выявить векторную структуру пространства».
В построении теории следует «отдать предпочтение
методам, основанным на фундаментальных понятиях, выкристаллизовавшихся за
двадцать веков развития математики: понятия множества, отношений эквивалентности
и порядка, алгебраических законах, векторном пространстве, симметрии и
геометрических преобразованиях».
Самому Г. Шоке не удалось разработать такую
теорию даже при существенном изменении традиционного содержания школьного курса
геометрии. В большей степени перечисленным требованиям удовлетворяет теория
А.Н. Колмогорова, положенная в настоящее время в основу школьных учебников. Эта
теория базируется на структуре метрического пространства.
Глава II.
Задачи, решаемые векторным способом
. Основные задачи о прямых и
плоскостях
1.Уравнение прямой, проходящей через две точки.
Пусть в пространстве задана общая декартова
система координат и две точки М1 и М2 с координатами (x1,y1,z1)
и (x2,y2,z2).
Чтобы написать уравнение прямой М1М2, примем М1
за начальную точку, а 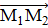 за направляющий
вектор. Этот вектор не нулевой, если точки не совпадают.
за направляющий
вектор. Этот вектор не нулевой, если точки не совпадают.
Получаем 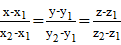 .
Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять
нулю соответствующий числитель.
.
Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять
нулю соответствующий числитель.
В планиметрии задача решается также. Отличие
только в том, что координаты точек теперь (x1,y1)
и (x2,y2),
и мы получаем 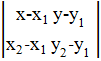 =0.
=0.
.Уравнение плоскости, проходящей через три
точки.
Пусть М1, М2,М3
- не лежащие на одной прямой точки с координатами (x1,y1,z1),
(x2,y2,z2)
и (x3,y3,z3)
в общей декартовой системе координат. Выберем М1 в качестве начальной точки, а 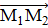 и
и
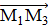 в
качестве направляющих векторов. Тогда получим уравнение плоскости
в
качестве направляющих векторов. Тогда получим уравнение плоскости 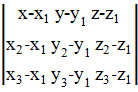 =0.
=0.
. Параллельность прямой и плоскости.
Пусть известен направляющий вектор прямой a(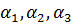 ),
а плоскость задана одним из уравнений (
),
а плоскость задана одним из уравнений ( )=0
или (
)=0
или (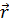 -
-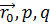 )=0.
Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда,
когда соответственно (
)=0.
Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда,
когда соответственно ( ,
,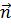 )=0
или (
)=0
или ( ,
,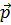 ,
,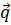 )=0.
Если плоскость задана линейным уравнением Ax+By+Cz+D=0,
то условию параллельности - A
)=0.
Если плоскость задана линейным уравнением Ax+By+Cz+D=0,
то условию параллельности - A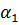 +B
+B +C
+C =0. Пусть прямая задана системой уравнений
=0. Пусть прямая задана системой уравнений 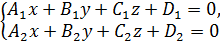 .
.
Тогда получаем A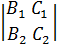 + B
+ B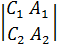 + C
+ C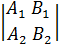 =0,
или
=0,
или 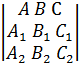 =0.
=0.
Все приведенные здесь условия являются не только
необходимыми, но и достаточными.
. Расстояние от точки до плоскости.
Пусть дана плоскость с уравнением ( )=0
и точка М с радиус вектором
)=0
и точка М с радиус вектором 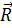 . Рассмотрим вектор
. Рассмотрим вектор
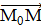 =
=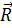 -
-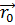 ,
соединяющий начальную точку плоскости с М(рис 1).Расстояние от точки до
плоскости равно модулю его скалярной проекции на вектор
,
соединяющий начальную точку плоскости с М(рис 1).Расстояние от точки до
плоскости равно модулю его скалярной проекции на вектор 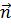 ,
то есть h=
,
то есть h=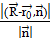 .
Если в декартовой прямоугольной системе координат точка М имеет координаты (X,Y,Z),
то равенство запишется следующим образом h=
.
Если в декартовой прямоугольной системе координат точка М имеет координаты (X,Y,Z),
то равенство запишется следующим образом h=
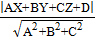
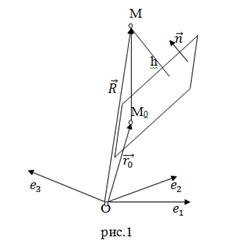
. Расстояние от точки до прямой.
Если прямая задана уравнением 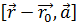 =0,
то можем найти расстояние h
от точки М с радиус - вектором
=0,
то можем найти расстояние h
от точки М с радиус - вектором 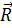 до этой прямой,
разделив площадь параллелограмма, построенного на векторах
до этой прямой,
разделив площадь параллелограмма, построенного на векторах 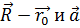 ,
на длину его основания (рис 2). Результат можно записать формулой h=
,
на длину его основания (рис 2). Результат можно записать формулой h=
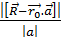 .
.
Для прямой в пространстве мы не будем получать
координатной записи этого выражения.
Рассмотрим прямую на плоскости, заданную
уравнением Ax+By+C=0
в декартовой прямоугольной системе координат. Пусть M0(x0,y0)
- начальная точка прямой, а M(X,Y)-
некоторая точка плоскости. В качестве направляющего вектора возьмём вектор 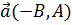 .
Площадь параллелограмма равна S=
.
Площадь параллелограмма равна S= .
Тогда S=
.
Тогда S=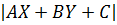 и
h =
и
h = 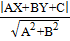 .
.
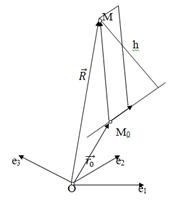
Рис.2
2. Доказательства и решения задач
Задача 1: Доказать, что диагонали ромба взаимно
перпендикулярны.
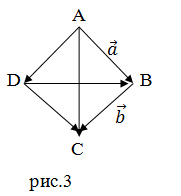
Доказательство: Пусть ABCD
- данный ромб (рис.3). Введем обозначения  =
= ,
,
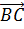 =
= .
Из определения ромба следует
.
Из определения ромба следует  =
=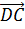 =
= ,
,
 =
=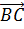 =
= .
.
По определению суммы и разности векторов 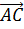 =
= +
+ ;
; =
= -
- .
.
Рассмотрим 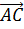 *
*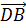 =
=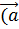 +
+ )(
)( -
- )=
)=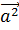 -
- .
Так как стороны ромба равны, то
.
Так как стороны ромба равны, то  =
= .
Следовательно,
.
Следовательно, 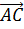 *
*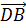 =0.
Из последнего условия следует что,
=0.
Из последнего условия следует что,  ,
что и требовалось доказать.
,
что и требовалось доказать.
Задача 2: Даны два вектора 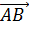 и
и
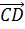 ,
причем А(-1;2;4), В (-4;5;4), С(-1;-2;2) и D(2;1;5). Определить,
перпендикулярны они друг другу или нет.
,
причем А(-1;2;4), В (-4;5;4), С(-1;-2;2) и D(2;1;5). Определить,
перпендикулярны они друг другу или нет.
Решение: Найдем сначала координаты векторов.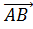 =(-3;3;0)
и
=(-3;3;0)
и 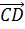 =(3;3;3).
=(3;3;3).
Вычислим теперь скалярное произведение этих
векторов:
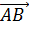 *
*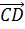 =(-3)*3 +3*3+0*3 = 0.
=(-3)*3 +3*3+0*3 = 0.
Последнее и означает, что 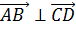
Задача 3: Дан произвольный треугольник АВС.
Доказать, что можно построить треугольник, стороны которого равны и параллельны
медианам треугольника АВС.

Решение: Обозначим медианы треугольника АВС
через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через 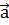 ,
,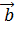 ,
,
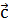 :
:
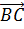 =
=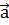 ,
,
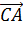 =
=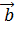 ,
, =
=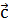 .
Тогда
.
Тогда  =
= +
+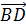 =
= +
+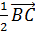 =
=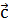 +
+ .
.
Аналогично определяются и другие медианы:
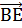 =
= ,
,
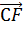 =
=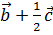 .
.
Так как, в силу замкнутости 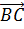 +
+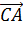 +
+ =
=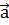 +
+ +
+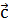 =0б
то мы имеем
=0б
то мы имеем
 +
+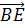 +
+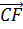 =(
=(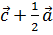 )+(
)+( )+(
)+(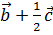 )=
)=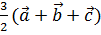 =
= *0=0.
*0=0.
Следовательно, отложив от точки В, вектор  =
=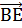 и от точки С1 - вектор
и от точки С1 - вектор 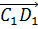 =
=
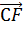 ,
мы получим.
,
мы получим.
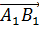 +
+ +
+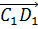 =
= +
+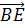 +
+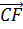 =0.
=0.
А это значит (в силу условия замкнутости), что
ломаная А1В1С1D1 является
замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1
(рис.5), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного
треугольника.
Задача 4: Доказать, что для любого треугольника
имеет место формула
c2
= a2+b2-2ab*соsС
(теорема косинусов)
Решение. Положим:
Тогда 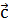 =
=  -
- ,
и мы имеем (учитывая, что угол между векторами
,
и мы имеем (учитывая, что угол между векторами 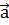 и
и
 равен
равен
С): с2 =(а-b)2
= а2 -2аb + b2
= а2-2аb*соsС+ b2.

Задача 5: Докажите, что сумма квадратов
диагоналей параллелограмма равна сумме квадратов его сторон.
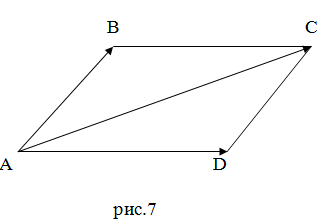
Решение: Пусть четырехугольник АВСD -
параллелограмм (рис.7). Имеем векторные равенства  +
+ =
=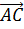 ,
,
 -
- =
=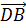 .
Возведем эти равенства в квадрат. Получим:
.
Возведем эти равенства в квадрат. Получим: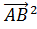 +2
+2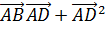 =
=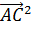 ,
,
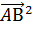 -2
-2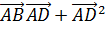 =
=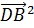
Сложим эти равенства почленно. Получим: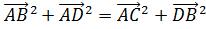 так как у параллелограмма противолежащие стороны равны, то это равенство и
означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов
его сторон, что и требовалось доказать.
так как у параллелограмма противолежащие стороны равны, то это равенство и
означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов
его сторон, что и требовалось доказать.
Задача 6: Даны три точки: А(1;1), В(-1;0),
С(0;1). Найдите такую точку D(х;y),
чтобы векторы  и
и 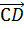 были
равны.
были
равны.
Решение: Вектор  имеет
координаты (-2, -1). Вектор
имеет
координаты (-2, -1). Вектор 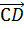 имеет координаты
(х-0, y-1). Так как
имеет координаты
(х-0, y-1). Так как  =
=
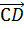 ,
то х-0 = -2, y-1 = -1. Отсюда
находим координаты точки D:
х =-2, y = 0.
,
то х-0 = -2, y-1 = -1. Отсюда
находим координаты точки D:
х =-2, y = 0.
Задача 7: Даны два вектора  и
и
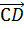 ,
причем А(-1;2;4), В(-4;5;4), С(-1;-2;2), D (2;1;5).Определить, перпендикулярны
они друг другу или нет.
,
причем А(-1;2;4), В(-4;5;4), С(-1;-2;2), D (2;1;5).Определить, перпендикулярны
они друг другу или нет.
Решение: Найдем сначала координаты векторов.  (-3;3;0)
и
(-3;3;0)
и 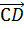 (3;3;3).
(3;3;3).
Вычислим теперь скалярное произведение этих
векторов:
 *
*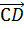 = (-3)*3 + 3*3 + 0*3 = 0.
= (-3)*3 + 3*3 + 0*3 = 0.
Последнее означает, что 
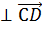
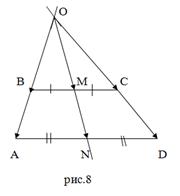
Задача 8: Доказать, что прямая проведенная через
середины оснований трапеции, проходит через точку пересечения продолжений
боковых сторон.
Доказательство: Пусть ABCD
- данная трапеция, М и N
- середины оснований BC
и AD, а O-точка
пересечения прямых AB
и CD (рис.8). Докажем,
что точка О лежит на прямой MN.
Треугольник OAD
и OBC подобны по первому
признаку подобия треугольников, поэтому 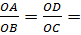 k.
Так как
k.
Так как 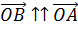 и
и
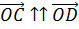 ,
то
,
то 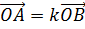 ,
,
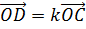 .
Точка М - середина отрезка ВС, поэтому
.
Точка М - середина отрезка ВС, поэтому  .
Аналогично
.
Аналогично 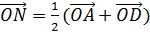 .
.
Подставив в это выражение равенство для 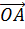 и
и
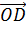 ,
получим:
,
получим:
 .
.
Отсюда следует, что векторы 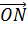 и
и
 коллинеарны,
и, значит, точка О лежит на прямой MN.
коллинеарны,
и, значит, точка О лежит на прямой MN.
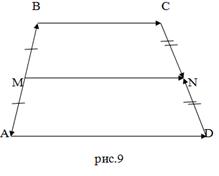
Задача 9: Доказать что средняя линия трапеции
параллельна основаниям и равна их полусумме.
Доказательство: Пусть MN
- средняя линия трапеции ABCD
(рис.9). Докажем, что MN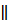 AD
и MN=
AD
и MN=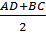 .
.
По правилу многоугольника  и
и
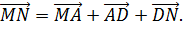 Сложив
эти равенства получим:
Сложив
эти равенства получим:
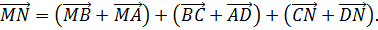
Но M
и N- середины сторон AB
и CD, поэтому 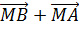 =
=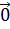 и
и 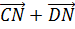 =
=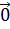 .
Следовательно, 2
.
Следовательно, 2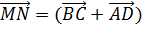 , откуда
, откуда 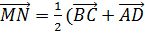 ).
).
Так как векторы  и
и
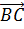 сонаправлены,
то векторы
сонаправлены,
то векторы 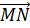 и
и  также
сонаправлены, а длина вектора
также
сонаправлены, а длина вектора 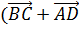 ) равна AD+BC.
Отсюда следует MN
) равна AD+BC.
Отсюда следует MN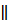 AD
и MN=
AD
и MN=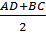 ,
что и требовалось доказать.
,
что и требовалось доказать.
Заключение
Целью моей работы было ознакомление с векторным
обоснованием евклидовой геометрии и рассмотрение основных видов задач, решаемых
векторным способом.
При написании данной работы были решены
следующие задачи:
- изучена биография Г. Вейля;
- изучены различные аксиоматики Вейля;
- выявлена взаимосвязь школьного курса
геометрии и аксиоматики Вейля;
- рассмотрены основные виды задач,
решаемые векторным способом.
В первой главе была рассмотрена биография
Германа Вейля, основные периоды его жизни и этапы его работ, также изучены
различные аксиоматики Вейля, доказана непротиворечивость и категоричность его
аксиоматики, способы задания прямой и плоскости, также выявлена взаимосвязь
современного курса геометрии и аксиоматики Вейля.
Во второй главе рассмотрены основные задачи,
решаемые векторным способом, и представлены решения этих задач.
В результате написания данной работы, я не
только изучила теоретический материал, касающийся темы работы, но и вспомнила,
как решаются основные задачи школьного курса геометрии векторным способом, а
также научилась решать задачи более высокого уровня.
Список литературы
1. Геометрия,
ч. 1: Атанасян Л.С.; Базылев В.Т. М.: Просвещение,1981 г.
. Векторное
изложение геометрии: Болтянский В.Г.; Волович М.Б.; Семушкин А.Д. М.:
Просвещение,1982 г.
. Элементарная
геометрия: Болтянский В.Г. М.: Просвещение,1985 г.
. Геометрия,
ч. 2: Вернер А.Л.; Кантор Б.Е.; Франгулов С.А. С-Пб.: Специальная литература,
1997г.
. Современные
основы школьного курса математики: Виленкин Н.Я. М.: Просвещение,1980 г.
. Курс
аналитической геометрии и линейной алгебры: Беклемишев Д.В. М.: ФИЗМАТЛИТ,2004
г.
. Сборник
задач по аналитической геометрии и линейной алгебре: Беклемишева Л.А. М.:
ФИЗМАТЛИТ,2003 г.
. Геометрия,
7-9: Атанасян Л.С.; Бутузов В.Ф М.: Просвещение,2002 г.
. Большая
советская энциклопедия (электронная версия)
. Новая
российская энциклопедия, том III
(2); М.: Издательство «Энциклопедия», 2007 г.
. http://ru.wikipedia.org/wiki