Регрессионные модели

Содержание

Введение

1. Основы построения регрессионных моделей

2. Построение регрессионных моделей

Заключение

Список использованной литературы

Введение

Обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных.

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

1. Основы построения регрессионных моделей

Метод наименьших квадратов - один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина прямой или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятности; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Большие затруднения представляются при определении из наблюдений величин, которые не могут быть измерены непосредственно. При этом, если бы число уравнений равнялось числу неизвестных, то для каждой неизвестной получилась бы одна определенная величина; если же число уравнений больше числа неизвестных, то, вследствие ошибок наблюдений, результаты решений отдельных групп этих уравнений в различных сочетаниях оказываются не совсем согласными между собой.

До начала XIX в. учёные не имели опредёленных правил для решения системы уравнений, в которой число неизвестных менее числа уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Лежандру (1805-06) и Гауссу (1794-95) принадлежит первое применение к решению указанной системы уравнений теории вероятности, исходя из начал, аналогичных с началом арифметической середины, уже издавна и, так сказать, бессознательно применяемых к выводам результатов в простейшем случае многократных измерений. Как и в случае арифметической середины, вновь изобретённый способ не даёт, конечно, истинных значений искомых, но даёт зато вероятнейшие значения. Этот способ распространён и усовершенствован дальнейшими изысканиями Лапласа, Энке, Бесселя, Ганзена и др. и получил название метода наименьших квадратов, потому что после подстановки в начальные уравнения неизвестных величин, выведенных этим способом, в правых частях уравнений получаются если и не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков, после подстановки каких бы то ни было других значений неизвестных. Помимо этого, решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть даёт величины, по которым судят о степени точности выводов.

Пусть дано решить систему уравнений

ax + by + cz… + n = 0x + b1y + c1z… + n1 = 0 (1)x + b2y + c2z… + n2 = 0

число которых более числа неизвестных x, у, z… Чтобы решить их по способу Н. квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные, уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной х и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной у и, сложив почленно, получают второе нормальное уравнение и т. д. Если означить для краткости:

[aa] = a1a1 + a2a2 +…

[ab] = a1b1 + a2b2 +…

[ac] = a1c1 + a2c2 +…

[bb] = b1b1 + b2b2 +…

[bc] = b1c1 + b2c2 +…

то нормальные уравнения представятся в следующем простом виде:

[aa]x + [ab]y + [ac]z +… [an] = 0

[ab]x + [bb]y + [bc]z +… [bn] = 0 (2)

[ac]x + [bc]y + [cc]z +… [cn] = 0

Легко заметить, что коэффициенты нормальных уравнений весьма легко составляются из коэффициентов данных, и притом коэффициент у первой неизвестной во втором уравнении равен коэффициенту у второй неизвестной в первом, коэффициент у первой неизвестной в третьем уравнении равен коэффициенту у третьей неизвестной в первом и т. д. Для пояснения сказанного ниже приведено решение пяти уравнений с двумя неизвестными:

5x - 8y - 16 = 0

x - y - 32 = 0

x + 8y - 55 = 0

x + 7y - 32 = 0

x + 20y - 29 = 0

Составив значения [aa], [ab].., получаем следующие нормальные уравнения:

507x + 323у - 1765 = 0

x + 578у - 1084 = 0,

откуда х = +3,55; у = -0,109. Уравнения (1) представляют систему линейных уравнений, то есть уравнений, в которых все неизвестные входят в первой степени. В большинстве случаев уравнения, связывающие наблюдаемые и искомые величины, бывают высших степеней и даже трансцендентные, но это не изменяет сущности дела: предварительными изысканиями всегда можно найти величины искомых с таким приближением, что затем, разложив соответствующие функции в ряды и пренебрегая высшими степенями искомых поправок, можно привести любое уравнение к линейному.

Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.

Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ). Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного анализа х на результативный признак у и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей.

Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типов функции может опираться на теоретические знания об изучаемом явлении, опят предыдущих аналогичных исследований, или осуществляться эмпирически - перебором и оценкой функций разных типов и т.п.

При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчётов преобразуют (путём логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной корреляционной связи имеет вид:

ŷ = a0 + a1x ,

где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии;, a1 - коэффициенты (параметры) уравнения регрессии.

Поскольку a0 является средним значением у в точке х=0, экономическая интерпретация часто затруднена или вообще невозможна.

Коэффициент парной линейной регрессии a1 имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Вышеприведенное уравнение показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, то есть вариацию у, приходящуюся на единицу вариации х. Знак a1 указывает направление этого изменения.

Параметры уравнения a0 , a1 находят методом наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), то есть в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выравненных ŷ :

(yi - ŷ)2 = S(yi - a0 - a1xi)2 = min

Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

Решим эту систему в общем виде:

Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:

Уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.

Коэффициент при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.

В статистической обработке данных используются следующие показатели

Математическое ожидание (expected value) случайной величины

В обычной жизни известно, как среднее арифметическое.

Несмотря на простоту, среднее арифметическое играет большую роль в математической статистике при анализе последовательностей случайных величин.

Дисперсия (variance) случайной величины. Одно из важнейших понятий математической статистики.

Cтандартное отклонение (standard deviation). Одно из важнейших понятий математической статистики. Другое название - среднеквадратичное отклонение.

Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии ( ), рассчитываемая по формуле

регрессионный корреляционный статистический дисперсия

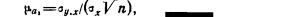
Где

уi, - i-e значение результативного признака; ŷi - i-e выравненное значение, полученное из уравнения (6.15); xi-i-e значение факторного признака; σx-среднее квадратическое отклонение х; n - число значений х или, что то же самое, значений у; m-число факгорных признаков (независимых переменных).

Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Последняя показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней арифметической, т. е. как t где t-величина, числовое значение которой определяется в зависимости от принятого уровня надежности.

Уравнение регрессии представляет собой функциональную связь, при которой по любому значению х можно однозначно определить значение у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание.

Метод наименьших квадратов применяется для расчета неизвестных параметров заранее выбранного вида функции, и вопрос о выборе наиболее подходящего для конкретных данных вида функции в рамках этого метода не ставится и не решается. Таким образом, при пользовании методом наименьших квадратов открытыми остаются два важных вопроса, а именно: существует ли связь и верен ли выбор вида функции, с помощью которой делается попытка описать форму связи.

Чтобы оценить, насколько точно уравнение регрессии описывает реальные соотношения между переменными, нужно ввести меру рассеяния фактических значений относительно вычисленных с помощью уравнения. Такой мерой служит средняя квадратическая ошибка регрессионного уравнения, вычисляемая по приведенной выше формуле

Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения - большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.

Рассмотрим следующую задачу. Была проведена серия измерений двух случайных величин X и Y, причем измерения проводились попарно: т.е. за одно измерение мы получали два значения - xi и yi . Имея выборку, состоящую из пар (xi , yi ), мы хотим определить, имеется ли между этими двумя переменными зависимость.

Зависимость между случайными величинами может иметь функциональный характер, т.е. быть строгим функциональным отношением, связывающим их значения. Однако при обработке экспериментальных данных гораздо чаще встречаются зависимости другого рода: статистические зависимости. Различие между двумя видами зависимостей состоит в том, что функциональная зависимость устанавливает строгую взаимосвязь между переменными, а статистическая зависимость лишь говорит о том, что распределение случайной величины Y зависит от того, какое значение принимает случайная величина X.

Одной из мер статистической зависимости между двумя переменными является коэффициент корреляции. Он показывает, насколько ярко выражена тенденция к росту одной переменной при увеличении другой. Коэффициент корреляции находится в диапазоне [-1, 1]. Нулевое значение коэффициента обозначает отсутствие такой тенденции (но не обязательно отсутствие зависимости вообще). Если тенденция ярко выражена, то коэффициент корреляции близок к +1 или -1 (в зависимости от знака зависимости), причем строгое равенство единице обозначает крайний случай статистической зависимости - функциональную зависимость. Промежуточные значения коэффициента корреляции говорят, что хотя тенденция к росту одной переменной при увеличении другой не очень ярко выражена, но в какой-то мере она все же присутствует.

Коэффициент корреляции, рассчитанный на основе выборки конечного размера, лишь приближенно равен истинному значению коэффициента корреляции между двумя случайными величинами. В частности, если две случайные величины не зависят друг от друга, коэффициент корреляции между ними равен нулю. Но рассчитав его на основе конечной выборки, мы скорее всего получим ненулевое значение. Чтобы определить, насколько значимо отличие коэффициента корреляции от ноля, можно воспользоваться соответствующим методом проверки гипотез.

Существует несколько различных коэффициентов корреляции, к каждому из которых относится сказанное выше. Наиболее широко известен коэффициент корреляции Пирсона, характеризующий степень линейной зависимости между переменными. Он определяется, как

Используя этот коэффициент, следует учитывать, что лучше всего он подходит для оценки взаимосвязи между двумя нормальными переменными. Если распределение переменных отличается от нормального, то он по-прежнему продолжает характеризовать степень взаимосвязи между ними, но к нему уже нельзя применять методы проверки на значимость. Также коэффициент корреляции Пирсона не очень устойчив к выбросам - при их наличии можно ошибочно сделать вывод о наличии корреляции между переменными. Поэтому если распределение исследуемых переменных отличается от нормального или возможны выбросы, то лучше воспользоваться непараметрическим аналогом - коэффициентом ранговой корреляции Спирмена.

Для словесного описания величин коэффициента корреляции применяется следующая таблица:

Пусть некоторые объекты обладают парой признаков каждый и гипотеза об их взаимосвязи не отвергается. Если признаки оказались взаимосвязаны, исследователя интересует сила их связи. Для описания такой связи было предложено много различных коэффициентов, называемых мерами связи.

В порядковых (ординальных) шкалах реальным содержанием измерений является тот порядок, в котором выстраиваются объекты (по степени выраженности измеряемого признака) и вместо значений чисел рассматривают их ранги. Здесь проверка нулевой гипотезы ведётся методом Спирмена. Пусть признаков два и каждый из n объектов характеризуется парой чисел (xi, yj) - своими значениями признаков А и В. От чисел переходим к их рангам (ri, sj). Cчитаем, что среди чисел xi и yj нет повторяющихся. Если признаки взаимосвязаны, то порядок, в котором следуют числа xi влияет на порядок, в котором следуют числа yj. Чем более тесно связаны эти признаки, тем в большей степени последовательность ri предопределяет последовательность sj. Если же признаки такой связи не проявляют, то порядок среди игреков случаен по отношению к порядку среди иксов. В этом случае все n! перестановок чисел 1, 2, ..., n, которые могут выступать как ранги, оказываются равновероятными при любом порядке чисел ri. По предложению Спирмена, близость двух рядов рангов ri и sj можно характеризовать статистикой:

Принято, что коэффициент корреляции должен изменяться от (-1) до 1. Поэтому нормированный и центрированный коэффициент связи Спирмена:

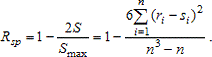
Крайние значения ±1 он принимает в случаях полной предсказуемости одной ранговой последовательности по другой. Значение S не зависит от первоначальной нумерации объектов. Поэтому обычно упорядочивают данные по одному из признаков. Последовательность рангов по этому признаку: 1, 2,..., n.

2. Построение регрессионных моделей

Расчёт ведётся в таблице Excel. Каждый лист соответствует одному заданию.

Задание 1 (лист 1)

Обозначим У - себестоимость добычи 1 т. руды, х1 - месячный объём добычи руды, х6 - объём отбитой руды за месяц в блоках, т.; х8 - удельный расход сжатого воздуха на добычу 1 тыс. т. руды. Средние значения

У ср. = 874,9/25=34,996

Х1 ср. = 1694,9/25=67,796

Х6 ср. = 1575,4/25= 63,016

Х8 ср. = 1400,8/25= 56,032

С помощью функции КВАДРОТКЛ, возвращающей сумму квадратов отклонений, находим дисперсию

По У - 95,6264

По Х1 - 472,9496

По Х6 - 11929,97

По Х8 - 544,9144

Среднеквадратичное отклонение равно квадратному корню из этой величины

По У - 9,7789

По Х1 - 21,7474

По Х6 - 109,2244

По Х8 - 23,3434

Средние величины по произведениям

УХ1 - 2474,3492

УХ6 - 2297,864

УХ8 - 2057,44

Ковариация

По паре У - Х1

2474,3492 - 34,996 х 67,796 = 101,760384

По паре У - Х6

2297,864 - 34,996 х 63,016 = 155,572064

По паре У - Х8

2057,44 - 34,996 х 56,032 = 96,544128

Коэффициент корреляции

По паре У - Х1

101,760384/(9,7789 х 21,7474) = 0,478 (связь плохая)

По паре У - Х6

155,572064/(9,7789 х 109,2244) = 0,146 (связь плохая)

По паре У - Х8

96,544128/(9,7789 х 23,3434) = 0,443 (связь плохая)

Везде мы имеем плохую связь, так как коэффициент корреляции меньше 0,5

Коэффициент линейной регрессии равен

По паре У - Х1

101,760384/472,9496 = 0,22

По паре У - Х6

155,572064/11929,97= 0,013

По паре У - Х8

96,544128/544,9144= 0,177

В данном случае нет необходимости строить уравнение линейной зависимости в силу очень слабой тесноты связи.

Задача 2 (лист 2)

Обозначим: Фондоотдача - У, доля активной части ОПФ - Х1, годовая производительность труда рабочих - Х2, фондовооружённость - Х3

Средние значения

Х1 ср. = 3,249/25=0,12996

Х2 ср. = 73195/25= 2927,8

Х3 ср. = 2241,55/25= 89,662

С помощью функции КВАДРОТКЛ, возвращающей сумму квадратов отклонений, находим дисперсию

По У - 101,9237

По Х1 - 0,000165

По Х2 - 1438792

По Х3 - 2749,043

Среднеквадратичное отклонение равно квадратному корню из этой величины

По У - 10,0957

По Х1 - 0,01285

По Х2 - 1199,4966

По Х3 - 52,4313

Средние величины по произведениям по таблице

УХ1 - 4,262986

УХ2 - 95947,8928

УХ3 - 2927,92654

Ковариация

По паре У - Х1

4,262986 - 10,0957х 0,000165= 4,262987

По паре У - Х2

95947,8928 - 10,0957х 1199,4966 = 83838,135

По паре У - Х3

2927,92654 - 10,0957х 52,4313 = 2398,645

Коэффициент корреляции

По паре У - Х1

4,262987 /(9,7789 х 21,7474) = 0,02 (связь практически отсутствует)

По паре У - Х2

83838,135/(9,7789 х 1199,4966) = 0,296 (связь плохая)

По паре У - Х3

2398,645/(9,7789 х 52,4313) = 0,502

(связь на уровне удовлетворительной)

Везде мы имеем плохую связь, так как коэффициент корреляции меньше 0,5. Только в последнем случае связь удовлетворительная

Коэффициент линейной регрессии равен

По паре У - Х1

4,262987 /0,000165 = 25818,18

По паре У - Х2

83838,135/2927,8= 28,635

По паре У - Х3

2398,645/2749,043= 0,8725

В данном случае нет необходимости строить уравнение линейной зависимости в силу очень слабой тесноты связи.

Задача 3 (лист 3)

Примем У - себестоимость, Х1 - годовая добыча, Х2 - коэффициент вскрышки, Х3 - фондовооружённость

Средние значения

У ср. = 56/25=2,24

Х1 ср. = 23234,41/25=929,3764

Х2 ср. = 85,82/25= 3,4328

Х3 ср. = 870,958/25= 56,032

С помощью функции КВАДРОТКЛ, возвращающей сумму квадратов отклонений, находим дисперсию

По У - 0,1648

По Х1 - 581570,3

По Х2 - 5,150904

По Х3 - 402,1078

Среднеквадратичное отклонение равно квадратному корню из этой величины

По У - 0,406

По Х1 - 762,608

По Х2 - 2,2696

По Х3 - 20,0526

Средние величины по произведениям

УХ1 - 2076,644612

УХ2 - 7,689872

УХ3 - 97,219315

Ковариация

По паре У - Х1

2076,644612- 2,24х 929,3764= -191,0472

По паре У - Х2

7,689872- 2,24х 3,4328 = 0,0004

По паре У - Х3

97,219315- 2,24х 3,4328= 89,53

Коэффициент корреляции

-191,0472/(9,7789 х 21,7474) = - 0,9 (связь очень хорошая и нисходящая)

По паре У - Х2

0,0004/(9,7789 х 109,2244) - близко к 0 (связь практически отсутствует)

По паре У - Х3

89,53/(9,7789 х 23,3434) = 0,39 (связь плохая)

Коэффициент линейной регрессии равен

По паре У - Х1

-191,0472/581570,3= - 0,003289

По паре У - Х2

0,0004/5,150904= 0,013

По паре У - Х3

89,53/402,1078= 0,177

В данном случае нет необходимости строить уравнение линейной зависимости в силу очень слабой тесноты связи по всем парам. Строим по первой паре, где коэффициент корреляции по модулю близок к 1.

Свободный член уравнения равен

(56 - (-0,003289) х 23234,41)/25 = 5,29672 т.е. У = 5,29672 - 0,003289 х Х1

Определим значение У и сравним их с фактическими. Сумма квадратов отклонений (дисперсия) по таблице равна 5,638

Критерий, равный отношению дисперсии модели к собственной дисперсии У равен

,638/0,1648=34,21

Достоверность модели равна (1- 1/34,21)^0,5= 0,985

Заключение

Основные выводы по итогам работы следующие:

1.       Подавляющее большинство пар показателей плохо коррелирует ли вовсе не корреллирует между собой (в семи случаях коэффициент корреляции меньше 0.5 и в одном - 0.5, причём в одном случае он стремится к 0). Поэтому модель не была построена, так как она не будет отражать адекватно зависимость величин.

2.       Только в одном случае получена хорошая корреляция, при этом соответствие модели на 98,5 %. Однако необходима дополнительная проверка - критериями Фишера или Стьюдента.

Список использованной литературы

1.       Виноградова Н.М., Евдокимов В.Т., Хитарова Е.М., Яковлева Н.И. Общая теория статистики. - М.: Статистика, 1998. - 312 с.

2.       Герчук Я.П. Графики в математико-статистическом анализе. - М.: Статистика, 1992. - 235 с.

.        Дружинин Н.К. Математическая статистика в экономике. Введ. в мат.-стат. методологию. - М.: Статистика, 2002. - 312 с.

.        Елисеева И.И., Юзбашев М.М. Общая теория статистики. - М.: Финансы и статистика, 2003. - 400 с.

.        Ефимова М.Р. Статистические методы в управлении производством.- М.: Финансы и статистика. 1998. - 336 с.

.        Ефимова М.Р., Рябцев В.М. Общая теория статистики.- М.: Финансы и статистика, 2001.- 272 с.

.        Рябушкин Т.В., Ефимова М.Р., Ипатова И.М., Яковлева Н.И. Общая теория статистики. - М.: Финансы и статистика, 2001. - 464 с.

.        Статистический анализ в экономике /Под ред. Г.Л. Громыко. - М.: Изд-во МГУ, 2002. - 434 с.

.        Статистическое моделирование и прогнозирование /Под ред. А.Г. Гранберга. - М.: Финансы и статистика, 2000. - 280 с.