Исследование математической модели движения материальной точки по заданным силам
СОДЕРЖАНИЕ
Введение
. Алгоритмический анализ
задачи
.1 Постановка задачи
.2 Описание входных и выходных
параметров
.3 Вывод дифференциального уравнения
движения груза
. Теоретическая часть
.1 Математическое моделирование
технических объектов
.2 Методы численного решения
дифференциальных уравнений
.3 Функции, предусматривающиеся для
численного решения дифференциальных уравнений в MathCAD
. Исследование математической
модели с помощью пакетов MathCAD и MathConnex
.1 Определение значений функций
движения
.2 Исследование влияния частоты
колебаний на движение груза
Заключение
Содержание
Литература
ВВЕДЕНИЕ
Компьютерная революция, свершившаяся на наших
глазах в течении двух последних десятилетий не могла не затронуть систему
народного образования. Рассматривая положение, которое в этой системе занял
персональный компьютер, мы должны, прежде всего, отметить уникальность этого
положения. С одной стороны, он стал естественным объектом учебного процесса, а
с другой стороны - сам явился ценным техническим средством обеспечения общего
процесса образования.
На ЭВМ хорошо решаются дифференциальные
уравнения, для решения алгебраических и трансцендентных уравнений требуется
применение нелинейных блоков, снижающих точность результатов до 5% от максимума
функции.
В деятельности инженера
компьютер стал необходимым инструментом, позволяющим осуществлять весь спектр
повседневных расчетов. Благодаря своей возможности проводить большое число
вычислений за короткое время, компьютер позволил современному инженеру
значительно усложнить методику расчетов, охватить большее количество
параметров, ускорить внедрение. Применение ЭВМ ликвидирует рутинные,
нетворческие этапы проектирования, но при этом усиливаются значение
неформальных элементов - оценки результатов, принятие решений и др. Умением
применять программные средства должен обладать каждый современный инженер.
С течением времени компьютеры
стали применяться повсюду. Они управляют работой кассовых аппаратов, следят за
работой автомобильных систем зажигания, ведут учёт семейного бюджета, или
просто используются в качестве развлекательного комплекса, но это только малая
часть возможностей современных компьютеров.
Облегчение, которое компьютер и созданные для
него программы принесли всем людям, работающим за письменным столом, настолько
значительны, что прежние методы работы воспринимаются ныне как кошмарный сон.
Большое значение в нашей жизни уделяется математическим расчётам, просто раньше
необходимые для их проведения знания были скрыты на страницах книг и за
высокими лбами специалистов. Трудоёмкость расчётов была велика, или вообще не
проводилась, или давалась с огромными затратами.
В данной курсовой работе проведено исследование
математической модели колебательного движения груза по заданным силам в среде MathCAD.использует
32-разрядную модель памяти, что обеспечивает повышенную точность и
быстродействие вычислений при полной совместимости как с обычным Windows 95/98
, так и с Windows NT/Xp.может
выполнять вычисления любой степени сложности, по своему объёму допустимые на
персональном компьютере. Помимо привычных численных расчётов Mathcad способен
делать символьные преобразования.обладает широкими графическими возможностями.
Множество типов графиков облегчают визуализацию и анализ данных.
1.
АЛГОРИТМИЧЕСКИЙ АНАЛИЗ ЗАДАЧИ
1.1 Постановка
задачи
Условие задачи:
Телу массой m
сообщена начальная скорость V0,
направленная вверх по наклонной плоскости. На тело действует сила P,
заданная кусочно-непрерывной функцией и направленная в ту же сторону (рис. 1,
2). Параметры зависимости силы P(t)
и коэффициент трения скольжения f
представлены в пункте 1.2. Данные о наклонной плоскости (рис. 2.).
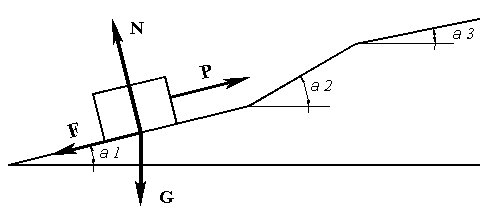
Рис. 1. Форма наклонной плоскости
Постановка задачи.
. Составить математическую модель
движения груза по заданной наклонной плоскости под воздействием силы P(t);
. В пакете MathCAD по полученной
математической модели определить значения функций движения, скорости и
ускорения тела;
. Построить графики функций движения,
скорости и ускорения тела;
. С помощью пакета MathConnex выполнить
моделирование влияния начальной скорости на движение тела и определить
минимальную начальную скорость V0
min при которой тело
поднимется на заданную высоту h;
. Для найденной начальной скорости V0
min построить графики
функций движения, скорости и ускорения тела.
1.2
Описание входных и выходных параметров.
Дано:
m=35 кг
V0=5.4 м/с
t0=0 c
t1=4 с
t2=10 с
t3=18 с
P0=100 Н
P1=200 Н
P2=150 Н
P3=250 Н
f=0,10
x1=5 м
x2=10 м
 град
град
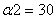 град
град
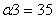 град
град
h=15 м,
где t1, t2, t3 - моменты
времени изменения силы P(t);
x1, x2 - длина
участка с углом наклона α1,
α2 соответственно.
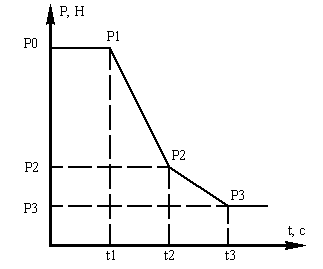
Рис. 2. Закон изменения силы P(t)
1.3 Вывод
дифференциального уравнения движения груза
Составим дифференциальное уравнение
движения тела:
m*a=∑F;*ax=∑Fx;*
d2 x/dt2=∑Fx ;
m*dV/dt=∑Fx(t);/dt=∑Fx(t)/m,/dt=V;
Так как
F=f*N, N=G*cos(α), то
dV/dt=P-f*G*cos(ά)-G*sin(ά),
dx/dt=V;
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
2.1
Математическое моделирование технических объектов
Моделирование.
Моделирование - представляет
собой процесс замещения объекта исследования некоторой его моделью и проведение
исследований на модели с целью получения необходимой информации об объекте.
Модель - это физический или абстрактный образ моделируемого объекта, удобный
для проведения исследований и позволяющий адекватно отображать интересующие
исследователя физические свойства и характеристики объекта.
Различают моделирование
предметное и абстрактное. При предметном моделировании строят физическую
модель, которая соответствующим образом отображает основные физические свойства
и характеристики моделируемого объекта. Если модель и объект одной и той же
физической природы, то моделирование называют физическим.
Математическая модель - это
совокупность математических объектов и отношений между ними, адекватно
отображающая физические свойства создаваемого технического объекта. В качестве
математических объектов выступают числа, переменные, множества, векторы,
матрицы и т. п. Процесс формирования математической модели и использования ее для
анализа и синтеза называется математическим моделированием. В конструкторской
практике под математическим моделированием обычно понимается процесс построения
математической модели, а проведение исследований на модели в процессе
проектирования называют вычислительным экспериментом.
Классификация математических
моделей.
При проектировании технических
объектов используют множество видов математических моделей, в зависимости от
уровня иерархии, степени декомпозиции системы, аспекта, стадии и этапа
проектирования.
На любом уровне иерархии объект
проектирования представляют в виде некоторой системы, состоящей из элементов. В
этой связи различают математические модели элементов и систем.
В общем случае уравнения
математической модели связывают физические величины, которые характеризуют
состояние объекта и не относятся к перечисленным выше выходным, внутренним и
внешним параметрам. Такими величинами являются: скорости и силы - в
механических системах; расходы и давления - в гидравлических и пневматических
системах; температуры и тепловые потоки - в тепловых системах; токи и
напряжения - в электрических системах.
Величины, характеризующие
состояние технического объекта в процессе его функционирования, называют
фазовыми переменными (фазовыми координатами). Вектор фазовых переменных задает
точку в пространстве, называемом фазовым пространством. Фазовое пространство, в
отличие от геометрического, многомерное. Его размерность определяется
количеством используемых фазовых координат.
Обычно в уравнениях
математической модели фигурируют не все фазовые переменные, а только часть из
них, достаточная для однозначной идентификации состояния объекта. Такие фазовые
переменные называют базисными координатами. Через базисные координаты могут
быть вычислены значения и всех остальных фазовых переменных.
К математическим моделям
предъявляются требования адекватности, экономичности, универсальности. Эти
требования противоречивы, поэтому обычно для проектирования каждого объекта
используют свою оригинальную модель.
Математические модели технических
объектов, используемые при проектировании, предназначены для анализа процессов
функционирования объектов и оценки их выходных параметров. Они должны
отображать физические свойства объектов, существенные для решения конкретных
задач проектирования. При этом математическая модель должна быть как можно
проще, но в то же время обеспечивать адекватное описание анализируемого
процесса.
Аналитическая модель
представляет собой явные зависимости искомых переменных от заданных величин
(обычно зависимости выходных параметров объекта от внутренних и внешних
параметров). Такие модели получают на основе физических законов, либо в
результате прямого интегрирования исходных дифференциальных уравнений,
используя табличные интегралы. К ним относятся также регрессионные модели,
получаемые на основе результатов эксперимента.
Графическая (схемная) модель
представляется в виде графов, эквивалентных схем, динамических моделей,
диаграмм и т. п. Для использования графических моделей должно существовать
правило однозначного соответствия условных изображений элементов графической и
компонентов инвариантной математических моделей.
Структурные модели отображают
только структуру объектов и используются при решении задач структурного
синтеза. Параметрами структурных моделей являются признаки функциональных или
конструктивных элементов, из которых состоит технический объект и по которым
один вариант структуры объекта отличается от другого. Эти параметры называют
морфологическими переменными. Структурные модели имеют форму таблиц, матриц и
графов. Наиболее перспективно применение древовидных графов типа дерева. Они
позволяют аккумулировать накопленный опыт, используя описания всех существующих
аналогов, известных из патентной литературы, и гипотетических объектов. Такие
модели наиболее широко используют на метауровне при выборе технического
решения.
Функциональные модели описывают
процессы функционирования технических объектов и имеют форму систем уравнений.
Теоретические модели получают
на основе описания физических процессов функционирования объекта, а
экспериментальные - на основе изучения поведения объекта во внешней среде,
рассматривая его как кибернетический "черный ящик". Эксперименты при
этом могут быть физические (на техническом объекте или его физической модели)
или вычислительные (на теоретической математической модели).
При построении теоретических
моделей используют физический и формальный подходы.
Физический подход сводится к
непосредственному применению физических законов для описания объектов,
например, законов Ньютона, Гука, Кирхгофа, Фурье и др.
Формальный подход использует
общие математические принципы и применяется при построении как теоретических,
так и экспериментальных моделей.
Линейные модели содержат только
линейные функции фазовых переменных и их производных. Характеристики многих
элементов реальных технических объектов нелинейные. Математические модели таких
объектов включают нелинейные функции фазовых переменных и (или) их производных
и относятся к нелинейным.
2.2
Методы численного решения дифференциальных уравнений
При разработке технических
устройств различного рода очень широко применяется математическое
моделирование, которое позволяет, избежав дорогостоящего построения реальных
прототипов устройств, рассчитать поведение основных элементов, основные параметры
системы.
Основным видом математических
моделей, применяемых в отношении технических устройств, являются аналитические
модели. Они представляются в виде системы алгебраических и/или дифференциальных
уравнений.
Дифференциальное уравнение
первого порядка - это уравнение вида
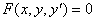 , (1)
, (1)
где 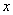 - независимая переменная,
- независимая переменная, 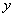 - искомая
функция,
- искомая
функция, 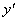 - ее
производная.
- ее
производная.
Производной функции 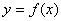 в точке
в точке 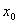 называется
предел отношения приращения функции к приращению аргумента при стремлении
последнего к нулю.
называется
предел отношения приращения функции к приращению аргумента при стремлении
последнего к нулю.
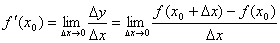
Если для некоторого значения 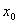 выполняется
условие
выполняется
условие
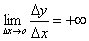 ( или
( или 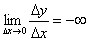 ),
),
то говорят, что в точке 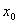 функция
имеет бесконечную производную знака плюс (или знака минус). В отличие от
бесконечной производной определенную выше производную функции иногда называют
конечной производной.
функция
имеет бесконечную производную знака плюс (или знака минус). В отличие от
бесконечной производной определенную выше производную функции иногда называют
конечной производной.
Если уравнение (1) можно разрешить
относительно 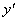 , то оно
принимает вид
, то оно
принимает вид
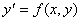 (2)
(2)
и называется уравнением первого
порядка, разрешенным относительно производной.
В некоторых случаях уравнение (2)
удобно записать в виде 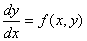 или в виде
или в виде 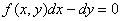 , являющемся
частным случаем более общего уравнения
, являющемся
частным случаем более общего уравнения
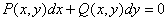 , (3)
, (3)
где 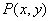 и
и 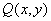 - известные функции. Уравнение в
симметричной форме (3) удобно тем, что переменные
- известные функции. Уравнение в
симметричной форме (3) удобно тем, что переменные 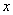 и
и 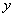 в нем
равноправны, то есть каждую из них можно рассматривать как функцию другой.
в нем
равноправны, то есть каждую из них можно рассматривать как функцию другой.
Найти точное решение этих уравнений,
как правило, не представляется возможным ввиду сложности уравнений описывающих
поведение модели. Поэтому в этих случаях широко применяются численные методы
решения. Для алгебраических уравнений основными численными методами являются:
1
метод
половинного деления;
2
метод
итераций;
3
метод
касательных;
4
метод
секущих;
5
комбинированный
метод.
Для дифференциальных уравнений
часто используются такие численные методы как:
6
метод
Эйлера;
7
метод
Рунге-Кутта;
8
метод
Адамса;
9
метод
Коуэлла-Субботина;
10
метод
квадратур.
Методы Эйлера.
Дифференциальные уравнения
находят широкое применение в прикладных задачах. Если рассматриваемая задача
сводится к решению системы обыкновенных линейных дифференциальных уравнений с
постоянными коэффициентами, как, например, большинство задач в теории
электрических цепей, то ее решение может быть найдено в явном виде. Если же
дифференциальные уравнения имеют переменные коэффициенты или являются
нелинейными, то их решение, как правило, приходиться искать численно. Использование
ЭВМ значительно облегчило использование дифференциальных уравнений, позволяет
решать такие задачи, к которым при ручном счете даже не приступали.
Рассмотрим дифференциальное уравнение
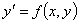 (1)
(1)
в предположении, что функция 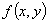 дифференцируема
в некоторой окрестности точки
дифференцируема
в некоторой окрестности точки  . Задача Коши для дифференциального
уравнения (1) формулируется так: найти решение
. Задача Коши для дифференциального
уравнения (1) формулируется так: найти решение 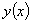 уравнения (1), удовлетворяющее
условию
уравнения (1), удовлетворяющее
условию 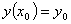 .
.
Метод Рунге - Кутта.
Допустим, что функция 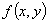 имеет
непрерывные частные производные до
имеет
непрерывные частные производные до 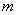 -го порядка включительно, тогда
решение
-го порядка включительно, тогда
решение 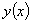 задачи Коши
для уравнения (1) будет обладать непрерывными производными до
задачи Коши
для уравнения (1) будет обладать непрерывными производными до 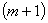 -го порядка
включительно и если значение
-го порядка
включительно и если значение 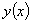 при
при 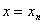 известно,
известно, 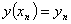 , то
справедливо равенство
, то
справедливо равенство
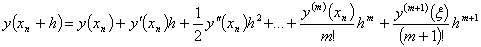 ,
,
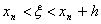 . (5)
. (5)
значения входящих сюда производных вычисляются
из уравнения (1) последовательным дифференцированием:
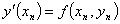 ,
,
 ,
,
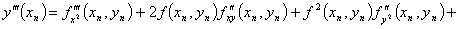
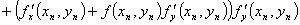 ,… (6)
,… (6)
дифференциальный
уравнение mathcad mathconnex
Подставляя значения 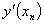 ,
, 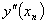 ,…,
определенные выражениями (6) в соотношении (5), можно вычислить значение
,…,
определенные выражениями (6) в соотношении (5), можно вычислить значение 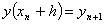 . Однако
такой расчет требует вычислений, сложность которых возрастает с увеличением
порядка производных. Для сокращения вычислительной работы Рунге предложил
значение
. Однако
такой расчет требует вычислений, сложность которых возрастает с увеличением
порядка производных. Для сокращения вычислительной работы Рунге предложил
значение 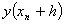 в виде:
в виде:
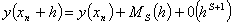 , (7)
, (7)
где 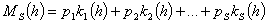 ,
,
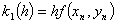 ;
; 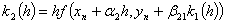 ,…,
,…,
 ,
, 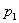 ,
,  , …,
, …, 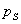 ,
, 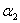 , …,
, …,  ,
, 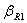 , …,
, …, 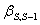 - некоторые параметры.
- некоторые параметры.
Формула (3) получается как частный
случай формулы (7) при 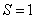 , а формула
(4) - при
, а формула
(4) - при 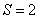 . Рассмотрим
вопрос о выборе параметров
. Рассмотрим
вопрос о выборе параметров 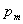 ,
, 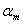 ,
, 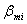 . Для простоты ограничимся случаем
. Для простоты ограничимся случаем 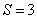 . Введем
обозначение:
. Введем
обозначение:
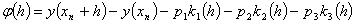 , (8)
, (8)
из выражения (7) следует, что
учитывая соотношения (6), из равенства (8)
найдем:
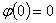 ,
,
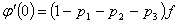 ,
,
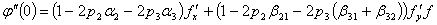 ,
,
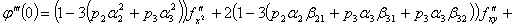
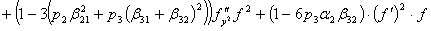 .
.
Условия (7) будут выполнятся, если справедливы
равенства:
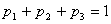 ,
,
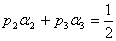 ,
,
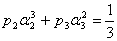 ;
;
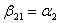 ;
; 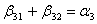 ;
;
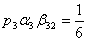 . (10)
. (10)
Эта система шести уравнений с восемью
неизвестными имеет бесчисленное множество решений. Наиболее употребительное
решение
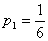 ,
, 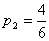 ,
, 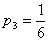 ,
, 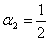 ,
, 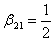 ,
, 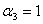 ,
, 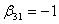 ,
, 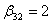
порождает расчетные формулы
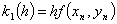
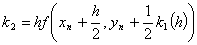 (11)
(11)
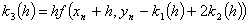 ,
,
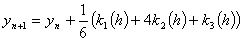 ,
, 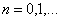
При  получаются расчетные формулы:
получаются расчетные формулы:
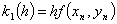 ,
,
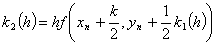 (12)
(12)
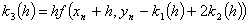 ,
,
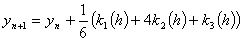 ,
, 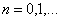
Оценка погрешности на каждом шаге
интегрирования уравнения (1) по методу Рунге-Кутта имеет порядок 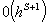 . Полную оценку
погрешности можно произвести аналогично тому, как это было сделано выше для
метода Эйлера.
. Полную оценку
погрешности можно произвести аналогично тому, как это было сделано выше для
метода Эйлера.
2.3 Функции,
предусматривающиеся для численного решения дифференциальных уравнений в MathCAD.
Системы MathCAD
пользуются огромной популярностью во всем мире, позволяя готовить вполне
профессиональные документы. Последние версии системы - MathCAD
2000 PRO и MathCAD
2000 Premium,
появившиеся в конце 1999 года, содержат тщательно сбалансированные средства
численных и символьных вычислений с графической визуализацией результатов в
сочетании с самым современным интерфейсом пользователя, мощной справочной
системой, обширными пакетами расширения и средствами для работы в интернете.
MathCAD
- это популярная система компьютерной математики, предназначенная для автоматизации
решения массовых математических задач в самых различных областях науки, техники
и образования.
Сегодня различные версии MathCAD
являются математически ориентированными универсальными системами. Помимо
собственно вычислений, как численных, так и аналитических, они позволяют с
блеском решать сложные оформительские задачи, которые с трудом даются
популярным текстовым редакторам или электронным таблицам.
С помощью MathCAD
можно, например, готовить статьи, книги, диссертации, научные отчеты, дипломные
и курсовые проекты не только с качественными текстами, но и с легко
осуществляемым набором самых сложных математических формул, изысканным
графическим представлением результатов вычислений и многочисленными “живыми”
примерами. А применение библиотек и пакетов расширения обеспечивает
профессиональную ориентацию MathCAD
на любую область науки, техники и образования.
Для решения дифференциальных уравнений в MathCAD
введен ряд функций. Вначале остановимся на функциях, дающих решения для систем
обыкновенных дифференциальных уравнений, представленных в обычной форме Коши:
·
rkadapt
(y, x1,
x2, acc,
n, F,
k, s)
- возвращает матрицу, содержащую таблицу значений решения задачи Коши на
интервале от х1 до х2 для системы обыкновенных дифференциальных уравнений,
вычисленную методом Рунге-Кутта с переменным шагом и начальными условиями в
векторе у (правые части системы записаны в векторе F,
n - число шагов, k
- максимальное число промежуточных точек решения, и s
- минимально допустимый интервал между точками);
·
Rkadapt
(y, x1,
x2, n,
F) - возвращает
матрицу решений методом Рунге-Кутта с переменным шагом для системы обыкновенных
дифференциальных уравнений с начальным условием в векторе у, правые части
которых записаны в символьном векторе F
на интервале от х1 до х2 при фиксированном числе шагов n;
·
rkfixed
(y, x1,
x2, n,
F) - возвращает
матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных
уравнений с начальным условием в векторе у, правые части которых записаны в
символьном векторе F на
интервале от х1 до х2 при фиксированном числе шагов n.
Функция Rkadapt
благодаря автоматическому изменению шага решения дает более точный результат.
Естественно, по скорости вычислений она проигрывает функции rkfixed,
хотя и не всегда - если решение меняется медленно, это может привести к
заметному уменьшению числа шагов. Таким образом, функция Rkadapt
наиболее привлекательна для решения систем дифференциальных уравнений, имеющих
относительно медленно изменяющиеся решения.
3. ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ С ПОМОЩЬЮ ПАКЕТОВ MathCAD
и MathConnex.
.1
Определение значений функций движения
В пакете MathCAD
по полученной математической модели определяю значения функций движения,
скорости и ускорения груза.

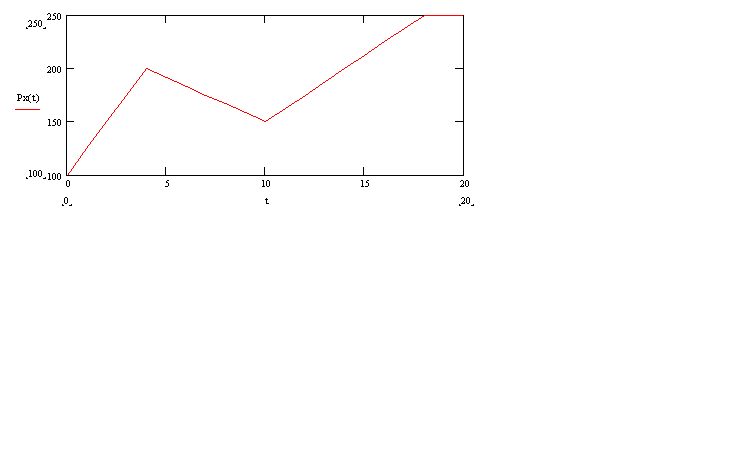
Рис. 1. Зависимость силы Px(t) от
времени t

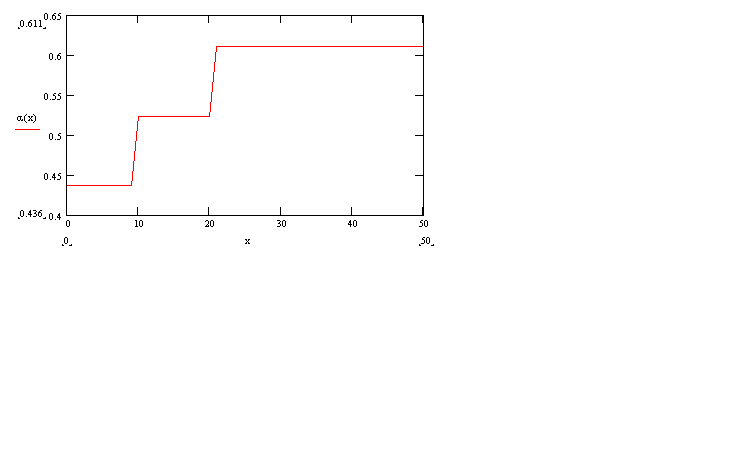
Рис. 2. Зависимость угла наклона от координаты х

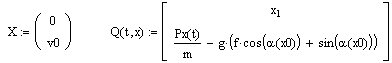
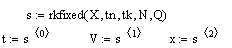
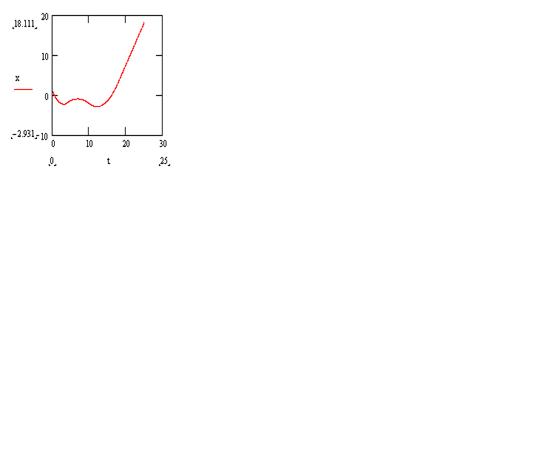
Рис. 3. Зависимость координаты х от
времени t

Рис. 4. Зависимость скорости V от
времени t
3.2
Исследование влияния частоты колебаний на движение груза
С помощью пакета MathConnex выполняю
моделирование влияния начальной скорости на движение тела и определяю
минимальную начальную скорость V0
min , при которой тело
поднимется на заданную высоту h.

Документ MathCAD,
вставленный в MathConnex.


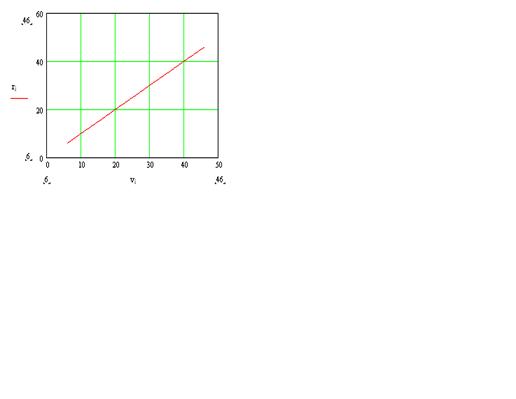
Рис. 5. Зависимость высоты от
скорости
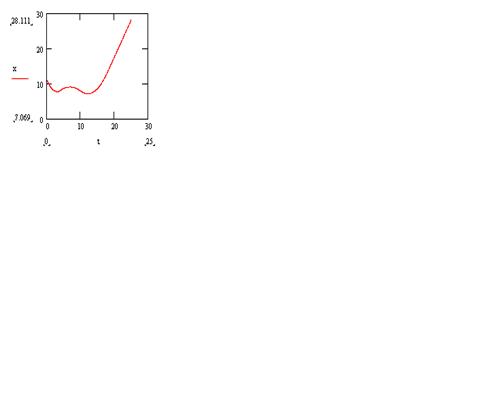
Рис. 6. Зависимость координаты х от
времени t
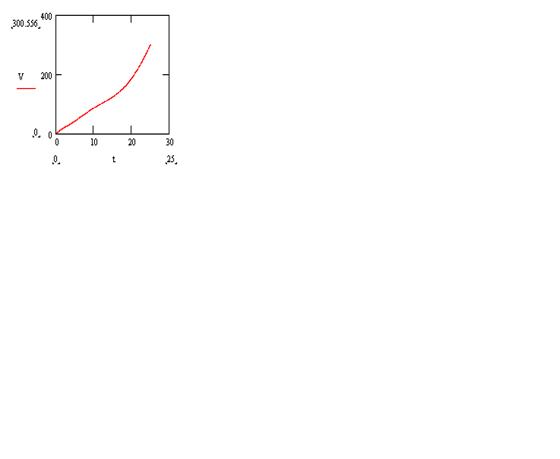
Рис. 7. Зависимость скорости V от времени t
Анализ результатов.
В ходе математического моделирования
влияния начальной скорости на движение тела определил, что минимальной
начальной скоростью V0 min, при
которой тело поднимется на заданную высоту h, является
11м/с.
ЗАКЛЮЧЕНИЕ
Данным курсовым проектом я оканчиваю курс
вычислительной техники и программирования. В ходе данной курсовой работы я
закрепила свои знания в области вычислительной техники, математики и
теоретической механики. Это связано с тем, что для создания программы
необходимо было исследовать механизм с колебательным движением груза и
произвести расчеты в среде MathCAD.
В данной работе была построена в среде MathCAD
модель работы механизма, с помощью пакета MathConnex
проведены исследования влияния от изменения определенных параметров на
максимальное отклонение груза от положения равновесия.
Первая глава посвящена алгоритмическому анализу
задачи. В ней приводится постановка задачи, на основании которой
разрабатывается графическая схема алгоритма решения задачи и таблица
соответствия переменных.
Документы MathCAD
и MathСоnnex
со всеми результатами приведен в третьей главе.
Построенная модель может быть использована для
исследования процессов в механизме. Работа в среде MathCAD
даёт значительное повышение точности в расчётах, облегчает процесс
программирования при вычислении функций, даёт возможность создания опрятных,
красочных, понятных любому пользователю документов.
ЛИТЕРАТУРА
1. Корн
Г., Корн T. Справочник по математике (для научных работников и инженеров). -
M.: Наука, 1978.
2. Токочаков
В. И. Практическое пособие по теме «Решение систем алгебраических и
дифференциальных уравнений в среде Mathcad для студентов всех специальностей
дневного и заочного отделений. - Гомель: ГГТУ, 2000.
. Mathcad
6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95. - M.:
Информационно-издательский дом «Филинъ», 1996.
. Тарг
С. М. Краткий курс теоретической механики. - М., 1970 г.
. Бать
М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и
задачах, т. II (Динамика). - М., 1972 г.
. Яблонский
А. А. Курс теоретической механики, ч.II.- М.,1966 г.
. Яблонский
А. А. Сборник заданий для курсовых работ по теоретической механике. - М., 1972
г.,
. Краскевич
В.Е.,Зеленский К.Х. Численные методы в инженерных исследованиях. - Киев:1986.
. Останина
А.М. Применение математических методов и ВМ.Мн.:1985.
. Тарасик
В.П. Математическое моделирование технических систем.- Мн.:1997.