Модель объекта в виде передаточной функции
Содержание
Введение
. Идентификация объекта управления
.1 Исходные данные
.2 Идентификация объекта методом последовательного
логарифмирования
.3 Идентификация объекта управления методом моментов
.4 Идентификация объекта методом наименьших квадратов
.5 Идентификация в среде Matlab
.6 Сравнение переходных функций
. Расчёт параметров настроек типовых регуляторов для
детерминированных типовых сигналов
.1 Выбор закона регулирования
.2 Настройка ПИ регулятора методом Циглера-Никольса
.3 Моделирование системы с настроечными параметрами ПИ
регулятора, полученными с помощью метода Циглера-Никольса
.4 Настройка ПИ регулятора методом РЧХ
.5 Моделирование системы управления с настроечными
параметрами ПИ регулятора, полученными с помощью метода РЧХ
.6 Расчёт и сравнение степени затухания
. Расчёт оптимального и квазиоптимального регуляторов
.1 Расчёт оптимального регулятора
.2 Расчёт квазиоптимального регулятора
.3 Анализ работы оптимального и квазиоптимального
регуляторов
. Расчёт систем управления многомерным объектом
.1 Расчёт комбинированной САР
.2 Расчёт каскадной САР
.3 Расчёт системы связанного регулирования двумерным
объектом
.4 Анализ работы систем управления
Заключение
Список используемой литературы
Введение
В данной курсовой работе при помощи кривой разгона необходимо получить
модель объекта в виде передаточной функции. Для того чтобы идентифицировать
объект мы будем использовать следующие методы: метод последовательного
логарифмирования, метод наименьших квадратов, метод моментов и идентификацию
объекта в программе Matlab.
Исходя из полученных данных устанавливаем, какая модель точнее описывает
заданный объект. Решение данной задачи в целом является достаточно актуальной
проблемой, поскольку зачастую мы имеем не саму математическую модель, а лишь ее
кривую разгона.
После выбора модели объекта производим расчет параметров ПИ-регулятора.
Расчет производим при помощи методов Циглера-Никольса и расширенных частотных
характеристик. Для того, чтобы определить по какому методу найдены наилучшие
настройки регулятора, используем в качестве критерия качества степень затухания
процесса.
Затем мы моделируем систему с оптимальным и квазиоптимальным регуляторами
и сравниваем дисперсию ошибки регулирования. Умение строить такие системы важно
в условиях, когда возмущение объекта носит стохастический, а не
детерминированный характер.
Затем мы синтезируем систему управления многомерным объектом трех видов:
комбинированную, каскадную и связанного регулирования. Рассчитываем параметры
настройки регуляторов и компенсаторов, исследуем отклик системы по различным
каналам на типовые воздействия.
Данные системы автоматического регулирования (многоконтурные) относятся к
классу многомерных систем, то есть таких систем, которые имеют не одну, а
несколько управляемых переменных. Знание таких систем так же является
необходимым при проектировании систем автоматического управления.
Целью курсовой работы является теоретическое изучение основных понятий,
методов расчета САУ, а также закрепление изученного материала на практике,
проведением расчетов (идентификация объекта управления, расчет настроек
регуляторов и моделирование замкнутой САУ в условиях различных входных
воздействий).
1.
Идентификация объекта управления
Идентификация - это определение взаимосвязи между выходными и входными
сигналами на качественном уровне.
1.1 Исходные данные
К=6*10=60=3=4
Передаточная функция объекта:
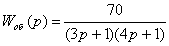
Шаг
∆τ=5Tmax/40=0.5
Таблица
значений:
Табл.
1.1.1
|
i
|
τ
|
h(τ)
|
|
1
|
0
|
0
|
|
2
|
0,5
|
0,5642
|
|
3
|
1
|
2,0581
|
|
4
|
1,5
|
4,2196
|
|
5
|
2
|
6,8406
|
|
6
|
2,5
|
9,7577
|
|
7
|
3
|
12,8433
|
|
8
|
3,5
|
15,9991
|
|
9
|
4
|
19,1504
|
|
10
|
4,5
|
22,2414
|
|
11
|
5
|
25,2316
|
|
12
|
5,5
|
28,0927
|
|
13
|
6
|
30,8055
|
|
14
|
6,5
|
33,3588
|
|
15
|
7
|
35,7467
|
|
16
|
7,5
|
37,9681
|
|
17
|
8
|
40,025
|
|
18
|
8,5
|
41,9219
|
|
19
|
9
|
43,665
|
|
20
|
9,5
|
45,2618
|
|
21
|
10
|
46,7206
|
|
22
|
10,5
|
48,0498
|
|
23
|
11
|
49,2584
|
|
24
|
11,5
|
50,355
|
|
25
|
12
|
51,3482
|
|
26
|
12,5
|
52,2462
|
|
27
|
13
|
53,0569
|
|
28
|
13,5
|
53,7877
|
|
29
|
14
|
54,4458
|
|
30
|
14,5
|
55,0375
|
|
31
|
15
|
55,5691
|

Рис. 1.1.1. Кривая разгона по исходным данным
1.2
Идентификация объекта управления методом последовательного логарифмирования
Метод последовательного логарифмирования применим для аппроксимации
гладких неколебательных апериодических переходных процессов.
Переходная функция должна быть представлена выражением вида:


Суть
метода заключается в последовательном приближении 
 сначала
решением уравнения первого порядка, то есть функцией
сначала
решением уравнения первого порядка, то есть функцией 
 . Если
эта аппроксимация неудовлетворительна на каком либо отрезке [0 , T], то вводится
в рассмотрение вторая составляющая
. Если
эта аппроксимация неудовлетворительна на каком либо отрезке [0 , T], то вводится
в рассмотрение вторая составляющая 
 .
.
Неизвестные
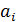
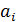 и
и 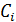
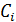 определяются
на каждом этапе аппроксимации с помощью операции логарифмирования, вследствие
чего этот способ и получил свое название.
определяются
на каждом этапе аппроксимации с помощью операции логарифмирования, вследствие
чего этот способ и получил свое название.
Поэтому
можно предположить, что 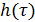
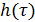 есть
решение линейного дифференциального уравнения первого порядка, и написать
приближенное равенство:
есть
решение линейного дифференциального уравнения первого порядка, и написать
приближенное равенство:


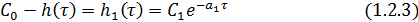
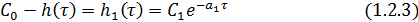
Прологарифмируем
функцию 
 и
получим уравнение прямой линии в полулогарифмическом масштабе по оси ординат:
и
получим уравнение прямой линии в полулогарифмическом масштабе по оси ординат: 
 .
.
Отсюда
нетрудно определить неизвестные величины 
 и
и 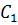
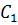 . Для
этого вычисляется функция
. Для
этого вычисляется функция 
 и строится
график
и строится
график 
 в
зависимости от времени
в
зависимости от времени 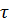
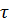 . Если
. Если 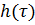
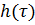 действительно
является решением дифференциального уравнения первого порядка, то функция:
действительно
является решением дифференциального уравнения первого порядка, то функция:


равна
нулю при всех а не только при больших значениях времени 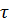
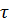 , т.е.
асимптота совпадает со всей функцией
, т.е.
асимптота совпадает со всей функцией 

Покажем
последовательность расчета:
) 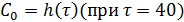
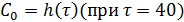 . Строим
вспомогательную функцию
. Строим
вспомогательную функцию 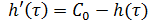
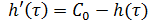 , из
которой исключается
, из
которой исключается 
 .
.
)По
полученным данным строим график зависимости 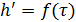
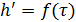 , для
удобства воспользовавшись ln(
, для
удобства воспользовавшись ln(
 .
.
По
графику находим 
 , как
точку пересечения графика с осью ординат, и
, как
точку пересечения графика с осью ординат, и 
 , как
тангенс угла наклона графика к оси абсцисс. Причем
, как
тангенс угла наклона графика к оси абсцисс. Причем 
 .
Полученные значения исключаем из исходной функции:
.
Полученные значения исключаем из исходной функции:
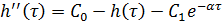
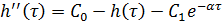 ,
,
) Строим
функцию откуда находим 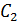
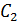 и
и 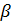
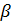 (см. п.2)
(см. п.2)
) Выполняем
проверку вычислений, исходя из условий:

 =0, при
=0, при 

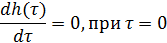

Табл. 1.2.1
|
τ
|
h(τ)
|
C0
|
h'(τ)=C0-h(τ)
|
ln(h'(τ))
|
metod log
|
|
0
|
0
|
60
|
60
|
4,0943
|
0
|
|
0,5
|
0,5642
|
60
|
59,4358
|
4,0849
|
0,2245
|
|
1
|
2,0581
|
60
|
57,9419
|
4,0594
|
0,8456
|
|
1,5
|
4,2196
|
60
|
55,7804
|
4,0214
|
1,7924
|
|
2
|
6,8406
|
60
|
53,1594
|
3,9733
|
3,0035
|
|
2,5
|
9,7577
|
60
|
50,2423
|
3,9169
|
4,4259
|
|
3
|
12,8433
|
60
|
47,1567
|
3,8535
|
6,0138
|
|
3,5
|
15,9991
|
60
|
44,0009
|
3,7842
|
7,7282
|
|
4
|
19,1504
|
60
|
40,8496
|
3,7099
|
9,5353
|
|
4,5
|
22,2414
|
60
|
37,7586
|
3,6312
|
11,407
|
|
5
|
25,2316
|
60
|
34,7684
|
3,5487
|
13,318
|
|
5,5
|
28,0927
|
60
|
31,9073
|
3,4628
|
15,248
|
|
6
|
30,8055
|
60
|
29,1945
|
3,374
|
17,18
|
|
6,5
|
33,3588
|
60
|
26,6412
|
3,2825
|
19,1
|
|
7
|
35,7467
|
60
|
24,2533
|
3,1886
|
20,996
|
|
7,5
|
37,9681
|
60
|
22,0319
|
3,0925
|
22,858
|
|
8
|
40,025
|
60
|
19,975
|
2,9945
|
24,678
|
|
8,5
|
41,9219
|
60
|
18,0781
|
2,8947
|
26,45
|
|
9
|
43,665
|
60
|
16,335
|
2,7933
|
28,169
|
|
9,5
|
45,2618
|
60
|
14,7382
|
2,6904
|
29,832
|
|
10
|
46,7206
|
60
|
13,2794
|
2,5862
|
31,435
|
|
10,5
|
48,0498
|
60
|
11,9502
|
2,4807
|
32,978
|
|
11
|
49,2584
|
60
|
10,7416
|
2,3741
|
34,459
|
|
11,5
|
50,355
|
60
|
9,645
|
2,2664
|
35,877
|
|
12
|
51,3482
|
60
|
8,6518
|
2,1578
|
37,234
|
|
12,5
|
52,2462
|
60
|
7,7538
|
2,0482
|
38,529
|
|
13
|
53,0569
|
60
|
6,9431
|
1,9377
|
39,763
|
|
13,5
|
53,7877
|
60
|
6,2123
|
1,8265
|
40,937
|
|
14
|
54,4458
|
60
|
5,5542
|
1,7146
|
42,054
|
|
14,5
|
55,0375
|
60
|
4,9625
|
1,6019
|
43,114
|
|
15
|
60
|
4,4309
|
1,4886
|
44,119
|
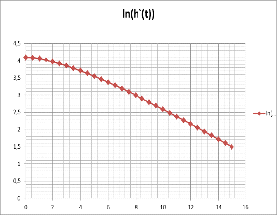
Рис.1.2.1. Нахождение величин α и C1 методом последовательного
логарифмирования
h(t)=C0+C1*e-α1*t+C2
*e-α2*t
C0+C1+C2=0=60 α1*C1+α2*C2=0
(C1)=4.63=102.5141=-162.514
Tg(γ)=0.44915/2=0.22457
Т1=1/ Tg(γ)=1/0.22457=4.45295
α1=1/Т1=0.22457
α2=α1*C1/C2
α2=0.14166
Т2=1/ α2=1/0.14166=7.0592
Представим результат в виде таблицы:
Таблица 1.2.2
|
C0
|
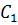
|
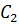
|
α1
|
α2
|
|
60
|
102.5141
|
-162.514
|
0.22457
|
0.14166
|
Итоговое уравнение по методу последовательного логарифмирования:
(t)=60+102.5141*e-0.22457*t-162.514*e-0.14166*t

Рис. 1.2.2. Сравнение исходной функции и полученной в результате метода
последовательного логарифмирования

Нахождение среднего квадратичного отклонения:
Таблица 1.2.3
|
τ
|
h(τ)
|
metod log
|
(h(τ)- metodlog)^2
|
|
0
|
0
|
0
|
0
|
|
0,5
|
0,5642
|
0,2245
|
0,115379
|
|
1
|
2,0581
|
0,8456
|
1,470139
|
|
1,5
|
4,2196
|
1,7924
|
5,8914
|
|
2
|
6,8406
|
3,0035
|
14,72357
|
|
2,5
|
9,7577
|
4,4259
|
28,42858
|
|
3
|
12,8433
|
6,0138
|
46,64141
|
|
3,5
|
15,9991
|
7,7282
|
68,40766
|
|
4
|
19,1504
|
9,5353
|
92,44944
|
|
4,5
|
22,2414
|
11,407
|
117,3931
|
|
5
|
25,2316
|
13,318
|
141,9423
|
|
5,5
|
28,0927
|
15,248
|
164,9873
|
|
6
|
30,8055
|
17,18
|
185,646
|
|
6,5
|
33,3588
|
19,1
|
203,305
|
|
7
|
35,7467
|
20,996
|
217,5816
|
|
7,5
|
37,9681
|
22,858
|
228,319
|
|
8
|
40,025
|
24,678
|
235,5333
|
|
8,5
|
41,9219
|
26,45
|
239,3819
|
|
9
|
43,665
|
28,169
|
240,1227
|
|
9,5
|
45,2618
|
29,832
|
238,0851
|
|
10
|
46,7206
|
31,435
|
233,6384
|
|
10,5
|
48,0498
|
32,978
|
227,157
|
|
11
|
49,2584
|
34,459
|
219,0255
|
|
11,5
|
50,355
|
35,877
|
209,6003
|
|
12
|
51,3482
|
37,234
|
199,2167
|
|
12,5
|
52,2462
|
38,529
|
188,1743
|
|
13
|
53,0569
|
39,763
|
176,739
|
|
13,5
|
53,7877
|
40,937
|
165,1377
|
|
14
|
54,4458
|
42,054
|
153,5678
|
|
14,5
|
55,0375
|
43,114
|
142,1812
|
|
15
|
55,5691
|
44,119
|
131,11
|

.3
Идентификация объекта управления методом моментов
При использовании метода моментов основной проблемой является нахождение
функциональной зависимости между моментом входной и выходной функции.
Для
вычисления моментов функции достаточно знать ее изображение по Лапласу (которое
часто найти гораздо легче, чем функцию). Действительно, согласно определению
преобразования по Лапласу функции 
 , ее
изображение:
, ее
изображение:


Равенство (1.3.1) при p=0 имеет вид:
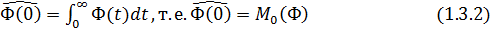
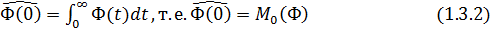
Найдем
значение 
 при
при 
 :
:
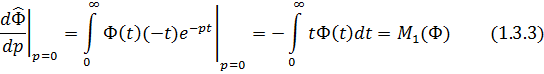
Аналогично,
для производных более высокого порядка получим:
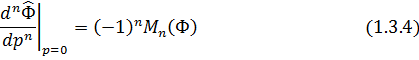
Таким
образом, для получения момента любого порядка некоторой функции 
 достаточно
продифференцировать по
достаточно
продифференцировать по 
 необходимое
число раз изображение
необходимое
число раз изображение 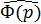
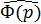 этой
функции и положить
этой
функции и положить 
 .
Получение явных выражений для момента с помощью выражения (1.3.4) имеет тот
недостаток, что при этом можно получить только моменты, являющиеся интегралами
по бесконечному промежутку времени.
.
Получение явных выражений для момента с помощью выражения (1.3.4) имеет тот
недостаток, что при этом можно получить только моменты, являющиеся интегралами
по бесконечному промежутку времени.
Итак,
передаточная функция описывается уравнением апериодического звена второго
порядка. Ее изображение по Лапласу имеет вид:
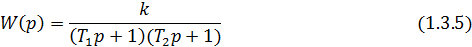
Тогда
выражение (1.3.4) примет вид:

Рассчитаем
нулевой момент:
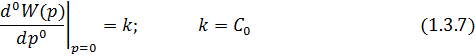
Рассчитаем
первый момент (математическое ожидание):

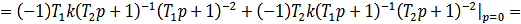




С
другой стороны, т.к. математическое ожидание - это среднее арифметическое
значений импульсной переходной функции 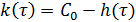
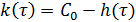 :
:

Рассчитаем
второй момент (дисперсию):

С
другой стороны, т.к. дисперсия - это квадрат отклонения значений 
 от
среднего арифметического
от
среднего арифметического 
 :
:
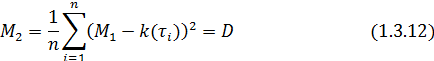
Итак,
получившаяся система уравнений позволяет найти 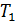
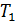 и
и 
 , а
следовательно и
, а
следовательно и 
 и
и 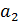
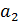 :
:

Расчет
в MathCAD:
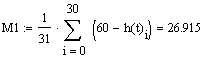

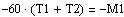
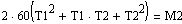
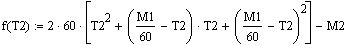

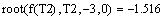

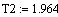






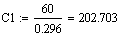
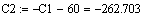
Итоговое уравнение по методу моментов:
(t)=60+202.703*e-0.66*t-262.703*e-0.509*t

Рис. 1.3.1. Сравнение исходной функции и полученной в результате метода
моментов
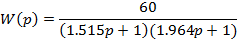
Нахождение среднего квадратичного отклонения:
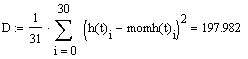
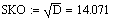
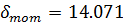
.4 Идентификация объекта методом наименьших квадратов
Метод наименьших квадратов (МНК) - метод оценки параметров модели на
основании экспериментальных данных.
В основе метода лежат следующие рассуждения: при замене точного
(неизвестного) параметра модели приблизительным значением необходимо
минимизировать разницу между экспериментальными данными и теоретическими
(вычисленными при помощи предложенной модели). Это позволяет рассчитать
параметры модели с помощью МНК с минимальной погрешностью.
Мерой разницы в методе наименьших квадратов служит сумма квадратов
отклонений действительных (экспериментальных) значений от теоретических.
Выбираются такие значения параметров модели, при которых сумма квадратов разностей
будет наименьшей - отсюда название метода.

где
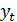
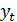 -
теоретическое значение измеряемой величины,
-
теоретическое значение измеряемой величины, 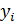
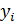 -
экспериментальное.
-
экспериментальное.
При
этом полученные с помощью МНК параметры модели являются наиболее вероятными.
Вычисления будем проводить в Mathcad.

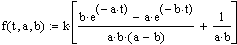
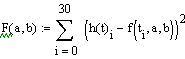

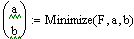
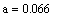
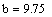

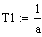
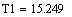

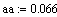

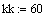
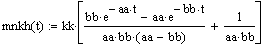

Рис. 1.4.1. Сравнение исходной функции и полученной в результате метода
наименьших квадратов

Нахождение среднего квадратичного отклонения:



.5 Идентификация объекта управления в программе Matlab
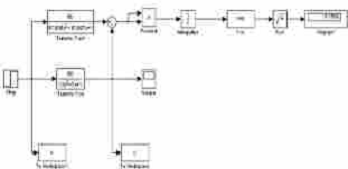
Рис. 1.5.1. Схема
С помощью Process Models находим значения T1 и T2.

Рис.
1.5.2. Полученная оценка параметров 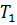
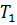 и
и 

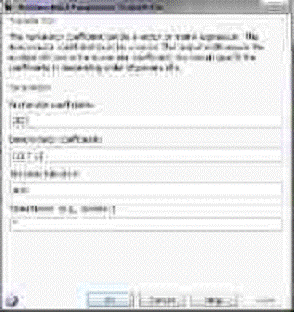
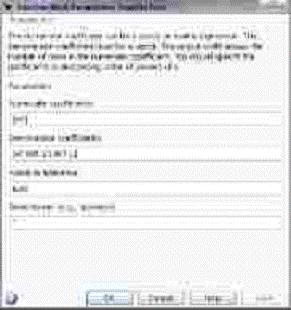
Рис. 1.5.3. Параметры блоков Transfer Fcn и Transfer Fcn2
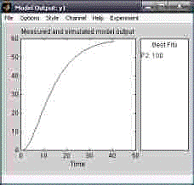
Рис. 1.4.4. Достоверность оценки
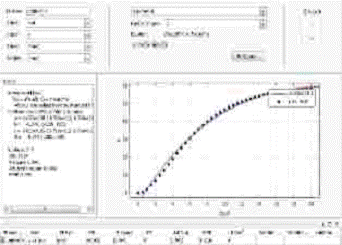
Рис. 1.5.5. Curve Fitting
Передаточная функция:
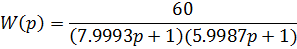
Среднеквадратическое отклонение:
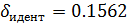
.6 Сравнение
переходных функций
Таблица 1.6.1
|
Метод последовательного
логарифмирования
|
Метод моментов
|
Метод наименьших квадратов
|
Идентификация в Matlab
|
|
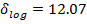
|
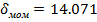
|

|
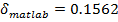
|
Среднее квадратичное отклонение передаточной функции, полученной при
помощи программы Matlab, от заданной функции меньше, чем соответствующие
значения для других методов, поэтому далее будем использовать передаточную
функцию, полученную этим методом:
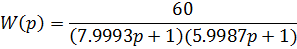
2. Выбор
закона управления
Для выбора закона регулирования будем использовать соотношение
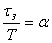
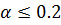
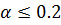 -
релейный закон регулирования
-
релейный закон регулирования

 -
пропорциональный закон
-
пропорциональный закон

 - ПИ
закон
- ПИ
закон

 - ПИД
закон
- ПИД
закон
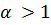
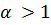 -
предикторы
-
предикторы
Передаточная
функция объекта:
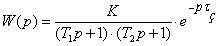
Тогда





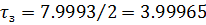
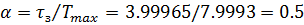

Исходя
из данных проведённого расчёта, выбираем ПИ-закон регулирования.
3. Расчёт
параметров настройки регулятора
.1 Метод
Циглера-Никольса
Этот метод основан на критерии Найквиста, суть которого заключается в
следующем: замкнутая система автоматического регулирования будет устойчивой,
если устойчива соответствующая разомкнутая система и годограф ее
амплитудно-фазовой характеристики не охватывает точку с координатами [-1, j0].
Этот критерий выполняется в случае, если разомкнутая система находится на границе
устойчивости при малых степенях астатизма.
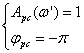 (3.1.1)
(3.1.1)
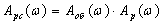 (3.1.2)
(3.1.2)
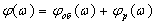 (3.1.3)
(3.1.3)
Метод
Циглера-Никольса состоит в том, что замкнутую систему искусственно выводят на
границу устойчивости.
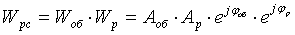
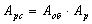

Выводим
систему на границу устойчивости.
 (3.1.4)
(3.1.4)
Для
определенной частоты, при которой выполняется система (3.1.4) (т.е. находится
на границе устойчивости) проводят расчет настроек ПИ-регулятора.
Определение
оптимальных настроек по формулам:
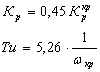 (3.1.5)
(3.1.5)
Надо
так же заметить, что метод применим лишь для объектов в совокупности по
числителю и знаменателю передаточной функции третьего и более высокого
порядков. В противном случае объект должен обладать запаздыванием.
Используя
данные полученные методом идентификации в MATLAB, рассчитаем параметры
регулятора для следующей передаточной функции:
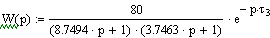
Поскольку
данный метод основан на частотном критерии Найквиста, то должно выполняться
условие:

 .
.
Листинг в программе MathCAD

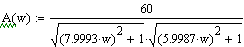



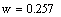
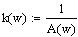

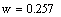




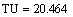

Исследуем реакцию системы на типовые сигналы по каналам управления и
возмущения.


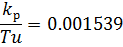


1. Переходная функция по каналу управления

Рис. 3.1.2. Система с переходной функцией по каналу управления
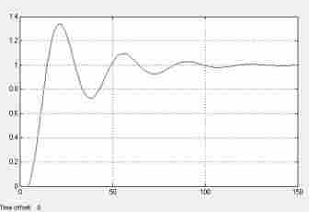
Рис. 3.1.3. Реакция системы по каналу управления на ступенчатую функцию
2. Импульсная функция по каналу управления

Рис. 3.1.4. Система с импульсной функцией по каналу управления

Рис. 3.1.5. Реакция системы по каналу управления на импульсную функцию
. Переходная функция по каналу возмущения
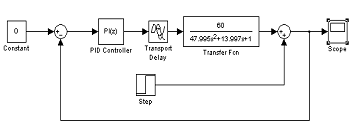
Рис. 3.1.6. Система с переходной функцией по каналу возмущения

. Импульсная функция по каналу возмущения

Рис. 3.1.8. Система с импульсной функцией по каналу возмущения
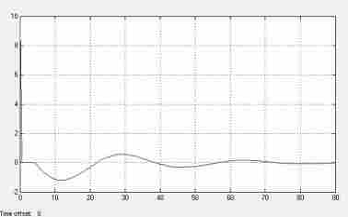
Рис. 3.1.9. Реакция системы по каналу возмущения на импульсную функцию
.2 Метод
расширенных частотных характеристик
Этот метод полностью основан на использовании модифицированного критерия
Найквиста (критерий Е. Дудникова), который гласит: если разомкнутая система
устойчива и ее расширенная амплитудно-фазовая характеристика проходит через
точку с координатами [-1, j0], то замкнутая система будет не только устойчива,
но и будет обладать некоторым запасом устойчивости, определяемым степенью
колебательности.


 -
расширенная АЧХ разомкнутой системы;
-
расширенная АЧХ разомкнутой системы;

 -расширенная
ФЧХ разомкнутой системы.
-расширенная
ФЧХ разомкнутой системы.
Этот
метод сводится, по существу, к решению системы уравнений (2.4.1) при заданных
характеристиках объекта регулирования и заданной степени колебательности m, то
есть по существу, при заданном запасе устойчивости.
Примем
степень затухания равную Ψ
= 0.85
Расчет
в среде Mathcad:
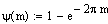




для Ψ = 0.85 m=0.302
Перейдем
в область расширенных частотных характеристик объекта. Для этого сделаем замену

 :
:
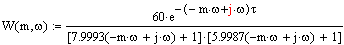
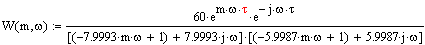

Расширенная амплитудно-частотная характеристика объекта:

Расширенная фазо-частотная характеристика объекта:

Для ПИ-регулятора расширенные частотные характеристики имеют вид:


После
некоторых преобразований второе уравнение системы можно записать:


Из
уравнения при известныхmи  можно определить
можно определить для
различных
для
различных  , а затем можно при различных
, а затем можно при различных 
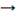
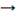 Tu.
Tu.
Далее,
используя первое уравнение системы можно записать:
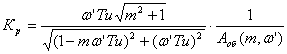
Отсюда,
зная  можно определить Кр при различных значениях частот
можно определить Кр при различных значениях частот .
.
Расчет
параметров настройки регулятора по методу расширенных частотных характеристик:
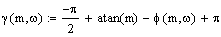
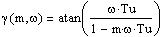




Нахождение первого внутреннего витка в методе РЧХ:
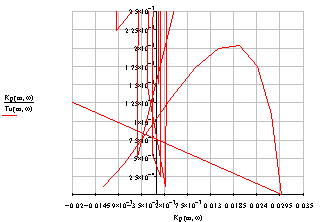
Из
графиков видно, что на первом витке 
 =
0.02=8.889
=
0.02=8.889
Исследуем реакцию системы на типовые сигналы по каналам управления и
возмущения.
. Переходная функция по каналу управления
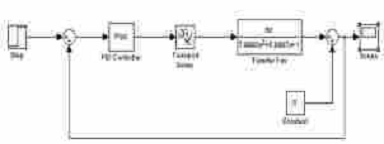
Рис. 3.2.2. Система с переходной функцией по каналу управления
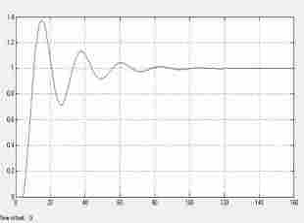
Рис. 3.2.3. Реакция системы по каналу управления на ступенчатую функцию
. Переходная функция по каналу возмущения

Рис. 3.2.6. Система с переходной функцией по каналу возмущения
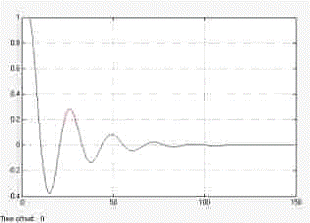
Рис. 3.2.7. Реакция системы по каналу возмущения на переходную функцию
.
Импульсная функция по каналу управления

Рис. 3.2.4. Система с импульсной функцией по каналу управления
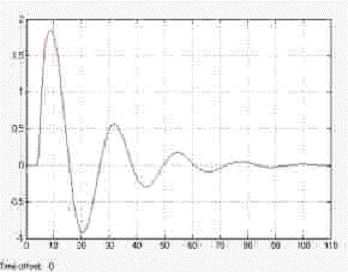
Рис. 3.2.5. Реакция системы по каналу управления на импульсную функцию
. Импульсная функция по каналу возмущения

Рис. 3.2.8. Система с импульсной функцией по каналу возмущения

Рис. 3.2.9. Реакция системы по каналу возмущения на импульсную функцию
.3 Сравнение качества работы системы управления
В данной курсовой работе основным критерием качества регулирования
является степень затухания переходного процесса, при воздействии двух типовых
воздействий: импульса и единичной ступеньки.
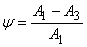 (3.3.1)
(3.3.1)
Рассчитаем значения степеней затухания для процессов, представленных на
рис. 3.1.2., рис. 3.1.4., рис. 3.1.6., рис. 3.1.8. и на рис. 3.2.3., рис.
3.2.5., рис. 3.2.7., рис. 3.2.9. по формуле (3.3.1.).
Метод Циглера-Никольса (рис. 3.1.2., рис. 3.1.4., рис. 3.1.6., рис.
3.1.8.)





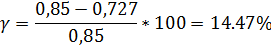
Метод расширенных частотных характеристик (рис. 3.2.3., рис. 3.2.5., рис.
3.2.7., рис. 3.2.9.)
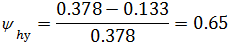
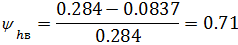


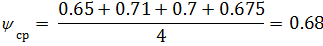

По результатам расчётов можно сделать вывод о том, что регулятор,
рассчитанный по методу Циглера-Никольса, справляется со своей задачей лучше,
чем регулятор, рассчитанный по методу расширенных частотных характеристик, так
как у него отклонение от заданной величины степени затухания 0,85 гораздо
меньше.
4. Расчёт
оптимального и квазиоптимального законов регулирования
.1 Расчёт
оптимального регулятора
В системах регулирования возмущающие воздействия зачастую являются случайными
функциями времени. Естественно поэтому оценивать качество функционирования
системы регулирования соответствующими вероятностными характеристиками:
математическое ожидание отклонения регулируемой величины и среднеквадратичным
ее значением.
Получим автокорреляционную функцию фильтра. Передаточная функция фильтра

Получим автокорреляционную функцию фильтра:

Рис. 3.1.1. Получение сглаженной автокорреляционной функции

Рис. 3.1.2 Автокорреляционная функция фильтра
Проведём аппроксимацию автокорреляционной функции фильтра методом
наименьших квадратов в программе MathCAD:
идентификация регулятор сигнал логарифмирование


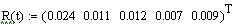

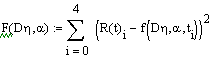
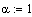

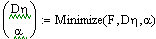
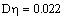
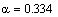




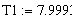

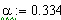


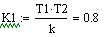

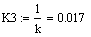
Смоделируем оптимальный регулятор:

Рис. 4.1.4. Схема оптимального регулятора
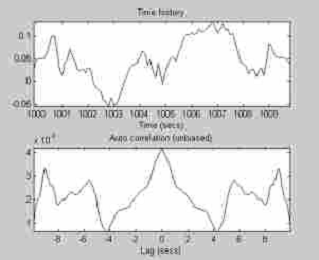
Рис. 4.1.5. Автокорреляционная функция оптимального регулятора

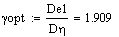
4.2 Расчёт
квазиоптимального регулятора
Передаточная функция квазиоптимального регулятора:

Из
уравнения (3.2.1) выразим 
 .
.
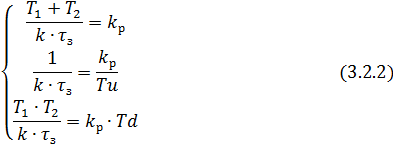
Подставим
исходные данные
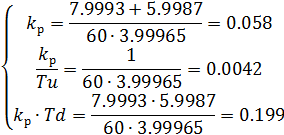
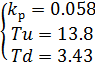
Построим
схему с квазиоптимальным регулятором:
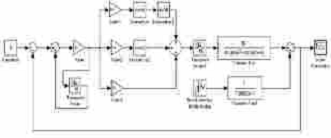
Рис. 3.2.1. Схема замкнутой САР с квазиоптимальным регулятором
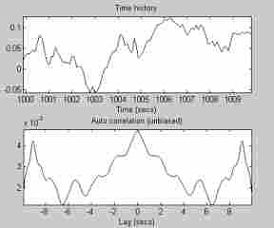
Рис. 3.2.2. Автокорреляционная функция квазиоптимального регулятора

.3 Анализ работы системы управления
Проведём анализ работы оптимального и квазиоптимального регуляторов. Для
этого подсчитаем отношения дисперсии установившегося состояния к дисперсии
фильтра.
 (4.3.1)
(4.3.1)
Если

 , то
система обладает нулевыми фильтрующими свойствами,
, то
система обладает нулевыми фильтрующими свойствами, 
 .
.
Если
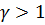
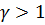 , то
система обладает отрицательными фильтрующими свойствами,
, то
система обладает отрицательными фильтрующими свойствами,
 .
.
Если

 , то
система обладает положительными фильтрующими свойствами,
, то
система обладает положительными фильтрующими свойствами, 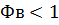
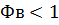 ,
, 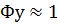
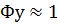 .
.
Чем
ближе 
 к нулю,
тем лучшими фильтрующими свойствами обладает система.
к нулю,
тем лучшими фильтрующими свойствами обладает система.
γ для оптимального регулятора:
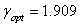
γ для квазиоптимального регулятора:

По результатам, полученным при расчётах можно сделать вывод о том, что
системы и с оптимальным и квазиоптимальным регулятором обладают отрицательными
фильтрующими свойствами. Система под управлением квазиоптимального регулятора
обладает более отрицательными фильтрующими свойствами.
5. Расчет систем управления многомерным объектом
.1 Комбинированная система управления
Существует случай, когда к объекту прилагаются жесткие воздействия,
которые можно измерить, но предлагается не одноконтурная система управления, а
так называемая комбинированная система, которая является комбинацией двух
принципов - принципа обратной связи и принципа компенсации возмущений.
Предлагается перехватывать возмущение раньше их воздействия на объект и с
помощью вспомогательного регулятора компенсировать их действия.


Рис. 5.1.1. Комбинированная система управления
Применим
к схеме, приведённой на Рис. 5.1.1, условие инвариантности выходной величины 
 по
отношению к возмущающему воздействию
по
отношению к возмущающему воздействию 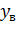
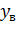 :
:
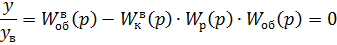
Принцип инвариантности к возмущению: чтобы система была инвариантна к
возмущению, её передаточная функция по каналу управления должна быть равна
нулю. Тогда передаточная функция компенсатора запишется так
 (5.1.1)
(5.1.1)
Рассчитаем ПИД-регулятор при помощи стандартных биномиальных форм
Ньютона.


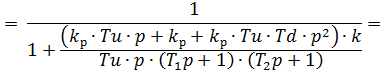




Приравняв полином знаменателя к нулю, получим выражение:
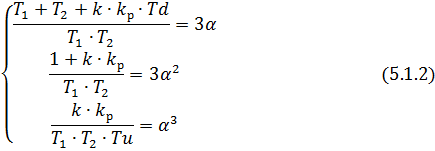
Рассчитаем ПИД-регулятор, используя формулу (5.1.2):

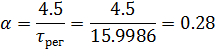

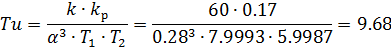

Рассчитаем компенсатор для нашей схемы, используя выражение (5.1.1):
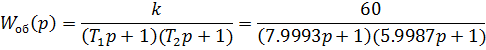
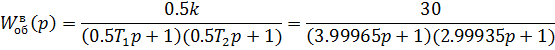
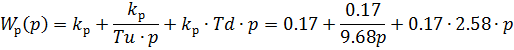

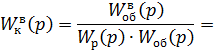
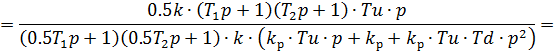
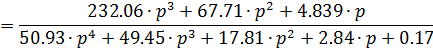
Теперь, когда получены все передаточные функции, проведём моделирование
системы.
Подсистема:
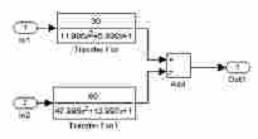
Рис. 5.1.2. Структура составного блока Subsystem
. Ступенчатое воздействие по каналу управления:

Рис. 5.1.3. Схема со ступенчатой функцией по каналу управления

Рис. 5.2.2. Настройки основного регулятора при Response time: 13 seconds
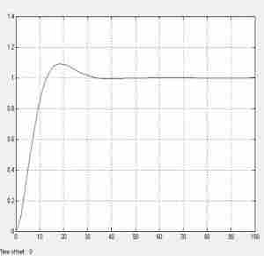
Рис. 5.1.4. Реакция на ступенчатую функцию по каналу управления
. Ступенчатое воздействие по каналу возмущения:

Рис. 5.1.5. Схема со ступенчатой функцией по каналу возмущения

Рис. 5.1.6. Реакция на ступенчатую функцию по каналу возмущения
. Импульсное воздействие по каналу управления:
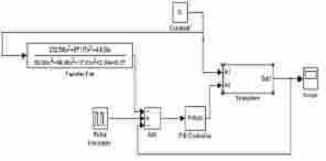
Рис. 5.1.7. Схема с импульсной функцией по каналу управления

Рис. 5.1.8. Реакция на импульсную функцию по каналу управления
. Импульсное воздействие по каналу возмущения:
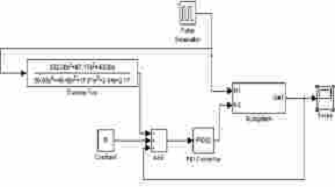
Рис. 5.1.9. Схема с импульсной функцией по каналу возмущения

Рис. 5.1.10. Реакция на импульсную функцию по каналу возмущения
.2 Каскадная система управления
Каскадные системы применяют для автоматизации объектов, обладающих
большой инерционностью по каналу регулирования, если можно выбрать менее
инерционную по отношению к наиболее опасным возмущениям промежуточную
координату и использовать для неё то же регулирующее воздействие, что и для
основного выхода объекта.
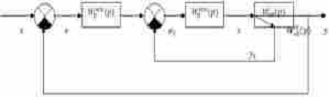
Рис. 5.2.1. Каскадная схема
В
этом случае в систему регулирования (рис.5.2.1) включают два регулятора -
основной (внешний) регулятор, служащий для стабилизации основного выхода
объекта 
 , и
вспомогательный (внутренний) регулятор, предназначенный для регулирования
вспомогательной координаты
, и
вспомогательный (внутренний) регулятор, предназначенный для регулирования
вспомогательной координаты 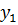
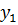 .
.
Заданием
для вспомогательного регулятора служит выходной сигнал основного регулятора.
Расчет
каскадной АСР предполагает определение настроек основного и вспомогательного
регуляторов при заданных динамических характеристиках объекта по основному и
вспомогательному каналам. Поскольку настройки основного и вспомогательного
регуляторов взаимозависимы, расчет их проводят методом итераций.
На
каждом шаге итерации рассчитывают приведенную одноконтурную АСР, в которой один
из регуляторов условно относится к эквивалентному объекту. Эквивалентный объект
для основного регулятора представляет собой последовательное соединение
замкнутого вспомогательного контура и основного канала регулирования; передаточная
его равна:
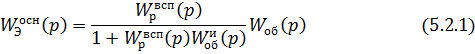
Эквивалентный
объект для вспомогательного регулятора является параллельным соединением
вспомогательного канала и основной разомкнутой системы. Его передаточная
функция имеет вид:
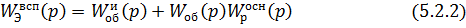
В
зависимости от первого шага итерации различают два метода расчетра каскадных
АСР.
-й
метод. Расчет начинают с основного регулятора. Метод используют в тех случаях,
когда инерционность вспомогательного канала намного меньше, чем основного.
На
первом шаге принимают допущение о том, что рабочая частота основного контура
намного меньше , чем вспомогательного. Тогда:
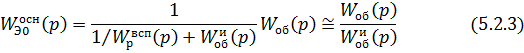
Таким
образом, в первом приближении настройки основного регулятора не зависят от настроек
вспомогательного регулятора и находятся по 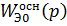
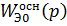 .
.
На
втором шаге рассчитывают настройки вспомогательного регулятора для
эквивалентного объекта (5.2.2).
В
случае приближенных расчетов ограничиваются первыми двумя шагами. При точных
расчетах их продолжают до тех пор, пока настройки регуляторов, найденные в двух
последовательных итерациях, не совпадут с заданной точностью.
-й
метод. Расчет начинают со вспомогательного регулятора. На первом шаге
предполагают, что внешний регулятор отключен, т. е.:
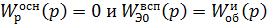
Таким
образом в первом приближении настройки вспомогательного регулятора находят по
одноконтурной АСР для вспомогательного канала регулирования. На втором шаге
рассчитывают настройки основного регулятора по передаточной функции
эквивалентного объекта 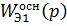
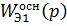 с учетом
настроек вспомогательного регулятора. Для уточнения настроек вспомогательного
регулятора расчет проводят по передаточной функции (5.2.2), в которую
подставляют найденные настройки основного регулятора. Расчеты проводят до тех
пор, пока настройки вспомогательного регулятора, найденные в двух
последовательных итерациях, не совпадут с заданной точностью.
с учетом
настроек вспомогательного регулятора. Для уточнения настроек вспомогательного
регулятора расчет проводят по передаточной функции (5.2.2), в которую
подставляют найденные настройки основного регулятора. Расчеты проводят до тех
пор, пока настройки вспомогательного регулятора, найденные в двух
последовательных итерациях, не совпадут с заданной точностью.
Выберем
в качестве вспомогательного закона регулирования ПИ-закон. Рассчитаем
ПИ-регулятор по формулам (5.1.2), исключив дифференциальную составляющую, для
объекта по вспомогательному каналу с передаточной функцией:


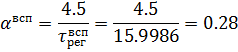

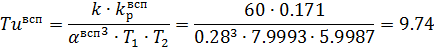
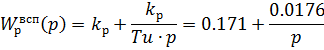
Основной регулятор рассчитаем при помощи автонастройки в программе
MATLAB:

Рис. 5.2.2. Настройки основного регулятора при Response time: 8.51seconds
Проведем моделирование системы:
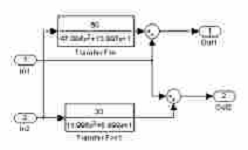
Рис. 5.2.3. Структурная схема блока Subsystem
. Ступенчатое воздействие по каналу управления:

Рис. 5.2.4. Система со ступенчатым воздействием по каналу управления

Рис. 5.2.5. Реакция на ступенчатую функцию
. Ступенчатое воздействие по каналу возмущения:

Рис. 5.2.5. Система со ступенчатым воздействием по каналу возмущения
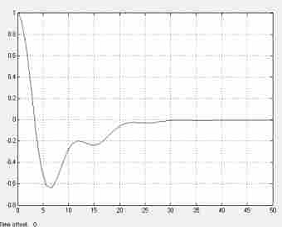
Рис. 5.2.6. Реакция на ступенчатую функцию
.
Импульсное воздействие по каналу управления:
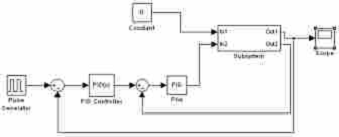
Рис. 5.2.5. Система с импульсным воздействием по каналу управления

Рис. 5.2.6. Реакция на импульсную функцию
. Импульсное воздействие по каналу возмущения:

Рис. 5.2.7. Система с импульсным воздействием по каналу возмущения

Рис. 5.2.8. Реакция на импульсную функцию
.3 Связанная система управления
При управлении многомерными объектами мы часто сталкиваемся со следующей
картиной:
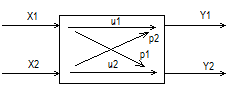
Рис. 5.3.1. Объект управления с двумя входными и двумя выходными
переменными
Где:, X2 - управляющие переменные, Y2 - управляемые переменные, U2 -
прямые связи, P2 - перекрестные связи.
Если для выходной переменной у1 выбрать в качестве регулирующей
переменной переменную х2, то за счет перекрестных каналов регулирующая
переменная х2 будет оказывать влияние через передаточную функцию W21 на
переменную у1, а регулирующая переменная х1 будет влиять через W12 на у2. Эти
обстоятельства существенно усложняют расчет такого рода системы.
Задача расчета значительно упрощается, если на систему наложить
дополнительные требования - требования автономности каналов регулирования.
Автономность каналов регулирования можно осуществить за счет введения
дополнительных связей между входными переменными, такого рода устройства
называются компенсаторами.

Рис. 5.3.2. Система управления двумерным объектом
В результате введения компенсаторов появились новые регулирующие
переменные, которые влияют на исходные переменные с учетом компенсирующих
воздействий.
Получим передаточные функции компенсаторов:
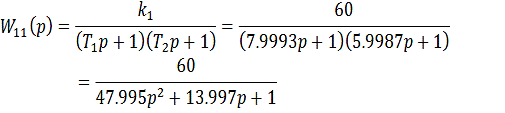

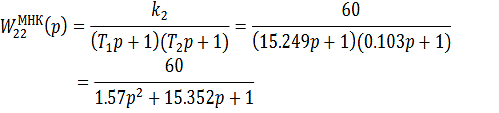

Передаточные функции компенсаторов:


Рассчитаем параметры настройки ПИД-регулятора при помощи стандартных биномиальных
форм Ньютона (воспользуемся формулой 5.1.2).
Рассчитаем первый ПИД-регулятор:
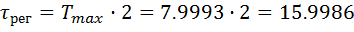


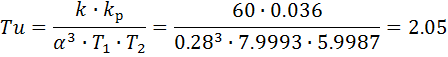

Рассчитаем второй ПИД-регулятор:
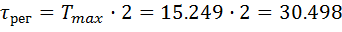


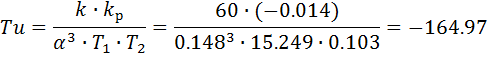

4.4 Анализ
работы систем управления
Для анализа работы комбинированной системы управления обратимся к рис.
4.1.3 - 4.1.6. По ним можно заключить, что компенсатор справляется со своей
задачей и система выходит на заданный режим.
Для анализа работы каскадной системы управления обратимся к рис.4.2.4 -
4.2.7. Из рисунков видно, что каскадная САР уменьшает динамическую ошибку и
выводит систему на заданный режим.
Для анализа работы системы управления двумерным объектом обратимся к рис.
4.3.4 - 4.3.7. Из рисунков делаем вывод, что перекрестные связи оказывают
влияние на выходные сигналы, не смотря на наличие компенсатора.
Заключение
В первом пункте работы были рассмотрены методы, применяемые для
аппроксимации функция, заданных таблично (в виде кривой разгона). Были
рассмотрены четыре метода: метод последовательного логарифмирования, метод
моментов, метод наименьших квадратов и идентификация объекта в программе
Matlab. Задача аппроксимации заключалась в поиске передаточных функций объекта.
По результатам аппроксимации была выбрана наиболее адекватная модель. Это
оказалась модель, полученная идентификацией объекта в программе Matlab.
Затем был определен закон регулирования и произведены расчеты настроек
ПИ-регулятора двумя методами: методом расширенных частотных характеристик и
методом Циглера-Никольса.
Третий пункт курсовой работы заключался в моделировании систем с оптимальным
и квазиоптимальным регуляторами. По полученным при моделировании результатам
можно сделать вывод, что система с оптимальным регулятором обладает лучшими
фильтрующими свойствами, чем система с квазиоптимальным регулятором.
Последний пункт курсовой работы заключался в моделировании многоконтурных
систем управления. Нами был проведен синтез и анализ трёх систем
автоматического управления. Была изучена реакция систем на типовые входные
воздействия. При моделировании систем была использована программа Matlab
(Simulink). В результате моделирования получили переходные функции.
Список
используемой литературы
1. Головушкин,
А. А. Теория автоматического управления : учеб. пособ. Ч. 1 : Линейные системы
автоматического управления / ИГХТА. - Иваново, 1993. 80 с.
. Головушкин,
А. А. Теория автоматического управления : учеб. пособие. Ч. 2 : Специальные
системы автоматического управления / ИГХТА. - Иваново, 1995. 88 с. - Библиогр.
: с. 87.
. Головушкин,
А. А. Теория автоматического управления. Математическое описание линейных
динамических систем : учеб. пособие. - Иваново : ИГХТА, 1994. 67с.
. Ротач
В.Я.
Теория
автоматического управления теплоэнергетическими процессами. - М.:
Энергоатомиздат. 1985. 296 с.
. Автоматическое
управление в химической промышленности. Под ред. Е.Г. Дудникова. - М.; Химия,
1987. 368 с.