Расчет стержневой конструкции на сложное сопротивление

Расчет стержневой конструкции на сложное сопротивление

Построение эпюр начнем со стержня l₁, для этого примем всю остальную конструкцию заделкой. Тогда рассматриваемый стержень можно считать консольным и не учитывать реакции в заделке.

Составим выражения для внутренних усилий в элементах бруса, пользуясь методом сечений. Возьмем сечение на расстоянии х₁ от свободного конца стержня.

Рассмотрим стержень l₁ в плоскости XoZ:

нормальная сила:

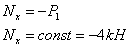
перерезывающая сила:

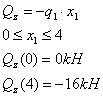
изгибающий момент:

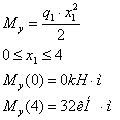
Далее рассмотрим стержень l₁ в плоскости XoY:

перерезывающая сила:

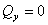
изгибающий момент: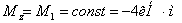

- крутящий момент: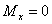

Далее таким же образом составим уравнения для стержня l₂:

Плоскость XoZ:

- нормальная сила: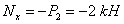

перерезывающая сила:

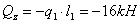
- изгибающий момент:

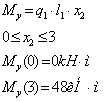
Плоскость XoY:

- перерезывающая сила: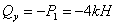

изгибающий момент:

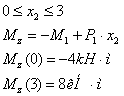
крутящий момент:

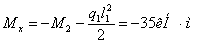
И последним рассмотрим стержень l₃:

Плоскость XoZ:

- нормальная сила:

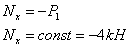
перерезывающая сила:

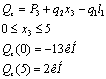
- изгибающий момент:

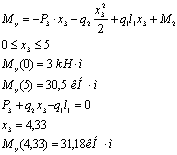
- крутящий момент:

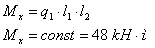
Плоскость XoY:

- перерезывающая сила:

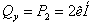
изгибающий момент:

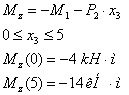
Эпюра перерезывающих сил Q_Y и Q_Z:

На основании построенных эпюр определяем вид деформаций.

Рассмотрим стержень l₁. Он работает на изгиб в 2-х плоскостях и вдобавок к этому подвергается сжатию. Поперечное сечение стержня круглое, поэтому изгиб будет плоским под действием результирующего момента.

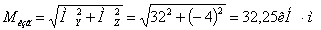
Условие прочности:

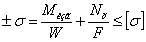
При подборе сечения напряжениями от нормальной силы, ввиду их малой величины, можно пренебречь, тогда предварительное условие прочности имеет вид:

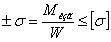
Момент сопротивления для круглого сечения: W=0,1d³

Из условия прочности:

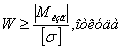
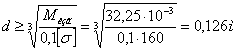
Вычислим нормальные и касательные напряжения:

Наибольшие нормальные напряжения при изгибе:

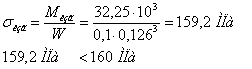
Условие прочности выполнено.

Наибольшие касательные напряжения при изгибе (по формуле Журавского для круглого сечения):

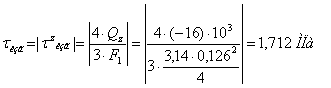
Нормальное напряжение от продольной силы:

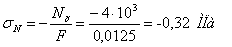 (сжатие)

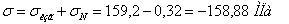
Обозначим смещение нейтральной оси с центра тяжести . Нормальные напряжения на нейтральной оси равны нулю. Тогда уравнение примет вид

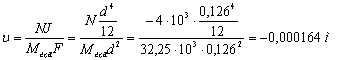
Далее рассмотрим стержень l₂. Работает на изгиб в двух плоскостях с кручением и сжатием. Поперечное сечение бруса круглое, поэтому изгиб будет плоским под действием результирующего момента.

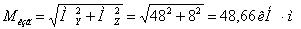
Условие прочности по третьей теории прочности (наибольших касательных напряжений) имеет вид:

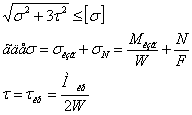
При подборе сечения напряжениями от нормальной силы s_N можно пренебречь в виду их малости, тогда условие прочности примет вид:

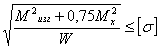
Момент сопротивления для круглого сечения: W=0,1d³

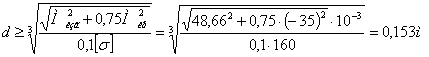
Вычислим нормальное напряжение:

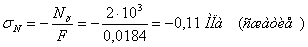
Наибольшие нормальные напряжения при изгибе:

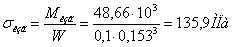
Наибольшие касательные напряжения при изгибе (по формуле Журавского для круглого сечения):

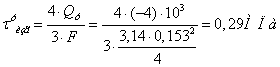
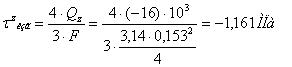
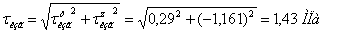
Наибольшие касательные напряжения при кручении

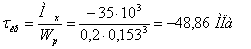
Нормальная сила смещает нейтральную ось с центра тяжести сечения. Определим новое положение нейтральной оси путём аналитического расчёта. Обозначим смещение нейтральной оси с центра тяжести через U. Нормальные напряжения от изгиба на нейтральной оси равны нулю.

Тогда уравнение примет вид:

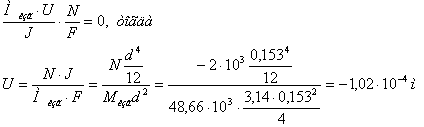
Для окончательной проверки подставим вычисленные напряжения в условие прочности:

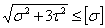
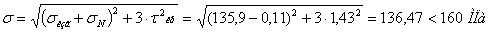
Условие прочности выполнено.

Последний стержень l₃ работает на изгиб в двух плоскостях с кручением и сжатием. Поперечное сечение бруса круглое, поэтому изгиб будет плоским под действием результирующего момента.

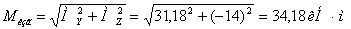
Условие прочности по третьей теории прочности (наибольших касательных напряжений) имеет вид:

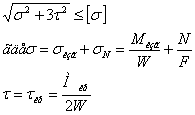
При подборе сечения напряжениями от нормальной силы s_N можно пренебречь в виду их малости, тогда условие прочности примет вид:

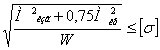
Момент сопротивления для круглого сечения: W=0,1d³

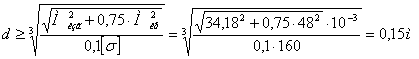
Вычислим нормальные и касательные напряжения:

Наибольшие нормальные напряжения при изгибе:

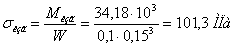
Наибольшие касательные напряжения при изгибе (по формуле Журавского для круглого сечения):

эпюра напряжение трубчатый стержень

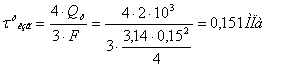
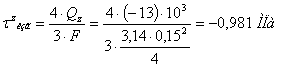
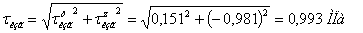
Наибольшие касательные напряжения при кручении

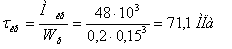
Наибольшие нормальные напряжения от продольной силы:

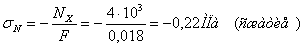
Нормальная сила смещает нейтральную ось с центра тяжести сечения. Определим новое положение нейтральной оси путём аналитического расчёта. Обозначим смещение нейтральной оси с центра тяжести через U. Нормальные напряжения от изгиба на нейтральной оси равны нулю. Тогда уравнение примет вид:

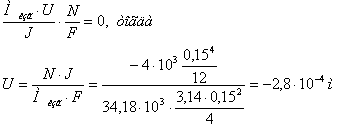
Для окончательной проверки подставим вычисленные напряжения в условие прочности:

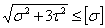
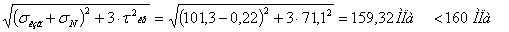
Условие прочности выполнено.

Пусть в условиях нашей задачи профиль поперечного сечения бруса на всех трёх участках одинаков. Необходимо выбрать наиболее экономичный с точки зрения металлоёмкости профиль из следующих трёх: круглый; прямоугольный с соотношением сторон h/b=2,0; трубчатый с соотношением диаметров d/D=0,75 (здесь d-внутренний, D-наружный диаметры).

На основании расчётов определим опасное сечение бруса. Для нашего случая оно будет находиться в точке с наибольшим значением изгибающего и крутящего моментов, т.е. в заделке.

Брус на этом участке работает на изгиб в двух плоскостях с кручением и сжатием.

Условие прочности имеет вид:

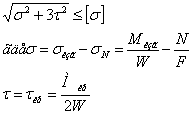
При подборе сечения напряжениями от нормальной силы пренебрегаем

Из условия прочности:

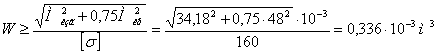
Определим площади поперечных сечений для различных профилей бруса:

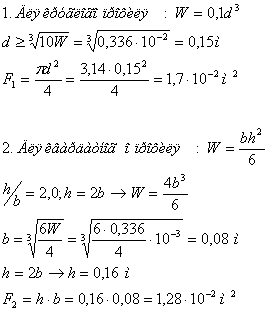
Таким образом, наименьшую площадь поперечного сечения имеет трубчатый профиль, т.е. он является наиболее экономичным по металлоёмкости.

В результате проделанной работы проведён расчёт стержневой конструкции на сложное сопротивление. В частности построены эпюры нормальных и перерезывающих сил, изгибающих и крутящих моментов. Так же рассчитаны размеры поперечных сечений и принят выбор трубчатого профиля стержня, как наиболее экономичного с точки зрения металлоёмкости.

Список литературы

1.   Расчёт стержневой конструкции на сложное сопротивление: Метод. указания по курсовому проектированию. Санкт-Петербургский государств. горный ин-т. СПб., 2009 г.

2.       Сопротивление материалов, Н.М. Беляев, М., Наука, 1976 г. - 608 с.