Планирование экспериментов и статистическая обработка данных
Оглавление
Введение
.Определение основных статистических оценок выборки
.1 Среднее арифметическое выборки
.2 Дисперсия
.3 Среднеквадратическое отклонение
.4 Отбраковка по критерию Шовене
.5 Правило «трёх сигм»
.6 Коэффициент вариации V
.7 Доверительный интервал
.8 Необходимое количество экспериментов
.9 Проверка закона распределения СВ
.10 Группировка данных
.Оценка значимости различия средних значений двух выборок
.1 Оценка значимости различия средних значений двух выборок с
использованием критерия Стьюдента
.2 Оценка значимости различия средних значений двух выборок с
использованием критерия Фишера
.Парный регрессионный анализ
.Множественный регрессионный анализ
.Полный факторный анализ
. Оценка качества эксперимента и уравнения регрессии
Заключение
Список литературы:
Введение
Решение любой
задачи всегда опирается на информацию о конкретной ситуации. Информация может
быть получена путём наблюдения и экспериментально. Современные
технологи-исследователи и работники технических средств разведочного бурения,
имеющие дело со случайными величинами, непрерывно изменяющиеся в процессе
наблюдения или эксперимента, не удовлетворяются использованием
детерминированных моделей изучаемых процессов (объектов) и переходят к
построению вероятностных (стохастических) моделей. Такие модели оказываются
более соответствующими реальному объекту, а полученные с их помощью решения -
более эффективными.
Систематизация, статистическое описание результатов лабораторных и
промысловых наблюдений и экспериментов с целью извлечения из них наибольшей
информации, построение и проверка различных математических моделей и принятие
на этой основе оптимальных решений составляют основное содержание
математической
статистики - одной из наиболее развитых прикладных наук, базирующейся на
теории вероятностей.
Эксперимент должен дать ответ на вопрос, какой будет результат. На
результат испытания влияют многочисленные факторы, поэтому эксперимент обычно
повторяют несколько раз. От умения правильно планировать и ставить эксперимент
зависят достоверность результата, продолжительность и затраты на его
проведение. Результаты эксперимента оцениваются методами теории вероятности и
математической статистики, которые позволяют не только судить о результатах, но
планировать объем и точность эксперимента, а также корректировать эти значения
по результатам проведенного эксперимента.
Цель курсовой работы - получить представление о принципах и особенностях
математического моделирования в разведочном бурении, овладеть основными
методами математической, преимущественно статистической, обработки информации и
научиться применять их для решения различных задач.
1.Определение основных статистических оценок выборки
Исходные
данные
Таблица №.1. Исходные данные.
|
77,90
|
81,71
|
82,81
|
86,46
|
87,02
|
84,39
|
94,80
|
85,15
|
88,82
|
88,79
|
|
80,80
|
76,67
|
78,72
|
80,33
|
73,12
|
91,44
|
95,73
|
79,75
|
79,11
|
76,37
|
|
86,59
|
77,83
|
84,46
|
80,56
|
82,42
|
82,78
|
88,84
|
83,52
|
78,48
|
|
|
79,35
|
77,56
|
76,77
|
92,16
|
85,52
|
92,37
|
72,05
|
80,06
|
87,15
|
|
|
84,19
|
73,70
|
78,55
|
85,94
|
84,62
|
83,22
|
87,57
|
77,29
|
71,36
|
|
|
88,24
|
82,32
|
72,90
|
79,21
|
89,19
|
83,94
|
81,69
|
79,56
|
83,64
|
|
1.1 Среднее
арифметическое выборки
Среднее значение - это среднеарифметическое из всех измеренных значений:
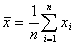 , (1.1.1)
, (1.1.1)
где
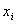 - значение случайной величины, n -
количество случайной величины;
- значение случайной величины, n -
количество случайной величины;
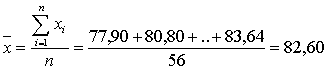
.2 Дисперсия
Мерой отклонения случайной величины от средних значений служит дисперсия
и среднеквадратическое отклонение. Дисперсия - это число, равное среднему
квадрату отклонений значений случайной величины от её среднего значения:
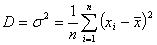 , (1.2.1)
, (1.2.1)
где D -
дисперсия.
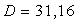
.3
Среднеквадратическое отклонение
Среднеквадратическое отклонение - это число, равное квадратному корню из
дисперсии:
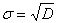 (1.3.1)
(1.3.1)
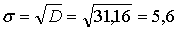
.4 Отбраковка
по критерию Шовене
арифметический выборка отклонение анализ
При проведение опытов при одинаковых условиях часто наблюдаются значения,
резко отличающиеся от остальных. Отбраковка таких значений производится с
помощью специальных методов. В работе мы использовали критерий Шовене.
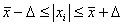 , (1.4.1)
, (1.4.1)
где
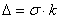 , k - коэффициент Шовене, для n=56 он равен
2,56.
, k - коэффициент Шовене, для n=56 он равен
2,56.
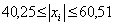 , все
элементы выборки вошли в интервал.
, все
элементы выборки вошли в интервал.
1.5 Правило
«трёх сигм»
Правило
«трёх сигм» основано на том, что случайная величина при нормальном законе
распределения практически полностью (на 99,7%) заключена в пределах от 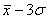 до
до 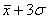 . Если
значение случайной величины отличается от среднего значения
. Если
значение случайной величины отличается от среднего значения 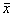 больше чем на 3
больше чем на 3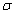 , то оно
является аномальным.
, то оно
является аномальным.
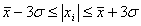 (1.5.1)
(1.5.1)
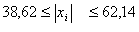 , все
элементы выборки вошли в интервал.
, все
элементы выборки вошли в интервал.
.6
Коэффициент вариации V
На практике широко применяют также характеристику рассеяния, называемую
коэффициентом вариации V,
который представляет собой отношение среднего квадратичного отклонения к
среднему значению. Коэффициент вариации показывает насколько велико рассеяние
по сравнению со средним значением случайной величины. Коэффициент вариации
выражается в долях единицы или в процентах. Вычисление коэффициента вариации
имеет смысл для положительных случайных величин:
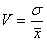 (1.6.1)
(1.6.1)
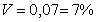
1.7
Доверительный интервал
Интервальная
оценка с принятой вероятностью p или уровнем значимости 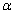 определяет
диапазон, в котором с определённой вероятностью будет находится истинное значение
средней величины
определяет
диапазон, в котором с определённой вероятностью будет находится истинное значение
средней величины
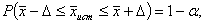 (1.7.1)
(1.7.1)
где Р - это доверительная вероятность, α - уровень значимости
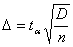 , (1.7.2)
, (1.7.2)
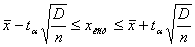 (1.7.3)
(1.7.3)
k=n-1, (1.7.4)
где
k - степень свободы, 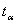 - критерий Стьюдента, для 56 равен 2,09 с α=0,05.
- критерий Стьюдента, для 56 равен 2,09 с α=0,05.
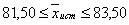
.8
Необходимое количество экспериментов
Зависит от точности, которую нам нужно получить.
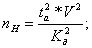 (1.8.1)
(1.8.1)
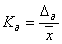 (1.8.2)
(1.8.2)
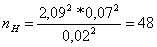
.9 Проверка
закона распределения СВ
Нормальный закон распределения выполняется в том случае, если соблюдается
два условия:
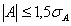 (1.9.1)
(1.9.1)
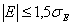 (1.9.2)
(1.9.2)
где A - показатель ассиметрии
(характеризует симметричность левой и правой ветвей кривой), равный
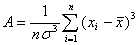 . (1.9.3)
. (1.9.3)
А=
0
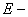 показатель
эксцесса (характеризует форму вершины кривой),
показатель
эксцесса (характеризует форму вершины кривой),
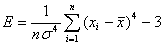 , (1.9.4)
, (1.9.4)
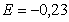
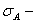 среднеквадратическое
отклонение ассиметрии нормального закона.
среднеквадратическое
отклонение ассиметрии нормального закона.
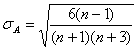 , (1.9.5)
, (1.9.5)
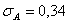
 среднеквадратическое
отклонение эксцесса нормального распределения
среднеквадратическое
отклонение эксцесса нормального распределения
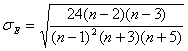 , (1.9.6)
, (1.9.6)
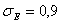
Оба
условия выполнены, следовательно, выборка подчиняется нормальному закону
распределения.
.10
Группировка данных
Весь диапазон данных разбивают на классы.
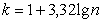 (1.10.1)
(1.10.1)
где
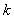 - количество классов.
- количество классов. 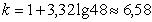 .
Результат округляем до целого. Размер каждого класса находим по формуле:
.
Результат округляем до целого. Размер каждого класса находим по формуле:
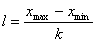 (1.10.2)
(1.10.2)
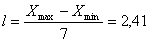
Таблица
№2
|
Класс
|
Частота
|
Частость
|
|
|
Дол.ед.
|
%
|
|
71,36
|
74,90
|
4
|
0,077
|
7,7
|
|
74,90
|
78,43
|
14
|
0,269
|
26,9
|
|
78,43
|
81,96
|
16
|
0,308
|
30,8
|
|
81,96
|
85,50
|
10
|
0,192
|
19,2
|
|
85,50
|
89,03
|
6
|
0,115
|
11,5
|
|
89,03
|
92,57
|
1
|
0,019
|
1,9
|
|
92,57
|
95,73
|
1
|
0,019
|
1,9
|
|
Проверка
|
52
|
1,000
|
100
|
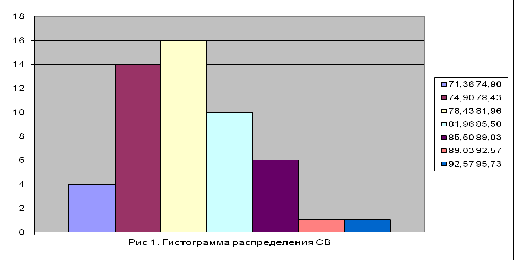
Рис. 1.10. Гистограмма.
Распределение случайной величины хорошо отражается приведённой
гистограммой.
Вывод
В данной работе были закреплены знания о статистических оценках выборки:
среднеарифметической выборки, дисперсии, среднеквадратичного отклонения,
коэффициента вариации. Было так же определено количество экспериментальных
опытов, которые в дальнейшем я проверила по закону распределения случайной
величины. Для наглядной оценки данной ситуации я построила гистограмму, что
значительно упрощает задачу и делает ее на много проще.
С помощью методов, используемых в данной работе, можно легко
проанализировать данные, полученные экспериментальным путем, и вычислить ошибку
в случае неудачи.
2.Оценка значимости различия средних значений двух выборок
Цель работы
Целью данной работы является оценка существенности различия средних
значений двух выборок.
Исходные данные.
Табл.1 Исходные данные
|
выборка №1
|
выборка№2
|
|
77,90
|
84,39
|
85,15
|
74,91
|
|
80,80
|
91,44
|
85,21
|
95,37
|
|
86,59
|
82,78
|
90,04
|
88,71
|
|
79,35
|
92,37
|
94,71
|
100,74
|
|
84,19
|
83,22
|
90,05
|
86,92
|
|
88,24
|
83,94
|
88,63
|
91,40
|
|
81,71
|
94,80
|
69,86
|
99,36
|
|
76,67
|
95,73
|
102,07
|
106,20
|
|
77,83
|
88,84
|
91,45
|
92,74
|
|
77,56
|
72,05
|
91,95
|
97,95
|
|
73,70
|
87,57
|
94,92
|
87,03
|
|
82,32
|
81,69
|
80,15
|
82,44
|
|
82,81
|
85,15
|
71,05
|
85,85
|
|
78,72
|
79,75
|
95,70
|
87,15
|
|
84,46
|
83,52
|
81,61
|
80,14
|
|
76,77
|
80,06
|
88,48
|
78,43
|
|
78,55
|
77,29
|
88,03
|
92,65
|
|
72,90
|
79,56
|
82,81
|
93,81
|
|
86,46
|
88,82
|
99,26
|
91,50
|
|
80,33
|
79,11
|
84,25
|
82,73
|
|
80,56
|
78,48
|
90,33
|
77,97
|
|
92,16
|
87,15
|
99,22
|
89,27
|
|
85,94
|
71,36
|
88,39
|
|
|
79,21
|
83,64
|
94,96
|
|
|
87,02
|
88,79
|
89,09
|
|
2.1 Оценка значимости различия средних значений двух выборок с
использованием критерия Стьюдента
Находим значение и дисперсию для двух выборок:
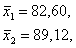
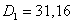 ,
,
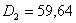 ,
,
Вычисляем
экспериментальный коэффициент Стьюдента:
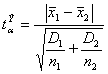 , (1)
, (1)
где
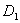 и
и 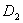 -
дисперсии выборок,
-
дисперсии выборок, 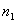 и
и 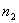 -
количество испытаний,
-
количество испытаний, 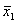 и
и 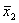 - среднее
значения выборок.
- среднее
значения выборок.
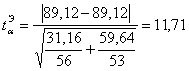 ,
,
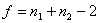 , (2)
, (2)
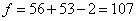 .
.
Определяем
табличное значение коэффициента Стьюдента при 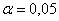 и
и 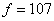 .
. 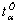 = 1,99.
= 1,99.
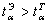 ; 11,71>1,99,
; 11,71>1,99,
Мы
видим, что различие коэффициентов существенно, следовательно, выборки не
относится к одной генеральной совокупности. Требуется дополнительное
исследование с помощью критерия Фишера.
.2
Оценка значимости различия средних значений двух выборок с использованием
критерия Фишера
Вычисляем
расчетное значение критерия Фишера:
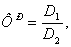 (3)
(3)
где
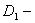 большее значение дисперсии.
большее значение дисперсии.
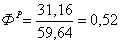 ,
,
Для
определения табличного значения коэффициента Фишера рассчитываем число степеней
свободы:
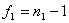 ; (4)
; (4)
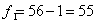 ;
;
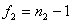 ; (5)
; (5)
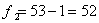 .
.
Табличное
значение для критерия Фишера при 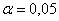 равно
1,65.
равно
1,65.
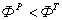 , 1,5 < 71,63- различие не существенно.
, 1,5 < 71,63- различие не существенно.
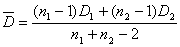 , (6)
, (6)
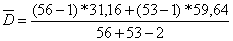 =5,72,
=5,72,
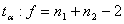 (7)
(7)
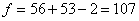 ,
,
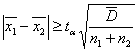 , (8)
, (8)
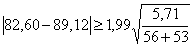
,97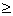 0,51
0,51
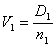 , (9)
, (9)
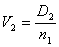
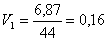 ,
,
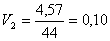
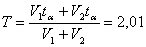 ,
, 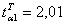
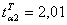 (10)
(10)
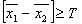 ,
,
,97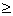 2,01.
2,01.
Вывод
Анализируя полученные результаты можно сделать вывод, что критерий
Стьюдента и критерий Фишера помогают нам оценить существенности различия
средних значений двух выработок. Для данной оценки лучше использовать оба
критерия, для получения более точной информации.
3.Парный регрессионный анализ
Исходные данные
Таблица 3.1 Исходные данные
|
x
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
y
|
0,84
|
4,73
|
5,11
|
5,81
|
7,23
|
8,85
|
Система
двух случайных величин имеет пять основных статистических характеристик:
средние значения 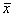 и
и 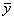 ,
дисперсии
,
дисперсии 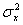 и
и 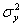 и
корреляционный момент (или ковариацию)
и
корреляционный момент (или ковариацию) 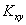 , которые
вычисляются по формулам:
, которые
вычисляются по формулам:
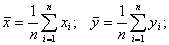 (3.1)
(3.1)
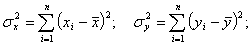 (3.2)
(3.2)
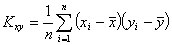 . (3.3)
. (3.3)
Особый интерес представляет формула корреляционного момента, которая
отражает взаимосвязь между случайными величинами x и y.
Поскольку корреляционный момент имеет размерность, его преобразуют в
безразмерную величину по формуле:
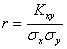 . (3.4)
. (3.4)
Величина
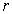 играет чрезвычайно большую роль в статистических
исследованиях и называется коэффициентом корреляции. Его значения заключены в
интервале между +1 и -1. Если коэффициент корреляции равен нулю, то линейная
связь между случайными величинами отсутствует. При
играет чрезвычайно большую роль в статистических
исследованиях и называется коэффициентом корреляции. Его значения заключены в
интервале между +1 и -1. Если коэффициент корреляции равен нулю, то линейная
связь между случайными величинами отсутствует. При 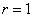 связь функциональная положительная. При
связь функциональная положительная. При 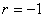 связь функциональная отрицательная. В реальных
условиях коэффициент корреляции не бывает равен единице (или минус единице) и
характеризует степень статистической связи между свойствами х и у. Чем ближе по
абсолютной величине
связь функциональная отрицательная. В реальных
условиях коэффициент корреляции не бывает равен единице (или минус единице) и
характеризует степень статистической связи между свойствами х и у. Чем ближе по
абсолютной величине 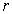 к единице, тем сильнее связь между свойствами; она
может быть положительной (
к единице, тем сильнее связь между свойствами; она
может быть положительной (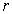 > 0) и отрицательной (
> 0) и отрицательной (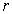 < 0). Таким образом, коэффициент корреляции
является мерой линейной зависимости между двумя величинами.
< 0). Таким образом, коэффициент корреляции
является мерой линейной зависимости между двумя величинами.
Если
значения 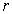 более 0,7-0,8, то можно считать связь сильной, при
более 0,7-0,8, то можно считать связь сильной, при 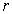 = 0,5-0,7 - связь средняя, а при
= 0,5-0,7 - связь средняя, а при 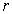 =0,2-0,5 - связь слабая. Принято считать, что линейной
корреляции нет, если
=0,2-0,5 - связь слабая. Принято считать, что линейной
корреляции нет, если 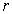 <0,4. Таким образом, для прямолинейной связи
коэффициент корреляции определяет меру связи между величинами. При малом
значении коэффициента корреляции теснота прямолинейной связи между исследуемыми
признаками оценивается критерием Стьюдента.
<0,4. Таким образом, для прямолинейной связи
коэффициент корреляции определяет меру связи между величинами. При малом
значении коэффициента корреляции теснота прямолинейной связи между исследуемыми
признаками оценивается критерием Стьюдента.
Различают два вида связи: 1) функциональная, 2) вероятностная
(стохастическая).
Уравнение множественной регрессии должно быть
адекватно изучаемому процессу. Коэффициенты в уравнении регрессии вычисляются
методами матричной алгебры.
Задачу решают проведением прямой линии через набор опытных точек и в
определении уравнения описывающего эту прямую. Обычно используется метод
наименьших квадратов. Суть метода состоит в том, что изучаемая зависимость
аппроксимируется таким алгебраическим выражением (трендом), который даёт
наименьшее расхождение с наблюдаемыми значениями.
Главный принцип метода заключается в требовании, чтобы сумма квадратов
всех отклонений от линии зависимости была минимальной:
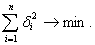 (3.5)
(3.5)
Если
между величинами 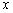 и
и 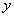 установлена
линейная статистическая зависимость, то представляет интерес найти ее выражение
в виде уравнения прямой линии
установлена
линейная статистическая зависимость, то представляет интерес найти ее выражение
в виде уравнения прямой линии
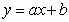 , (3.6)
, (3.6)
где
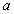 и
и 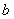 -
коэффициенты.
-
коэффициенты.
Такое
уравнение называется уравнением регрессии. Если величина 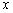 неслучайная, то существует одно уравнение регрессии.
Если обе величины
неслучайная, то существует одно уравнение регрессии.
Если обе величины 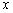 и
и 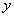 случайные,
то имеется два уравнения регрессии и можно вычислять зависимости как
случайные,
то имеется два уравнения регрессии и можно вычислять зависимости как 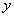 от
от 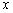 , так и
, так и 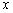 от
от 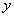 . Расчёт
уравнения сводится к определению наиболее вероятного значения у, когда известно
значение х.
. Расчёт
уравнения сводится к определению наиболее вероятного значения у, когда известно
значение х.
Коэффициенты
уравнения регрессии 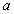 и
и 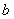 :
:
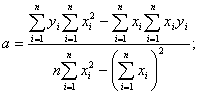 (3.7)
(3.7)
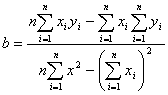 . (3.8)
. (3.8)
Коэффициент
корреляции:
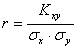 . (3.9)
. (3.9)
Если
опытные точки в декартовой системе координат явно лежат не вблизи прямой, то
метод наименьших квадратов неприменим.
Для
применения метода наименьших квадратов необходимо преобразовать систему
координат таким образом, чтобы опытные точки располагались вблизи воображаемой
прямой линии, т. е. выполнить так называемую линеаризацию (трансформировать
систему координат).
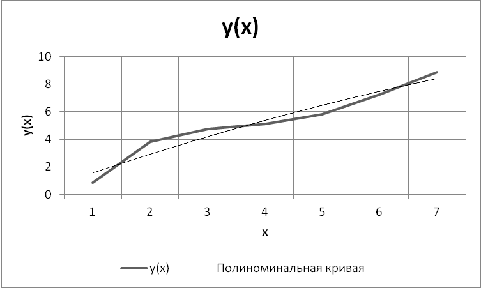
Имеется
нелинейная зависимость (рис.1). Требуется рассчитать нелинейную параболическую
зависимость по методу наименьших квадратов. Уравнение параболы имеет вид
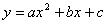 (3.10)
(3.10)
 9
9
Рис.3.1.
График параболы
Следовательно,
для каждой точки графика справедливо соотношение:
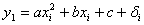 (3.11)
(3.11)
Из
этого выражения найдём отклонения 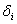 и сумму квадратов
отклонений, которая является функцией
и сумму квадратов
отклонений, которая является функцией 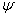 от
неизвестных коэффициентов a, b, c:
от
неизвестных коэффициентов a, b, c:
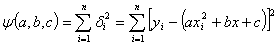
Таблица
3.2
Расчёт
параболической зависимости.
|
№
|
xi
|
yi
|
xi2
|
xi3
|
xi4
|
xiyi
|
xi2yi
|
yi2
|
|
1
|
1
|
0,84
|
1,00
|
1,00
|
1,00
|
0,84
|
0,84
|
0,71
|
|
2
|
2
|
3,81
|
4,00
|
8,00
|
16,00
|
7,62
|
15,24
|
14,52
|
|
3
|
3
|
4,73
|
9,00
|
27,00
|
81,00
|
14,19
|
42,57
|
22,37
|
|
4
|
4
|
5,11
|
16,00
|
64,00
|
256,00
|
20,44
|
81,76
|
26,11
|
|
5
|
5
|
5,81
|
25,00
|
125,00
|
625,00
|
29,05
|
145,25
|
33,76
|
|
6
|
6
|
7,23
|
36,00
|
216,00
|
1296,00
|
43,38
|
260,28
|
52,27
|
|
7
|
7
|
8,85
|
49,00
|
343,00
|
2401,00
|
61,95
|
433,65
|
78,32
|
|
|
|
|
|
|
|
|
|
|
CУММА
|
28
|
36,38
|
140,00
|
784,00
|
4676,00
|
177,47
|
979,59
|
228,06
|
|
|
|
|
|
|
|
|
|
|
средзнач
|
4
|
5,20
|
20,00
|
112,00
|
668,00
|
25,35
|
139,94
|
32,58
|
Чтобы
отыскать минимум функции 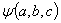 , необходимо найти частные производные от функции по
неизвестным a, b, c и приравнять производные нулю. После раскрытия и
преобразования получаем систему трёх уравнений с тремя неизвестными:
, необходимо найти частные производные от функции по
неизвестным a, b, c и приравнять производные нулю. После раскрытия и
преобразования получаем систему трёх уравнений с тремя неизвестными:
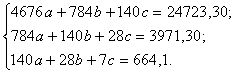
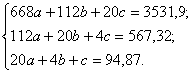
Решая
систему, находим коэффициенты a=10,98167; b=-40,8933; c=38,81.
Следовательно, уравнение аппроксимирующей параболы имеет вид:
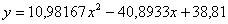
Таблица
3.3
Сравнение
фактической yi и теоретической yт
|
№
|
x
|
y
|
yт
|
сигма
|
сигма 2
|
|
1
|
1
|
0,84
|
1,066
|
0,06
|
0,004102
|
|
2
|
2
|
3,81
|
1,522
|
-0,08
|
0,006748
|
|
3
|
3
|
4,73
|
2,741
|
-0,04
|
0,001717
|
|
4
|
4
|
5,11
|
4,724
|
0,02
|
0,000262
|
|
5
|
5
|
5,81
|
7,469
|
0,06
|
0,003684
|
|
6
|
6
|
7,23
|
10,978
|
0,02
|
0,000489
|
|
7
|
7
|
8,85
|
15,250
|
-0,04
|
0,001565
|
|
|
|
|
|
|
|
сумма
|
28
|
36,38
|
43,75
|
0,00
|
0,02
|
|
|
|
|
|
|
|
средзнач
|
4
|
5,20
|
6,250
|
0,000
|
0,002
|
Сравнение
фактических 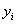 и теоретических
и теоретических 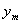 ,
рассчитанных по уравнению параболы, свидетельствует об удовлетворительном их
совпадении (табл.2). Расхождения
,
рассчитанных по уравнению параболы, свидетельствует об удовлетворительном их
совпадении (табл.2). Расхождения 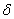 между
фактическими и теоретическими значениями позволяют найти дисперсию случайных
отклонений
между
фактическими и теоретическими значениями позволяют найти дисперсию случайных
отклонений 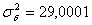 .
.
Далее
вычисляем дисперсию исходных значений: 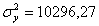 .
.
Определяем
корреляционное отношение: 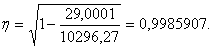
Корреляционное
отношение близко к единице, следовательно, параболическая зависимость хорошо
аппроксимирует эмпирические данные.
Вывод
Метод наименьших квадратов применим, если опытные точки в декартовой
системе координат явно лежат вблизи воображаемой прямой линии, а если нет, то
надо выполнить так называемую линеаризацию. На графике видно, что разброс точек
относительно линий регрессии незначителен, следовательно и коэффициент
корреляции близок к единице.
4.Множественный регрессионный анализ
Цель работы
По результатам наблюдений xi и yi (i = 1, 2 …n)
найти оценки неизвестных параметров а0, а1 и аm . Для линейной зависимости модель множественной регрессии
записывается в виде:
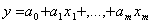 , (1)
, (1)
Исходные данные.
Таблица 1. Исходные данные.
|
Вариант № 1
|
|
|
|
х1
|
х2
|
y
|
|
№
|
Na2CO3, %
|
КМЦ, %
|
Т, с
|
|
1
|
0
|
0
|
20
|
|
2
|
8
|
0
|
22
|
|
3
|
0
|
2
|
25
|
|
4
|
8
|
2
|
28
|
|
5
|
0
|
1
|
23
|
|
6
|
9,76
|
1
|
26
|
|
7
|
4
|
0
|
21
|
|
8
|
4
|
2,4
|
27
|
|
9
|
4
|
1
|
25
|
|
10
|
4
|
1
|
25
|
Вычисление переменных.
Процедуру вычисления коэффициентов множественной регрессии рассмотрим на
примере регрессии с двумя переменными (факторами):
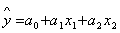 , (2)
, (2)
Для
того, чтобы найти коэффициенты а0, а1 и а2 найдем некоторые произведения,
представленные в таблице 2.
|
х1
|
х2
|
y
|
Произведения
|
|
№
|
Na2CO3, %
|
КМЦ, %
|
Т, с
|
x12
|
x22
|
y2
|
x1x2
|
x1y
|
x2y
|
|
1
|
0
|
0
|
20
|
0
|
0
|
400
|
0
|
0
|
0
|
|
2
|
8
|
0
|
22
|
64
|
0
|
484
|
0
|
176
|
0
|
|
3
|
0
|
2
|
25
|
0
|
4
|
625
|
0
|
0
|
50
|
|
4
|
8
|
2
|
28
|
64
|
4
|
784
|
16
|
224
|
56
|
|
5
|
0
|
1
|
23
|
0
|
1
|
529
|
0
|
0
|
23
|
|
6
|
9,76
|
1
|
26
|
95,2576
|
1
|
676
|
9,76
|
253,76
|
26
|
|
7
|
4
|
0
|
21
|
16
|
0
|
441
|
0
|
84
|
0
|
|
8
|
4
|
2,4
|
27
|
16
|
5,76
|
9,6
|
108
|
64,8
|
|
9
|
4
|
1
|
25
|
16
|
1
|
625
|
4
|
100
|
25
|
|
10
|
4
|
1
|
25
|
16
|
1
|
625
|
4
|
100
|
25
|
|
|
|
|
|
|
|
|
|
|
|
СУММЫ
|
41,76
|
10,4
|
242
|
287,2576
|
17,76
|
5918
|
43,36
|
1045,76
|
269,8
|
|
|
|
|
|
|
|
|
|
|
|
средзнач
|
4,176
|
1,04
|
24,2
|
28,72576
|
1,776
|
591,8
|
4,336
|
104,576
|
26,98
|
Таблица 2.
Найдя суммы полученных произведений можно найти коэффициенты а1 и а2 по
формулам:
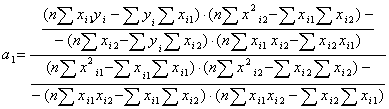 , (3)
, (3)
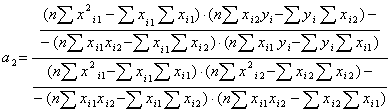 . (4)
. (4)
Подставив
известные значения в формулы (3) и (4) получим:
а1= 0,2899
а2= 2,6126
Зная коэффициенты а1 и а2 а также средних значений x1i , x2i и yi найдем значение коэффициента а0 по формуле:
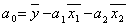 , (5)
, (5)
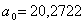
Зная
значения коэффициентов а0, а1 и а2 можно найти значений 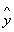 по формуле (2). Вычисления
по формуле (2). Вычисления 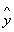 представлены в таблице 3.
представлены в таблице 3.
Таблица
3.
|
№
|
Na2CO3, %
|
КМЦ, %
|
Т, с
|
y"
|
|
1
|
0
|
0
|
20
|
32,64
|
|
2
|
8
|
0
|
22
|
28,64
|
|
3
|
0
|
2
|
25
|
15,23
|
|
4
|
8
|
2
|
28
|
11,24
|
|
5
|
0
|
1
|
23
|
23,93
|
|
6
|
9,76
|
1
|
26
|
19,06
|
|
7
|
4
|
0
|
21
|
30,64
|
|
8
|
4
|
2,4
|
27
|
9,75
|
|
9
|
4
|
1
|
25
|
21,94
|
|
10
|
4
|
1
|
25
|
21,94
|
|
|
|
|
|
|
СУММЫ
|
41,76
|
10,4
|
242
|
215,00
|
|
|
|
|
|
|
средзнач
|
4,176
|
1,04
|
24,2
|
21,50
|
Вывод
Мы
видим, что полученные значения 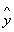 очень
близки к значениям y, а суммы и средние значения одинаковы. Следовательно,
коэффициенты а0, а1 и а2 были найдены правильно. Полученные данные позволяет
нам найти зависимость
очень
близки к значениям y, а суммы и средние значения одинаковы. Следовательно,
коэффициенты а0, а1 и а2 были найдены правильно. Полученные данные позволяет
нам найти зависимость 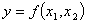 , в нашем случае
, в нашем случае 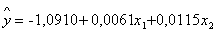
5.Полный факторный анализ
Исходные данные.
Факторный эксперимент связан с варьированием одновременно всех факторов с
проверкой достоверности результатов математико-статистическими методами. В этом
разделе производится оценка влияния концентраций двух химических реагентов CaCl2 и КССБ (концентрированная
сульфидспиртовая барда) на величину предельного напряжения сдвига бурового
раствора.
Пределы изменения концентраций реагентов:
. CaCl2: 0 - 2 %;
. КССБ: 1 - 3 %.
Проведено четыре эксперимента (N=4) по три параллельных опыта в каждом (n=3).
Исходные данные представлены в табл.5.1.
Таблица 5.1
Исходные данные
|
N
|
N
|
|
Y1
|
Y2
|
Y3
|
|
1
|
18
|
19
|
20
|
|
2
|
8
|
7
|
7
|
|
3
|
24
|
23
|
23,2
|
|
4
|
9
|
9,4
|
11
|
5. Полный факторный эксперимент и обработка его результатов
Стандартная
матрица планирования эксперимента в общем виде представлена в табл.5.2.
Таблица 5.1.1
Стандартная матрица планирования эксперимента в общем виде
|
N
|
N
|
|
Y1
|
Y2
|
Y3
|
|
1
|
Y11
|
Y12
|
Y13
|
|
2
|
Y21
|
Y22
|
Y23
|
|
3
|
Y31
|
Y32
|
Y33
|
|
4
|
Y41
|
Y42
|
Y43
|
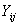 -
значение функции отклика.
-
значение функции отклика.
Общая
концентрации реагентов вычисляется по формулам:
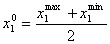 (5.1.1)
(5.1.1)
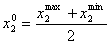 ,
,
где
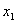 - концентрация хлорида кальция и
- концентрация хлорида кальция и 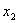 - концентрация КССБ.
- концентрация КССБ.
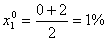
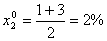
Интервал
варьирования факторов определяется по формулам:
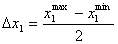 (5.1.2)
(5.1.2)
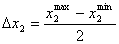
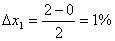
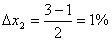
В планировании эксперимента применяется метод кодирования. Каждый фактор
имеет только одно из двух значений: «+1» - наибольшее значение уровня
варьирования фактора и «-1» - наименьшее значение. Допустим, что под воздействием
изменения концентраций предельное напряжение сдвига бурового раствора
изменяется прямо пропорционально (линейная модель). В этом случае стандартная
матрица планирования с учетом взаимодействия факторов между собой выглядит
следующим образом:
Таблица 5.1.3
Стандартная матрица планирования с учетом взаимодействия факторов
|
№
|
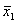 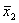 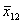 Y1Y2Y3YSi2 Y1Y2Y3YSi2
|
|
|
|
|
|
|
|
|
1
|
-1
|
-1
|
1
|
Y11
|
Y12
|
Y13
|
Y1
|
S12
|
|
2
|
-1
|
1
|
-1
|
Y21
|
Y22
|
Y23
|
Y2
|
S22
|
|
3
|
1
|
-1
|
-1
|
Y31
|
Y32
|
Y33
|
Y3
|
S32
|
|
4
|
1
|
1
|
1
|
Y41
|
Y42
|
Y43
|
Y4
|
S42
|
- дисперсия.
Уравнение регрессии
Строим модель уравнение регрессии. Предположим, что под воздействием
изменения концентраций химических реагентов величина предельного напряжения
сдвига изменяется прямо пропорционально.
Общий вид значения функции отклика.
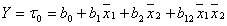 , (5.1.3)
, (5.1.3)
где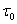 - величина предельного напряжения сдвига; bi -
коэффициенты уравнения регрессии.
- величина предельного напряжения сдвига; bi -
коэффициенты уравнения регрессии.
Определим средние значения функции отклика по каждому из четырех
экспериментов, используя формулу:
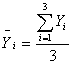 ; (5.1.4)
; (5.1.4)
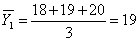
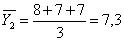
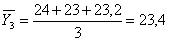
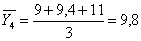
Расчет
коэффициентов уравнения регрессии выполняется по следующим формулам:
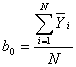 и
и 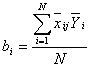 ; (5.1.5)
; (5.1.5)
где
b0 - свободный член уравнения; N -количество
экспериментов (N = 4).
Выполнив
вычисления по формуле (5), получаем:
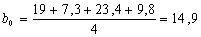
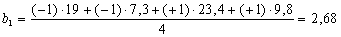
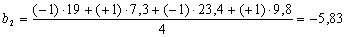
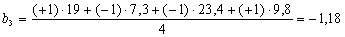
Уравнение
регрессии:
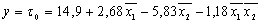
Вывод
Было
составлено уравнение регрессии.
6. Оценка качества эксперимента и уравнения регрессии
Оценим значимость коэффициентов уравнения регрессии (существенность
влияния факторов). Для этого определяем дисперсию экспериментов по формуле:
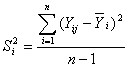 ; (6.1.1)
; (6.1.1)
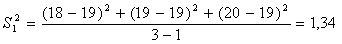
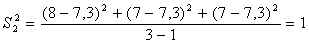
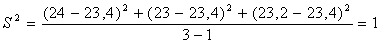
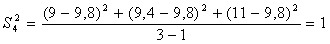
Дисперсия воспроизводимости или средняя дисперсия:
 ;
(6.1.2)
;
(6.1.2)
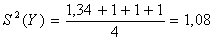
Дисперсия коэффициентов уравнения регрессии:
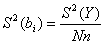 ;
(6.1.3)
;
(6.1.3)
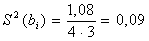
Адекватность уравнения регрессии оценивается в целом по критерию Фишера:
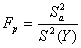 , (6.1.4)
, (6.1.4)
где
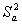 - остаточная дисперсия, оценивающая разброс расчетных
и опытных данных:
- остаточная дисперсия, оценивающая разброс расчетных
и опытных данных:
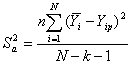 ,
(6.1.5)
,
(6.1.5)
где
Yiр - рассчитанное по уравнению регрессии ожидаемое
значение функции отклика; k -количество факторов (k = 2).
Для
расчета Yiр необходимо раскодировать 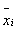 , то есть перейти к натуральным единицам измерения - к
процентам.
, то есть перейти к натуральным единицам измерения - к
процентам.
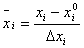 ,
,
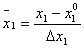 ; (6.1.6)
; (6.1.6)
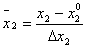 .
.
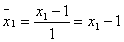 ;
;
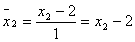 .
.
где
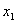 и
и 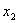 -
концентрации данных химических реагентов в процентах (задаются любыми, но
только в исследуемом диапазоне: 0-2% для CaCl2 и 1-3% для
КССБ). Подставив в уравнение
-
концентрации данных химических реагентов в процентах (задаются любыми, но
только в исследуемом диапазоне: 0-2% для CaCl2 и 1-3% для
КССБ). Подставив в уравнение 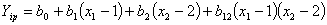 численные
значения переменных, получаем:
численные
значения переменных, получаем:
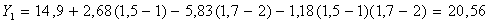
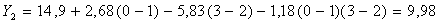
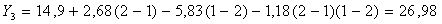
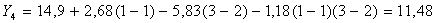
Таким
образом, по формуле (5.2.5):
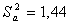
Рассчитываем
значение критерия Фишера по формуле (6.1.4):
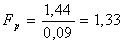
Сравним
рассчитанное значение критерия Фишера с табличным, которое находится при двух
степенях свободы:
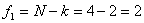 ,
,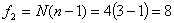 .
. 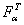 =4,46.
=4,46.
Расчетное
значение критерия Фишера меньше табличного, значит уравнение регрессии
адекватно.
Вывод: Метод планирования экспериментов повышает эффективность научных
исследований в несколько раз, тем самым обеспечивая принятие оптимальных
решений на различных стадиях исследовательской работы. Доказано, что на
результаты экспериментов влияние оказывают только химические реагенты,
коэффициенты уравнения регрессии статистически значимы и уравнение регрессии
адекватно. Основное преимущество многофакторных экспериментов - более высокая
точность полученных результатов.
Заключение
Изучение свойств горных пород, прогнозирование, проектирование новой буровой
техники, разработка оптимальных режимов бурения и решение других
технологических задач требует постановки сложных и дорогостоящих экспериментов.
Большое значение имеет планирование эксперимента, т.е. процедура выбора числа и
условий проведения опытов, необходимых и достаточных для решения поставленной
задачи с требуемой точностью.
Данная работа показала, что для решения и анализа прикладных
математических задач лучше всего использовать современную компьютерную технику,
т.к. это эффективно и быстро.
Любой инженер должен уметь пользоваться данной техникой, чтоб проводить
правильный и логический анализ поставленной задачи.
С помощью данной работы я овладела базовыми знаниями, необходимыми для
оценок выборок, их сравнении, вычисления средних отклонений и т.д. Также мною
были освоены такие офисные пакеты как MS Excel и MS Word.
Список литературы
1. Ганджумян
Р.А. “Математическая статистика в разведочном бурении”, М.: Недра,1990.
. Материалы
выполненных по курсу математических методов в бурении заданий.