Расчет аппроксимаций экспериментальных данных методом наименьших квадратов посредством программных средств Microsoft Excel, MathCAD и MatLAB

Расчет аппроксимаций экспериментальных данных методом наименьших квадратов посредством программных средств Microsoft Excel, MathCAD и MatLAB

Введение

Целью данной работы является решение поставленной задачи, связанной с исследованиями функций, а также развитие и закрепление навыков работы с различными программными средствами.

Задачей работы является расчёт аппроксимаций экспериментальных данных методом наименьших квадратов посредством программных средств Microsoft Excel, MathCAD и MatLAB.

Аппроксимация - это процесс подбора эмпирической функции φ(х) для установления из опыта функциональной зависимости y= φ(х). Пусть величина y является функцией аргумента x. Это означает, что любому значению x из области определения поставлено в соответствии значение y. Вместе с тем на практике часто неизвестна явная связь между y и x, т.е. невозможно записать эту связь в виде y=f(x). Наиболее распространенным и практически важным случаем, когда вид связи между параметрами x и y неизвестен, является задание этой связи в виде некоторой таблицы {x_i y_i}. Это означает, что дискретному множеству значений аргумента {x_i} поставлено в соответствие множество значений функции {y_i} (i=0,1.n). Эти значения - либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значение величины y и в других точках, отличных от узлов x_i. Однако получить эти значения можно лишь путем очень сложных расчетов или провидением дорогостоящих экспериментов. Таким образом, с точки зрения экономии времени и средств появляется необходимость использования имеющихся табличных данных для приближенного вычисления искомого параметра y при любом значении (из некоторой области) определяющего параметра x, поскольку точная связь y=f(x) неизвестна. Этой цели и служит задача об аппроксимации функций: данную функцию f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией g(x) так, чтобы отклонение (в некотором смысле) g(x) от f(x) в заданной области было минимальным. Функция g(x) при этом называется аппроксимирующей.

Обычно определение параметров при известном виде зависимости осуществляют по методу наименьших квадратов. Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно. Именно поэтому он является полезным при обработке экспериментальных данных.

Теоретические сведения. Метод наименьших квадратов

Пусть задана некоторая функция f(х) и существует некоторая функция φ(х). При этом функция φ(x) считается наилучшим приближением к f(x), если для нее сумма квадратов невязок ε_i=f(x_i)-φ(x_i) или отклонений “теоретических” значений φ(x_i), найденных по эмпирической формуле, от соответствующих опытных значений y_i, имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.

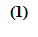
Используя методы дифференциального исчисления, метод наименьших квадратов формулирует аналитические условия достижения суммой квадратов отклонений σ (1) своего наименьшего значения. Так, если функция φ(x) вполне определяется своими параметрами a, b, c, … , то наилучшие значения этих параметров находятся из решения системы уравнений.

Например, в простейшем случае, когда функция φ(x) представлена линейным уравнением y=ax+b, система имеет вид:

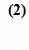
Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек (x_i, y_i) на координатной плоскости.

Например, пусть точки расположены так, как показано на рис.1.

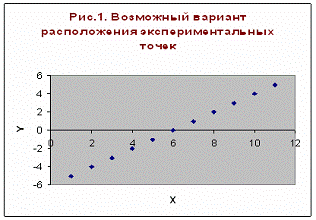
Рис.1.

Учитывая то, что практические данные получены с некоторой погрешностью, обусловленной неточностью измерений, необходимостью округления результатов и т.д., естественно предположить, что здесь имеет место линейная зависимость y=ax+b. Чтобы функция приняла конкретный вид, необходимо каким-то образом вычислить a и b. Для этого можно решить систему (2) <#"577644.files/image006.gif"> 

Рис.2.

Таким образом, расположение экспериментальных точек может иметь самый различный вид, и каждому соответствует конкретный тип функции. Построение эмпирической функции сводится к вычислению входящих в нее параметров, так чтобы из всех функций такого вида выбрать ту, которая лучше других описывает зависимость между изучаемыми величинами. То есть сумма квадратов разности между табличными значениями функции в некоторых точках и значениями, вычислениями по полученной формуле, должна быть минимальна.

Аппроксимация экспериментальных данных в программе Microsoft Excel

Microsoft Excel (также иногда называется Microsoft Office Excel) - программа для работы с электронными таблицами, созданная корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. Она предоставляет возможности экономико-статистических расчетов, графические инструменты и, за исключением Excel 2008 под Mac OS X <#"577644.files/image007.gif">

Для расчёта исходные данные подставляются в таблицу 2. В ячейках А1:А25 и В1:В25 (табл. 1) занесены значения х и у соответственно.

Таблица 2 Вычисление средних значений и их сумм

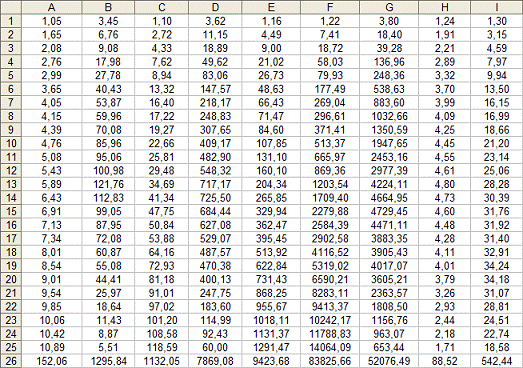
В ячейку С1 вводится формула =А1^2. Затем она копируется в ячейки С2:С25.

В ячейку D1 вводится формула =А1*В1. Затем она копируется в ячейки D2:D25.

В ячейку Е1 вводится формула =А1^3. Затем она копируется в ячейки Е2:Е25.

В ячейку F1 вводится формула =А1^4. Ячейки F2:F25 заполняются копированием.

В ячейку G1 вводится формула = А1^2*В1. Ячейки G2:G25 заполняются копированием.

В ячейку Н1 вводится формула = LN(В1). Ячейки Н2:Н25 заполняются копированием.

В ячейку I1 вводится формула =А1*LN(В1). Ячейки I2:I25 заполняются копированием.

Ячейки А26:I26 являются суммами всех ячеек соответствующих столбцов.

Линейная аппроксимация функции:

Решив систему (1), воспользовавшись значениями, расположенными в ячейках А26, В26, С26, D26, находим а₁ и а₂ (табл. 3).

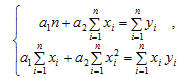
Таблица 3 Нахождение коэффициентов а₁ и а₂

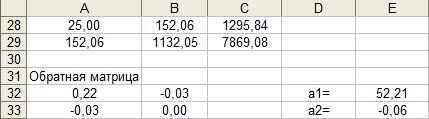
Линейная аппроксимация имеет вид:

у = 52,21 - 0,06* х.

В ячейках А32:В33 записана формула {=МОБР(А28:В29)}.

В ячейках Е22:Е33 записана формула

{=МУМНОЖ(А32:В33,С28:С29)}.

Квадратичная аппроксимация функции:

Для аппроксимации функции у=f(х) квадратичной функцией  решим систему (2) используя значения, расположенные в ячейках А26, В26, С26, D26, Е26, F26, G26. Таким образом определим коэффициенты а₁, а₂, а₃ (табл. 4).

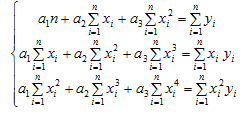
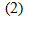
Таблица 4 Нахождение коэффициентов а₁, а₂, а₃

Квадратичная аппроксимация имеет вид: у=-74,14+53,72*х-4,39*х².

В ячейках А41:С43 записана формула {=МОБР(А36:С38)}.

В ячейках F41:F43 записана формула {=МУМНОЖ(А41:А43,D36:D38)}.

Экспоненциальная аппроксимация функции:

Аппроксимируем функцию у=f(х) экспоненциальной функцией 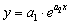. Определим коэффициенты а₁ и а₂ прологарифмировав значения у и использую значения, полученные в ячейках А26, С26, Н26, I26 получим систему:

,

где с = ln(а₁).

Решив систему (3), нашли с и а₂, а₁ нашли потенцированием (табл. 5).

Таблица 5 Нахождение коэффициентов с, а₁, а₂

В ячейках А50:А51 записана формула {=МОБР(А46:В47)}.

В ячейках Е49:Е50 записана формула {=МУМНОЖ(А50:В51,С46:С47)}.

В ячейке Е51 записана формула = ЕХР(Е49).

Среднее арифметическое всех х и у вычисляется по формулам:

наименьший квадрат аппроксимация matlab

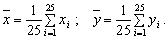(табл. 6)

Таблица 6 Нахождение среднего арифметического всех х и у

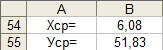
В ячейке В54 записана формула =А26/25.

В ячейке В55 записана формула =В26/25.

Расчёт коэффициента корреляции и коэффициента детерминации:

Данные занесём в таблицу 7 , которая является продолжением таблицы 2.

Таблица 7

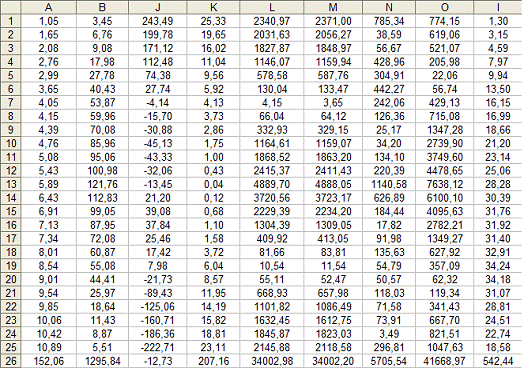
В ячейку J1 вводим формулу =(А1-$В$54)*(В1-$В$55).

Ячейки J2:J25 заполняются копированием.

В ячейку К1 вводим формулу =(А1-$В$54)^2.

Ячейки К2:К25 заполняются копированием.

В ячейку L1 вводится формула =(В1-$В$55)^2. Ячейки L2:L25 заполняются копированием.

В ячейку М1 вводится формула =($Е$32+$Е$33*А1-В1)^2. Ячейки М2:М25 заполняются копированием.

В ячейку N1 вводим формулу =($F$41+$F$42*А1+$F$43*А1^2-В1)^2. Ячейки N2:N25 заполняются копированием.

В ячейку О1 вводим формулу =($Е$51*ЕХР($Е$50*А1)-В1)^2. Ячейки О2:О25 заполняются копированием.

Ячейки J26:О26 являются суммами всех ячеек соответствующих столбцов.

По формулам (4) и (5) рассчитаем коэффициенты корреляции и детерминации (табл. 8). Коэффициент корреляции рассчитывается только для линейной аппроксимации.

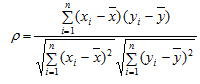
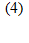
где , 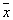и 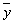 ¾ среднее арифметическое значение соответственно по x и y.

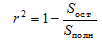
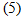
где S_ост - остаточная сумма квадратов, S_полн - сумма остаточной суммы квадратов и регрессионной суммы квадратов.

Таблица 8 Нахождение коэффициента корреляции и коэффициента детерминации

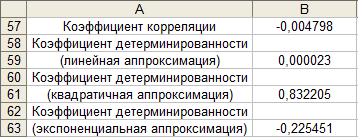
В ячейку В57 вводим формулу =J26/(К26*L26)^(1/2).

В ячейку В59 вводим формулу =1-М26/L26.

В ячейку В61 вводим формулу =1-N26/L26.

В ячейку В63 вводим формулу =1-О26/L26.

Построение графика в Excel и использование функции ЛИНЕЙН:

Построим график функции и линию тренда, которой является прямая у=а₁+а₂*х. Для построения линии тренда необходимо:

.        Активизируем диаграмму дважды щёлкнув по ней и нажимаем на одну из точек.

.        Пункт меню Вставка-«Линия тренда».

.        На вкладке «Тип» выбираем линейный тип для графика линейной аппроксимации (рис.3.), полиномиальный тип степень 2 для графика квадратичной аппроксимации (рис.4.) и экспоненциальный тип для графика экспоненциальной аппроксимации (рис.5.).

.        На вкладке «Параметры» потребуем показать уравнение тренда и значение R².

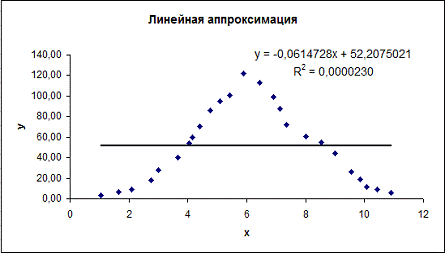
Рис.3. Исходная функция и линия тренда для линейной аппроксимации.

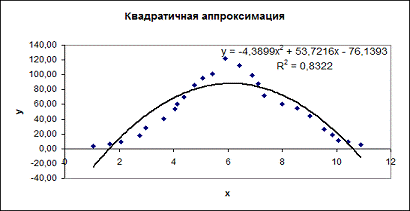
Рис.4. Исходная функция и линия тренда для квадратичной аппроксимации.

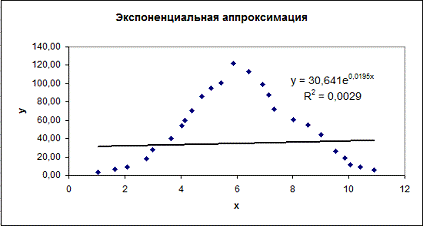
Рис.5. Исходная функция и линия тренда для экспоненциальной аппроксимации.

Получение числовых характеристик зависимости:

Выделяем область А65:В69 и вызываем Мастер функций. Выбираем функцию ЛИНЕЙН. В качестве «изв_знач_у» указываем В1:В25, а «изв_знач_х» А1:А25. В поле «стат» выбираем истина. Нажимаем Закончить. Устанавливаем курсор в строку формул и нажимаем Ctrl+Shift+Enter (табл. 9).

Таблица 9 Числовые характеристики зависимости

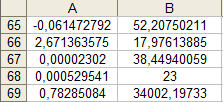
В ячейке А65 расположено значения коэффициента а₂, в ячейке В65 расположено значение коэффициента а₁.

В А66 расположено значение стандартной ошибки а₁, в В66 расположено значение стандартной ошибки коэффициента а₂.

В ячейке А67 расположено значение коэффициента детерминированности.

В ячейке А68 расположено значение F-критерия, в ячейке В68 расположено число степеней свободы.

В ячейке В69 расположено значение остаточной суммы квадратов, а в ячейке А69 значение регрессионной суммы квадратов.

В ходе расчётов выяснили, что квадратичная аппроксимация наилучшим способом описывает экспериментальные данные. Сравнивая результаты, полученные при помощи функции ЛИНЕЙН, видим, что они полностью совпадают с вычислениями, проведёнными выше. Полученное при построении линии тренда значения коэффициента детерминированности для экспоненциальной зависимости R² = 0,0029 не совпадает с истинным значением R² = -0,2254 поскольку при вычислении коэффициента детерминированности с помощью функции ЛИНЕЙН используются не истинные значения у, а преобразованные значения lnу с дальнейшей линеаризацией.

Расчёт аппроксимации экспериментальных данных с использованием MathCAD

Ввод исходных данных:

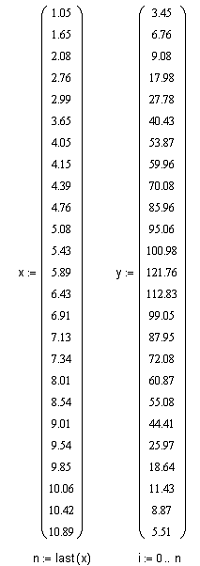
Линейная аппроксимация функции:

Нахождение коэффициентов А и В.

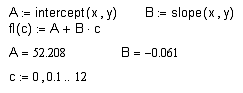
Построение графика линейной аппроксимации в MathCAD:

Рис.6. Исходная функция и линия тренда для линейной аппроксимации.

Квадратичная аппроксимация данных:

Нахождение коэффициентов d2, f2(c), k2.

Построение графика квадратичной аппроксимации в MathCAD:

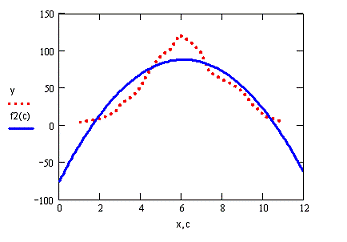
Рис.7. Исходная функция и линия тренда для квадратичной аппроксимации.

Экспоненциальная аппроксимация данных:

Нахождение коэффициентов а1, а2, z.

Построение графика экспоненциальной аппроксимации в MathCAD:

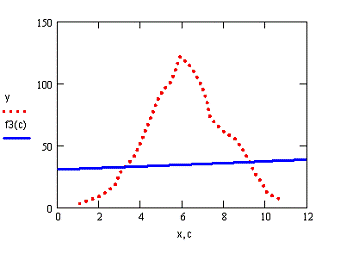
Рис.8. Исходная функция и линия тренда для экспоненциальной аппроксимации.

Расчёт аппроксимации экспериментальных данных с использованием MatLAB

Ввод исходных данных:

>> x=[1.05 1.65 2.08 2.76 2.99 3.65 4.05 4.15 4.39 4.76 5.08 5.43 5.89 6.43 6.91 7.13 7.34 8.01 8.54 9.01 9.54 9.85 10.06 10.42 10.89];

>> y=[3.45 6.76 9.08 17.98 27.78 40.43 53.87 59.96 70.08 85.96 95.06 100.98 121.76 112.83 99.05 87.95 72.08 60.87 55.08 44.41 25.97 18.64 11.43 8.87 5.51];

Линейная аппроксимация функции:

Нахождение коэффициентов линейной функции.

>> p=polyfit(x,y,1)=

>> t=polyval(p,x);

>> plot(x,y,'ob',x,t,'-g')

>> 

Построение графика линейной аппроксимации в MatLAB:

Рис.9. Исходные данные и линия тренда для линейной аппроксимации.

Квадратичная аппроксимация данных:

Нахождение коэффициентов квадратичной функции.

>> p=polyfit(x,y,2)=

.3899 53.7216 -76.1393

>> t=polyval(p,x);

>> plot(x,y,'ob',x,t,'-g')

>> 

Построение графика квадратичной аппроксимации в MatLAB:

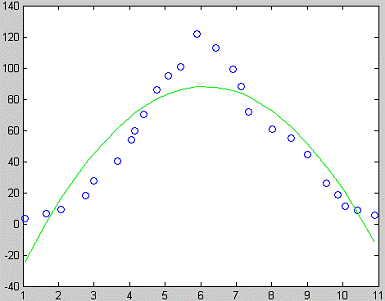
Рис.10. Исходные данные и линия тренда для квадратичной аппроксимации.

Экспоненциальная аппроксимация данных:

Нахождение коэффициентов экспоненциальной функции.

>> b=log(y);

>> p=polyfit(x,b,1)=

.0195 3.4223

>> c=3.4223=

.4223

>> a2=0.0195=

.0195

>> a1=exp(c)=

.6398

>> t=a1*exp(a2*x);

>> plot(x,y,'ob',x,t,'-g')

>> 

Построение графика экспоненциальной аппроксимации в MatLAB:

Рис.11. Исходные данные и линия тренда для экспоненциальной аппроксимации

Заключение

В данной курсовой работе я посчитала аппроксимацию экспериментальных данных методом наименьших квадратов с помощью различных программных средств, таких как Microsoft Excel, MathCAD и MatLAB.

Исходя из произведённых расчётов, выяснила, что квадратичная аппроксимация наилучшим способом описывает экспериментальные данные.

Сравнивая результаты, полученные при помощи функции ЛИНЕЙН в Microsoft Excel, увидела, что они полностью совпадают с вычислениями, проведёнными выше. А коэффициент детерминированности для экспоненциальной зависимости не совпадает с истинным значением, поскольку при вычислении коэффициента детерминированности с помощью функции ЛИНЕЙН используются не истинные значения у, а преобразованные значения lnу с дальнейшей линеаризацией.

Результаты, полученные в программах Microsoft Excel, MathCAD, MatLAB совпадают, следовательно, расчёты выполнены верно

Список использованных источников

1.   Акулич И. Л. Математическое программирование в примерах и задачах: Учебное пособие для студентов экономических специализированных вузов. - М.: «Высшая школа», 1986.- С.365

2.       Гурьяшова Р. Н. , Шеянов А. В. Информатика. Пакет MathCAD. - М.: «ФГОУ ВПО», 2005. - С.140.

3.       Дьяконов В. П. MATLAB 6/6.1/6.5 + Simulink 4/5 в математике и моделировании. Основы применения. Полное руководство пользователя. - М.: «СОЛОН-Пресс» <http://ru.wikipedia.org/w/index.php?title=%D0%9C%D0%BE%D1%81%D0%BA%D0%B2%D0%B0._%28%D0%B8%D0%B7%D0%B4%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE%29&action=edit&redlink=1>, 2003. - С. 576.

.        Курбатова Е. А. MATLAB 7. Самоучитель - М.: «Диалектика» <http://ru.wikipedia.org/w/index.php?title=%D0%94%D0%B8%D0%B0%D0%BB%D0%B5%D0%BA%D1%82%D0%B8%D0%BA%D0%B0_%28%D0%B8%D0%B7%D0%B4%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE%29&action=edit&redlink=1>, 2005. - С. 256.

.        Макаров Е. Г. MathCAD: учебный курс. - СПб.: «Питер», 2009.- С.384.