Программа интерполяции в MATLAB
1. Основная
часть
1.1 О
назначении и возможностях пакета MATLAB
Название MATLAB является сокращением от Matrix Laboratory, и
первоначально пакет MATLAB разрабатывался как средство доступа к библиотекам
программ LINPACK и EISPACK, предназначенных для матричных вычислений. Пакет
MATLAB создан компанией MathWorks около двадцати лет назад. Работа сотен ученых
и программистов направлена на постоянное расширение его возможностей и
совершенствование заложенных алгоритмов. В настоящее время MATLAB является мощным
и универсальным средством решения задач, возникающих в различных областях
человеческой деятельности. Спектр проблем, исследование которых может быть
осуществлено при помощи MATLAB и его расширений (Toolbox), охватывает:
матричный анализ, обработку сигналов и изображений, задачи математической
физики, оптимизационные задачи, финансовые задачи, обработку и визуализацию
данных, работу с картографическими изображениями, нейронные сети, нечеткую
логику и многое другое. Около сорока специализированных Toolbox могут быть
выборочно установлены вместе с MATLAB по желанию пользователя. В состав многих
Toolbox входят приложения с графическим интерфейсом пользователя, которые
обеспечивают быстрый и наглядный доступ к основным функциям. Пакет Simulink,
поставляемый вместе с MATLAB, предназначен для интерактивного моделирования
нелинейных динамических систем, состоящих из стандартных блоков.
Обширная и удобная справочная система MATLAB способна
удовлетворить потребности как начинающего, так и достаточно опытного пользователя.
Полная гипертекстовая информационная система (на английском языке) содержит
описание встроенных функций и достаточно большое число примеров их
использования. Ссылки позволяют переходить к разделам, имеющим отношение к
изучаемому вопросу, что облегчает самостоятельный поиск интересующей
информации. Доступ из командной строки к кратким сведениям о встроенных
функциях обеспечивает возможность быстрого выбора нужного варианта обращения к
функциям. Инженерам и научным работникам, проводящим самостоятельные исследования,
оказываются полезными прилагаемые к пакету электронные книги в формате PDF.
Данные книги не только дублируют справочную систему MATLAB и каждого Toolbox,
но и содержат теоретические сведения и математическую базу, необходимые для
осознанного использования описываемых, средств. Справочная система снабжена
ссылками на книги и статьи, посвященные реализованным алгоритмам в MATLAB и
Toolbox, что позволяет исследователю и разработчику собственных алгоритмов
вникнуть в суть дела.обладает хорошо развитыми возможностями визуализации
двумерных и трехмерных данных. Высокоуровневые графические функции призваны
сократить усилия пользователя до минимума, обеспечивая, тем не менее, получение
качественных результатов. Интерактивная среда для построения графиков позволяет
обойтись бел графических функций для визуализации данных. Кроме того, она
служит и для оформления результата желаемым образом: размещения поясняющих
надписей, задания цвета и стиля линий и поверхностей, словом, для получения
изображения, пригодного для включения в отчет или статью. Полный доступ к
изменению свойств отображаемых графиков дают низкоуровневые функции, применение
которых подразумевает понимание принципов компьютерной графики и владение
приемами программирования.
В MATLAB реализованы классические численные алгоритмы решения
уравнений, задач линейной алгебры, нахождения значений определенных интегралов,
аппроксимации, решения систем или отдельных дифференциальных уравнений. Для
применения базовых вычислительных возможностей достаточно знания основных
численных методов в рамках программы технических вузов. Решение специальных
задач, разумеется, невозможно без соответствующей теоретической подготовки;
впрочем, сведения, изложенные в справочной системе, оказываются неоценимым
подспорьем для желающих самостоятельно разобраться в обширных возможностях
пакета MATLAB.
Простой встроенный язык программирования позволяет легко
создавать собственные алгоритмы. Простота языка программирования компенсируется
огромным множеством функций MATLAB и Toolbox. Данное сочетание позволяет
достаточно быстро разрабатывать эффективные программы, направленные на решение
практически важных задач.
Визуальная среда GUIDE предназначена для написания приложений
с графическим интерфейсом пользователя. Работа в среде GUIDE проста, но
предполагает владение основами программирования и дескрипторной графики.
Наличие определенного навыка работы в среде GUIDE предоставляет возможность
создать визуальную среду для проведения собственных исследований, что
значительно облегчает работу и существенно экономит время.
Объектно-ориентированный подход, заложенный в основу MATLAB,
обеспечивает современную эффективную технологию программирования. С учетом
специфики решаемой задачи разработчик приложений MATLAB в дополнение к
существующим классам имеет возможность создавать собственные со своими
методами.прекрасно интегрируется со многими приложениями и средами
программирования. Связь MATLAB и MS Word обеспечивает возможность написания в
редакторе MS Word интерактивных документов, так называемых М-книг, основанных
на специальном шаблоне. Пользователь, работающий с М-книгой, может запускать
блоки команд MATLAB непосредственно из документа MS Word, причем результат
выполнения команд отображается в М-книге. Данное средство прекрасно подходит для
создания электронных отчетов и учебных пособий.
Надстройка MS Excel Link, поставляемая вместе с MATLAB,
существенно расширяет возможности MS Excel, обеспечивая доступ пользователя к
функциям MATLAB и Toolbox. Подготовка данных осуществляется непосредственно в
электронных таблицах, а обращение к функциям производится либо из ячеек
рабочего листа, либо в модуле, написанном на Visual Basic (VBA). MATLAB Builder
for MS Excel позволяет реализовывать алгоритмы MATLAB в виде СОМ-объектов и
использовать их в приложениях на VBA.
Информация, хранящаяся в базах данных многих популярных
форматов, может быть импортирована в MATLAB, нужным образом обработана и
исследована при помощи функций MATLAB, а затем экспортирована в какую-либо
другую базу данных. Для обмена данными используются команды языка запросов SQL.
Поддерживается, в частности, связь с Microsoft Access, Microsoft SQL Server,
Oracle. Имеется приложение с графическим интерфейсом, которое облегчает работу
пользователей, не знакомых с языком запросов SQL.
Символические вычисления в MATLAB основаны на библиотеке,
являющейся ядром пакета Maple. Решение уравнений и систем, интегрирование и
дифференцирование, вычисление пределов, разложение в ряд и суммирование рядов,
поиск решения дифференциальных уравнений и систем, упрощение выражений - вот
далеко не полный перечень возможностей MATLAB для проведения аналитических
выкладок и расчетов. Поддерживаются вычисления с произвольной точностью.
Пользователи, имеющие опыт работы в Maple, могут напрямую обращаться ко всем функциям
данного пакета (кроме графических) и вызывать процедуры, написанные на
встроенном языке Maple.
Программный интерфейс приложения (API) реализует связь среды
MATLAB с программами, написанными на С, Fortran или Java. Библиотека
программного интерфейса позволяет вызывать имеющиеся модули на С, Fortran или
Java из среды или программ MATLAB, обращаться к функциям MATLAB из программ на
С или Fortran, осуществлять обмен данными между приложениями MATLAB и другими
программами. Средства MATLAB Builder for СОМ предназначены для преобразования
программ MATLAB в СОМ-объекты, доступные в других приложениях.
Для разработки интернет-приложений MATLAB создан MATLAB Web
Server, причем процесс создания приложения достаточно прост - кроме умения
программировать в MATLAB требуется только знание основ HTML.
Подводя итог вышесказанному, можно сделать вывод, что
начинающий пользователь MATLAB может в процессе работы совершенствовать свои
знания как в области моделирования и численных методов, так и программирования,
и визуализации данных. Огромным преимуществом MATLAB является открытость кода,
что дает возможность опытным пользователям разбираться в запрограммированных
алгоритмах и, при необходимости, изменять их. Впрочем, разнообразие набора
функций MATLAB и Toolbox допускает решение большинства задач без каких-либо
предварительных модификаций.
1.2 Цель
интерполирования
В вычислительной математике существенную роль играет
интерполяция функций, т.е. построение по заданной функции другой (как правило,
более простой), значения которой совпадают со значениями заданной функции в
некотором числе точек. Причем интерполяция имеет как практическое, так и
теоретическое значение. На практике часто возникает задача о восстановлении
непрерывной функции по ее табличным значениям, например полученным в ходе
некоторого эксперимента. Для вычисления многих функций оказывается эффективно
приблизить их полиномами или дробно-рациональными функциями. Теория
интерполирования используется при построении и исследовании квадратурных формул
для численного интегрирования, для получения методов решения дифференциальных и
интегральных уравнений.
Все перечисленные выше вопросы рассмотрены в классических
учебниках по численным методам. Простота языка пакета MATLAB в сочетании с
широким набором его функций, в том числе и графических, позволяет вместо
написания собственных программ интерполяции и визуализации результатов
сосредоточиться на исследовании большого числа примеров, что может быть
использовано при проведении лабораторных работ по численным методам для
студентов технических факультетов вузов и институтов.
1.3 Суть
метода
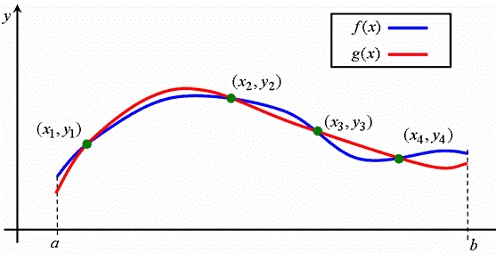
Пусть на отрезке [a, b] задана функция ƒ(x). Задача интерполяции (или интерполирования) состоит в построении
функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек
{x1, x2,…, xn+1} из отрезка [a, b] (эти точки
называются узлами интерполяции), т.е. должны выполняться условия:
(xk)=yk, k=1,2,…, n+1,
где yk - известные значения функции ƒ(x) в точках xk. Функция g(x) называется интерполянтом
функции ƒ(x).
Пример интерполяции с четырьмя узлами приведен на следующем
рисунке, из которого видно, что узлы интерполяции не обязательно должны
располагаться равномерно на отрезке [a, b].
Если ƒ(x) табличная функция,
скажем полученная из эксперимента, т.е. известны только ее значения yk
в точках xk, то, вообще говоря, о качестве полученного приближения
судить трудно.
Мы рассмотрим только линейную интерполяцию, т.е. такую, при
которой функция g(x) разыскивается в виде линейной комбинации некоторых функций
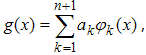
где для k=1,2,…, n+1: φk(x) - заданные функции, а
ak - искомые коэффициенты.
Ясно, что из постановки задачи интерполяции (т.е. из
совпадения значений интерполянта g(x) и интерполируемой функции ƒ(x) в точках xk) следует, что коэффициенты ak
определяются из решения следующей системы линейных алгебраических уравнений:
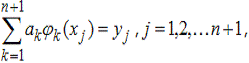
или в развернутой форме
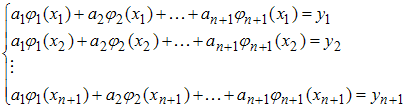
Совершенно ясно, почему число коэффициентов ak
должно совпадать с числом узлов интерполяции xk. Это нужно для того,
чтобы матрица системы была квадратной (т.е. число неизвестных совпадало бы с
числом условий, из которых находятся эти неизвестные). Кроме того, для
однозначной разрешимости данной системы (при произвольной правой части)
необходимо и достаточно, чтобы ее определитель был отличен от нуля, т.е.
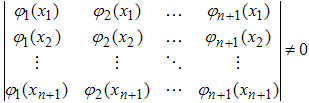
Очень часто в качестве системы функций φk(x) выбирают полиномы, например степени x, именно:
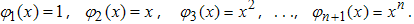
Тогда соответствующий интерполянт называют интерполяционным
полиномом. Существование и единственность интерполяционного полинома
гарантируется, если все узлы интерполяции xk различны.
Действительно, определитель системы линейных алгебраических уравнений для
нахождения коэффициентов ak
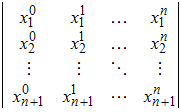
является определителем Вандермонда, который, как известно,
равен
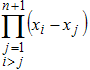
и, следовательно, отличен от нуля в случае, когда все узлы xk
различны. Поскольку матрица системы невырождена, то решение системы существует
и единственно. Итак, интерполяционный полином существует и единственный.
Можно рассуждать и по-другому. Предположим, что есть два
интерполяционных полинома gk и hk степени n такие, что
для произвольного набора значений выполняются равенства g(xk) = h(xk)
= yk) для всех k=1,2,…, n+1, т.е. для n+1-ой точки. Тогда их
разность hk - gk является полиномом степени не выше n, но
обращается в ноль в n+1-ой точке. По известной теореме алгебры у полинома
степени n не может быть больше чем n корней, следовательно hk - gk
≡ 0 и hk ≡ gk. Единственность установлена. А
так как полином единственный, то у соответствующей системы линейных
алгебраических уравнений есть только одно решение (для произвольной правой
части). Из результатов линейной алгебры известно, что у системы может быть либо
бесконечное число решений при некоторых правых частях, либо единственное, для
произвольной правой части. Последнее как раз и выполняется.
Итак, число узлов интерполяционного полинома всегда должно
быть на единицу больше его степени. Это понятно также из следующих простых
соображений: через две точки проходит единственная прямая, через три -
единственная парабола и т.д. Полином может получиться и степени меньшей, чем,
например, если три точки лежат на одной прямой, то через них проходит
единственный полином первой степени, однако это не нарушает наших рассуждений
(просто коэффициент при старшей степени равен нулю). Однако, существует
бесконечно много парабол, проходящих через две точки.
Казалось бы, при практической реализации интерполяционного
процесса коэффициенты интерполяционного полинома ak можно найти,
непосредственно решая систему линейных алгебраических уравнений
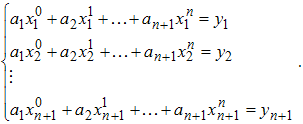
2.
Практическая часть
2.1 Интерполирование
и сглаживание
Табличные данные очень часто удобно интерпретировать как
некоторую функцию, в частности, полиномиальную или сплайн - гладкую функцию,
которая на отрезках области определения равна полиномам определенной степени.
Будем различать два критерия приближения табличных функций: интерполирование,
при котором аппроксимирующая функция совпадает с табличной в узлах, и
сглаживание, основанное на минимизации некоторого критерия, например, суммы
квадратов отклонений в узлах. Итак, возникает задача о построении
полиномиальной или кусочно-полиномиальной функции для приближения некоторых
дискретных данных. Набор вычислительных функций MATLAB содержит функции для
решения таких задач, как в случае одномерных, так и многомерных данных. Самым
простым способом интерполяции является аппроксимация данных сплайном нулевого
порядка (на каждом участке степень полинома равна нулю), при которой значение в
каждой промежуточной точке принимается равным ближайшему значению, заданному в
таблице. В результате данные приближаются ступенчатой функцией, а само
приближение называется интерполяцией по соседним точкам. Линейная интерполяция
основана на соединении соседних точек отрезками прямых - табличные данные
приближаются ломаной линией (сплайн первого порядка дефекта единица). Для
получения более гладкой функции следует применять интерполяцию кубическими
сплайнами.
2.2 Постановка
задачи
Определить по кривой (рис. 1), при α=0° (для оцифровки графиков удобно
воспользоваться программой GetData) значение 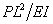 в интервале
в интервале 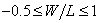 , и интерполировать полученные данные с
помощью кусочно-линейной интерполяцией и кубическим сплайном. Результаты
интерполяции представить графически. Определить площадь под кривой численным
интегрированием.
, и интерполировать полученные данные с
помощью кусочно-линейной интерполяцией и кубическим сплайном. Результаты
интерполяции представить графически. Определить площадь под кривой численным
интегрированием.
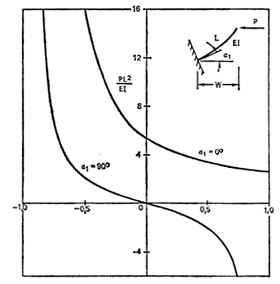
Рис. 1. Кривая зависимости безразмерной величины нагрузки 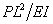 от безразмерной деформации
от безразмерной деформации 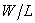
2.3 Решение
задачи
Схема решения данной задачи в MATLAB состоит из следующих
этапов:
1. Определение по кривой при α=0° значений 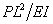 в интервале
в интервале 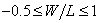 .
.
. Интерполирование полученных данных с помощью
кусочно-линейной интерполяции и кубическим сплайном.
. Построение графиков исходной зависимости и графиков
интерполянтов.
. Определение площади под кривой численным интегрированием
(метод трапеций).
Значения 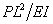 в интервале
в интервале 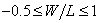 были найдены с помощью оцифровки графика
программой GetData:
были найдены с помощью оцифровки графика
программой GetData:
§ нанесение координатных осей (Команды →
Установить систему координат);
§ оцифровка графика (Команды → Авто
трассировка линий);
§ удаление ненужных точек (Команды → Ластик
точек данных);
§ сохранение массивов точек в файл (Файл →
Экспорт данных).
Данные способы интерполяции реализованы в функции interp1.
Функция yi = interp1 (x, y, xi) строит интерполирующую
кривую для одномерного массива y, заданного на сетке x; выходной массив yi может быть определен на
более мелкой сетке xi. Если Y - двумерный массив, то интерполирующая кривая строится для
каждого столбца. По умолчанию реализована линейная интерполяция.
Для использования yi = interp1 (x, y, xi, ‘<метод>»)
следует задать координаты абсцисс промежуточных точек, в которых вычисляются
значения интерполянта, и способ интерполирования:
§ 'linear' - линейная интерполяция (применяется по
умолчанию, если способ интерполирования не задан);
При линейной интерполяции MATLAB соединяет существующие точки
данных прямыми линиями. Использует векторы данных 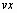 и
и 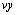 , чтобы возвратить
интерполируемое значение
, чтобы возвратить
интерполируемое значение 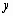 , соответствующее третьему аргументу
, соответствующее третьему аргументу 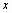 . Аргументы
. Аргументы 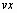 и
и 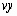 должны быть векторами
одинаковой длины. Вектор
должны быть векторами
одинаковой длины. Вектор 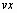 должен содержать вещественные значения,
расположенные в порядке возрастания. Эта функция соединяет точки данных
отрезками прямых, создавая таким образом ломаную. Интерполируемое значение для
конкретного х есть ордината у соответствующей точки ломаной. Для значений
должен содержать вещественные значения,
расположенные в порядке возрастания. Эта функция соединяет точки данных
отрезками прямых, создавая таким образом ломаную. Интерполируемое значение для
конкретного х есть ордината у соответствующей точки ломаной. Для значений 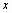 , расположенных перед
первой точкой в векторе
, расположенных перед
первой точкой в векторе 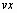 , MATLAB продолжает ломаную прямой линией,
проходящей через первые две точки данных. Для значений
, MATLAB продолжает ломаную прямой линией,
проходящей через первые две точки данных. Для значений 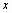 , расположенных за
последней точкой
, расположенных за
последней точкой 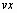 , MATLAB продолжает ломаную прямой линией,
проходящей через последние две точки данных. Для получения наилучших
результатов
, MATLAB продолжает ломаную прямой линией,
проходящей через последние две точки данных. Для получения наилучших
результатов 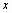 должно находится между самыми большими и самыми
маленькими значениями
должно находится между самыми большими и самыми
маленькими значениями 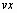 - маловероятно, что будут полезны значения,
вычисленные для
- маловероятно, что будут полезны значения,
вычисленные для 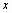 вне этого диапазона.
вне этого диапазона.
§ 'spline' - интерполяция кубическими сплайнами;
Сплайн-интерполяция используется для представления данных
отрезками полиномов невысокой степени - чаще всего третьей. При этом кубическая
интерполяция обеспечивает непрерывность первой и второй производных результата
интерполяции в узловых точках. Из этого вытекают следующие свойства кубической
сплайн-интерполяции:
§ в узловых точках нет разрывов и резких перегибов
функции;
§ благодаря низкой степени полиномов погрешность
между узловыми точками обычно достаточно мала;
§ связь между числом узловых точек и степенью
полинома отсутствует;
§ поскольку используется множество полиномов,
появляется возможность аппроксимации функций с множеством пиков и впадин.
В переводе spline означает «гибкая линейка». График
интерполирующей функции при этом виде интерполяции можно уподобить кривой, по
которой изгибается гибкая линейка, закрепленная в узловых точках.
Сплайн-интерполяция дает неплохие результаты для функций, не имеющих разрывов и
резких перегибов. Особенно хорошие результаты получаются для монотонных
функций.
Методы линейной и кубической интерполяции реализуются
довольно просто; что же касается интерполяции сплайнами, то в этом случае
используются вспомогательные функции ppval, mkpp, unmkpp, которые образуют небольшой пакет для работы с
кусочно-гладкими полиномами.
Выходным аргументом interp1 является вектор значений
интерполянта в промежуточных точках.
Графики в декартовой системе координат строят с помощью
команды plot. Команда plot имеет различные формы, связанные с входными
параметрами. Результат выводится в специальном окне. Команда plot (x, у, «цвет_стиль_маркер') - позволяет задавать
цвет, стиль линий и маркеры. Аргумент 'цвет_стиль_маркер» - это
строковая константа, составленная из символов цвета, стиля линий и маркеров.
Если определить только тип маркеров, но не указать стиль линий, MATLAB выведет на график только
маркеры.
Нанесение надписей и сетки на графике:
§ xlabel ('TEXT') - маркировка оси х.
§ ylabel ('TEXT') - маркировка оси у.
§ legend ('TEXT1', 'TEXT2', …) - легенда.
Команда grid осуществляет нанесение координатной сетки. По
умолчанию на двумерных графиках сетка не наносится. Для задания сетки нужно
выполнить команду grid on, а убрать по команде grid off. Команда grid без параметров действует
как переключатель.
Добавление кривых на существующий график:
§ hold on - обеспечивает
продолжение вывода графиков в текущее окно;
§ hold off - отменяет режим
продолжения;
§ hold - работает как
переключатель с одного режима на другой.
Интегрирование методом трапеций:
§ I = trapz (x, y)
Функция I = trapz (x, y) вычисляет интеграл от
функции y
по переменной x,
используя метод трапеций. Аргументы x и y могут быть одномерными массивами одинакового размера, либо
массив Y
может быть двумерным, но тогда должно выполняться условие size (Y, 1) = length(x). В последнем случае
вычисляется интеграл для каждого столбца.
Листинг 1. Файл-программа interpoljacija
|
% заполнение массивов для табличной функции x
= [-0.5 -0.4677 -0.4343 -0.3952 -0.3493 -0.2951 -0.2278 -0.1431 -0.0394
0.0803 0.2099 0.3445 0.4816 0.6225 0.7647 0.9009 1]; y = [16 14.6264
13.2183 11.8263 10.4538 9.1135 7.8345 6.6780 5.7083 4.9382 4.3355 3.8454
3.4550 3.1773 2.9703 2.7792 2.7]; % вывод графика табличной функции
маркерами plot (x, y, 'ko') % задание промежyточныx точек для
интерполирования xi = [x(1):0.1:x (length(x))]; % вычисление
кyсочно-линейной фyнкции в промежyточныx точкаx yline =
interp1 (x, y, xi, 'linear'); % вычисление кyбического сплайна в
промежyточныx точкаx yspline = interp1 (x, y, xi, 'spline'); % для построения
графиков в одном окне hold on % нанесение измерительной сетки
grid on % построение графиков интерполянтов plot (xi,
yline, 'k-', xi, yspline, 'k - .') % нанесение названий координатных осей %
вывод легенды legend ('табличная фyнкция', 'линейная (linear)',
'кyбический сплайн (spline)') % задание интервала x1=-0.5:0.1:1;
% задание функции y1 = interp1 (x, y, x1, 'spline'); % нахождение площади
под графиком S=trapz (x1, y1)
|
интерполяция инженерный сплайн matlab
Выполнение файл-программы interpoljacija приводит к
появлению графика, изображенного на рис. 2., отражающего график табличной
функции и графики интерполянты. Как видно, интерполяция кубическим сплайном
является более точным методом интерполяции, чем кусочно-линейная, вследствие
чего график сплайна располагается ближе к графику табличной функции. Также мы
нашли площадь под графиком табличной функции: S = 8.1882 (кв. ед.).
Заключение
Из данной работы видно, насколько прост и удобен в
использовании пакет MATLAB. Для работы с ней необходимо иметь самые
элементарные навыки работы на ПК.
Говоря о математических аспектах MATLAB, нужно отметить, что
его обозначения очень близки к тем, которые давно используются в математике, и
это заметно упрощает освоение многочисленных математических команд.
Этот пакет может использоваться во всех сферах вычислений
начиная с самых простых, заканчивая самыми сложными. С его помощью можно
работать с массивами чисел, выполнять операции над многочленами, решать
различные уравнения, строить графики. Пакет MATLAB включает различные
интерфейсы для получения доступа к внешним подпрограммам, написанным на других
языках программирования.
Итогом написания данной курсовой работы является компьютерная
реализация решения инженерной задачи по интерполяции табличной функции 2
различными методами (кусочно-линейной интерполяцией и кубическим сплайном), а
также построение их графиков.