Математическое программирование
Лекция 1.
1.Общая задача оптимизации
1.1. Математическая задача оптимизации
На практике часто возникает ситуация, когда достичь
какого-либо результата можно не одним, а многими различными способами.
Естественно, когда решений много, возникает
желание и необходимость выбрать в каком-то смысле наилучшее из них.
•
Чтобы применить математический аппарат для нахождения наилучшего надо
описать ситуацию и понятие наилучшего на математическом языке.
•
Описать математическую постановку задачи оптимизации.
|
•
Выбрать
независимые переменные (варьируемые параметры)
•
Описать
ограничения на эти переменные, область допустимых значений, которая
задается обычно системой неравенств
•
Описать
функцию цели, минимум или максимум которой надо найти
|
|
Математическая постановка
задачи оптимизации состоит в следующем:
В этой задаче ищется не только само максимальное (минимальное) значение, но и значения независимых переменных,
при которых достигается максимальное (минимальное) значение
Значения независимых
переменных, при которых достигается максимальное (минимальное)
значение называется оптимальным решением,
а множество всех оптимальных решений называется оптимальным
множеством.
Задачи такого рода получили название задач
математического программирования.
1.2. Задача о станции
•
Задан прямолинейный участок железной дороги и два населенных пункта A и B на некотором
расстоянии от нее. Требуется построить железнодорожную станцию C для обслуживания пунктов A
и B.
Очевидно, что станцию можно построить в различных точках
железной дороги, и, соответственно, необходимо найти наилучшее решение по ее
размещению
Эта задача пока что не является задачей математической
оптимизации.
Для постановки математической задачи оптимизации
необходимо:
a)
выбрать независимые переменные;
b)
описать ограничения на переменные;
c) описать
функцию цели, зависящую от переменных.
Вариант 1. Математическая постановка задачи о станции
Построим прямоугольную систему координат, (ось 0х
направим вдоль железной дороги, ось 0у пусть проходит через пункт А в
направлении от железной дороги к пункту А).
Тогда:
a) независимые
переменные: – неизвестные координаты точки C;
b) ограничения:
(станция должна находиться на железной дороге);
c)
функция цели: (разность расстояний от станции до пунктов A и B должна быть
минимальной равной нулю. Никого не обидеть, на одинаковом расстоянии) или
Вариант 2.
Сократим число переменных и возьмем другую цель: минимальное суммарное
расстояние до населенных пунктов от станции C
(меньше строить автодорог):
a) независимая
переменная одна – x, координата точки C на оси Ox;
b)
ограничений нет;
c) необходимо
найти минимум:
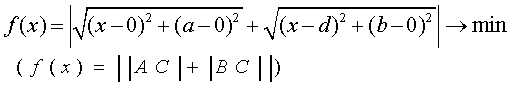
1.3. Линейное программирование
В зависимости от характера функций выделяют различные
виды задач математического программирования.
•
Наиболее простой и чаще всего встречающийся вид, когда эти функции
являются линейными, т.е. имеют вид:
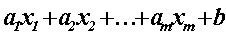
, (1)
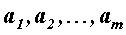 где и
b – заданные числа, для каждой
функции свои.
где и
b – заданные числа, для каждой
функции свои.
Если
функции
– линейные, т.е. имеют вид (1), то говорят о задаче
линейного программирования.
•
Линейное программирование как раздел прикладной математики появилось
в 40-х гг. прошлого столетия.
•
В настоящее время около 85% всех решаемых на практике задач являются
задачами линейного программирования
Замечание
Каждая задача на нахождение максимума может быть сведена
к задаче на нахождение минимума и наоборот.
Для этого достаточно функцию цели
умножить на -1.
1.4. Задача о банке
Пусть собственные средства банка вместе с депозитами
составляют 100 млн. долларов
Часть из этих средств, но не менее 35 млн. долларов,
должна находиться в кредитах. Эти средства являются неликвидными активами
банка, т.к. в случае непредвиденной потребности банка в наличности обратить эти
кредиты в наличность без ущерба невозможно.
Другая часть должна находиться в ценных бумагах.
Их можно в любой момент продать, получить некоторую
прибыль или, во всяком случае, не получить большого убытка.
Поэтому для банков существует правило, согласно которому
они должны покупать в определенной пропорции ценные бумаги (ликвидные активы),
чтобы компенсировать неликвидность кредита.
•
В нашем примере ликвидное ограничение таково: ценные бумаги должны
составлять не менее 30% средств, размещенных в кредитах и ценных бумагах.
Доходность ценных бумаг равна 0,1, доходность кредитов
0,15.
Какую часть средств банк должен размещать в ценных
бумагах, а какую – в кредитах?
Постановка задачи линейного программирования.
a) независимые
переменные: x – средства (в млн. долл.),
размещенные в кредитах, а y – средства,
размещенные в ценных бумагах.
b) Ограничения:
c) доходность
банка
Функция цели и все функции в ограничениях являются
линейными, поэтому поставленная задача есть задача линейного программирования.
На свиноферме производится откорм свиней. Известно, что
каждая свинья должна получать не менее 6 единиц вещества K, не менее 8 единиц вещества L
и не менее 12 единиц вещества M. Вещества
K, L,
M могут обозначать, например, белки, жиры
и углеводы.
Для откорма свиней можно закупить три вида кормов: I, II, III. Например, картофель, жмых, комбикорма. Содержание
каждого вещества в различных кормах и стоимость единицы каждого корма зададим с
помощью таблицы:
|
Вид
корма
|
Вещества
|
Стоимость
единицы корма
|
|
K
|
L
|
M
|
|
I
|
2
|
1
|
3
|
2
|
|
II
|
1
|
2
|
4
|
3
|
|
III
|
1,5
|
2
|
2,5
|
2,5
|
Требуется обеспечить наиболее дешевый рацион откорма и
при этом дать все необходимое свиньям.
Составим математическую модель.
a)
Независимые переменные:
Х1 – количество корма I
вида, которое надо давать свинье;
Х2 – количество корма II
вида, которое надо давать свинье;
Х3– количество корма III
вида, которое надо давать свинье;
b) Ограничения:
Цель – дешевый рацион, т.е.
1.6. Задача об использовании ресурсов
Задача
Для изготовления шкафов и буфетов деревообрабатывающий
завод применяет древесину 4‑х видов. Запасы по каждому виду ограничены и
составляют соответственно 120, 160, 120, 80.
Количество единиц древесины каждого вида, необходимой для
изготовления 1 шкафа и 1 буфета, а также прибыль, получаемую заводом
от реализации единицы продукции, зададим с помощью таблицы:
|
Вид
Древесины
|
Запасы
|
Количество на
1 единицу продукции
|
|
Шкаф
|
Буфет
|
|
I
|
120
|
0
|
4
|
|
II
|
160
|
4
|
0
|
|
III
|
120
|
2
|
2
|
|
IV
|
80
|
1
|
2
|
|
Прибыль
|
2
|
3
|
Требуется составить такой план выпуска продукции, который
обеспечил бы предприятию наибольшую прибыль от реализации всей продукции.
Математическая модель:
a) Независимые
переменные: x – количество шкафов,
y – количество буфетов, которые
необходимо выпустить.
b) Ограничения:
 Цель: наибольшая прибыль от
реализации продукции, т.е.
Цель: наибольшая прибыль от
реализации продукции, т.е.
Эта задача, так же, как и все предыдущие (кроме задачи о
станции), является задачей линейного программирования, т.е. все функции,
описывающие ограничения, и функция цели являются линейными.
1.7. Транспортная задача
Уголь, добываемый в двух месторождениях, отправляется
трем потребителям (заводам, электростанциям и т.п.). Известно, сколько угля
добывается с каждого месторождения, например за месяц, и известно, сколько его
требуется в этот же срок каждому потребителю.
Известны также расстояния между месторождениями и
потребителями и условия сообщения между ними.
Учитывая эти данные, можно подсчитать, во что обойдется
перевозка каждой тонны угля из любого месторождения в любой пункт назначения.
Нужно спланировать перевозки угля так, чтобы затраты на
них были минимальными.
|
 потребители потребители
отправители
|
П1
|
П2
|
П3
|
Всего
отправлено
|
|
О1
|
c11
x11
|
c12
x12
|
c13
x13
|
а1
|
|
О2
|
c21
x21
|
c22
x22
|
c23
x23
|
а2
|
|
Всего
привезено
|
b1
|
b2
|
b3
|
а1+а2=
= b1+b2+b3
|
Построим математическую
модель:
a)
хkn количество тонн угля, которое нужно
перевезти от Ok до Пn;
b) ограничения:
c) цель – затраты на перевозку должны быть
минимальными, т.е
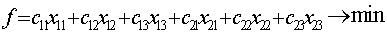
2. Каноническая и стандартная задачи
линейного программирования
2.1. Каноническая задача линейного
программирования
В
канонической задаче система ограничений, помимо тривиальных, содержит только
уравнения. Примером канонической задачи может служить транспортная задача.
2.2. Стандартная задача линейного
программирования
В
стандартной задаче все ограничения состоят только из неравенств.
Примерами стандартных задач являются задача о
диете, задача о банке, задача об использовании ресурсов.
Стандартная и каноническая задачи сводятся одна к другой.
2.3. Сведение стандартной задачи линейного программирования
к канонической на примере задачи о диете.
Стандартная Каноническая
|
a)
x1, х2, x3
b)
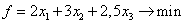 с) с)
|
a)
x1, х2, x3, x4,
х5,
x6
b)
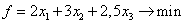 с) с)
|
x4, х5, x6 - балансовые переменные
2.4. Сведение канонической задачи к стандартной
Пусть дана задача
a)
x1, х2, x3 ,
х4
b)

a)
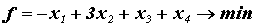
Возьмем первые 2 равенства системы ограничений и методом
Гаусса выделим базисные неизвестные.
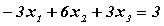 Сложим 2 первых уравнения:
Сложим 2 первых уравнения:
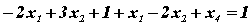 Найдем х4
Найдем х4
Найденные значения подставим в функцию цели
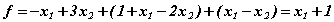
 Получим задачу
Получим задачу
Получим стандартную задачу
3. Геометрия задач линейного программирования
Допустимое множество, заданное с помощью линейных
ограничений
(уравнений или неравенств), называется выпуклой многогранной областью.
Примеры выпуклых множеств
Теорема 1
Если в задаче линейного программирования допустимое
множество не пусто и целевая функция ограничена, то существует хотя бы одно
оптимальное решение.
Теорема 1 указывает, когда существует оптимальное
решение, но не дает метода нахождения этого решения
Определение
Угловой точкой называется точка множества X, если она не является внутренней точкой ни для какого
отрезка, целиком лежащего в X.
Примеры
Теорема 2
Если в задаче линейного программирования на минимум
(максимум) допустимое множество имеет хотя бы одну угловую точку, а целевая
функция ограничена, то угловая точка допустимого множества, в которой функция
принимает минимальное (максимальное) значение среди всех угловых точек,
является оптимальным решением данной задачи.
Теорема 2 позволяет для ограниченных целевых функций при
малом числе угловых точек указать процедуру нахождения оптимального решения.
Процедура выглядит следующим образом:
- Находятся все угловые точки допустимого множества.
- Среди этих точек находится точка с минимальным
(максимальным) значением целевой функции. Найденная точка и есть
оптимальное решение.
При большом числе угловых точек эта процедура является
громоздкой, требует множества вычислений.
При небольшом же их числе ее можно и даже желательно
применять.
Задача
 А) x1,
x2
А) x1,
x2
B
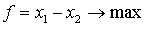 C)
C)
План решения
•
Построим область допустимых значений
•
Найдем угловые точки
•
Найдем значения функции цели в угловых точках
•
Найдем максимальное среди этих значений
Замечание
Оптимальное решение возможно не единственное.
Замечание
Если ограничений много, то эта процедура очень
громоздкая, перебор всех вершин труден.
Существуют более целенаправленные процедуры перебора
вершин.
Графический метод, симплекс-метод.