Развитие познавательного интереса на математическом кружке для 5-6 классов

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

"Московский педагогический государственный университет"

математический факультет

кафедра теории чисел

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

по теме "Развитие познавательного интереса на математическом кружке для 5-6 классов"

по специальности "Математика" с дополнительной специальностью "Информатика"

Выполнила:

Студентка

группы 5 курса

Торхова Анна Юрьевна

Научный руководитель

Котова Л.В.

Москва 2012

Содержание

 

Глава I. Познавательный интерес как фактор развития активности самостоятельности учения во время внеклассной работе по математике

§1. Некоторые теоретические подходы к определению понятия "познавательный интерес"

§2. Формирование познавательного интереса в обучении

§3. Формы и методы формирования познавательного интереса у школьников

§4. Внеклассная работа по математике как средство развития познавательного интереса

§5. Математический кружок как форма внеклассной работы по математике

Требования к организации кружкового занятия

§ 6. Анализ программ математических кружков

Глава II. Математический кружок для 5-6 классов как средство развития познавательного интереса

§1. Учебно-тематический план кружка

§2. Вводное занятие

§3. Признаки делимости

§4. Магические квадраты

§5. Решение задач методом с "конца". Решение задач на все действия с дробными числами

§6. Задачи на разрезание и перекраивание фигур

§7. Задачи на взвешивание и переливание

§8. Элементы комбинаторики. Принцип Дирихле

§9. Графы. Применение графов к решению задач

§10. Круги Эйлера

§11. Математические шифры

§12. Геометрия на спичках

§13. Фокусы

§ 14. Математическая регата

Глава I. Познавательный интерес как фактор развития активности самостоятельности учения во время внеклассной работе по математике

§1. Некоторые теоретические подходы к определению понятия "познавательный интерес"

Проблема интереса в современной науке представлена с различных позиций. В исследованиях М.Ф. Беляева, А.А. Невского изучается психологическая природа интереса; в работах Ю.К. Бабанского познавательный интерес выступает в основном как средство обучения. Познавательный интерес рассматривается В.Н. Мясищевым как отношение личности к предметам и явлениям окружающей действительности. Ряд авторов исследуют интерес как условие повышения продуктивности учебного процесса.

Приступая к рассмотрению проблемы развития познавательного интереса у детей среднего школьного возраста, мы считаем целесообразным, прежде всего, рассмотреть теоретические основы самого понятия "интерес".

В научной литературе, посвященной данной проблеме, можно встретить разнообразные, иногда противоречивые толкования этого понятия. Под познавательным интересом зачастую понимают различные состояния человека, всего лишь объединенные позитивной направленностью к его деятельности: увлечения, склонности, любопытство и другие. На смешение различных по содержанию понятий при определении познавательного интереса указывается в работах Л.И. Божович, Н.Г. Морозовой, Н.А. Беляевой.

Для более четкого определения ключевого для нашей работы понятия необходимо обратиться к психологическим и педагогическим исследованиям, специально посвященным изучению сущности интереса.

математический кружок познавательный интерес

Анализ литературы по проблеме показал, что в психологии существуют различные определения интереса. Так, С.И. Рубинштейн определил это понятие как "… сосредоточенность на определенном предмете мыслей, помыслов личности, вызывающая стремление ближе познакомиться с предметом, глубже в него проникнуть, не упускать из поля своего зрения".

В.А. Крутецкий дает следующее определение: "Интерес - это активная познавательная направленность человека на тот или иной предмет или явление действительности, связанная обычно с положительно эмоционально-окрашенным отношением к познанию объекта или к овладению той или иной деятельностью". В.А. Крутецкий считает, что интерес носит избирательный характер и влечет за собой тенденцию обращать внимание на объекты определенного рода.

Д.А. Кикнадзе считает, что интерес - это потребность, прошедшая стадию мотивации; сознательная направленность человека на удовлетворение познавательной потребности.

А.Н. Леонтьев, определяя сущность интереса, исходит из анализа структуры деятельности субъекта: "Интерес объективно выражается в направленности деятельности на те или иные цели"

М.Ф. Беляев в работе "Психология интереса" дает следующее определение интереса: "Интерес есть одна из психологических активностей, характеризующая как общая сознательная устремленность личности к объекту, проникнутая отношением близости к объекту, эмоционально насыщенная и влияющая на повышение продуктивности деятельности".

Это определение, на наш взгляд является наиболее полным, так как позволяет выделить следующие специфические признаки:

объективная отнесенность, из которой следует, что беспредметных интересов быть не может;

сознательное стремление к объекту, что отличает интерес от влечения;

эмоциональная насыщенность, указывающая на то, что удовлетворение интереса связано с положительными эмоциями, а невозможность удовлетворения интереса вызывает отрицательные эмоции;

благотворное влияние на продуктивность деятельности, что делает интерес особо ценным в педагогическом отношении.

Таким образом можно сделать вывод, что, несмотря на различные трактовки сущности интереса, большинство психологов относят интерес к категории направленности, то есть к стремлению личности к объекту или деятельности. Психологическое понятие "интерес" отображает множество значимых процессов от единичных до их совокупности.

Исходя из анализа психолого-педагогической литературы, мы считаем, что интерес выступает перед нами:

и как избирательная направленность психологических процессов человека на объекты и явления окружающего мира;

и как тенденция, стремление, потребность личности заниматься именно данной областью явлений, данной деятельностью, которая приносит удовлетворение;

и как мощный побудитель активности личности, под влиянием которого все психологические процессы протекают особенно интенсивно и напряженно, а деятельность становится увлекательной и продуктивной;

и, наконец, как особое избирательное отношение к окружающему миру, к его объектам, явлениям, процессам.

По предметной направленности интересов вполне правомерно различать интересы художественные, спортивные, технические и другие.

Одной из самых значительных областей общего феномена "интерес" является познавательные интересы, имеющие особое значение в школьном возрасте. Под познавательным интересом различные его исследователи понимают особую избирательную направленность личности на процесс познания, избирательный характер которой выражается в той или иной предметной области (С.Л. Рубинштейн); стремление человека обращать на что-то внимание, познавать какие-либо предметы и явления (Ф.Н. Гоноболин); особое избирательное, наполненное активным замыслом, сильными эмоциями, устремлениями отношение личности к окружающему миру, к его объектам, явлениям, процессам (Г.И. Щукина); эмоционально окрашенную потребность, прошедшую стадию мотивации и придающую деятельности человека увлекательный характер (И.Ф. Харламов).

Для более глубокого изучения понятия познавательного интереса рассмотрим различные подходы к его классификации, к выделению уровней познавательного интереса.

Интерес к какому-нибудь предмету, к занятию, отрасли знаний, как и внимание, может быть прямым (непосредственным) и косвенным (опосредованным). В случае прямого интереса человека привлекает сам предмет, деятельность определенного вида. Но нередко случается и так, что прямого интереса, например, к математике, ученик не испытывает, но он интересуется физикой и понимает, что без математики в этой области ничего сделать нельзя. В этом случае к математике проявляется косвенный интерес. Знание учителем непосредственных и косвенных интересов учащихся помогает осуществлению индивидуального подхода.

В развитии познавательного интереса можно выделить ряд уровней: любопытство, любознательность, собственно познавательный интерес, творческий интерес. Эти уровни определяют разную степень избирательной направленности, избирательного отношения к предмету и, соответственно, степень влияния познавательного интереса на личность.

Любопытство - элементарная стадия познавательного интереса. Оно обусловлено чисто внешними обстоятельствами, привлекающими внимание человека. На этой стадии отсутствует подлинное стремление к познанию, но любопытство может быть его начальным толчком. Человек при этом является пассивным объектом внешнего воздействия. Любопытство - есть реакция на изменение обстановки, на появление нового в окружающем мире.

Интерес этого уровня - поверхностный, фрагментарный, ситуативный, связанный с переживанием своего отношения к предмету в данный момент. Любопытство особенно характерно для младшего школьного возраста, когда вступающему в жизнь интересно все. Но интерес этот неглубок. Любопытство в среднем школьном возрасте совсем не исчезает. Оно приобретает другую форму. Поле его действия ограничивается. Появляется более высокий уровень познавательного интереса - любознательность. Там, где для любопытства уже нет материала, для любознательного только начинается работа. Это - работа мысли; разбуженной случайным фактом. Это стремление к более глубокому анализу явлений действительности, к познанию новой неизвестной закономерности. Для любознательного при решении задачи исчезает время и пространство.

На этапе любознательности интерес еще в полной мере не освободился от интереса к фабуле, к описаниям. И тем не менее он уже носит поисковый характер, связанный с желанием проникнуть в более глубокие основания знаний. При этом импульс активности исходит уже не со стороны, а от самого человека, что в корне меняет характер интереса. Такой интерес не угасает с окончанием той или иной ситуации, он заставляет все глубже погружаться в интересующую деятельность. Привлекательной для ученика становится сама деятельность. Постоянное погружение в деятельность предполагает наличие возможностей самостоятельной работы. Ученик становится субъектом деятельности. А познавательный интерес с уровня любознательности переходит на более высокий уровень познавательного интереса.

Под творческим интересом понимают такой уровень познавательного интереса, когда ученик стремится осуществить самостоятельную, творческую, поисковую деятельность. Это, в основном, узкий интерес к определенной отрасли знаний, переходящий в профессиональный интерес.

В разные периоды жизни можно выделить предпочтительный уровень развития познавательного интереса, хотя переход с более низкого уровня на более высокий очень индивидуален.

У младших школьников этот интерес имеет яркую эмоциональную окраску. Это интерес к впечатлениям, описаниям, наблюдениям. Познавательный интерес школьников среднего возраста в значительной мере определяется новообразованием этого возраста - стремлением к взрослению, стремлением к самостоятельности. Познавательный процесс в этом возрасте, хотя не освободился еще от интереса к фабуле, но уже связан с желанием проникнуть в основание знаний, в существующие закономерности.

§2. Формирование познавательного интереса в обучении

Однажды известного физика Альберта Эйнштейна спросили: “Как делаются открытия? ” Эйнштейн ответил: “А так: все знают, что вот этого нельзя. И вдруг появляется такой человек, который не знает, что этого нельзя. Он и делает открытие”. Конечно, это была лишь шутка. Но все же, вероятно, Эйнштейн вкладывал в нее глубокий смысл. Может быть, он намекал в том числе и на собственное открытие более правильной и точной картины мироздания, изложенное им в знаменитой теории относительности. Может быть, он из озорства гения высказал серьезную мысль в шутливой форме. Дело не в том, чтобы “не знать”. Знать надо! А дело в том, чтобы “сомневаться”, не брать на веру все, чему учили деды. И вдруг появляется человек, которого не останавливает инерция привычных представлений. Вот он и делает открытие.

Актуальность формирования познавательного интереса обусловлена тем, что системы образования в любой стране призваны способствовать реализации основных задач развития общества, так как именно школа, а затем и вуз готовят человека к активной деятельности в разных сферах жизни общества, поэтому способность образовательного учреждения гибко реагировать на актуальные запросы общества имеет важное значение. Развитие современного общества, внедрение научных идей в школьную практику требуют особого внимания к проблемам обучения и воспитания школьников, адекватной реакции учителя на происходящие изменения.

Уже в школе нужно привить ученику стремление к постоянному пополнению своих знаний с помощью самообразования, воспитать у него внутреннее побуждение расширять свой общий и профессиональный кругозор, чтобы стать специалистом, который способен не только быть хорошим исполнителем задачи, но и совершенствовать свой труд, поднимать его на уровень творческой деятельности. Реализовывать эту задачу необходимо в условиях стремительного "обновления" циркулирующей в обществе информации, когда одни данные устаревают и перестают использоваться, другие приходят им на смену и занимают прочное место как в различных профессиональных областях, так и в повседневной жизни человека.

Следовательно, актуальной проблемой современного образования является формирование и развитие познавательных интересов учащегося, личность которого является центральной фигурой образовательного процесса, и так как именно интерес к познавательной деятельности, воспитанный в школе, впоследствии станет основой для развития способности ученика в любых условиях идти в ногу со временем. "Познавательный интерес можно назвать избирательной деятельностью человека на познание предметов, явлений, событий окружающего мира, активизирующей психические процессы, деятельность человека, его познавательные возможности". В настоящее время изменения в нашем обществе сопровождаются сменой приоритетов в сфере социальных ценностей, что, в свою очередь, актуализирует потребность в личностно-ориентированном образовании, исходным моментом которого является создание условий для проявления субъективности учащегося, и в частности, формирования познавательного интереса. Потребность познать мир, объединить представления о себе и мире; освоить общекультурные человеческие ценности с целью обоснования собственной жизненной концепции - это характерные черты среднего школьного возраста (Л.И. Божович); познавательный интерес для этого периода имеет специфические особенности (Ф.К. Савина).

Познавательный интерес, как и всякая черта личности и мотив деятельности школьника, развивается и формируется в деятельности, и, прежде всего, в учении. Формирование познавательных интересов учащихся в обучении может происходить по двум основным каналам, с одной стороны само содержание учебных предметов содержит в себе эту возможность, а с другой - путем определенной организации познавательной деятельности учащихся. Первое, что является предметом познавательного интереса для школьников - это новые знания о мире. Вот почему глубоко продуманный отбор содержания учебного материала, показ богатства, заключенного в научных знаниях, являются важнейшим звеном формирования интереса к учению. Каковы же пути осуществления этой задачи? Прежде всего, интерес возбуждает и подкрепляет такой учебный материал, который является для учащихся новым, неизвестным, поражает их воображение, заставляет удивляться.

Удивление - сильный стимул познания, его первичный элемент. Удивляясь, человек как бы стремится заглянуть вперед. Он находится в состоянии ожидания чего-то нового. Но познавательный интерес к учебному материалу не может поддерживаться все время только яркими фактами, а его привлекательность невозможно сводить к удивляющему и поражающему воображение. Еще К.Д. Ушинский писал о том, что предмет, для того чтобы стать интересным, должен быть лишь отчасти нов, а отчасти знаком. Новое и неожиданное всегда в учебном материале выступает на фоне уже известного и знакомого. Вот почему для поддержания познавательного интереса важно учить школьников умению в знакомом видеть новое. Такое преподавание подводит к осознанию того, что у обыденных, повторяющихся явлений окружающего мира множество удивительных сторон, о которых он сможет узнать на уроках. И то, почему растения тянутся к свету, и о свойствах талого снега, и о том, что простое колесо, без которого сейчас не обходится ни один сложный механизм, является величайшим изобретением. Все значительные явления жизни, ставшие обычными для ребенка в силу своей повторяемости, могут и должны приобрести для него в обучении неожиданно новое, полное смысла, совсем иное звучание. И это обязательно явится стимулом интереса ученика к познанию. Именно поэтому учителю необходимо переводить школьников со ступени его чисто житейских, достаточно узких и бедных представлений о мире - на уровень научных понятий, обобщений, понимания закономерностей. Интересу к познанию содействует также показ новейших достижений науки. Сейчас, больше чем когда-либо, необходимо расширять рамки программ, знакомить учеников с основными направлениями научных поисков, открытиями. Далеко не все в учебном материале может быть для учащихся интересно. И тогда выступает еще один, не менее важный источник познавательного интереса - сам процесс деятельности. Чтобы возбудить желание учиться, нужно развивать потребность ученика заниматься познавательной деятельностью, а это значит, что в самом процессе ее школьник должен находить привлекательные стороны, чтобы сам процесс учения содержал в себе положительные заряды интереса. Путь к нему лежит, прежде всего, через разнообразную самостоятельную работу учащихся, организованную в соответствии с особенностью интереса.

§3. Формы и методы формирования познавательного интереса у школьников

Формирование и развитие познавательных интересов - часть широкой проблемы воспитания всесторонне развитой личности. Если определить эту проблему более конкретно, то ее можно сформулировать так: должен быть путь, с помощью которого можно, добиваясь полноценного усвоения учащимися школьной программы, обеспечивать развитие их познавательных возможностей, не допуская при этом перегрузки. Именно эта задача наиболее остро стоит перед школой, т.е. школа должна найти оптимальные пути ее решения.

Условия, соблюдение которых способствует формированию, развитию и укреплению познавательного интереса школьников:

·              максимальная опора на активную мыслительную деятельность учащихся. Главной почвой для развития познавательных сил и возможностей учащихся, как и для развития, подлинно познавательного интереса, являются ситуации решения познавательных задач, ситуации активного поиска, догадок, размышления, ситуации мыслительного напряжения, ситуации противоречивости суждений, столкновений различных позиций, в которых необходимо разобраться самому, принять решение, встать на определённую точку зрения.

·              учебный процесс должен проходить на оптимальном уровне развития учащихся. В реальном процессе обучения учителю приходится иметь дело с тем, чтобы постоянно обучать учащихся множеству умений и навыков, в постоянном усложнении учебного труда, в овладении всё более сложными и более совершенными умениями, позволяющими решать более трудные задачи познания, состоит суть развивающего обучения, неуклонно укрепляющего познавательные силы, интерес и стремления школьника.

·              создание благоприятной эмоциональной атмосферы познавательной деятельности учащихся.

·              благоприятное общение в учебном процессе. Стремление к общению с товарищами, с учителем само по себе может быть сильным мотивом учения и в то же время способствовать укреплению познавательного интереса.

Специальные исследования, посвященные проблеме формирования познавательного интереса, показывают, что интерес во всех его видах и на всех этапах развития характеризуется по крайней мере тремя обязательными моментами:

) положительной эмоцией по отношению к деятельности,

) наличием познавательной стороны этой эмоции,

) наличием непосредственного мотива, идущего от самой деятельности (Г.И. Щукина, Н.Г. Морозова).

Отсюда следует, что в процессе обучения важно обеспечивать возникновение положительных эмоций по отношению к учебной деятельности, к ее содержанию, формам и методам осуществления. Эмоциональное состояние всегда связано с переживанием душевного волнения: отклика, сочувствия, радости, гнева, удивления. Именно поэтому к процессам внимания, запоминания, осмысливания в таком состоянии подключаются глубокие внутренние переживания личности, которые делают эти процессы интенсивно протекающими и оттого более эффективными в смысле достигаемых целей.

Одним из приемов, входящих в метод эмоционального стимулирования учения, можно назвать прием создания на уроке ситуаций занимательности - введение в учебный процесс занимательных примеров, опытов, парадоксальных фактов. Подбор таких занимательных фактов вызывает неизменный отклик у учеников. Часто школьникам самим поручается подбирать такие примеры.

Многие учителя используют для повышения интереса к учению анализ отрывков из художественной литературы, посвященных жизни и деятельности выдающихся ученых и общественных деятелей. Успешно применяются и такие приемы повышения занимательности обучения, как рассказы о применении в современных условиях тех или иных предсказаний научных фантастов, показ занимательных опытов. Передовые учителя умело применяют метод и входящие в него приемы создания эмоционально-нравственной ситуации. Прежде всего они используют прием создания ситуаций нравственных переживаний.

В роли приема, входящего в методы формирования интереса к учению, выступают и занимательные аналогии.

Эмоциональные переживания вызывают путем применения приема удивления. Необычность приводимого факта, парадоксальность опыта, демонстрируемого на уроке - все это при умелом сопоставлении данных, при убедительности этих примеров неизменно вызывает глубокие эмоциональные переживания у учеников.

Одним из приемов стимулирования является сопоставление научных и житейских толкований отдельных природных явлений.

Для создания эмоциональных ситуаций в ходе уроков большое значение имеет художественность, яркость, эмоциональность речи учителя. Без всего этого речь учителя, конечно, остается информативно полезной, но она не реализует в должной мере функцию стимулирования учебно-познавательной деятельности учеников. В этом, между прочим, еще раз проявляется отличие методов организации познавательной деятельности от методов ее стимулирования.

Входящие в методы формирования интереса приемы художественности, образности, яркости, занимательности, удивления, нравственного переживания вызывают эмоциональную приподнятость, которая в свою очередь возбуждает положительное отношение к учебной деятельности и служит первым шагом на пути к формированию познавательного интереса. Вместе с тем среди основных моментов, характеризующих интерес, было подчеркнуто не просто возбуждение эмоциональности, но наличие у этих эмоций собственно показательной стороны, которая проявляется в радости познания.

Основным источником интересов к самой учебной деятельности является прежде всего ее содержание. Для того чтобы содержание оказало особенно сильное стимулирующее влияние, оно должно отвечать целому ряду требований, сформулированных в принципах обучения (научность, связь с жизнью, систематичность и последовательность, комплексное образовательное, воспитывающее и развивающее влияние и т.д.) Однако имеются и некоторые специальные приемы, направленные на повышение стимулирующего влияния содержания обучения. К ним в первую очередь можно отнести создание ситуации новизны, актуальности, приближения содержания к самым важным открытиям в науке, технике, к достижениям современной культуры, искусства, литературы, к явлениям общественно-политической внутренней и международной жизни. С этой целью учителя подбирают специальные примеры, факты, иллюстрации, которые в данный момент вызывают особый интерес у всей общественности страны, публикуются в печати, сообщаются по телевидению и радио. В этом случае ученики значительно ярче и глубже осознают важность, значимость изучаемых вопросов и оттого относятся к ним с большим интересом.

Ценным методом стимулирования интереса к учению можно назвать метод познавательных игр, который опирается на создание в учебном процессе игровых ситуаций. Игра давно уже используется как средство возбуждения интереса к учению. В практике работы учителей используются настольные игры с познавательным содержанием.

К методам стимулирования и мотивации учения мы относим также метод создания ситуаций познавательного спора. Известно, что в споре рождается истина. Но спор вызывает и повышенный интерес к теме. Некоторые учителя умело используют этот метод активизации учения. Они, во-первых, умело используют исторические факты борьбы различных научных точек зрения по той или иной проблеме. Научные споры ведутся и на современном этапе развития науки. Включение учеников в ситуации научных споров не только углубляет их знания по соответствующим вопросам, но и невольно приковывает их внимание к теме, а на этой основе вызывает новый прилив интереса к учению.

Однако ситуации спора, учебные дискуссии учителя создают и в момент изучения обычных учебных вопросов на любом уроке. Для этого, например, специально предлагается ученикам высказать свои мнения о причинах того или иного явления, обосновать ту или иную точку зрения. Здесь традиционным стал уже вопрос типа: "А кто думает иначе?" И если такой прием вызывает спор, то ученики невольно распределяются на сторонников и противников того или иного объяснения и с интересом ждут аргументированного заключения учителя. Так учебный спор выступает в роли метода стимулирования интереса к учению.

Все чаще можно встретить в практике работы школы и специально организуемые на уроках учебные дискуссии уже не игрового характера. В этом случае ученики выступают как бы сторонниками различных концепций. Естественно, нельзя ожидать, что школьники выскажут окончательное решение о справедливости той или иной точки зрения. Этот прием используется для того, чтобы вызвать повышенный интерес к более углубленному изучению тех или иных вопросов. Особенно широко применяются учебные дискуссии на факультативных занятиях по углубленному изучению различных учебных предметов.

В качестве приема стимулирования учения в ряде школ используется анализ жизненных ситуаций. Этот метод обучения непосредственно стимулирует учение за счет максимально возможной конкретизации знаний.

Одним из действенных приемов стимулирования интереса к учению является создание в учебном процессе ситуаций успеха у школьников, испытывающих определенные затруднения в учебе. Известно, что без переживания радости успеха невозможно по-настоящему рассчитывать на дальнейшие успехи в преодолении учебных затруднений. Вот почему опытные учителя так подбирают для учеников задания, чтобы те из них, которые нуждаются в стимулировании, получили бы на соответствующем этапе доступное для них задание, а затем уже переходили бы к выполнению более сложных упражнений. Например, с этой целью используются специальные сдвоенные задания, одно из которых вполне доступно для ученика и создает базу для последующих усилий по решению более сложной задачи. Ситуации успеха создаются и путем дифференциации помощи школьникам в выполнении учебных заданий одной и той же сложности. Так, слабоуспевающим школьникам могут быть даны карточки-консультации, планы предстоящего ответа, которые позволяют им на данном уровне подготовленности справиться с соответствующим заданием, а затем уже выполнить упражнение, аналогичное первому, самостоятельно. Ситуации успеха организуются учителем и путем поощрения промежуточных действий школьников, т.е. путем специального подбадривания его на новые усилия. Важную роль в создании ситуации успеха играет обеспечение благоприятной морально-психологической атмосферы в ходе выполнения тех или иных учебных заданий. Благоприятный микроклимат во время учебы снижает чувство неуверенности, боязни. Состояние тревожности при этом сменяется состоянием уверенности. Итак, мы весьма кратко охарактеризовали группу методов и входящих в них разнообразных приемов стимулирования интереса к учению.

Основной побудительной силой деятельности личности является потребности. На основании потребностей возникает и развивается интерес. Потребности и интерес побуждают человека к деятельности, к приобретению новых знаний и умений.

Избирательная направленность характеризуется постоянным стремлением к познанию, к новым, более полным и глубоким знаниям. Систематически укрепляясь и развиваясь, познавательный интерес становится основой положительного отношения к учению.

Познавательный интерес носит поисковый характер. Под его влиянием у человека постоянно возникают вопросы, ответы на которые он сам постоянно и активно ищет. При этом поисковая деятельность школьника совершается с увеличением, он испытывает эмоциональный подъем, радость от удачи. Познавательный процесс положительно влияет не только на процесс и результат деятельности, но и на протекание психических процессов - мышления, воображения, памяти, внимания, которые под влиянием познавательного интереса приобретают особую активность и направленность.

Познавательный интерес при правильной педагогической организации деятельности учащихся и систематической и целенаправленной воспитательной деятельности может и должен стать устойчивой чертой личности школьника и оказывает сильное влияние на его развитие.

В настоящее время исследования ученых убедительно показали, что возможности людей, которых обычно называют талантливыми, гениальными - не аномалия, а норма. Задача заключается лишь в том, чтобы раскрепостить мышление человека, повысить коэффициент его полезного действия, наконец, использовать те богатейшие возможности, которые дала ему природа, и о существовании которых многие подчас и не подозревают.

§4. Внеклассная работа по математике как средство развития познавательного интереса

Отношение учащихся к тому или иному предмету определяется различными факторами: индивидуальными особенностями личности, особенностями самого предмета, методикой его преподавания. По отношению к математике всегда имеются некоторые категории учащихся, проявляющие повышенный интерес к ней; занимающиеся ею по мере необходимости и особенного интереса к предмету не проявляющие; ученики, считающие математику скучным, сухим и вообще не любимым предметом. Поэтому уже с первых классов начинается резкое расслоение коллектива учащихся: на тех, кто легко и с интересом усваивают программный материал по математике, на тех, кто добивается при математике лишь удовлетворительных результатов, и тех, кому успешное изучение математики дается с большим трудом. Это приводит к необходимости индивидуализации обучения математике, одной из форм которой является внеклассная работа.

Под внеклассной работой по математике понимают необязательные систематические занятия учащихся с преподавателем во внеурочное время.

Одна из основных причин сравнительно плохой успеваемости по математике - слабый интерес многих учащихся к этому предмету. Интерес к предмету зависит, прежде всего, от качества учебной работы на уроке, В то же время с помощью продуманной системы внеурочных занятий можно значительно повысить интерес школьников к математике.

Внеклассная работа имеет целью оказывать содействие повышению уровня знаний, закреплению умений и привычек, приобретенных учениками на уроках математики, развивать математические способности, сообразительность, изобретательность, обнаруживать наиболее одаренных и способных детей и оказывать содействие их дальнейшему развитию.

Систематической внеклассной работой по математике должно быть охвачено большинство школьников, в ней должны быть заняты не только ученики, увлеченные математикой, но и те учащиеся, которые не тяготеют еще к математике, не выявили своих способностей и наклонностей. Это особенно важно в младшем и среднем возрасте, когда еще формируются, а иногда определяются постоянные интересы и склонности к тому или иному предмету. Именно в этот период нужно стремиться раскрыть притягательные стороны математики перед всеми учащимися, используя для этой цели все возможности, в том числе и особенности внеклассных занятий.

Внеклассная работа по математике является составной частью учебного процесса, естественным продолжением работы на уроке. Она отличается от классной работы тем, что строится на принципе добровольности. Государственных программ по внеклассной работе нет, как нет и норм оценок. Для внеклассной работы учитель подбирает материал повышенной трудности или материал, дополняющий изучение основного курса математики, но с учётом преемственности с классной работой. Здесь может широко использоваться упражнения в занимательной форме.

Несмотря на свою необязательность для школы, внеурочные занятия по математике заслуживают самого пристального внимания каждого учителя, преподающего этот предмет, так как часы на основной курс математики сокращаются.

Учитель может на внеклассных занятиях по математике в максимальной мере учесть возможности, запросы и интересы своих учеников. Внеклассная работа по математике дополняет обязательную учебную работу по предмету и должна, прежде всего, способствовать более глубокому усвоению учащимися материала, предусмотренного программой.

Главное назначение внеклассной работы - не только расширение и

углубление теоретического материала, изученного на уроках, но и развитие

умений применять полученные на уроках знания к решению нестандартных

задач, воспитание у учеников определенной культуры работы над задачей. Дети нуждаются в том, чтобы первоначальное знакомство с математическими истинами носило не сухой и скучный характер, а пробуждало бы интерес к науке, которую большинство считает сухой и неинтересной.

Внеклассная работа является неотъемлемой частью учебно-воспитательной работы в школе. Она способствует углублению знаний учащихся, развитию их дарований, логического мышления, расширяет кругозор. Кроме того, внеклассная работа по математике имеет большое воспитательное значение, ибо цель её не только в том, чтобы осветить какой-либо узкий вопрос, но и в том, чтобы заинтересовать учащихся предметом, вовлечь их в серьёзную самостоятельную работу. Изучение любой науки - тяжелый труд, требующий усердия, внимания, трудолюбия, а иногда и заучивания материала. В полной мере это относится и к математике - науке точной, "сухой" и часто нелюбимой детьми. Поэтому желательно превратить этот тяжелый труд в игру. Разумеется, в серьезную игру, направленную на достижение важной и серьезной цели - пробуждения у детей интереса и любви к математике!

Существуют следующие виды внеклассной работы по математике:

.        Работа с учащимися, отстающими от других в изучении программного материала;

2.      Работа с учащимися, проявляющими к изучению математики повышенный интерес и способности;

.        Работа с учащимися по развитию интереса в изучении математики.

В третьем случае задачей учителя заключается в том, чтобы заинтересовать учащихся математикой.

В связи с указанными выше видами внеклассной работы по математике можно выделить в ней следующие цели:

·        Своевременная ликвидация (и предупреждение) имеющихся у учащихся пробелов в знаниях и умениях по курсу математики;

·        Пробуждение и развитие устойчивого интереса учащихся к математике и её приложениям;

·        Расширение и углубление знаний учащихся по программному материалу;

·        Оптимальное развитие математических способностей у учащихся и привитие учащимся определённых навыков научно - исследовательского характера;

·        Воспитание высокой культуры математического мышления;

·        Развитие у школьников умения самостоятельно и творчески работать с учебной и научно - популярной литературой;

·        Расширение и углубление представлений учащихся о практическом значении математики;

·        Воспитание у учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной;

·        Установление более тесных деловых контактов между учителем математики и учащимися и на этой основе более глубокое изучение познавательных интересов и запросов школьников;

·        Создание актива, способного оказать учителю математики помощь в организации эффективного обучения математике всего коллектива данного класса.

Предполагается, что реализация этих целей частично осуществляется на уроках. Однако в процессе классных занятий, ограниченных рамками учебного времени и программы, это не удаётся сделать с достаточной полнотой. Поэтому окончательная и полная реализация этих целей переносится на внеклассные занятия этого вида.

Учителя математики, которые работают творчески, с огоньком, большое значение в своей работе отводят формированию познавательных интересов в процессе обучения, поиску методов, форм, средств, приемов, побуждающих учащихся к активной мыслительной деятельности. Добиться, чтобы большинство школьников испытали и осознали притягательные стороны математики, ее возможности в совершенствовании умственных способностей, полюбили думать, преодолевать трудности, - сложная, но очень нужная и важная сторона обучения математике. Возникновение интереса к математике у большинства учащихся зависит в большей степени от методики его преподнесения, оттого, насколько тонко и умело будет построена учебная работа.

Дышинский Е.А. выделяет три основные задачи внеклассной работы по математике:

·        Повысить уровень математического мышления, углубить теоретические знания и развить практические навыки учащихся, проявивших математические способности;

·        Способствовать возникновению интереса у большинства учеников, привлечение некоторых из них в ряды "любителей математики";

·        Организовать досуг учащихся в свободное от учебы время.

За последние десятилетия в математике возникли новые направления, имеющие не только большое практическое значение, но и большой познавательный интерес. Экспериментальные исследования, проведенные в ряде школ, показали, что многие вопросы так называемой современной математики (в объеме своих начальных понятий) вполне доступны и весьма интересны для изучения их учащимися, начиная с 5 класса. На это справедливо указывал Н.Я. Виленкин. Предлагая на внеклассных занятиях по математике знакомить учащихся с элементами вычислительной математики, производной и интегралом, основными понятиями математической логики, современной алгебры, комбинаторики, теории информации и т.д.Н.Я. Виленкин рекомендует обращать внимание и на практическую направленность внеклассных занятий и ее занимательность, которые можно реализовать рассмотрением соответствующих задач.

В процессе учебной деятельности большую роль играет уровень развития познавательных процессов: мышления, внимания, памяти, воображения, речи; а так же способностей учащихся. Их развитие и совершенствование повлечёт за собой и расширение познавательных возможностей детей. Для этого необходимо включать ребёнка в доступную его возрасту деятельность. Деятельность должна вызывать у школьника сильные и устойчивые положительные эмоции, удовольствие; она должна быть по возможности творческой; ученик должен преследовать цели, всегда немного превосходящие его возможности, то есть идёт активное развитие познавательного интереса учащихся. Этому содействуют различные формы внеклассной работы по математике.

Вместе с тем "Между учебно-воспитательной работой, проводимой на уроках, и внеклассной работой существует тесная взаимосвязь: учебные занятия, развивая у учащихся интерес к знаниям, содействуют развертыванию внеклассной работы, и, наоборот, внеклассные занятия, позволяющие учащимся применить знания на практике, расширяющие и углубляющие эти знания, повышают успеваемость учащихся и их интерес к учению. Однако внеклассная работа не должна дублировать учебную работу, иначе она превратится в обычные дополнительные занятия.

Выделяют следующие формы проведения внеклассной работы с учащимися:

математические кружки;

математические викторины, конкурсы и олимпиады;

математические вечера; математические экскурсии;

математические игры;

математические рефераты и сочинения; школьная математическая печать.

Указанные формы часто пересекаются и поэтому трудно провести между ними резкие границы. Более того, элементы многих форм могут быть использованы при организации работы по какой либо одной из них. Например, при проведении математического вечера можно использовать викторины, конкурсы, доклады и т.д.

При проведении внеклассной работы по математике регулярно используются системы специальных задач и заданий, которые направлены на развитие познавательных возможностей и способностей, на расширение математического кругозора школьников. А также способствуют математическому развитию, повышают качество математической подготовленности, позволяют детям более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни. При проведении внеклассной работы по математике учитель опирается на знания, которые уже есть у ученика, ученик же открывает для себя что-то новое, неизведанное. Таким образом, внеклассная работа по математике выступает средством развития познавательного интереса учащихся через свои цели, задачи, содержание и формы проведения.

§5. Математический кружок как форма внеклассной работы по математике

"Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным. "

Блез Паскаль

Математические олимпиады обычно посвящаются решению задач, но возможны олимпиады по вычислению на счетах, в навыках быстрых и безошибочных подсчетов. Проведение олимпиад должно быть предусмотрено планом работы учителя. Участие детей носит добровольный характер. Олимпиада проводится в 3 тура. В начале полугодия учитель намечает ряд задач, которые решаются во внеурочное время дополнительно к задачам, решаемым по программе. Когда задачи решены, учитель организует проверочную письменную работу (1-3 задачи). К работе во втором туре допускаются ученики, решившие 2-3 задачи из трех. Они получают новый набор задачи по истечении 1-1,5 месяца снова выполняют письменную проверочную работу. Ученики, справившиеся с решением 2-3 задач, готовятся к третьему туру, на котором определяются победители олимпиады и проводится премирование.

Математические конкурсы и викторины относятся к наиболее легко организуемым видам математических соревнований. Для конкурса учитель намечает тему, дает списки задач, указывает, что нужно повторить и назначает срок состязания. До конкурса ученики не знают тех задач и вопросов, с которыми они встретятся на состязании.

При проведении викторины ученики заблаговременно задания не получают, а готовятся к ответам экспромтом. В проведении викторины может принять участие каждый желающий. Викторины бывают слуховые (ответы на вопрос), зрительные (по рисункам и чертежам) и смешанные. Содержанием их являются теоретические вопросы и занимательные задачи.

Командные соревнования проводятся между параллельными классами или внутри класса. Они могут охватывать всех учащихся или одинаковые по численности (8-10 человек) команды от каждого класса. Если командные состязания проводятся в одном классе, команды выделяются от каждого звена (по 2-3 человека). В команды выделяются ученики с учетом мнения детей.

Каждой команде предлагается в определенный срок (30-45 минут) решить несколько задач и примеров. По истечении назначенного срока работы сдаются учителям, которые устанавливают победителя в командных соревнованиях.

Математические вечера вызывают большой интерес у учащихся. Они обычно являются заключительным этапом при проведении тематической недели. Хотя может проводиться и как самостоятельная разновидность внеклассной работы.

В школе наиболее удобно проводить математические вечера для учащихся параллельных классов.

Подготовку к вечеру нужно начать заранее, лучше всего за полтора - два месяца до вечера. Для руководства всей подготовительной работой выделяется комиссия, в которую входит учитель математики и несколько (4-5) учащихся. Члены комиссии, посоветовавшись с другими учащимися и взвесив возможности, составляют план вечера и выделяют для каждого участка ответственного и исполнителей (с их согласия). Комиссия устанавливает крайний срок, к которому вся подготовительная работа должны быть завершена. Проверку качества подготовки каждого выступления тоже следует поручать учащимся, хотя за всем придется следить самому учителю.

Учитывая то, что основная цель вечера - повышение интереса к математике, желательно привлечь к его организации как можно больше учащихся. Если ученику будет поручена подготовка какого-то номера программы, то его интерес к вечеру значительно возрастет.

За несколько дней до вечера вывешивается красочное объявление о месте и времени проведения вечера и его программе. На вечер обычно приглашаются учащиеся других классов той же школы или параллельных классов соседней школы.

Программа вечера может быть различной по своему содержанию. Важно, чтобы тематика вечера была тесно связано с изучаемым программным материалом. Это будет способствовать расширению и углублению математических знаний учащихся. В программу вечера, кроме докладов, включаются рассказы, сообщения, математические софизмы, фокусы, развлечения, инсценировки, математическая световая газета.

Длительность вечера - обычно два-три часа.

Математические экскурсии. Математические экскурсии - исключительно интересная, но сравнительно редко применяемая форма внеурочных занятий. Не следует думать, что они сводятся только к геодезическим работам на местности. Во время экскурсии ученик видит, где на практике встречаются и применяются различные геометрические фигуры, изученные им в школе, знакомится с применениями математики в различных областях народного хозяйства. На экскурсии ученик видит немало случаев, когда приходится использовать известные ему формулы для вычисления тех или иных геометрических величин (длин, площадей, объемов). Хорошо поставленные экскурсии укрепят уверенность учащегося в том, что с математикой действительно сталкиваешься на каждом шагу, что "математика всюду", что она действительно необходима человечеству. У учащихся значительно повышается интерес к этому предмету. Хорошо подготовленные экскурсии приводят к лучшему пониманию учащимися отдельных вопросов курса математики.

В их планировании и проведении полезно соблюдать следующие рекомендации:

. Организация и проведение экскурсий слагаются из следующих этапов:

) подготовка к экскурсии учителя и составление плана,

) подготовка детей - участников экскурсии,

) работа детей во время экскурсии,

) подведение итога экскурсии и использование наблюдений и материалов, собранных во время экскурсии.

. Руководителю экскурсии заранее следует посетить место проведения экскурсии, осмотреть объекты, побеседовать с теми специалистами, которые помогут провести экскурсию.

. В плане проведения экскурсии определяют ее цели и организационные вопросы. Все это потом доводится до сведения учащихся в виде подробного инструктажа (куда и зачем идем, что будем делать, что и как записывать и т.п.).

. В ходе экскурсии руководитель контролирует выполнение учащимися поставленных перед ними задач и занятость каждого участника.

. При подведении итогов, кроме прочего, выясняют, что нового узнали дети.

Математические игры. Большую роль на внеклассных занятиях по математике играют игры, главным образом дидактические. Основная их ценность в том, что они возбуждают интерес детей, усиливают эффект самого обучения. Создание игровых ситуаций приводит к тому, что дети увлечены игрой и незаметно для себя и без особого труда и напряжения приобретают определенные знания, умения и навыки. Игра делает отдельные элементы внеклассной работы по математике эмоционально насыщенными, вносит бодрый настрой в детский коллектив, помогает эстетически воспринимать ситуацию, связанную с математикой: праздничное оформление класса, красочные оригинальные газеты, красоту древней легенды, включающей задачу, драматизацию математического задания, наконец, стройность мыслей при решении логических задач. Игра так же содействует воспитанию дисциплинированности, так как проводится по правилам.

Чтобы игра была наиболее эффективной, необходимо, чтобы учитель тоже включался в игру. Но не следует забывать, что игра это не самоцель, а средство для развития интереса к математике. Поэтому математическая сторона должна выдвигаться на передний план. Однако при проведении математических игр учителю необходимо соблюдать некоторые правила:

·        Игра не должна вызывать слишком бурной реакции детей.

·        Дидактический материал должен быть прост в изготовлении и удобен в использовании.

·        Если игра предполагает соревнование команд, то должен быть контроль и открытый учет результатов.

·        Дети должны активно участвовать в игре, а не бездействовать в длительном ожидании.

·        Легкие игры должны чередоваться с более трудными. В конце должна быть проведена наиболее легкая и живая игра.

·        Если на нескольких занятиях проводятся игры, связанные со сходными мыслительными действиями, то по содержанию математического материала должен соблюдаться принцип ¾ от простого к сложному, от конкретного к абстрактному.

·        Подвижные игры должны чередоваться со спокойными.

·        Игровой характер проведения внеклассных занятий по математике должен иметь определенную меру.

·        Игры имеют познавательное значение, поэтому на первом плане должны оказаться умственные задания, для решения которых в мыслительной деятельности должны использоваться сравнение, анализ и синтез, суждения и умозаключения. Надо предоставлять детям возможность высказаться.

·        В процессе игры должно быть выполнено определенное законченное действие, решено конкретное задание, а после игры сделан вывод.

Школьная математическая печать. Полезной формой внеклассной работы является также стенная математическая печать. Важно, чтобы она была действительной, т.е. содержащиеся в ней материалы использовались активно.

Важное место во внеклассной работе по математике может занять изготовление учащимися различных моделей и наглядных пособий. Этот вид работы имеет большое воспитательное значение, кроме того, в процессе изготовления этих пособий учащиеся могут связать изучение математики с выработкой трудовых навыков. Желательно, чтобы подготовительные модели и пособия использовались в учебном процессе.

Для выпуска математической стенгазеты не обязательно наличие математического кружка. Иногда математическая стенгазета выпускается в период организации кружка, когда нужно привлечь внимание учащихся по кружку. Специальный номер математической стенгазеты выпускается к школьному математическому вечеру.

Однако мы будем ориентироваться на тот наиболее важный и наиболее реальный случай, когда газета выходит как орган кружка. Основная цель такой газеты - пропаганда математических знаний среди учащихся, не состоящих в кружке, повышение их интереса к математике, привлечение их к кружку, освещение опыта работы кружка. Известную часть газеты занимают материалы, которые не рассматриваются на заседаниях кружка. Газета как бы дополняет кружковые занятия.

Школьникам, выпускающим газету, эта работа приносит большую пользу, так как приходится подбирать материалы для газеты, а для этого они знакомятся с различными книгами, выбирают из них нужный материал, отделяют самое главное, литературно обрабатывают отобранное. Все это благотворно сказывается на расширении математического кругозора учащихся, на их речи и грамотности.

Содержание стенгазеты должно быть разнообразным, в противном случае она очень скоро надоест учащимся.

В коротких заметках обычно сообщают о новом в науке и технике, о результатах конкурсов и олимпиад. Полезно помещать решение отдельных задач с обязательным указанием фамилий учеников, решивших эти задачи. Конкурсные задачи должны быть разной степени трудности. Легкие задачи нужны для того, чтобы заинтересовать более равнодушных и заставить поверить в свои силы более слабых.

С интересом читают учащиеся коротенькие сообщения под рубрикой "А знаете ли вы?" Материал для этих заметок, а также сообщения о новостях науки и техники можно подбирать из различных журналов, газет, из книг по занимательной математике, физике, астрономии и механике.

Математическая газета должна выпускаться регулярно и не реже одного раза в месяц.

Математический кружок. Самой распространенной формой внеклассной работы является математический кружок. Математический кружок - это самостоятельное объединение учащихся под руководством педагога, в рамках которого проводятся систематические занятия с учащимися во внеурочное время. Вопросы организации, содержания и методики его работы достаточно полно освещены в методической литературе. В ней можно найти рекомендации по построению занятий, перечень тематики и библиографию источников, домашние и творческие задания для участников кружка и т.д.

В работе математических кружков можно выделить два направления. Первое в основном ориентировано на развитие мышления и формирование первоначального интереса к математике, второе на углубление знаний по математике и параллельно с этим на дальнейшую работу по развитию мышления.

В работе математического кружка большое значение имеет занимательность материала и систематичность его изложения. Занимательность повышает интерес к предмету и способствует осмыслению важной идеи: математика окружает нас, она есть везде. Систематичность изложения материала может быть направлена на общее умственное развитие учащихся.

Математический кружок - это одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружков работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь ввиду, что иногда и слабо успевающие учащиеся изъявляют желание учувствовать в работе математического кружка и не редко весьма успешно занимаются там. Но не всегда такие ученики изъявляют желание посещать такие занятия. Учителю не следует препятствовать посещению таких учащихся. Необходимо лишь более внимательно отнестись к таким ученикам, постараться укрепить имеющиеся у них ростки интереса к математики, проследить за тем, чтобы работа в математическом кружке оказалась для них посильной. Конечно, наличие слабоуспевающих учащихся среди членов математического кружка затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем участникам кружка, можно в некоторой степени ослабить эти трудности. Главное - сохранить массовый характер кружков занятий по математики.

При организации математического кружка необходимо заинтересовать учащихся, показать им, что работа в кружке не является дублированием классных занятий, четко сформулировать цели и раскрыть характер предстоящей работы (для этого целесообразно выделить часть времени на одном из уроков математики, с тем чтобы обратиться с сообщением об организации кружка ко всему классу).

Занятия кружка целесообразно проводить один раз в неделю, выделяя на каждое занятие по одному часу. К организации работы математического кружка целесообразно привлекать самих учащихся (поручать им подготовку небольших сообщений по изученной теме, подбор задач и упражнений по конкретной теме, подготовку справок исторического характера, изготовление моделей и рисунков к данному занятию и т.д.). На занятия математического кружка учитель должен создать "атмосферу" свободного обмена мнениями и активной дискуссии. Тематика кружковых занятий по математике в современной школе весьма разнообразна. В тематике кружковых занятий для 5-6 классов находят место вопросы, связанные с историей математики, жизнью и деятельностью Российских и зарубежных, известных математиков. Так же занятия способствуют развитию интереса у учащихся к предмету, математического кругозора, их творческих способностей. Их дополняют разовые мероприятия проводимые как в школе (математические вечера, викторины, олимпиады, КВН, соревнование команд и др.) так и вне школы (математические конкурсы, занятия в физико-математических школах, конкурсы по решению задач и др.).

В основном формирование состава кружка часто происходит после проведения школьной математической олимпиады среди учащихся пятых классов, где выявляется уровень математических способностей учащихся.

Целевая установка деятельности математического кружка 5-6 классов.

Развитие продуктивной мыслительной деятельности учащихся, для повышения интеллектуальной готовности детей к обучению их в дальнейшем.

Воспитание устойчивой мотивации к изучению математики.

Воспитание у детей коммуникативных качеств в условиях работы в новом коллективе.

В процессе изучения математики дети на основе решения задач различных типов учатся анализировать данные, выделять из них существенные и не существенные, разрабатывать алгоритм решения задач, а затем его реализовывать. Этот процесс развития мыслительной деятельности приводит к тому, что многие дети в дальнейшем могут самостоятельно решать довольно сложные задачи.

Особенности понимания детьми условий задач прослеживается при решении серии однотипных задач при возрастании сложности условия и решения. При решении нестандартных задач одного типа важно выявить признак типа, принцип решения задач данного типа и на все более усложняющихся примерах (с добавлением условия, с переходом к обратным задачам) отработать их решение. Это служит пропедевтикой методов решения нестандартных задач на факультативах и специальных курсах в старшем классах.

Деятельность математического кружка направлена на формирование у детей умения детально и последовательно разбираться в постановке задач, в исследовании их решения и получении правила, принципа решения задач данного типа.

Цели математического кружка заключаются в следующем:

Развитие математических знаний и умений учащихся;

Развитие интеллектуальных способностей учащихся.

Привитие интереса к предмету;

Решение нестандартных задач, предлагаемых на математических олимпиадах.

Одной из основных целей работы математического кружка на урока математики в 5-6 классах может являться своевременная ликвидация (и предупреждения) имеющихся у учащихся пробелов в знаниях и умениях по курсу математики. Задания из учебников, не всегда могут заинтересовать учащихся, а нестандартные, интересные задания, особенно наглядные могут вызвать интерес даже у отстающих учеников.

Для учеников которые уже проявляют интерес к математике, на таких занятиях могут быть следующие цели:

. Расширение и углубление знаний учащихся по программному материалу.

. Оптимальное развитие математических способностей у учащихся и привитие учащимся определенных навыков научно - исследовательского характера.

. Воспитание высокой культуры математического мышления.

. Развитие у учащихся умения самостоятельно и творчески работать с учебной и научно - популярной литературой.

. Расширение и углубление представлений учащихся о практическом значении математики в технике и практике социалистического строительства.

. Расширение и углубление представлений учащихся о культурно - исторической ценности математики.

. Воспитание у учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной.

. Установление более тесных деловых контактов между учителем математики и учащимися, и на этой основе более глубокое изучение познавательных интересов и запросов школьника.

. Создание актива, способного оказать учителю математики помощь в организации эффективного обучения математики всего коллектива данного класса (помощь в изготовлении наглядных пособий, занятий с отстающими, в пропаганде математических знаний среди других учащихся).

Учителю математики необходимо постоянно анализировать причины отставания учеников при изучении ими математики, изучать типичные ошибки, допускаемые учащимися при изучении той или иной темы. И с помощью элементов кружковых занятий (то есть с помощью нестандартных, увлекательных заданий) на уроках попробовать заполнить пробелы в знаниях. Таким образом, можно сделать вывод о том, что математические кружки являются полезными занятиями для интеллектуального развития школьников.

Математический кружок - одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружковой работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъявляют желание участвовать в работе математического кружка и нередко весьма успешно занимаются там; учителю математике не следует этому препятствовать. Необходимо лишь более внимательно отнестись к таким учащимся, постараться укрепить имеющиеся у них ростки интереса к математике, проследить за тем, чтоб работа в математическом кружке оказалась для них посильной. Конечно, наличие слабо успевающих учащихся среди членов математического кружка затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем кружковцам, можно в некоторой степени ослабить эти трудности. Главное - сохранить массовый характер кружковых занятий по математике, являющийся следствием доступности посещения кружковых занятий всеми желающими.

Основными целями проведения занятий являются:

·        Привитие интереса учащимся к математике;

·        Углубление и расширение знаний (а также умений и навыков) учащихся по математике;

·        Развитие математического кругозора, мышления, исследовательских умений учащихся и их творческих способностей;

·        Воспитание настойчивости, инициативы;

·        Научить учащихся самостоятельно добывать знания из дополнительной литературы.

Основными задачами математического кружка являются:

·        Воспитание творческой активности учащихся в процессе изучения математики;

·        Оказание конкретной помощи обучающимся в решении задач ЕГЭ, олимпиадных задач;

·        Повышение интереса учащихся к математике, развитие логического мышления.

Главное - не научить определённому набору методов решения стандартных задач, а приучить школьников к логически строгим рассуждениям, показать красоту и гармонию математики. Участие в кружке поможет школьникам, имеющим склонность к математике, обнаружить в себе эти способности, заинтересоваться математикой.

Но, наверное, самым важным является то, что в кружке создаётся своя особая среда - среда единомышленников. Многие дети, придя в кружок, находят там новых друзей, получают возможность общаться со сверстниками, с которыми у них есть общий интерес - интерес к познанию.

Требования к организации кружкового занятия

Проведение кружковых занятий в значительной степени близко к урокам. Сходство классных и внеклассных занятий определяется организационной формой коллективной учебной работы, когда учитель ведет занятие с группой учащихся, проводит необходимые пояснения, спрашивает учащихся. При этом целесообразно учащимся предоставлять собственные суждения по обсуждаемому вопросу. Надо учесть, что иногда "неправильные" рассуждения и их опровержения, тренировка в "разговоре" на математические темы дает учащимся больше пользы, чем сообщение учителем готовых решений. Это необходимо для развития у учащихся собственной инициативы, личного подхода к решению данной задачи.

Важно чаще практиковать различные способы решения задачи, не стремиться навязывать свое решение. Лучше решить одну задачу двумя-тремя способами, чем одним способом три задачи.

Вместе с тем учителю необходимо следить за тем, чтобы тематика кружковых занятий была разнообразной. Темп проведения кружковых занятий должен постепенно возрастать. Ценность содержания внеклассной работы определяется разнообразием тематики и методов решения задач, новизной по отношению к содержанию урока математики в классе. Школьников обязательно надо учить ориентироваться в незнакомых ситуациях и областях, решать задачу на незнакомую фабулу, с непривычным для них математическим содержанием.

В работе математического кружка большое значение имеет занимательность материала и систематичность его изложения. Занимательность повышает интерес к предмету и способствует осмыслению важной идеи: математика окружает нас, она везде. Систематичность изложения материала может быть направлена на общее умственное развитие учащихся.

Нецелесообразно на кружковых занятиях по математике проводить систематическое повторение пройденных вопросов, так как сообщение учащимся математических фактов, подлежащих обязательному усвоению, не является основной задачей внеклассной работы.

Итак, чтобы работа кружка по математике для учащихся 5-6 класса проходила интересно, необходимо:

Систематичность в работе;

Приобщение учащихся к чтению дополнительной литературы по предмету;

Организация соревнования в процессе кружковых занятий;

Изготовление учащимися различных форм пособий;

Применение разнообразных игровых форм работы, пробуждающих интерес ребят.

А.С. Макаренко писал: “Игра обязательно должна присутствовать в детском коллективе. Детский коллектив, не играющий, не будет настоящим детским коллективом. В детском возрасте игра это норма и ребенок должен всегда играть, даже когда делает серьезное дело”.

Исходя из вышесказанного, занятия математического кружка проводится должны с использованием элементов игры или вообще все занятия в игровой форме.

Организация работы кружка.

Уже при организации математического кружка, необходимо заинтересовать учащихся, показать им, что работа в кружке не является дублированием классных занятий, четко сформулировать цели и раскрыть характер предстоящей работы (для этого целесообразно выделить часть времени на одном из уроков математики, с тем, чтобы обратиться с сообщением об организации кружка по всему классу).

В разработке математического кружка представлена система занятий на полгода, то есть начать рекомендуется с третьей четверти и закончить в мае. В течение года кружковые занятия должны увязываться с другими формами внеклассной работы по математике, в подготовке которых активное участие должны принимать члены кружка. В каникулы предметные кружки проводить не рекомендуется.

Занятия кружка целесообразно проводить один раз в неделю (можно проводить и два раза), выделяя на каждое занятие в среднем по одному часу. Продолжительность кружка для учащихся 5 классов может быть 30-45 минут. На занятиях математического кружка учитель должен создать атмосферу свободного обмена мнениями и активной дискуссии.

§ 6. Анализ программ математических кружков

Мною было рассмотрено 10 планов проведения кружковых занятий для 5-6 классов на одно полугодие.

Математика в школе 6 выпуск 1971 г.: воспитать у детей желание и потребность заниматься математикой, возбуждать, поддерживать и развивать у учащихся интерес к математике. (пересечение и объединение множеств, составление задач учащимися на пересечение и объединение множеств, геометрические задачи, подготовка к математической олимпиаде, математический вечер, математический).

Глава II. Математический кружок для 5-6 классов как средство развития познавательного интереса

§1. Учебно-тематический план кружка

Внеклассная работа по математике является неотъемлемой частью учебно-воспитательного процесса в школе. Она способствует углублению знаний учащихся, развитию логического мышления, расширяет кругозор. Кружок также имеет сильное воспитательное значение, так как его целью является не только освещение какого-нибудь узкого вопроса, но и то, что учащихся надо заинтересовать, вовлечь их в самостоятельную деятельность.

Математические кружки по математике являются основной формой внеклассной работы с учащимися в 5-6 классах. В данной работе представлена разработка такого математического кружка.

Для занятий математического кружка "Занимательная математика" предлагаются несколько небольших фрагментов, которые, с одной стороны, тесно примыкают к основному курсу, а с другой - позволяют познакомить учащихся с новыми идеями и методами, расширить представления об изучаемом материале и, главное, порешать интересные задачи.

Уровень сложности этих заданий таков, что к их рассмотрению можно привлечь значительное число учащихся, а не только наиболее сильных. Как показывает опыт, они интересны и доступны обучающимся, не требуют основательной предшествующей подготовки и особого уровня развития.

Основные требования к программе кружка:

) связь содержания программы кружка с изучением программного материала;

) использование занимательности;

) использование исторического материала;

) решение нестандартных, олимпиадных задач;

) учет желаний учащихся;

) особенности школы;

) наличие необходимой литературы у учителя.

Для тех школьников, которые пока не проявляет заметной склонности к математике, эти занятия могут стать толчком в развитии их интереса к предмету и вызвать желание узнать больше. Кроме того, хотя эти вопросы и выходят за рамки обязательного содержания, они, безусловно, будут способствовать совершенствованию и развитию важнейших математических умений, предусмотренных программой.

Настоящая программа рассчитана на полгода обучения и предназначена для работы с обучающимися 5 класса в возрасте 10 - 12 лет. Занятия проводятся 1 раз в неделю, и по времени рассчитано на 45 минут, увеличивать время не рекомендуется, так как это не соответствует возрастным особенностям учащихся.

Основными целями кружка являются:

1. Формировать у учащихся качества мышления, характерные для математической деятельности и необходимые для продуктивной жизни в обществе.

. Развивать у учащихся интерес к математике.

. Развивать творческие способности учащихся.

. Способствовать расширению математического кругозора школьников.

. Добиваться выработки умений у учащихся решать нестандартные, логические, комбинаторные задачи.

. Сформировать у учащихся приемы и навыки решения прикладных задач.

А также изучение различных исторических фактов об известных математиках, их открытиях, воспитание трудолюбия, самостоятельности у учащихся.

Учебно-тематический план кружка (1 час в неделю)

№ занятия	Тема занятия	Количество часов	Примечания
1	Введение	1
	Все о числах	3
2	Великаны и карлики в мире чисел.	1
3	Признаки делимости.	1
4	Магические квадраты.	1
	Мы умеем решать задачи.	6
5	Решение задач методом "с конца".	1
6	Задачи на разрезание и перекраивание.	1
7	Задачи на взвешивания и переливания.	1
8	Элементы комбинаторики.	1
9	Графы.	1
10	Круги Эйлера.	1
	Занимательная математика.	3
11	Математические шифры.	1
12	Геометрия на спичках.	1	знакомит учащихся, в игровой форме, с некоторыми элементами геометрии, развивает пространственное мышление.
13	Фокусы.	1
14	Заключительное занятие.	1

§2. Вводное занятие

В начале первого занятия учитель приветствует учащихся, рассказывает о работе кружка. То есть кратко говорит о темах занятий (о признаках делимости, о принципе Дирихле, об инвариантах, шифрах, магических квадратах и т.д.), о том, что занятия будут проходить не только в формах лекций и семинаров, но и в различных других (беседы, викторины, исторические путешествия, лабораторная работа, урок-представление).

Первое занятие проводится в форме игры. Учитель делит участников кружка на команды (желательно, чтобы в каждой команде было человека 3-4). Школьникам предлагаются различные задания, часть из них по тем темам, которые запланированы учителем для изучения в процессе работы кружка: принцип Дирихле, задачи, решаемые с конца, логические задачи, задачи-шутки (которые используются в качестве разминки для учащихся), задачи на делимость. На первом этапе игры даются задачи-шутки, которые развивают быстроту мышления и логику у детей. На второй этапе каждой команде предлагаются одинаковые по тематике и сложности задания. На каждую задачу отводится определенное количество времени, после чего задания проверяются и выставляются баллы за их решение. На третьем этапе целесообразно предложить учащимся задачи более трудные. Даются несколько одинаковых заданий каждой из команды, кто быстрее справляется с ними, объясняет решение другим командам, если у тех, в свою очередь, возникли трудности.

В конце занятия подводятся итоги, считаются баллы, которые заработали каждая из команд участников.

При решении заданий команды сообщают об этом учителю. Проверяются задания решением на доске. Если все команды допустили в решении ошибки или не знают, как его делать, то разбираются в решении вместе с учителем. Если только одна команда справилась с заданием, то представитель этой команды объясняет решение остальным участникам.

Великаны и карлики в мире чисел.

1). Сообщение ученика на тему "Легенда о шахматной доске".

2). Рассказ учителя о числах-великанах.

Предложить учащихся вспомнить, какие самые большие числа знают они? (миллион, миллиард, секстиллион …). На данном занятии мы и будем узнавать, какие же самые большие и маленькие числа знает человечество.

Для таких "гигантов" придуман сокращенный способ обозначения. Весьма большие числа в научных сочинениях (по астрономии, физике) обозначаются так:

000 000=10⁶

400 000 000=4·10⁸

6 квадриллионов =6·10¹⁵

Теперь попробуем представить себе столь большие числа на практике. Толщина человеческого волоса - около 0,07 мм. Мы округлим ее для удобства вычислений до 0,1 мм. Представьте себе, что рядом, бок-о-бок, положен миллион волос. Какой ширины получилась бы полоса?

Оказывается, что ширина полосы из миллиона волос достигала бы примерно ста метров. Это кажется невероятным, но давайте проведем подсчет: 0,1мм·1 000000 - 0,1м·1000 = 0,1км = 100м (Мы проделали здесь умножение следующим путем: вместо умножения числа, мы дважды заменили самую единицу меры другою, в тысячу раз большею. Этот прием очень удобен для устных подсчетов, и им следует пользоваться).

Задачи для самостоятельного решения:

1). Сколько времени потребуется человеку, чтобы сосчитать миллиард зерен, если он в минуту будет считать по 100 зерен.

2). От земли до Марса около 60млн. км. Сколько времени придется лететь на ракете от земли до Марса, если скорость ракеты будет 10км/ч? Сколько времени потребовалось бы самолету, летящему со скоростью 1000км/ч, чтобы преодолеть это расстояние?

3). В нашей стране проживают около 250 млн. человек. Если все люди встанут в одну шеренгу, то какой длины будет эта шеренга? (Пусть каждый человек занимает место длиной в 50см).

4). Каких размеров достигает обыкновенный комар, увеличенный в миллион раз? Длина комара приблизительно равна 5мм.

5). Узнайте свой рост, увеличенный в миллион раз?

6). Сколько километров займет миллион людей, построенных в один ряд плечом к плечу?

3). Рассказ учителя о числах - карликах.

В конце занятия обобщим знания, полученные на данном занятии.

Сверхгигант и сверхлилипут.

Наши беседы о великанах и карликах из мира чисел были бы неполны, если не рассказать одной изумительной диковинке этого рода - диковинке, правда, не новой, но стоящей дюжины новинок. Чтобы подойти к ней, начнем со следующей, на вид весьма незамысловатой задачи.

Какое самое большое число можно написать тремя цифрами, не употребляя никаких знаков действий?

Решение:

Хочется ответить: 999,-но, вероятно, вы уже подозреваете, что ответ иной; иначе задача была бы чересчур проста. И, действительно, правильный ответ пишется так:

Выражение это означает: "девять в степени девять в девятой степени".

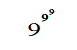
Если хватит терпения выполнить перемножение девяти девяток, вы получите число: 387 420 489. Другими словами: нужно составить произведение из стольких девяток, сколько единиц в результате умножения: 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9. Достаточно только начать вычисление, чтобы ощутить огромность ожидаемого результата: 9^387420489, т.е. произведение 387 420 489 девяток. Придется сделать круглым счетом 400 миллионов умножений.

Познакомившись с этим замаскированным гигантом, попытайтесь найти его противоположность. (Соответствующий числовой лилипут получится, если разделим единицу на это число. Будем иметь: 1/9^387420489).

Архимед вычислил некогда, сколько песчинок заключал бы в себе мир, если бы весь он, до неподвижных звезд, наполнен был тончайшим песком. У него получился результат, не превышающий единицы с 63 нолями. Наше число состоит не из 64, а из 370 миллионов цифр - следовательно, оно неизмеримо превышает огромное число Архимеда.

В качестве домашнего задания можно предложить посчитать, сколько песчинок понадобится, чтобы устлать весь пол в квартире каждого учащегося в один ряд. Для этого необходимо узнать у родителей метраж квартиры. Размер песчинки приблизительно равен 0,125миллиметра.

 

§3. Признаки делимости

Учащиеся 6 класса уже владеют понятиями: "простые и составные числа", "Делители натурального числа", НОК и НОД, умеют применять свойства и признаки делимости. Поэтому в объяснении нового для 5-классников материала будут принимать участие ученики 6 класса, заранее подготовленные с учителем.

Рассмотри задачу: в доме, где всего один подъезд - 35 квартир. Может ли дом быть семиэтажным? (Сколько тогда квартир на одном этаже). А четырехэтажным? Сколько этажей еще может быть в доме? Таким образом, мы можем сказать, что количество этажей - это число, на которое 35 делится без остатка, то есть нацело. Если одно натуральное число нацело делится на другое натуральное число, то первое называют кратным второму, а второе - делителем первого. Например, 35: 7 = 5, из этого следует, что 35 кратно 7, а 7 - делитель числа 35.

Можем ответить на вопросы нашей задачи: если на каждом этаже по одной квартире (что маловероятно), то этажей 35. Следуя данному рассуждению, мы делим 35 на 5 и получаем 7. То есть дом может быть пятиэтажным, на каждом этаже по 7 квартир. А четырехэтажным дом не может быть, поскольку 35 не делится на 4 нацело.

Признаки делимости представлены в виде таблицы. (Предложить учащимся сделать себе памятки в виде таблицы, для дальнейшего ее использования).

Признаки делимости		Пример:
на 2	На 2 делятся все четные натуральные числа.	172, 94,67 838, 1670.
на 3	На 3 делятся все натуральные числа, сумма цифр которых кратна 3.	16 734 (1+6+7+3+4=21; 21: 3 = 7).
на 4	На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4.	124 (24: 4=6); 103 456 (56: 4 = 14).
на 5	На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0.	125; 10 720.
на 6	На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно (все четные числа, которые делятся на 3).	126 (6 - четное, 1 + 2 + 6 = 9, 9: 3 = 3).
на 9	На 9 делятся те натуральные числа, сумма цифр которых кратна 9.	179 (1 + 1 + 7 + 9 = 18,18: 9 = 2).
на 10	На 10 делятся все натуральные числа, оканчивающиеся на 0.	30; 980; 1 200; 1 570.
на 11	На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11.	105787 (1 + 5 + 8 = 14 и 0 + 7 + 7 = 14); 9 163 627 (9 + 6 + б + 7 = 28 и 1+3+2=6); 28 - 6 = 22; 22: 11 = 2).
на 25	На 25 делятся те натуральные числа, две последние цифры которых - нули или составляют число, кратное 25.	2300; 650 (50: 25 = 2); 1475 (75: 25 = 3).

Задачи для работы по теме занятия.

1). Перечислите все цифры, которые следует поставить вместо звездочки в записи 3*16, чтобы получившиеся число делились на 3?

Решение: вспомним признак делимости на 3. сложим цифры, которые уже известны в данном числе, 3+1+6=10. Нам необходимо к 10 прибавить такое натуральное число, которое в сумме с 10 нацело делило бы число 3. Заметим, что следующее число после 10, которое делится 3 нацело, число 12. Соответственно мы нашли одно из чисел (2), удовлетворяющих условию задачи. Следующие числа, которые делится на 3 без остатка, - числа 15 и 18. Тем самым мы получили три числа (2, 5,8), которые нам подходят.

2). К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

Решение: Обозначим неизвестные нам цифры через a и b. Тогда четырехзначное число можно записать в виде a10b. Данный вид записи подразумевает под собой то, что, например, число вида abc = a·100+b·10+c (как пример можно привести: 123=1·100+2·10+3). Это значит, что данное число представлено в виде: a10b = a·1000+1·100+5·10+b.

В условии задачи мы имеем: полученное число должно делиться на 15. Что это значит? Что мы должны рассмотреть признак делимости числа 15. То есть b либо равно 5, либо 0.

По признаку делимости на 5: b=0 или b=5. Рассмотрим оба случая.

а). Пусть b=0.

Полученное число a150 должно делиться на 15. (Подобно первой задаче находим число а). О признаке делимости на 5 мы сказали ранее, а на 3 число делится - тогда и только тогда, когда сумма его цифр, равная a+1+5, делится на 3. Отсюда получаем, что а=3, 6, 9.

б). Рассмотрим второй случай. Пусть b=5.

Здесь получаем, что полученное число a10b делится на 5, а на 3 - тогда и только тогда, когда сумма его цифр, равная а+1+5+5, делится на 3. Получаем, что а=1, 4, 7.

Ответ: четырехзначные числа равны: 3150, 6150, 9150, 1155, 4155, 7155.

3). Найдите наибольшее натуральное число, делящееся на 36, в записи которого участвуют все 10 цифр по одному разу.

Решение: Число делится на 36 тогда и только тогда, когда оно делится на 9 и на 4. Проверим, что сумма всех десяти цифр делится на 9 (1+2+3+4+5+6+7+8+9=45; 45: 9=5). Поэтому любое число, в записи которого участвуют все 10 цифр по одному разу, делится на 9. Самым большим таким числом является число 9876543210. Но оно не делится на 4 (ибо число делится на 4 тогда и только тогда, когда две его последние цифры образуют число, делящееся на 4). Нужно добиться делимости на 4, минимально уменьшив при этом число. Очевидно, число 9876543120 делится на 4. Больше него только числа 9876543210 и 9876543201, которые на 4 не делятся.

Ответ: 9876543120.

Целесообразно дать учащимся подобные задачи для самостоятельного решения.

4). Замените звёздочки в записи числа 72*3* цифрами так, чтобы число делилось без остатка на 45.

5). Найти натуральные числа, дающие при делении на 2, 4, 5, 6 остаток 1, и, кроме того, делящиеся на

6). Заполните столбики таблицы, предлагаемыми числами:

, 192, 304, 766, 845, 900, 975, 5555, 6000.

Делятся на 2	Делятся на 5	Делятся на 10	Делятся на 2 и на 5 одновременно	Делятся на 2, но не делятся на 5	Делятся на 5, но не делятся на 2

7). Докажите, что число записанное шестью одинаковыми цифрами, делится на 3, 7, 11, 13, 37.

В заключении хотелось бы представить участникам кружка четыре изумительных десятизначных числа:

438 195 760

785 942 160

753 869 120

876 391 520

В каждом из них есть все цифры от 0 до 9, причем каждая цифра только по одному разу и каждое из этих чисел делится на 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, и 18. (Можно в виде домашнего задания предложить учащимся проверить несколько чисел).

§4. Магические квадраты

Вступительное слово учителя.

"В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты" - Бенджамин Франклин.

Одно из самых загадочных произведений изобразительного искусства хранится в Кунстхалле города Карлсруэ. Речь идет о гравюре Альбрехта Дюрера "Меланхолия I" (1514).

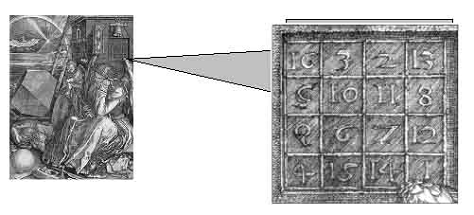
Значимая деталь, изображенная на гравюре "Меланхолия I" - составленный впервые в европейском искусстве магический квадрат 4 Х 4. Сумма чисел в любой строке или столбце равна 34. Два средних числа в нижнем ряду указывают дату создания картины 1514 год.

Размерность квадрата 4*4. Он заполнен числами от 1 до 4*4 (16) интересным образом. Учащимся самим предстоит узнать все о магическом квадрате, посчитать, чему равна сумма чисел по любой вертикали, горизонтали и диагонали (34). Учитель, в свою очередь, должен спросить, заметил ли кто-нибудь из них, в каких еще конструкциях встречается данная сумма (сумма встречается в угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных "ходом коня" (2+8+9+15 и 3+5+12+14), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12).

Магические квадраты - это таблицы чисел, в которых суммы чисел в каждой строке, в каждом столбце и в каждой из двух диагоналей квадрата все равны между собой. Из всякого магического квадрата путем различных перестановок составляющих его чисел можно получить множество новых магических квадратов, обладающих теми же свойствами.

Известно, что магических квадратов 2х2 не существует (предложить попытаться составить квадрат 2х2 и доказать, почему же его все таки не существует). Магический квадрат 3х3 только один. Магических квадратов 4х4, как на картине Дюрера, составлено уже 800, а количество магических квадратов 5х5 близко к четверти миллиона!

Заметка в тетрадь: каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n² клеток и называется квадратом n-го порядка.

Рассмотрим удобный способ заполнения магического квадрата 3-го порядка и составим магический квадрат третьего порядка. После чего участникам кружка предлагается самостоятельно составить магические квадраты.

Слово учителя о магическом квадрате Пифагора.

§5. Решение задач методом с "конца". Решение задач на все действия с дробными числами

Вступительное слово учителя.

Простейшим примером задачи, решаемой с "конца" может служить игра в лабиринты, нарисованные на бумаге, которые нужно проходить с помощью карандаша. Многие из этих лабиринтов содержат несколько возможных путей, и среди них только один верный путь, который приведет в конец лабиринта к заветной цели. Ускорить решение такой задачки-лабиринта можно, если пойти в обратном направлении, начав движение с конечной точки и прорисовывая путь к началу лабиринта.

Стратегия решения с конца очень удобна. На данном занятии мы в этом убедимся. При решении следующих задач необходимо выполнять проверку.

Задача 1: Я задумала число, умножила его на 7, прибавила 15 и получила 50. Какое число я задумала?

Решение: начнем решение задачи с "конца". В результате всех действий мы получили число 50. Далее от 50 отнимаем 15 и получаем число (35), до прибавления 15. Затем число, полученное в первом действии делим на семь, тем самым получаем искомое число 5.

Проверка: 5·7=35; 35+15=50.

Таким образом, пользуясь обратным ходом, мы легко решили эту задачу.

Задача 2: Группа туристов отправилась в поход. В первый день они прошли 1/3 пути, во второй - 1/3 остатка, в третий - 1/3 нового остатка. В результате им осталось пройти 32км. Сколько километров был маршрут туристов?

Решение: Так как осталось 32км, а в третий день туристы прошли остаток, то 32км будут составлять последнего 2/3 остатка, тогда сам последний остаток будет равен 32: 2/3 = 48 (км). Эти 48км будут составлять 2/3 длины маршрута, оставшегося пройти после первого дня. Тогда весь маршрут, который осталось пройти, будет равен 48: 2/3 = 72 (км). Эти 72км составляют вновь 2/3, но уже всего маршрута туристов, а значит, весь маршрут будет равен 72: 2/3 = 108 (км). Задача решена.

Проверка: 108: 3·1=36 км - прошли в первый день; 108-36=72, 72: 3·1=24 км - во второй день; 72-24=48, 48: 3·1=16 км - в третий день; 48-16=32 км - осталось пройти.

Решение олимпиадных задач:

1). Средний из трех братьев старше младшего на 2 года, а возраст старшего брата превышает сумму лет двух остальных братьев четырьмя годами. Найдите возраст каждого брата, если вместе им 96 лет.

Решение: Удвоенные возраст старшего брата на 4 года больше от суммы лет всех троих братьев и равен поэтому 96+4=100 годам. Значит, возраст старшего брата равен 100: 2=50 годам. Удвоенный возраст среднего брата на 2 года больше от суммы его лет и лет младшего брата и равен поэтому (96-50) +2=48. Значит возраст среднего брата равен 48: 2=24 годам. Теперь осталось найти возраст младшего брата: 96-50-24=22 года. Получаем ответ: младшему - 22, среднему - 24, старшему - 50

2). Однажды купец предложил бездельнику заработать. "Как только ты перейдешь через этот мост, - сказал он, - твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 рубля". Бездельник согласился и … после третьего перехода остался без денег. Сколько денег у него было сначала?

Решение: Так как после третьего перехода у бездельника денег не осталось, то после перехода моста в третий раз у него было 24 рубля, а до перехода третьего моста - 12 рублей. Тогда после перехода второго моста у бездельника было 12 + 24 = 36 (рублей), а до перехода второго моста - 36: 2 = 18 (рублей). Рассуждая аналогично, получим, что после перехода первого моста у бездельника стало 18 + 24 = 42 (рубля), а перед переходом первого моста - 42: 2 = 21 (рубль). Таким образом, у бездельника сначала был 21 рубль.

Задачи для самостоятельного решения:

1). Я задумал число, умножил его на 8, результат уменьшил на 10 и новый результат умножил на 5. Получилось 70. Какое число я задумал. [дидактические материалы к учебнику Г.В. Дорофеева, И.Ф. Шарыгина "математика 6"]

2). Библиотека из фонда детских книг передала интернату половину книг и еще тридцать книг, после этого она передала половину оставшихся и еще десять книг. В библиотеке осталось 150 детских книг. Сколько детских книг было в библиотеке первоначально? [дидактические материалы к учебнику Г.В. Дорофеева, И.Ф. Шарыгина "математика 6"]

3). Маша принесла своим друзьям медведям торт. Известно, что старший медведь съедает торт за 2 дня, средний медведь - за 3 дня, младший медведь - за 6 дней. За сколько дней три медведя вместе съедят торт?

4). "Мишины котята". Увидит Миша где-нибудь брошенного котенка, непременно подберет и принесет домой. Всегда воспитывается у него несколько котят, а сколько именно он не любит говорить, чтобы над ним не смеялись. Бывало, спросят у него:

Сколько у тебя теперь котят?

Немного, - ответит он. - Три четверти их числа, да еще три четверти одного котенка.

Товарищи думали, что он просто балагурит. А между тем Миша задавал им задачу, которую решить совсем нетрудно. Сколько было у Миши котят? [Е.Г. Козлова. Сказки и подсказки. Задачи для математического кружка].

§6. Задачи на разрезание и перекраивание фигур

Данное занятие предполагается провести в виде "лабораторной" работы. Разбить участников кружка на группы по 2-3 человека. Каждой из групп предоставить заранее подготовленные учителем фигуры. Учащиеся располагают линейкой (с делениями), карандашом, ножницами. Разрешается производить с помощью ножниц лишь прямолинейные разрезы. Разрезав какую-нибудь фигуру на части, необходимо составить другую фигуру из тех же частей.

В начале занятия дать учащимся небольшую историческую справку: Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками, китайцами, но первый систематический трактат на эту тему принадлежит перу Абуль-Вефа. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее построение другой фигуры в начале 20 века. Одним из основателей этого раздела был знаменитый основатель головоломок Генри Э. Дьюдени.

В наши дни любители головоломок увлекаются решением задач на разрезание прежде потому, что универсального метода решения таких задач не существует, и каждый, кто берется их решать, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. (На занятии мы будем указывать лишь один из возможных примеров разрезания. Можно допустить, что у учащихся может получиться какая-то другая верная комбинация - не надо этого бояться).

В конце занятия предложить учащимся просмотреть презентацию с заданиями.  (презентация)  <C:\Users\Максим\Desktop\по диплому\razrezanie.pptx>.

§7. Задачи на взвешивание и переливание

Данное занятие предлагается провести в виде практического занятия. Разбить класс на 2 группы. Каждой из групп предложить по задаче на взвешивание и переливание, после чего команда должна рассказать (показать) решение. Для следующих задач необходимо заранее подготовить сосуды емкостью 300мл, 400мл, 500мл, 900мл (из пластиковых бутылок), весы без циферблата, современные монеты, и монеты Советского союза достоинством 10р. и 900г крупы.

Группа 1. Задание 1: В бочке налита вода. Как отлить из нее 600мл с помощью сосудов вместимостью 900мл и 500мл? Подсказка: обращать внимание не только на то, сколько воды в каждом из сосудов, но и сколько осталось пустого места. Каждой группе дать для наглядности по таблице.

.        Заполняем 500миллилитровую бутыль полностью.

2.      Выливаем ее полностью в 900миллилитровую бутыль. В 900миллилитровой остается место еще для 400мл.

.        Снова набираем 500миллилитровую бутыль полностью и выливаем ее в 900миллилитровую. Итого в 500миллилитровой останется 100мл.

.        Выливаем из 900миллилитровой все содержимое. И теперь в пустую 900миллилитровую бутыль выливаем 100мл из 500миллилитровой.

.        Снова наполняем 500миллилитровую полностью и переливаем воду из нее в 900миллилитровую. Тем самым мы получаем, что в 900миллилитровой у нас 600мл.

Задание 2: Имеется 80 монет, одна из которых фальшивая, причем она легче других. За какое наименьшее число взвешиваний на весах без гирь можно найти фальшивую монету?

Наводящие вопросы:

1.      Как выделить наличие фальшивой монеты? Какое количество действий при этом получается?

2.      Сколько действий будет, если кучки с монетами постоянно делить пополам?

.        Как оптимизировать количество действий?

.        Что будет, если монеты поделить на 3 и большее количество частей?

Решение: Выберем самое оптимальное решение, где количество действий наименьшее. Фальшивую монету можно определить за 4 взвешивания. Алгоритм следующий. Первое взвешивание: кладем на чаши по 27 монет. В случае равновесия фальшивая среди оставшихся 26. Если одна чаша легче, то фальшивая среди лежащих на ней 27. Второе взвешивание: кладем на обе чаши по 9 монет из числа "подозреваемых" и рассуждаем аналогично. В третьем взвешивании положим на чаши по 3 монеты, а в четвертом - по одной. Как видим, здесь деление не пополам, а на три по возможности равные части.

Группа 2: Задание 1: есть две пустые емкости 300мл и 500мл. Как отмерить 400мл воды? (Воду можно наливать и выливать бесконечное количество раз).

.        Заполняем 500миллилитровую бутыль полностью.

2.      Выливаем из нее 3 литра в 300миллилитровую бутыль. В 500миллилитровой остается 200мл.

.        Выливаем из 300миллилитровой бутыли всю воду и переливаем в неё оставшиеся 200мл из 500миллилитровой. В 300миллилитровой осталось свободное место для ста миллилитров.

Наполняем 500миллилитровую бутыль. Переливаем из неё 100мл в 300миллилитровую бутыль. В 500миллилитровой остается 400мл.

Задание 2: Имеется 900г крупы и чашечные весы с гирями в 5г и 20г. Попробуйте в три приема отвесить 200г этой крупы.

Наводящие вопросы:

1.      Каким образом и сколько крупы мы можем отвесить сразу, не пользуясь гирями?

2.      Сколько раз мы можем повторить шаг 1? Какое наименьшее количество крупы нам необходимо получить?

.        Сколько грамм составляют гири вместе?

Решение: Нужно развесить крупу на две равные части по 450г; затем развесить одну из этих частей еще раз пополам, то есть по 225г, и от одной из этих частей отнять при помощи двух имеющихся гирь 25г. Таким образом, Вы получите вес в 200г.

Решение типовых задач:

1). Имеются шестилитровая банка сока и две пустые банки: трех - и четырехлитровая. Как налить 1литр сока в трехлитровую банку? (Предложить учащимся сначала заполнить таблицу, а затем составить алгоритм выполнения действий.

Решение: для решения данной задачи составим таблицу

Банки	6 литров	4 литра	3 литра
До переливания	6	0	0
После 1-го переливания	2	4	0
После 2-го переливания	2	1	3
После 3-го переливания	5	1	0
После 4-го переливания	5	0	1

·        Заполняем соком из 6-литровой банки 4-литровую банку полностью. В 6-литровой остается 2 литра сока.

·        Действуем аналогично: из 4-литровой выливаем 3литра в 3-литровую. Тем самым в 4-литровой остается 1литр.

·        Содержимое 3-литровой выливаем в 6-литровую банку.

·        Из 4-литровой банки переливаем литр содержимого в банку 3-литровую. В 6-литровой - 5литров; в 3-литровой - 1литр; 4-литровая банка - пустая.

2). В мешке 24кг. гвоздей. Как, имея только чашечные весы без гирь, отмерить 9кг гвоздей?

Решение: составим таблицу

	1 куча	2 куча	3 куча	4 куча
1-й шаг	12кг	12кг
2-й шаг	12кг	6кг	6кг
3-й шаг	12кг	6кг	3кг	3кг

·        разделить все гвозди на 2 равные части, по 12кг.

·        Одну из частей продолжаем разбивать пополам, по 6кг.

·        Теперь уже кучу в 6кг разбиваем на 2 равные части по 3кг. Имеем 4 кучки с гвоздями: 12кг, 6кг, 3кг, 3кг.

·        Из имеющихся кучек мы легко сможем "отмерить" 9кг гвоздей.

Задачи для самостоятельного решения:

1). Как, имея пятилитровое ведро и девятилитровую банку, набрать из реки ровно три литра воды?

2). Есть три бидона емкостью 14, 9 и 5литров. В большом бидоне 14л молока, остальные пусты. Как с помощью этих бидонов разделить молоко пополам?

3). Из 27 монет одна фальшивая. Фальшивая монета легче остальных. За какое наименьшее число взвешиваний на чашечных весах без гирь можно определить фальшивую монету?

4). Как развесить 20фунтов чая в 10 коробок по 2фунта в каждой за девять развесов имея только гири на 5 и на 9фунтов?

5). Двое должны разделить поровну 8 ведер кваса, находящегося в восьмиведерном бочонке. Но у них есть только два пустых бочонка, в один из которых входит 5 ведер, а в другой - 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками?

§8. Элементы комбинаторики. Принцип Дирихле

В начале занятия кратко рассказать историю зарождения комбинаторики и об областях ее применения.

Определение. Задачи на составление числа возможных соединений элементов с определенными свойствами, которые можно составить из элементов заданного множества, называются комбинаторными.

Задача 1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?

Решение: Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.

11	14	17
41	44	47
71	74	77

Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Данный метод называется методом перебора.

Однако существует другой подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название - дерево возможных вариантов.

Вернемся к задаче о составлении двузначных чисел из цифр 1, 4 и 7. Для ее решения можно построить специальную схему.

Эта схема действительно похожа на дерево, правда, "вверх ногами" и без ствола. Знак “*” изображает корень дерева, ветви дерева - различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 4 или 7. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 4 и 7.

Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 4 или 7. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 4 или 7. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.

Дополнительная подзадача: Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры десятков и единиц не повторяются?

Задача 2. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

Способ 1: Обозначим города их первыми буквами. Тогда код каждого маршрута будет состоять из трех букв: В, Р и Ф, каждая из которых должна быть использована только один раз, например, ВФР или ФРВ.

Варианты путешествия получаются следующие: ВРФ, ВФР, РВФ, РФВ, ФВР, ФРВ, что хорошо видно из дерева вариантов.

Путешествие можно начинать в любом из трех городов. Если первой посетить Венецию, то затем можно поехать в Рим или во Флоренцию. Если вторым посетить Рим, то третьей будет Флоренция, если второй будет Флоренция, то третьим будет Рим. Это первые два варианта путешествия. Таким образом, всего существует 6 вариантов путешествия.

Способ 2: Для каждого из трех городов существует 2 варианта маршрута по оставшимся городам. Если 3 умножить на 2, получится 6. Такой же ответ получится при помощи дерева вариантов.

Про второй способ рассуждений обычно говорят так: мы использовали правило умножения.

Комбинаторные задачи бывают самых разных видов. Но большинство из них решается с помощью двух основных правил - правила суммы и правила произведения. Продолжим знакомиться с правилом произведения (умножения), сформулируем утверждение: Если первую компоненту пары можно выбрать n способами, а вторую можно выбрать k способами, то число всевозможных комбинаций пар равно произведению чисел n и k.

Задача 3: Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?

Решение: Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:

№1 - Саша - есть возможность выбрать из 5 вариантов (стульев) №2 - Петя - 4 варианта №3 - Денис - 3 варианта №4 - Оля - 2 варианта №5 - Настя - 1 вариант

Используя правило умножения, получаем: 5х4х3х2х1=120

Теперь решим задачу, применяя правило сложения.

Задача 4: В коробке 6 синих карандашей и 12 красных. Сколько всего карандашей в коробке?

Решение: Мы легко можем ответить на вопрос, сложив число синих и красных карандашей, 6+12=18.

Изменим вопрос к задаче: сколькими способами можно выбрать из коробки один карандаш? Получим комбинаторную задачу. Число способов выбора одного карандаша равно числу всех карандашей в коробке, т.е.18. Но 18 - это сумма 6 и 12, где 6 - число способов выбора синего карандаша, а 12 - число выбора красного карандаша. Т.о. правило суммы можно сформулировать следующим образом.

Если объект а можно выбрать n способами, а объект b можно выбрать k способами, то выбор a или b можно сделать n+k способами.

Принцип Дирихле.

В несерьёзной форме принцип Дирихле гласит: "Нельзя посадить 7 кроликов в 3 клетки, чтобы в каждой было не больше 2 кроликов. "

Более общая формулировка: "Если z зайцев сидят в k клетках, то найдётся клетка, в которой не менее z/k зайцев." Не надо бояться дробного числf зайцев: если получается, что в ящике не меньше 7/3 зайцев, значит, их больше двух.

Доказательство принципа Дирихле очень простое, но заслуживает внимания, поскольку похожие рассуждения"от противного" часто встречаются. Допустим, что в каждой клетке число зайцев меньше, чем z/k. Тогда в k клетках зайцев меньше, чем k · z/k = z. Противоречие!

Решение задачи с помощью принципа Дирихле сводится к выбору "кроликов" и "клеток". Иногда не совсем очевидно, кто в данной задаче является "кроликом", и что служит "клеткой".

1). В классе 30 человек. В диктанте Стас Иванов сделал 13 ошибок, а остальные - меньше. Докажите, что по крайней мере три ученика сделали ошибок поровну (может быть, по 9 ошибок).

Решение: Это доказывается с помощью принципа Дирихле. Подумайте, кто здесь зайцы, и где клетки. (Здесь "зайцы" - ученики, а "клетки" - число сделанных ошибок). В клетку 0 "посадим" всех, кто не сделал ни одной ошибки, в клетку 1 - тех, у кого одна ошибка, в клетку 2 - две,. и так до клетки 13, куда попал один Стас Иванов.

Теперь применим принцип Дирихле, докажем утверждение задачи от противного.

Предположим, никакие три ученика не сделали по одинаковому числу ошибок, то есть в каждую из клеток 0, 1,., 12 попало меньше трех школьников.

Тогда в каждой из них два человека или меньше, а всего в этих 13 клетках не больше 26 человек. Добавив Стаса Иванова, все равно не наберем 30 ребят. Противоречие.

Можно ли утверждать, что ровно трое сделали поровну ошибок? Нет, конечно. Возможно, что все ребята, кроме Стаса, написали диктант без единой ошибки, то есть, все сделали по 0 ошибок. Можно ли считать, что по крайней мере четверо попали в одну "клетку"? Нет, нельзя. Класс, в котором по 3 человека сделали 0, 1, 2 ошибки, по 2 человека - 3, 4,., 12 ошибок и один - 13, удовлетворяет условию задачи.

2). В одном доме живут 13 учеников одной и той же школы. В этой школе 12 классов. Докажите, что хотя бы два ученика, живущие в этом доме, учатся в одном и том же классе

Решение. В данной задаче классы - это клетки, а учащиеся - кролики. У нас имеется 13 "кроликов" и 12 "клеток". Учитывая принцип Дирихле, мы получаем, что хотя бы в одной клетке "кроликов" два. То есть, если в школе 12 классов, то максимум в них может учиться 12 учеников. А 13 ученик все равно будет учиться в одном из этих 12 классов.

Задачи для самостоятельного решения:

1). В магазине "Все для чая" есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем? 2). Сколько существует 6-значных чисел, все цифры которых имеют одинаковую четность? 3). У Васи на куртке 3 кармана. Каким числом способов он может положить в эти карманы две одинаковые монетки?

4). В корзине сидят котята - 2 черных, 2 рыжих и 1 полосатый. Сколькими способами можно выбрать трех котят так, чтобы они все были разной окраски?

5). В корзине лежат яблоки двух сортов. Наугад берут из этой корзины несколько яблок. Какое наименьшее число яблок нужно взять, чтобы среди них оказались хотя бы два яблока одного сорта?

6). Докажите, что любое число рублей можно уплатить, если покупатель и кассир имеют лишь трехрублевые и пятирублевые денежные знаки.

 

§9. Графы. Применение графов к решению задач

Графы - это рисунки, которые состоят из точек и линий, соединяющих эти точки.

Каждая пара точек в графе может быть соединена линиями. Линия указывает на связь между двумя точками. Точки называются вершинами графа, а линии - рёбрами.

С какими графами вы встречаетесь повседневной в жизни? (схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах - изображение железных дорог). С помощью графов изображаются схемы дорог, газопроводов, тепло и электросетей.

Особым видом графа является дерево. Дерево (граф) - это способ организации информации об отношениях между объектами, в нем нет циклов, то есть нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Примером такого дерева может служить генеалогическое дерево Рюриковичей и Романовых.

 

 

Рассмотрим одну из простейших задач: Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля - Меркурий; Плутон - Венера; Земля - Плутон; Плутон - Меркурий; Меркурий - Венера; Уран - Нептун; Нептун - Сатурн; Сатурн - Юпитер; Юпитер - Марс и Марс - Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение: Нарисуем схему условия: планеты изобразим точками, их у нас 9, а маршруты ракет - направляющими линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.

1). В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра - провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа - 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным15·5/2=37,5. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.

Ответ. Соединить телефоны таким образом невозможно.

2). В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.

Решение. Подсчитаем общее количество выходящих городов дорог - 100.4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза - она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.

3). Обрисовать фигуру, не отрывая карандаша от бумаги и не проводя два раза по одной линии. Обозначьте точки пересечения, в скобках укажите, сколько линий выходит из данной точки. Если число линий четное - то вершина четная, если число линий нечетное - то вершина нечетная. Пометить вершину, с которой надо начинать обход.

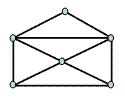1. 2. 3.

.

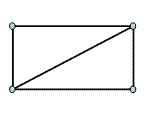
Все ли фигуры у вас получилось нарисовать? (все, кроме фигуры №1). Как вы думаете почему? Как это связано с количеством четных и нечетных вершин?

Сделаем вывод:

·        Если все вершины графа четные, то нарисовать фигуру возможно, и начать можно с любой вершины (№4).

·        Если же из этих вершин две нечетные, то нарисовать фигуру можно, но только начинать необходимо в одной из этих двух нечетных вершин, а заканчивать во второй нечетной вершине (№2, №3).

·        Если в графе более двух нечетных вершин, то нарисовать фигуру невозможно (№1).

Вопрос о разрешимости таких задач входит в теорию графов. Впервые ее исследовал Л. Эйлер в 1736г., решая задачу о Кенигсбергских мостах.

4). Город Кенигсберг расположен на берегах и двух островах реки Преголя. Части города соединены между собой семью мостами. В воскресные дни горожане совершили прогулки по городу. И возник вопрос, можно ли выбрать такой маршрут, чтобы пройти по каждому мосту только один раз и вернуться в начальную точку пути?

 

Попробуем разрешить эту задачу. Но сначала составим план города, как это сделал Л. Эйлер. Он обозначил части города точками (вершины), а переходы по мостам - линиями (ребра). Получил граф.

Ответ: обход по всем мостам только один раз невозможен, т.к. все вершины графа нечетные.

Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

[<#"564905.files/image015.gif">

Нам очевидно, что общая часть кругов М и Б состоит из тех ребят, которые одновременно увлекаются и математикой, и биологией. Теперь давайте посчитаем. Всего внутри прямоугольника 35 ребят. Внутри двух маленьких кругов М и Б будет 35-9= 26 ребят, поскольку нам известно, что 9 ребят не посещают кружки. Внутри "математического" круга 19 ребят, значит, в той части "биологического" круга, которая расположена вне круга М, находится 26-19= 7 биологов, не посещающих математический кружок. Остальные биологи, их 10-7= 3, находятся в общей части кругов МБ. Таким образом, 3 биолога увлекаются математикой.

Изображение различных множеств в виде кругов широко использовал в своих научных трудах великий математик ХVIII века Леонард Эйлер. Именно поэтому рисунки, подобные в задаче, которую разобрали выше, обычно называют "кругами Эйлера". Эйлер отмечал, что изображение множеств в виде кругов "очень подходит для того, чтобы облегчить наши рассуждения".

Круги Эйлера - геометрическая схема, с помощью которой можно изобразить отношения между подмножествами.

2). В киоске около школы продается мороженое двух видов: "Спортивное" и "Мальвина". На перемене 24 ученика успели купить мороженое. При этом 15 из них купили "Спортивное", а 17 - мороженое "Мальвина". Сколько человек купили мороженое обоих сортов?

Решение. Попробуем изобразить данные задачи с помощью кругов.

Общая часть кругов состоит из тех школьников, которые купили мороженое обоих сортов. Всего мороженое купили 24 ученика. Внутри круга М 17 учеников, а в круге С - 15 учеников. Возьмем, например, учащихся, купивших мороженое "Мальвина". Получим 24-17=7 учащихся, которые купили мороженое "Спортивное", но не купили мороженое "Мальвина". Остальные учащиеся: 15-7= 5 купили и мороженое "Спортивное", и "Мальвина". Таким образом, мы получили 5 учеников, которые купили оба вида мороженого.

3). Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек. Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.

Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским - 30 человек. По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно,20 человек не владеют ни одним из данных языков.

Ответ: только английским владеет 13 человек, только французским - 30, только немецким - 20 человек.20 человек не знают ни одного из этих языков.

4). В классе 30 человек.20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

Решение: Для решения опять воспользуемся кругами Эйлера.

Пусть х - человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом - (10 − х) человек, только автобусом и троллейбусом - (9 − х) человек, только метро и автобусом - (12 − х) человек. Найдем, сколько человек пользуется одним только метро: 20 − (12 − х) − (10 − х) − х = х − 2. Аналогично получаем: х − 6 - только автобусом и х + 4 - только троллейбусом, так как всего 30 человек, составляем уравнение: х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30, отсюда х = 3.

Задачи для самостоятельного решения:

1). В трех шестых классах 70 ребят. Из них 28 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

2). В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом, а 2 школьника увлекаются сразу тремя видами спорта. Сколько ребят увлекается лишь одним из этих видов спорта?

3). Из 100 человек 85 знают английский язык.80 - испанский, 75 - немецкий. Сколько человек знают только один язык, если все три знают 10 человек?

4). В классе 30 человек.20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

5). Контрольная работа по математике состояла из задачи, уравнения и неравенства. Контрольную работу писали 40 человек. Правильно решили только задачу 2 ученика, только неравенство - 4 человека, только уравнение - 3 человека. Не решили только задачу 7 человек, только уравнение - 5 человек, только пример - 6 человек. Остальные выполнили всю работу правильно. Сколько таких учащихся?

§11. Математические шифры

Занятие по математическим шифрам проводится в виде игры - исторического путешествия. В начале занятия кратко о шифрах рассказывает учитель, а затем слово предоставляется учащимся. Участники кружка рассказывают о разных шифрах, придуманных в разных странах (Афинах, Греции, России). Обыграть историческое путешествие по шифрам можно следующим образом: рефераты рассказывать от первого лица. То есть учащийся, рассказывая, например, о шифре "скитала", говорит от лица полководца Лисандра, приводит конкретный пример на шифр и предлагает остальным участникам кружка зашифровать или, наоборот, расшифровать предложенное сообщения.

Вступительное слово учителя:

Издавна люди изыскивали способы уберечь некоторые важные сообщения от посторонних глаз. Рассказывают, как один царь обрил голову гонца, написал на ней послание и отослал гонца к своему союзнику лишь тогда, когда волосы на его голове отросли. Развитие химии дало удобное средство для тайнописи: симпатические чернила, записи которыми не видны до тех пор, пока бумагу не нагреют или обработают каким-нибудь химикатом. Но чаще стали применять шифры: сначала ими пользовались пираты, отмечая расположение кладов, алхимики, купцы, заговорщики. Впоследствии - дипломаты, стремящиеся сохранить тайны переговоров, военоначальники, скрывающие от противника отданные распоряжения, разведчики и так далее.

При шифровании должны выполняться определенные условия. Во-первых, различные буквы должны обозначаться разными знаками: иначе получатель должен будет гадать, какую из нескольких букв обозначает тот или иной знак. Далее, шифр должен быть трудно разгадываемым - легкие шифры можно применять лишь при условии, что у противника нет времени на разгадку. Наконец, секретность шифра должна сочетаться со сравнительной несложностью операций кодирования и раскодирования: иначе у них уйдет столько времени, что переданная информация устареет. Впрочем, в наше время данные операции могут быть поручены ЭВМ. А если раскодирование потребует слишком много усилий, то можно оказаться в положении легендарного писца. Он писал за плату письма на восточном базаре, но при этом взимал плату еще и как гонец. Дело было в том, что написанное им никто, кроме него самого, понять не мог.

Шифрование методом решетки Кардано.

Кроме замены букв другими буквами или числами, применяются методы шифрования, основанные на перестановке букв. Рассмотрим один из более современных методов перестановки букв - решетке Кардано. Решётка Кардано - инструмент кодирования и декодирования, представляющий собой специальную прямоугольную (в частном случае - квадратную) таблицу-карточку, часть ячеек которой вырезана.

Описание решетки Кардано.

Решетка Кардано сделана из листа картона или пергамента, или же из тонкого металла. Чтобы обозначить линии письма, бумагу разлиновывают, и между этими линиями вырезают прямоугольные области через интервалы произвольной длины. (Показать изготовленную заранее решетку). Шифратор помещает решетку на лист бумаги и пишет сообщение в прямоугольных отверстиях, в которых помещается отдельный символ, слог или целое слово. При передвижении решётки фрагменты заполняются, образуя запись, искажающую исходное сообщение.

У получателя сообщения должна быть такая же решетка. Копии решетки вырезаются из первичного шаблона, однако для взаимно-однозначного соответствия можно было бы сделать множество других шаблонов. Решетку можно разместить в 4 положениях - лицом вверх, лицом вниз, вертикально и в перевернутом положении, что вчетверо увеличивает число возможных размещений сетки.

Чтобы прочитать закодированное сообщение, необходимо наложить решётку Кардано на текст нужное число раз и прочитать буквы, расположенные в вырезанных ячейках. Решётки Кардано представляют собой квадратные таблицы, где четверть ячеек прорезана так, что при четырёх поворотах они показывают весь квадрат. Вписание в прорезанные ячейки текста и повороты решётки продолжаются до тех пор, пока весь квадрат не будет заполнен. Например, на рисунке ниже показан процесс шифровки решеткой 4 на 4:

При зашифровке таким способом, мы получили шифр текст: СЗДО_ЕИКТБОМАРУ_.

Необходимо указать на недостатки этого метода, что он является медленным и требует наличия литературных навыков. Но самое главное, что любой шифровальный аппарат может быть утерян, украден или конфискован. Таким образом, потерять одну решетку - значит потерять всю секретную переписку, шифровавшуюся с помощью этой решетки.

§12. Геометрия на спичках

В работе над задачками можно использовать спички, счётные палочки или просто рисунок на бумаге. Спички имеют стандартную длину и это свойство позволяет строить из них различные геометрические фигуры. Одна спичка - это модель отрезка.

Данное занятие целесообразно провести в форме викторины. Разделить участников кружка на команды (желательно на 2 команды, а также несколько человек сделать независимым жюри). Дать учащимся время на выбор в каждой команде капитана, название команды. По окончании игры можно подарить каждой команде сувениры, приготовленные заранее.

§13. Фокусы

В начале занятия учитель сообщает учащимся, что он - телепат, и может угадать трехзначное число, которое любой из учащихся загадает.

Учитель (обращаясь к одному из участников кружка):

·        Возьми бумажку. Запиши на ней трехзначное число. Мне не показывай!

·        Припиши к нему это же число еще раз.

·        Теперь передай своему соседу.

·        Теперь второй учащийся должен разделить это число на 7 и передать бумажку дальше.

·        Следующий нам разделит это число на 11, запишет его на чистой бумажке и отдаст результат учителю.

·        Слушаем ответ! Правильно? Конечно правильно, это и называется телепатия.

Секрет: последний результат надо разделить на 13 и мы получим исходное число.

Разъяснение: Когда мы к трехзначному числу приписали такое же число, то мы тем самым умножили его на 1001, а затем, разделив последовательно на 7, 11, 13, мы разделили его на 1001, то есть получили задуманное трехзначное число.

Учитель:

·        просит загадать любого участника кружка одно из чисел, изображенных на кругу и не говорить его.

·        Сам выбирает произвольное число n (также из круга).

·        Указывает его ученику.

·        Предлагает продолжить счет от задуманного учеником числа против часовой стрелки, стартуя с числа, указанного учителем и закончив на числе n+12.

Когда же учащийся досчитает, то как раз сам укажет на задуманное им число.

"Угадать возраст"

Предложить умножить человеку, у которого пытаемся узнать возраст, число лет на 2, прибавить 5, а сумму снова умножить на 5. Полученное число сообщить.

Секрет фокуса: Нетрудно догадаться, что последней цифрой результата будет цифра 5. Ее необходимо отбросить а от оставшегося числа отнять 2. Разность и есть искомый результат.

"Угадывание дня, месяца и года рождения"

Предложить одному из учащихся выполнить следующие действия: “Умножить номер месяца, в котором он родились, на 100, затем прибавить день рождения, результат умножить на 2, к полученному числу прибавить 2, результат умножить на 5, к полученному числу прибавить 1, к результату приписать 0, к полученному числу прибавить еще 1 и, наконец, прибавьте число его лет. После этого он должен сообщить, какое число у него получилось.

Секрет фокуса: от названного числа отнять 111, а потом остаток разбить на три грани справа налево по две цифры. Средние две цифры обозначают день рождения, первые две или одна - номер месяца, а последние две цифры - число лет, зная число лет, определяется год рождения.

Фокусы с предметами.

"День недели" <#"564905.files/image024.gif">

 

Смысл фокуса заключается в том, чтобы высший разряд привести в "порядок", расположить цифры в порядке возрастания, с разницей между ними в единицу.

"В какой руке монета?  <http://goodmagic.ru/v-kakoi-ruke-moneta>"

Вот старинный фокус, в котором используется числовое значение монеты. Пусть кого-нибудь возьмет в один кулак 10 рублей, а в другой - 10 копеек. Затем предложите умножить числовое значение монеты, лежащей в правом кулаке, на восемь (или любое другое четное число), а числовое значение другой монеты на пять (или любое нечетное число, какое вам захочется).

Сложив эти два числа, зритель должен сказать вам, четное или нечетное число получилось. После этого вы говорите ему, какая монета у него в какой руке.

Секрет фокуса: Если сумма четная, то в правой руке - 10 копеек; если нечетная - 10 рублей.

Учащимся заранее раздаются сообщения по теме "фокусы". На занятии

ученик рассказывает о фокусе, показывает. По возможности готовит материал к занятию: плакаты или какой-либо раздаточный материал.

"Сколько палочек в кулаке?"

Для этого фокуса необходимо заготовить коробочку с 20 палочками. Фокусник должен повернуться спиной к зрителю и попросить его вытянуть из коробки несколько палочек, но не больше 10, и положить в карман. После этого зритель должен пересчитать палочки, которые остались в коробке. Предположим, их осталось 14. Это число он должен записать на бумаге следующим образом: единица изображается одной палочкой, положенной слева, а четверка - четырьмя палочками справа. Эти пять палочек нужно взять из оставшихся в коробке палочек. Затем палочки, изображавшие число 14, кладутся в карман. В результате зритель вынимает из коробки еще несколько палочек и зажимает их в кулаке. После этого фокусник поворачивается лицом к зрителям, выкладывает палочки из коробки на стол и незамедлительно называет число палочек, зажатых в кулаке.

Секрет фокуса: Чтобы узнать ответ, необходимо отнять из девяти число палочек, рассыпанных на столе.

Кто взял резинку, а кто карандаш?

Отвернитесь и предложите двум участникам фокуса, пусть это будут Женя и Саша, взять одному карандаш, а другому резинку. Далее скажите:

Обладателю карандаша назначаю число 7, обладателю резинки - число 9 (числа могут быть и иными, причем обязательно одно простое, а другое составное, но не делящееся на первое). - Женя, умножь свое число на 2, а Саша на 3 (одно из этих чисел должно целое число раз содержаться в назначенном вами составном числе, как, например, 3 и 9, а другое должно быть с ним взаимно простым, как, например, 3 и 2).

Сложите результаты и скажите мне сумму или скажите, делится ли эта сумма без остатка на 3 (на то данное вам число, которое содержится множителем в назначенном составном числе). Узнав это, вы тотчас можете определить, кто взял карандаш, а кто резинку.

В самом деле, если полученная сумма делится на 3, - это значит, что на 3 умножено число, не делящееся на 3, то есть 7. Зная, кто умножал свое число на 3 (Саша) и что число 7 назначено обладателю карандаша, вы заключаете, что карандаш у Саши. Наоборот, если полученная сумма не делится на 3, то это значит, что на 3 было умножено число, делящееся на 3, то есть 9. В этом случае у Саши - резинка. Как вы докажите этот фокус?

Доказательство. Пусть A - простое число, B - составное, но не делящееся на A. два других числа x и y - взаимно простые, причем y - один из делителей числа B. После требуемых умножений может получиться сумма Ax+By или Ay+Bx. Ясно, что первая сумма не делится на y, а вторая делится. Следовательно, по тому, делится или нет окончательный результат на y, однозначно определяем, было ли умножено на y число A или B.

В качестве домашнего задания предложить детям найти или придумать свои фокусы и объяснить разгадку к ним.

§ 14. Математическая регата

Математическая регата - увлекательное соревнование, которое может быть проведено не только во внеурочное время, но и во время уроков. Она проводится с целью активизации математических знаний учащихся и повышения интереса к предмету. В данном мероприятии представлены задания на различные темы, которые изучались учащимися во время занятия.

Соревнование проводится в 4 тура, то есть своеобразные заезды. Поскольку занятие получается объемное по содержанию, что целесообразнее провести его либо в два урока по 45 минут (по два этапа), либо два занятия подряд, выделив для этого непосредственно 90 минут. Два тура представляют собой коллективное письменное решение задач. Любая задача оформляется и сдается на отдельном листе. Третий тур представляет собой конкурс капитанов. Задания, представленные для решения, также оформляются и сдаются на отдельном листе. Четвертый, завершающий, тур представлен в качестве коллективного творческого задания. То есть каждая из команд зашифровывает сообщение по одному из шифров, которые они знают, по предложенной теме. Данный этап - конкурс можно обыграть: например, одна из команд выбрала Египет. Один из участников кратко рассказывает о стране (сообщение готовят сами учащиеся), а затем представляют текст, который остальные учащиеся должны расшифровать.

Ведущий "Математической регаты" объявляет о начале мероприятия, что в программе ожидаются заезды "одиночек" (конкурс капитанов), а также заезды "четверок", "пятерок" (в зависимости от участников в каждой команде).

Регатой руководит Координатор. Он организует раздачу задания и сбор листов с решениями; проводит разбор задач и объявляет итоги проверки. Координатором может быть учитель.

Время, отведенное командам для решения и "ценность" задач каждого тура в баллах указаны на листах с условиями задач.

Жюри осуществляет проверку решений после окончания каждого тура.

Параллельно с проверкой Координатор проводит разбор задач для учащихся, а затем объявляет итоги проверки. После объявления итогов тура команды, не согласные с тем, как оценены их решения, имеют право подать заявки на апелляцию.

В случае получения такой заявки, комиссия повторно проверяет и, после этого, может изменить свою оценку. Если оценка не изменена, то апелляции эта же комиссия принимает после окончания всех туров регаты, но до окончательного подведения итогов. В результате апелляции оценка решения может быть как повышена, так и понижена, или оставлена без изменения.

В спорных случаях окончательное решение об итогах проверки принимает председатель жюри.

Команды-победители и призеры регаты определяются по сумме баллов, набранных каждой командой во всех турах.