Разработка единого системного подхода к решению задачи оптимального оценивания
Разработка единого системного
подхода к решению задачи оптимального оценивания
Введение
При разработке перспективных и
оптимизации существующих информационно-измерительных систем (ИИС) различного
назначения, широко используемых в гражданских и военных сферах, особое внимание
уделяется вопросам оптимизации обработки измерений, содержащих всевозможные
помехи. Данные помехи могут иметь различную физическую природу и для уменьшения
степени их влияния на работу ИИС используются известные методы статистической
обработки измерений (метод наименьших квадратов (МНК), метод максимального
правдоподобия, метод максимума апостериорной плотности вероятности, байесовские
методы, квазиоптимальные методы, регуляризованные методы, робастные методы и
другие).
Среди указанных методов наиболее
широкое распространение на практике получил МНК и его различные модификации.
Известно, что МНК дает зачастую приемлемые по точности результаты (в задачах
линейного и нелинейного оценивания) при наличии в измерениях случайных
флуктуационных ошибок. В ряде работ рассмотрен вопрос построения устойчивых МНК
- оценок при наличии в измерениях как случайных, так и систематических ошибок
различной физической природы. При этом используется традиционная процедура
расширения пространства состояния, которая на практике зачастую приводит к
известному эффекту «размазывания точности», росту объема вычислительных затрат
и усложнению структур систем обработки измерений.
Более сложной является задача
оценивания в условиях сингулярных помех (СП), математические модели которых
предполагают задание некоторого конечного функционального базиса с точностью до
вектора неизвестных коэффициентов. Зачастую, оптимальное решение такой задачи
удается найти с использованием принципа инвариантности при соблюдении
соответствующих условий регулярности и несмещенности. СП зачастую возникают в
задачах, характеризующихся переходными процессами. Примером может служить
доплеровский измеритель скорости инерциальной навигационной системы, у которой
возникает задача распознавания полезного сигнала на фоне скачкообразно
изменяющихся помех вследствие естественных и искусственных возмущений.
В дипломной работе развивается
системный подход к решению указанной задачи в наиболее общей постановке,
включающей в себя не только оценивание коэффициентов модели полезного сигнала,
но и его производных различного порядка в условиях сингулярных помех (СП) и
флуктуационных шумов (ФШ).
В работе принят широко используемый
в радиотехнике подход к представлению полезных сигналов в классе функций с
финитным спектром (ФФС). Поскольку реальные сигналы не обладают таким спектром,
то в работе исследованы вопросы интерполяции, аппроксимации и дифференцирования
на основе известной теоремы отсчетов с использованием ряда Котельникова, при
этом учтены ограничения на полезный сигнал во временной и частотной областях.
Дипломная работа включает: список
принятых сокращений, введение, три раздела, заключение, список литературы.
сингулярная помеха радиотехника
оценивание финитный спектр
1. Системный подход к задаче
оценивания
.1 Общие положения
В работах
отечественных и зарубежных ученых неоднократно поднималась проблема разработки
единого системного подхода к решению задачи оптимального оценивания. Были
сформулированы условия правильности (регулярности) математической постановки
задач этого класса, которые могли бы гарантировать получение единственного
решения с заданными оптимальными свойствами.
В рамках системного
подхода можно получить комплексное решение вопросов выбора адекватных
математических моделей и функционирования систем обработки измерительной
информации; рационального критерия качества оценивания; оптимальной стратегии
измерений и т.п. При декомпозиции исходной задачи оценивания на составные части
(элементы) основное внимание уделяется их структурным взаимосвязям, влияющим на
характер и качество ее решения.
В настоящее время
для проверки условий регулярности постановки задачи оценивания в основном
используется математический аппарат, базирующийся на теореме о неявных функциях
и предполагающий вычисление рангов соответствующих функциональных матриц для
проверки взаимной однозначности отображений. Однако исследование сложной задачи
трудно осуществить в рамках какого-то одного раздела математики, одной теории
или метода. Постоянное ужесточение требований к качеству и срокам
проектирования систем обработки измерительной информации являются основной
причиной активизации поиска адекватного математического аппарата,
соответствующего основным принципам системного подхода.
В данной главе,
опираясь на [2, 3, 16, 25, 27, 28, 30], в сжатой форме изложены основные
принципы системного подхода к решению задач оценивания. Основное внимание
уделено условиям правильности (регулярности) математической постановки задач
этого класса, которые могли бы гарантировать получение единственного решения с
заданными оптимальными свойствами. На базе известной из математического анализа
теоремы о неявных функциях дается анализ структурных свойств задачи оценивания:
адекватности используемых математических моделей, наблюдаемости измеряемых
параметров, состоятельности критерия качества.
Следуя [16], введем
понятие регулярности (правильности) математической постановки задачи
оценивания. Задачу будем считать регулярной, если в рамках принятой
математической постановки существует единственное решение этой задачи с
требуемыми предельными свойствами по объему выборки измерений.
Рассмотрим
математическую постановку задачи оценивания в рамках системного подхода, т.е. с
учетом структурных взаимосвязей, существующих между элементами задачи.
.2 Основные
элементы задачи. Условия регулярности
Пусть известно, что
оцениваемый процесс (вектор состояния) на отрезке времени [t0, T] характеризуется
вектором 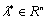 .
Для описания данного процесса воспользуемся приближенной математической моделью
G. В отличие от
.
Для описания данного процесса воспользуемся приближенной математической моделью
G. В отличие от 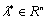 вектор состояния,
соответствующий модели G,
будем обозначать через
вектор состояния,
соответствующий модели G,
будем обозначать через 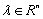 .
.
К модели G предъявляются следующие требования:
модель G должна однозначным образом описывать оцениваемый процесс;
модель G должна в некотором смысле наиболее точно описывать оцениваемый
процесс (адекватность модели);
модель G должна быть достаточно простой в вычислительном отношении.
Функциональное
соответствие между вектором состояния  и вектором измеряемых
параметров у задается математической моделью S.
В большинстве случаев
и вектором измеряемых
параметров у задается математической моделью S.
В большинстве случаев
 (1.1)
(1.1)
Поскольку погрешности,
возникающие при задании модели S,
незначительны, то считаем, что вектор  действительных
измеряемых параметров определяется в соответствии с уравнением
действительных
измеряемых параметров определяется в соответствии с уравнением
 . (1.2)
. (1.2)
Для полного описания
условий функционирования системы обработки измерительной информации,
характеризующих способ комбинации ошибок измерений с измеряемыми параметрами и
вероятностные характеристики ошибок измерений, используется модель Q. В простейшем случае данной модели отвечает следующее
функциональное соответствие:
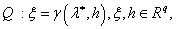 (1.3)
(1.3)
где  -
вектор результатов измерений; h
- вектор ошибок измерений.
-
вектор результатов измерений; h
- вектор ошибок измерений.
Измерения на отрезке
времени  могут
производиться как в дискретные моменты времени ti,
могут
производиться как в дискретные моменты времени ti,
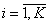 ,
так и непрерывно
,
так и непрерывно  В
первом случае qK-мерный вектор ошибок измерений
В
первом случае qK-мерный вектор ошибок измерений
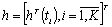
полностью характеризуется
плотностью вероятности р(h).
Если плотность вероятности р(h)
является гауссовской, то будем писать

где  -
вектор математических ожиданий ошибок измерений и Kh
- ковариационная матрица. Во втором случае (непрерывное наблюдение) случайный
процесс h = h(t) характеризуется соответствующим функционалом плотности
вероятности.
-
вектор математических ожиданий ошибок измерений и Kh
- ковариационная матрица. Во втором случае (непрерывное наблюдение) случайный
процесс h = h(t) характеризуется соответствующим функционалом плотности
вероятности.
Следующим элементом
задачи оценивания является критерий качества К. Наибольшее распространение в
настоящее время получил критерий минимума среднего риска (байесов критерий).
Данный критерий применяется в условиях полной априорной определенности. Если же
априорное распределение  неизвестно,
используются другие критерии: минимума условного риска, максимального
правдоподобия, минимаксный.
неизвестно,
используются другие критерии: минимума условного риска, максимального
правдоподобия, минимаксный.
Полагаем, что система
обработки измерительной информации характеризуется нерандомизированным решающим
правилом 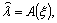 когда
устанавливается детерминированная функциональная связь между оценкой
когда
устанавливается детерминированная функциональная связь между оценкой  и
вектором измерений
и
вектором измерений  .
.
Условным риском называют
риск 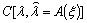 ,
усредненный по условному распределению
,
усредненный по условному распределению  т.е. по функции
правдоподобия
т.е. по функции
правдоподобия 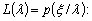
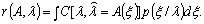 (1.4)
(1.4)
Важным является понятие
апостериорного риска, т.е. риска  , усредненного по
апостериорной плотности вероятности:
, усредненного по
апостериорной плотности вероятности:
 (1.5)
(1.5)
где k - нормировочный коэффициент.
Апостериорный риск
определяется как
 (1.6)
(1.6)
Средний риск, т.е. риск,
усредненный по  и
и
 ,
связан с апостериорным риском простой зависимостью
,
связан с апостериорным риском простой зависимостью
 (1.7)
(1.7)
Отсюда следует, что
байесов критерий оптимальности - критерий минимума среднего риска -
эквивалентен критерию минимума апостериорного риска. Это означает, что
оптимальный байесов алгоритм  должен выбираться из
условия минимизации функционала
должен выбираться из
условия минимизации функционала
 (1.8)
(1.8)
т.е.
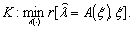 (1.9)
(1.9)
Конкретный алгоритм 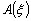 зависит
от выбранной функции потерь
зависит
от выбранной функции потерь  , которая задает меру
отклонения получаемого решения от истинного. Очевидно, что функция потерь и
риск должны отвечать ряду свойств, при которых обеспечивается корректность
применения байесова критерия оптимальности.
, которая задает меру
отклонения получаемого решения от истинного. Очевидно, что функция потерь и
риск должны отвечать ряду свойств, при которых обеспечивается корректность
применения байесова критерия оптимальности.
1.3 Адекватность моделей
задачи оценивания
Условие адекватности
определяет некоторое отношение на множестве математических моделей. Введем в
рассмотрение метрическое пространство  непрерывных на отрезке
[t0, T] вектор-функций
непрерывных на отрезке
[t0, T] вектор-функций  ,
расстояние в котором между элементами
,
расстояние в котором между элементами
 и
и 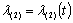
некоторой
неотрицательной действительной функцией 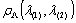 . В практике оценивания
наиболее распространено расстояние
. В практике оценивания
наиболее распространено расстояние
 (1.10)
(1.10)
которое, как известно,
приводит к метрическому пространству, не являющемуся полным. Полное метрическое
пространство получится в том случае, если в  ввести расстояние по
формуле
ввести расстояние по
формуле
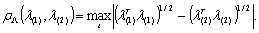 (1.11)
(1.11)
Предпочтение на практике
отдается метрическому пространству  с
расстоянием (1.10), несмотря на то, что оно не является полным. Данное
расстояние может использоваться в качестве меры близости между R и
G (где R и G - соответственно реальное и модельное поведение сигнала). С его
помощью вводятся важные понятия математической модели G,
локально или глобально ε-адекватной реальному полезному сигналу. Величина ε
представляет собой среднеквадратическое расстояние
с
расстоянием (1.10), несмотря на то, что оно не является полным. Данное
расстояние может использоваться в качестве меры близости между R и
G (где R и G - соответственно реальное и модельное поведение сигнала). С его
помощью вводятся важные понятия математической модели G,
локально или глобально ε-адекватной реальному полезному сигналу. Величина ε
представляет собой среднеквадратическое расстояние  между
реальным процессом и его моделью. Она может быть назначена из чисто физических
соображений или получена путем расчета.
между
реальным процессом и его моделью. Она может быть назначена из чисто физических
соображений или получена путем расчета.
По аналогии с  вводится
метрическое пространство
вводится
метрическое пространство 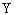 непрерывных
на отрезке [t0, Т] вектор-функций у = у(t)
с расстоянием
непрерывных
на отрезке [t0, Т] вектор-функций у = у(t)
с расстоянием 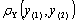 ,
определяемым, например, выражениями типа (1.10) и (1.11). Это позволяет
рассматривать элемент
,
определяемым, например, выражениями типа (1.10) и (1.11). Это позволяет
рассматривать элемент
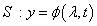 (1.12)
(1.12)
как непрерывное
отображение 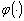 метрического
пространства
метрического
пространства  в
метрическое пространство
в
метрическое пространство 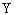 .
При этом необходимое условие ε-адекватности
(локальной и глобальной) в пространстве измеряемых параметров выглядит так:
.
При этом необходимое условие ε-адекватности
(локальной и глобальной) в пространстве измеряемых параметров выглядит так:
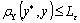 , (1.13)
, (1.13)
где 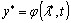 ;
L - постоянная Липшица для отображения
;
L - постоянная Липшица для отображения 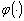 ,
удовлетворяющая условию
,
удовлетворяющая условию
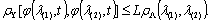 (1.14)
(1.14)
Так, для случая
квадратичной метрики и линейного преобразования
 , (1.15)
, (1.15)
где H - матрица соответствующей размерности, условие (1.14) имеет вид
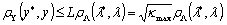 (1.16)
(1.16)
В последнем выражении κmax - максимальное характеристическое число матрицы НТН.
Для получения
необходимых и достаточных условий ε-адекватности
в пространстве измеряемых параметров на отображение 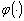 накладываются
определенные ограничения. Так, если отображение
накладываются
определенные ограничения. Так, если отображение 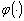 является гемеоморфным,
то для ε-адекватности математической модели G реальному движению R
необходимо и достаточно, чтобы выполнялось неравенство
является гемеоморфным,
то для ε-адекватности математической модели G реальному движению R
необходимо и достаточно, чтобы выполнялось неравенство
 (1.17)
(1.17)
где
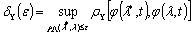 (1.18)
(1.18)
В случае изометрического
отображения 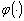 ,
например, когда
,
например, когда 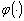 задается
матрицей ортогонального преобразования
задается
матрицей ортогонального преобразования 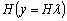 , адекватность
обеспечивается при выполнении неравенства
, адекватность
обеспечивается при выполнении неравенства 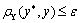 , где ε
находится из условия
, где ε
находится из условия 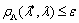 .
.
Для использования приведенных
выше критериев необходимо вычислить значение  . Оно может быть найдено
по результатам измерений, если ошибками измерений практически можно пренебречь.
В противном случае условие адекватности приобретает статистический характер.
. Оно может быть найдено
по результатам измерений, если ошибками измерений практически можно пренебречь.
В противном случае условие адекватности приобретает статистический характер.
В пространстве выборок
статистическое условие адекватности формулируется следующим образом: если
отображение 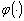 является
гомеоморфным, то для ε-адекватности математической модели G
с вероятностью (надежностью) Р0 реальному поведению R необходимо и достаточно, чтобы выполнялось неравенство
является
гомеоморфным, то для ε-адекватности математической модели G
с вероятностью (надежностью) Р0 реальному поведению R необходимо и достаточно, чтобы выполнялось неравенство
 , (1.19)
, (1.19)
где 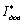 -
верхняя граница доверительного интервала Iдов,
накрывающего с вероятностью Р0 неизвестное значение
-
верхняя граница доверительного интервала Iдов,
накрывающего с вероятностью Р0 неизвестное значение  ;
;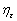 - значение правой части одного из условий ε-адекватности,
сформулированного ранее.
- значение правой части одного из условий ε-адекватности,
сформулированного ранее.
Будем полагать, что
критерий качества K в случае
эквивалентности модели G
реальному поведению R(ε
= 0) обеспечивает получение решения  , обладающего свойством
сильной сходимости:
, обладающего свойством
сильной сходимости:
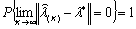 , (1.20)
, (1.20)
где 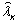 -
оценка
-
оценка  вектора
вектора
 ,
полученная по измерениям, выполненным в дискретные моменты времени
,
полученная по измерениям, выполненным в дискретные моменты времени 
Сформулированное
статистическое условие адекватности оказывается связанным с предположением о
сильной сходимости оценок к своим действительным значениям. Сильная сходимость
лежите основе понятия состоятельности критерия качества K. Состоятельность критерия качества является необходимым условием
для однозначного вывода, получаемого с использованием статистического условия
адекватности. В свою очередь состоятельный критерий качества обеспечивает
сходимость оценок к их действительным значениям только с той точностью, которую
гарантирует величина ε в условии адекватности.
Если условие
состоятельности не выполняется, то результат проверки условия адекватности
относится не только к вопросу близости модели G и реального поведения R, но и к отношению между критерием качества К и условиями опыта Q. Какое из этих двух отношений не удовлетворяет требованиям
регулярности, в данном случае установить трудно.
Условие адекватности
(1.19) не только служит показателем близости G и R, но и является качественным
показателем точности получаемого решения  . Последнее свойство
статистического условия адекватности является очень важным, так как
количественно оценить точность решения в сложных задачах оценивания практически
не представляется возможным.
. Последнее свойство
статистического условия адекватности является очень важным, так как
количественно оценить точность решения в сложных задачах оценивания практически
не представляется возможным.
.4 Состоятельность
критерия качества
Полагая 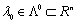 и
учитывая, что оценка
и
учитывая, что оценка 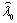 действительного
значения
действительного
значения  вектора
вектора
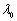 зависит
от мощности выборки (т.е.
зависит
от мощности выборки (т.е. 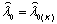 ),
введем в Rn
расстояние с помощью нормы
),
введем в Rn
расстояние с помощью нормы
 . (1.21)
. (1.21)
Рассмотрим известные
статистические свойства оценок.
. Состоятельность,
 , (1.22)
, (1.22)
где  -
любое положительное число; Р{Q)}
- вероятность события Q.
-
любое положительное число; Р{Q)}
- вероятность события Q.
. Несмещенность,
 . (1.23)
. (1.23)
где М{·} - символ
математического ожидания.
. Эффективность (оценка
называется эффективной, если по сравнению с любой другой она обладает
наименьшим разбросом).
. Достаточность (оценка
называется достаточной, если она определяется через достаточные статистики как
функция от них).
Опыт показывает, что в
большинстве случаев невозможно найти такой критерий качества K, чтобы названные статистические свойства оценок удовлетворялись в
совокупности, хотя они и не являются противоречащими друг другу. Данные
свойства называются вторичными оптимальными свойствами оценок, поскольку
первичное свойство определяется критерием качества.
Для решения вопроса о
выборе критерия качества, обеспечивающего получение оценок, обладающих
какими-то вторичными свойствами, необходимо из всех вторичных свойств выбрать
одно или несколько свойств, чтобы множество методов оценивания было разбито на
два класса. В первый класс должны войти методы, обеспечивающие выбранные свойства
(множество состоятельных методов), во второй - все остальные (множество
несостоятельных методов). Среди состоятельных методов оценивания (состоятельных
критериев качества) далее можно искать метод, которому соответствует наиболее
эффективная вычислительная процедура решения задачи.
Из перечисленных выше
статических свойств оценок наименее ограничительными является свойство
состоятельности. Однако условие (1.22) обеспечивает лишь слабую сходимость или
сходимость по вероятности, что не является достаточной гарантией для получения
желательной оценки. Поэтому на практике используются еще два вида сходимости
[2, 3].
. Сходимость сильная,
или почти наверное,
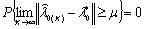 . (1.24)
. (1.24)
. Сходимость в среднем
квадратическом,
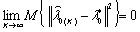 .(1.25)
.(1.25)
Если выбрать в качестве
оптимального свойства сильную сходимость, то получим следующее определение
состоятельности критерия K.
Критерий качества К называется состоятельным по отношению к паре G - S, если
соответствующее ему решение 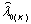 является единственным и
обладает свойством сильной сходимости к действительному значению
является единственным и
обладает свойством сильной сходимости к действительному значению  .
.
В случае, когда модель G эквивалентна реальному поведению R,
то 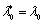 .
Если условие эквивалентности не выполняется, но выполняется условие ε-адекватности,
то начальные условия могут не совпадать. Расстояние между ними будет
.
Если условие эквивалентности не выполняется, но выполняется условие ε-адекватности,
то начальные условия могут не совпадать. Расстояние между ними будет
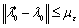 , (1.26)
, (1.26)
где 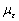 -
некоторое число, зависящее от ε . В этом случае условие (1.24) в
определении состоятельности критерия качества должно выполняться не для всякого
μ > 0, а только для
-
некоторое число, зависящее от ε . В этом случае условие (1.24) в
определении состоятельности критерия качества должно выполняться не для всякого
μ > 0, а только для  .
.
Если решение задачи
оценивания получено в аналитическом виде и имеется плотность вероятности р(ξ)
выборочного вектора ξ, то появляется возможность использования необходимых или
достаточных условий состоятельности, когда критерий K
обеспечивает получение единственного решения  .
.
Если учесть, что из
сильной сходимости следует слабая сходимость, то имеем следующий критерий: для
состоятельности критерия качества К по отношению к паре G - Q необходимо, чтобы
оценка  обладала
свойством сходимости по вероятности
обладала
свойством сходимости по вероятности
 . (1.27)
. (1.27)
Признаком слабой
сходимости может быть выполнение следующего условия: для каждого ε
> 0 существует такое натуральное число К, при котором для любого l > 0 справедливо неравенство
 . (1.28)
. (1.28)
Если все оценки
ограничены в совокупности, то данный признак является также и необходимым.
Следующий критерий,
отражающий достаточные условия состоятельности K,
выглядит так: для состоятельности критерия качества K
по отношению к паре G - Q достаточно, чтобы оценка  обладала свойством
сходимости в среднем квадратическом:
обладала свойством
сходимости в среднем квадратическом:
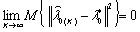 (1.29)
(1.29)
и чтобы
 . (1.30)
. (1.30)
Данным критерием можно
пользоваться, если имеется выражение для математического ожидания квадрата
нормы отклонения оценки  от
действительного значения
от
действительного значения  в
зависимости от числа К результатов измерений.
в
зависимости от числа К результатов измерений.
Сформулированные
критерии задают некоторые границы состоятельности критерия качества К. С
использованием неравенства Чебышева можно сформулировать следующие менее
сложные с практической точки зрения критерии, выполнение которых гарантирует
необходимое условие состоятельности K.
Первый критерий: если оценка  обладает свойством
сходимости в среднем квадратическом
обладает свойством
сходимости в среднем квадратическом
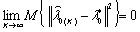 (1.31)
(1.31)
то она обладает
свойством слабой сходимости. Второй критерий: если оценка  обладает
свойством асимптотической несмещенности
обладает
свойством асимптотической несмещенности
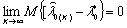 (1.32)
(1.32)
И
 , (1.33)
, (1.33)
то она обладает
свойством слабой сходимости.
В [2, 3] дана
характеристика наиболее распространенных на практике функций потерь, которые
задают многообразие критериев качества, применяемых в задачах оценивания. Там
же перечисляются основные свойства риска  , непосредственно
вытекающие из свойств применяемой функции потерь.
, непосредственно
вытекающие из свойств применяемой функции потерь.
2. Приближение и
дифференцирование полезных сигналов в классе функций с финитным спектром
.1 Интерполяция функций
с финитным спектром
В данном разделе в
качестве моделей полезных сигналов используются функции с финитным спектром
(ФФС) [29], для которых в соответствии с известной теоремой отсчетов
справедливо представление в виде ряда Котельникова. На базе ФФС развивается
метод косвенного оценивания локальных характеристик полезного сигнала, который
в отличие от традиционных подходов в меньшей степени чувствителен к случайным
ошибкам измерений и может быть применен для вычисления соответствующей
производной в любой точке фиксированного интервала наблюдения.
Следует отметить, что
необходимость оценивания локальных характеристик до N-гo порядка включительно возникает довольно часто при решении
широкого круга прикладных задач. При этом на практике, как правило,
используются достаточно простые в вычислительном плане косвенные методы
оценивания, основанные на численном дифференцировании измеренных сигналов с
использованием разностных шаблонов. Среди данных методов наиболее
распространены методы скользящего дифференцирования [26, 27], предполагающие
разложение дифференцируемой функции в соответствующий конечный ряд Тейлора и
вычисление искомой производной только для одной (средней) точки выбранного
интервала измерений. Основной недостаток указанных методов состоит в следующем.
Для уменьшения остаточной (методической) погрешности требуется либо уменьшать
шаг дискретизации по времени либо повышать порядок используемых разностей. Но и
в том, и в другом случаях резко возрастают погрешности, вызываемые случайными
ошибками измерений. Как показано в [26], численные методы, основанные на
разностных представлениях, относятся к классу некорректных, поскольку теряют
устойчивость при наличии случайных ошибок, которые неизбежно сопутствуют
процессу измерений.
Метод N-кратного дифференцирования ФФС, предлагаемый в данном разделе,
позволяет разрабатывать алгоритмы косвенного оценивания, которые в отличие от
традиционных являются корректными в вычислительном плане.
Ниже обсуждаются
отдельные результаты [4, 5, 12], касающиеся интерполяции и аппроксимации ФФС и
функций с нефинитным спектром, которые будут использованы нами при изложении
основного материала.
Пусть функция f(t), интегрируемая в квадрате на всей вещественной оси, представима
в виде
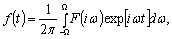 (2.1)
(2.1)
где F(iω) - спектральная плотность функции f(t),
 (2.2)
(2.2)
Согласно известной
теореме Винера-Пэли-Шварца, для того чтобы f(t) была функцией с финитным интегрируемым в квадрате спектром F(iω), необходимо и достаточно, чтобы f(t) могла быть доопределена в комплексной плоскости как целая функция
конечной степени, интегрируемая в квадрате на всей вещественной оси. Следуя
[29], обозначим через 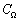 класс
функций f(t) с финитным интегрируемым в квадрате спектром F(iω), для которого справедливо представление (2.1).
класс
функций f(t) с финитным интегрируемым в квадрате спектром F(iω), для которого справедливо представление (2.1).
Поскольку f(t) может быть доопределена как целая функция конечной степени, то
можно воспользоваться следующей интерполяционной формулой Котельникова:
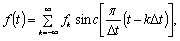 (2.3)
(2.3)
где 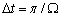 -
шаг между отсчетами fk
= f(kΔt) функции f(t); sincx = sinx/x.
-
шаг между отсчетами fk
= f(kΔt) функции f(t); sincx = sinx/x.
Формула (2.3)
показывает, что для восстановления ФФС f(t) на всей вещественной оси необходимо использовать лишь значения
этой функции fk, называемые отсчетами, которые
выбираются через равные интервалы 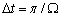 . В разложении (2.3)
можно воспользоваться отсчетами
. В разложении (2.3)
можно воспользоваться отсчетами 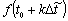 , взятыми в
периодической последовательности точек при любом фиксированном t0, которое указывает лишь начало отсчета переменной t, и при любом
, взятыми в
периодической последовательности точек при любом фиксированном t0, которое указывает лишь начало отсчета переменной t, и при любом 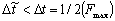 . Последнее утверждение
следует из того, что если спектр f(t) сосредоточен в интервале (-2πFmax, 2πFmax) = (-Ω,
Ω), то он подавно сосредоточен в большем интервале
. Последнее утверждение
следует из того, что если спектр f(t) сосредоточен в интервале (-2πFmax, 2πFmax) = (-Ω,
Ω), то он подавно сосредоточен в большем интервале  ,
где
,
где  .
Если функция f(t) принадлежит пространству
.
Если функция f(t) принадлежит пространству 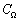 , причем интервал (-Ω,
Ω) - это наименьший интервал, вне которого спектр F(iω) тождественно равен нулю, то величина Δt = π/Ω = l/(2Fmax) указывает наибольший возможный
интервал между отсчетами, при котором представление (2.3) еще справедливо.
, причем интервал (-Ω,
Ω) - это наименьший интервал, вне которого спектр F(iω) тождественно равен нулю, то величина Δt = π/Ω = l/(2Fmax) указывает наибольший возможный
интервал между отсчетами, при котором представление (2.3) еще справедливо.
Таким образом, формула
(2.3) отражает замечательное свойство ФФС - свойство однозначной
восстановимости значений функции на всей оси по ее значениям в дискретной
(периодической) последовательности точек.
В формуле (2.3)
предполагается использование неограниченного числа отсчетов функции f(t). Очевидно, что для конечного числа отсчетов применение формулы
(2.3) без дополнительных ограничений приводит к неединственности решения
интерполяционной задачи. Для того чтобы данное решение было единственным, обычно
сужают класс функций, в котором решается интерполяционная задача. Укажем три
известных способа введения указанных ограничений.
Первый способ состоит в
специальном задании отсчетов вне того интервала, на котором определена функция.
Второй способ заключается во введении дополнительного ограничения
экстремального типа: из всех ФФС в интервале (-Ω,
Ω), обладающих заданными величинами отсчетов в конечном числе
узлов, выбирается та, которая минимизирует некоторый функционал. Третий способ
предполагает ограничение энергии функции вне заданного интервала и подбор
минимального числа степеней свободы (свободных параметров), при котором
достигается требуемая точность приближения функции.
Рассмотрим конкретные
примеры применения этих различных подходов.
При первом подходе
положим равными нулю все отсчеты функции f(t), кроме тех, которые заданы на отрезке [0, Т]. Отсчеты берутся в
моменты
0 ≤ t0 < t1
< ... < tK ≤
Т. Такая интерполяционная задача имеет бесконечное множество решений, поскольку
не заданы отсчеты функции f(t) вне отрезка [0,T].
Если же положить
f(tk) = 0 (2.4)
при k < 0 и k
> К, т.е. считать, что все отсчеты вне отрезка [0, Т] равны нулю, то
интерполяционная задача имеет единственное решение. Например, в случае
равномерно следующих отсчетов из формулы (2.3) получаем общее представление для
множества функций из класса 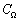 , отсчеты которых равны
нулю вне отрезка [0, T]:
, отсчеты которых равны
нулю вне отрезка [0, T]:
 (2.5)
(2.5)
Число отсчетов, которые
берутся внутри отрезка [0, T],
здесь равно К + 1 = 2FmaxT
+ 1, т.е. считаем, что на отрезке [0, T]
укладывается целое число интервалов длительности Δt. Следует особо подчеркнуть, что если все отсчеты вне отрезка [0, T] равны нулю, то из этого вовсе не вытекает, что функция f(t) тождественно равна нулю вне отрезка [0, T].
Обратимся теперь ко
второму из указанных подходов к ограничению класса функций. В качестве примера
рассмотрим функции с минимальной энергией. Среди всех функций класса 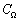 выделим
ту, для которой полная энергия минимальна:
выделим
ту, для которой полная энергия минимальна:
 (2.6)
(2.6)
Нетрудно указать
представление для этого класса функций с минимальной энергией, который мы
обозначим через 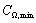 .
Класс
.
Класс 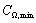 -
это подмножество класса
-
это подмножество класса 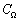 ,
следовательно, по теореме отсчетов для любой из функций
,
следовательно, по теореме отсчетов для любой из функций 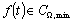 имеем
представление вида (2.3).
имеем
представление вида (2.3).
Члены ряда (2.3) попарно
ортогональны на всей оси в силу соотношений
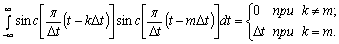 (2.7)
(2.7)
Поэтому, возводя обе
части равенства (2.3) в квадрат, раскрывая скобки и интегрируя почленно,
получаем
 (2.8)
(2.8)
Предположим сначала, что
отсчеты на отрезке [0, T]
берутся в моменты 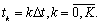 Поскольку
в правой части равенства (2.8) стоит ряд из неотрицательных величин, причем
отсчеты fk,
Поскольку
в правой части равенства (2.8) стоит ряд из неотрицательных величин, причем
отсчеты fk, 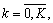 фиксированы,
выражение (2.8) достигает минимума, когда все остальные отсчеты обращаются в
нуль. Следовательно, в том случае, когда отсчеты на отрезке [0, T] берутся в моменты
фиксированы,
выражение (2.8) достигает минимума, когда все остальные отсчеты обращаются в
нуль. Следовательно, в том случае, когда отсчеты на отрезке [0, T] берутся в моменты  , ФФС и минимальной
энергией задаются формулой (2.5).
, ФФС и минимальной
энергией задаются формулой (2.5).
Таким образом, для
восстановления функции рассматриваемого класса достаточно знать лишь отсчеты fk, 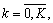 и в классе
и в классе 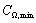 эта
интерполяционная задача имеет единственное решение.
эта
интерполяционная задача имеет единственное решение.
.2 Аппроксимация функций
с финитным спектром
Рассмотрим теперь
возможность аппроксимации с заданной точностью
ε > 0 на отрезке [0, T] функции  при
помощи конечного числа членов ряда Котельникова (2.3). Очевидно, что такая
возможность существует, поскольку ряд (2.3) сходится равномерно в каждой
ограниченной области. Таким образом, для каждого отрезка [0, T] и заданного ε > 0 можно
указать такие числа i и т, что при 0 ≤ t ≤ T
будет выполняться неравенство
при
помощи конечного числа членов ряда Котельникова (2.3). Очевидно, что такая
возможность существует, поскольку ряд (2.3) сходится равномерно в каждой
ограниченной области. Таким образом, для каждого отрезка [0, T] и заданного ε > 0 можно
указать такие числа i и т, что при 0 ≤ t ≤ T
будет выполняться неравенство
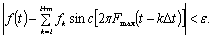 (2.9)
(2.9)
Однако длительность mΔt интервала времени, на
котором в данном случае берутся отсчеты, может значительно превосходить
величину Т. Поэтому возникает вопрос о том, с какой точностью приближается
функция  ,
задаваемая рядом (2.3), если воспользоваться лишь некоторым фиксированным
числом членов этого ряда.
,
задаваемая рядом (2.3), если воспользоваться лишь некоторым фиксированным
числом членов этого ряда.
Рассмотрим частную сумму
ряда (2.3) при нечетном числе отсчетов, равном 2K
+ 1:
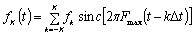 (2.10)
(2.10)
Введем невязку
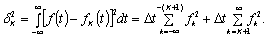 (2.11)
(2.11)
Из (2.11) следует, что
отбрасывание «хвостов» ряда Котельникова приводит к среднеквадратической ошибке
аппроксимации ФФС. Эта ошибка равна энергии «хвостов».
Для оценки погрешности,
возникающей при замене ряда Котельникова частной суммой вида (2.10),
целесообразно ввести определенные предположения относительно скорости убывания
функции f(t) при |t| → ∞.
Предположим, что
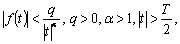 (2.12)
(2.12)
(для удобства вместо [0,
Т] рассматривается отрезок [-T/2,
T/2]).
Используя результаты
работ [4, 12], не сложно показать, что ограничение (2.12) приводит к следующей
оценке
 (2.13)
(2.13)
Анализ функции εK(t) показывает, что в точках  она обращается в нуль, а
ее максимумы растут по мере приближения к краям отрезка [-KΔt, KΔt].
она обращается в нуль, а
ее максимумы растут по мере приближения к краям отрезка [-KΔt, KΔt].
Приведенные в данном
подразделе результаты составляют основу аппроксимации функций, которые
встречаются в задачах оценивания и могут быть отнесены к классу ФФС. Однако на
практике у реальных функций спектр не может быть финитным. Таким образом, для
построения адекватных моделей необходимо выяснить влияние отбрасываемых
«хвостов» спектра функции на качество ее аппроксимаций.
2.3 Аппроксимация
функций с нефинитным спектром
Прежде всего,
рассмотрим задачу приближения произвольных функций с конечной полной энергией
(т.е. интегрируемых в квадрате на всей оси) при помощи ФФС и конечной полной
энергией.
Пусть φ(t) - произвольная
функция, интегрируемая в квадрате на всей оси -∞ < t < ∞, и пусть . Рассмотрим выражение
. Рассмотрим выражение
 (2.14)
(2.14)
которое имеет смысл
полной энергии разности этих функций и равно квадрату среднеквадратической
погрешности при аппроксимацией функции φ(t) функцией f(t).
Поставим перед собой
задачу: среди всех функций f(t) пространства 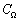 найти
ту, которая обращает в минимум величину
найти
ту, которая обращает в минимум величину  , т.е. осуществляет
наилучшие приближенные функции φ(t) в
среднеквадратическом смысле.
, т.е. осуществляет
наилучшие приближенные функции φ(t) в
среднеквадратическом смысле.
Для решения задачи
заметим, что разность φ(t) - f(t) также интегрируема в квадрате на всей оси. Поэтому, используя
равенство Парсеваля имеем
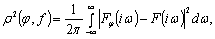 (2.15)
(2.15)
где Fφ(iω) - спектральная
плотность функции φ(t).
Представим себе теперь,
что мы хотим применить метод, основанный на теореме отсчетов, для аппроксимации
функции с нефинитным спектром. Если выбрать шаг между моментами отсчета равным Δt = π/Ω и составить ряд Котельникова для функции φ(t),
спектр которой не финитен, то получим новую функцию
 (2.16)
(2.16)
где φk = φ(kΔt).
Для того чтобы ряд
(2.16) сходился равномерно в каждой ограниченной области, а функция  принадлежала
пространству
принадлежала
пространству 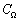 ,
нужно наложить определенные ограничения на поведение чисел φk, т.е. сузить класс рассматриваемых функций φ(t).
Будем для простоты предполагать функцию Fφ(iω) непрерывной на всей оси и убывающей при |ω|
→ ∞ быстрее, чем
,
нужно наложить определенные ограничения на поведение чисел φk, т.е. сузить класс рассматриваемых функций φ(t).
Будем для простоты предполагать функцию Fφ(iω) непрерывной на всей оси и убывающей при |ω|
→ ∞ быстрее, чем  при некоторых σ
> 0, β > 1. Эти условия обеспечивают интегрируемость в первой степени
и в квадрате спектральной плотности Fφ(iω) на всей оси, и, следовательно, обеспечивают непрерывность
функции
при некоторых σ
> 0, β > 1. Эти условия обеспечивают интегрируемость в первой степени
и в квадрате спектральной плотности Fφ(iω) на всей оси, и, следовательно, обеспечивают непрерывность
функции  и
ее квадратичную интегрируемость.
и
ее квадратичную интегрируемость.
Функция  имеет
финитный спектр в интервале (-Ω, Ω).
Оценка разности
имеет
финитный спектр в интервале (-Ω, Ω).
Оценка разности 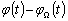 по
абсолютной величине:
по
абсолютной величине:
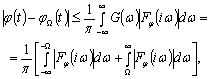 (2.17)
(2.17)
где
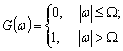 (2.18)
(2.18)
Таким образом, при
анализе и синтезе моделей на основе рядов Котельникова необходимо учитывать
результирующую погрешность приближения (аппроксимации), обусловленную ошибками
двух типов. Ошибки первого типа обусловлены усечением в частотной области (т.е.
осуществляется переход к функциям с финитным спектром из класса 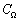 ), а ошибки второго типа - усечением в
пространственной (временной) области (т.е. осуществляется ограничение числа
отсчетов аппроксимируемой функции).
), а ошибки второго типа - усечением в
пространственной (временной) области (т.е. осуществляется ограничение числа
отсчетов аппроксимируемой функции).
2.4
Дифференцирование функций с финитным спектром
Рассмотрим новый
метод N-кратного дифференцирования, базирующийся на применении ряда
Котельникова, который по сравнению с известными методами в большой степени ориентирован
на решение конкретных задач оценивания.
Пусть задана
функция f(t), принадлежащая к классу 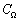 , для которой справедливо разложение в виде ряда Котельникова
(2.3). Рассмотрим производную N-го порядка f(N)(t) от функции f(t), представимой рядом (2.3).
Относительно функции f(N)(t) (
, для которой справедливо разложение в виде ряда Котельникова
(2.3). Рассмотрим производную N-го порядка f(N)(t) от функции f(t), представимой рядом (2.3).
Относительно функции f(N)(t) ( ) можно утверждать, что она, так же как и функция f(t), может быть доопределена в
комплексной плоскости как целая функция конечной степени, интегрируемая в
квадрате на всей вещественной оси, и для нее справедливо представление
) можно утверждать, что она, так же как и функция f(t), может быть доопределена в
комплексной плоскости как целая функция конечной степени, интегрируемая в
квадрате на всей вещественной оси, и для нее справедливо представление
 (2.19)
(2.19)
где 
Таким образом,
располагая совокупностью отсчетов  , в соответствии с (2.19) можно однозначно восстановить
всю функцию
, в соответствии с (2.19) можно однозначно восстановить
всю функцию  .
.
Поставим задачу
найти точные аналитические выражения для отсчетов 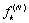 , позволяющие по заданной совокупности
, позволяющие по заданной совокупности 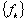 находить искомую совокупность
находить искомую совокупность  , а на ее основе восстановить функцию
, а на ее основе восстановить функцию  .
.
Для случая
произвольного N применительно к функциям  , заданным бесконечной совокупностью отсчетов, можно
воспользоваться следующим результатом.
, заданным бесконечной совокупностью отсчетов, можно
воспользоваться следующим результатом.
Для класса 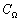 ф
ункций f(t) с финитным спектром производная N-гo порядка f(N)(t) в отсчетных точках вычисляется по таким формулам:
ф
ункций f(t) с финитным спектром производная N-гo порядка f(N)(t) в отсчетных точках вычисляется по таким формулам:
для четных 
 (2.20)
(2.20)
для нечетных 
 (2.21)
(2.21)
([х] - целая часть
числа х).
Вывод данных формул
(опущен в силу громоздкости) базируется на использовании формулы Лейбница для N-кратного дифференцирования
произведения двух функций и раскрытии неопределенностей типа 0/0, появляющихся
при переходе к отсчетным точкам.
Остановимся на
вопросе дифференцирования функции fK(t), которая задается в виде конечного ряда Котельникова и
интерполирует исходную функцию . Очевидно, что спектр
функции fK(t) сосредоточен в интервале (-Ω, Ω), и, следовательно,
. Очевидно, что спектр
функции fK(t) сосредоточен в интервале (-Ω, Ω), и, следовательно,  . Производная
N-гo порядка от функции
. Производная
N-гo порядка от функции  в отсчетных точках вычисляется по формулам:
в отсчетных точках вычисляется по формулам:
для четных 
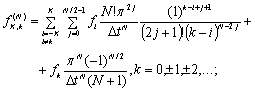 (2.22)
(2.22)
для нечетных 
 (2.23)
(2.23)
Формулы (2.22),
(2.23) непосредственно следуют из (2.20), (2.21), если в последних перейти от
бесконечных сумм по индексу i к конечным суммам.
Формулы (2.22) и
(2.23) также допускают векторно-матричную форму записи:
 (2.24)
(2.24)
где 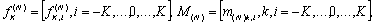
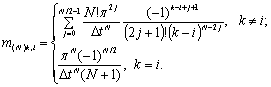 (2.25)
(2.25)
для четных 
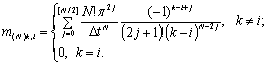 (2.26)
(2.26)
для нечетных 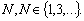
.5 Погрешности
дифференцирования функций с финитным спектром
Для оценки
погрешностей дифференцирования введем ограничение на поведение функции  при
при  Положим,
что для интегрируемой в квадрате функции
Положим,
что для интегрируемой в квадрате функции  , выполняется неравенство (2.12).
, выполняется неравенство (2.12).
Введем теперь меру
отклонения функций f(N)(t) и  в отсчетных точках отрезка [-Т, Т]:
в отсчетных точках отрезка [-Т, Т]:
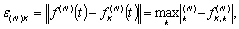 (2.27)
(2.27)
где 
Рассмотрим первый
случай, когда при фиксированных
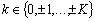 и d > 1 последовательность
и d > 1 последовательность 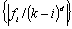 монотонно убывает
монотонно убывает
(при i = - К - 1, - К - 2,... и i = K + 1, K + 2,...).
Если
последовательность 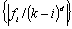 монотонно
убывает
монотонно
убывает
(при i = - К - 1, - К - 2,... и i = K + 1, K + 2,...) и, кроме того, выполняется
условие (2.12), то для погрешности 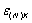 дифференцирования функции
дифференцирования функции  справедлива оценка
справедлива оценка
 (2.28)
(2.28)
где
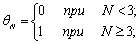
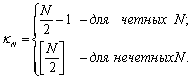
При получении
оценки (2.28) был использован известный признак Лейбница для установления
сходимости знакочередующихся рядов.
Поскольку для
функций f(t) из класса 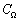 величина
величина
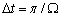 является фиксированной, то в формуле (2.28) варьируемыми
оказываются параметры Т и К. Значения данных параметров выбираются из условия
обеспечения требуемой точности N-кратного дифференцирования.
является фиксированной, то в формуле (2.28) варьируемыми
оказываются параметры Т и К. Значения данных параметров выбираются из условия
обеспечения требуемой точности N-кратного дифференцирования.
Рассмотрим теперь
более общий случай, когда последовательность 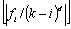 может не являться монотонно убывающей, однако условие (2.12)
выполняется.
может не являться монотонно убывающей, однако условие (2.12)
выполняется.
Если выполняется
условие (2.12), то для погрешности 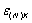 дифференцирования функции
дифференцирования функции  справедлива оценка
справедлива оценка
 (2.29)
(2.29)
Введем теперь меру
отклонения функций  и
и 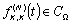 :
:
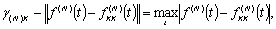 (2.30)
(2.30)
где 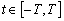
Если выполняется
условие (2.12), то для погрешности 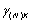 дифференцирования функции
дифференцирования функции  на отрезке [-Т, T] справедлива оценка
на отрезке [-Т, T] справедлива оценка
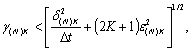 (2.31)
(2.31)
где 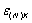 в зависимости от характера поведения f(t) при
в зависимости от характера поведения f(t) при  удовлетворяет неравенствам (2.28) или (2.29),
удовлетворяет неравенствам (2.28) или (2.29),
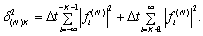 (2.32)
(2.32)
При расчетах в
соответствии с формулой (2.31) можно воспользоваться оценкой
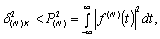 (2.33)
(2.33)
которая показывает,
что величина среднеквадратического отклонения 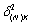 не превосходит полной энергии
не превосходит полной энергии  функции
функции 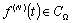 . В
этом случае
. В
этом случае
 (2.34)
(2.34)
Если ввести
ограничения на поведение функции  :
:
 (2.35)
(2.35)
то применительно к 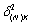 можно воспользоваться более строгой оценкой
можно воспользоваться более строгой оценкой
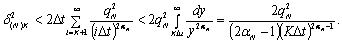 (2.36)
(2.36)
2.6
Дифференцирование функций с нефинитным спектром
Рассмотрим
возможность применения изложенного в предыдущих подразделах математического
аппарата для N-кратного дифференцирования функций с нефинитным спектром.
Пусть φ(t) - произвольная функция, у которой
производная  абсолютно
непрерывна на каждом конечном интервале и
абсолютно
непрерывна на каждом конечном интервале и 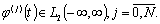 Для непрерывной на всей оси спектральной плотности
Для непрерывной на всей оси спектральной плотности 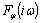 функции φ(t) введем следующее ограничение
функции φ(t) введем следующее ограничение
 (2.37)
(2.37)
Допустим, что среди
всех функций из класса 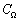 выбрана
та f(t), которая обращает в минимум
выражение
выбрана
та f(t), которая обращает в минимум
выражение
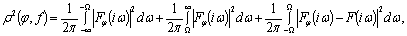 (2.38)
(2.38)
где 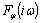 и
и 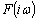 -
спектральные плотности функций φ(t) и f(t) соответственно.
-
спектральные плотности функций φ(t) и f(t) соответственно.
Как указывалось в
подразд. 2.3, минимум  достигается
тогда, когда
достигается
тогда, когда
 (2.39)
(2.39)
при этом
 (2.40)
(2.40)
Отклонение функций  и
и 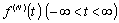
 (2.41)
(2.41)
при выполнении
условий (2.37), (2.39) удовлетворяет неравенству
 (2.42)
(2.42)
где  .
.
Результирующую
погрешность находится так
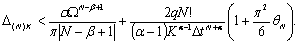 (2.43)
(2.43)
Таким образом,
полученные формулы позволяют оценить результирующую погрешность N-кратного дифференцирования,
возникающую при использовании ФФС к реальным сигналам.
.7
Дифференцирование финитных функций
Обратимся теперь к
наиболее распространенному в практике случаю, когда дифференцируемые функции
являются финитными на временной оси, и, следовательно, не принадлежат классу
ФФС.
Анализ приведенных
ранее аналитических зависимостей показывает, что погрешность N-кратного дифференцирования на
основе ряда Котельникова определяется уровнями усечения функции и ее спектра, а
также скоростями их убывания соответственно в пространственной (временной) и
частотной областях. Для функций, имеющих высокую скорость убывания в указанных
областях, рассмотренный математический аппарат позволяет обеспечить требуемую
точность N-кратного дифференцирования на заданном отрезке [-Т, Т], если
уровни усечения не превышают некоторых заранее установленных значений.
Рассмотрим возможность применения данного аппарата для вычисления производных
соответствующего порядка от финитных функций 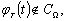 имеющих «плохие» спектральные свойства и большие уровни усечения
в пространственной (временной) области.
имеющих «плохие» спектральные свойства и большие уровни усечения
в пространственной (временной) области.
Первый подход к дифференцированию
финитных функций, основанный на сплайн-продолжениях, состоит в следующем. Пусть
 - произвольная финитная функция (рис. 2.1), у которой производная
- произвольная финитная функция (рис. 2.1), у которой производная  непрерывна, а
непрерывна, а 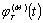 кусочно-непрерывна
на отрезке [-Т, Т]. Используя операцию сплайн-продолжения, перейдем от функции
кусочно-непрерывна
на отрезке [-Т, Т]. Используя операцию сплайн-продолжения, перейдем от функции 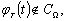 заданной на отрезке [-Т, Т], к новой функции
заданной на отрезке [-Т, Т], к новой функции 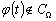 , заданной на всей вещественной оси (рис. 2.2):
, заданной на всей вещественной оси (рис. 2.2):
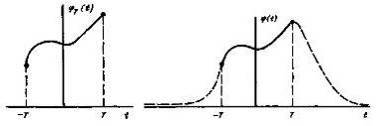
Рисунок 2.1 Рисунок
2.2
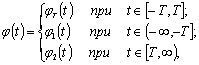 (2.44)
(2.44)
где φ1(t) и φ2(t) - вспомогательные функции, у
которых производные  и
и 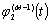 непрерывны при
непрерывны при  и
и  соответственно, и, кроме того, выполняются равенства (условия
«стыковки»)
соответственно, и, кроме того, выполняются равенства (условия
«стыковки»)
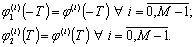 (2.45)
(2.45)
Таким образом, из
исходной финитной функции  получили
сплайн-продолженную функцию φ(t), заданную на интервале (-∞, ∞), состоящем из
основного информационного отрезка [-Т, Т] и двух вспомогательных
неинформационных полуоткрытых интервалов
получили
сплайн-продолженную функцию φ(t), заданную на интервале (-∞, ∞), состоящем из
основного информационного отрезка [-Т, Т] и двух вспомогательных
неинформационных полуоткрытых интервалов 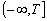 и
и  .
.
Далее, вводя
оператор  усечения в пространственной (временной) области перейдем от φ(t) к финитной функции
усечения в пространственной (временной) области перейдем от φ(t) к финитной функции  , заданной на отрезке
, заданной на отрезке  (рис. 2.3). При этом потребуем выполнения следующего условия:
(рис. 2.3). При этом потребуем выполнения следующего условия:
 (2.46)
(2.46)
где  - уровни усечения функции φ(t) и ее производных
- уровни усечения функции φ(t) и ее производных  ,
которые выбираются с учетом полученных в предыдущих подразделах аналитических
зависимостей исходя из условия минимизации результирующей погрешности N-кратного дифференцирования (N < M).
,
которые выбираются с учетом полученных в предыдущих подразделах аналитических
зависимостей исходя из условия минимизации результирующей погрешности N-кратного дифференцирования (N < M).

Рисунок 2.3
Очевидно, что
периодически (с периодом  )
продолженная на всю числовую ось функция
)
продолженная на всю числовую ось функция  остается непрерывной на этой оси вместе со своими производными до
(М - 1)-го порядка включительно. Вспомогательные функции φ1(t) и φ2(t), удовлетворяющие условиям (2.45),
(2.46), могут быть достаточно произвольного вида. Однако полагаем, что
независимо от вида финитной функции
остается непрерывной на этой оси вместе со своими производными до
(М - 1)-го порядка включительно. Вспомогательные функции φ1(t) и φ2(t), удовлетворяющие условиям (2.45),
(2.46), могут быть достаточно произвольного вида. Однако полагаем, что
независимо от вида финитной функции  в качестве φ1(t) и φ2(t) используются функции,
интегрируемые в квадрате, т.е.
в качестве φ1(t) и φ2(t) используются функции,
интегрируемые в квадрате, т.е. 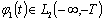 и
и  . Каждая из функций φ1(t) и φ2(t) должна удовлетворять 2М условиям
(2.45), (2.46) и поэтому имеет 2М подлежащих определению коэффициентов.
. Каждая из функций φ1(t) и φ2(t) должна удовлетворять 2М условиям
(2.45), (2.46) и поэтому имеет 2М подлежащих определению коэффициентов.
Необходимость
введения условий (2.45), (2.46) можно обосновать из следующих соображений. Если
финитную функцию  периодически
продолжить на всю числовую ось (обозначим полученную функцию через
периодически
продолжить на всю числовую ось (обозначим полученную функцию через  ), то коэффициенты соответствующего ряда Фурье можно определить по
формуле
), то коэффициенты соответствующего ряда Фурье можно определить по
формуле
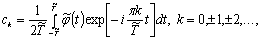 (2.47)
(2.47)
при этом скорость
убывания коэффициентов ck с возрастанием  определяется
дифференциальными свойствами данной периодической функции.
определяется
дифференциальными свойствами данной периодической функции.
Близким по своей
сути к подходу, основанному на сплайн-продолжении, является известный метод
Малиева разложения функций в быстросходящиеся ряды Фурье. Однако данный метод
предполагает лишь одностороннее продолжение исходной финитной функции с
обеспечением выполнения условия непрерывности соответствующей периодической
функции и ее производных различных порядков.
Построение же
функции φ(t) (2.44) требует двухстороннего
продолжения  ,
выполнения указанного условия непрерывности (2.45) и обеспечения требуемых
уровней усечения функции φ(t) и ее производных
,
выполнения указанного условия непрерывности (2.45) и обеспечения требуемых
уровней усечения функции φ(t) и ее производных

в пространственной
(временной) области (см. (2.46)).
Второй подход к
дифференцированию финитных функций, имеющих «плохие» спектральные свойства,
состоит в домножении исходной функции  заданной на отрезке [-Т, Т], на некоторую функцию-регуляризатор
заданной на отрезке [-Т, Т], на некоторую функцию-регуляризатор 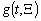 (где Ξ - вектор постоянных параметров), заданную на том же отрезке [-Т, T] или на расширенном отрезке
(где Ξ - вектор постоянных параметров), заданную на том же отрезке [-Т, T] или на расширенном отрезке  :
:
 (2.48)
(2.48)
где 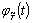 является продолжением функции
является продолжением функции  с отрезка [-Т, T] на отрезок
с отрезка [-Т, T] на отрезок 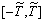 с
сохранением свойства непрерывности. Для функции
с
сохранением свойства непрерывности. Для функции 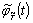 и ее производных различных порядков на краях отрезка
и ее производных различных порядков на краях отрезка 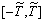 можно задать соответствующие уровни усечения (по аналогии с
(2.46)) исходя из условия минимизации результирующей погрешности N-кратного дифференцирования.
можно задать соответствующие уровни усечения (по аналогии с
(2.46)) исходя из условия минимизации результирующей погрешности N-кратного дифференцирования.
В качестве
функции-регуляризатора 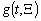 можно
рассматривать функцию вида
можно
рассматривать функцию вида
 (2.49)
(2.49)
где 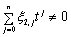 при
при 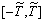 .
.
В простейшем случае
в качестве 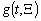 можно
рассматривать гауссовскую кривую, характеризующуюся двумя параметрами. Известно
[29], что такая кривая имеет максимально возможную скорость убывания в
пространственной и частотной областях и реализует знак равенства в известном
«соотношении неопределенности». Выбор значений параметров гауссовской кривой,
обеспечивающих требуемое поведение функции
можно
рассматривать гауссовскую кривую, характеризующуюся двумя параметрами. Известно
[29], что такая кривая имеет максимально возможную скорость убывания в
пространственной и частотной областях и реализует знак равенства в известном
«соотношении неопределенности». Выбор значений параметров гауссовской кривой,
обеспечивающих требуемое поведение функции 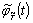 и ее спектра соответственно в пространственной (временной) и
частотной областях, не представляет затруднений, поскольку известно, что
и ее спектра соответственно в пространственной (временной) и
частотной областях, не представляет затруднений, поскольку известно, что 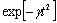 убывает на бесконечности быстрее любой степени t при γ > 0.
убывает на бесконечности быстрее любой степени t при γ > 0.

Рисунок 2.4
Если найдена
производная 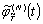 , то
вычисление искомой производной
, то
вычисление искомой производной  осуществляется
в соответствии с известной формулой [4], в которой необходимо заменить
осуществляется
в соответствии с известной формулой [4], в которой необходимо заменить 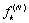 на
на  на
на 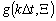 и
и 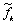 на
на 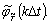 Для того чтобы избежать трудоемкой в вычислительном плане
операции восстановления искомой производной в соответствии с указанной
формулой, можно использовать в качестве
Для того чтобы избежать трудоемкой в вычислительном плане
операции восстановления искомой производной в соответствии с указанной
формулой, можно использовать в качестве 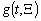 функцию-регуляризатор срезывающего типа [4]. Данная функция
является бесконечно дифференцируемой на всей вещественной оси (-∞, ∞)
и вместе со своими производными тождественно равна нулю для всех
функцию-регуляризатор срезывающего типа [4]. Данная функция
является бесконечно дифференцируемой на всей вещественной оси (-∞, ∞)
и вместе со своими производными тождественно равна нулю для всех 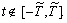 Кроме того, функция-регуляризатор срезывающего типа на отрезке
[-Т, T] тождественно равна единице, и, следовательно, составная функция
Кроме того, функция-регуляризатор срезывающего типа на отрезке
[-Т, T] тождественно равна единице, и, следовательно, составная функция 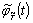 на отрезке [-T, T] повторяет исходную функцию
на отрезке [-T, T] повторяет исходную функцию  . Однако построение срезывающих функций сводится к вычислению
соответствующих определенных интегралов, что создает определенные неудобства на
практике по сравнению с функциями типа (2.49).
. Однако построение срезывающих функций сводится к вычислению
соответствующих определенных интегралов, что создает определенные неудобства на
практике по сравнению с функциями типа (2.49).
Ниже приводятся
результаты численного эксперимента, направленного на вычисление первой и второй
производных от финитных функций 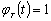 (рис.
2.4),
(рис.
2.4),  (рис. 2.5) и
(рис. 2.5) и 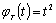 (рис.
2.6), существующих на отрезке [-Т, T]. В качестве продолженных использовались соответственно функции
(рис.
2.6), существующих на отрезке [-Т, T]. В качестве продолженных использовались соответственно функции  ,
, 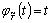 и
и 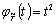 , существующие на отрезке
, существующие на отрезке 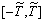 , а в качестве
, а в качестве 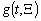 -
функция-регуляризатор (2.49):
-
функция-регуляризатор (2.49):

Рис. 2.5 Рис.
2.6

где 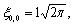
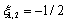 (полагалось,
что в векторе Ξ
все параметры равны нулю, за исключением
(полагалось,
что в векторе Ξ
все параметры равны нулю, за исключением  и
и 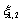 , а
параметр
, а
параметр  ),
),


где 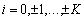 ,
,

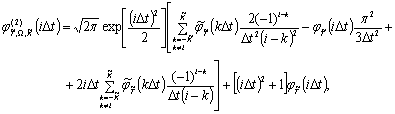
Данные выражения
позволяют находить приближенные значения производных  и
и 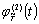 в
отсчетных точках
в
отсчетных точках 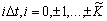 ,
отрезка
,
отрезка 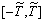 . При практических расчетах необходимо помнить, что отрезку [-Т,
Т] соответствует сетка интерполяции объемом 2К + 1, а отрезку
. При практических расчетах необходимо помнить, что отрезку [-Т,
Т] соответствует сетка интерполяции объемом 2К + 1, а отрезку 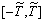 - сетка объемом
- сетка объемом 
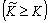 . При
этом узлы отрезка
. При
этом узлы отрезка 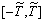 образуются
путем добавления к узлам
образуются
путем добавления к узлам 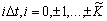 , слева
и справа соответствующего числа узлов.
, слева
и справа соответствующего числа узлов.

Рисунок 2.7 Рисунок
2.8
На рис. 2.7
приведены зависимости относительной погрешности вычисления (для случая, когда  )
)

от объема сетки
аппроксимации 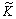 для
функций
для
функций 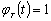 (кривая 1),
(кривая 1),  (кривая
2) и
(кривая
2) и 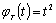 (кривая 3) при следующих исходных данных:
(кривая 3) при следующих исходных данных:
T = 3, 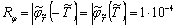 ,
, 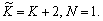 Кривые 1,2 и 3 на рис. 2.8 показывают зависимость
Кривые 1,2 и 3 на рис. 2.8 показывают зависимость 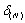 от
от 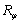 для
функций
для
функций 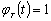 ,
,  и
и 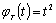 соответственно при Т = 3, К = К + 2 = 8, N = 1.
соответственно при Т = 3, К = К + 2 = 8, N = 1.
Анализ графиков
(см. рис. 2.7 и 2.8) показывает: во-первых, высокая точность вычисления
производных обеспечивается при достаточно малых объемах сетки интерполяции;
во-вторых, точность расчетов существенно зависит от выбора значений параметров 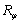 и
и 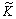 , которые определяются исходя из условия минимизации
результирующей погрешности дифференцирования с учетом формул, полученных в
предыдущих подразделах.
, которые определяются исходя из условия минимизации
результирующей погрешности дифференцирования с учетом формул, полученных в
предыдущих подразделах.
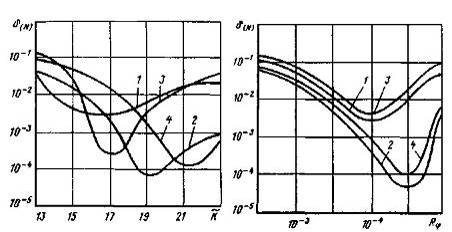
Рисунок 2.9 Рисунок
2.10
На рис. 2.9 и 2.10 приведены
аналогичные зависимости 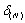 от
параметров
от
параметров 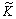 и
и 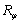 для N = 2 (кривые 1, 2 - для функции
для N = 2 (кривые 1, 2 - для функции  , кривые 3, 4 - для функции
, кривые 3, 4 - для функции 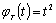 ). Зависимости рассчитывались при следующих исходных данных: на
рис. 2.9 кривые 1, 3 -
). Зависимости рассчитывались при следующих исходных данных: на
рис. 2.9 кривые 1, 3 -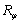 = 4∙10-4,
Т = 3,
= 4∙10-4,
Т = 3,  кривые 2, 4 -
кривые 2, 4 -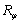 = 4∙10-5,
Т = 3,
= 4∙10-5,
Т = 3,  на рис. 2.10 кривые 1, 3 -
на рис. 2.10 кривые 1, 3 -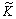 = К + 3 = 8, Т = 3; кривые 2, 4 -
= К + 3 = 8, Т = 3; кривые 2, 4 -  = К + 4 = 9, Т = 3.
= К + 4 = 9, Т = 3.
Анализ графиков
(см. рис. 2.9 и 2.10) показывает, что погрешности вычисления второй производной
близки к погрешностям вычисления первой производной (по порядку и характеру
поведения кривых). При этом лишь незначительно (4 и 6 точек) увеличивается
объем сетки отрезка [-Т, Т], обеспечивающий требуемую точность вычислений.
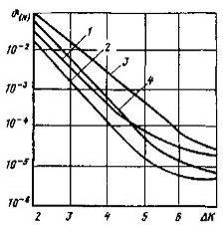
Рисунок 2.11
На рис. 2.11
представлены зависимости 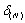 от
от 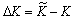 при следующих исходных данных: кривая
при следующих исходных данных: кривая 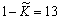 ,
, 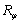 = 1∙10-5,
T = = 3,
N = 1;
кривая 2 -
= 1∙10-5,
T = = 3,
N = 1;
кривая 2 - 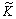 = 14,
= 14, 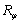 = 1∙10-5, T = 3, N= 1; кривая
= 1∙10-5, T = 3, N= 1; кривая 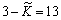 ,
, 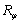 = 1∙10-5,
T = 3, N = 2; кривая
= 1∙10-5,
T = 3, N = 2; кривая  ,
, 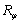 = =1∙10-5,
T = 3, N = 1.
= =1∙10-5,
T = 3, N = 1.
Анализ графиков
(см. рис. 2.11) показывает, что точность вычислений существенно зависит от
числа дополнительных точек, причем с добавлением каждой новой пары точек
погрешность дифференцирования уменьшается более чем на порядок и уже при 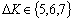 дальнейшее приращение в точности становится практически
незначительным.
дальнейшее приращение в точности становится практически
незначительным.
2.8 Влияние
погрешностей задания отсчетов функций на точность дифференцирования
При практической
реализации численных алгоритмов дифференцирования на ЭВМ принципиальным
является вопрос, связанный с устойчивостью разрабатываемых алгоритмов по
отношению к методическим погрешностям и погрешностям задания отсчетов
дифференцируемых функций. Последний вид погрешностей связан, например, с
ошибками округления или измерения, которые необходимо учитывать при решении
задачи оценивания.
Покажем, что
математический аппарат N-кратного дифференцирования на основе ряда Котельникова в
большинстве практически важных случаев является более устойчивым по отношению к
случайным ошибкам задания отсчетов дифференцируемых функций по сравнению с
традиционными методами, предполагающими использование конечно-разностных схем.
Пусть φ(t) - произвольная функция,
методическая погрешность N-кратного дифференцирования которой не превышает величины 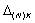 . Считаем также заданным вектор отсчетов
. Считаем также заданным вектор отсчетов 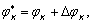 где
где 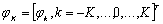 -
вектор-столбец отсчетов дифференцируемой функции φ(t);
-
вектор-столбец отсчетов дифференцируемой функции φ(t); 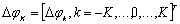 -
вектор-столбец ошибок задания отсчетов
-
вектор-столбец ошибок задания отсчетов  исходной функции φ(t) на отрезке [-Т, Т]. Принимаем, что ошибка
исходной функции φ(t) на отрезке [-Т, Т]. Принимаем, что ошибка 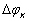 является векторной случайной величиной, имеющей нулевое
математическое ожидание и соответствующую корреляционную матрицу
является векторной случайной величиной, имеющей нулевое
математическое ожидание и соответствующую корреляционную матрицу 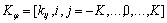 где
где  -
дисперсия.
-
дисперсия.
Учитывая, что
модель отсчетов предполагает наличие гауссовских ошибок, а формулы N-кратного дифференцирования на
основе ряда Котельникова соответствуют линейным преобразованиям над отсчетами
исходной функции, корреляционную матрицу 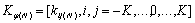 ошибок вычисления значений компонент вектора производных
ошибок вычисления значений компонент вектора производных 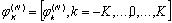 можно представить в следующем виде [2]:
можно представить в следующем виде [2]:
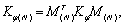 (2.50)
(2.50)
где 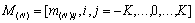 - матрица дифференцирования.
- матрица дифференцирования.
Если матрица 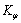 является диагональной, причем
является диагональной, причем 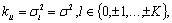
то элементы 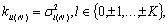 матрицы
матрицы  можно
определить следующим образом:
можно
определить следующим образом:
 (2.51)
(2.51)
для четных  ;
;
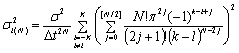 (2.52)
(2.52)
для нечетных  .
.
Анализ выражений
(2.51) и (2.52) показывает, что степень устойчивости результатов
дифференцирования к случайным ошибкам задания отсчетов функции φ(t) в основном определяется величиной 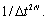 Поскольку метод N-кратного дифференцирования на основе ряда Котельникова
работоспособен при достаточно больших значениях Δt (для функций с «хорошими»
спектральными свойствами), а традиционные (конечно-разностные) методы - лишь
при малых значениях
Поскольку метод N-кратного дифференцирования на основе ряда Котельникова
работоспособен при достаточно больших значениях Δt (для функций с «хорошими»
спектральными свойствами), а традиционные (конечно-разностные) методы - лишь
при малых значениях  , то
можно утверждать, что в большинстве практически важных случаев, встречающихся
при решении задач оценивания, может быть достигнута более высокая устойчивость
к указанным ошибкам. Очевидно, что чем «лучше» спектральные свойства функции φ(t) (уже ее спектр), тем больше Δt, и, следовательно, меньшие значения дисперсии
, то
можно утверждать, что в большинстве практически важных случаев, встречающихся
при решении задач оценивания, может быть достигнута более высокая устойчивость
к указанным ошибкам. Очевидно, что чем «лучше» спектральные свойства функции φ(t) (уже ее спектр), тем больше Δt, и, следовательно, меньшие значения дисперсии 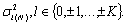
По аналогии с [2] в
качестве величины, характеризующей суммарную ошибку алгоритма N-кратного дифференцирования,
основанного на применении ряда Котельникова, можно взять сумму квадратов
максимальной случайной ошибки 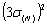 и
методической ошибки
и
методической ошибки 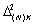 :
:
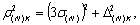 (2.53)
(2.53)
где 
Поскольку за счет
рационального выбора параметров методическая ошибка 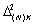 может быть сведена к сколь угодно малой величине, то очевидно,
что результирующая ошибка N-кратного дифференцирования будет в основном определяться
величиной
может быть сведена к сколь угодно малой величине, то очевидно,
что результирующая ошибка N-кратного дифференцирования будет в основном определяться
величиной 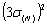 .
.
Рассмотрим
следующий иллюстративный пример. Пусть требуется оценить радиальную скорость  изменения дальности
изменения дальности 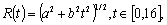 где а и b - некоторые константы. Данная формула соответствует движению
летательного аппарата на постоянной высоте и с постоянной скоростью. Интервал
отсчетов 2Т = 16 (здесь и далее все величины полагаем безразмерными), а = 104,
b = 2,5∙102,
ошибки
где а и b - некоторые константы. Данная формула соответствует движению
летательного аппарата на постоянной высоте и с постоянной скоростью. Интервал
отсчетов 2Т = 16 (здесь и далее все величины полагаем безразмерными), а = 104,
b = 2,5∙102,
ошибки  , взаимно не коррелированы, распределены по нормальному закону с
нулевым математическим ожиданием и дисперсией
, взаимно не коррелированы, распределены по нормальному закону с
нулевым математическим ожиданием и дисперсией  . В качестве функции-регуляризатора
. В качестве функции-регуляризатора 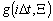 использована функция вида
использована функция вида 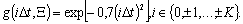

Рисунок 2.12
Проведенный анализ
показал, что для обеспечения абсолютной методической погрешности  вычисления искомых производных радиальной дальности R(t) на основе разработанного алгоритма
(2.23) достаточно выбрать шаг Δt = 0,8. При расчетах же методом
скользящего дифференцирования необходим шаг Δt = 0,1.
вычисления искомых производных радиальной дальности R(t) на основе разработанного алгоритма
(2.23) достаточно выбрать шаг Δt = 0,8. При расчетах же методом
скользящего дифференцирования необходим шаг Δt = 0,1.
На рис. 2.12
изображены графики, иллюстрирующие зависимость относительной погрешности
вычислений  от
от  :
:
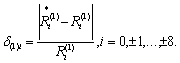
Анализ графиков для
различных значений σ2 показывает, что метод N-кратного дифференцирования на
основе ряда Котельникова обеспечивает высокую точность косвенного оценивания локальных
характеристик движения летательного аппарата при достаточно малых объемах сетки
интерполяции. При этом наивысшая точность достигается в середине интервала [-Т,
Т]. При аналогичном расчете для метода скользящего среднего при тех же исходных
данных видно, что вычислительная процедура уже при σ2 = 1,5 становится неустойчивой.
О преимуществах
рассмотренного в разделе 2 математического аппарата свидетельствует также
анализ единичных дисперсий ошибок оценивания величин  Для метода скользящего дифференцирования (при заданном уровне
методической погрешности)
Для метода скользящего дифференцирования (при заданном уровне
методической погрешности)
 а для
подхода, основанного на применении ряда Котельникова,
а для
подхода, основанного на применении ряда Котельникова, 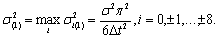
Используя исходные
данные иллюстративного примера убеждаемся, что применение ряда Котельникова
позволило снизить дисперсию ошибки оценивания радиальной скорости в 19,5 раза.
Следует отметить,
что полученные в иллюстративном примере оценки являются единичными. Дальнейшее
повышение точности может быть достигнуто путем оптимальной статистической
обработки семейства единичных замеров.
3 Метод оценивания числовых
характеристик полезных сигналов на фоне сингулярных помех в классе функций с
финитным спектром
.1 Общие положения
В настоящем разделе в
классе функций с финитным спектром разработан метод оптимального вычисления
операторов 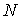 -
кратного дифференцирования, позволяющий формировать несмещенные значения
соответствующих производных, инвариантные к сингулярным погрешностям входных
данных. Получены оценки сверху на методическую и флуктуационную погрешности
вычислений. Дан иллюстративный пример.
-
кратного дифференцирования, позволяющий формировать несмещенные значения
соответствующих производных, инвариантные к сингулярным погрешностям входных
данных. Получены оценки сверху на методическую и флуктуационную погрешности
вычислений. Дан иллюстративный пример.
При решении широкого
круга математических и прикладных задач зачастую возникает необходимость 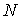 -
кратного дифференцирования функций, заданных на некоторой системе точек [4, 5,
12].
-
кратного дифференцирования функций, заданных на некоторой системе точек [4, 5,
12].
В работе [4], с
использованием интерполяционной формулы Котельникова развит математический
аппарат 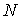 -
кратного дифференцирования в классе функций с финитным спектром, получены
оценки сверху на соответствующие погрешности вычислений. Однако в [4] отсчеты
значений дифференцируемых функций полагались известными точно. Вместе с тем, на
практике вычислительный процесс всегда сопровождается ошибками, при этом
результирующая погрешность входных данных в общем случае содержит как
случайную, так и сингулярную составляющие. Известно, что оптимальное решение
данной задачи можно получить в рамках метода наименьших квадратов (МНК). Однако
непосредственное применение последнего зачастую приводит к решению задач
высокой размерности либо к получению смещенных оценок из-за наличия сингулярных
погрешностей.
-
кратного дифференцирования в классе функций с финитным спектром, получены
оценки сверху на соответствующие погрешности вычислений. Однако в [4] отсчеты
значений дифференцируемых функций полагались известными точно. Вместе с тем, на
практике вычислительный процесс всегда сопровождается ошибками, при этом
результирующая погрешность входных данных в общем случае содержит как
случайную, так и сингулярную составляющие. Известно, что оптимальное решение
данной задачи можно получить в рамках метода наименьших квадратов (МНК). Однако
непосредственное применение последнего зачастую приводит к решению задач
высокой размерности либо к получению смещенных оценок из-за наличия сингулярных
погрешностей.
С учетом вышесказанного
вполне правомерно поставить вопрос о развитии полученных ранее результатов и
разработке универсального метода оптимального оценивания значений операторов 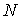 -
кратного дифференцирования, позволяющего формировать несмещенные оценки
соответствующих производных, устойчивые к сингулярным погрешностям входных
данных. Требование устойчивости вычислительных алгоритмов к сингулярным
погрешностям является принципиально важным, поскольку нескомпенсированность
последних практически полностью обесценивает получаемые результаты и приводит к
невозможности достоверной интерпретации вычислительного эксперимента [2, 3, 23,
24, 27]. Решению вышеперечисленного круга проблем посвящена настоящая работа.
-
кратного дифференцирования, позволяющего формировать несмещенные оценки
соответствующих производных, устойчивые к сингулярным погрешностям входных
данных. Требование устойчивости вычислительных алгоритмов к сингулярным
погрешностям является принципиально важным, поскольку нескомпенсированность
последних практически полностью обесценивает получаемые результаты и приводит к
невозможности достоверной интерпретации вычислительного эксперимента [2, 3, 23,
24, 27]. Решению вышеперечисленного круга проблем посвящена настоящая работа.
.2 Математическая постановка задачи
Пусть функция  представима
в виде
представима
в виде
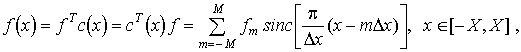 (3.1)
(3.1)
где  -
вектор неизвестных отсчетов функции
-
вектор неизвестных отсчетов функции
 ,
, 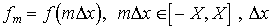
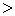 0,
0, 
=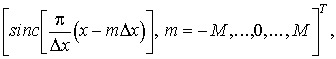
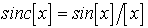 .
.
Зададим сетку  ,
узлам которой ставятся в соответствие значения
,
узлам которой ставятся в соответствие значения

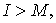 (3.2)
(3.2)
где  и
и
 -
соответственно сингулярная
-
соответственно сингулярная 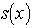 и случайная
и случайная  составляющие
результирующей погрешности в узле
составляющие
результирующей погрешности в узле  .
.
Для описания сингулярной
погрешности 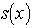 воспользуемся
следующей моделью
воспользуемся
следующей моделью
 ,
(3.3)
,
(3.3)
где  -
вектор неизвестных коэффициентов,
-
вектор неизвестных коэффициентов,
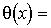
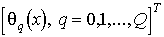 - вектор
линейно-независимых функций.
- вектор
линейно-независимых функций.
В дальнейшем помимо
(3.2) нам потребуется следующая векторная форма записи
 , (3.4)
, (3.4)
где 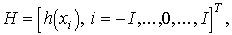
 ,
,
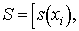
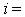
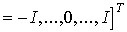 ,
, 
Считаем, что случайный
вектор  характеризуется
нулевым математическим ожиданием и корреляционной матрицей
характеризуется
нулевым математическим ожиданием и корреляционной матрицей 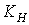 .
.
Введем следующий
оператор 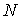 -кратного
дифференцирования
-кратного
дифференцирования 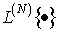 :
:
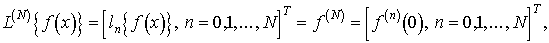
где 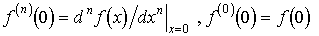 ,
то есть рассматривается вопрос, связанный с вычислением значений функции
,
то есть рассматривается вопрос, связанный с вычислением значений функции  и
ее производных до
и
ее производных до 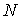 -
го порядка включительно в центральной точке интервала
-
го порядка включительно в центральной точке интервала  .
.
Поставим задачу
оптимального оценивания значений данного оператора на основе конечномерной
выборки (3.4), содержащей сингулярную  и случайную
и случайную  погрешности.
Искомый оптимальный оператор
погрешности.
Искомый оптимальный оператор 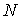 - кратного
дифференцирования
- кратного
дифференцирования 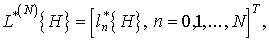 значения
которого близки (в смысле определяемого ниже критерия оптимальности) к
значениям
значения
которого близки (в смысле определяемого ниже критерия оптимальности) к
значениям 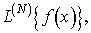 будем
искать в виде
будем
искать в виде
 (3.5)
(3.5)
где 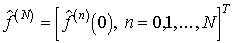 -
вектор оценок искомых производных в точке
-
вектор оценок искомых производных в точке  ,
,
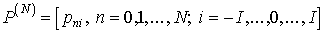 - матрица искомых
коэффициентов оптимального оператора
- матрица искомых
коэффициентов оптимального оператора  .
.
В дальнейшем полагаем,
что составная матрица
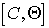 , где
, где 

 и
и 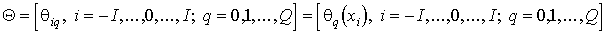 имеет
ранг, равный
имеет
ранг, равный 

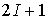 , то есть поставленная
выше задача разрешима.
, то есть поставленная
выше задача разрешима.
Корреляционная матрица
оценки (3.5) для принятой модели случайного вектора  находится
по правилу
находится
по правилу
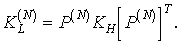 (3.6)
(3.6)
Требуется найти вид
матрицы  оператора
оператора
 ,
которая обеспечивает минимизацию следа матрицы
,
которая обеспечивает минимизацию следа матрицы 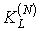 (то есть величины
(то есть величины
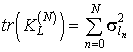 , где
, где 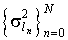 -
диагональные члены матрицы
-
диагональные члены матрицы 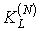 ), а
), а
также выполнение условия
несмещенности оценки значений линейного оператора 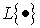
 (3.7)
(3.7)
и условия инвариантности
оператора  к
сингулярным ошибкам измерений
к
сингулярным ошибкам измерений
 , (3.8)
, (3.8)
где  -
нулевой вектор-столбец размерности
-
нулевой вектор-столбец размерности 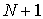 .
.
Ставится также задача
проанализировать влияние неадекватности модели (3.1) на результаты оптимального
оценивания значений оператора 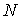 - кратного
дифференцирования.
- кратного
дифференцирования.
3.3 Решение задачи
С учетом (3.1), (3.5), и
(3.7), замечая, что  ,
имеем
,
имеем

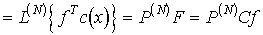 , (3.9)
, (3.9)
откуда вытекает
следующее условие несмещенности
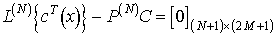 ,
(3.10)
,
(3.10)
где  -
нулевая матрица размерности
-
нулевая матрица размерности
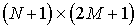 ,
, 
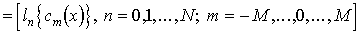 .
.
Принимая во внимание
(3.8), получим
 , (3.11)
, (3.11)
откуда вытекает
следующее условие инвариантности
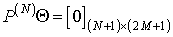 . (3.12)
. (3.12)
Для компактности
последующих выкладок введем следующие обозначения:
 ,
, 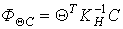 ,
,
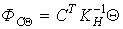 ,
,
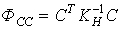 ,
,
 ,
,
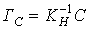 ,
,

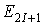 -
единичная матрица
-
единичная матрица
размерности 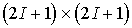 .
С учетом данных обозначений, а также полагая, что система уравнений (3.10),
(3.12) совместна, сформулируем и докажем следующую теорему.
.
С учетом данных обозначений, а также полагая, что система уравнений (3.10),
(3.12) совместна, сформулируем и докажем следующую теорему.
Матрица 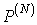 линейного
оператора
линейного
оператора 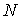 -
кратного дифференцирования
-
кратного дифференцирования 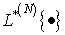 , обеспечивающая
минимизацию следа корреляционной матрицы
, обеспечивающая
минимизацию следа корреляционной матрицы 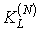 и выполнение условий
несмещенности (3.10) и инвариантности (3.12), определяется по следующей формуле
[9, 10, 14, 15]:
и выполнение условий
несмещенности (3.10) и инвариантности (3.12), определяется по следующей формуле
[9, 10, 14, 15]:
 , (3.13)
, (3.13)
где  ,
,
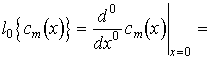
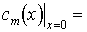
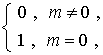 (3.14)
(3.14)
для 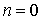 ;
;
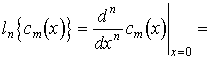

 (3.15)
(3.15)
для  ;
;
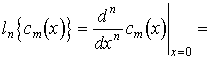
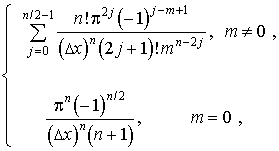 (3.16)
(3.16)
для  ,
,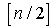 - целая часть числа
- целая часть числа  .
.
Доказательство
осуществляется в соответствии с методом множителей Лагранжа.
С учетом (3.1) для
оптимальной оценки 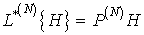 минимальный
след матрицы
минимальный
след матрицы 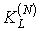 находится
по следующему правилу
находится
по следующему правилу
 , (3.17)
, (3.17)
где
 , (3.18)
, (3.18)
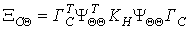 . (3.19)
. (3.19)
Соотношения (3.13) -
(3.16), а также (3.17) - (3.19) составляют математическую основу развитого
оптимального метода инвариантного оценивания значений операторов 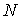 -
кратного дифференцирования при наличии во входных данных как случайных, так и
сингулярных ошибок.
-
кратного дифференцирования при наличии во входных данных как случайных, так и
сингулярных ошибок.
Несложный анализ
показывает, что необходимыми и достаточными условиями практической
реализуемости данного метода являются:
наличие ненулевых матриц
в (3.13) и невырожденность исходных матриц поставленной задачи ;
совместность условий
несмещенности (3.7) и инвариантности (3.8), то есть базисные функции в (3.1) и
(3.3) должны быть линейно независимыми и , следовательно, составная матрица
должна иметь ранг, равный  ;
;
количество узлов в (3.2)
должно превышать общее число неизвестных коэффициентов в моделях (3.1) и (3.3),
то есть 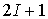 >
>
3.4 Оценка
методической погрешности
Дадим теперь оценку
методической погрешности оптимального оценивания, обусловленной неадекватностью
принятой математической модели (3.1). Пусть истинная функция  имеет
следующее аналитическое представление
имеет
следующее аналитическое представление


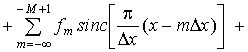
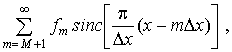 (3.20)
(3.20)
при этом функцию  считаем
интегрируемой в квадрате на всей вещественной оси, для которой [29]
считаем
интегрируемой в квадрате на всей вещественной оси, для которой [29]
 , (3.21)
, (3.21)
где  при
при
 при
при

 .
.
Пусть для функции  выполняются
следующие ограничения:
выполняются
следующие ограничения:


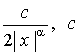
 0,
0, 
 1,
1, 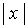
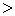
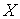 . (3.22)
. (3.22)
Введем меру отклонения
функций  и
и
 :
:
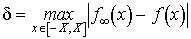 . (3.23)
. (3.23)
Опираясь на результаты
второго раздела можно получить ряд оценок сверху на методические погрешности.
Так, отклонение функций  и
и
 при
выполнении ограничения (3.22) удовлетворяет неравенству
при
выполнении ограничения (3.22) удовлетворяет неравенству


 . (3.24)
. (3.24)
Соответственно для
оценки погрешности 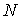 -
кратного дифференцирования введем меру отклонения функций
-
кратного дифференцирования введем меру отклонения функций  и
и
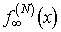 в
точке
в
точке  :
:
 .
(3.25)
.
(3.25)
Для погрешности 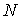 -
кратного дифференцирования, обусловленной усечением ряда Котельникова функции
-
кратного дифференцирования, обусловленной усечением ряда Котельникова функции  в
пространственной области, при выполнении условия (3.22) справедлива оценка
в
пространственной области, при выполнении условия (3.22) справедлива оценка


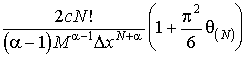 , (3.26)
, (3.26)
где 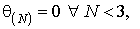
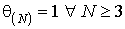 .
.
Введем результирующую
погрешность 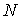 -
кратного дифференцирования в точке
-
кратного дифференцирования в точке  :
:
 ,
(3.27)
,
(3.27)
где  -
погрешность, обусловленная переходом от функции
-
погрешность, обусловленная переходом от функции  с нефинитным спектром к
функции
с нефинитным спектром к
функции  с
финитным спектром (усечение в частотной области),
с
финитным спектром (усечение в частотной области),  -
погрешность, обусловленная переходом от
-
погрешность, обусловленная переходом от  к функции
к функции  с
финитным спектром (усечение в пространственной области).
с
финитным спектром (усечение в пространственной области).
Отклонение функций  и
и
 в
точке
в
точке  удовлетворяет
неравенству
удовлетворяет
неравенству
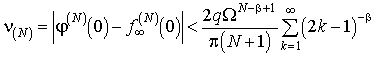 .(3.28)
.(3.28)
Найдем теперь среднее
значение методической ошибки, полагая, что для истинной модели справедливо
следующее представление
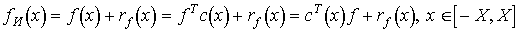 , (3.29)
, (3.29)
где 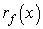 -
остаточный член.
-
остаточный член.
Используя символ
математического ожидания 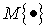 и
учитывая, что
и
учитывая, что
 и
и 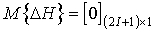 ,
найдем среднее значение методической ошибки
,
найдем среднее значение методической ошибки 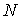 - кратного
дифференцирования:
- кратного
дифференцирования:


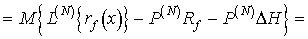
 ,
(3.30)
,
(3.30)
где  .
.
Непосредственно из
(3.29) и (3.30) следует, что методическая погрешность целиком определяется
свойствами линейных операторов 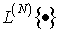 и
и 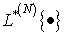 ,
а также величиной остаточного члена
,
а также величиной остаточного члена 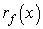 и его дискретного
аналога
и его дискретного
аналога  .
Следует отметить, что минимизация результирующей погрешности оценивания
значений оператора
.
Следует отметить, что минимизация результирующей погрешности оценивания
значений оператора  ,
которая характеризуется величинами
,
которая характеризуется величинами  и
и 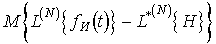 ,
достигается на практике путем рационального варьирования параметрами
,
достигается на практике путем рационального варьирования параметрами 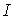 и
и
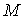 .
В качестве такой результирующей погрешности можно, например, принять следующую
величину
.
В качестве такой результирующей погрешности можно, например, принять следующую
величину
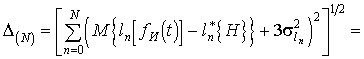
=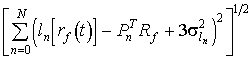 .
(3.31)
.
(3.31)
.5 Сравнительный анализ
разработанного метода с методом наименьших квадратов
Рассмотрим случай, когда
 и
, следовательно,
и
, следовательно, 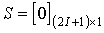 .
Оценка
.
Оценка  вектора
вектора
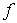 в
соответствии с классическим МНК имеет вид [23]
в
соответствии с классическим МНК имеет вид [23]

 (3.32)
(3.32)
Принимая во внимание,
что  ,
оптимальная оценка
,
оптимальная оценка 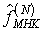 вектора
вектора
 с
учетом (4.1) находится следующим образом
с
учетом (4.1) находится следующим образом
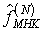
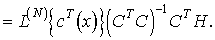 (3.33)
(3.33)
С учетом того, что в
рассматриваемом случае 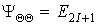 получаем
получаем
 (3.34)
(3.34)
Поскольку  (где
(где
 -
оптимальная оценка вектора
-
оптимальная оценка вектора  , построенная согласно
развиваемому в статье подходу), то с учетом (3.34) имеем
, построенная согласно
развиваемому в статье подходу), то с учетом (3.34) имеем
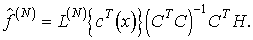 (3.35)
(3.35)
Анализ формул (4.33) и
(4.35) показывает, что для случая, когда  , оценки по методу МНК и
оценки, соответствующие разработанному методу, совпадают. Данный вывод не
является неожиданным, поскольку обе оценки являются несмещенными, при этом
, оценки по методу МНК и
оценки, соответствующие разработанному методу, совпадают. Данный вывод не
является неожиданным, поскольку обе оценки являются несмещенными, при этом

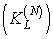
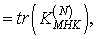 где
где 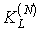 и
и
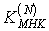 -
корреляционные матрицы оценок (4.33) и (4.35) соответственно.
-
корреляционные матрицы оценок (4.33) и (4.35) соответственно.
Основное достоинство
развиваемого в статье подхода состоит в том, что он не требует увеличения
размерности решаемой задачи при построении оптимальных несмещенных оценок,
инвариантных к сингулярным погрешностям. Можно сказать, что развит
модифицированный МНК, обладающий внутренним свойством инвариантности к
сингулярным погрешностям измерений заданного класса.
3.6 Результаты вычислительного
эксперимента
Рассмотрим задачу оптимального
оценивания при наличии сингулярной и флуктуационной помех для следующих
исходных данных:
 ,
, 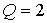 ,
,
 ,
,
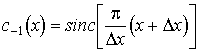 ,
,
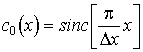 ,
,
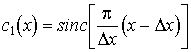 и
и
 ,
,
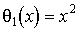 ,
,
 ,
то есть
,
то есть 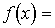
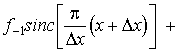
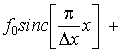
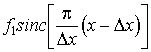 ,
,
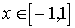 ,
,
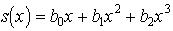 ,
,
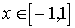 .
.
Принимая 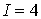 ,
,
 ,
,
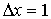 ,
с учетом (1.2) в узлах сетки
,
с учетом (1.2) в узлах сетки  имеем
имеем


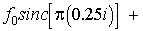
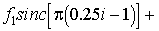
 ,
,  .
.
Поскольку  в
данном случае рассматривалась задача оценивания сглаженного значения функции
в
данном случае рассматривалась задача оценивания сглаженного значения функции  и
ее первой производной
и
ее первой производной  в
средней точке
в
средней точке  отрезка
отрезка
 .
.
При моделировании вектор
случайных погрешностей  полагался
распределенным по нормальному закону с нулевым математическим ожиданием и
корреляционной матрицей
полагался
распределенным по нормальному закону с нулевым математическим ожиданием и
корреляционной матрицей
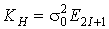 , где
, где 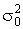 -
заданная положительная константа.
-
заданная положительная константа.
Кроме того, полагалось,
что на отрезке  выполнялось
тождественное равенство
выполнялось
тождественное равенство  ,
то есть
,
то есть 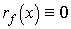 .
Вычисления проводились с точностью
.
Вычисления проводились с точностью 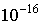 .
.
Раскроем далее основные
вектора и матрицы (здесь и далее числа округлены до третьего знака после
запятой) с учетом специфики рассматриваемого примера:

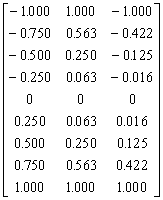 ,
, 
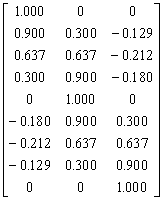 ,
,
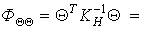
 ,
,

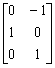 ,
,
 ,
,

 .
.
Исходя из условий
практической реализуемости развитого метода, сформулированных во втором
параграфе, в данном примере система базисных функций  выбрана
линейно независимой. При этом ранг расширенной матрицы
выбрана
линейно независимой. При этом ранг расширенной матрицы  равен
6, что обеспечивает совместность условий несмещенности и инвариантности.
равен
6, что обеспечивает совместность условий несмещенности и инвариантности.
Искомая матрица  выглядит
так
выглядит
так
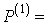
 .
.
Для принятых исходных
данных имеем следующие значения дисперсий ошибок оценивания: 
 (для
(для
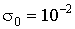 ).
).
Рассмотрим теперь более
общий случай, когда для заданного отрезка  число
число 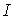 -
произвольное число натурального ряда, то есть
-
произвольное число натурального ряда, то есть 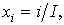
 .
Примем также
.
Примем также  ,
,
 .
.
Для моделирования на ЭВМ
случайных погрешностей 
 использовался датчик
случайных чисел, генерирующий квазислучайную последовательность с нормальным
распределением, характеризующимся нулевым математическим ожиданием и
соответствующей дисперсией
использовался датчик
случайных чисел, генерирующий квазислучайную последовательность с нормальным
распределением, характеризующимся нулевым математическим ожиданием и
соответствующей дисперсией 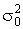 .
.
Результаты моделирования
отображены в виде таблицы, показывающей зависимость результирующих оптимальных
оценок 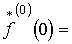
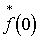 и
и 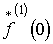 ,
а также евклидовой нормы вектора сингулярной ошибки
,
а также евклидовой нормы вектора сингулярной ошибки 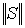 от
числа
от
числа 
 для
для 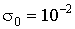 и
и
 соответственно.
При этом указанные оценки формировались путем усреднения единичных оценок
величин
соответственно.
При этом указанные оценки формировались путем усреднения единичных оценок
величин 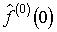 и
и
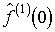 ,
полученных на основе пятидесяти реализаций, генерируемых датчиком случайных
чисел.
,
полученных на основе пятидесяти реализаций, генерируемых датчиком случайных
чисел.
Таблица 3.1
|
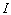 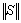 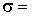  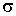 
|
|
|
|
|
|
   
|
|
|
|
|
4
|
15.157
|
1.226
|
0.684
|
0.989
|
0.208
|
|
10
|
20.686
|
1.124
|
0.314
|
0.996
|
0.189
|
|
20
|
27.717
|
1.032
|
0.263
|
0.998
|
0.121
|
|
30
|
33.321
|
1.021
|
0.097
|
0.999
|
0.016
|
|
40
|
38.114
|
1.007
|
0.028
|
1.000
|
0.009
|
|
50
|
42.371
|
1.000
|
0.007
|
1.000
|
0
|
Анализ результатов
моделирования показывает инвариантность получаемых оценок к сингулярным
погрешностям (в условиях отсутствия случайных погрешностей результаты расчетов
совпадают с точными значениями  ) и высокую степень
устойчивости к случайным возмущениям.
) и высокую степень
устойчивости к случайным возмущениям.
Развитый метод является
основой для решения задач оптимального оценивания значений операторов 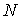 -
кратного дифференцирования в классе функций с финитным спектром. Метод
позволяет существенно повысить устойчивость вычислительных процедур как к
случайным, так и к сингулярным ошибкам заданного класса.
-
кратного дифференцирования в классе функций с финитным спектром. Метод
позволяет существенно повысить устойчивость вычислительных процедур как к
случайным, так и к сингулярным ошибкам заданного класса.
Основное достоинство
предложенного подхода состоит в том, что, в отличие от абсолютного большинства
известных методов [2, 3, 23-25, 28, 30], в данном случае не требуется
увеличения размерности решаемой задачи при построении оптимальных несмещенных
оценок, инвариантных к сингулярным погрешностям.
Достоинством метода
также является его универсальность, поскольку решение получено в конечно -
аналитическом виде, допускающем компактную векторно-матричную форму записи, что
весьма удобно при практической реализации на базе цифровых вычислительных машин
различных классов.
Поскольку возможность применения
полученных в работе результатов тесно связана с понятием «наблюдаемости»
(разрешимости) поставленной задачи, то в практических случаях выбор подпространства
сингулярных ошибок можно производить, опираясь на результаты работ [2, 3, 16],
в которых дано всестороннее теоретическое и прикладное обоснование понятия
«наблюдаемости».
Выводы и рекомендации
В дипломной работе решалась задача
развития оптимального метода линейного оценивания различных числовых
характеристик полезных сигналов в классе ФФС по результатам измерений,
содержащих как флуктуационную, так и сингулярную помеху. Дан всесторонний
анализ возможности использования известной теоремы отсчетов (ряда Котельникова)
для решения задач интерполяции, аппроксимации и дифференцирования как ФФС, так
и других классов функций, которые нельзя отнести к классу ФФС. Получены
различные оценки сверху на методические погрешности, обусловленные рядом ограничений
на полезные сигналы как во временной, так и в частотной областях.
Результаты вычислительных
экспериментов наглядно подтверждают эффективность развитого метода для
обработки измерений при наличии сингулярных и флуктуационных погрешностей.
Найденная векторно-матричная форма представления основного результата допускает
несложную практическую реализацию как на универсальных, так и
специализированных ЭВМ.
Развитый метод может найти широкое
применение в различных областях гражданского и военного назначения, связанных с
автоматизацией процессов сбора, хранения и обработки измерительной информации,
подверженной воздействию различного рода помех естественного и искусственного
происхождения. Полученные результаты без особых финансово-экономических затрат
могут быть реализованы как в существующих, так и перспективных
информационно-измерительных системах различного типа.
Применение метода целесообразно при
оценивании характеристик динамичных информационных процессов, например,
траекторий летательных аппаратов на участках маневра, входа в плотные слои
атмосферы, посадки. Кроме того, метод может быть использован при обработке
измерительной информации в комплексированных навигационных системах, в которых,
как правило, при переходе от одной измерительной структуры к другой возникают
высокодинамичные переходные процессы и каждый измеритель характеризуется своей
сингулярной помехой.
Полученные в дипломной работе
результаты хорошо согласуются с известными подходами, применяемыми при
оптимальной и квазиоптимальной обработке измерений.
Материалы, полученные в дипломной
работе, нашли отражение в статьях [5-8] и докладах на научных конференциях
различного уровня [9-15].
Перечень сокращений
В настоящей
пояснительной записке применяются следующие обозначения и сокращения:
ФФС - функция с финитным спектром;
МНК - метод наименьших квадратов;
СП - сингулярная помеха;
ИИС - информационно - измерительная
система;
ФШ - флуктуационный шум.
Библиографический список
1. Березин И.С., Жидков Н.П. Методы вычислений. Т.1.M.: Наука, 1966.
2. Брандин В.Н., Васильев А.А., Худяков С.Т. Основы
экспериментальной космической баллистики. М-: Машиностроение, 1974.
. Брандин В.Н., Разоренов Г.Н. Определение траекторий
космических аппаратов. М.: Машиностроение, 1978.
. Булычев Ю.Г., Бурлай И.В. Оптимальное вычисление
производных различных порядков в классе функций с финитным спектром. - Журнал
вычислительной математики и математической физики, 2000, т.40, № 4, С.505-516.
5. Булычев В.Ю., Булычев Ю.Г., Лапсарь А.П. Алгоритм
оценки вектора состояния управляемых технических объектов на основе теоремы
Котельникова // Автометрия, 2010, Т. 46, № 3, стр. 30 - 40.
6. Булычев В.Ю., Булычев Ю.Г., Манин А.П., Семенов И.Г.
Прикладные аспекты теории нелинейной фильтрации в задачах оценивания движения
ЛА // Общероссийский НТ журнал «Полет», Москва, 2010, №6, стр. 52 - 60.
. Булычев В.Ю., Булычев Ю.Г., Мозоль А.А., Помысов А.С.,
Семенов И.Г. Компенсация систематических ошибок измерений на основе инвариантов
движения объекта // Известия вузов. Радиоэлектроника, Киев, 2010, Т. 53, №9,
стр. 18 - 26.
. Булычев Ю.Г., Булычев В.Ю., Мозоль А.А., Пархоменко Н.Г.
Использование непрерывных групп преобразований в задачах синтеза следящих
измерителей // Известия вузов России. Радиоэлектроника. 2011, Вып. 1,стр. 9 -
16.
. Булычев Ю.Г., Булычев В.Ю., Елисеев А.В., Мозоль А.А.,
Помысов А.С., Сергеев М.Ю. Алгоритм обработки измерений по полной выборке в
условиях структурно-параметрической неопределенности модели помех// Современные
проблемы радиоэлектроники. Материалы III международной конференции. Секция 2. Ростов-на-Дону. - 2010, стр.
100 - 102.
. Булычев Ю.Г., Булычев В.Ю., Елисеев А.В., Мозоль А.А.,
Помысов А.С., Глянько В.Е. Метод параметрической идентификации модели
информационного процесса, инвариантный к сингулярной помехе // Современные
проблемы радиоэлектроники. Материалы III международной конференции. Секция 2. Ростов-на-Дону. - 2010, стр.
106 - 109.
. Булычев Ю.Г., Булычев В.Ю., Челахова Т.Н., Челахов В.М.,
Декомпозиционный подход к решению плохообусловленных задач параметрической
идентификации // X Международная научно-практическая конференция «Моделирование.
Теория, методы и средства». Новочеркасск. ЮРГТУ. - 2010, стр. 125 - 132.
. Булычев Ю.Г., Булычев В.Ю., Челахова Т.Н., Челахов В.М.
Вопросы интерполяции, аппроксимации и дифференцирование в классе функций с
финитным спектром // Порядковый анализ и смежные вопросы математического
моделирования: тезисы докладов VIII международной научной конференции. Владикавказ. - 2010, стр. 81.
. Булычев Ю.Г., Булычев В.Ю., Челахова Т.Н., Челахов В.М.
Декомпозиционный подход к решению плохообусловленных задач параметрической
идентификации // Порядковый анализ и смежные вопросы математического
моделирования: тезисы докладов VIII международной научной конференции. Владикавказ. - 2010, стр. 266.
. Булычев Ю.Г., Булычев В.Ю., Челахова Т.Н., Челахов В.М.
Вычислительная схема инвариантно-несмещенного оценивания значений линейных
функционалов // Порядковый анализ и смежные вопросы математического
моделирования: тезисы докладов VIII международной научной конференции. Владикавказ. - 2010, стр. 267
- 268.
15. Булычев В.Ю., Кийко А.С., Касьянов Е.Е. Оптимальное
обобщенное оценивание без расширения пространства состояния // Сборник трудов VIII Всероссийской научной
конференции молодых ученых, аспирантов и студентов «Информационные технологии,
системный анализ и управление». Таганрог. - 2010, стр. 315 - 320.
16. Булычев Ю.Г., Манин
А.П. Математические аспекты определения движения летательных аппаратов. М.:
Машиностроение, 2000.
17. Волков Е.А. Численные
методы. М.: Наука, 1987. 248 С.
18. Гоноровский И.С. Радиотехнические цепи и сигналы. М.:
Радио и связь. 1986. 512с.
. Иванов В.В. Методы вычислений на ЭВМ. Справочное
пособие. Киев: Наук, думка, 1986.584с.
. Корн Г., Корн Т. Справочник по математике. М.: Наука,
1978. 832 с.
. Леонов В.А., Поплавский Б.К. Метод линейных
преобразований идентификации динамических систем. - Техническая кибернетика,
1990, № 2, С. 73-79.
. Леонов В.А., Поплавский Б.К. Фильтрация ошибок измерений
при оценивании линейного преобразования полезного сигнала. - Техническая
кибернетика, 1992, № 1, С. 163-164.
. Линник Ю.В. Метод наименьших квадратов и основы
математической обработки наблюдений. - М.: Физматгиз, 1962.
. Лысенко Л.Н., Нгуен Танг Кыонг.Теоретические и
прикладные аспекты синтеза мультиструктурных схем рекуррентной обработки
информации в навигационных системах летательных аппаратов. - Известия АН.
Теория и системы управления, 1997, № 6, С.38-48.
. Рао С.Р. Линейные статистические методы и их применение.
М.: Наука, 1974. 548 с.
. Самарский А.А., Гулин А.В. Численные методы. М.: Наука,
1989
. Тихонов А.Н., Уфимцев М.В. Статистическая обработка
результатов экспериментов. - М.: Издательство МГУ, 1988.
. Тихонов В.И., Кульман Н.К. Нелинейная фильтрация и
квазикогерентный прием сигналов. М.: Сов. радио, 1975. 704с.
. Хургин Я.И., Яковлев В.П. Финитные функции в физике и
технике. М.: Наука, 1971.
30. Ширман Я.Д., Манжос
В.Н. Теория и техника обработки информации на фоне помех М.: Радио и связь.
1981. 416 с.