Жизненные формы харовых водорослей (Charophyta) Северного Казахстана
Зміст
Вступ
1. 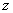 - вкладення тихонівських
просторів у ширші простори
- вкладення тихонівських
просторів у ширші простори
. Характеризація лінделефовості тихонівських
просторів
. Характеризація компактності тихонівських
просторів
Література
Вступ
тихонівський простір теорема
Вважатимемо, що всі простори
є Тихонівськими просторами. Для підпростору  простору
простору  , говорять,
що
, говорять,
що  є
є 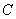 - вкладеним
(відовідно
- вкладеним
(відовідно  - вкладеним)
в
- вкладеним)
в  , якщо кожна
дійсно значена (відповідно кожна обмежена дійснозначна) неперервна функція на
, якщо кожна
дійсно значена (відповідно кожна обмежена дійснозначна) неперервна функція на  може може
бути неперервним продовженням на
може може
бути неперервним продовженням на  . Говорять, що підпростір
. Говорять, що підпростір  простору
простору  є
є 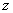 - вкладеним
в
- вкладеним
в  , якщо для
кожної функціонально замкненої множини
, якщо для
кожної функціонально замкненої множини 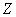 в
в  існує функціонально замкнена
множина
існує функціонально замкнена
множина 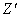 в
в  така, що
така, що 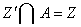 . Зрозуміло
що з
. Зрозуміло
що з 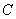 -
вкладеності випливає
-
вкладеності випливає  -
вкладеність, а з останнього випливає
-
вкладеність, а з останнього випливає 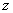 - вкладеність. Добре відомо, що
існує декілька результатів про
- вкладеність. Добре відомо, що
існує декілька результатів про 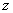 - вкладеність, які тісно пов’язують
її з
- вкладеність, які тісно пов’язують
її з 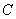 або
або  -
вкладеністю та іншими властивостями продовження (див [1]). Згадаємо наступну
теорему, яка описує так звані абсолютні
-
вкладеністю та іншими властивостями продовження (див [1]). Згадаємо наступну
теорему, яка описує так звані абсолютні  - вкладення або абсолютні
- вкладення або абсолютні 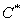 - вкладення.
Говорять, що тихонівський простір є майже компактним, якщо
- вкладення.
Говорять, що тихонівський простір є майже компактним, якщо 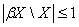 , де
, де 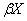 означає
модифікацію Стоуна-Чеха простору
означає
модифікацію Стоуна-Чеха простору  .
.
Дана робота присвячена
перекладу і методичному опрацюванню результатів роботи [19].
1. 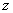 - вкладення
тихонівських просторів у ширші простори
- вкладення
тихонівських просторів у ширші простори
Теорема 1. (Досс [9]),
Гьюітт [14], Смірнов
[16]:
див також [1], [11]).
Тихонівський простір  є абсолютно
є абсолютно
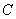 (або
рівносильно,
(або
рівносильно, 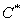 ) вкладеним
в кожний більший тихонівський простір тоді і тільки тоді, коли
) вкладеним
в кожний більший тихонівський простір тоді і тільки тоді, коли  є майже
компактним.
є майже
компактним.
Що стосується 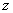 -
вкладення, нагадаймо наступний результат, який належить Джерісону (див [13,
Лемма 5,3.] або
[1,
теорема 7,8]).
-
вкладення, нагадаймо наступний результат, який належить Джерісону (див [13,
Лемма 5,3.] або
[1,
теорема 7,8]).
Теорема 2. (Джерісона). Якщо  є лінделефовим
підпростором тихоновського простору
є лінделефовим
підпростором тихоновського простору  ,тоді
,тоді  є
є 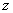 - вкладеним в
- вкладеним в  .
.
Відповідно до теореми 1
наступний результат, що характеризує так звані абсолютні 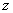 -
вкладення, встановлений Блером [7],
Блером-Гагером
[8] I Гагером
-Джонсоном [12]
частини ”
тоді
”
випливає безпосередньо з теореми 1 і 2.
-
вкладення, встановлений Блером [7],
Блером-Гагером
[8] I Гагером
-Джонсоном [12]
частини ”
тоді
”
випливає безпосередньо з теореми 1 і 2.
Теорема 3. (Блер [7],
Блер-Гагер
[8],
Гагер-Джонсон [12]).
Тихонівський простір  є
є 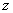 - вкладеним
у кожний більший тихонівський простір, тоді і тільки тоді, коли
- вкладеним
у кожний більший тихонівський простір, тоді і тільки тоді, коли  є майже
компактом або лінделефовим.
є майже
компактом або лінделефовим.
Доведення частини «тільки
тоді»: теореми 3 подане у [7], [8] і [12] і отримується з допомогою наслідків,
які мають самостійний інтерес , і які стосуються повних за Г’юітом просторів
або кільця неперервних функцій. В цій роботі ми подаємо альтернативне і просте
доведення цієї теореми, яке використовує лише наступний добре відомий факт:
тихонівський простір  є
лінделефовим тоді і тільки тоді, коли для кожного компактного підпростору
є
лінделефовим тоді і тільки тоді, коли для кожного компактного підпростору  простору
простору 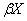 з
з 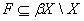 існує
функціонально замкнена множина
існує
функціонально замкнена множина 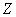 у просторі
у просторі 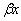 така, що
така, що 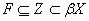 (див
[10,3.12.25(в)]). Іншу термінологію можна знайти в [1], [10] і [11].
(див
[10,3.12.25(в)]). Іншу термінологію можна знайти в [1], [10] і [11].
Доведення частини «тільки
тоді теореми 3».
Припустимо, що  є
є 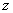 - вкладеним
у кожний більший тихонівський простір. Припустимо що
- вкладеним
у кожний більший тихонівський простір. Припустимо що  не є майже
компактним. Ми покажемо, що
не є майже
компактним. Ми покажемо, що  є лінделефовим. Нехай
є лінделефовим. Нехай  компактний
підпростір
компактний
підпростір 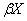 з
з 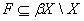 .
.
Твердження. Для кожного 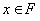 існує
відкритий окіл
існує
відкритий окіл  точки
точки  в просторі
в просторі  і
функціонально замкнена множина
і
функціонально замкнена множина 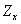 в посторі
в посторі 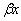 такі,що
такі,що 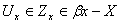 .
.
Нехай 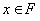 оскільки
оскільки  , то
візьмемо точку
, то
візьмемо точку 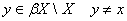 . Нехай
. Нехай 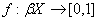 неперервна
функція, яка задовільняє умови
неперервна
функція, яка задовільняє умови  і
і 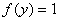 . Нехай
. Нехай  фактор
простір який отримується з простору
фактор
простір який отримується з простору 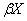 шляхом ототожнення всіх точок з
множини
шляхом ототожнення всіх точок з
множини 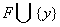 з однією
такою точкою
з однією
такою точкою 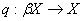 , яке буде
фактор відображенням. Оскільки
, яке буде
фактор відображенням. Оскільки 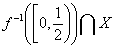 є функціонально замкненою множиною
в просторі
є функціонально замкненою множиною
в просторі  , а
, а 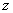 - вкладений
в
- вкладений
в  , то існує
функціонально замкнена множина
, то існує
функціонально замкнена множина 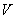 в просторі
в просторі  така, що
така, що  . Тоді
. Тоді 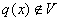 . Справді,
якщо
. Справді,
якщо  , то
, то 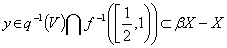 , що
приводить до суперечності. Покладемо
, що
приводить до суперечності. Покладемо 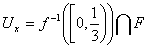 і
і 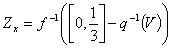 . Це ті множини, що нам
потрібні. Це факт і показує вірність даного твердження.
. Це ті множини, що нам
потрібні. Це факт і показує вірність даного твердження.
На завершення, для деякої
скінченної послідовності  з
з 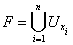 покладемо
покладемо 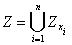 . Тоді
. Тоді 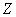 є
функціонально замкненою множиною в
є
функціонально замкненою множиною в  просторі
просторі 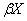 і
і 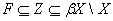 . Отже
. Отже  є
лінделефовим простором. Це і завершує доведення.
є
лінделефовим простором. Це і завершує доведення.
2. Характеризація
лінделефовості тихонівських просторів
Ми застосуємо нашу техніку у
вище наведеному доведенню, щоб навести просте доведення теореми, яка нещодавно
була доведена Белломі Ященко [6], їх
доведення довге і складне.
Теорема 4. (Белла-Ященко [6]).
Для тихоновського простору  наступні твердження рівносильні:
наступні твердження рівносильні:
) якщо тихонівський
простір  містить дві
замкнені множини
містить дві
замкнені множини 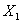 і
і  , що
неперетинаються, то ці множини можна відокремити в
, що
неперетинаються, то ці множини можна відокремити в  відкритими
множинами;
відкритими
множинами;
)  є
лінделефовим.
є
лінделефовим.
Дивись [3] для
мотивації теореми 4, яка буде сформульована нижче. Нагадаймо що підмножини  та
та 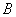 топологічного
простору
топологічного
простору  називаються
відокремними, якщо
називаються
відокремними, якщо 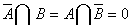 .
.
(*) Якщо тихонівський простір
 містить дві
копії
містить дві
копії 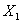 і
і  простору
простору  , які є
відокремними підмножинами, то ці копії можуть бути відокремленими в просторі
, які є
відокремними підмножинами, то ці копії можуть бути відокремленими в просторі  функціонально
замкненими множинами.
функціонально
замкненими множинами.
Доведення теореми 4. (1) 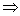 (2).
(2).
Припустимо (1). Спочатку ми
доведемо що (*) має місце. Нехай 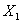 і
і  копії простору
копії простору  і
припустимо, що віни є відокремними підмножинами тихоновського простору
і
припустимо, що віни є відокремними підмножинами тихоновського простору  . Вкладемо
простір
. Вкладемо
простір  в
тихоновський куб. Крім того, вкладемо
в
тихоновський куб. Крім того, вкладемо  в добуток
в добуток 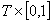 , як
підпростір
, як
підпростір 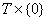 і позначемо
підпростір
і позначемо
підпростір 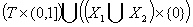 через
через 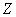 . Оскільки
. Оскільки 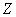 є щільною
підмножиною простору
є щільною
підмножиною простору 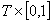 то ці
відкриті множини можуть бути продовжені до відкритих множин
то ці
відкриті множини можуть бути продовжені до відкритих множин  і
і  , що не перетинаються,
в просторі
, що не перетинаються,
в просторі 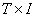 . Оскільки
. Оскільки 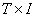 є
тихоновським кубом, то вівдомо, що
є
тихоновським кубом, то вівдомо, що  і
і  можуть бути відокремлені за допомогою
функціонально замкнених множин
можуть бути відокремлені за допомогою
функціонально замкнених множин 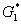 і
і 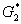 в
в 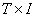 (для цього потрібно застосувати
[15, теорема 2] і [17, теорема 2]. Тоді звідси випливає, що
(для цього потрібно застосувати
[15, теорема 2] і [17, теорема 2]. Тоді звідси випливає, що  ,
, 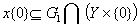 при
при 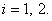 Звідси
випливає, що
Звідси
випливає, що 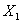 і
і  можуть
відокремлюватися функціонально замкненими множинами в просторі
можуть
відокремлюватися функціонально замкненими множинами в просторі  точніше (*)
має місце.
точніше (*)
має місце.
Тепер ми доведемо, що  є
лінделефовим. Нехай
є
лінделефовим. Нехай  компактний
підпростір простору
компактний
підпростір простору 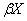
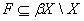 і нехай
і нехай 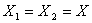 . Позначемо
множину
. Позначемо
множину  в
в 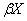 через
через 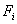 при
при 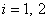 . Нехай
. Нехай 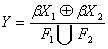 фактор
простору який одержується з простору
фактор
простору який одержується з простору 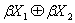 ототожненням всіх точок множини
однією точкою, а
ототожненням всіх точок множини
однією точкою, а 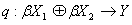 - фактор
відображеня. Оскільки
- фактор
відображеня. Оскільки 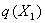 і
і 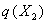 є
відокремленими підмножинами в
є
відокремленими підмножинами в  , то згідно з (*) існують
функціонально замкнені множини, що не перетинаються, і
, то згідно з (*) існують
функціонально замкнені множини, що не перетинаються, і 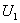 і
і 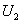 в просторі
в просторі  такі що
такі що  при
при 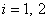 . Можна
припустити, що
. Можна
припустити, що  . Тоді
. Тоді  і
і  є
функціонально замкненою множиною в
є
функціонально замкненою множиною в  . Отже
. Отже 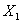 (а значить
і
(а значить
і  ) є
лінелефовим. Імплікація
) є
лінелефовим. Імплікація є
очевидною.
є
очевидною.
Слід зазначити в теоремі 1
(відповідно теоремі 3), що  може також бути
може також бути 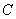 або
або 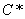 (відповідно
(відповідно
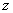 ) вкладеним
в кожний тихонівський простір, в якому
) вкладеним
в кожний тихонівський простір, в якому  є вкладеним, як замкнена підмножина
([4], [14], [16]). Так само, як може бути доведена аналогічна властивість(*).
є вкладеним, як замкнена підмножина
([4], [14], [16]). Так само, як може бути доведена аналогічна властивість(*).
Яджіма подав деякі
узагальнення теореми 4 і характеризації паракомпактності [18].
. Характеризація компактності
тихонівських просторів
Далі наведемо деякі
результати, що стосуються теореми 4. При цьому використовується техніка
побудови допоміжного простору, визначеного деякими просторами і тихоновським
розширенням, що є популярним в теорії відносних топологічних властивостей .
Теорема 5. Для тихоновського
простору  твердження
є рівносильними:
твердження
є рівносильними:
) якщо тихонівський
простір  містить дві
замкнені копії
містить дві
замкнені копії 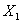 і
і  простору що
не перетинаються, то ці копії можуть бути повністю відокремними в просторі
простору що
не перетинаються, то ці копії можуть бути повністю відокремними в просторі  ;
;
)  є
компактом.
є
компактом.
Доведення: 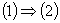 . Припустимо
. Припустимо
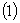 згідно з
теоремою 4
згідно з
теоремою 4  є
лінделефовим. Достатньо показати, що кожна замкнена дискретна множина в
просторі
є
лінделефовим. Достатньо показати, що кожна замкнена дискретна множина в
просторі  є
скінченною. Щоб довести цей факт, припустимо протилежне і нехай
є
скінченною. Щоб довести цей факт, припустимо протилежне і нехай 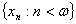 замкнена
дискретна множина, що складається з різних точок. Нехай
замкнена
дискретна множина, що складається з різних точок. Нехай 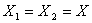 і позначимо
множини
і позначимо
множини 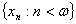 в просторі
в просторі  через
через 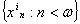 при
при  . Нехай
. Нехай 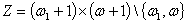 тихоновське
розширення. Нехай
тихоновське
розширення. Нехай 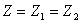 і позначимо
правий край
і позначимо
правий край 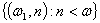 , простору
, простору  через
через  , а верхній
край
, а верхній
край  постору
постору 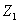 , через
, через  при
при  . Для
. Для  визначимо
відображення
визначимо
відображення 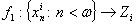 наступним
чином
наступним
чином  . Розглянемо
просторове об’єднання
. Розглянемо
просторове об’єднання 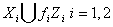 . (див. [10, с.93]). Означимо відображення
. (див. [10, с.93]). Означимо відображення
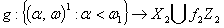 наступним
чином
наступним
чином  . Нехай
. Нехай  простір
об’єднання
простір
об’єднання 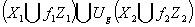 . Оскільки
. Оскільки  є
тихоновським простором і
є
тихоновським простором і  та
та  замкнені
підмножини в просторі
замкнені
підмножини в просторі  , то згідно
з припущенням
, то згідно
з припущенням 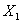 та
та  є
відокремними в просторі С. Це приводить до суперечності.
є
відокремними в просторі С. Це приводить до суперечності.
Теорема 6. Для тихоновського
простору  твердження
рівносильні:
твердження
рівносильні:
) якщо тихонівський
простір  містить
копію
містить
копію 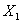 простору
простору  і замкнену
підмножину
і замкнену
підмножину  , що не
перетинається, то
, що не
перетинається, то 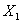 і
і  можуть бути
цілком відокремленими в просторі
можуть бути
цілком відокремленими в просторі  ;
;
) якщо тихонівський
простір  містить
замкнену копію
містить
замкнену копію 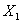 простору
простору  і замкнену
підмножину
і замкнену
підмножину  , що не
перетинаються, то
, що не
перетинаються, то 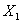 і
і  можуть бути
відокремленими в
можуть бути
відокремленими в  відкритими
множинами;
відкритими
множинами;
)  є
компактним.
є
компактним.
Наступні імплікації
доведені також:
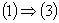 доведено Блером-Гагером [8,
твердження 4.3]
доведено Блером-Гагером [8,
твердження 4.3]
 доведено Аулемом [5,
теорема 1(в]).
доведено Аулемом [5,
теорема 1(в]).
Теорема 7 (Блер-Гагер
[8],
Аул [5]). Для  тихоновського
простору справедливі такі твердження:
тихоновського
простору справедливі такі твердження:
1) якщо тихонівський
простір  містить
копію
містить
копію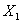 , простору
, простору  і
функціонально замкнену множину
і
функціонально замкнену множину  , що не перетинаються то
, що не перетинаються то 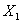 і
і  можуть бути
цілком відкритими в
можуть бути
цілком відкритими в  .
.
2) якщо тихонівський
простір  містить
замкнену копію
містить
замкнену копію 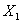 простору
простору  і
функціонально замкнену множину
і
функціонально замкнену множину  , що не перетинаються то то
, що не перетинаються то то 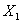 і
і  можуть бути
відкритими в
можуть бути
відкритими в  множинами.
множинами.
3)  є
псевдокомпактом.
є
псевдокомпактом.
Доведення .
Імплікацяі 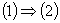 є
очевидною.
є
очевидною.
 . Пропустимо що
. Пропустимо що 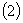 виконується
і припустимо що
виконується
і припустимо що  не є
псевдокомпактом. Нехай
не є
псевдокомпактом. Нехай 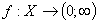 є
додатна, необмежена, неперервна функція. Тоді, існує замкнена дискретна підмножина
є
додатна, необмежена, неперервна функція. Тоді, існує замкнена дискретна підмножина
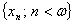 в просторі
в просторі  така, що
така, що 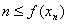 для кожного
для кожного
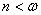 . Розглянемо
простір-об’єднаня
. Розглянемо
простір-об’єднаня 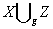 де
де 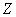 площина
Тихонова і
площина
Тихонова і 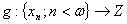 є
відображенням, визначене наступним чином:
є
відображенням, визначене наступним чином: 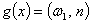 при
при 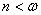 . Тоді зауважимо, що верхній край
простору
. Тоді зауважимо, що верхній край
простору 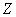 є
функціонально замкненою множиною в просторі
є
функціонально замкненою множиною в просторі 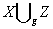 . Справді визначимо неперервну
функцію
. Справді визначимо неперервну
функцію 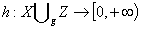 наступним
чином:
наступним
чином: 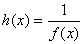 , якщо
, якщо  ;
; 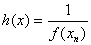 , якщо
, якщо 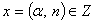 ,
, 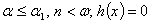 , якщо
, якщо 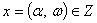
 . Оскільки
верхній край простору
. Оскільки
верхній край простору 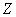 дорівнює
дорівнює 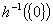 , то умова
, то умова 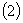 призводить
до суперечності.
призводить
до суперечності.
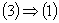
Згідно з [наслідком 3.6] (див
також [1]) простір  простору
простору  є
є 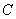 - вкладеним
в
- вкладеним
в  тоді і тільки
тоді, коли
тоді і тільки
тоді, коли 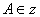 - вкладеним
і добре вкладеним в
- вкладеним
і добре вкладеним в  , якщо
будь-яка функціонально земкнена множина в посторі
, якщо
будь-яка функціонально земкнена множина в посторі  , яка не
перетинється з
, яка не
перетинється з  і може бути
цілком відкритою в
і може бути
цілком відкритою в  відносно
відносно  , слід
відзначити що з теореми 3 і 7 випливає теорема 1.
, слід
відзначити що з теореми 3 і 7 випливає теорема 1.
Література
[1]. Alo R.A., Shapiro H.L.,
Normal Topological Spaces. Comment University press. Cambridge. 1974.
[2]. Arhangel’skii A.V.,
Relative topological properties and relative topological spaces, Topology Appl.
70 (1996). 87-89.
[3]. Arhangel’skii A.V.,
Tartir J., A characterization of compactness by relative separation property.
Questions Answers Ger. Topological 14 (1996), 49-52.
[5]. Aull C.E., On
well-embeddings, General Topological and Applications (Middletown, CT, 1998),
pp. 1-5: Lecture Notes in Pure and Appl. Math., 123, Dekker, New York.
[6]. Bella A., Yaschenco I.V.
Lindelöf property and absolute embeddings, Proc. Amer. Math. Soc. 127
(1999), 907-913.
[7]. Brail R.L., On 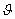 -embeddings
sets in topological spaces, TOPO 72- General Topology and its Applications
(Proc. Second Pittsburgh Internat. Conf., Pittsburgh, Pa., 1972; dedicated to
the memory of Johannes H. de Groot). pp. 46-79; Lecture Notes in Math., Vol.
378, Springer. Berlin. 1974.
-embeddings
sets in topological spaces, TOPO 72- General Topology and its Applications
(Proc. Second Pittsburgh Internat. Conf., Pittsburgh, Pa., 1972; dedicated to
the memory of Johannes H. de Groot). pp. 46-79; Lecture Notes in Math., Vol.
378, Springer. Berlin. 1974.
[8]. Brail R.L., Hager A.,W.,
Extensions of zero-sets and of real-valued functions, Math. Z. 136 (1974),
41-52.
[9]. Doss R.L., On uniform spaces
with a unique structure, Amer. J. Math. 71 (1949), 19-23.
[10]. Engelking R., General
Topology, Heldermann Verlag Berlin, 1989.
[11]. Gillman L. Jerison M., Rings
of Continuous Functions, Van Nostrand, Princeton, 1960.
[12]. Hager A., W., Johnson D.G., A
note on certain subalgebras of 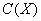 , Canad. Math. 20 (1968), 389-393.
, Canad. Math. 20 (1968), 389-393.
[13]. Henriksen M., Johnson D. G.,
A note structure of a class of archimedian lattice-ordered algebras. Fund.
Math. 50 (1961), 73-94.
[14]. Hewitt E., A note on
extensions of continuous functions, An. Acad. Brazil. Ci. 21 (1949), 175-179.
[15]. Noble N., 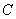 - embedded
subsets of product, Proc. Amer. Math. Soc. 31 (1972), 613-614/
- embedded
subsets of product, Proc. Amer. Math. Soc. 31 (1972), 613-614/
[16]. Smirnov Y., Mappings of
systems of open sets (in Russian), Mat. Sb. 31 (1952), 152-166.
[17]. Teraga T., Note on 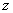 -,
-, 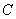 -, and
-, and 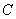 - embedding,
Sci. Rep. Tokyo Kyoiku Daigaku Sect. A. 13 (1975), 129-132.
- embedding,
Sci. Rep. Tokyo Kyoiku Daigaku Sect. A. 13 (1975), 129-132.
[18]. XXX Characterizations of
paracompactness and Lindelöfness by separation property, preprint.
[19]. Yamasaki K. A proof the
Blair-Hager-Johnson theorem on absolute 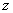 - embedding. Comment.Math.Univ.Varoline
43, 1 (2002) p.175-179
- embedding. Comment.Math.Univ.Varoline
43, 1 (2002) p.175-179