Возможности использования ИКТ в изучении линий второго порядка в школьном курсе алгебры
Введение
Понятие линии определилось в сознании человека в
доисторические времена. Траектория брошенного камня, струя воды, лучи света и
другие явления природы привлекали внимание наших предков и, наблюдаемые
многократно, послужили основой для постепенного установления понятия линии.
Однако потребовался большой исторический период
прежде чем люди стали сравнивать между собой формы кривых линий и отличать одну
кривую от другой.
Линии второго порядка возникли как сечения
конических поверхностей плоскостью и имеют особенно большое значение в науке и
технике.
Одним из первых, кто начал изучать конические
сечения был ученик знаменитого Платона, древнегреческий математик Менехм (IV и.
до н.э.). Решая задачу об удвоении куба, Менехм задумался: «А что случится, если
разрезать конус плоскостью, перпендикулярной его образующей?». Так, изменяя
угол при вершине прямой круговой поверхности, Менехм получил три вида кривых:
эллипс - если плоскость будет перпендикулярна к образующей конической
поверхности; гиперболу - если плоскость будет параллельна оси конической
поверхности; параболу - если плоскость будет параллельна образующей конической
поверхности. Но названия этих кривых придумал не Менехм, их предложил один из
крупнейших геометров древности Аполлоний Пергский, посвятивший замечательным
кривым трактат из восьми книг «Конические сечения». Аполлоний показал, что
кривые можно получить, проводя различные сечения одной и той же конической
поверхности. Вид конического сечения зависит от расположения плоскости
относительно оси или образующих конической поверхности.
Основная часть работы направлена на рассмотрение
вопросов методики изучения линий второго порядка и методики использования ЦОР в
VII-IX классах школьного курса алгебры.
Объект исследования - методика организации изучения
линий второго порядка.
Предмет исследования - возможности использования
ИКТ в организации изучения линий второго порядка в школьном курсе алгебры 7-9
классов.
Цель данной работы: установить возможности
использования ИКТ в изучении линий второго порядка в школьном курсе алгебры.
Основные задачи работы:
Проанализировать и систематизировать содержание
линий второго порядка в элементарной математике;
Проанализировать содержание и возможности
использования для изучения линий второго порядка имеющиеся ЦОР по математике;
Проанализировать содержание темы «Линии 2го
порядка» в школьных учебниках;
Рассмотреть примеры использования ИКТ в решении
задач с линиями второго порядка
Глава 1. Теоретические и
методические аспекты изучения линий второго порядка
.1 Теория линий второго порядка и
использования ИКТ в обучении
Понятие линии второго порядка в аналитической
геометрии
Аналитическая геометрия описывает свойства линий
на плоскости через их уравнения. В аналитической геометрии систематически
исследуются так называемые алгебраические линии второго порядка (эти линии в
декартовых прямоугольных координатах определяются соответственно
алгебраическими уравнениями второй степени). Линии второго порядка определяются
уравнениями вида 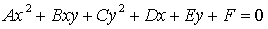 . Основной метод
исследования и классификации этих линий заключается в подборе такой декартовой
прямоугольной системы координат, в которой уравнение линии имеет наиболее
простой (канонический) вид, удобный для исследования.
. Основной метод
исследования и классификации этих линий заключается в подборе такой декартовой
прямоугольной системы координат, в которой уравнение линии имеет наиболее
простой (канонический) вид, удобный для исследования.
Определение 1. Линией второго порядка называется
множество всех точек  плоскости,
координаты которых удовлетворяют уравнению:
плоскости,
координаты которых удовлетворяют уравнению:
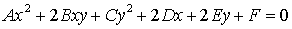
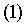
где A,B,C,D,E,F - вещественные коэффициенты,
причем 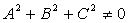 .
.
Исследуем уравнение и узнаем, что представляет
собой произвольная линия второго порядка.
Приведение общего уравнения линии второго
порядка к каноническому виду
Для исследований приведем общее уравнение линии
второго порядка к одному из канонических видов.
Существует такая система координат, в которой
уравнение (1) не содержит произведения xy, то есть B = 0.
Пусть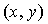 координаты точки M в системе координат XOY. Повернем оси координат на угол
координаты точки M в системе координат XOY. Повернем оси координат на угол 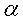 в
положительном направлении и обозначим (x', y') координаты точки M в новой
системе координат X'OY'.(чертеж 1.)
в
положительном направлении и обозначим (x', y') координаты точки M в новой
системе координат X'OY'.(чертеж 1.)
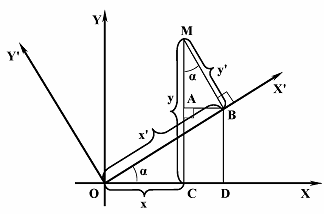
Чертеж 1
Найдем связь между этими координатами. Очевидно,
что:
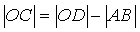 (так как
(так как 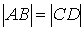 );
(2)
);
(2)
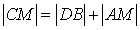 (так как
(так как  );
(3)
);
(3)
Рассмотрим  .
Так как он прямоугольный, то
.
Так как он прямоугольный, то 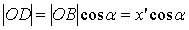 ,
,  .
(4)
.
(4)
Рассмотрим теперь 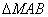 .
Он также прямоугольный, поэтому
.
Он также прямоугольный, поэтому 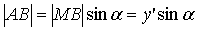 ,
, 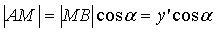 .
(5)
.
(5)
Таким образом, с учетом того, что 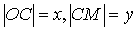 ,
из равенств (2)-(5) получим:
,
из равенств (2)-(5) получим: (6)
(6)
Следовательно, система (6) представляет собой
выражение старых координат 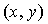 через новые
через новые 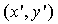 при
повороте XOY на угол α вокруг О
(0,0).
при
повороте XOY на угол α вокруг О
(0,0).
Замечание. Для того чтобы получить выражение
новых координат через старые, достаточно угол α в
формулах (6) заменить на угол (−α), так
как при повороте системы координат X′OY ′ на угол (−α)
мы
получим систему XOY.
Подставим формулы (6) в уравнение (1), получим:
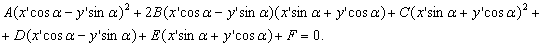
Соберем коэффициенты при соответствующих
неизвестных.
При  ,
получим:
,
получим:
 ,
,
При 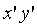 :
:
 , (7)
, (7)
При 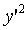 :
:
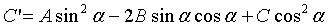 ,
,
При 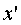 :
:
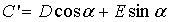 ,
,
При 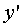 :
:
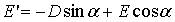 .
.
Таким образом, уравнение (1) с учётом замены (6)
принимает вид:
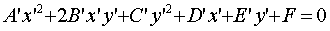 (8)
(8)
Подберем угол 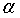 таким
образом, чтобы коэффициент
таким
образом, чтобы коэффициент 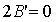 . Из (7) следует,
что
. Из (7) следует,
что  поэтому
поэтому
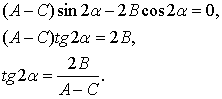
После данного преобразования уравнение (1)
примет вид:
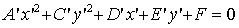 . (9)
. (9)
Докажем, что при повороте на любой угол α
имеет
место равенство:
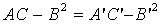 (10)
(10)
Так как мы подобрали угол α
так,
что 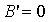 ,
то из (10) следует, что
,
то из (10) следует, что
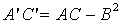 . (11)
. (11)
Чтобы проанализировать уравнение кривой (9),
рассмотрим три
случая:
)  (эллиптический
случай);
(эллиптический
случай);
) 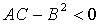 (гиперболический
случай);
(гиперболический
случай);
) 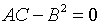 (параболический
случай).
(параболический
случай).
Подробнее рассмотрим эллиптический случай. Из  следует,
что
следует,
что 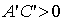 ,
то есть знаки
,
то есть знаки 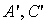 совпадают. Пусть A′
> 0, C′ > 0. Выделим полные квадраты при неизвестных x′, y′,
получим:
совпадают. Пусть A′
> 0, C′ > 0. Выделим полные квадраты при неизвестных x′, y′,
получим:
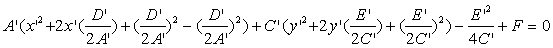
Дополним члены, содержащие x’ и y’,до полного
квадрата:
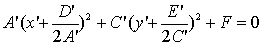 , (12)
, (12)
где 
Положим 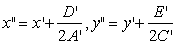 ,
тогда уравнение (12) примет вид:
,
тогда уравнение (12) примет вид: 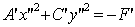 .
(13)
.
(13)
Пусть 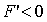 .
Разделим обе части уравнения (13) на
.
Разделим обе части уравнения (13) на  ,
получим:
,
получим:
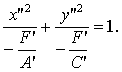 (14)
(14)
Так как 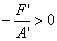 и
и
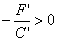 ,
то предположим, что
,
то предположим, что  . (15)
. (15)
Из (14) и (15) следует, что мы получили
каноническое уравнение эллипса 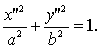
Пусть F′ > 0, тогда в уравнении (13)
слева стоит неотрицательное число, а справа - отрицательное, поэтому точек,
удовлетворяющих данному уравнению, не существует.
Пусть F′ = 0. Тогда уравнению (13)
удовлетворяет только одна точка  , то есть точка с
координатами
, то есть точка с
координатами 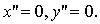
Рассмотрим гиперболический случай. Из 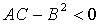 следует,
что
следует,
что 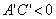 ,
то есть числа
,
то есть числа 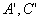 имеют разные знаки.
Выполняя аналогичные преобразования, как и для эллиптического случая, получим
уравнение кривой:
имеют разные знаки.
Выполняя аналогичные преобразования, как и для эллиптического случая, получим
уравнение кривой: 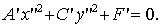
Предположим, что 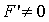 .
Отсюда:
.
Отсюда:
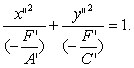 (16)
(16)
Так как 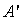 и
и
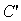 разных
знаков, следовательно, одна из скобок больше нуля, другая скобка меньше нуля.
Пусть
разных
знаков, следовательно, одна из скобок больше нуля, другая скобка меньше нуля.
Пусть 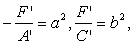 (17)
(17)
тогда мы получаем каноническое уравнение
гиперболы:
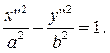
При  уравнение
принимает вид:
уравнение
принимает вид:  (18)
(18)
Пусть  ,
тогда
,
тогда  и
уравнение (18) примет вид:
и
уравнение (18) примет вид: 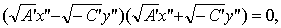 откуда
откуда  Таким
образом, получили уравнения двух пересекающихся прямых.
Таким
образом, получили уравнения двух пересекающихся прямых.
Рассмотрим параболический случай. Так как 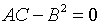 ,
то
,
то  .
.
Пусть  .
Так как после поворота
.
Так как после поворота 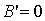 , то уравнение (9)
преобразуется до вида:
, то уравнение (9)
преобразуется до вида: 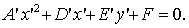 (19)
(19)
Соберём члены, содержащие 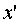 ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
 тогда уравнение
(19) примет вид:
тогда уравнение
(19) примет вид: 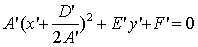 или
или  ,
(20)
,
(20)
где 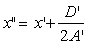 .
Из (20) следует, что
.
Из (20) следует, что 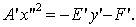
Рассмотрим два случая:
Пусть 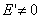 ,
тогда
,
тогда 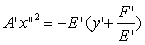 ,
то есть
,
то есть 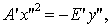 (21)
(21)
где 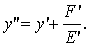
Положим  ,
тогда уравнение (21) примет вид:
,
тогда уравнение (21) примет вид: 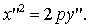
Это каноническое уравнение параболы,
симметричной относительно
оси (OY ).
Пусть 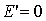 ,
тогда уравнение (20) перепишется в виде
,
тогда уравнение (20) перепишется в виде
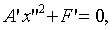 (22)
(22)
. Если 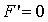 ,
то получим уравнение оси (OY )
,
то получим уравнение оси (OY )  .
.
. Если 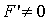 ,
то возможны два случая. Если A′ и F′ одного знака, то точек,
удовлетворяющих данному уравнению, нет; если же A′ и F′ разных
знаков, то
,
то возможны два случая. Если A′ и F′ одного знака, то точек,
удовлетворяющих данному уравнению, нет; если же A′ и F′ разных
знаков, то  , где
, где 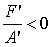 ,
поэтому
,
поэтому  и
уравнение (22) описывает две параллельные прямые:
и
уравнение (22) описывает две параллельные прямые: 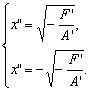 )
Пусть
)
Пусть 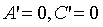 ,
тогда уравнение (9) примет вид
,
тогда уравнение (9) примет вид
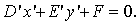 (23)
(23)
Если 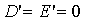 ,
а
,
а 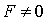 ,
то точек, удовлетворяющих уравнению (23), нет; если же
,
то точек, удовлетворяющих уравнению (23), нет; если же  или
или
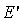 отличны
от нуля, то уравнение (23) описывает прямую.
отличны
от нуля, то уравнение (23) описывает прямую.
Вывод. Путем преобразований кривой второго
порядка, определяемой уравнением (1) мы можем получить уравнения таких линии
второго порядка, как:
 - уравнение эллипса
- уравнение эллипса
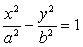 - уравнение
гиперболы
- уравнение
гиперболы
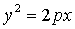 - уравнение
параболы
- уравнение
параболы
 - совокупности двуз
пересекающихся прямых
- совокупности двуз
пересекающихся прямых
 - совокупности двух
параллельных прямых
- совокупности двух
параллельных прямых
Содержание темы «Линии второго порядка» в элементарной
математике
В математике рассматриваются линии второго
порядка, как конические сечения: окружность, эллипс, гипербола, парабола; или
как множество точек обладающих некоторыми свойствами.
Рассмотрим каждую линию второго порядка
подробнее, определяя линии как множество точек.
ОКРУЖНОСТЬ
Определение 1.1. Окружность - множество точек
плоскости, равноудаленных от данной точки М0, называемой ее центром.[9.С.65]
Общий вид уравнения 
Исследование свойств окружности по её уравнению
Пресечение с осями координат:
С ОХ: Пусть у=0, тогда  .
Отсюда делаем вывод, что (-R;0), (R;0)- точки пересечения с осью ОХ.
.
Отсюда делаем вывод, что (-R;0), (R;0)- точки пересечения с осью ОХ.
С ОУ: Пусть х=0, тогда 02+у2=R2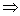
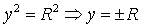 . Отсюда делаем
вывод, что (0;-R),(0;R)- точки пресечения с осью ОУ.
. Отсюда делаем
вывод, что (0;-R),(0;R)- точки пресечения с осью ОУ.
Следовательно, у окружности с центром в начале
координат область допустимых значений для 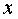 и
для
и
для  закрытый
интервал
закрытый
интервал  .
.
Вывод: Окружность вписана в квадрат с размером
стороны 2R.[1.С.99]
) Симметрия окружности:
Относительно оси ОХ и оси ОУ, так как окружность
имеет общие точки пересечения с осями координат.
Пусть  принадлежит
окружности, т. Е
принадлежит
окружности, т. Е 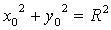 - верное равенство.
- верное равенство.
Точка 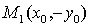 симметрична
точке М0 относительно оси ОХ. Подставим координаты точки М1 в уравнение
окружности
симметрична
точке М0 относительно оси ОХ. Подставим координаты точки М1 в уравнение
окружности 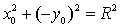 ,отсюда имеем:
,отсюда имеем: 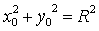 -
верное равенство.
-
верное равенство.
Следовательно, М1 принадлежит окружности, отсюда
следует, что окружность симметрична относительно оси ОХ.
Точка 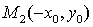 симметрична
точке М0 относительно оси ОУ, следовательно, окружность симметрична
относительно оси ОУ.
симметрична
точке М0 относительно оси ОУ, следовательно, окружность симметрична
относительно оси ОУ.
Точка 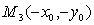 симметрична
точке М0 относительно О (центра), следовательно, окружность симметрична
относительно начала координат. [1.С.99-100]
симметрична
точке М0 относительно О (центра), следовательно, окружность симметрична
относительно начала координат. [1.С.99-100]
Эксцентриситет окружности:
Определение 1.2. Отношение  называется
эксцентриситетом окружности. Для окружности эксцентриситет окружности равен
нулю.
называется
эксцентриситетом окружности. Для окружности эксцентриситет окружности равен
нулю.
Касательная к окружности:
Определение 1.3. Прямая, имеющая с окружностью
ровно одну общую точку, называется касательной
<#"562771.files/image127.gif"> принадлежит
окружности, тогда уравнение касательной к окружности в данной точке имеет вид:
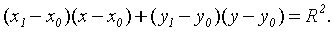 [1.С.100]
[1.С.100]
ЭЛЛИПС
Определение 2.1. Эллипс - множество точек
плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2
этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина,
равная 2а, а > 0, большая, чем расстояние между фокусами 2с, с > 0.
Общий вид уравнения 
Исследование свойств эллипса по его уравнению
) Пересечение эллипса с осями координат:
Найдем точки пересечения эллипса с осью ОХ:
Пусть y=0, тогда уравнение эллипса имеет вид: 
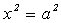 , следовательно
, следовательно 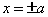 .
.
Отсюда следует, что точки (-a,0),(a,0) являются
точками пересечения с осью ОХ.
Найдем точки пересечения эллипса с осью ОУ:
Пусть х=0,отсюда имеем: 
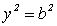 ,
отсюда
,
отсюда 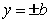 .
.
Следовательно, точки (-b,0),(b,0)являются
точками пересечения с осью ОУ.
Отсюда заключаем, что границы эллипса 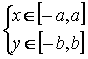 ,
отображающие его схематичное построение. (чертеж 2) [1.С. 105]
,
отображающие его схематичное построение. (чертеж 2) [1.С. 105]
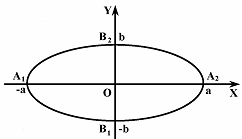
Чертеж 2
Расстояние |A1A2| = 2a называется большой
(фокальной) осью эллипса, расстояние |B1B2| = 2b называется малой осью эллипса.
Расстояния от начала координат до вершин A2(a, 0), B2(0, b) называются
соответственно большой и малой полуосями эллипса.
Вывод: Таким образом, заключаем, что эллипс
вписан в прямоугольник с размерами 2a, 2b (чертеж 3).
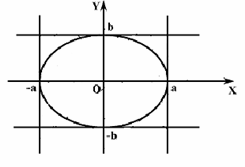
Чертеж 3
2) Симметрия эллипса относительно координатных
осей OX и OY:
Пусть  принадлежит
эллипсу, т. е
принадлежит
эллипсу, т. е 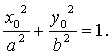 - верное
равенство.
- верное
равенство.
Точка 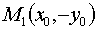 симметрична
точке
симметрична
точке 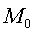 относительно
оси ОХ
относительно
оси ОХ

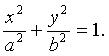 - верное равенство.
- верное равенство.
Следовательно, 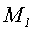 принадлежит
эллипсу, отсюда заключаем, что эллипс симметричен относительно ОХ
принадлежит
эллипсу, отсюда заключаем, что эллипс симметричен относительно ОХ
Точка  симметрична
точке
симметрична
точке 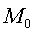 относительно
оси ОУ, следовательно, эллипс симметричен относительно оси ОУ.
относительно
оси ОУ, следовательно, эллипс симметричен относительно оси ОУ.
Точка 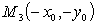 симметрична
точке
симметрична
точке 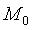 относительно
О (центра), следовательно, эллипс симметричен относительно начала
координат.[1.С.105-106]
относительно
О (центра), следовательно, эллипс симметричен относительно начала
координат.[1.С.105-106]
Фокусы эллипса:
Пусть фокусы эллипса лежат на оси ОX.
Межфокусное расстояние эллипса равно  причем
причем
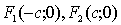 .
Заметим, что
.
Заметим, что 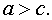

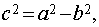
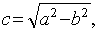
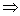
 . [1.С.106]
. [1.С.106]
4) Эксцентриситет эллипса:
Определение 2.2. Эксцентриситетом эллипса 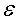 называют
отношение межфокусного расстояния 2с к длине большой оси 2а.
называют
отношение межфокусного расстояния 2с к длине большой оси 2а.
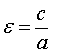 .
.
Так как 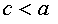 ,
следовательно,
,
следовательно, 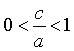 .
.
Если  стремится
к нулю при постоянном значении
стремится
к нулю при постоянном значении 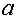 , то
, то  стремится
к нулю. При этом величина
стремится
к нулю. При этом величина  стремится к
стремится к  .
В предельном случаи уравнение эллипса принимает вид:
.
В предельном случаи уравнение эллипса принимает вид: 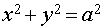 .
Это уравнение окружности. Если
.
Это уравнение окружности. Если 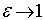 , то
, то 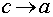 .
При этом малая ось эллипса неограниченно уменьшается, эллипс стремится к
отрезку. (чертеж 4) [1.С.106]
.
При этом малая ось эллипса неограниченно уменьшается, эллипс стремится к
отрезку. (чертеж 4) [1.С.106]
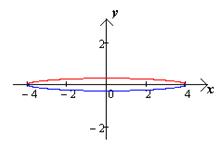
Чертеж 4
) Диаметры эллипса:
Всякая хорда, проходящая через центр эллипса,
называется диаметром эллипса. В частности, диаметрами эллипса является его
большая ось 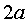 и малая ось
и малая ось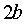 .
Всякий диаметр эллипса, не являющийся его осью, больше малой оси, но меньше
большой оси (чертеж 5). [1.С.106-107]
.
Всякий диаметр эллипса, не являющийся его осью, больше малой оси, но меньше
большой оси (чертеж 5). [1.С.106-107]
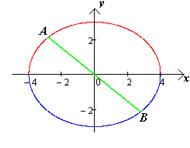
Чертеж 5
) Касательная к эллипсу:
Уравнение касательной к эллипсу  где
где
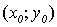 -
координаты точки касания и
-
координаты точки касания и  соответственно
большая и меньшая полуоси эллипса (чертеж 6).
соответственно
большая и меньшая полуоси эллипса (чертеж 6).
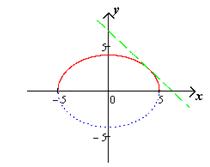
Чертеж 6
) Частный случай эллипса - окружность:

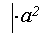
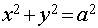 , где
, где 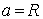 окружности.
окружности.
) Взаимное расположение точек и эллипса:
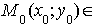 эллипсу, если
эллипсу, если 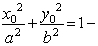 верное
равенство,
верное
равенство,
Если 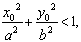 то
то
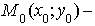 лежит
внутри эллипса,
лежит
внутри эллипса,
Если  то
то
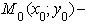 лежит
вне эллипса. [1.С.100]
лежит
вне эллипса. [1.С.100]
) Уравнения директрис эллипса:
Пусть эллипс задан уравнением 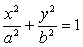 и
если при этом
и
если при этом  , то
, то  и
и
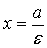 уравнения
директрис эллипса, если
уравнения
директрис эллипса, если  , то директрисы
определяются уравнениями
, то директрисы
определяются уравнениями 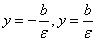 .
.
ГИПЕРБОЛА
Определение 3.1. Гипербола - множество точек
плоскости, модуль разности расстояний от которых до двух данных точек  этой
плоскости, называемых фокусами гиперболы, есть заданная постоянная величина
этой
плоскости, называемых фокусами гиперболы, есть заданная постоянная величина  меньшая,
чем расстояние между фокусами
меньшая,
чем расстояние между фокусами  [8.С.510]
[8.С.510]
Общий вид уравнения 
Исследование свойств гиперболы по ее уравнению
) Пересечение гиперболы с осями координат:
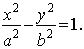
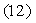
Очевидно, что гипербола состоит из двух ветвей:
правой и левой, простирающихся в бесконечность.
В уравнении (12) положим, что y=0, получим: 
 отсюда
отсюда
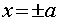 .
Следовательно, точки
.
Следовательно, точки  являются точками
пересечения гиперболы с осью
являются точками
пересечения гиперболы с осью 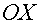 (чертеж 7).
(чертеж 7).

Чертеж 7
Положим, что в уравнении (12) х=0, и получим: 
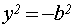 ,
следовательно, уравнение гиперболы не пересекает ось
,
следовательно, уравнение гиперболы не пересекает ось 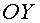 .
.
ЗАМЕЧАНИЕ: Если мнимая ось гиперболы имеет длину
2a и направлена по оси (OX), а действительная ось длиной 2b совпадает с осью
(OY), то уравнение гиперболы имеет вид: 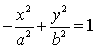 .
[1.С.107-108]
.
[1.С.107-108]
Определение 3.2. Гиперболы, заданные уравнениями
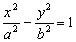 и
и
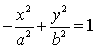 ,
называются сопряженными гиперболами.
,
называются сопряженными гиперболами.
Определение 3.3. Если a=b, гипербола называется
равносторонней.
) Симметрии гиперболы относительно координатных
осей 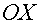 и
и
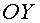 :
:
Пусть 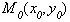 принадлежит
гиперболе, то есть
принадлежит
гиперболе, то есть 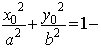 верное равенство.
Точка
верное равенство.
Точка 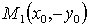 симметрична
точке
симметрична
точке 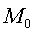 относительно
оси ОХ:
относительно
оси ОХ:
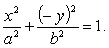
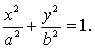 - верное
равенство. Следовательно,
- верное
равенство. Следовательно, 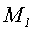 принадлежит
гиперболе, следовательно, гипербола симметрична относительно ОХ.
принадлежит
гиперболе, следовательно, гипербола симметрична относительно ОХ.
Точка  симметрична
точке
симметрична
точке 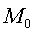 относительно
оси ОУ, следовательно, гипербола симметрична относительно оси ОУ.
относительно
оси ОУ, следовательно, гипербола симметрична относительно оси ОУ.
Точка  симметрична
точке
симметрична
точке 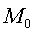 относительно
О (центра), отсюда следует, что гипербола симметрична относительно начала
координат. [1.С.108]
относительно
О (центра), отсюда следует, что гипербола симметрична относительно начала
координат. [1.С.108]
) Асимптоты гиперболы:
Текущая точка гиперболы при движении по ней в
бесконечность неограниченно приближается к некоторой прямой, которая называется
асимптотой гиперболы. Асимптотами являются прямые, которые имеют следующие
уравнения:
 и
и  ,
,
Пусть текущая точка гиперболы, 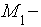 ее
проекция на ось абсцисс. Прямая
ее
проекция на ось абсцисс. Прямая 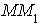 пересекает прямую
пересекает прямую 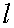 ,
заданную указанным уравнением в точке
,
заданную указанным уравнением в точке 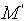 .
Докажем: что
.
Докажем: что 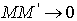 при
при  .
.
Доказательство:
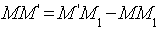 .Расстояние
.Расстояние  это
ордината точки
это
ордината точки 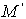 , лежащей на прямой
, лежащей на прямой
 .
Она равна
.
Она равна  . Расстояние
. Расстояние 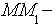 это
ордината точки
это
ордината точки 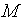 гиперболы, которую
находим из её канонического уравнения:
гиперболы, которую
находим из её канонического уравнения: 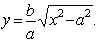 Тогда
Тогда

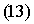
Умножим и разделим равенство (13) на ( ),следовательно,
получим:
),следовательно,
получим:
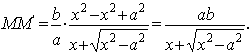
При 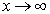 знаменатель
дроби неограниченно увеличивается, следовательно, дробь стремится к нулю.
знаменатель
дроби неограниченно увеличивается, следовательно, дробь стремится к нулю.
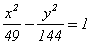 - уравнение
гиперболы, в которой
- уравнение
гиперболы, в которой  а
а 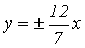 -
являются асимптотами гиперболы. (чертеж 20.) [1.С.108]
-
являются асимптотами гиперболы. (чертеж 20.) [1.С.108]
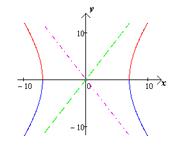
Чертеж 8
) Фокусы гиперболы:
Пусть фокусы гиперболы лежат на оси Ох.
Межфокусное расстояние гиперболы равно  причем
причем
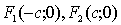 .
Заметим, что
.
Заметим, что  по определению
гиперболы.
по определению
гиперболы.
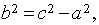

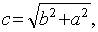
Следовательно,  фокусы
гиперболы. [1.С.109]
фокусы
гиперболы. [1.С.109]
) Директориальное свойство гиперболы:
Определение 3.4. Директрисами гиперболы
называются прямые, параллельные канонической оси ОУ и отстоящие от этой оси на
расстояние 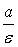 .
.
Уравнения директрис гиперболы имеют вид: ++ и
и
 ,
если гипербола задана уравнением
,
если гипербола задана уравнением 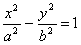 .
Если гипербола задана уравнением
.
Если гипербола задана уравнением 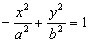 ,
то директрисы определяются уравнениями
,
то директрисы определяются уравнениями 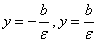 .
.
) Эксцентриситет гиперболы:
Определение 3.5. Отношение  называется
эксцентриситетом гиперболы. Так как
называется
эксцентриситетом гиперболы. Так как 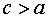 ,
то
,
то 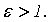
Если при постоянном значении 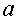 ,
число
,
число  будет
изменяться от нуля до бесконечности, то
будет
изменяться от нуля до бесконечности, то 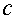
 будет
измениться от
будет
измениться от 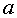 до бесконечности.
Если
до бесконечности.
Если 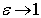 ,
то гипербола будет стремиться к лучам (чертеж 9).
,
то гипербола будет стремиться к лучам (чертеж 9).

Чертеж 9
Если 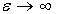 ,
то гипербола будет стремиться к параллельным прямым (чертеж 10). [1.С.109]
,
то гипербола будет стремиться к параллельным прямым (чертеж 10). [1.С.109]
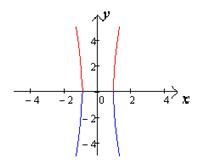
Чертеж 10
) Касательная к гиперболе:
Уравнение касательной к гиперболе 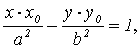 ,
где
,
где 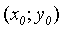 -
координаты точки касания, а
-
координаты точки касания, а 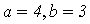 соответственно
действительная и мнимая полуоси гиперболы (чертеж 11).
соответственно
действительная и мнимая полуоси гиперболы (чертеж 11).
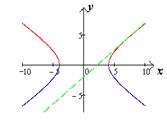
Чертеж 11
8) Диаметр гиперболы:
Если гипербола задана уравнением 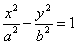 ,
то её диамерт, сопряженный хордам с угловым коэффициентом k, определяется
уравнением
,
то её диамерт, сопряженный хордам с угловым коэффициентом k, определяется
уравнением 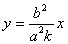 .
.
ПАРАБОЛА
Определение 4.1.Парабола- это геометрическое
множество точек, для каждой из которых расстояние от некоторой фиксированной
точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой
директрисой (директриса не проходит через фокус). [8.С.589]
Общий вид уравнения  .
.
Исследование свойств параболы
) Вершина параболы:
Уравнению (15) удовлетворяют числа 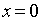 и
и
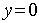 ,
следовательно, парабола проходит через начало координат.[1.c.109-110]
,
следовательно, парабола проходит через начало координат.[1.c.109-110]
) Симметрия параболы:
Пусть 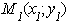 принадлежит
параболе, т.е.
принадлежит
параболе, т.е.  верное равенство.
Точка
верное равенство.
Точка  симметрична
точке
симметрична
точке  относительно
оси
относительно
оси  ,
следовательно, парабола симметрична относительно оси абсцисс. [1.С.110]
,
следовательно, парабола симметрична относительно оси абсцисс. [1.С.110]
Эксцентриситет параболы:
Определение 4.2. Эксцентриситетом параболы
называется число 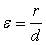 , равное единице.
, равное единице.
 , так как по
определению параболы
, так как по
определению параболы 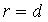 .[1.С.110-111]
.[1.С.110-111]
) Касательная параболы:
Касательная к параболе в точке касания  определяется
уравнением
определяется
уравнением
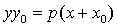 , где
, где 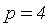 (чертеж
12)
(чертеж
12)
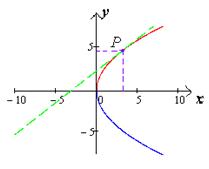
Чертеж 12
Фокус параболы:
Если уравнение параболы имеет вид 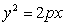 ,
то её фокус имеет координаты
,
то её фокус имеет координаты 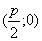 .
.
Если уравнение параболы имеет вид  ,
то её фокус будет иметь координаты
,
то её фокус будет иметь координаты  .
.
Диаметр параболы:
Если парабола задана уравнением 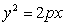 ,
то её диаметр определяется уравнением
,
то её диаметр определяется уравнением 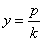 ,где
k угловой коэффициент.
,где
k угловой коэффициент.
Уравнения директрис параболы:
Если уравнение параболы имеет вид 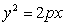 ,
то директриса параболы имеет уравнение:
,
то директриса параболы имеет уравнение:  .
Если уравнение параболы имеет вид
.
Если уравнение параболы имеет вид  ,
то уравнение директрисы параболы имеет вид:
,
то уравнение директрисы параболы имеет вид: 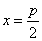
Чтобы обобщить работу по теории линий второго
порядка в элементарной математике и для удобства использования информации о
линиях при решении задач, заключим все данные о линиях второго порядка в
таблицу № 1.
Таблица 1 - Линии второго порядка в элементарной
математике
|
Название
линии 2-го порядка
|
Окружность
|
Эллипс
|
Гипербола
|
Парабола
|
|
Характеристические
свойства
|
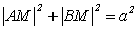
|
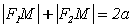
|
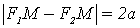
|
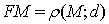
|
|
Уравнение
линии
|
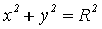
|
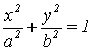
|
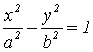
|
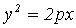
|
|
Эксцентриситет
|
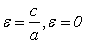
|
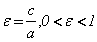
|

|
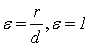
|
|
Уравнение
касательной в точке (x0;y0)
|

|
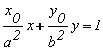
|
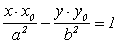
|
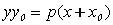
|
|
Фокус
|
|
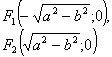
|
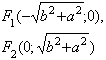
|
 , если
уравнение параболы: , если
уравнение параболы: 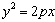 . .  , если
уравнение параболы имеет вид: , если
уравнение параболы имеет вид:
|
|
Диаметры
линий
|
|
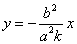 , где k-
угловой коэффициент , где k-
угловой коэффициент
|
 , где k
угловой коэффициент , где k
угловой коэффициент
|
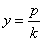 , где k-
угловой коэффициент , где k-
угловой коэффициент
|
|
Уравнения
директрис
|
|
 , если , если  . . 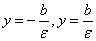 , если , если 
|
 , если
уравнение гиперболы имеет вид: , если
уравнение гиперболы имеет вид: 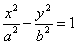 . . 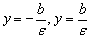 , если уравнение гиперболы имеет
вид: , если уравнение гиперболы имеет
вид:  . .
|
 ,если
уравнение параболы имеет вид: ,если
уравнение параболы имеет вид: 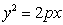 . .
|
Возможности использования ИКТ в изучении линий
второго порядка
Сегодня современные информационные технологии
становятся важнейшим инструментом модернизации школы в целом - от управления до
воспитания и обеспечения доступности образования.
Процесс информатизации, охвативший все стороны
жизни современного общества, имеет несколько приоритетных направлений, к
которым, безусловно, следует отнести информатизацию образования. Она является
первоосновой глобальной рационализации интеллектуальной деятельности человека
за счет использования информационно-коммуникационных технологий (ИКТ).
Середина 90-х годов прошлого века и до
сегодняшнего дня, характеризуется массовостью и доступностью персональных
компьютеров в России, широким использованием телекоммуникаций, что позволяет
внедрять разрабатываемые информационные технологии обучения в образовательный
процесс, совершенствуя и модернизируя его, улучшая качество знаний, повышая
мотивацию к обучению, максимально используя принцип индивидуализации обучения.
Информационные технологии обучения являются необходимым инструментом на данном
этапе информатизации образования.
Информационные технологии не только облегчают
доступ к информации и открывают возможности вариативности учебной деятельности,
ее индивидуализации и дифференциации, но и позволяют по-новому организовать
взаимодействие всех субъектов обучения, построить образовательную систему, в
которой ученик был бы активным и равноправным участником образовательной
деятельности.
Формирование новых информационных технологий в
рамках предметных уроков стимулируют потребность в создании новых
программно-методических комплексов направленных на качественное повышение
эффективности урока. Поэтому, для успешного и целенаправленного использования в
учебном процессе средств информационных технологий, преподаватели должны знать
общее описание принципов функционирования и дидактические возможности
программно- прикладных средств, а затем, исходя из своего опыта и рекомендаций,
"встраивать" их в учебный процесс.
Изучение математики в настоящее время сопряжено
с целым рядом особенностей и трудностей развития школьного образования в нашей
стране.
Появился так называемый кризис математического
образования. Причины его состоят в следующем:
в изменении приоритетов в обществе и в науке, то
есть в настоящее время идет рост приоритета гуманитарных наук;
в сокращении количества уроков математики в
школе;
в оторванности содержания математического
образования от жизни;
в малом воздействии на чувства и эмоции
учащихся.
Сегодня остается открытым вопрос: «Как же
наиболее эффективно использовать потенциальные возможности современных
информационных и коммуникационных технологий при обучении школьников, в том
числе, при обучении математике?».
Компьютер - отличный помощник в изучении такой
темы, как “Квадратичная функция”, потому что, используя специальные программы
можно строить графики различных функций, исследовать функцию, легко определить
координаты точек пересечения, вычислить площади замкнутых фигур и т.д.
Например, на уроке алгебры в 9-м классе, посвящённом преобразованию графика
(растяжения, сжатия, переносы координатных осей) можно увидеть лишь застывший
результат построения, а на экране монитора прослеживается вся динамика
последовательных действий учителя и ученика.
Компьютер, как ни одно техническое средство,
точно, наглядно и увлекательно открывает перед учеником идеальные
математические модели, т.е. то, к чему должен стремиться ребенок в своих
практических действиях.
Сколько трудностей приходится испытывать учителю
математики для того, чтобы убедить учеников в том, что касательная к графику
квадратичной функции в точке касания практически сливается с графиком функции.
На компьютере этот факт продемонстрировать очень просто- достаточно сузить
интервал по оси Ох и обнаружить, что в очень маленькой окрестности точки
касания график функции и касательная совпадают. Все эти действия происходят на
глазах у учеников. Этот пример дает толчок к активным размышлениям на уроке.
Для активизации познавательной деятельности
использование ИКТ может происходить на всех этапах и при разных типах уроков.
На вводных уроках важно заинтересовать ребят
яркими, запоминающимися образами, которые можно создать с помощью библиотеки
электронных наглядных пособий или образовательных ресурсов сети Интернет.
Увеличения доли информации, представляемой в визуальной форме, открывает
принципиально новые возможности для усвоения нового материала, развития
внимания и сообразительности.
При формировании новых знаний может быть
использовано электронное сопровождение в виде презентации, на которой отражены
основные понятия, схемы, алгоритм применения правил.
На уроках закрепления можно использовать
электронный тренажер или возможности цифрового образовательного ресурса, с
помощью которых обучающиеся не только могут применить свои знания в процессе
практической деятельности, но и увидеть личный результат.
Использование цифровых образовательных ресурсов
на уроке контроля позволяет организовать проверочную работу, при которой ученик
не только получает отметку и оценку своих знаний, но и анализ всего хода
выполнения работы (количество правильных и неправильных ответов, на какие
правила была допущена ошибка, какой материал необходимо повторить и т.д.)
Тем самым использование компьютера возможно как
в ходе объяснения нового материала на уроке, так и на этапе контроля. При
помощи программ, например «My Test», ученик самостоятельно может проверить свой
уровень знаний по теории, выполнить теоретико-практические задания. Программа
удобна своей универсальностью. Она может быть использована и для самоконтроля,
и для контроля со стороны учителя.
Разумная интеграция математики и компьютерных
технологий позволит богаче и глубже взглянуть на процесс решения задачи, ход
осмысления математических закономерностей. Кроме того, компьютер поможет
сформировать графическую, математическую и мыслительную культуру учеников, а
также с помощью компьютера можно подготовить дидактические материалы: карточки,
листы опроса, тесты и др. При этом давать возможность ребятам самостоятельно
разрабатывать тесты по теме, в ходе чего развивается интерес и творческий
подход.
Грамотное спользование ИКТ дает возможность:
повысить мотивацию обучения;
увеличить индивидуальную активность учащихся;
сформировать информационную компетенцию;
для свободного творчества;
для интерактивность обучения;
активизировать познавательную деятельность и
повысить качество успеваемости школьников;
для развития навыков самообразования и
самоконтроля;
повышения уровня комфортности обучения;
снизить дидактически затруднений у учащихся;
развивать информационное мышление;
проводить уроки на высоком эстетическом уровне;
индивидуально подойти к ученику, применяя
разноуровневые задания.
А для учителя, информационные технологии
способны решать многие педагогические задачи, предоставляя новые возможности
для творчества, приобретения и закрепления профессиональных навыков, позволяют
реализовывать принципиально новые формы и методы обучения.
Таким образом ИКТ становятся неотъемлемой частью
современного учебного процесса, способствующей повышению качества образования.
А значат есть необходимость и возможности применения компьютера на уроках
математики достаточно широко. Использование информационных технологий будет
способствовать повышению качества знаний, расширит горизонты изучения
квадратичной функции, следовательно, поможет найти новые перспективы для
поддержания интереса учащихся к предмету и к теме.
1.2 Методические аспекты изучения
линий второго порядка в школьном курсе алгебры 7-9 классов
Анализ содержания темы «Линии 2го порядка» в
школьных учебниках. (учебники по алгебре под редакцией Г. В. Дорофеева, Ш. Ф.
Алимова, А. Г. Мордковича)
Обязательной и неотъемлемой частью учебного
процесса, а также изучения линий второго порядка является тематическое
планирование и учебники. Из анализа комплектов учебников по алгебре 7-9 классов
таких авторов, как: А.Г. Мордкович, Ш. А. Алимов и Г.В. Дорофеев выяснили
содержание темы «Линии 2го порядка». ( Приложение 2. Таблица №3.)
Таблица 2 - Содержание темы «Линии 2го порядка»
в школьных учебниках
|
Линии
второго порядка
|
Алгебра,
автор А. Г. Мордкович
|
Алгебра,
автор Ш. А. Алимов, Ю. М. Колягин.
|
«Математика:
арифметика. Алгебра. Анализ данных», автор Г. В. Дорофеев, С. Б. Суворова.
|
|
Функция

|
с
какого класса узнают
|
с
7-го
|
|
|
|
|
с
8-го
|
|
+
|
+
|
|
|
с
9-го
|
|
|
|
|
название
|
+
|
+
|
+
|
|
исследования
свойств по уравнению
|
+
|
+
|
+
|
|
построение
графика:
|
+
|
+
|
+
|
|
по
точкам
|
+
|
+
|
+
|
|
по
свойствам
|
-
|
-
|
-
|
|
методом
преобразований
|
-
|
-
|
-
|
|
Функция
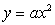
|
с
какого класса узнают
|
с
7-го
|
|
|
|
|
|
с
8-го
|
+
|
+
|
|
|
|
с
9-го
|
|
|
+
|
|
название
|
+
|
+
|
+
|
|
исследования
свойств по уравнению
|
+
|
+
|
+
|
|
построение
графика:
|
+
|
+
|
+
|
|
по
точкам
|
+
|
+
|
+
|
|
по
свойствам
|
+
|
+
|
+
|
|
методом
преобразований
|
-
|
-
|
-
|
|
Функция

|
с
какого класса узнают
|
с
7-го
|
|
|
|
|
|
с
8-го
|
+
|
+
|
|
|
|
с
9-го
|
|
|
+
|
|
название
|
+
|
+
|
+
|
|
исследования
свойств по уравнению
|
+
|
+
|
+
|
|
построение
графика:
|
+
|
+
|
+
|
|
по
точкам
|
+
|
+
|
+
|
|
по
свойствам
|
+
|
+
|
+
|
|
методом
преобразований
|
+
|
+
|
+
|
|
Функция

|
с
какого класса узнают
|
с
7-го
|
|
|
+
|
|
|
с
8-го
|
+
|
|
|
|
|
с
9-го
|
|
+
|
|
|
название
|
+
|
+
|
+
|
|
исследования
свойств по уравнению
|
+
|
+
|
+
|
|
построение
графика:
|
+
|
+
|
+
|
|
по
точкам
|
+
|
+
|
+
|
|
по
свойствам
|
-
|
-
|
-
|
|
методом
преобразований
|
-
|
-
|
-
|
|
|
|
|
|
|
|
Проанализировав содержание темы «Линии второго
порядка» в школьном курсе алгебры трех авторов, таких как Александра
Григорьевича Мордкович, Шавката Арифджановича Алимова, Георгия Владимировича
Дорофеева, было выявлено, что изложение теоретического материала наиболее полно
раскрыто у Дорофеева. Автор придерживается определенного алгоритма для каждой
функциональной линии:
пример и запись функции;
определение(как множество точек);
построение графика функции (по точкам, с
использованием свойств, методом преобразований );
исследование его свойств.
При этом Георгий Владимирович плавно подводит
под изучение нового материала, за счет повторения узученного. Изложенный
материал подкреплен соответствующими рисунками. По завершению главы «квадратичная
функция» автор отдельной главой выделяет изучение линий второго порядка:
История изучения плоских кривых;
Способы образования линий второго порядка;
Эллипс;
Гипербола;
Парабола.
Изучение данной главы идет при непосредственной
опоре и сравнении с изученными ранее квадратичными и дробно- рациональной
функциями.
В учебниках А.Г. Мордкович и Ш.А. Алимова
теоретическая часть представлена в меньшем объеме. Изучения новой функции не
предпологает повторение изученного материала, но при этом изучение каждой функциональной
линии начинается с примера (осуществляется межпредметная связь).
Рассматривая степень наглядности теоретического
материала, является необходимым отметить, что у Александра Григорьевича
теоретическая часть сопровождается большим количеством наглядности при:
приведении примеров (отмечание точек на одной
координатной плоскости и построение линии на другой координатной плоскости);
исследовании свойств (некоторые свойства
отображены на разных рисунках);
рассмотрение построения частей одной функции в разных
четвертях (при построении графика функции  ).
).
При это рисунки представлены на разлинованном
поле, что дает возможность легко находить координаты точек.
В учебниках Дорофеева графики отображены в
меньшем количестве (изображение нескольких функциий в одной системе координат),
но при этом, как и у Мордковича, прямоугольная система координат представлена в
разлиновоном виде.
У Шавката Арифджановича наглядность очень мала,
и по данным черчежам затруднительно вести исследования (т.к ни одна точка линии
не имеет точной координаты).
При сравнении практической части комплектов
учебников, заключаем, что в учебниках Александра Григорьевича Мордковича в
практической части представлены задания на закрепление изученного
теоретического материала, как на построение функций в явной форме, так и
построение по заданным значениям, свойствам. Практические задания разбиты по
уровню сложности, а также имеются задания на исследование уже построенных
функций по рисункам.
У Алимова практическая часть следует сразу после
теоретической и содержит задания, разбитые на три уровня сложности, каждый из
которых в среднем содержит по четыре задачи.
Рассматривая комплект учебников по алгебре 7-9
классов под редакцией Георгия Владимировича Дорофеева, можно сказать, что
содержащаяся для каждого параграфа практическая часть разделена на две части по
уровню сложности. Первую часть обозначают буквой А и в неё помещены упражнения,
требующие от учеников о основном умения решать по алгоритму. А во вторую часть,
обозначаемой буквой В, включены упражнения, при решении которых требуется
умение мыслить и анализировать. В основном в каждой части В (в конце)
содержится задача - исследование. При этом формулировки упражнений интересны,
разнообразны, и местами прослеживается непосредственная связь с другими
предметами (физика, геометрия). Каждый параграф заканчивается контрольными
вопросвми и заданиями. Учебники содержат не только разнообразные упражнения, но
и дополнительный материал в рублике «Для тех, кому интересно», «Вопросы для
повторения», Задачи для самопроверки»
Особенности изучения линий второго порядка в
школьном курсе алгебры
Изучение линий второго порядка в школьном курсе
алгебры начинается с 8-9 класса. Где данной теме уделяется 16 часов.
(приложение 2.)
Линии второго порядка представлены квадратичной
и дробно - рациональной функциями. Дробно - рациональная функция изучается в 8
классе, в течении 3 часов. Понятие функции учащиеся усваивают, начиная с 7
класса средней школы; идет постепенное изучение свойств функций и
функциональных зависимостей. Рассматриваются различные классы функций: начиная
с простейших линейных функций и их графиков, затем следуют квадратичные
функции, функции обратной пропорциональности и дробно-линейные функции.
В данной работе подробно рассмотрим особенности
изучения учащимися квадратичной функции и функции выражающей обратно
пропорциональную зависимость.
К изучению класса квадратичных функций учащиеся
знают, как строить график линейной функции:
метод «загущения» точек на графике;
построение по двум точкам;
Однако для построения параболы нужны новые
приёмы:
приём, основанный на преобразованиях, приводящих
функцию к виду  , и использования
геометрических преобразований для построения графика произвольной квадратичной
функции из параболы стандартного вида - графика функции
, и использования
геометрических преобразований для построения графика произвольной квадратичной
функции из параболы стандартного вида - графика функции 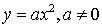 ;
;
построение по характеристическим точкам и с
учетом свойств симметрии. При построении графика функции по характеристическим
точкам и с учетом свойств симметрии необходимо использовать следующий алгоритм:
Выяснить направление ветвей. Если 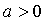 ,
то ветви параболы направлены вверх, если
,
то ветви параболы направлены вверх, если 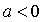 ,
то ветви направлены вниз.
,
то ветви направлены вниз.
Вычислить координаты вершины параболы  по
формулам
по
формулам 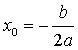 и
и
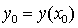 .
.
Найти нули функции 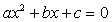 и
построить на оси абсцисс соответствующие точки параболы.
и
построить на оси абсцисс соответствующие точки параболы.
Вычисляем координаты точки пересечения параболы
с осью ординат:  и строим точку,
симметричную ей относительно оси параболы.
и строим точку,
симметричную ей относительно оси параболы.
Через построенные точки проводим параболу.
Квадратичная функция вводится и изучается в
тесной связи квадратичными уравнениями и неравенствами, что дает возможность
активно использовать график функции в их решении.
На подготовительном этапе к изучению линий
второго порядка, рассматривается функция 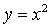 .
По своим свойствам, прежде всего, эта функция немонотонна, в отличие от
линейной функции. Чтобы подчеркнуть указанное отличие, полезно предложить
учащимся следующее задание: Функция задана формулой
.
По своим свойствам, прежде всего, эта функция немонотонна, в отличие от
линейной функции. Чтобы подчеркнуть указанное отличие, полезно предложить
учащимся следующее задание: Функция задана формулой  на
промежутке
на
промежутке 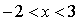 . Найти множество
значений этой функции.
. Найти множество
значений этой функции.
Перенося свойство монотонности с класса линейных
функций на  , учащиеся могут
допустить ошибку, именно поэтому следует рассмотреть график функции
, учащиеся могут
допустить ошибку, именно поэтому следует рассмотреть график функции  и
его построение:
и
его построение:
методом «загущения точек;
по характеристическим точкам.
Другое отличие состоит в том, что характер
изменения значений функции  неравномерный: на
одних участках она растет быстрее, на других - медленнее. Эта особенность
выявляется при построении графика, причем целесообразно рассмотреть два
графика: один - в крупном масштабе на промежутке
неравномерный: на
одних участках она растет быстрее, на других - медленнее. Эта особенность
выявляется при построении графика, причем целесообразно рассмотреть два
графика: один - в крупном масштабе на промежутке  ,
другой-в мелком масштабе на промежутке, например,
,
другой-в мелком масштабе на промежутке, например, 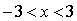 .
Построение можно вести описанным выше методом загущения. Важно отметить
свойство параболы - симметричность относительно оси абсцисс. В дальнейшем это
свойство приведет к рассмотрению класса четных функций, причем именно функция
.
Построение можно вести описанным выше методом загущения. Важно отметить
свойство параболы - симметричность относительно оси абсцисс. В дальнейшем это
свойство приведет к рассмотрению класса четных функций, причем именно функция  будет
ведущим примером функции этого класса.
будет
ведущим примером функции этого класса.
Изучение класса квадратичных функций начинается
с изучения функций вида  ; при этом
выясняется геометрический смысл коэффициента а, путем построения и сравнения
нескольких графиков функции в одной системе координат:
; при этом
выясняется геометрический смысл коэффициента а, путем построения и сравнения
нескольких графиков функции в одной системе координат:  .После
чего рассматриваются свойства функции при
.После
чего рассматриваются свойства функции при 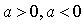 ,
вводится понятие области определения. При этом сначала рассуждения проводятся с
использованием геометрической терминологии и с опорой на график, а затем те же
самые факты формулируются на алгебраическом языке. Таким образом, формирование
таких понятий, как наименьшее (или наибольшее) значение квадратичной функции,
неограниченность сверху (или снизу) происходит с опорой на наглядные
представления. Школьники должны знать и о симметрии графиков функции
,
вводится понятие области определения. При этом сначала рассуждения проводятся с
использованием геометрической терминологии и с опорой на график, а затем те же
самые факты формулируются на алгебраическом языке. Таким образом, формирование
таких понятий, как наименьшее (или наибольшее) значение квадратичной функции,
неограниченность сверху (или снизу) происходит с опорой на наглядные
представления. Школьники должны знать и о симметрии графиков функции  относительно
оси OX при противоположных значениях a, и об изменении «крутизны» параболы при
изменении a.
относительно
оси OX при противоположных значениях a, и об изменении «крутизны» параболы при
изменении a.
Далее вводится более широкий класс функций,
имеющий вид 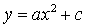 . И здесь также
коэффициент
. И здесь также
коэффициент 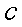 получает ясную
геометрическую интерпретацию. При этом справедливо следующее утверждение: чтобы
построить график функции
получает ясную
геометрическую интерпретацию. При этом справедливо следующее утверждение: чтобы
построить график функции 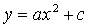 , где c- заданное
положительное число, надо сдвинуть график функции
, где c- заданное
положительное число, надо сдвинуть график функции 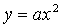 вдоль
оси OY на c единиц масштаба вверх; чтобы построить график функции
вдоль
оси OY на c единиц масштаба вверх; чтобы построить график функции 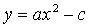 ,
где c- заданное положительное число, надо сдвинуть график функции
,
где c- заданное положительное число, надо сдвинуть график функции 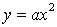 вдоль
оси OY на c единиц масштаба вниз.
вдоль
оси OY на c единиц масштаба вниз.
Пример 1. Задан график функции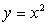 .
Построить на этом чертеже график функции
.
Построить на этом чертеже график функции 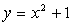 .
.
Заметим, что при заданном значении аргумента Х0
значения функции 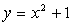 на одно и то же
число, равное 1, больше значений функции
на одно и то же
число, равное 1, больше значений функции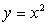 .
Поэтому для построения соответствующей точки второй функции на графике достаточно
поднять на одну единицу график первой функции с абсциссой Х0. Следовательно,
чтобы построить весь график второй функции, нужно поднять на 1 единицу весь
график первой функции. Доказывается теорема о том, что график любой функции
вида
.
Поэтому для построения соответствующей точки второй функции на графике достаточно
поднять на одну единицу график первой функции с абсциссой Х0. Следовательно,
чтобы построить весь график второй функции, нужно поднять на 1 единицу весь
график первой функции. Доказывается теорема о том, что график любой функции
вида  может
быть получен путем сдвигов вдоль координатных осей параболы
может
быть получен путем сдвигов вдоль координатных осей параболы  .
.
После этой подготовки, казалось бы, можно
приступить к изучению графиков произвольных квадратичных функций. Но здесь
возникает трудность: коэффициент при первой степени неизвестного не имеет для
квадратичной функции  достаточно
простого геометрического смысла. Именно поэтому приходится идти обходным путем,
следуя тем же преобразованиям, которые производились при выводе формулы решения
квадратного уравнения, и вводить в рассмотрение новый подкласс квадратичных
функций вида
достаточно
простого геометрического смысла. Именно поэтому приходится идти обходным путем,
следуя тем же преобразованиям, которые производились при выводе формулы решения
квадратного уравнения, и вводить в рассмотрение новый подкласс квадратичных
функций вида 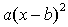 . Объяснения при
построении графиков здесь в целом могут быть такими же, как при рассмотрении
функций вида
. Объяснения при
построении графиков здесь в целом могут быть такими же, как при рассмотрении
функций вида 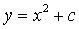 , однако
усваивается предлагаемый способ здесь с большим трудом, так как требует
дополнительных геометрических преобразований, поэтому требуется достаточное
количество упражнений для закрепления. После таких приготовлений построение
графика, а также изучение его свойств происходят без принципиальных
затруднений.
, однако
усваивается предлагаемый способ здесь с большим трудом, так как требует
дополнительных геометрических преобразований, поэтому требуется достаточное
количество упражнений для закрепления. После таких приготовлений построение
графика, а также изучение его свойств происходят без принципиальных
затруднений.
Отметим здесь один частный, но полезный прием,
который состоит в использовании системы заданий, имеющих цель - дать
представление о тех или иных чертах данной функции или целого класса без
указания точного значения величин, связанных с рассматриваемым вопросом. Его
можно назвать качественным или оценочным исследованием функции. Приведем два
примера применения приема, связанные с изучением квадратичных функций.
Пример 2. На рисунке изображены графики функций  и
и
 .
Как относительно их пройдет график функции
.
Как относительно их пройдет график функции 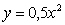 ;
; ;
;
 ?
Это задание не предполагает «точного» построения искомого графика; достаточно
лишь указание на область, где он расположен, или его эскизное построение.
?
Это задание не предполагает «точного» построения искомого графика; достаточно
лишь указание на область, где он расположен, или его эскизное построение.
Пример 3. На рисунке изображен график функции 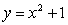 ,
пользуясь этим чертежом, изобразить от руки график функции
,
пользуясь этим чертежом, изобразить от руки график функции  .
Проверить правильность сделанного эскиза, вычислить значения функции
.
Проверить правильность сделанного эскиза, вычислить значения функции  при
при
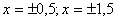 и
отметить точки графика. Каким преобразованием можно перевести график функции
и
отметить точки графика. Каким преобразованием можно перевести график функции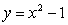 в график функции
в график функции  ?
?

Рис. 1 - График функции 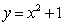
Теперь учащиеся по коэффициентам квадратного
трехчлена  могут представить
общий вид соответствующей параболы и вычислить координаты её вершины, путём
выделения полного квадрата в данном трёхчлене. В результате выполнения
практических заданий, на построение графика квадратичной функции необходимо в
строгой последовательности проговорить и зафиксировать алгоритм построения
функции
могут представить
общий вид соответствующей параболы и вычислить координаты её вершины, путём
выделения полного квадрата в данном трёхчлене. В результате выполнения
практических заданий, на построение графика квадратичной функции необходимо в
строгой последовательности проговорить и зафиксировать алгоритм построения
функции 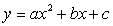 .
.
В системе упражнений, учебников по алгебре,
значительное место отводится задачам прикладного характера. Завершается тема
рассмотрением вопроса о решении квадратных неравенств, выбор решения основан на
использовании графиков.
При работе с теоретической частью и выполнении
заданий учащиеся должны будут проводить наблюдение, выдвигать гипотезы,
рассуждать, доказывать, переходить от одной системы терминов к другой.
Затем отмечается, что график любой квадратичной
функции - это парабола и приведены различные виды парабол.
В восьмом классе идет изучение функции ,
изложение материала начинается с анализа примеров реальных зависимостей.
Учащимся предлагается рассмотреть зависимость времени движения пешехода от его
скорости, длины стороны прямоугольника заданной площади от длины другой его
стороны, количества товара, которое можно купить на определенную сумму денег,
от цены этого товара. Обобщая эти примеры постепенно приходим к определению
функции
,
изложение материала начинается с анализа примеров реальных зависимостей.
Учащимся предлагается рассмотреть зависимость времени движения пешехода от его
скорости, длины стороны прямоугольника заданной площади от длины другой его
стороны, количества товара, которое можно купить на определенную сумму денег,
от цены этого товара. Обобщая эти примеры постепенно приходим к определению
функции  (называемой
обратной пропорциональностью).
(называемой
обратной пропорциональностью).
Все свойства и график функции в учебнике
рассматриваются на примере конкретных функций (Например, 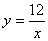 ).
По точкам строится график данной функции и вводится его название (гипербола).
Здесь из свойств выделяются только область определения, промежутки убывания и
возрастания функции и делается замечание, что график данной функции не
пересекает координатные оси. Исследование проводится подробно для первого
случая, когда
).
По точкам строится график данной функции и вводится его название (гипербола).
Здесь из свойств выделяются только область определения, промежутки убывания и
возрастания функции и делается замечание, что график данной функции не
пересекает координатные оси. Исследование проводится подробно для первого
случая, когда 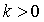 , а для второго
случая (
, а для второго
случая (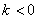 ) приведены только конечные выводы и результаты.
) приведены только конечные выводы и результаты.
Традиционно построение графика обратной
пропорциональности вызывает у учащихся трудности. Многие строят его небрежно,
не соблюдая симметрии ветвей, ветви бывают очень короткие, очень часто в
работах учащихся одна из ветвей гиперболы сначала приближается, например, к оси
х, а затем удаляется от нее. Для предупреждения подобных ошибок очень важно
проанализировать особенности графика, обратив внимание учащихся на то, что
график состоит из двух ветвей, симметричных друг другу относительно начала
координат. Каждая ветвь гиперболы по мере удаления от начала координат
становится все ближе и ближе к осям, но не пересекает их. Бесконечное
приближение ветвей к осям координат можно проиллюстрировать в ходе небольшого
числового опыта: например, подставить в формулу вместо х несколько достаточно
больших чисел в порядке их возрастания и понаблюдать, как изменяется при этом
значение  .
.
Глава 2. Практическое применение ИКТ
при изучении линий второго порядка учащимися
.1 Систематизация ЦОР, содержащих
линии второго порядка
Анализируя компьютерные программы, рассмотрим
те, которые помогают решать задачи, изучать свойства линий второго порядка, а
также строить графики функций, задающих данные линии. К этим программам
относятся: математический пакет «MathCAD», программы «Maple» и «Живая
геометрия», а также такая программа, как «Advanced Grapher».
Математический пакет «MathCAD» - универсальный
математический пакет, предназначенный для выполнения инженерных и научных
расчетов. Основное преимущество пакета - естественный математический язык, на
котором формируются решаемые задачи. Имеет операторы для построения двухмерных
графиков. Для построения линий второго порядка в MathCAD необходимо:
задать диапазон значений аргумента;
задать функцию;
установить курсор в то место, где должен быть
построен график.
Главным достоинством пакета являются:
простота в использовании;
проведение численных и аналитических
математических расчетов;
получение различной справочной информации из
области математики и многое другое.
Недостатки программы:
не задает направление системы координат;
не задаёт название осей системы координат.
[8.С.543]
Программа «Maple»- система компьютерной
математики, способная выполнять быстро и эффективно не только символьные, но и
численные расчеты, причем сочетает это с превосходными средствами графической
визуализации и подготовки электронных документов. позволяет:
строить графики многих функций, также и графики
линий второго порядка с различными типами осей (с линейным и логарифмическим
масштабом);
строить графики функций в декартовой и полярной
системах координат;
задание пользователем окраски графиков.
Недостатки программы:
не задает направление системы координат;
не задаёт название осей системы координат;
необходимо знать много названий, помогающий
задать функцию, цвет линии, толщину линии и т.д. [11.С.3-16]
Программа «Живая геометрия» - электронный альбом
для геометрических чертежей. При помощи этой программы выполняются построения
линий второго порядка. Программа позволяет:
Создавать хорошие чертежи, проще, чем на бумаге;
"Оживлять" их, плавно изменяя
положение исходных точек ("мышкой" илиавтоматически.). Дает
возможность:
создавать десятки обучающих и исследовательских
"живых" чертежей;
использовать архивы чертежей;
обозначать каждую построенную прямую или
отмеченную точку буквой английского или русского алфавита. [8.С.359-360]
Программа «Advanced Grapher» - мощная и простая
в использовании программа для построения графиков и их анализа. Дает
возможность строить графики линий второго порядка. Поддерживает построение
графиков функций вида Y(x), X(y), в полярных координатах, заданных
параметрическими уравнениями.
Вычислительные возможности: нахождение нулей и
экстремумов функций, точек пересечения графиков, уравнений касательных и
нормалей. Большое количество параметров графиков и координатной плоскости.
Имеет возможности печати, сохранения и копирования графиков в виде рисунков, многодокументный
настраиваемый интерфейс. Поддерживает интерфейс на русском языке и при его
выборе может использоваться в некоммерческих целях бесплатно.
Программа позволяет:
строить разнообразные графики на плоскости, а
также проводить исследование функций;
одновременно на чертеже изобразить до 100
геометрических объектов (это могут быть графики функций, заданных явно или
неявно в декартовых координатах, параметрически, в полярных координатах, а
также заштрихованные области, лежащие между двумя графиками функций).
в начале работы выбрать готовый шаблон с
системой координат или создать новый;
изменить систему координат и ее настройки в
любой момент работы с данным чертежом;
фиксировать построенные объекты в списке функций
в левой части окна программы;
скрывать отдельные функции на плоскости чертежа,
отмеченные «галочкой» (это удобно для объяснения учебного материала).
Программа «MyTest» - программа тестирования
учащихся, редактор тестов для создания и проведения компьютерного тестирования,
сбора и анализа результатов, выставления оценки по указанной в тесте шкале.
Программа дает возможность:
создавать тесты для промежуточного и итогового
контроля знаний по линиям второго порядка;
сохранить параметры тестирования, задания и
рисунки в одном файле текста;
для различных заданий выставить разное время для
выполнения;
быстро и относительно точно оценить большое
количество испытуемых.
Обобщим возможности использования ЭСО в изучении
линий второго порядка в таблицу (Таблица № 3).
Таблица 3 - Линии 2го порядка в ЦОР
|
№
п/п.
|
Дидактические
единицы
|
Математический
пакет «MathCAD»
|
Программа
«Maple»
|
Программа
«Живая геометрия»
|
Программа
«Advanced Grapher»
|
|
1.
|
Определение
|
-
|
-
|
+
|
-
|
|
2.
|
Вывод
уравнения
|
-
|
-
|
-
|
-
|
|
3.
|
Исследование
свойств по уравнению
|
+
|
-
|
+
|
+
|
|
4.
|
Изображение
линий
|
+
|
+
|
+
|
+
|
Вывод: Проанализировав имеющиеся компьютерные
программы по математике, позволяющие строить линии второго порядка, заключаем,
что данные программы не дают возможность реализовать все дидактические единицы
темы «Линии второго порядка в элементарной математике». Рассматривая таблицу,
видим, что главной функцией программ является построение графиков, их
визуализация и исследование свойств линии по ее уравнению. Программы «MathCAD»,
«Maple» и «Живая геометрия», интересны тем, что они позволяют исследовать
линии, при изменении параметров в их уравнениях. Прогоамма «Advanced Grapher»
позволяет не только исследовать линии, но и фиксировать построения в списке
функций, а также скрывать отдельные функции на плоскости черчежа.
Программа «MyTest» не дает возможности ни
строить,ни исследовать линии второго порядка. Основной функцией «MyTest»
является создание тестов для усвоения и закрепления изученного материала.
2.2 Особенности использования ЦОР в
изучении линий второго порядка на уроках алгебры
Для того чтобы соответствовать требованиям
современного информационного общества школа должна подготовить выпускников,
которые являются не только хорошими специалистами в своей области, но и владеют
одной из ключевых компетенций - умением применять информационно-коммуникационные
технологии. Использование ИКТ в обучении способствует активизации
образовательного процесса, развитию познавательного интереса и, как следствие,
повышению качества знаний, что приводит к достижению учащимися максимальных
результатов в различных областях.
Рассмотрим особенности использования описанных в
работе ЦОР на уроках алгебры 7-9 классов. При проведении уроков математики с
компьютерным сопровождением лучше использовать электронную версию уроков
«Кирилла и Мефодия», разработки компании «Физикон», !Открытая математика.
Планиметрия» (7- 9 кл.), «Открытая математика. Графики и функции» (7- 9 кл.),
«Интерактивная математика» (5- 9 кл.) издательства «Дрофа», «Алгебра не для
отличников» и другие. Они содержат материалы по многим темам программы, по истории
математики, видеосюжеты, а иногда сопровождается и звуковым объяснением
материала.
В настоящее время существует множество программ,
позволяющих рисовать графики функций, выполнять построения, проводить
доказательства, проводить исследования и т.д. Они позволяют давать иллюстрацию
важнейших понятий, причем сделать это наглядно и быстро, что повышает и
активизирует познавательную активность учащихся. Появляется возможность
оптимально сочетать практические и аналитические виды деятельности в соответствии
с индивидуальными особенностями каждого ученика. К таким программам относятся:
«Живая геометрия», «Mathcad», «Maple». Одной из таких программ является
ADVANCED GRAPHER. Эта программа давно известна. Использовать ее можно
практически на всех уроках при изучении графиков функций. Особенно эффективно
применение программы при изучении следующих разделов математики:
взаимное расположение графиков линейных функций
(7 класс);
графический способ решения системы линейных
уравнений (7 класс);
графический способ решения уравнений (8 класс);
построение графика квадратичной функции (9
класс);
графический способ решения систем уравнений (9
класс);GRAPHER можно использовать и на внеклассных занятиях, так как программа
позволяет строить кривые, заданные параметрическими уравнениями или уравнениями
в полярных координатах, изображать на плоскости области, являющиеся решением
неравенств.
Проектная деятельность на основе ИКТ позволяет
разнообразить учебную
деятельность. При этом повышается мотивация
учащихся к самостоятельному изучению математики.
Плюсы и минусы при использовании ИКТ на уроках
Положительные стороны использования ИКТ:
Конечно же, использование компьютера в учебном
процессе способствует:
развитию познавательного интереса;
активизирует речемыслительную деятельность;
позволяет в увлекательной творческой форме
продуктивно решать все задачи урока;
индивидуализация обучения, позволяющая ученику
развиваться в соответствии с его способностями и особенностями.
Компьютер в школе, особенно в кабинете
математики - это не просто атрибут современного урока, это, прежде всего,
возможность повышения мотивации к изучению математики, повышения качества
обучения и развития творческих способностей учащихся. Создавая презентации,
весь материал " как на ладони", наглядность, доступность и т.д.
Большая экономия времени на уроке при использовании ИКТ, в этом я убедилась на
практике.
Можно создавать тренажёры и использовать их на
уроках в целях закрепления или итогового контроля, появляется интерес к
изучаемому.
Отрицательные стороны использования ИКТ:
Использование ИКТ на уроке должно быть
методически правильным (безусловно, с соблюдением санитарно-гигиенических
требований), разумным и целесообразным. Есть определенные требования к уроку.
Про сбережение здоровья забывать не имеем права. Нельзя весь урок работать у
компьютера. Дети перестают говорить и рассуждать. Все должно быть в меру. От
мастерства учителя зависит, сможет ли он найти эту меру и не навредить.
Даже самая умная машина не сможет заменить живое
общение учителя и ученика, яркого, грамотного, эмоционального слова учителя.
Сегодня современные информационные технологии
становятся важнейшим инструментом модернизации школы в целом - от управления до
воспитания и обеспечения доступности образования. Учитель решает, исходя из
индивидуальных особенностей ученика, какого характера программы более
целесообразно использовать на том или ином этапе обучения. Осуществляя
личностно-ориентированное обучение с использованием компьютера и новых
информационных технологий, надо помнить о том, что необходимо обеспечить
ученику возможность реализации личностных устремлений, индивидуальности,
инициативы и самостоятельности. А учителю важно получать достаточно полную и
объективную информацию о процессах личностного становления ученика, всячески
содействуя этому процессу.
Заключение
В работе отражено историческое развитие теории
линий второго порядка. Систематизированный материал по каждой линии второго
порядка был раскрыт и разбит по дидактическим единицам: определение, вывод
уравнения, исследование свойств, изображение линий. Для обобщения работы по
теории линий второго порядка в элементарной математике и для удобства
использования информации о линиях при решении задач, все данные о линиях
второго порядка были занесены в таблицу (Таблица №1). Во второй части первой
главы описано изучение и анализ комплектов учебников по алгебре таких авторов,
как Г.В. Дорофеева, Ш.Ф. Алимова, А.Г. Мордковича по теме «Линии второго
порядка». Содержание данной темы в школьных учебниках отображено в таблице № 2.
Внедрение компьютерных технологий в процесс
обучения, которые становятся неотъемлемой частью целостного образовательного
процесса, значительно повышают его эффективность. Учитывая развитие новых
технологий, встал вопрос: «Возможно ли изучение линий второго порядка в
школьном курсе алгебры, при помощи использования ИКТ?». Рассматривая этот
вопрос, большое внимание уделялось рассмотрению компьютерных программ. Исследуя
геометрические программы, как: «MathCAD», «Maple», «Живая геометрия», «Advanced
Grapher» результат показал, что данные программы дают возможность изучения
отдельных дидактических единиц линий второго порядка (Таблица №3). Они
позволяют активно работать, оперируя их возможностями. Во время работы
предоставляется возможность изучения закономерностей изменения линий за счет
изменения параметров.
Во второй главе выпускной квалификационной
работы раскрыто практическое применение ИКТ при изучении линий второго порядка
учащимися: систематизированы ЦОР, содержащии линии второго порядка; рассмотрены
особенности использования ЦОР в изучении линий второго порядка на уроках
алгебры; разработаны и реализованы на практике фрагменты уроков по алгебре на
тему «Линии второго порядка».
Целью данной работы являлось: установить
возможности использования ИКТ в изучении линий второго порядка в школьном курсе
алгебры.
Основные задачи работы:
. Проанализировать и систематизировать
содержание линий второго порядка в элементарной математике;
.Проанализировать содержание и возможности
использования для изучения линий второго порядка имеющиеся ЦОР по математике;
. Проанализировать содержание темы «Линии 2го
порядка» в школьных учебниках;
.Рассмотреть примеры использования ИКТ в решении
задач с линиями второго порядка
В ходе выполнения работы достигнута цель и
частично решены поставленные задачи:
проанализировано и систематизировано содержание
линий второго порядка в элементарной математике;
проанализировано содержание и возможности
использования для изучения линий второго порядка трех ЦОР по математике;
рассмотрены примеры использования ЦОР в решении
задач с линиями второго порядка.
Литература
1. Алгебра.
7 класс: Учеб. для общеобразовательных учеб. заведений / К.С. Муравин, Г.К.
Муравин, Г.В. Дорофеев. - М.: Дрофа, 1999.
2. Алгебра.
7 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г.
Мордкович. - М.: Мнемозина, 2000.
. Алгебра.
8 класс: Учеб. для общеобразовательных учеб. заведений / К.С. Муравин, Г.К.
Муравин, Г.В. Дорофеев. - М.: Дрофа, 2001.
. Алгебра.
9 класс: Учеб. для общеобразовательных учеб. заведений / К.С. Муравин, Г.К.
Муравин, Г.В. Дорофеев. - М.: Дрофа, 1999.
. Алгебра.
9 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г.
Мордкович. - М.: Мнемозина, 2000.
. Алгебра.
8 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г.
Мордкович. - М.: Мнемозина, 2000.
. Алгебра.
Учеб. для 7 класса средней школы / Ш.А. Алимов, Ю.М. Колягин и др. - М.:
Просвещение, 2000.
. Алгебра.
Учеб. для 8 класса средней школы / Ш.А. Алимов, Ю.М. Колягин и др. - М.:
Просвещение, 2001.
. Алгебра.
Учеб. для 9 класса средней школы / Ш.А. Алимов, Ю.М. Колягин и др. - М.:
Просвещение, 2001.
. Анищенко
А.С. Лекции по геометрии. Ч.1.-Красноярск: РИО КГПУ, 2004.-144 с.
. Беклемишев
Д.В. Курс аналитической геометрии и линейной алгебры: учебник для студ. Вузов.
/ Д.В. Беклемишев. М.: Физматлит, 2002.- 374 с.
. Глушакова
Т.Н., Решение задач по аналитической геометрии. Линии второго порядка. -
Воронеж, 2008 г.- 47 с.
. Гусак
А.А. Аналитическая геометрия и линейная алгебра.- Мн.: Тетрасистемс, 1998.- 143
с.
. Ефимов
А.В., Демидович Б.П. Сборник задач по математике для ВТУЗов (4 части). - М.:
Наука, 1993.-98 с.
. Ильин
В.А., Позняк Г. Аналитическая геометрия. - М.: Наука, 1974.- 218 с.
. Калиновский
Ю.Л. Пособие для выполнения курсовых работ по линейной алгебре и аналитической
геометрии, 2005.-32 с.
. Клетеник
Д.И. Сборник задач по аналитической геометрии. М.: Наука, 1980.- 198 с.
. Математический
энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С.
Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П.
Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с.
. Мышкис
А.Д. Лекции по высшей математике./ А.Д. Мышкис. М.: Наука, 1969.- 640 с.
. Погорелов
А.В. Геометрия: Учебник для 7-11 кл. общеобразоват. Учреждений.-9-е изд.- М.:
Просвещение,1999.-383 с.
. Овсеец
М.И., Светлая Е.М. Сборник задач по высшей математике. Учебное издание.- Мн.:
ЧИУиП, 2006.- 67 с.
. Савелов
А.А. Плоские кривые. - М.: ГИФ-МЛ, 1960.
. Савотченко
С.Е., Кузьмичева Т.Г. Методы решения математических задач в Maple. Учебное
пособие.- Белгород, 2001.- 58 с.
. Дубровский
В.Н., Поздняков С.Н. Динамическая геометрия в школе. Стереометрия в двух мерных
средах. Учебное пособие.-2008.-76 с.
.
<#"562771.files/image369.gif"> начинается
в 7 классе с § 37, где переход от линейной функции к квадратичной
осуществляется на примере. (пусть x - сторона квадрата, y - его площадь, то  ).
Затем независимой переменной x дают конкретные значения, чтобы рассчитать
значения y и вводится таблица вида:
).
Затем независимой переменной x дают конкретные значения, чтобы рассчитать
значения y и вводится таблица вида:
Вводится понятие таблица значений, а затем
полученные координаты строятся в прямоугольной системе координат. И сразу же
говорится, что построенная линия называется параболой. Далее перечисляются
геометрические свойства параболы:
симметричность относительно оси OY;
дается определение ветвей параболы;
вершина и её координаты;
наибольшее и наименьшее функции;
Убывание, возрастание;
Фокус параболы.
Построение функции  и
и
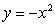 ,
сравнивание, и анализ графика.
,
сравнивание, и анализ графика.
Весь материал представлен параллельно с
примерами и изображенными графиками функций.
Функция 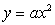 рассматривается
в 8 классе в 3-ей главе § 17. И здесь говориться о том, что функция
рассматривается
в 8 классе в 3-ей главе § 17. И здесь говориться о том, что функция 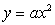 аналогична
функции
аналогична
функции  при
a=1. Затем рассматриваются функции,
при
a=1. Затем рассматриваются функции, 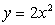 и
и
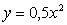 ,
составляется таблица значений, строятся графики (наглядность построения) и
сравниваются. Затем идет пояснение, что каждая линия- парабола, а осьy -ось
симметрии. Далее рассматривается случай при a=-1, выполняется построение
графика, и делается вывод о направлении ветвей параболы. После чего дается
определение функции
,
составляется таблица значений, строятся графики (наглядность построения) и
сравниваются. Затем идет пояснение, что каждая линия- парабола, а осьy -ось
симметрии. Далее рассматривается случай при a=-1, выполняется построение
графика, и делается вывод о направлении ветвей параболы. После чего дается
определение функции 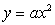 . Отдельным пунктом
автор выделяет свойства
. Отдельным пунктом
автор выделяет свойства 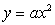 при a>0:
при a>0:
Область определения функции (-∞;+∞);=0
при x=0;y>0 при x≠0;
Непрерывна;наим=0 при x=0, yнаиб - не
существует;
 возрастает при x≥0
и убывает при x≤0;
возрастает при x≥0
и убывает при x≤0;
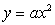 ограничена снизу, не
ограничена сверху;
ограничена снизу, не
ограничена сверху;
Функция выпукла вниз.
И при a<0 с непосредственной опорой на
геометрическую модель-параболу.
После теоретической части идут непосредственно,
задания на усвоение:
) Найти наиб. И наим. Значения функции 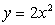 на
отрезках: [0;2], [-2;-1], [-1;1,5].
на
отрезках: [0;2], [-2;-1], [-1;1,5].
) Решить уравнение 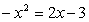 и
другие.
и
другие.
Задания на закрепление, охватывают всю
теоретическую часть и представлены в большом количестве. Здесь приведены
задания на построение функции как в явной форме, так и построение линии по
заданным значениям, свойствам. Также имеются задания на исследование уже
построенных функций по рисункам.
В 8 классе с § 37 изучается функция 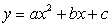 и
её свойства. Изучение начинается с рассмотрения многочлена
и
её свойства. Изучение начинается с рассмотрения многочлена 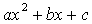 ,
где a,b,c-числа, причем a≠0. И поясняется, что это квадратичный трехчлен.
Затем рассматривается функция
,
где a,b,c-числа, причем a≠0. И поясняется, что это квадратичный трехчлен.
Затем рассматривается функция  и дается ее
определение. При этом рассматривается несколько функций:
и дается ее
определение. При этом рассматривается несколько функций: 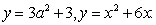 и
делается обобщение, что эти функции являются квадратичными. Автор предлагает
рассмотреть квадратный трехчлен
и
делается обобщение, что эти функции являются квадратичными. Автор предлагает
рассмотреть квадратный трехчлен  и путем
преобразований привести его к виду
и путем
преобразований привести его к виду 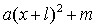 ,
где
,
где 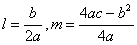 .
Затем вводится формула
.
Затем вводится формула  и поясняется, что
это формула для вычисления вершины параболы.
и поясняется, что
это формула для вычисления вершины параболы.
При этом дается задание: Не выполняя построения
графика функции  , ответить на
следующие вопросы:
, ответить на
следующие вопросы:
Какая прямая служит осью параболы?
Каковы координаты вершины параболы?
Куда направлены ветви параболы?
После построения графика данной функции вводится
алгоритм построения параболы  .
.
Практическая часть содержит большой объем
заданий: легких, средней сложности и повышенной сложности.
В 8 классе в § 18 Мордкович предлогает
познакомимся с функцией 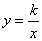 , где коэффициент k
может принимать любые значения, кроме k=0. И предлагается рассмотреть функцию
при k=1, составляется таблица значений при x>0, и строится график функции
, где коэффициент k
может принимать любые значения, кроме k=0. И предлагается рассмотреть функцию
при k=1, составляется таблица значений при x>0, и строится график функции 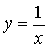 ,
а затем при x<0. Дальше говориться, что этот график функции
,
а затем при x<0. Дальше говориться, что этот график функции 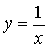 называется
гиперболой. По чертежу перечисляются основные свойства:
называется
гиперболой. По чертежу перечисляются основные свойства:
Гипербола симметрична относительно центра;
Имеет две асимптоты: ось x и ось y;
Имеет оси симметрии: y=x и y=-x.
Затем дается пример: Найти наименьшее и
наибольшее значение функции  : на отрезке
[1/2;4], на полуинтервале [-8;-1] и подробно расписывается ход действий.
: на отрезке
[1/2;4], на полуинтервале [-8;-1] и подробно расписывается ход действий.
Далее вводится определение графика функции 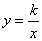 .
.
И поясняется, что две величины x и y обратно
пропорциональны, если они связаны отношением xy=k (где k - число, отличное от
нуля)
Дальше автор по отдельности выделяет свойства
функции 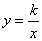 при
k>0 и при k<0. Для усвоения изученного материала предлагается решить
уравнение
при
k>0 и при k<0. Для усвоения изученного материала предлагается решить
уравнение 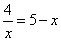 .
.
Практическая часть для закрепления и усвоения
данного материала содержит большое количество заданий трех уровней сложности.
При этом это задачи как на построение графика функции, так и на исследование
его свойств по строящимся чертежам, так и по готовым рисункам.
Анализ содержания темы «Линии 2го порядка» в
школьных учебниках по алгебре автора Ш. Ф. Алимова.
В 8 классе в §35на примере тела, брошенного
вверх со скоростью v, выводится формула 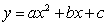 ,
и дается определение квадратичной функции.
,
и дается определение квадратичной функции.
Начиная с §36, рассматривается функция 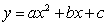 при
a=1,b=c=0. Составляется таблица значений, строятся точки, кривую называют
параболой. Сразу рассматриваются её свойства:
при
a=1,b=c=0. Составляется таблица значений, строятся точки, кривую называют
параболой. Сразу рассматриваются её свойства:
Проходит через начало координат
Симметричность относительно OY.
Вершина параболы
Убывание и возрастание на промежутках.
Фокус параболы (с ссылкой на рисунок)
В конце параграфа представлена система заданий
на усвоение и закрепление материала.
Такие задания, как:
Построить график функции  ,
найти значение y при
,
найти значение y при 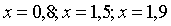 и т.д.;
и т.д.;
При каких x значения функции 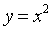 больше
9, меньше 16?
больше
9, меньше 16?
Найти координаты точек пересечения  и
прямой
и
прямой 
Функция 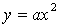 рассматривается
в 8 классе в § 37. Изучение сразу начинается с построения графика функции
рассматривается
в 8 классе в § 37. Изучение сразу начинается с построения графика функции 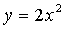 и
и
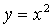 с
помощью таблицы значений. Сравнивая графики, делается вывод о том, что каждую
точку графика функции
с
помощью таблицы значений. Сравнивая графики, делается вывод о том, что каждую
точку графика функции  можно получить из
точки графика функции
можно получить из
точки графика функции  с той же абсциссой
увеличением её ординаты в 2 раза. Далее дается определение функции
с той же абсциссой
увеличением её ординаты в 2 раза. Далее дается определение функции 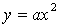 и
перечисляются свойства при a≠0:
и
перечисляются свойства при a≠0:
Если a>0, то функция 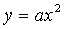 принимает
положительные значения, если a<0-отрицательные. И если значение функции
принимает
положительные значения, если a<0-отрицательные. И если значение функции 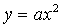 равно
0, значит x=0.
равно
0, значит x=0.
Парабола симметрична относительно оси ординат
Если a>0, то функция  возрастает
при x≥0 и убывает при x≤0;если a<0, то функция
возрастает
при x≥0 и убывает при x≤0;если a<0, то функция 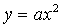 убывает
при x≥0 и возрастает при x≤0.
убывает
при x≥0 и возрастает при x≤0.
Затем задается задача:
На одной координатной плоскости построить
графики функций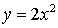 и
и 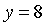 .
С помощью этих графиков решить неравенство
.
С помощью этих графиков решить неравенство 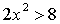 .
.
Упражнения представлены в конце параграфа и
содержат как легкие, так и повышенной сложности задания.
Изучение графика функции  начинается
с §38, где сразу дается задание:
начинается
с §38, где сразу дается задание:
Построить график функции 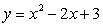 и
сравнить его с графиком функции
и
сравнить его с графиком функции 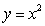 . После проведенных
рассуждений делается заключение, что графиком функции
. После проведенных
рассуждений делается заключение, что графиком функции  является
парабола, полученная сдвигом параболы
является
парабола, полученная сдвигом параболы 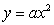 вдоль
координатных осей. И перечисляются свойства:
вдоль
координатных осей. И перечисляются свойства:
Вершина параболы 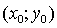 ,
где
,
где  ;
;
Ось симметрии параболы параллельна оси ординат и
проходит через вершину параболы;
Направление ветвей параболы, если a>0- вверх,
если a<0-вниз.
Практическая часть разделена на уровни по
сложности, каждый из уровней имеет по 6 заданий. Некоторые из них:
Найти координаты вершины параболы  .
.
Найти координаты точек пересечения параболы с
осями координат: 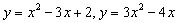 .
.
Записать уравнение параболы, пересекающей ось
абсцисс в точках x=-1 и x=3, а ось ординат в точке y=2.
Функция  изучается
в 9 классе, начиная с §15. Изучение начинается с задания: Построить график
функции
изучается
в 9 классе, начиная с §15. Изучение начинается с задания: Построить график
функции  .
И по графику начинается изучение свойств:
.
И по графику начинается изучение свойств:
Область определения
(-∞;0)˅(0;+∞);
) нечетная, так как 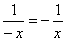 при
при
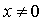 .
.
) убывает на промежутке x>0;
) При x>0 функция принимает положительные
значения;
Затем говорится, что график функции  называется
гиперболой, а две части, из которых она состоит, называются ветвями гиперболы.
называется
гиперболой, а две части, из которых она состоит, называются ветвями гиперболы.
Сразу дается на рассмотрение задача 2: Построить
график функции  при k=2 и k=-2.
при k=2 и k=-2.
Исследуя две функции поясняется, что функции
симметричны относительно оси абсцисс.
Функция 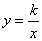 соотносится
с функцией
соотносится
с функцией  и говорится, что
и говорится, что 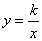 обладает
теми же свойствами, что и
обладает
теми же свойствами, что и  .
.
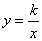 при k>0
выражает обратную пропорциональную зависимость между x и y. И приводится пример
из физики. Далее следует практическая часть, состоящая по сложности из уровней.
Каждый из уровней содержат по четыре задачи на закрепление.
при k>0
выражает обратную пропорциональную зависимость между x и y. И приводится пример
из физики. Далее следует практическая часть, состоящая по сложности из уровней.
Каждый из уровней содержат по четыре задачи на закрепление.
Анализ содержания темы «Линии 2го порядка» в
школьных учебниках по алгебре под редакцией Г.В. Дорофеева
Функция изучается с §22 по §23. В §22 на
рассмотрение выносится две задачи:
За t секунд велосипедист проезжает 600 км.
Какова его скорость?
Площадь прямоугольника с основанием ф (м) равна
40 м2. Какую высоту имеет этот прямоугольник?
В первой задаче, если скорость обозначить за v,
тогда 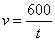 .
А во второй задаче, если обозначить высоту за h, получим:
.
А во второй задаче, если обозначить высоту за h, получим:  .
Обобщая эти задачи, говорится, что функции в каждой из них получаются делением
некоторого отличного от нуля числа на соответствующее значение аргумента.
Обозначив число буквой k, а аргумент и функцию соответственно x и y получаем
общий вид формул:
.
Обобщая эти задачи, говорится, что функции в каждой из них получаются делением
некоторого отличного от нуля числа на соответствующее значение аргумента.
Обозначив число буквой k, а аргумент и функцию соответственно x и y получаем
общий вид формул:  , где k- число,
отличное от нуля. После чего рассматривается пропорция
, где k- число,
отличное от нуля. После чего рассматривается пропорция 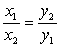 ,
говорится, что частное двух значений переменной x обратно частному
соответствующих им значений переменной y. И такие переменные называют обратно
пропорциональными. К данному параграфу прилагаются практические задания по
уровню сложности на составление пропорции, на нахождение одного из компонентов
формулы
,
говорится, что частное двух значений переменной x обратно частному
соответствующих им значений переменной y. И такие переменные называют обратно
пропорциональными. К данному параграфу прилагаются практические задания по
уровню сложности на составление пропорции, на нахождение одного из компонентов
формулы  .
В §23 рассматривается график функции
.
В §23 рассматривается график функции  при
k=12. Составляется таблица значений для положительными абсциссами, а затем с
отрицательными и выполняется построение. Анализируя построенные графики
функции, выделяются следующие свойства:
при
k=12. Составляется таблица значений для положительными абсциссами, а затем с
отрицательными и выполняется построение. Анализируя построенные графики
функции, выделяются следующие свойства:
Графики не имеют общих точек пересечения с осями
координат;
Ветви графика функции  расположены
симметрично относительно начала координат: если k>0, то ветви расположены в
I и III координатных четвертях; а если k<0, то во II и IV координатных
четвертях.
расположены
симметрично относительно начала координат: если k>0, то ветви расположены в
I и III координатных четвертях; а если k<0, то во II и IV координатных
четвертях.
После выделенных свойств, говорится, что кривые
вида  называются
гиперболами.
называются
гиперболами.
На этом теоретическая часть заканчивается, и
начинается практическая часть, состоящая из двух уровней сложности, по
количеству заданий и их характеру для изучаемой темы возможно достаточно хорошо
усвоить и закрепить материал, так как все задания различны.
Приложение 2
Примерное распределение учебного
материала «Линии 2-го порядка» к школьному учебнику по алгебре под редакцией
Г.В. Дорофеева
|
№
п/п
|
Тема
урока
|
Кол-во
часов
|
|
1.
|
Функция
у =х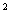 , её
свойства и график. , её
свойства и график.
|
1
|
|
2.
|
Функция
у= х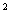 , её
свойства и график. Функция у = -х2 , её
свойства и график. Функция у = -х2
|
1
|
|
3.
|
Контрольная
работа
|
1
|
|
4.
|
Функция
у=aх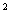 , её
свойства и график , её
свойства и график
|
1
|
|
5.
|
Функция
у=aх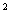 , её
свойства и график , её
свойства и график
|
1
|
|
6.
|
Функция
у=aх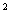 , её
свойства и график , её
свойства и график
|
1
|
|
7.
|
Контрольная
работа
|
1
|
|
8.
|
Функция
у = k/x, её свойства и график
|
1
|
|
9.
|
Функция
у = k/x, её свойства и график
|
1
|
|
10.
|
Контрольная
работа
|
1
|
|
11.
|
Функция
у=ax2+bx+c, её свойства и график
|
1
|
|
12.
|
Функция
у=ax2+bx+c, её свойства и график
|
1
|
|
13.
|
Функция
у=ax2+ bx+c, её свойства и график
|
1
|
|
14.
|
Квадратные
неравенства
|
1
|
|
15.
|
Контрольная
работа
|
1
|
|
16.
|
Итоговый
урок
|
1
|
Приложение 3
линия порядок алгебра урок
Вывод уравнения окружности
Введем прямоугольную систему координат так, что:
М0(x0;y0) - центр окружности, совпадающий с
началом системы координат и  . Пусть
. Пусть  -
текущая точка окружности.(чертеж 13)
-
текущая точка окружности.(чертеж 13)
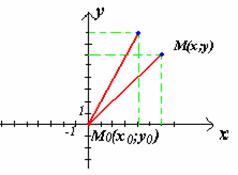
Чертеж 13
Если центр окружности находится в начале
координат, то x0=0, y0=0. В этом случае уравнение окружности имеет вид:
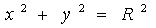 ,
,
так как 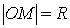 по
определению окружности и
по
определению окружности и  .) Пусть
.) Пусть 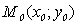 не
совпадает с началом системы координат. По построению окружности:
не
совпадает с началом системы координат. По построению окружности:
 =
=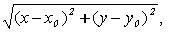 тогда
тогда
 или
возведя обе части в квадрат получим:
или
возведя обе части в квадрат получим:
 (1)
(1)
где  уравнение
окружности радиуса R c центром в точке
уравнение
окружности радиуса R c центром в точке 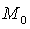 с
координатами
с
координатами 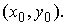 (чертеж 14)
(чертеж 14)
Иногда уравнение окружности пишут так:  -
канонический вид уравнения окружности с центром в точке
-
канонический вид уравнения окружности с центром в точке 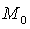 с
координатами
с
координатами
 и радиусом R.
и радиусом R.

Чертеж 14
Изображение окружности
Построим окружность центром в точке  и
радиусом равным 1.
и
радиусом равным 1.
Построение без использования ИКТ: Для построения
окружности задаем прямоугольную систему координат с центром в точке О и
единичный отрезок. Строим циркулем окружность с центром О и радиусом, равным 1
(чертеж 15).

Чертеж 15
) Построение с использованием ЭСО- Mathcad:
Уравнение окружности имеет вид: 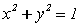 .
Для построения линии в программе Mathcad уравнение нужно привести к виду:
.
Для построения линии в программе Mathcad уравнение нужно привести к виду: 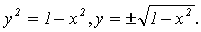 (чертеж
16)
(чертеж
16)

Чертеж 16
Построим окружность центром в точке 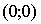 и
радиусом равным 5.
и
радиусом равным 5.
Построение без использования ИКТ: Для построения
окружности задаем прямоугольную систему координат с центром в точке О и
единичный отрезок. Строим циркулем окружность с центром О и радиусом, равным 5
(чертеж 17).

Чертеж 17
) Построение с использованием ЭСО- Mathcad:
Уравнение окружности имеет вид: 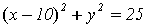 .
Для построения линии в программе Mathcad уравнение нужно привести к виду:
.
Для построения линии в программе Mathcad уравнение нужно привести к виду: 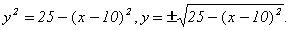 (чертеж
19)
(чертеж
19)
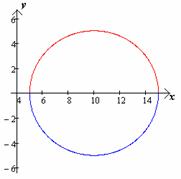
Чертеж 18
Вывод уравнения эллипса
Введем прямоугольную систему координат. Пусть
фокусы эллипса лежат на оси Х, причем 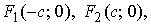 т.
Е.
т.
Е.  -
межфокусное расстояние эллипса. (чертеж 8.) [8.С.467]
-
межфокусное расстояние эллипса. (чертеж 8.) [8.С.467]
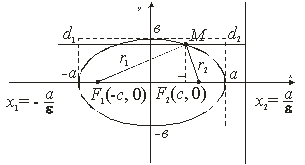
Чертеж 19
Пусть 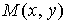 -
произвольная точка эллипса. Величины
-
произвольная точка эллипса. Величины 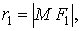
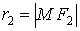 называются
фокальными радиусами точки М эллипса. По определению эллипса: r1 + r2 = 2a, а
> c. Из прямоугольных треугольников, по теореме Пифагора, имеем:
называются
фокальными радиусами точки М эллипса. По определению эллипса: r1 + r2 = 2a, а
> c. Из прямоугольных треугольников, по теореме Пифагора, имеем:
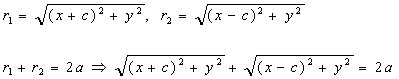
Преобразуем уравнение, умножим уравнение (2) на 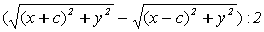 ,
получим:
,
получим:
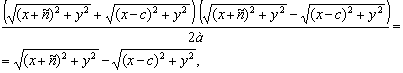
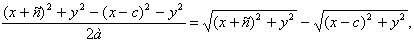
 (3)
(3)
Сложим уравнения (2) и (3):

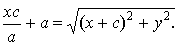 (4)
(4)
Возведем равенство(4) в квадрат, получим:


Пусть 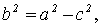 так
как
так
как 
 , откуда уравнение
имеет вид:
, откуда уравнение
имеет вид:
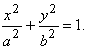
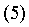
где (5) каноническое уравнение эллипса с центром
в начале координат.
Соответственно, отсюда получаем уравнение:


где  каноническое
уравнение эллипса с центром в точке
каноническое
уравнение эллипса с центром в точке 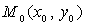 .
Где числа а и b соответственно большая и малая полуоси эллипса. Заметим, что а
>с Если а <
.
Где числа а и b соответственно большая и малая полуоси эллипса. Заметим, что а
>с Если а < 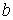 , то фокусы эллипса
будут лежать на оси ОУ, если а =
, то фокусы эллипса
будут лежать на оси ОУ, если а = 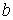 ,
то эллипс превращается в окружность.
,
то эллипс превращается в окружность.
Точки 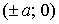 ,
,
 называются
вершинами эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника,
ограниченного прямыми
называются
вершинами эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника,
ограниченного прямыми 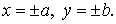
Изображение эллипса
Построим эллипс с центром в точке  и
с большей осью равной 14 и меньшей осью равной 10.
и
с большей осью равной 14 и меньшей осью равной 10.
Построение без использования ИКТ: Для построения
эллипса построим прямоугольную систему координат с центром в точке О и
единичный отрезок. Построим прямоугольник со сторонами 2a=14,2b=10 и впишем в
него эллипс так, чтобы координаты точек (-7;0),(7;0),(0;-5),(0;5) принадлежали
эллипсу (чертеж 21).

Чертеж 20
С использованием ЭСО- Mathcad:
Полученное уравнение эллипса имеет вид: 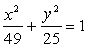 .
Для построения линии второго порядка в программе Mathcad приводим уравнение к
виду:
.
Для построения линии второго порядка в программе Mathcad приводим уравнение к
виду: 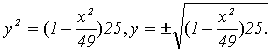 (чертеж
22)
(чертеж
22)
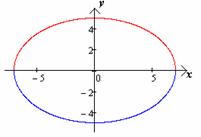
Чертеж 21
Дано параметрическое уравнение эллипса 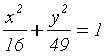 ,
построить данную линию второго порядка.
,
построить данную линию второго порядка.
Построение без использования ИКТ: Для построения
эллипса построим прямоугольную систему координат с центром в точке О и
единичный отрезок. Построим прямоугольник со сторонами 2a=8,2b=14 и впишем в
него эллипс так, чтобы координаты точек (-4;0),(4;0),(0;-7),(0;7) принадлежали
эллипсу (чертеж 23).
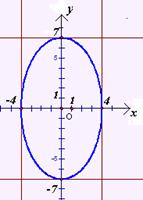
Чертеж 22
С использованием ЭСО- Mathcad:
Для построения линии в Mathcad приведем ее к
виду:  ,
,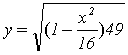 .(чертеж
24)
.(чертеж
24)
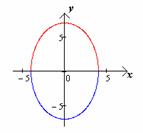
Чертеж 23
Изображение гиперболы
Построим гиперболу с действительной осью равной
4 и мнимой осью равной 4.
Построение без использования ИКТ: Для построения
гиперболы задаем прямоугольную систему координат с центром в точке О и
единичный отрезок. Строим прямоугольник со сторонами 2a=4,2b=4, проводим
диагонали прямоугольника. Выполняем построение ветвей гиперболы так, чтобы
координаты точек (-2;0),(2;0) являлись их вершинами, и ветви гиперболы не
пересекали диагоналей прямоугольника.(чертеж 25)

Чертеж 24
С использованием ЭСО- Mathcad:
Полученное уравнение линии имеет вид:  .
Для построения линии второго порядка в программе Mathcad приводим уравнение к
виду:
.
Для построения линии второго порядка в программе Mathcad приводим уравнение к
виду: 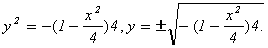 (чертеж
26)
(чертеж
26)
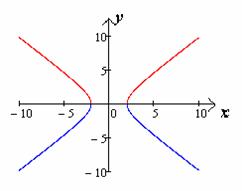
Чертеж 25
Построим гиперболу с действительной осью равной
10 и мнимой осью равной 8.
а) Построение без использования ИКТ: Для
построения гиперболы задаем прямоугольную систему координат с центром в точке О
и единичный отрезок. Строим прямоугольник со сторонами 2a=10,2b=8, проводим
диагонали прямоугольника. Выполняем построение ветвей гиперболы так, чтобы
координаты точек (0;4),(0;-4) являлись их вершинами, и ветви гиперболы не
пересекали диагоналей прямоугольника (чертеж 26)

Чертеж 26
) С использованием ЭСО- Mathcad:
Полученное уравнение имеет вид: 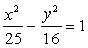 .
Для построения линии второго порядка в программе Mathcad приводим уравнение к виду:
.
Для построения линии второго порядка в программе Mathcad приводим уравнение к виду:
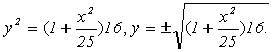 (чертеж
27)
(чертеж
27)
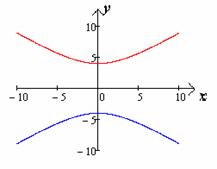
Чертеж 27
Вывод уравнения параболы
Введем прямоугольную систему координат, где  .
Пусть ось
.
Пусть ось  проходит через
фокус F параболы и перпендикулярен директрисе, а ось
проходит через
фокус F параболы и перпендикулярен директрисе, а ось  проходит
посередине между фокусом и директрисой. Обозначим через
проходит
посередине между фокусом и директрисой. Обозначим через 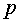 расстояние
между фокусом и директрисой. Тогда
расстояние
между фокусом и директрисой. Тогда  а
уравнение директрисы
а
уравнение директрисы 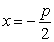 .
.
Число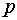 -
называется фокальным параметром параболы. Пусть
-
называется фокальным параметром параболы. Пусть  -
текущая точка параболы. Пусть
-
текущая точка параболы. Пусть 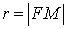 - фокальный радиус
точки
- фокальный радиус
точки  гиперболы.
гиперболы.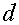 -расстояние
от точки
-расстояние
от точки  до
директрисы. Тогда
до
директрисы. Тогда  (чертеж 28)
(чертеж 28)

Чертеж 28
По определению параболы  .
Следовательно,
.
Следовательно,

Отсюда:


Возведем уравнение  в
квадрат, получим:
в
квадрат, получим:
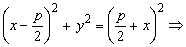
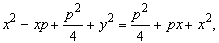
 (15)
(15)
где (15) каноническое уравнение параболы,
симметричной относительно оси 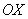 и проходящей через
начало координат.
и проходящей через
начало координат.
Изображение параболы
Построим параболу с вершиной в точке 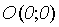 и
и
 .
.
Построение без использования ИКТ: Для построения
параболы задаем прямоугольную систему координат с центром в точке О и единичный
отрезок. Отмечаем на оси ОХ фокус 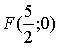 ,так
как
,так
как 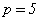 ,
проводим
,
проводим 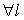 такую,
что
такую,
что 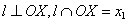 ,
и директрису параболы
,
и директрису параболы  . Выполняем
построение окружности в точке
. Выполняем
построение окружности в точке 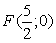 и радиусом равным
расстоянию от прямой
и радиусом равным
расстоянию от прямой 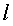 до директрисы
параболы. Окружность пересекает прямую
до директрисы
параболы. Окружность пересекает прямую 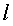 в
точках
в
точках 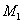 и
и
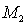 .
Строим параболу так, чтобы она проходила через начало координат и через точки
.
Строим параболу так, чтобы она проходила через начало координат и через точки 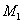 и
и
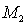 .(чертеж
29.)
.(чертеж
29.)
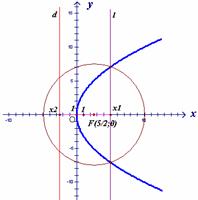
Чертеж 29
С использованием ЭСО- Mathcad:
Полученное уравнение имеет вид: 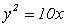 .
Для построения линии второго порядка в программе Mathcad приводим уравнение к виду
(чертеж 30)
.
Для построения линии второго порядка в программе Mathcad приводим уравнение к виду
(чертеж 30)
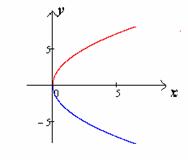
Чертеж 30
Построим параболу с вершиной в точке  и
и
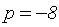 .)
Построение без использования ИКТ: Для построения параболы задаем прямоугольную
систему координат с центром в точке О и единичный отрезок. Отмечаем на оси ОХ
фокус
.)
Построение без использования ИКТ: Для построения параболы задаем прямоугольную
систему координат с центром в точке О и единичный отрезок. Отмечаем на оси ОХ
фокус 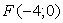 ,так
как
,так
как 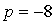 ,
проводим
,
проводим 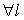 такую,
что
такую,
что 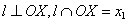 ,
и директрису параболы
,
и директрису параболы 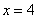 . Выполняем
построение окружности в точке
. Выполняем
построение окружности в точке  и радиусом равным
расстоянию от прямой
и радиусом равным
расстоянию от прямой 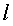 до директрисы
параболы. Окружность пересекает прямую
до директрисы
параболы. Окружность пересекает прямую 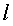 в
точках
в
точках 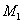 и
и
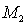 .
Строим параболу так, чтобы она проходила через начало координат и через точки
.
Строим параболу так, чтобы она проходила через начало координат и через точки  и
и
 (чертеж
31).
(чертеж
31).
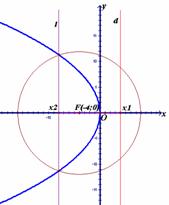
Чертеж 31
)С использованием ЭСО- Mathcad:
Полученное уравнение имеет вид:  .
Для построения линии второго порядка в программе Mathcad приводим уравнение к
виду:
.
Для построения линии второго порядка в программе Mathcad приводим уравнение к
виду:  .(чертеж
32)
.(чертеж
32)
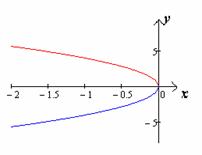
Чертеж 32