Теория принятия решений
СОДЕРЖАНИЕ
Задача 1.
Многокритериальный анализ вариантов
Задача 2.
Стратегии принятия решений
Задача 3.
Принятие решений в условиях неопределенности
Задача 4.
Методы прогнозирования
Задача 5.
Полный факторный эксперимент
Задача 6.
Имитационное моделирование
Задача 7.
Динамическое программирование
Задача 8.
Теория игр. Игра 2х2
Задача 9.
Контрольные карты Шухарта
Задача 1. Многокритериальный анализ вариантов
Дано: Из ноутбуков четырёх фирм: «HP», «ASUS»,
«Samsung», «Acer» нужно выбрать лучший. С дальнейшей целью его
покупки.
Для оценки эксперты воспользовались следующими критериями:
S = {S1, S2, S3, S4};
C1 -
популярность фирмы;
C2 -
оригинальность дизайна;
C3 -
высокая производительность процессора;
C4 -
средняя цена;
C5 -
размер матрицы.
При сравнении были получены следующие высказывания:
С1:
) отсутствие преимущества S3 над
S2;
) существенное преимущество 4 над 1;
) слабое преимущество 1 над 2;
) явное преимущество 4 над 3;
) явное преимущество 4 над 2;
) слабое преимущество 3 над 1.
С2:
) абсолютное преимущество 1 над 2;
) слабое преимущество 3над 4;
) слабое преимущество 1 над 3;
) существенное преимущество 1 над 4;
) нет преимущества 4 над 2;
) слабое преимущество 3 над 2.
С3:
) отсутствие преимущества 3 над 4;
) явное преимущество 4 над 2;
) абсолютное преимущество 3 над 1;
) абсолютное преимущество 4 над 1;
) слабое преимущество 2 над 1;
) явное преимущество 3 над 2.
С4:
) отсутствие преимущества 2 над 4;
) слабое преимущество 4 над 1;
) существенное преимущество 4 над 3;
) существенное преимущество 2 над 3;
) слабое преимущество 2 над 1;
) слабое преимущество 1 над 3.
С5:
) слабое преимущество 1 над 2
) абсолютное преимущество 4 над 2
) существенное преимущество 4 над 1
) отсутствие преимущества 3 над 2
) абсолютное преимущество 3 над 2
) существенное преимущество 3 над 1
Ход решения:
5 матриц 4x4
S1 S2 S3 S4
А(С1) = 
Составим нечеткое множество:
Просуммируем числа в столбце, получив определенное число, далее нужно
единицу разделить на это число. И так для каждого столбца.
С’1 = {  ;
; 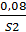 ;
; 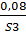 ;
; 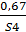 }
}
S1 S2 S3 S4
А(С2) = 
Составим нечеткое множество:
С’ 2= {
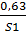 ;
;  ;
; 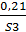 ;
; 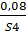 }S2 S3 S4
}S2 S3 S4
А(С3) = 
Составим нечеткое множество:
С’3 = {
 ;
; 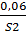 ;
; 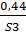 ;
; 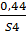 }S2 S3 S4
}S2 S3 S4
А(С4) = 
Составим нечеткое множество:
С’4 = {
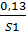 ;
;  ;
; 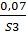 ;
; 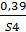 }S2 S3 S4
}S2 S3 S4
А(С5) = 
Составим нечеткое множество:
С’5 = {  ;
;  ;
; 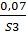 ;
; 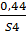 }
}
Составим результирующее множество:
С’1 = {  ;
; 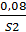 ;
; 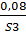 ;
; 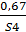 }
}
С’ 2= { 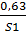 ;
;  ;
; 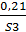 ;
; 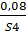 }
}
С’3 = {  ;
; 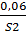 ;
; 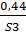 ;
; 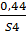 }
}
С’4 = { 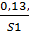 ;
; 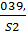 ;
; 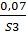 ;
; 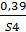 }
}
С’5 = {  ;
;  ;
; 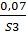 ;
; 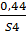 }
}
Из каждого получившегося столбца берем минимальное значение.
D = {  ;
; 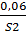 ;
; 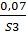 ;
; 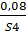 }
}
S1:=
4место;
S2:=
3место;
S3:=
2место;
S4:=
1место;
Неравновесные критерии:
w1 =
0,1 - степень важности критерия С1;
w2 =
0,1 - степень важности критерия С2;
w3 =
0,4 - степень важности критерия С3;
w4 =
0,2 - степень важности критерия С4;
w5 =
0,2 - степень важности критерия С5.
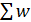 = 1
= 1
С’1 = { 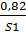 ;
;  ;
; 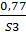 ;
; 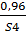 };
};
С’ 2= { 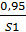 ;
; 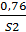 ;
; 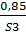 ;
; 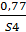 };
};
С’3 = {  ;
;  ;
;  ;
; 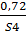 };
};
С’4 = { 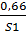 ;
;  ;
; 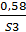 ;
; 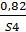 };
};
С’5 = { 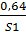 ;
; 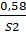 ;
; 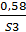 ;
; 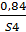 }.
}.
Из каждого получившегося столбца берем минимальное значение.
D’ = {
 ;
;  ;
; 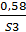 ;
; 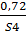 }
}
S1:=
4место;
S2:=
3место;
S3:=
2место;
S4:=
1место;
Вывод: по результатам расчетов многокритериального анализа , самый
лучший, рекомендуемый для покупки ноутбук - это Acer.
Задача 2. Стратегии принятия решений
Дано: С целью определения наилучшего варианта места отдыха семья
будет рассматривать 5 критериев:
) к1 - стоимость путевки;
) к2 - количество дней отдыха;
) к3- количество пересадок;
) к4- число торговых точек;
) к5- количество звёзд отеля.
Для нахождения оптимального решения, рассматриваются 8 альтернативных
вариантов:
) а - Турция;
) b - Греция;
) c - Таиланд;
) d - ОАЭ;
) e - Франция;
) f - Испания;
) g - Италия;
) h - Египет.
Таблица 1 - Исходные данные
|
|
k1
|
ран
|
k2
|
ран
|
k3
|
ран
|
k4
|
ран
|
k5
|
ран
|
|
a
|
25000
|
10
|
14
|
10
|
2
|
7
|
20
|
4
|
3
|
5
|
|
b
|
50000
|
1
|
7
|
3
|
3
|
4
|
15
|
2
|
4
|
7
|
|
c
|
23000
|
10
|
10
|
6
|
1
|
10
|
11
|
1
|
2
|
3
|
|
d
|
30000
|
8
|
7
|
3
|
4
|
3
|
13
|
1
|
2
|
3
|
|
e
|
45000
|
3
|
10
|
6
|
3
|
4
|
40
|
10
|
4
|
3
|
|
f
|
52000
|
1
|
12
|
8
|
2
|
7
|
35
|
9
|
4
|
7
|
|
g
|
32000
|
7
|
6
|
2
|
1
|
10
|
30
|
7
|
3
|
5
|
|
h
|
40000
|
5
|
5
|
1
|
3
|
4
|
26
|
6
|
5
|
10
|
|
Утопическая тч
|
23000
|
|
14
|
|
1
|
|
40
|
|
5
|
|
Ход решения:
.Некомпенсирующие методы
Лексикографический
Строился список критериев в порядке важности и выбирался самый наилучший
по важности критерий.
В принятии решения важным критерием является стоимость путевки,
Наиболее подходящей альтернативой является - с (Таиланд).
Метод оптимизации по основному частному критерию
Среди частных критериев выбирается самый важный, но на остальные
накладываются определенные условия.
В принятии решения важным критерием является стоимость путевки.
Мы стремимся к сокращению затрат и выдвигаем дополнительные условия -
количество дней не менее 5, количество звезд отеля не менее 3.
После первого этапа отбора будем минимизировать стоимость и просматривать
дни и звёзды: a,b,e,f,g,h
По стоимости, приоритетным вариантом остается - а.
Метод последовательных уступок
Ранжируются критерии по степени важности. На первом этапе решается
однокритериальная задача для наиболее важного критерия и далее устанавливается
уступка, которая определяет границы допустимых значений и так далее для каждого
критерия.
Главный критерий - торговые точки, второстепенный критерий - количество
звёзд отеля, третий - число пересадок до места прибытия.
Лучший вариант по максимуму торговых точек - e (Франция).
Но нам важно так же ещё количество звезд отеля, поэтому уступка будет
составлять 40% по главному критерию, приемлемые интервалы от 24 до 40.
На первом этапе выделились альтернативы (уже с уступкой) - e, f, h, g.
Уступка по критерию звезд составляет ,% то есть от 4 до 5
На этом этапе остаются альтернативы: e, f, h.
На втором этапе сравнивали число пересадок
Прошла f-альтернатива. По наименьшему числу
пересадок равному 2.
Метод разумной достаточности
Подразумевается выбор первой попавшейся альтернативы, которая
удовлетворяет заданным условиям одновременно по всем критериям, для
объективного восприятия исходные значения были проранжированы в диапазоне от 1
до 10.
Зададим условие на выбор альтернативы: все критерии должны быть больше
или равно 4.
Заданному условию по всем критериям подходит только a (Турция).
Метод исключения
Основная цель данного метода это постепенное отсеивание альтернатив в
несколько этапов удовлетворяющих ранжированной шкале и установленному условию ki >6.
На первом этапе отбрасываются альтернативы не подходящие данному условию
и рассматриваются оставшиеся альтернативы дальше по следующим критериям.
этап условию удовлетворяют по критерию k1 - a, c, d, g.
.1 этап условию удовлетворяют по критерию k2 - a, c.
.2 этап условию удовлетворяют по критерию k3 - a, c.
По остальным критериям нет альтернатив, удовлетворяющих условию, поэтому
в результате выбирается первая, попавшаяся по последнему критерию альтернатива a (Турция).
2.Компенсирующие методы
Обобщенный скалярный критерий
Направить ЛПР на достижение наилучшего результата, для этого определяются
координаты утопической точки (координата точки с наилучшими показателями по
каждому критерию).
Таблица 2 - Обобщенный скалярный критерий
|
F(x)
|
|
|
|
|
сумма
|
|
0,086
|
0
|
1
|
0,5
|
0,4
|
1,98
|
|
1,17
|
0,5
|
2
|
0,62
|
0,2
|
4,49
|
|
0
|
0,28
|
0
|
0,72
|
0,6
|
1,61
|
|
0,30
|
0,5
|
3
|
0,67
|
0,6
|
5,07
|
|
0,95
|
0,28
|
2
|
0
|
0,2
|
3,44
|
|
1,26
|
0,14
|
1
|
0,12
|
0,2
|
2,72
|
|
0,39
|
0,57
|
0
|
0,25
|
0,4
|
1,61
|
|
0,73
|
0,64
|
2
|
0,35
|
0
|
3,73
|
Необходимо взять минимальное значение суммы т. к. расчет производили по
модулю относительно утопической точки.
По результатам суммы критериев наилучшей альтернативой является C(Таиланд).
Модифицированный метод
Таблица 3 - Модифицированный метод
|
F(x)
|
|
|
|
|
сумма
|
|
0
|
0
|
0,3
|
0,6
|
0,5
|
1,4
|
|
0,9
|
0,7
|
0,6
|
0,8
|
0,3
|
3,3
|
|
0
|
0,4
|
0
|
0,9
|
0,7
|
2
|
|
0,2
|
0,7
|
0,7
|
0,9
|
0,7
|
3,2
|
|
0,7
|
0,4
|
0,6
|
0
|
0,7
|
|
0,9
|
0,2
|
0,3
|
0,1
|
0,3
|
1,8
|
|
0,3
|
0,8
|
0
|
0,3
|
0,5
|
1,9
|
|
0,5
|
0,9
|
0,6
|
0,4
|
0
|
2,4
|
Модификация заключается в применении выше изложенного метода к
ранжированным частным критериям.
По результатам метода, наилучшей альтернативой является максимальное
значение т.к. оценке 10 соответствует наилучшее значение частного критерия.
По результатам анализа получили результат b (Греция).
Метод идеальной точки
Таблица 4 - Метод идеальной точки
|
F(x)
|
|
|
|
|
сумма
|
корень
|
|
0
|
0
|
9
|
36
|
25
|
70
|
8
|
|
81
|
49
|
36
|
64
|
9
|
239
|
15
|
|
0
|
16
|
0
|
81
|
49
|
146
|
12
|
|
4
|
49
|
49
|
81
|
49
|
232
|
15
|
|
49
|
16
|
36
|
0
|
49
|
150
|
12
|
|
81
|
4
|
9
|
1
|
9
|
104
|
10
|
|
9
|
64
|
0
|
9
|
25
|
107
|
10
|
|
25
|
81
|
36
|
16
|
0
|
158
|
13
|
На содержательном уровне данный метод находит расстояние до этой
идеальной точки, минимальное расстояние и покажет расстояние до этой идеальной
точки.
По результатам данного метода наилучшей альтернативой является вариант а
(Турция)
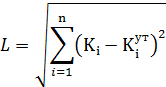
Метод аддитивной оптимизации
Вводятся коэффициенты важности (веса), для каждого отдельного критерия,
затем формулируется скалярный критерий.
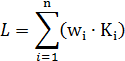
. Критерии должны быть соизмеримы по важности
. Критерии должны иметь размерность позволяющие сравнение и оценку
разных величин (применение нормировки)
Нормировка относительно среднего значения
 ,
,
где - нормированное значение критерия
- нормированное значение критерия
 - текущее значение
- текущее значение
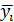 - среднее значение по данному критерию
- среднее значение по данному критерию
 - среднеквадратическое отклонение у.
- среднеквадратическое отклонение у.
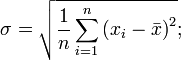
Сумма баллов максимальное значение взять вариант а.
Таблица 5 - Метод аддитивной оптимизации
|
|
k1
|
ран
|
k2
|
ран
|
k3
|
ран
|
k4
|
ран
|
k5
|
ран
|
|
a
|
25000
|
10
|
14
|
10
|
2
|
7
|
20
|
4
|
3
|
5
|
|
b
|
50000
|
1
|
7
|
3
|
3
|
4
|
15
|
2
|
4
|
7
|
|
c
|
23000
|
10
|
10
|
6
|
1
|
10
|
11
|
1
|
2
|
3
|
|
d
|
30000
|
8
|
7
|
3
|
4
|
3
|
13
|
1
|
2
|
3
|
|
e
|
45000
|
3
|
10
|
6
|
3
|
4
|
40
|
10
|
4
|
3
|
|
f
|
52000
|
1
|
12
|
8
|
2
|
7
|
35
|
9
|
4
|
7
|
|
g
|
32000
|
7
|
6
|
2
|
1
|
10
|
30
|
7
|
3
|
5
|
|
h
|
40000
|
5
|
5
|
1
|
3
|
4
|
26
|
6
|
5
|
10
|
|
Утоп тч
|
23000
|
10
|
14
|
10
|
1
|
10
|
40
|
10
|
5
|
10
|
|
значимость
|
0,4
|
|
0,2
|
|
0,1
|
|
0,2
|
|
0,1
|
|
|
сред знач
|
37125
|
|
8,87
|
|
2,37
|
|
23,8
|
|
3,37
|
|
|
среднеквадр
отклонен
|
11217,81
|
|
3,13
|
|
1,06
|
|
10,7
|
|
1,06
|
|
|
Нормированные значения
должны быть в диапозоне от -1 до 1
|
|
-1,08
|
|
1,63
|
|
-0,35
|
|
-0,35
|
|
-0,35
|
|
|
1,14
|
|
-0,59
|
|
0,58
|
|
-0,81
|
|
0,58
|
|
|
-1,25
|
|
0,35
|
|
-1,29
|
|
-1,19
|
|
-1,29
|
|
|
-0,63
|
|
-0,59
|
|
1,53
|
|
-1,00
|
|
-1,29
|
|
|
0,70
|
|
0,35
|
|
0,58
|
|
1,51
|
|
0,58
|
|
|
1,32
|
|
0,99
|
|
-0,35
|
|
1,05
|
|
0,58
|
|
|
-0,45
|
|
-0,91
|
|
-1,29
|
|
0,58
|
|
-0,35
|
|
|
0,25
|
|
-1,23
|
|
0,58
|
|
0,21
|
|
1,53
|
|
|
сумма
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
|
миним
|
|
макс
|
|
мин
|
|
макс
|
|
макс
|
|
|
корректируем направление
причесывания все максимизировать
|
|
1,08
|
|
-1,82
|
|
0,35
|
|
-1,21
|
|
-2,18
|
|
|
-1,14
|
|
-2,82
|
|
-0,58
|
|
-2,21
|
|
-3,18
|
|
|
1,25
|
|
-2,30
|
|
1,29
|
|
-2,24
|
|
-3,51
|
|
|
0,63
|
|
-3,0
|
|
-1,53
|
|
-2,29
|
|
-2,62
|
|
|
-0,70
|
|
-2,71
|
|
-0,58
|
|
-2,32
|
|
-4,40
|
|
|
-1,32
|
|
-3,01
|
|
0,35
|
|
-2,31
|
|
-4,40
|
|
|
0,45
|
|
-2,71
|
|
1,29
|
|
-2,07
|
|
-2,62
|
|
|
-0,25
|
|
-2,51
|
|
-0,58
|
|
-2,11
|
|
-2,62
|
|
Таблица 6 - Метод аддитивной оптимизации
|
Значения F(x) после
нормализации в метод аддитивной оптимизации с весами критериев
|
|
0,43
|
-0,36
|
0,03
|
-0,24
|
-0,21
|
-0,35
|
|
-0,45
|
-0,56
|
-0,05
|
-0,44
|
-0,31
|
-1,84
|
|
0,50
|
-0,46
|
0,12
|
-0,44
|
-0,35
|
-0,62
|
|
0,25
|
-0,60
|
-0,15
|
-0,45
|
-0,26
|
-1,22
|
|
-0,28
|
-0,54
|
-0,05
|
-0,46
|
-1,78
|
|
-0,53
|
-0,60
|
0,03
|
-0,46
|
-0,44
|
-2,00
|
|
0,18
|
-0,54
|
0,12
|
-0,41
|
-0,26
|
-0,90
|
|
-0,10
|
-0,50
|
-0,05
|
-0,42
|
-0,26
|
-1,35
|
|
к1
|
к2
|
к3
|
к4
|
к5
|
сумма
|
По максимальному значению с учетом веса критериев и их нормализации
определили наилучшую альтернативу - это a (Турция).
Метод суммы оценок частных критериев
Данный подход упрощает процесс принятия решения посредством пренебрежения
информацией по относительной важности критериев, можно использовать
ранжирование значений критериев и среди альтернатив предлагают ту в которой
сумма значений показателей максимальна.
Таблица 7 - Метод суммы оценок частных критериев
|
Сумма по ранжированию
|
|
36
|
|
17
|
|
30
|
|
18
|
|
26
|
|
32
|
|
31
|
|
26
|
По результатам данного метода наилучшей альтернативой является вариант а
(Турция).
Задача3. Принятие решений в условиях неопределенности
Дано: Необходимо проанализировать данные по
критериям Лапласа, Вальда, Сервиджа, Гурвица, Гермейера и выбрать наилучший
объект по признакам, при этом идет ориентирование на величину потерь.
Торговая
компания должна определить наиболее выигрышную стратегию в выборе продажи
определенного товара в зависимости от уровня доходов покупателей. Для каждого
уровня доходов определенна стратегия продажи товара, а отклонение от этого
уровня ведет к дополнительным затратам, представленным в таблице. Необходимо
определить наиболее удачную стратегию.
Таблица 1 - Исходные данные
|
Стратегии
|
Спрос на услуги
|
|
S1
|
S2
|
S3
|
S4
|
S5
|
|
R1
|
9
|
18
|
26
|
14
|
7
|
|
R2
|
7
|
14
|
20
|
8
|
5
|
|
R3
|
22
|
10
|
9
|
21
|
12
|
|
R4
|
20
|
25
|
16
|
24
|
22
|
|
R5
|
15
|
18
|
22
|
20
|
12
|
Ход решения:
. Критерий Лапласа
Данный критерий предполагает, что S1-S5 все состояния
являются равновероятными:
qi=1/n=1/5=0,2
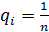 ,
,
 ,
,
где n - это количество состояний природы.
Следовательно, 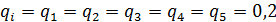 .
.
Таблица 2 - Критерий Лапласа
|
Z(R1)
|
0,2∙(9+18+26+14+7)
|
14,8
|
|
Z(R2)
|
0,2∙(7+14+20+8+5)
|
10,8
|
|
Z(R3)
|
0,2∙(22+10+9+21+12)
|
14,8
|
|
Z(R4)
|
0,2∙(20+26+16+24+22)
|
21,4
|
|
Z(R5)
|
0,2∙(15+18+22+20+12)
|
17,4
|
По критерию Лапласа наилучшей стратегией будет стратегия R2.
2. Критерий Вальда
(Минимаксный или максиминный)
Данный критерий опирается на принцип наибольшей осторожности и
основывается на выборе наилучшей из наихудших стратегий, то есть, лицо,
принимающее решение (ЛПР), не может столкнуться с худшим результатом, чем тот,
на который оно ориентируется.
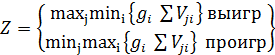
Так как начальная матрица представляет затраты, то применим максиминный
критерий.
стратегия решение прогнозирование имитационный
программирование
Таблица 3 - Критерий Вальда
|
Стратегии
|
Спрос на услуги
|
Max {Vij}
|
Min max {Vji}
|
|
S1
|
S2
|
S3
|
S4
|
S5
|
|
|
|
R1
|
9
|
18
|
26
|
14
|
7
|
26
|
-
|
|
R2
|
7
|
14
|
20
|
8
|
5
|
20
|
20
|
|
R3
|
22
|
10
|
9
|
21
|
12
|
22
|
-
|
|
R4
|
20
|
25
|
16
|
24
|
22
|
25
|
-
|
|
R5
|
15
|
18
|
22
|
20
|
12
|
22
|
|
По критерию Вальда наилучшей стратегией будет стратегия R2.
3. Критерий Сервиджа
Критерий использует матрицу рисков и рекомендует в условиях
неопределенности выбрать ту стратегию, при которой величина риска принимает
наименьшее значение в самой неблагоприятной ситуации.

Используем матрицу рисков.
Таблица 4 - Критерий Сервиджа
|
Стратегии
|
Спрос на услуги
|
Max {Vij}
|
Min max {Vji}
|
|
S1
|
S2
|
S3
|
S4
|
S5
|
|
|
|
R1
|
9(2)
|
18(8)
|
26(17)
|
14(6)
|
7(2)
|
26
|
17
|
-
|
-
|
|
R2
|
7(0)
|
14(4)
|
20(11)
|
8(0)
|
5(0)
|
20
|
11
|
20
|
11
|
|
R3
|
22(15)
|
10(0)
|
9(0)
|
21(13)
|
12(7)
|
22
|
15
|
-
|
-
|
|
R4
|
20(13)
|
25(15)
|
16(7)
|
24(16)
|
22(17)
|
25
|
17
|
-
|
-
|
|
R5
|
15(8)
|
18(8)
|
22(13)
|
20(12)
|
12(7)
|
22
|
13
|
|
|
Матрица рисков строится по принципу: выбирается min значение по столбцу и от каждого значения в столбце
отнимается выбранное min
значение по столбцу.
По критерию Сервиджа наилучшей стратегией будет стратегия R2.
4. Критерий Гурвица
Данный критерий основан на следующих предположениях:
Природа может находиться в самом невыгодном состоянии с вероятностью (1- α)
и в самом выгодном
состоянии с вероятностью α;
- Критерий устанавливает баланс между случаями крайнего пессимизма и
крайнего оптимизма путем введения соответствующих коэффициентов.
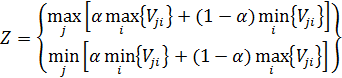
α=0,5
Таблица 5 - Критерий Гурвица
|
min V
|
max V
|
W=α∙min V+(1-α)∙max V
|
Min W
|
|
7
|
26
|
16,5
|
-
|
|
5
|
20
|
12,5
|
12,5
|
|
9
|
22
|
15,5
|
-
|
|
16
|
25
|
21
|
-
|
|
12
|
22
|
17
|
|
По критерию Гурвица наилучшей стратегией будет стратегия R2.
5. Критерий Гермейера
Правило выбора согласно критерию Гермейера формулируется следующим
образом:
Матрица решений Wij
дополняется ещё одной строкой содержащей в каждом стролбце наименьшее
произведение имеющегося в нем результата на вероятность соответствующего
состояния. Выбираются те варианты в стролбцах которых находится наибольшее
значение Wij этой строки.
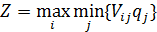
Так как в условии не даны вероятности каждой состояний, то возьмем их
случайно:
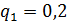
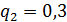
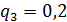

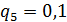
Таблица 6 - Критерий Гермейера
|
Стратегии
|
Спрос на услуги
|
Min {Vij}
|
Max min {Vji}
|
Z
|
|
S1
|
S2
|
S3
|
S4
|
S5
|
|
|
|
|
R1
|
9(1.8)
|
18(3.6)
|
26(5.2)
|
14(2.8)
|
7(1.4)
|
26
|
1.4
|
|
|
5,4
|
|
R2
|
7(2.1)
|
14(4.2)
|
20(6)
|
8(2.4)
|
5(1.5)
|
20
|
1.5
|
|
|
4,2
|
|
R3
|
22(4.4)
|
10(2)
|
9(1.8)
|
21(4.2)
|
12(2.4)
|
22
|
1.8
|
|
|
4,4
|
|
R4
|
20(4)
|
25(5)
|
16(3.2)
|
24(4.8)
|
22(4.4)
|
25
|
3.2
|
25
|
3.2
|
7,5
|
|
R5
|
15(1.5)
|
18(1.8)
|
22(2.2)
|
20(2)
|
12(1.2)
|
22
|
1.2
|
|
|
|
Для того, чтобы найти Z,
нужно составить следующую таблицу, в которой:
каждый столбец умножить на соответствующие вероятности q1, q2,q3,q4,q5
По критерию Гермейера наилучшей стратегией будет стратегия R2.
Вывод: Проделав расчеты по всем критериям, можно смело отметить,
что наиболее лучшей альтернативой является стратегия R2.
Задача 4. Методы прогнозирования
Взять статистику из 25 значений. За основу для прогнозирования взять 20
значений. С использованием прогнозных процедур сделать прогноз на 2 дня вперед.
Дано: На эмпирическом временном ряде из 20 значений, используя процедуры
обычной регрессии, Хэмминга (А и Б-метод) и Брауна, выполнить прогноз на один
шаг и на три-четыре шага вперед для каждого метода соответственно. Сравнить
прогнозные процедуры. Сделать выводы.
Таблица 1 - Исходные данные
|
t
|
Y(t)
|
t
|
Y(t)
|
t
|
Y(t)
|
t
|
Y(t)
|
t
|
Y(t)
|
|
1
|
50
|
6
|
54
|
11
|
61
|
16
|
59,5
|
21
|
63,7
|
|
2
|
7
|
53,5
|
12
|
62
|
17
|
60,5
|
22
|
63,5
|
|
3
|
56,5
|
8
|
60
|
13
|
58
|
18
|
61
|
23
|
64
|
|
4
|
53,5
|
9
|
59
|
14
|
57
|
19
|
62
|
24
|
64,5
|
|
5
|
51
|
10
|
60
|
15
|
57,5
|
20
|
62,5
|
25
|
65
|
Ход решения:
. «Наивные» методы
Наивные методы предполагают, что некоторый последний период
прогнозируемого времени ряда лучше всего оценивает будущее этого ряда.
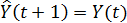 (21) = Y (20)
= 62,5
(21) = Y (20)
= 62,5
Модели, основанные на скользящих средних

Y(21)
= 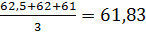
Модели, основанные на экспоненциальном сглаживании

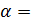 0,6
0,6
Y(21)
=63,04
Y(22)
= 63,31
Y(23)
= 63,72
Y(24)
= 64,19
График 1 - Экспоненциальное сглаживание
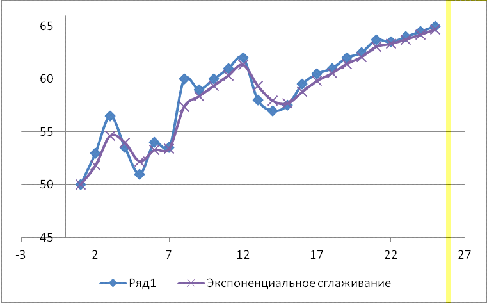
Коэффициент сглаживания найден экспериментальным путем, отвечающим
наиболее близкому приближению прогнозируемых значений к исходным данным.
2. Метод Хемминга
Метод Хемминга обладает достоинствами, связанными с простотой и
относительно небольшой погрешностью. Существует в двух модификациях. Базовый
алгоритм (А-метод Хемминга) применяется для прогнозирования относительно
стабильных или слабо изменяющихся динамических рядов, имеющих фиксированную
структуру.
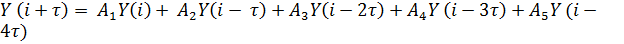
где  - прогнозное значение;
- прогнозное значение;
Y-
значение функции;
i -
порядковый номер элемента, входящего в состав исследуемого объекта;
 - время запаздывания или исследование обрабатываемых данных
(реализация функций объекта);
- время запаздывания или исследование обрабатываемых данных
(реализация функций объекта);
A1, A2, A3, A4, A5 - коэффициенты настройки, задаваемые
жестко, в виде числа.
Наиболее удачными, по мнению Хемминга, являются коэффициенты для 3 и 5
слагаемых
Таблица 2 - Метод Хемминга
|
А1
|
А2
|
А3
|
А4
|
А5
|
|
для трех
|
0,60
|
0,30
|
0,10
|
|
|
|
для пяти
|
0,6
|
0,25
|
0,10
|
0,04
|
0,01
|
Таблица 2.1 - Прогнозируемые значения по методу Хемминга
|
Y(21) =
|
59,04
|
|
Y(22) =
|
58,625
|
|
Y(23) =
|
58,685
|
|
Y(24) =
|
57,59
|
|
Y(25) =
|
57,29
|
Прогнозные значение на основе базового алгоритма Хэмминга (А-метод ):
Yp(21) = A1 Y(20)+ A2
Y(20)+ A2  Y(19)+ A3
Y(19)+ A3  Y(18)+ A4
Y(18)+ A4  Y(17)+ A5
Y(17)+ A5  Y(16);p(22) = A1
Y(16);p(22) = A1 Y(20)+ A2
Y(20)+ A2  Y(18)+ A3
Y(18)+ A3  Y(16)+ A4
Y(16)+ A4  Y(14)+ A5
Y(14)+ A5  Y(12);p(23) = A1
Y(12);p(23) = A1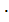 Y(20)+ A2
Y(20)+ A2  Y(17)+ A3
Y(17)+ A3 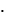 Y(14)+ A4
Y(14)+ A4  Y(11)+ A5
Y(11)+ A5  Y(8);p(24) = A1
Y(8);p(24) = A1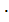 Y(20)+ A2
Y(20)+ A2  Y(16)+ A3
Y(16)+ A3 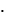 Y(12)+ A4
Y(12)+ A4  Y(8)+ A5
Y(8)+ A5  Y(4);p(25) = A1
Y(4);p(25) = A1 Y(20)+ A2
Y(20)+ A2  Y(15)+ A3
Y(15)+ A3  Y(10)+ A4
Y(10)+ A4  Y(5)+ A5
Y(5)+ A5  Y(0);
Y(0);
На основе полученных данных построим график прогнозирования по адаптивной
модели Хемминга
График 2 - График прогнозирования по модели Хемминга
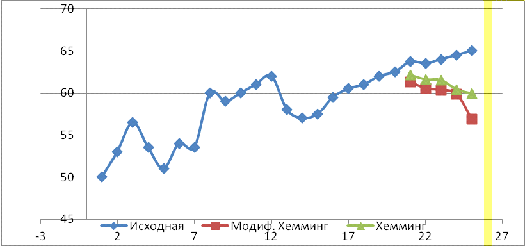
Таблица 3.1 - Расчетные коэффициенты Хемминга
|
А1
|
0,863
|
0,25
|
|
А2
|
0,742
|
0,22
|
|
А3
|
0,672
|
0,19
|
|
А4
|
0,622
|
0,18
|
|
А5
|
0,538
|
0,16
|
|
Сумма
|
3,439
|
1
|
Модифицированный метод Хемминга предполагает использования алгоритма
вычисления коэффициентов, путем автокорреляционного метода, с помощью которого
подбираются соответствующие коэффициенты, показанные в таблице 3.1.
Далее, расчетные коэффициенты используются в формуле (1), для расчета,
прогнозируемых значений Y21, Y22
Yp(21) = A1 Y(20)+ A2
Y(20)+ A2  Y(19)+ A3
Y(19)+ A3 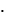 Y(18)+ A4
Y(18)+ A4  Y(17)+ A5
Y(17)+ A5  Y(16);p(22) = A1
Y(16);p(22) = A1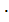 Y(20)+ A2
Y(20)+ A2  Y(18)+ A3
Y(18)+ A3 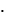 Y(16)+ A4
Y(16)+ A4  Y(14)+ A5
Y(14)+ A5  Y(12);p(23) = A1
Y(12);p(23) = A1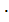 Y(20)+ A2
Y(20)+ A2  Y(17)+ A3
Y(17)+ A3 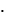 Y(14)+ A4
Y(14)+ A4  Y(11)+ A5
Y(11)+ A5  Y(8);p(24) = A1
Y(8);p(24) = A1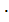 Y(20)+ A2
Y(20)+ A2  Y(16)+ A3
Y(16)+ A3 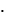 Y(12)+ A4
Y(12)+ A4  Y(8)+ A5
Y(8)+ A5  Y(4);p(25) = A1
Y(4);p(25) = A1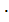 Y(20)+ A2
Y(20)+ A2  Y(15)+ A3
Y(15)+ A3 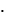 Y(10)+ A4
Y(10)+ A4  Y(5)+ A5
Y(5)+ A5  Y(0);
Y(0);
Таблица 3.2 - Модифицированный метод Хемминга
|
Y(21) =
|
61,265
|
|
Y(22) =
|
60,53
|
|
Y(23) =
|
60,345
|
|
Y(24) =
|
59,855
|
|
Y(25) =
|
56,855
|
3. Метод Брауна
Также считается адаптивным алгоритмом прогнозирования, и в основном
используется при краткосрочном прогнозировании.
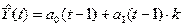
где k - количество шагов прогнозирования (k=1).
Это значение сравнивается с фактическим уровнем
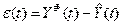 ,
,
который затем используется для корректировки модели.
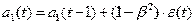 ,
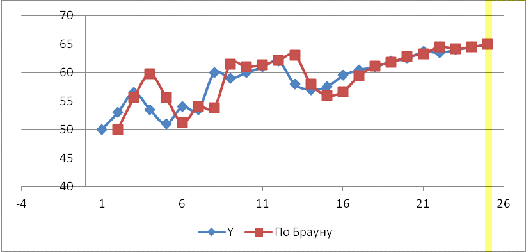
,
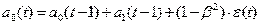 ,
,
где β - коэффициент дисконтирования данных, отражает большую степень
доверия к более поздним данным, 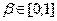 .
.
Начальные оценки параметров получим по первым пяти точкам по формулам:
 ,
, 
Для расчета этой таблицы нам понадобилось tср=3 и Yср=52,8.
Результаты моделирования по методу Брауна представлены в таблице
Таблица 4 - Метод Брауна
|
№
|
Y
|
Q
|
t
|
Y -прогноз
|
|
1
|
50
|
|
|
|
|
2
|
53
|
53
|
3
|
|
|
3
|
56,5
|
53,25
|
2,45
|
|
|
4
|
53,5
|
52,15
|
1,74
|
|
|
5
|
51
|
50,705
|
1,103
|
|
|
6
|
54
|
51,801
|
1,101
|
|
|
7
|
53,5
|
52,099
|
0,941
|
|
|
8
|
60
|
55,579
|
1,448
|
|
|
9
|
59
|
56,565
|
1,356
|
|
|
10
|
60
|
57,604
|
1,292
|
|
|
11
|
61
|
58,655
|
1,244
|
|
|
12
|
62
|
59,705
|
1,205
|
|
|
13
|
58
|
58,250
|
0,673
|
|
|
14
|
57
|
57,288
|
0,346
|
|
|
15
|
57,5
|
57,221
|
0,263
|
|
|
16
|
59,5
|
58,228
|
0,412
|
|
|
17
|
60,5
|
59,158
|
0,515
|
|
|
18
|
61
|
59,821
|
0,545
|
|
|
19
|
62
|
60,637
|
0,599
|
|
|
20
|
62,5
|
61,269
|
0,605
|
|
|
21
|
63,7
|
62,181
|
0,667
|
61,875
|
|
22
|
63,5
|
62,507
|
0,598
|
63,516
|
|
23
|
64
|
62,954
|
0,568
|
64,303
|
|
24
|
64,5
|
63,442
|
0,552
|
65,228
|
|
25
|
65
|
63,945
|
0,542
|
66,205
|
Y(21)
=62,18
Y(22)
=62,50
Y(23)
=62,95
Y(24)
=63,44
Y(25)
=63,94
График 3 - Метод Хемминга (А, В)

Для осуществления прогноза на несколько точек вперед рассмотрели
полученную на последнем шаге модель

Прогнозные оценки по этой модели получаются подстановкой в нее значений k = 21, k = 22, k =
23, k = 24 таким образом:
На основе полученных данных построим график прогнозирования по адаптивной
модели Брауна
Таблица 6 - Расчет метода Брауна
|
номер
|
Y
|
A0
|
A1
|
ε
|
Y- прогноз
|
|
1
|
50
|
48
|
2
|
50
|
|
|
2
|
53
|
52,52
|
3,08
|
3
|
50
|
|
3
|
56,5
|
56,36
|
3,40
|
0,9
|
55,6
|
|
4
|
53,5
|
54,50
|
1,15
|
-6,26
|
59,76
|
|
5
|
51
|
51,74
|
-0,52
|
-4,65
|
55,65
|
|
6
|
54
|
53,55
|
0,47
|
2,78
|
51,22
|
|
7
|
53,5
|
53,58
|
0,28
|
-0,53
|
54,03
|
|
8
|
60
|
59,01
|
2,49
|
6,12
|
53,87
|
|
9
|
59
|
59,40
|
1,58
|
-2,51
|
61,51
|
|
10
|
60
|
60,15
|
1,23
|
-0,98
|
60,98
|
|
11
|
61
|
61,06
|
1,09
|
-0,38
|
61,38
|
|
12
|
62
|
62,02
|
1,03
|
-0,15
|
62,15
|
|
13
|
58
|
58,80
|
-0,78
|
-5,06
|
63,06
|
|
14
|
57,16
|
-1,15
|
-1,02
|
58,02
|
|
15
|
57,5
|
57,26
|
-0,61
|
1,49
|
56,009
|
|
16
|
59,5
|
59,04
|
0,41
|
2,85
|
56,64
|
|
17
|
60,5
|
60,33
|
0,78
|
1,04
|
59,45
|
|
18
|
61
|
61,01
|
0,74
|
-0,11
|
61,11
|
|
19
|
62
|
61,96
|
0,82
|
0,23
|
61,76
|
|
20
|
62,5
|
62,54
|
0,72
|
-0,29
|
62,79
|
|
21
|
63,7
|
63,63
|
0,87
|
0,42
|
63,27
|
|
22
|
63,5
|
63,66
|
0,51
|
-1,01
|
64,51
|
|
23
|
64
|
64,02
|
0,45
|
-0,17
|
64,17
|
|
24
|
64,5
|
64,49
|
0,45
|
0,02
|
64,47
|
|
25
|
65
|
64,99
|
0,47
|
0,04
|
64,95
|
График 2 - График прогнозирования по модели Брауна
. Метод Хольта - Уинтерса
Данную модель удобно использовать при небольшом объёме исходных данных.
Таблица 7 - Метод Хольта - Уинтерса
|
t
|
Y(t)
|
Yp(t)
|
Y(t)-Yср
|
t-tср
|
(Y(t)-Yср)*(t-tср)
|
(t-tср)^2
|
e(t)=Y(t)-Yp(t)
|
|
0
|
|
|
|
|
|
|
0
|
|
1
|
50
|
52,6
|
-8,9
|
-12
|
106,7
|
144
|
-2,600
|
|
2
|
53
|
53,1
|
-5,9
|
-11
|
64,8
|
121
|
-0,124
|
|
3
|
56,5
|
53,6
|
-2,4
|
-10
|
23,9
|
100
|
2,851
|
|
4
|
53,5
|
54,2
|
-5,4
|
-9
|
48,5
|
81
|
-0,672
|
|
5
|
51
|
54,7
|
-7,9
|
-8
|
63,1
|
64
|
-3,696
|
|
6
|
54
|
55,2
|
-4,9
|
-7
|
34,2
|
49
|
-1,220
|
|
7
|
53,5
|
55,7
|
-5,4
|
-6
|
32,3
|
36
|
-2,244
|
|
8
|
60
|
56,3
|
1,1
|
-5
|
-5,6
|
25
|
3,731
|
|
9
|
59
|
56,8
|
0,1
|
-4
|
-0,4
|
16
|
2,207
|
|
10
|
60
|
57,3
|
1,1
|
-3
|
-3,3
|
9
|
2,683
|
|
11
|
61
|
57,8
|
2,1
|
-2
|
-4,2
|
4
|
3,159
|
|
12
|
62
|
58,4
|
3,1
|
-1
|
-3,1
|
1
|
3,635
|
|
13
|
58
|
58,9
|
-0,9
|
0
|
0,0
|
0
|
-0,888
|
|
14
|
57
|
59,4
|
-1,9
|
1
|
-1,9
|
1
|
-2,411
|
|
15
|
57,5
|
59,9
|
-1,4
|
2
|
-2,8
|
4
|
-2,435
|
|
16
|
59,5
|
60,5
|
0,6
|
3
|
1,8
|
9
|
-0,959
|
|
17
|
60,5
|
61,0
|
1,6
|
4
|
6,4
|
16
|
-0,483
|
|
18
|
61
|
61,5
|
2,1
|
5
|
10,6
|
25
|
-0,507
|
|
19
|
62
|
62,0
|
3,1
|
6
|
18,7
|
36
|
-0,031
|
|
20
|
62,5
|
62,6
|
3,6
|
7
|
25,3
|
49
|
-0,055
|
|
21
|
63,7
|
63,1
|
4,8
|
8
|
38,5
|
64
|
0,620
|
|
22
|
63,5
|
63,6
|
4,6
|
9
|
41,5
|
81
|
-0,103
|
|
23
|
64
|
64,1
|
5,1
|
10
|
51,1
|
100
|
-0,127
|
|
24
|
64,5
|
64,7
|
5,6
|
11
|
61,7
|
121
|
-0,151
|
|
25
|
65
|
65,2
|
6,1
|
12
|
73,3
|
144
|
-0,175
|
Расчетные коэффициенты
|
b(0)
|
0,5
|
|
a(0)
|
52,1
|
|
Параметры
сглаживания
|
|
а1
|
0,3
|
|
аF
|
0,6
|
|
а3
|
0,3
|
|
F(-3)=
[Y(1)/Yp(1)+Y(5)/Yp(5)]/2 =
|
0,94
|
|
F(-2)=
[Y(2)/Yp(2)+Y(6)/Yp(6)]/2 =
|
0,99
|
|
F(-1)=
[Y(3)/Yp(3)+Y(7)/Yp(7)]/2 =
|
1,01
|
|
F(0)=
[Y(4)/Yp(4)+Y(8)/Yp(8)]/2 =
|
1,03
|
График 3 - Метод Хольта - Уинтерса
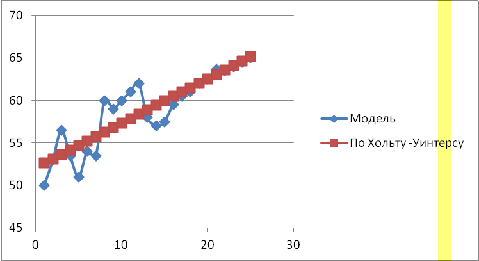
Вывод: Исследуя значения, используя процедуры обычной регрессии,
Хэмминга (А и Б-метод), Брауна и методом Хольта -Уинтерса, мы выполнили прогноз
на один шаг и на три-четыре шага вперед для каждого метода соответственно. Наши
прогнозы не сильно отличаются от значения функции, а следовательно, наши
прогнозы - годны.
Задача 5. Полный факторный эксперимент
Дано: Проводился эксперимент типа 23, где
число факторов k=3, число уровней р=2, число опытов N=8, число повторных опытов n=5.
Матрица планирования приведена в таблице 1.
Таблица 1 - Матрица планирования
|
x1
|
x2
|
x3
|
y1
|
y2
|
y3
|
yср
|
|
1
|
1
|
1
|
10,622
|
10,422
|
11,242
|
10,762
|
|
1
|
1
|
-1
|
8,253
|
8,093
|
8,213
|
8,183
|
|
1
|
-1
|
1
|
4,428
|
3,938
|
4,348
|
4,238
|
|
1
|
-1
|
-1
|
6,517
|
5,557
|
5,99
|
|
-1
|
1
|
1
|
4,049
|
4,329
|
4,839
|
4,405
|
|
-1
|
1
|
-1
|
2,663
|
2,203
|
2,543
|
2,469
|
|
-1
|
-1
|
1
|
5,311
|
5,041
|
4,561
|
4,971
|
|
-1
|
-1
|
-1
|
4,881
|
4,371
|
5,061
|
4,771
|
Ход решения:
После проведения опытов выполнена статистическая обработка
результатов. Сначала определяли ошибки повторных (параллельных) опытов.
Среднеквадратичное отклонение определяем по выражению:
Si2 = 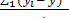 ,
,
где y - среднее арифметическое значение параметра
оптимизации из пяти повторных опытов (значения приведены в табл. 1).
Уравнение математической модели с учетом парных
взаимодействий имеет вид:
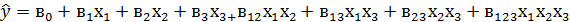
Коэффициенты регрессии при полном факторном эксперименте
определяют по выражениям:
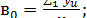


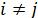
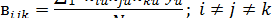
Коэффициенты регрессии, рассчитанные по вышеприведенным
выражениям, равны:
|
b0
|
5,72
|
|
b1
|
1,570
|
|
b2
|
0,731
|
|
b3
|
0,369
|
|
b12
|
1,447
|
|
b13
|
-0,164
|
|
b23
|
0,758
|
С учетом значения дисперсии воспроизводимости S2{y} = 0,123079 с
доверительной вероятностью а = 0,95 находим границы доверительных
интервалов для коэффициентов регрессии, табличное значение критерия Стьюдента
для трех повторных опытов с вероятностью 0,95 равно 4,3 :
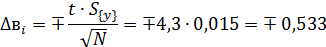
Сравнивая значения коэффициентов регрессии с границами
доверительных интервалов видим, что коэффициенты в3, в13
незначимы. Теперь уравнение математической модели имеет вид:
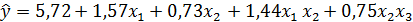
Проверяем адекватность полученного уравнения.
Вычисляем теоретические значения параметра оптимизации 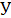 , величину ошибки
, величину ошибки 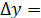
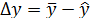 результаты занесены в
таблицу 3:
результаты занесены в
таблицу 3:
Таблица 3 - Результаты вычисления оптимизации
|
Номер опыта
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
y
|
10,762
|
8,186
|
4,238
|
5,997
|
4,405
|
2,467
|
4,971
|
4,771
|
|
Δy
|
10,232
|
8,715
|
4,357
|
5,874
|
4,196
|
2,679
|
4,11
|
5,629
|
|
Δy2
|
0,280
|
0,280
|
0,014
|
0,014
|
0,043
|
0,043
|
0,73
|
0,7368
|
Рассчитаем дисперсию адекватности:
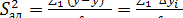 ,
,
где 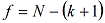 - число степеней свободы.
- число степеней свободы.
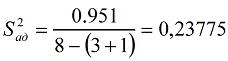
Адекватной математической модели определяем по критерию
Фишера
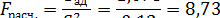
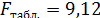
 следовательно, модель адекватна.
следовательно, модель адекватна.
Вывод: Выполнив полный факторный эксперимент, мы пришли к выводу,
что данная модель является адекватной, т.к.  и по ней вполне можно проводить
дальнейшие исследования.
и по ней вполне можно проводить
дальнейшие исследования.
Задача 6. Имитационное моделирование
Дано: Городская администрация контролирует услуги микроавтобусов, которые
развозят пассажиров с железнодорожного вокзала в различные части города. О
потоке пассажиров были собраны в данных о потоке пассажиров:
|
Промежуток между
появлениями пассажиров, мин
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Вероятность
|
0,04
|
0,16
|
0,24
|
0,16
|
0,10
|
0,10
|
0,02
|
По расписанию микроавтобусы должны прибывать каждые 10 минут, однако
изменчивость транспортных условий приводит к следующему распределению
интервалов между прибытиями автобусов:
|
Интервал между
прибытиями автобусов, мин
|
8
|
10
|
12
|
14
|
16
|
|
Вероятность
|
0,10
|
0,38
|
0,28
|
0,15
|
0,09
|
Предполагается, что в автобусе все пассажиры должны находится на сидячих
местах. Число свободных мест определяется следующим распределением:
|
Количество свободных
мест, шт.
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Вероятность
|
0,06
|
0,18
|
0,27
|
0,34
|
0,11
|
0,03
|
0,01
|
Пассажир, которому не хватило места, остается ждать следующего автобуса
на остановке. Очередь движется по принципу «обслуживания в порядке прибытия» (FIFO).
Требуется построить имитационную модель потока из 30 пассажиров, в
предположении, что моделируемый счетчик времени установлен на нулевой отметке.
Оценить:
среднее время ожидания автобуса пассажиром;
среднюю длину очереди.
Ход решения:
Модель появления пассажиров вероятностная модель
|
I, min
|
P
|
|
СЧ
|
|
0
|
0,04
|
0,04
|
0-3
|
|
1
|
0,16
|
0,2
|
4-19
|
|
2
|
0,24
|
0,44
|
20-43
|
|
3
|
0,28
|
0,72
|
44-71
|
|
4
|
0,16
|
0,88
|
72-87
|
|
5
|
0,1
|
0,98
|
88-97
|
|
6
|
0,02
|
1
|
98-99
|
|
|
|
|
|
W, min
|
P
|
|
СЧ
|
|
8
|
0,1
|
0,1
|
0-9
|
|
10
|
0,38
|
0,48
|
10-47
|
|
12
|
0,28
|
0,76
|
48-75
|
|
14
|
0,15
|
0,91
|
76-90
|
|
16
|
0,09
|
1
|
91-99
|
|
|
|
|
|
N
|
P
|
|
СЧ
|
|
0
|
0,06
|
0,06
|
0-5
|
|
1
|
0,18
|
0,24
|
6-23
|
|
2
|
0,27
|
0,51
|
24-50
|
|
3
|
0,34
|
0,85
|
51-84
|
|
4
|
0,11
|
0,96
|
85-95
|
|
5
|
0,03
|
0,99
|
96-98
|
|
6
|
0,01
|
1
|
99
|
В данном случае имитационную модель можно свести в Таблице 1:
Таблица 1 - Имитационная модель
|
№, п/п
|
Поток
пассажиров
|
Прибытие
автобусов
|
Свободные места
|
Время ожидания,
мин
|
№ уехавших
|
|
СЧ
|
I, мин
|
Время от начала
|
Очередь
|
СЧ
|
W, мин
|
Время от начала
|
СЧ
|
Кол-во мест
|
Кол-во уехавших
|
Общее кол-во
уехавших
|
|
|
|
1
|
39
|
2
|
2
|
1
|
3
|
8
|
|
|
|
|
|
6
|
|
|
2
|
29
|
2
|
4
|
2
|
|
|
|
|
|
|
|
4
|
|
|
3
|
27
|
2
|
6
|
3
|
95
|
16
|
8
|
24
|
2
|
2
|
2
|
18
|
1,2
|
|
4
|
63
|
3
|
9
|
2
|
|
|
|
|
|
|
|
15
|
|
|
5
|
72
|
4
|
13
|
3
|
|
|
|
|
|
|
|
11
|
|
|
6
|
27
|
2
|
15
|
4
|
|
|
|
|
|
|
|
17
|
|
|
7
|
59
|
3
|
18
|
5
|
|
|
|
|
|
|
|
14
|
|
|
8
|
72
|
4
|
22
|
6
|
9
|
8
|
24
|
59
|
3
|
3
|
5
|
10
|
3,4,5
|
|
9
|
96
|
5
|
27
|
4
|
|
|
|
|
|
|
|
5
|
|
|
10
|
22
|
2
|
29
|
36
|
10
|
32
|
85
|
4
|
4
|
9
|
13
|
6,7,8,9
|
|
11
|
83
|
4
|
33
|
2
|
|
|
|
|
|
|
|
9
|
|
|
12
|
10
|
1
|
34
|
3
|
|
|
|
|
|
|
|
8
|
|
|
13
|
92
|
5
|
39
|
4
|
|
|
|
|
|
|
|
17
|
|
|
14
|
28
|
2
|
41
|
5
|
|
|
|
|
|
|
|
25
|
|
|
15
|
15
|
1
|
42
|
6
|
87
|
14
|
42
|
75
|
3
|
3
|
12
|
24
|
10,11,12
|
|
16
|
46
|
3
|
45
|
4
|
|
|
|
|
|
|
|
21
|
|
|
17
|
81
|
4
|
49
|
5
|
|
|
|
|
|
|
|
27
|
|
|
18
|
12
|
1
|
50
|
6
|
|
|
|
|
|
|
|
26
|
|
|
19
|
53
|
3
|
53
|
7
|
|
|
|
|
|
|
|
|
|
|
20
|
50
|
3
|
56
|
8
|
34
|
10
|
56
|
12
|
1
|
1
|
13
|
|
13
|
|
21
|
25
|
2
|
58
|
8
|
|
|
|
|
|
|
|
|
|
|
22
|
54
|
3
|
61
|
9
|
|
|
|
|
|
|
|
|
|
|
23
|
35
|
2
|
63
|
10
|
14
|
10
|
66
|
53
|
3
|
3
|
16
|
|
14,15,16
|
|
24
|
99
|
6
|
69
|
8
|
|
|
|
|
|
|
|
|
|
|
25
|
17
|
1
|
70
|
9
|
|
|
|
|
|
|
|
|
|
|
26
|
7
|
1
|
71
|
10
|
74
|
12
|
76
|
28
|
2
|
2
|
18
|
|
17,18
|
|
27
|
99
|
6
|
77
|
9
|
|
|
|
|
|
|
|
|
|
|
28
|
76
|
4
|
81
|
10
|
|
|
|
|
|
|
|
|
|
|
29
|
24
|
2
|
83
|
11
|
|
|
|
|
|
|
|
|
|
|
30
|
29
|
2
|
85
|
12
|
|
|
|
|
|
|
|
|
|
Средняя длина очереди: 6,625 человек. Среднее время ожидания автобуса
пассажиром: 15 минут.
Вывод: Анализ данной имитационной модели
показывает, что время ожидания автобуса пассажиром составляет, в среднем, 15
минут, при этом, средняя длина очереди пассажиров до прибытия микроавтобуса
равна 7 человек, тогда как максимальное количество мест - 6. Так же при анализе
модели потока из 30 пассажиров было установлено, что за 85 минут от начала
эксперимента уехать смогли всего 18 человек, т.е 60 % от общего потока
пассажиров, 12 человек так и остались ждать на остановке.
Принимая во внимание все вышеизложенное, можно сделать вывод,
что для более эффективной работы нужно увеличить количество микроавтобусов,
соответственно уменьшив интервалы между прибытиями, либо пустить транспортные
средства с более высоким числом посадочных мест.
Задача. 7. Динамическое программирование
1. Дано: Задача о распределении инвестиций, задача о кратчайшем пути в
транспортной сети.
Имеются четыре предприятия, между которыми необходимо распределить 100
тыс. усл.ед. средств. Необходимо составить оптимальный план распределения
средств, позволяющий максимизировать общий прирост выпуска продукции. Значения
прироста выпуска продукции на предприятиях в зависимости от выделенных средств
X представлены в следующей таблице:
Таблица 1 - Исходные данные
|
  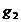  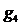
|
|
|
|
|
|
0
|
0
|
0
|
0
|
0
|
|
20
|
42
|
40
|
25
|
24
|
|
40
|
34
|
52
|
36
|
45
|
|
60
|
47
|
50
|
46
|
32
|
|
80
|
51
|
48
|
57
|
36
|
|
100
|
62
|
60
|
67
|
54
|
где g - это предприятие.
Ход решения:
Шаг 1:
K = 4
Предполагается что все средства (100 ден. единиц) переданы на 4-е
предприятие, в этом случае функция Беллмана выглядит след образом
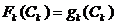
 -
количество оставшихся средств на К-ом шаге
-
количество оставшихся средств на К-ом шаге
Таблица
2 - Расчёт на первом шаге
|
C4
|
X4
|
|
С4*
|
|
0
|
20
|
40
|
60
|
80
|
100
|
F4(C4)
|
|
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
0
|
0
|
|
20
|
-
|
24
|
-
|
-
|
-
|
-
|
24
|
20
|
|
40
|
-
|
-
|
45
|
-
|
-
|
-
|
45
|
40
|
|
60
|
-
|
-
|
-
|
32
|
-
|
-
|
32
|
60
|
|
80
|
-
|
-
|
-
|
-
|
36
|
-
|
36
|
80
|
|
100
|
-
|
-
|
-
|
-
|
-
|
54
|
54
|
100
|
Шаг: 2
K = 3
Определяем оптимальную стратегию инвестирования в остальные предприятия.
При этом функция Беллмана для всех последующих шагов, будет выглядеть след
образом:
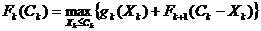
Таблица 3 - Расчёт на втором шаге
|
C3
|
X3
|
|
С3*
|
|
0
|
20
|
40
|
60
|
80
|
100
|
F3(C3)
|
|
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
0
|
0
|
|
20
|
24
|
25+0
|
-
|
-
|
-
|
-
|
25
|
20
|
|
40
|
45
|
25+24
|
36+0
|
-
|
-
|
-
|
49
|
20
|
|
60
|
32
|
25+45
|
36+24
|
46+0
|
-
|
-
|
70
|
20
|
|
80
|
36
|
25+32
|
36+45
|
46+24
|
57+0
|
-
|
81
|
40
|
|
100
|
54
|
25+36
|
36+32
|
46+45
|
57+24
|
67+0
|
91
|
60
|
Шаг:3
K = 2
Таблица 3 - Расчёт на третьем шаге
|
C2
|
X2
|
|
С2*
|
|
0
|
20
|
40
|
60
|
80
|
100
|
F2(C2)
|
|
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
0
|
0
|
25
|
40+0
|
-
|
-
|
-
|
-
|
40
|
20
|
|
40
|
49
|
40+25
|
52+0
|
-
|
-
|
-
|
65
|
20
|
|
60
|
70
|
40+49
|
52+25
|
50+0
|
-
|
-
|
89
|
20
|
|
80
|
81
|
40+70
|
52+49
|
50+25
|
48+0
|
-
|
110
|
20
|
|
100
|
91
|
40+81
|
52+70
|
50+49
|
48+25
|
60+0
|
122
|
40
|
Шаг:4 = 1
Таблица 4 - Расчёт на четвертом шаге
|
C1
|
X1
|
|
С1*
|
|
0
|
20
|
40
|
60
|
80
|
100
|
F1(C1)
|
|
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
0
|
0
|
|
20
|
40
|
42+0
|
-
|
-
|
-
|
-
|
42
|
20
|
|
40
|
65
|
42+40
|
34+0
|
-
|
-
|
-
|
82
|
20
|
|
60
|
89
|
42+65
|
34+40
|
47+0
|
-
|
-
|
107
|
20
|
|
80
|
110
|
42+89
|
34+65
|
47+40
|
51+0
|
-
|
131
|
20
|
|
100
|
122
|
42+110
|
34+89
|
47+65
|
51+40
|
62+0
|
152
|
20
|
Этап 2: безусловная оптимизация.
1 предприятие - 20
ден. Ед
-20=80
предприятие - 20 ден. Ед
предприятие - 20 ден. Ед
предприятие - 40 ден. Ед
Таким образом, оптимальный план составит (20;20;20;40)
Вывод: Доведя данный метод до своего логического завершения, мы
установили, что оптимальный план составит (20;20;20;40).
2. Дано: В предложенной транспортной сети (см. Рис.1) имеется
несколько маршрутов по проезду из начального пункта (1) в конечный пункт (11).
Стоимость проезда между отдельными пунктами транспортной сети придумать
самостоятельно и представить в соответствующей таблице (T(i,j)). Необходимо определить оптимальный маршрут проезда
из пункта 1 в пункт 11 с минимальными транспортными расходами.

Рисунок 1 - Граф исходных данных
Ход решения:
1) Выбор оптимального пути в транспортной сети.
Пусть задана какая-либо сеть.(Рис.2)
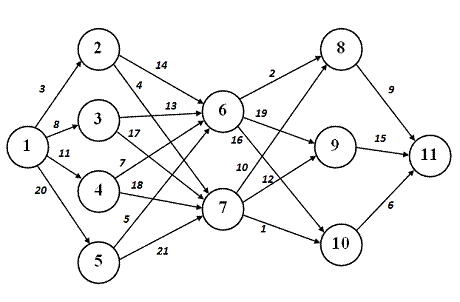
Рисунок 2 - Взвешенный граф
В задаче имеется ограничение - двигаться по изображенным на схеме
маршрутам можно только слева на право, т.е. попав, например, в пункт 8, мы
имеем право переместиться только в пункт 11 и не можем возвратиться обратно в
6-й или 7-й. Эта особенность транспортной сети дает право отнести каждый из
одиннадцати пунктов к одному из поясов. Будем считать, что пункт принадлежит
k-му поясу, если из него попасть в конечный пункт ровно за k шагов, т.е. с
заездом ровно в (k - 1)-й промежуточный пункт. Таким образом, пункты 8, 9 и 10
принадлежат к первому поясу, 6 и 7 - ко второму, 2, 3, 4 и 5 - к третьему и 1 -
к четвертому. Тогда на k-м шаге будем находить оптимальные маршруты из пунктов
k-го пояса до конечного пункта. Оптимизацию будем производить с конца процесса,
и потому, дойдя до k-го шага, неизвестно, в каком из пунктов k-го пояса
окажется груз, перевозимый из первого пункта.
Введем обозначения: - номер шага (k = 1, 2,3,4); - пункт начала маршрута
(i = 1,2,..., 9); - пункт назначения (j = 2,3,.., 11);
Сi, j - веса из пункта i в пункт j. k (i) -
минимальные затраты прохождения маршрута на k-м шаге решения задачи из пункта i
до конечного пункта.
Очевидно, что минимум затрат из пунктов k-го пояса до пункта 11 будет
зависеть от того, в каком пункте этого пояса мы оказались. Номер i пункта,
принадлежащего k-му поясу, будет являться переменной состояния системы на k-м
шаге. Поскольку оптимизация осуществляется с конца процесса, то, находясь в
некотором пункте i k-го пояса, принимается решение о прохождении в один из
пунктов (k - 1)-го пояса, а направление дальнейшего движения известно из
предыдущих шагов. Номер j пункта (k - 1)-го пояса будет переменной управления
на k-м шаге.

Минимум
затрат достигается на некотором значении J*, которое
является оптимальным направлением движения из пункта i в конечный пункт. На
четвертом шаге попадаем на 4-й пояс и состояние системы становится определенным
i = 1. Функция F4(1) представляет собой минимально возможные затраты
по прохождению маршрута из 1-го пункта в 11-й. Оптимальный маршрут определяется
в результате анализа всех шагов в обратном порядке, а выбор некоторого
управления j на k-м шаге приводит к тому, что состояние системы на (k - 1)-м
шаге становится определенным.
I
этап. Условная оптимизация
-й
шаг. k = 1 (i) = Сi 11
На
первом шаге в пункт 10 груз может быть доставлен из пунктов 7,8 или 9.
Таблица 2.1 -1 шаг
|
S
|
  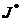
|
|
|
|
i = 8
|
9
|
9
|
11
|
|
i = 9
|
15
|
15
|
11
|
|
i = 10
|
6
|
6
|
11
|
-й шаг. k = 2
Функциональное уравнение на втором шаге принимает вид:
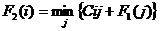
Таблица
2.2 - 2 шаг
|
S
|
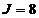 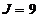 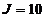 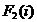 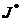
|
|
|
|
|
|
i = 6
|
2+9
|
10+15
|
16+6
|
11
|
8
|
|
i = 7
|
10+9
|
12+15
|
1+6
|
7
|
10
|
3-й шаг. k = 3

Таблица
2.3 - 3 шаг
|
S
|
  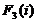 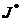
|
|
|
|
|
i = 2
|
14+11
|
4+7
|
11
|
7
|
|
i = 3
|
13+11
|
17+7
|
24
|
6;7
|
|
i = 4
|
7+11
|
18+7
|
18
|
6
|
|
i = 5
|
5+11
|
21+7
|
16
|
6
|
-й шаг. k = 4
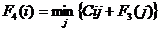
Таблица
2.4 - 4 шаг
|
S
|
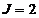  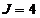 J = 5 J = 5 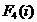 
|
|
|
|
|
|
|
i =1
|
3+11
|
8+24
|
11+18
|
20+16
|
14
|
2
|
II этап. Безусловная оптимизация
На этапе условной оптимизации получено, что минимальные затраты на
перевозку груза из пункта 1 в пункт 11 составляют F4(1) = 14. Данный результат достигается при движении из 1-го
пункта в 2-й. По данным таблиц, из пункта 2 необходимо двигаться в пункт 7 (см.
табл.2.3), затем - в пункт 10 (см. табл.2.2) и из него - в конечный пункт (см.
Табл. 2.1). Таким образом, оптимальный маршрут: 1 => 2 => 7 => 10
=> 11.
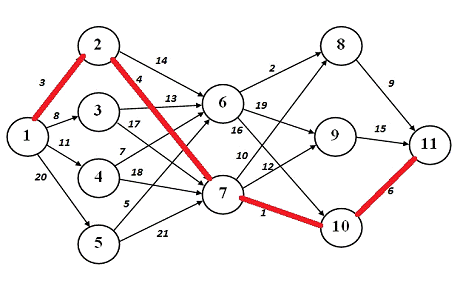
Рисунок 3 - Оптимальный маршрут
Вывод: Оптимальный маршрут: 1 => 2 => 7 => 10 => 11.
Задача
8.Теория игр
Дано: Игра 2х2 (численный и графический способ решения)
Поиск оптимальной смешанной стратегии для двух игроков. Исходные данные
представлены в Таблице 1.
Таблица 1 - Исходные данные
|
Стратегия
природы
|
|
Стратегия
игрока
|
|
Q1
|
Q2
|
|
a1
|
3
|
5
|
|
a2
|
8
|
2
|
Ход решения:
Пусть игра задана платежной матрицей
 ,
,
тогда
формулы для нахождения оптимальной стратегии 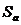 будут
следующие:
будут
следующие:
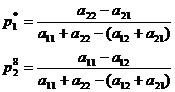
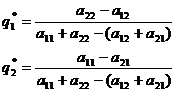
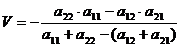 ,
,
где
V - цена игры.
Максиминная стратегия говорит о том, что в обоих случаях выигрыш составит
не более чем 9 и не менее чем 9.
Верхняя цена игры (α) = 3
Нижняя цена игры (β) = 5
Если допустить смешанные стратегии, то можно для каждой конечной игры
найти решение, то есть пару устойчивых оптимальных стратегий игрока.
Найдем решение в виде смешанной стратегии.
|
p1=0,75
|
|
|
q1=0,375
|
|
|
p2=0,25
|
|
|
q2=0,625
|
|
|
|
|
|
|
|
V= 4,25
|
|
|
|
|
На основании приведенных расчётов можно сделать следующие выводы:
Пара смешанных стратегий для игрока 1 будет(0,75; 0,25), для игрока 2 -
(0,375; 0,625)
Таблица 2 - Верхняя и нижняя цена игры
|
Q1
|
Q2
|
β
|
|
a1
|
3
|
5
|
3
|
|
a2
|
8
|
2
|
2
|
|
 α α
|
8
|
5
|
|
Рисунок 1 - Геометрическая интерпретация игры
Задача 9. Карты Шухарта
Дано: Контрольные карты Шухарта (любая задача по 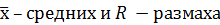 картам).
картам).
На предприятии ведется мониторинг индекса работоспособности процесса
термомеханического упрочнения арматурного проката диаметром 12 мм класса А500С
по ДСТУ 3760. Данные о величине индекса работоспособности за 15 последних
месяцев приведены в Таблице 1. Необходимо построить карту Шухарта
индивидуальных значений и текущего размаха для наблюдаемого процесса.
Мы имеем 15 значений исследуемого параметра. По мнению автора, это -
минимальное количество значений, по которым можно оценить процесс и построить
его x-R карту. Если на полученной карте не будет особых точек, то
процесс построения карты можно будет завершить на основании имеющихся данных.
Если же при анализу карты нам придется удалить какие-то точки, то данных будет
недостаточно. Тогда необходимо дополнить данные последними месяцами 2006 года,
либо ждать новых данных за апрель 2008 года и т.д.
Ход решения:
Строим расчетную таблицу:
Расчетная таблица для построения контрольной x-R карты
Таблица 1 - Расчетная карта Шухарта
|
№№ п/п
|
Месяц
|
Значение xi
|
Размах Ri
|
|
1
|
Январь 2007 г.
|
1.40
|
|
|
2
|
Февраль
|
1.42
|
0.02
|
|
3
|
Март
|
1.43
|
0.01
|
|
4
|
Апрель
|
1.36
|
0.07
|
|
5
|
Май
|
1.52
|
0.16
|
|
6
|
Июнь
|
1.53
|
0.01
|
|
7
|
Июль
|
1.49
|
0.04
|
|
8
|
Август
|
1.27
|
0.22
|
|
9
|
Сентябрь
|
1.28
|
0.01
|
|
10
|
Октябрь
|
1.41
|
0.13
|
|
11
|
Ноябрь
|
1.25
|
0.16
|
|
12
|
Декабрь
|
1.50
|
0.25
|
|
13
|
Январь 2008 г.
|
1.43
|
0.07
|
|
14
|
Февраль
|
1.50
|
0.07
|
|
15
|
Март
|
1.43
|
0.07
|
Шаг 1. Строим две диаграммы
- верхняя диаграмма: x-карта (текущие значения xi),
нижняя диаграмма: R-карта (текущий размах Ri).

Рисунок 1 - Диаграммы Шухарта
На первом шаге построения можно провести два теста:
Тест “6”: Шесть последовательных точек расположены по возрастанию или по убыванию
Примечание: тестирование контрольных карт Шухарта необходимо начинать с
нижней карты (R-карт или S-карт). В рассматриваемом случае начинаем с карты
размахов.
На R-карте самая длинная растущая последовательность наблюдается в
сентябре - декабре 2007 г. (0.01 - 0.13 - 0.16 - 0.25, 4 точки). Если
перестраховаться, и считать постоянные значения растущими (убывающими), то
самая длинная убывающая последовательность наблюдается в декабре 2007 г. -
марте 2008 г. (0.25 - 0.07 - 0.07 - 0.07, 4 точки). Таким образом, Тест “6”
дает отрицательный результат, т.е. у нас нет оснований считать какие-нибудь из
анализируемых точек R-карты особыми.
На x-карте максимальные растущие последовательности наблюдаются в январе
- марте, апреле - июне и августе - октябре 2007 г., а максимальная убывающая
последовательность - в июне - августе 2007 г. Во всех случаях длина
последовательности составляет 3 точки. Поэтому Тест “6” для x-карты также дает
отрицательный результат.
Тест “14”: Есть 14 последовательных точек, чередующихся вверх-вниз
Выше нами было сделано предложение считать ряд неизменных значений “в
пользу теста”. Если использовать этот подход, то максимальный знакочередующийся
рад на R-карте наблюдается на участке ноябрь 2007 г. - март 2008 г. (0.16 ↑
0.25 ↓ 0.07 ↑ 0.07 ↓ 0.07, 5 точек). Тест “14” для R-карты
дает отрицательный результат.
Для x-карты максимальная знакочередующаяся последовательность наблюдается
в сентябре 2007 г. - марте 2008 г. - 7 точек. Тест “14” для x-карты также дает
отрицательный результат.
Таким образом, Тест “6” и Тест “14” не выявили особых точек на строящейся
диаграмме Шухарта.
Шаг 2. Определяем параметры диаграммы
● среднее значение параметра
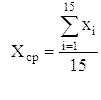 ср=1.41;
ср=1.41;
● среднее значение текущего размаха
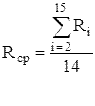 ср=0.092.
ср=0.092.
Принимаем для x-карты значение центральной линии CL=1.41. Для R-карты
значение центральной линии принимаем равной CL=0.09.
Линии контрольных карт
Таблица 2 - Верхняя и нижняя границы карты
|
Параметр
|
x-карта
|
R-карта
|
|
UCL
|
1.645
|
0.295
|
|
UCL 2/3
|
1.565
|
0.225
|
|
UCL 1/3
|
1.485
|
0.155
|
|
CL
|
1.41
|
0.09
|
|
LCL 1/3
|
1.335
|
0.025
|
|
LCL 2/3
|
1.255
|
-
|
|
LCL
|
1.175
|
-
|
Определяем верхнюю и нижнюю границы:
● для x-карты
=CL+2.660ˑRср=1.41+2.660ˑ0.09=1.649≈1.645,=CL-2.660ˑRср=1.41-2.660ˑ0.09=1.171≈1.175;
● для R-карты
=3.267ˑRср=0.294≈0.295.
Примечания:
1. Нижняя контрольная граница LCL для R-карты отсутствует, так как она
меньше нуля.
. Границы для контрольных карт необходимо принимать таким образом, чтобы
наносимые значения не могли принадлежать какой-либо контрольной линии. Если,
например, точность измерения обеспечивает 0.01 единицу, то для границы значение
надо принимать в виде x.xx5. В этом случае, к примеру, параметр может принять
значение 1.32 или 1.33, но никак не 1.325. Искомая точка при этом будет обязательно
лежать ниже или выше границы.
Наносим контрольные пределы на диаграмму.
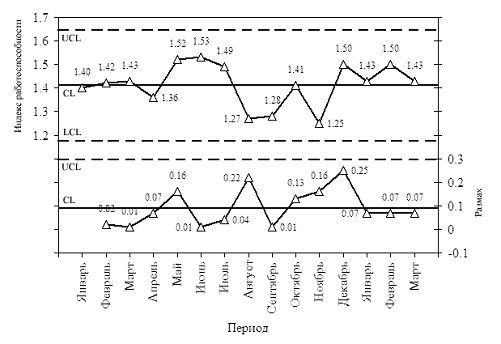
Рисунок 2 - Контрольная карта Шухарта
На втором шаге построения также можно провести два теста:
Тест одной точки: Точка выходит за контрольные пределы
Ни одна из исследуемых точек не выходит за контрольные пределы, т.е. не
лежит выше UCL или ниже LCL.
Тест “9”: Девять последовательных точек находятся с одной стороны от центральной
линии
На R-карте максимальные последовательности одного знака состоят из трех
точек (точки за октябрь - декабрь 2007 г. находятся выше CL, а за январь - март
2008 г. - ниже CL).
На x-карте максимальные последовательности одного знака состоят из
четырех точек (точки за август - ноябрь 2007 г. находятся ниже CL, а за декабрь
2007 г. - март 2008 г. - выше CL).
Таким образом, Тест одной точки и Тест “9” не выявили особых точек на
строящейся диаграмме Шухарта.
Шаг 3. Определяем зоны A, B и C на контрольных картах.
Для x-карты определяем ширину зоны:
∆x = (UCL - LCL)/6 = (1.645 - 1.175)/6 = 0.078.
Рассчитываем границы зон A, B и C:
/3 = UCL - ∆x = 1.645 - 0.078 = 1.567 ≈ 1.565,/3 = CL + ∆x
= 1.41 + 0.078 = 1.488 ≈ 1.485,/3 = CL - ∆x = 1.41 - 0.078 = 1.332 ≈
1.335,/3 = LCL + ∆x = 1.175 + 0.078 = 1.253 ≈ 1.255.
Разбиваем на зоны R-карту:
∆R = (UCL - CL)/3 = (0.295 - 0.09)/3 = 0.068./3 = UCL - ∆R =
0.295 - 0.068 = 0.227 ≈ 0.225,/3 = CL + ∆R = 0.09 + 0.068 = 0.158 ≈
0.155,/3 = CL - ∆R = 0.09 - 0.068 = 0.022 ≈ 0.025.
Примечание: LCL2/3 для карты текущих размахов отсутствует, т.к. она
меньше нуля. Как следствие, отсутствует для карты текущих размахов и нижняя
зона A.
На третьем (завершающем) шаге построения проводят еще четыре теста:
Тест “3”: Две из трех последовательных точек находятся с одной стороны от
центральной линии в зоне A или дальше
На R-карте в зоне A находятся только одна точка: декабрь 2007 г. На
x-карте в зоне A нет ни одной точки. Тест “3” для карты Шухарта отрицательный.
Тест “5”: Четыре из пяти последовательных точек находятся с одной стороны от
центральной линии в зоне B или дальше
Для R-карты составим таблицу:
Таблица 3 - Проверка карт Шухарта
|
Исследуемый период из 5
месяцев
|
Количество точек
|
|
В верхних зонах A и B
|
В нижних зонах A и B
|
|
Февраль - июнь 2007 г.
|
1
|
2
|
|
Март - июль 2007 г.
|
1
|
2
|
|
Апрель - август 2007 г.
|
2
|
1
|
|
Май - сентябрь 2007 г.
|
2
|
2
|
|
Июнь - октябрь 2007 г.
|
1
|
2
|
|
Июль - ноябрь 2007 г.
|
2
|
1
|
|
Август - декабрь 2007 г.
|
3
|
1
|
|
Сентябрь 2007 г. - январь
2008 г.
|
2
|
1
|
|
Октябрь 2007 г. - февраль
2008 г.
|
2
|
0
|
Максимальное количество точек находящихся с одной стороны от центральной
линии в зоне B или дальше за период 5 месяцев составляет 3 (август, ноябрь и
декабрь 2007 г.).
Для x-карты аналогично получаем два случая с тремя точками находящимися с
одной стороны от центральной линии в зоне B или дальше за период 5 месяцев
(май, июнь, июль и август, сентябрь, ноябрь 2007 г.
Тест “5” для карты Шухарта отрицательный.
Тест “8”: Восемь последовательных точек находятся вне зоны C с обеих сторон от
центральной линии
Для R-карты рассмотрим все случаи выхода за зону C:
март 2007 г. - 1 точка,
май, июнь 2007 г. - 2 точки,
август, сентябрь 2007 г. - 2 точки,
ноябрь, декабрь 2007 г. - 2 точки,
т.е. максимальное количество последовательных точек вне зоны C составляет
2. Особых точек нет. Тест “8” для R-карты отрицательный.
Аналогично рассматриваем последовательности для x-карты. Максимальная
длина ряда последовательных точек вне зоны C равна 5 (май - сентябрь 2007 г.).
Тест “8” для x-карты отрицательный.
Тест “15”: Есть 15 последовательных точек в зоне C (по обе стороны от
центральной линии).
Для R-карты максимальная длина ряда последовательных точек в зоне C равна
3 (январь - март 2008 г.). Для x-карты - 4 (январь - апрель 2007 г.).
Тест “15” для строящейся карты отрицательный.
Вывод: Таким образом, все 8 тестов дали отрицательный результат.
Особых точек на карте Шухарта не обнаружено. Причин отклонить предположение о
том, что рассматриваемая последовательность подчинена нормальному закону со
средним 1.41 и средним размахом 0.09 нет.