Оптимальные экономико-математические модели
19. (Транспортная задача)
Имеется пять поставщиков однородной
продукции с объемами поставок  и пять потребителей с объемами
потребления
и пять потребителей с объемами
потребления 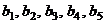 .
.
Решить транспортную задачу
Исходная матрица планирования
|
Матрица
планирования
|
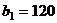    
|
|
|
|
|
|
 5179711 5179711
|
|
|
|
|
|
|
 676106 676106
|
|
|
|
|
|
|
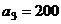 979612 979612
|
|
|
|
|
|
|
 8101477 8101477
|
|
|
|
|
|
|
 1189115 1189115
|
|
|
|
|
|
Решение
Так как
 и
и 
(т.е.  ), то исходная транспортная задача
является закрытой.
), то исходная транспортная задача
является закрытой.
Найдем начальный опорный план
методом минимальной стоимости, а затем оптимизируем его методом потенциалов.
1. Построение начального опорного плана
Из таблицы стоимостей выберем наименьшую
стоимость
 .
.
Заполним клетку (1,1)
 .
.
В клетку (1, 1) помещаем 120
ед.груза и исключаем из дальнейшего рассмотрения первый столбец (потребности
потребителя  полностью
удовлетворены).
полностью
удовлетворены).
Заполним клетку (5, 5)

В клетку (5, 5) помещаем 100
ед.груза и исключаем из дальнейшего рассмотрения пятый столбец (потребности
потребителя  полностью
удовлетворены).
полностью
удовлетворены).
В оставшейся таблице стоимостей
наименьшей является стоимость
 .
.
Заполним клетку (2, 3)
 .
.
В клетку (2, 3) помещаем 280
ед.груза и исключаем из дальнейшего рассмотрения третий столбец (потребности
потребителя  полностью
удовлетворены).
полностью
удовлетворены).
Заполним клетку (3, 4)
 .
.
В клетку (3, 4) помещаем 200
ед.груза и исключаем из дальнейшего рассмотрения третью строку (запасы
поставщика  полностью
израсходованы).
полностью
израсходованы).
В оставшейся таблице стоимостей
наименьшей является стоимость

Заполним клетку (1, 4)
 .
.
В клетку (1, 4) помещаем 90 ед.груза
и исключаем из дальнейшего рассмотрения четвертый столбец (потребности
потребителя  полностью
удовлетворены).
полностью
удовлетворены).
Заполним клетку (2, 2)
 .
.
В клетку (2, 2) помещаем 10 ед.груза
и исключаем из дальнейшего рассмотрения вторую строку (запасы поставщика  полностью израсходованы).
полностью израсходованы).
В оставшейся таблице стоимостей
наименьшей является стоимость
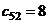
Заполним клетку (5,2)
 .
.
ед.груза помещаем в клетку (5, 2),
тем самым полностью расходуя запасы поставщика  .
.
В оставшейся таблице стоимостей
наименьшей является стоимость

Заполним клетку (4, 2)
 .
.
ед.груза помещаем в клетку (4, 2),
тем самым полностью расходуя запасы поставщика  .
.
Заполним клетку (1, 2)
 .
.
ед.груза помещаем в клетку (1, 2),
тем самым полностью израсходовав запасы поставщика  и полностью
удовлетворив потребности потребителя
и полностью
удовлетворив потребности потребителя  .
.
В результате получаем план

|
Матрица
планирования
|
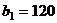    
|
|
|
|
|
|
 51201770979011 51201770979011
|
|
|
|
|
|
|
 67106280106 67106280106
|
|
|
|
|
|
|
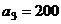 979620012 979620012
|
|
|
|
|
|
|
 8101101477 8101101477
|
|
|
|
|
|
|
 118209115100 118209115100
|
|
|
|
|
|
Определим стоимость плана

. Метод потенциалов
Построим систему потенциалов.
Положим  . Найдем
остальные потенциалы по формулам:
. Найдем
остальные потенциалы по формулам:  .
.



 5
5
-
17
+
7
|
9011
|
|
|
|
|
|
|
 67
67
|
280106
|
|
|
|
|
|
|
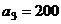 9+ 7
9+ 7
х9-
6
|
20012
|
|
|
|
|
|
|
 810
810
|
1101477
|
|
|
|
|
|
|
 118
118
По найденной системе потенциалов вычислим оценки
незанятых клеток по формуле:





Условия оптимальности ( ) нарушаются
в клетках (1, 3), (1, 5), (3, 2), (3, 3), (3, 5). Поэтому найденный опорный
план не является оптимальным. Следовательно, одна из этих клеток должна быть
загружена некоторым объемом поставок. В первую очередь заполняется та клетка,
для которой достигается максимум среди
) нарушаются
в клетках (1, 3), (1, 5), (3, 2), (3, 3), (3, 5). Поэтому найденный опорный
план не является оптимальным. Следовательно, одна из этих клеток должна быть
загружена некоторым объемом поставок. В первую очередь заполняется та клетка,
для которой достигается максимум среди  :
:  . Значит, включим переменную
. Значит, включим переменную 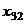 в число
базисных. Пометим ее знаком «х» и построим цикл, который начинается и
заканчивается в этой клетке (3, 2), а вершины цикла располагаются в занятых
клетках.
в число
базисных. Пометим ее знаком «х» и построим цикл, который начинается и
заканчивается в этой клетке (3, 2), а вершины цикла располагаются в занятых
клетках.
(3, 2) - (3, 4) - (1, 4) - (1, 2).
Клетка (3, 2) помечается знаком «+»,
затем клетки, находящиеся в вершинах цикла отмечаются чередующимися знаками «-»
и «+». Величина поставок, перемещаемая в клетку (3, 2), равна минимуму из
поставок со знаком «-», т.е.
 .
.
Величина  вычитается
из объемов поставок клеток со знаком «-» и прибавляется к объемам поставок
клеток со знаком «+». В результате получаем новый опорный план, затраты на
реализацию которого составляют
вычитается
из объемов поставок клеток со знаком «-» и прибавляется к объемам поставок
клеток со знаком «+». В результате получаем новый опорный план, затраты на
реализацию которого составляют
поставка
опорный план потребитель

 5
5
|
16011
|
|
|
|
|
|
|
 67
67
|
280106
|
|
|
|
|
|
|
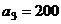 9+ 7
9+ 7
-
6
|
13012
|
|
|
|
|
|
|
 8- 10
8- 10
+
7
|
х7
|
|
|
|
|
|
|
 118
118
В новом опорном плане вычислим
потенциалы занятых клеток и оценки незанятых клеток. Положим  (т.к. во
втором столбце наибольшее число заполненных клеток).
(т.к. во
втором столбце наибольшее число заполненных клеток).







Условия оптимальности ( ) нарушаются
в клетках (4, 4). Поэтому найденный опорный план не является оптимальным.
) нарушаются
в клетках (4, 4). Поэтому найденный опорный план не является оптимальным.
Следовательно, эта клетка должна
быть загружена некоторым объемом поставок. Включим переменную  в число
базисных.
в число
базисных.
Пометим ее знаком «х» и построим
цикл, который начинается и заканчивается в этой клетке (4, 4), а вершины цикла
располагаются в занятых клетках.
Клетка (4, 4) помечается знаком «+»,
затем клетки, находящиеся в вершинах цикла отмечаются чередующимися знаками «-»
и «+».
Величина поставок, перемещаемая в
клетку (4, 4), равна минимуму из поставок со знаком «-», т.е.
 .
.
Величина  вычитается
из объемов поставок клеток со знаком «-» и прибавляется к объемам поставок
клеток со знаком «+».
вычитается
из объемов поставок клеток со знаком «-» и прибавляется к объемам поставок
клеток со знаком «+».
В результате получаем новый опорный
план, затраты на реализацию которого составляют:

 5
5
|
16011
|
|
|
|
|
|
|
 67
67
|
280106
|
|
|
|
|
|
|
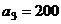 97
97
|
2012
|
|
|
|
|
|
|
 810
810
|
1107
|
|
|
|
|
|
|
 118
118
В новом опорном плане вычислим
потенциалы занятых клеток и оценки незанятых клеток. Положим  (т.к. во
втором столбце наибольшее число заполненных клеток).
(т.к. во
втором столбце наибольшее число заполненных клеток).



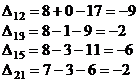



Так как все  , то условия
оптимальности выполняются, следовательно, полученный план является оптимальным.
, то условия
оптимальности выполняются, следовательно, полученный план является оптимальным.
Все поставщики полностью
израсходовали свои запасы, а потребности полностью удовлетворили свои
потребности.
Значение целевой функции


Ответ: 
. (Задача о назначениях).
Решить задачу о назначениях со
следующей матрицей затрат:
|
5
|
17
|
9
|
7
|
11
|
|
6
|
7
|
6
|
10
|
6
|
|
9
|
7
|
9
|
6
|
12
|
|
8
|
10
|
14
|
7
|
7
|
|
11
|
8
|
9
|
11
|
5
|
Решение
Вычтем из элементов каждой строки минимальное
значение в этой строке





Произведя вычисления, получим
матрицу (новые значения затрат записаны в левых нижних углах клеток):
|
1
|
1
|
1
|
1
|
1
|
|
1
|
5
0
|
17
12
|
9
4
|
7
2
|
11
6
|
|
1
|
6
0
|
7
1
|
6
0
|
10
4
|
6
0
|
|
1
|
9
3
|
7
1
|
9
3
|
6
0
|
12
6
|
|
1
|
8
1
|
10
3
|
14
7
|
7
0
|
7
0
|
|
1
|
11
6
|
8
3
|
9
4
|
11
6
|
5
0
|
Теперь вычтем из элементов каждого столбца
минимальное значение в этом столбце:




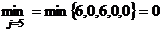
Получим новую матрицу затрат:
|
1
|
1
|
1
|
1
|
1
|
|
1
|
0
|
11
|
4
|
2
|
6
|
|
1
|
0
|
0
|
0
|
4
|
0
|
|
1
|
3
|
0
|
3
|
0
|
6
|
|
1
|
1
|
2
|
7
|
0
|
0
|
|
1
|
6
|
2
|
4
|
6
|
0
|
В полученной матрице можно распределить единицы
(один вид работы) в клетки с нулевыми затратами таким образом, чтобы в каждой
строке и в каждом столбце была только одна единица:
 .
.
Получили распределение работ по
станкам с минимальными затратами:

Чтобы найти значение целевой функции
сложим значения затрат из первоначальной матрицы тех клеток, в которые были
размещены единицы, т.е.
 .
.
Таким образом, первую работу следует
выполнять на первом станке, вторую на третьем, третью на втором, четвертую на
четвертом, пятую на пятом.
Ответ: 
49. (Минимизация сети)
Построить набор дуг, соединяющих все вершины
сети и имеющих минимальную протяженность.

Решение
Итерация 1.
Начнем построение с вершины 1. Обозначим:
С - множество связанных вершин
 - множество несвязанных вершин.
- множество несвязанных вершин.
Тогда 
Итерация 2.
Ближе всех к связанному множеству
вершин расположена вершина 5, так как

Тогда 

Итерация 3.
Ближе всех к связанному множеству вершин
расположены вершины 2 и 6, так как
 .
.
Включим во множество связанных
вершин вершину 2.
Тогда 

Итерация 4.
Ближе всех к связанному множеству
вершин расположена вершина 6, так как

Тогда

Итерация 5.
Ближе всех к связанному множеству
вершин расположены вершины 3 и 4, так как

Включим во множество связанных
вершин вершину 3.
Тогда 

Итерация 6.
Ближе всех к связанному множеству
вершин расположена вершина 7, так как

Тогда 

Итерация 7.
Ближе всех к связанному множеству
вершин расположена вершина 9, так как

Тогда 

Итерация 8.
Ближе всех к связанному множеству
вершин расположена вершина 11, так как
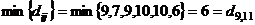
Тогда 

Итерация 9.
Ближе всех к связанному множеству
вершин расположена вершина 12, так как

Тогда 

Итерация 10.
Ближе всех к связанному множеству вершин
расположена вершина 10, так как

Тогда 

Итерация 11.
Ближе всех к связанному множеству
вершин расположена вершина 4, так как
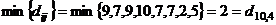
Тогда 

Итерация 12.
Ближе всех к связанному множеству вершин
расположена вершина 8, так как


Тогда 

В связанное множество вершин С
попали все вершины, значит, минимальная сеть построена, ее суммарная длина
равна:
 .
.
Ответ: 
. (СПУ) Задана следующая
последовательность работ с их временными характеристиками:
|
Работа
|
1-2
|
1-3
|
1-4
|
2-4
|
2-5
|
3-4
|
3-6
|
4-5
|
4-6
|
4-7
|
|
Длительность
|
19
|
5
|
9
|
7
|
18
|
10
|
17
|
8
|
6
|
|
Работа
|
5-7
|
5-8
|
6-7
|
6-8
|
6-9
|
7-8
|
7-9
|
7-10
|
8-10
|
9-10
|
|
Длительность
|
5
|
8
|
5
|
8
|
12
|
5
|
15
|
13
|
6
|
5
|
Построить сетевой график; найти критический
путь; определить полные и свободные резервы времени некритических операций.
Решение
Построим сетевой график так, чтобы все дуги -
работы были направлены слева направо. Над дугами проставим длительности работ.

I этап - прямой ход
Находим ранние сроки всех событий по формуле:

Считаем, что 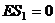 .
.
Событию 2 предшествует только работа
(1, 2), а событию 3 - работа (1, 3). Поэтому:
 (из 1)
(из 1)
 (из 1)
(из 1)
Далее находим:
 (из 2)
(из 2)
 (из 2)
(из 2)
 (из 4)
(из 4)
 (из 5)
(из 5)
 (из 7)
(из 7)
 (из 7)
(из 7)
 (из 9)
(из 9)
Критический путь состоит из работ:
(1, 2) - (2, 5) - (5, 7) - (7, 9) -
(9, 10)
и его длительность - 62.

II этап -
обратный ход
Определим поздние сроки всех событий
по формуле:

Считаем, что

Тогда  ;
; 




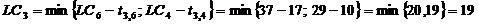


Над каждым событием запишем дробь, в
числителе которой проставим ранний срок начала операций, выходящих из этого
события, а в знаменателе поздний срок окончания операций, входящих в это событие.
Таким образом, получим:
1) ранние сроки наступления событий
(числители дробей);
2) поздние сроки наступления событий
(знаменатели дробей);
) резервы времени событий (разность между
знаменателями и числителями);
4) поздние сроки начала работ  (знаменатели
дробей конечных событий за вычетом длительностей работ);
(знаменатели
дробей конечных событий за вычетом длительностей работ);
) ранние сроки окончания
работ  (суммы
числителей начальных событий и длительностей работ);
(суммы
числителей начальных событий и длительностей работ);
) общие резервы времени работ
(разности между знаменателями конечных событий и числителями событий за вычетом
длительностей работ);
) свободные резервы времени
работ (разность между числителями начальных и конечных событий за вычетом
длительностей работ).
Временные характеристики некритических работ
|
некритические
работы
|
продолжительность
|
ранние
сроки начала работ
|
поздние
сроки окончания работ
|
ранние
сроки окончания работ
|
поздние
сроки начала работ
|
общий
резерв времени
|
свободный
резерв времени
|
|
1-3
|
5
|
0
|
19
|
5
|
14
|
14
|
0
|
|
1-4
|
9
|
0
|
29
|
9
|
20
|
20
|
17
|
|
2-4
|
7
|
19
|
29
|
26
|
22
|
3
|
0
|
|
3-4
|
10
|
5
|
29
|
15
|
19
|
14
|
11
|
|
3-6
|
17
|
5
|
37
|
22
|
20
|
15
|
10
|
|
4-5
|
8
|
26
|
37
|
34
|
29
|
3
|
3
|
|
4-6
|
6
|
26
|
37
|
32
|
31
|
5
|
0
|
|
4-7
|
13
|
26
|
42
|
39
|
29
|
3
|
3
|
|
5-8
|
8
|
37
|
56
|
45
|
48
|
11
|
2
|
|
6-7
|
5
|
32
|
42
|
37
|
37
|
5
|
5
|
|
6-8
|
8
|
32
|
56
|
40
|
48
|
16
|
7
|
|
6-9
|
12
|
32
|
57
|
44
|
45
|
13
|
13
|
|
7-8
|
5
|
42
|
56
|
47
|
51
|
9
|
0
|
|
7-10
|
13
|
42
|
62
|
55
|
49
|
7
|
7
|
|
8-10
|
6
|
47
|
62
|
53
|
56
|
9
|
9
|