Оптимальное одношаговое управление. Транспортная задача

Оптимальное одношаговое управление. Транспортная задача

Задание. Исходные данные

Транспортная подсистема завода обслуживает три заготовительных А_i , i=1,2,3 и три сборочных В_j , j=1,2,3 цеха, находящихся на значительном расстоянии друг от друга. Каждый заготовительный цех производит весь набор комплектующих изделий, необходимый для работы сборочных цехов. Заготовительный цех A_i производит в сутки a_i. комплектов изделий, а сборочный цех B_j реализует в сутки b_j комплектов, i, j=1,2,3. Известны стоимости S_ij перевозки одного комплекта из цеха А_i в цех В_j.

Необходимо организовать перевозки комплектов из заготовительных цехов в сборочный таким образом, чтобы обеспечить бесперебойную работу всех цехов и чтобы суммарная стоимость всех перевозок была минимальной.

Как должна быть скорректирована работа транспортной подсистемы, если вышел из строя один заготовительный цех (например, А₁) и его функции взял на себя другой цех (например, А₂)?

Таблицы исходных данных

Таблица1

Таблица2

Транспортная подсистема как объект управления

Данную задачу можно рассматривать как задачу одношагового управления статическим объектом (транспортной подсистемой завода), имеющим несколько входов и один выход (рис .1).

Рис.1

На входы объекта ОУ поступают материальные потоки суточные количества комплектов изделий. Их можно трактовать как управляющие воздействия. На выходе объекта имеем информацию о затратах на реализацию этих потоков общую стоимость перевозок комплектов. Ее можно трактовать как выходной параметр объекта. Задача управления объектом состоит в надлежащем выборе поступающих на объект управляющих воздействий, обеспечивающих минимизацию его выходного параметра.

Построение математической модели

заготовительный математический аварийный транспортный

На первом этапе строится математическая модель транспортной подсистемы завода соответственно возложенным на нее функциям.

Обозначим через x_ij количество перевозимых комплектов из заготовительного цеха А_i в сборочный цех В_j, а через S суммарную стоимость перевозок. В этих обозначениях транспортную подсистему можно представить в виде объекта управления ОУ с управляющими воздействиями x_ij и выходным параметром S. Внутреннее состояние объекта описывается суточными производительностями а_i и b_j заготовительных и сборочных цехов, а также стоимостями S_ij перевозок грузов из первых во вторые, i, j=1,2,3 (рис. 2).

Рис.2

Реальные условия функционирования объекта накладывают ограничения на его управляющие воздействия :

x₁₁+x₁₂+x₁₃=a₁₂₁+x₂₂+x₂₃=a₂₃₁+x₃₂+x₃₃=a₃  (1)₁₁+x₂₁+x₃₁=b₁₁₂+x₂₂+x₃₂=b₂₁₃+x₂₃+x₃₃=b₃

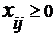, i,j=1,2,3.(2)

Уравнения системы (1) вытекают из требования бесперебойности работы заготовительных и сборочных цехов (рис. 3). Неравенства (2) (их 9) отражают условия физической реализуемости потоков грузов.

Выходной параметр объекта предстает в виде линейной комбинации его управляющих воздействий:

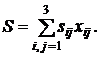(3)

Соотношение (3) совместно с ограничениями (1) и (2) можно рассматривать как математическую модель объекта. Она дает исчерпывающую информацию для решения связанных с его функционированием задач.

Задача управления, в отличие от классических математических задач, имеет не одно, а множество решений. Применительно к рассматриваемому объекту управления любые значения его управляющих воздействий x_ij (в дальнейшем будем именовать их переменными), удовлетворяющие условиям (1) и (2), являются таким решением. Совокупность всех решений в пространстве переменных x_ij образуют n-мерный (в нашем случае n=9) многогранник, именуемый многогранником допустимых решений. В каждой из точек многогранника выходной параметр S объекта управления принимает разные значения. Этот параметр служит одновременно и показателем качества управления объектом. В тех случаях, когда ставится задача минимизации показателя качества, последний именуется целевой функцией.

В свете изложенного, математическая формулировка решаемой нами задачи выглядит так: найти переменные x_ij ,i , j=1,2,3, минимизирующие целевую функцию (3) на многограннике допустимых решений (1), (2).

Нетрудно показать, что искомое решение соответствует одной из вершин этого многогранника. Алгоритм решения сводится, таким образом, к поиску этих вершин и их направленному перебору.

Анализ математической модели

На втором этапе решения задачи анализируется математическая модель объекта и преобразуется к более удобному для последующих действий виду.

Бесперебойное функционирование объекта возможно лишь в том случае, если общее количество комплектов a₁+a₂+a₃ , изготовленных в сутки заготовительными цехами, равно общему количеству комплектов b₁+b₂+b₃ , используемых в сутки сборочными цехами. Коль скоро так, суммы трех первых и трех последних уравнений системы (1) дают один и тот же результат. Отсюда следует, что уравнения системы зависимы, и, значит, одно из них может быть опущено. Какое уравнение опустить, существенной роли не играет. Пусть для конкретности последующих рассуждений опущено третье уравнение.

Итак, система (1) предстает как система пяти уравнений с девятью переменными:

x₁₁+x₁₂+x₁₃=a₁

x₂₁+x₂₂+x₂₃=a₂

x₁₁+x₂₁+x₃₁=b₁ (4)

x₁₂+x₂₂+x₃₂=b₂

x₁₃+x₂₃+x₃₃=b₃

В этой системе четыре переменных (9-5=4) могут принимать любые значения в пределах ограничений (2), а остальные пять будут зависеть от них. Первые называют свободными, вторые базисными переменными.

После того как свободные переменные приняли некоторые значения, система (4) превращается в систему пяти уравнений с пятью неизвестными. Она имеет единственное решение. Решение исходной системы (4), при котором свободные переменные полагаются равными нулю, называется базисным решением. Если при этом базисные переменные оказались неотрицательными, оно именуется допустимым базисным решением.

Разбиение переменных на свободные и базисные в известной степени произвольно. Следует учитывать лишь одно условие: свободными переменными не могут быть одновременно три переменных с одинаковыми первыми или вторыми индексами.

Далеко не всякое базисное решение является допустимым базисным решением. Между тем для нас представляют интерес только эти последние. В теории линейного программирования доказывается, что допустимые базисные решения являются вершинами многогранника допустимых решений. Отсюда следует, что решение поставленной задачи следует искать среди допустимых базисных решений.

если для какого-либо сочетания i , j и k выполняется неравенство:

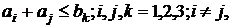 (5)

в качестве комбинации свободных переменных, обеспечивающей допустимое базисное решение, может быть выбрана совокупность:

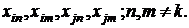 (6)

Проиллюстрируем примером, который будет использован в дальнейшем. Пусть 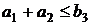. Тогда i=1, j=2, k=3; индексы т и п могут быть либо "1", либо "2", причем, если т =1, то n=2 , и наоборот.

То же правило остается в силе, если 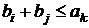. Тогда в совокупности (6) первые и вторые индексы следует поменять местами.

Если соотношений типа (5) установить нельзя, как в моем случае, комбинация (6) в качестве совокупности свободных переменных не годится. Тогда такую совокупность можно составить из трех диагональных переменных x₁₁,x₂₂,x₃₃ и одной недиагональной 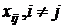, с индексами i и j, соответствующими наименьшим значениям величин a_i и b_j.

Исходя из этого: x₁₁, x₂₂, x₃₃, x₁₂ - свободные переменные(7)

x₁₃, x₂₁, x₂₃, x₃₁, x₃₂ - базисные переменные

Исходное базисное решение

Алгоритм направленного перебора вершин многогранника допустимых решений (или, что то же, - допустимых базисных решений) базируется на так называемом симплекс-методе, главном детище теории линейного программирования. Для "работы" метода необходимо иметь какое-либо одно (любое) допустимое базисное решение. Как найти такое решение, мы разобрали в предыдущем разделе (этапе). Здесь рассматривается формализованное представление этого решения, удобное для использования в симплекс-методе.

Как видно из приведенных данных таблицы1, в качестве совокупности свободных переменных выберем набор (7). Подставим данные табл.1 в систему (4) и выразим базисные переменные через свободные :

x₁₁+x₁₂+x₁₃=150

x₂₁+x₂₂+x₂₃=250

x₁₁+x₂₁+x₃₁=300

x₁₂+x₂₂+x₃₂=200

x₁₃+x₂₃+x₃₃=300

x₁₃=150-x₁₁-x₁₂

x₂₁=100-x₂₂-x₁₁-x₁₂+x₃₃

x₃₁=200-x₃₃+x₁₂+x₂₂(8)

x₃₂=200-x₁₂-x₂₂

x₂₃=150+x₁₁+x₁₂-x₃₃

Из этой записи наглядно просматривается соответствующее выбранной совокупности свободных переменных базисное решение :

x₁₁=0, x₂₂=0, x₃₃=0, x₁₂=0,

x₁₃=150, x₂₁=100, x₃₁=200, x₃₂=200, x₂₃=150.

Поскольку все переменные неотрицательные, оно является допустимым базисным решением. Подставив его в выражение для целевой функции (3), получим:

S=s₁₃x₁₃+s₂₁x₂₁+s₃₁x₃₁+s₃₂x₃₂+s₂₃x₂₃=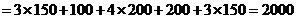(10)

Данному решению отвечает схема транспорта грузов, приведенная на рис. 4.

Уместен вопрос: быть может, данное решение является оптимальным? Этот вопрос возникает на каждом шаге последовательного перебора вершин многогранника допустимых решений. Для аргументированного ответа на него, выразим целевую функцию через свободные переменные. Подставим (8) в (3) и приведем подобные члены:

S=s₁₁x₁₁+s₁₂x₁₂+s₁₃x₁₃+s₂₁x₂₁+s₂₂x₂₂+s₂₃x₂₃+s₃₁x₃₁+s₃₂x₃₂+s₃₃x₃₃=

=2x₁₁+x₁₂+3(150-x₁₁-x₁₂)+100-x₂₂-x₁₁-x₁₂+x₃₃+4x₂₂+

+3(150+x₁₁+x₁₂-x₃₃)+4(200+x₂₂+x₁₂-x₃₃)+200-x₁₂-x₂₂+x₃₃= (11)

=2000+x₁₁+3x₁₂+6x₂₂-5x_33.

Как и следовало ожидать, исходному базисному решению соответствует значение целевой функции, определяемое свободным членом выражения (11). Однако это выражение несет в себе гораздо большую информацию. Оно справедливо, независимо от того, являются ли переменные x₁₁, x₁₂, x₃₃ свободными или базисными. Переменная x₃₃ имеет в нем отрицательный коэффициент. Если бы эта переменная была не свободной, а базисной переменной, то она была бы положительной (по крайней мере, неотрицательной). А это значит (см. (11)), что значение целевой функции S уменьшилось бы. Таким образом, данное допустимое базисное решение (9) не оптимально. И индикатором этого заключения является наличие в (11) отрицательных коэффициентов.

Отсюда вывод: для того, чтобы допустимое базисное решение было оптимальным, необходимо, чтобы в записи целевой функции, выраженной через свободные переменные, коэффициенты при этих переменных были неотрицательными.

Поскольку данное решение оказалось неоптимальным, следует перейти к другому допустимому базисному решению, имеющему меньшее значение S. В теории линейного программирования разработан специальный метод, именуемый симплекс-методом, формализующий процедуру такого (направленного) перехода. Он предусматривает запись соотношений (11) и (8) в форме специальной матрицы (симплекс-матрицы) и ее преобразование по определенному алгоритму в другую такую же матрицу. Последняя анализируется на оптимальность и при отсутствии таковой вновь преобразуется по тому же алгоритму. Процедура повторяется до тех пор, пока не будет получено оптимальное решение.

Исходная симплекс-таблица и ее преобразование

Симплекс-таблицей называется таблица упорядоченного расположения записей (11) и (8). В левом верхнем углу клеток записываются коэффициенты целевой функции (верхняя строка) и базисных переменных (следующие строки), выраженных через свободные переменные (табл.3).

Неотрицательные элементы первого столбца таблицы (табл.3, слева) свидетельствуют о том, что исходное базисное решение является допустимым базисным. Наличие в верхней строке таблицы отрицательных элементов свидетельствует о неоптимальности решения. Для перехода к следующей симплекс-таблице выполним такие действия.

Остановим свой выбор на каком-либо из отрицательных элементов первой строки, в данном случае он один, это коэффициент при переменной x₃₃. Переведем ее в базисные переменные. Соответствующий ей столбец симплекс-таблицы обведем двойными линиями. (Этих и последующих построений удобно придерживаться с точки зрения формализации процедуры ручного перехода). На место переменной x₃₃ из базисных переменных нужно перевести ту, которая быстрее всего обращается в нуль, т.е. ту, для которой отношение коэффициента при x₃₃ к соответствующему свободному члену наименьшее (с учетом знака). В правой части таблицы3 приведены эти отношения. Очевидно, наименьшее из них "-1/150". Это значит, что свободная переменная x₃₃ должна поменяться с базисной переменной x₂₃ Обведем соответствующую ей строку таблицы двойными линиями. Элементы этой строки назовем строчными коэффициентами и обведем рамкой.

В клетке на пересечении выделенных строки и столбца запишем обратную величину стоящего в ней коэффициента (внизу справа). В нашем примере ею будет "-1". Назовем ее генеральным столбцовым коэффициентом и возьмем в двойную рамку. Далее заполним выделенный столбец как произведение генерального столбцового коэффициента на соответствующие элементы клеток таблицы. Полученные значения записываем в правых нижних углах соответствующих клеток. Назовем их столбцовыми коэффициентами и обведем рамками. В оставшихся клетках симплекс-таблицы запишем взятое с обратным знаком произведение строчного коэффициента на столбцовый, включая генеральный.

После этого переходим к составлению второй симплекс-таблицы, в которой свободная и базисная переменные поменялись местами.

Составление второй (и последующих) симплекс-таблиц и их анализ

Как и ранее, начнем с заполнения ее левых верхних углов. Строку и столбец, соответствующие новым свободным и базисным переменным, заполним нижними элементами строки и столбца предыдущей таблицы. В остальные клетки запишем суммы значений, стоящие в соответствующих клетках прежней таблицы. Это и будет матричная запись целевой функции и базисных переменных, выраженных через новые свободные переменные (табл.4).

Убедимся, что базисное решение, задаваемое новой таблицей, остается допустимым базисным. Признаком этого служит неотрицательность всех элементов первого столбца составленной симплекс-таблицы. Если какой-либо элемент оказался отрицательным, в выполненные выше расчеты вкралась ошибка. Проверьте их.

Проверяем полученное решение на оптимальность. Признаком оптимальности служит неотрицательность всех элементов первой строки таблицы. В нашем случае коэффициенты отрицателеные. Это означает, что новое допустимое базисное решение также неоптимально. Тем не менее оно лучше предыдущего решения, ибо суммарные затраты на перевозку грузов оказались меньшими (см. первую клетку первой строки). Данному решению отвечает схема транспорта грузов, приведенная на рис.5. Наличие отрицательных элемента первой строки свидетельствует, что возможности улучшения решения не исчерпаны.

Повторим построения и расчеты, проведенные в предыдущем пункте, применительно к данной симплекс-таблице. В результате придем к следующей, третьей симплекс-таблице (табл. 5). Из ее анализа видно, что полученное решение не оптимально и, значит, повторим построения и расчеты, проведенные в предыдущем пункте, применительно к данной симплекс-таблице. Соответствующая схема транспорта груза приведена на рис. 6.

Повторим построения и расчеты, проведенные в предыдущем пункте, применительно к данной симплекс-таблице. В результате придем к следующей, четвертой симплекс-таблице (табл. 6). Из ее анализа видно, что полученное решение оптимально и, значит, окончательно. Лучшего решения наша задача не имеет. Соответствующая схема транспорта груза приведена на рис. 7.

Х₃₁

Х₁₃

Х₂₂

Х₂₃

S

850

2

2

4

3

Х₁₂

100

1

-1

-1

-1

Х₂₁

250

0

0

-1

-1

Х₃₃

300

0

-1

0

-1

Х₁₁

50

-1

0

1

1

В данном случае оптимальное решение получено в результате трех симплекс-переходов. При иных исходных данных или ином выборе свободных и базисных переменных число таких переходов может быть другим.

Решение задачи в условиях аварийной ситуации

Решим ту же задачу в предположении, что вышел из строя один из заготовительных цехов, например, цех А₁, и его функции взял на себя цех А₃. Очевидно, в этом случае, вместо системы (1), будем иметь систему из пяти уравнений:

x₂₁+x₂₂+x₂₃=а₂^’

x₃₁+x₃₂+x₃₃=a₃ (12)

x₂₁+x₃₁=b₁

x₂₂+x₃₂=b₂

x₂₃+x₃₃=b₃

x₂₁+x₂₂+x₂₃=400

x₃₁+x₃₂+x₃₃=400

x₂₁+x₃₁=300

x₂₂+x₃₂=200

x₂₃+x₃₃=300

одно из которых может быть опущено, 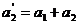. Вычеркнем второе уравнение. Таким образом, имеем систему из четырех уравнений с шестью переменными, две из которых свободные, остальные базисные. Выберем в качестве свободных переменных x₂₂, x_33, а в качестве базисных переменных x₂₃, x₃₁, ₃₂, x₂₁ и, как и раньше, выразим через них целевую функцию и базисные переменные:

x₂₃=300-x₂₂

x₃₂=200-x₂₂

x₂₁=100-x₂₂-x₃₃ (13)

x₃₁=200-x₃₃+x₂₂

S=s₂₁x₂₁+s₂₂x₂₂+s₂₃x₂₃+s₃₁x₃₁+s₃₂x₃₂+s₃₃x₃₃=

=100-x₂₂+x₃₃+4x₂₂+3(300-x₃₃)+4(200-x₃₃+ x₂₂)+200-x₂₂+x₃₃=

=2000+6x₂₂-5x₃₃(14)

На основании соотношений (13) и (14) составляем исходную симплекс-таблицу, соответствующую рассматриваемой ситуации (табл.5).

Повторяя действия, изложенные в предыдущем пункте, приходим к заключительной симплекс-таблице (табл.8).

Это решение есть окончательным, потому что нет отрицательных коэффициентов.

Исходные и заключительные схемы транспорта грузов приведены на рис.6 , рис.7.

Заключение

В данной курсовой работе решается производственная задача в которой мне необходимо было организовать перевозки комплектов из заготовительных цехов в сборочные таким образом, чтобы обеспечить бесперебойную работу всех цехов и чтобы суммарная стоимость всех перевозок была минимальной.

Также данная задача решается в условиях аварийной ситуации, то есть при выходе из строя одного из заготовительных цехов.

В теории линейного программирования разработан специальный метод, именуемый симплекс-методом. Он предусматривает запись коэффициентов целевой функции и базисных переменных, выраженных через свободные переменные в форме специальной матрицы(симплекс матрицы) и ее преобразования по определенному алгоритму в другую такую же матрицу. Полученная таблица анализируется на оптимальность и при отсутствии таковой, вновь преобразуется по тому же алгоритму. Преобразования продолжаются до тех пор, пока не будет получено оптимальное решение.

Для нахождения оптимального решения при нормальном режиме работы понадобилось три симплекс-шага, а при аварийной ситуации - один симплекс-шаг.

Список использованной литературы

1.      Болычевцев А.Д., Быстрицькая Л.Б. Математические основы теории электронных систем: Методические указания по курсовому проектированию для студентов специальности 7.010104.05. - Харьков: УИПА, 2003. - 20с.

.        Коршунов Ю.М. Математические основы кибернетики. - М.: Энергоатомиздат. 1987.

.        Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике. - М.: Наука, 1984.